A New Model of Solar Illumination of Earth’s Atmosphere during Night-Time
Abstract
:1. Introduction
2. Materials and Methods
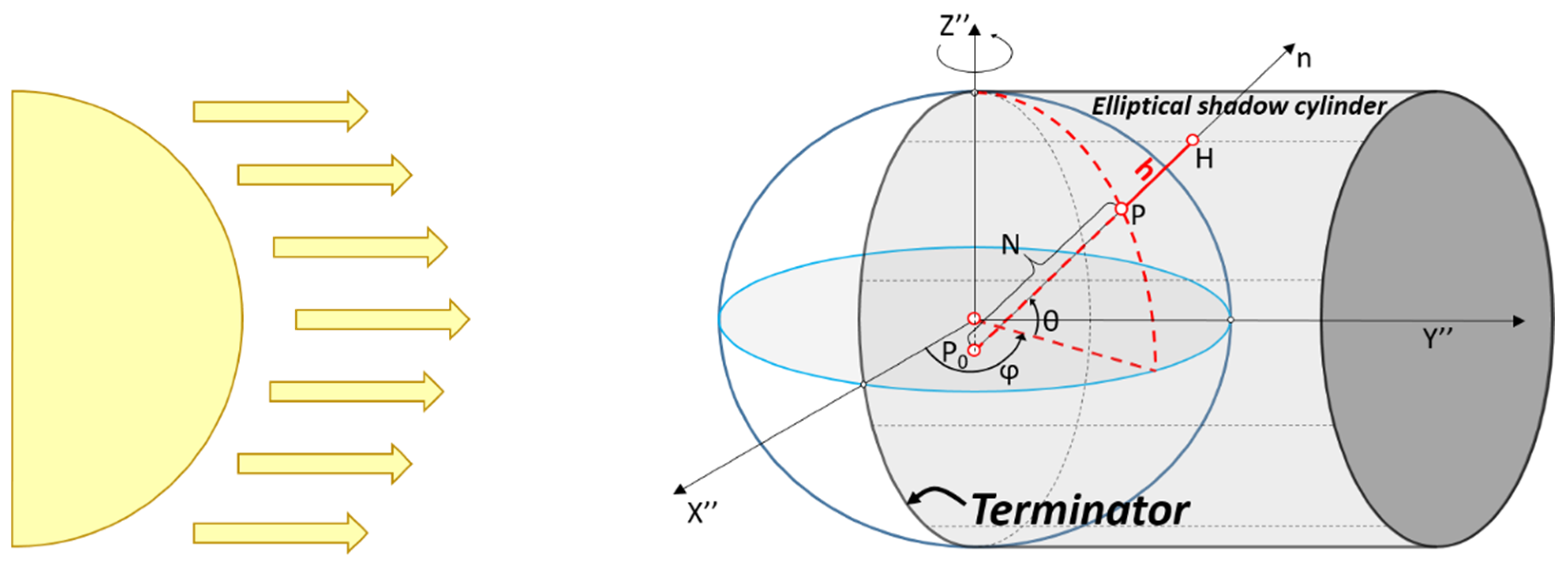
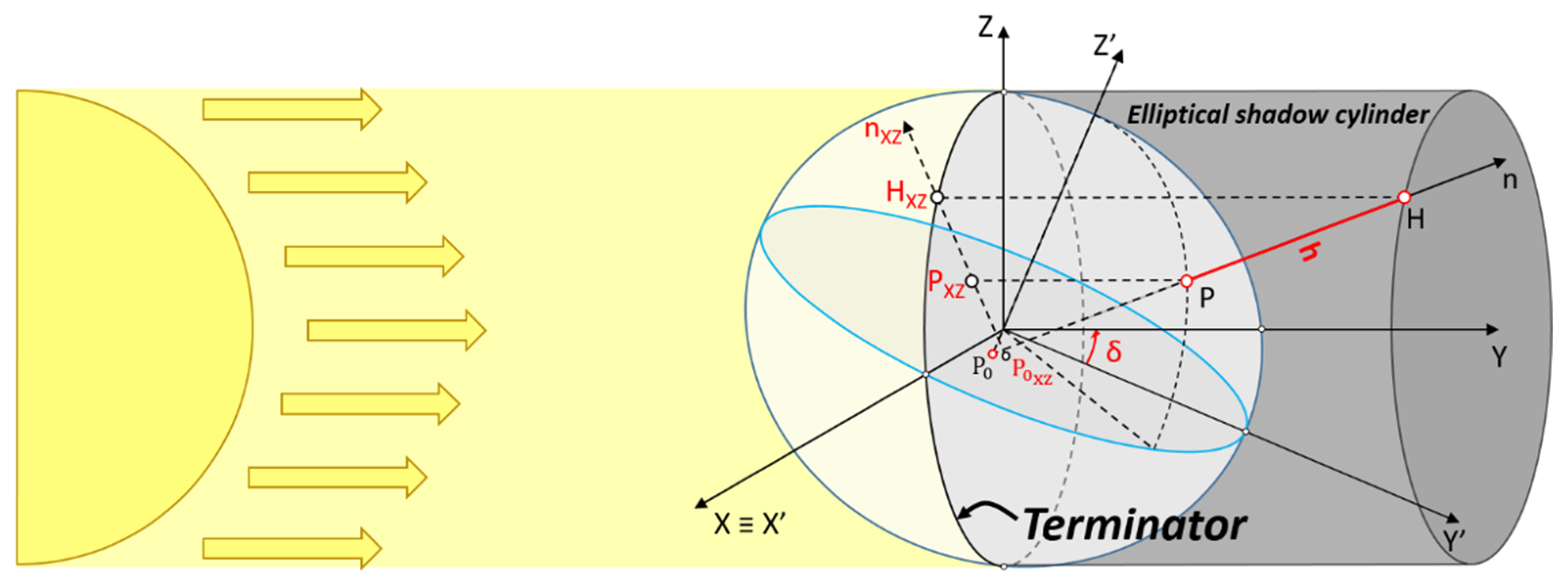
2.1. Solar Terminator Height Determination
- H is the terminal point of the ellipsoidal height h;
- is the length of the straight line coinciding with the ellipsoid’s normal n connecting the point P and the point of intersection between n and Z″ axis P0 (length in Figure 1);
- e2 and a, respectively equal to 0.00669438 and to 6,378,137 m, are the ellipsoidal parameters first eccentricity squared and semi-major axis of the reference ellipsoid used (WGS84);
- θ and φ are, respectively, the geodetic latitude and the longitude.
- Solar declination angle δ;
- Local hour angle from sunset λ;
- Solar elevation angle α.
2.1.1. Solar Declination Angle: δ
2.1.2. Equation of Time: ET (min)
2.1.3. Local Hour Angle from Sunset λ
- HD (min/UTC), the hour of the day hh:mm:ss UTC of point P expressed in minutes, is calculated:
- 2.
- TST (min/UTC), the true solar time of point P expressed in minutes, is obtained as follows:
- 3.
- LHA (°), the local hour angle of point P expressed in degrees, is given by:
- 4.
- λ (°), local hour angle from sunset expressed in degrees, then, is:
2.1.4. Solar Elevation Angle α
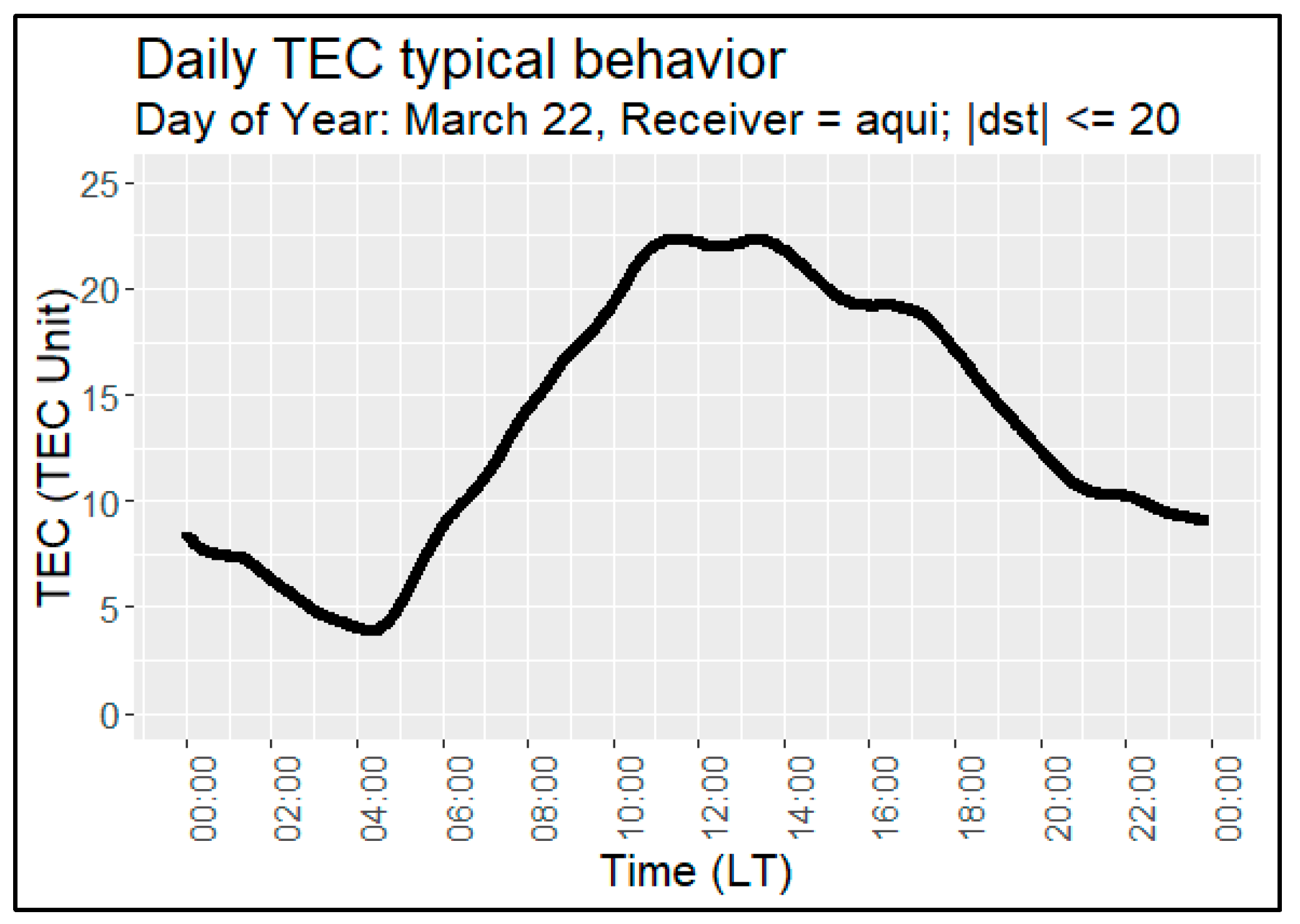
2.2. STH–TEC Correlation Analysis
Collection of TEC Data Samples
3. Results
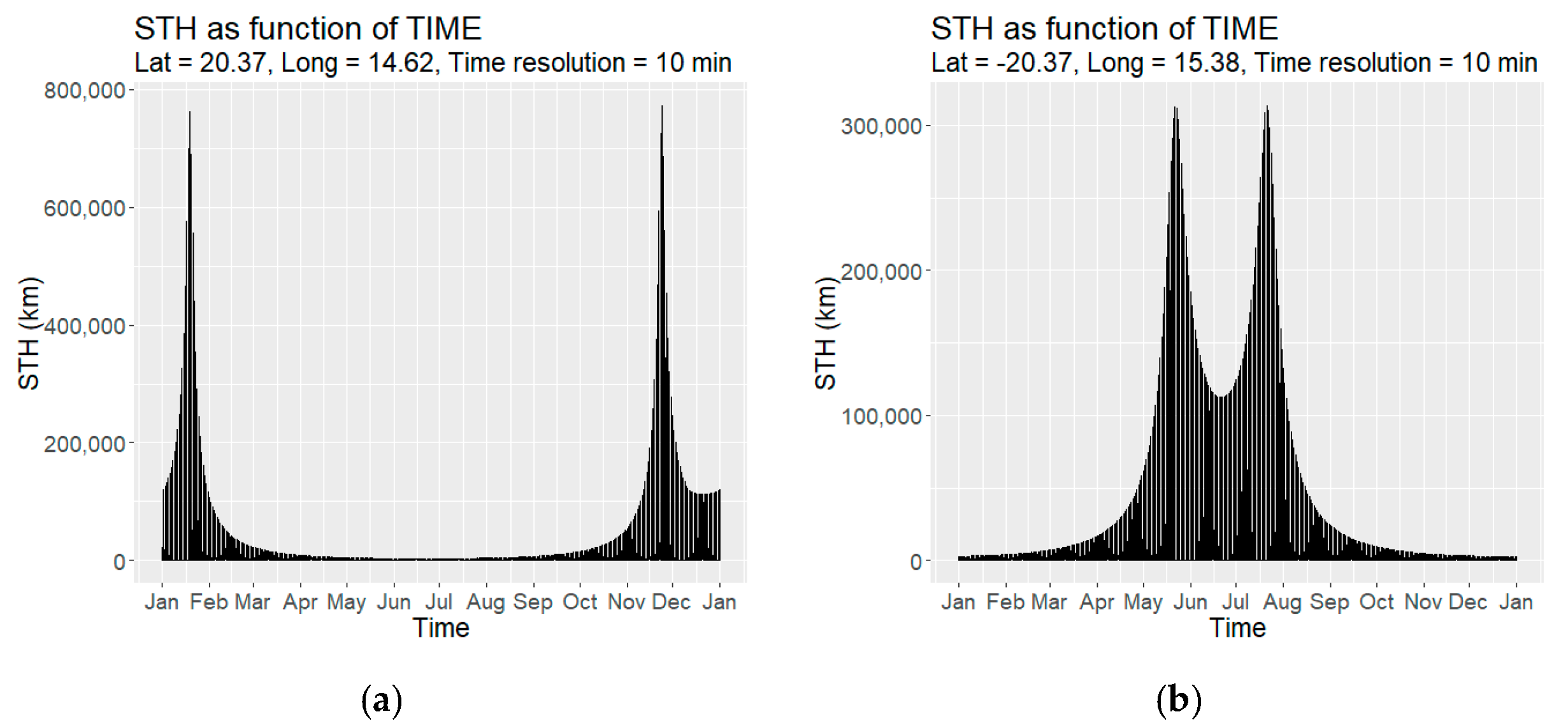
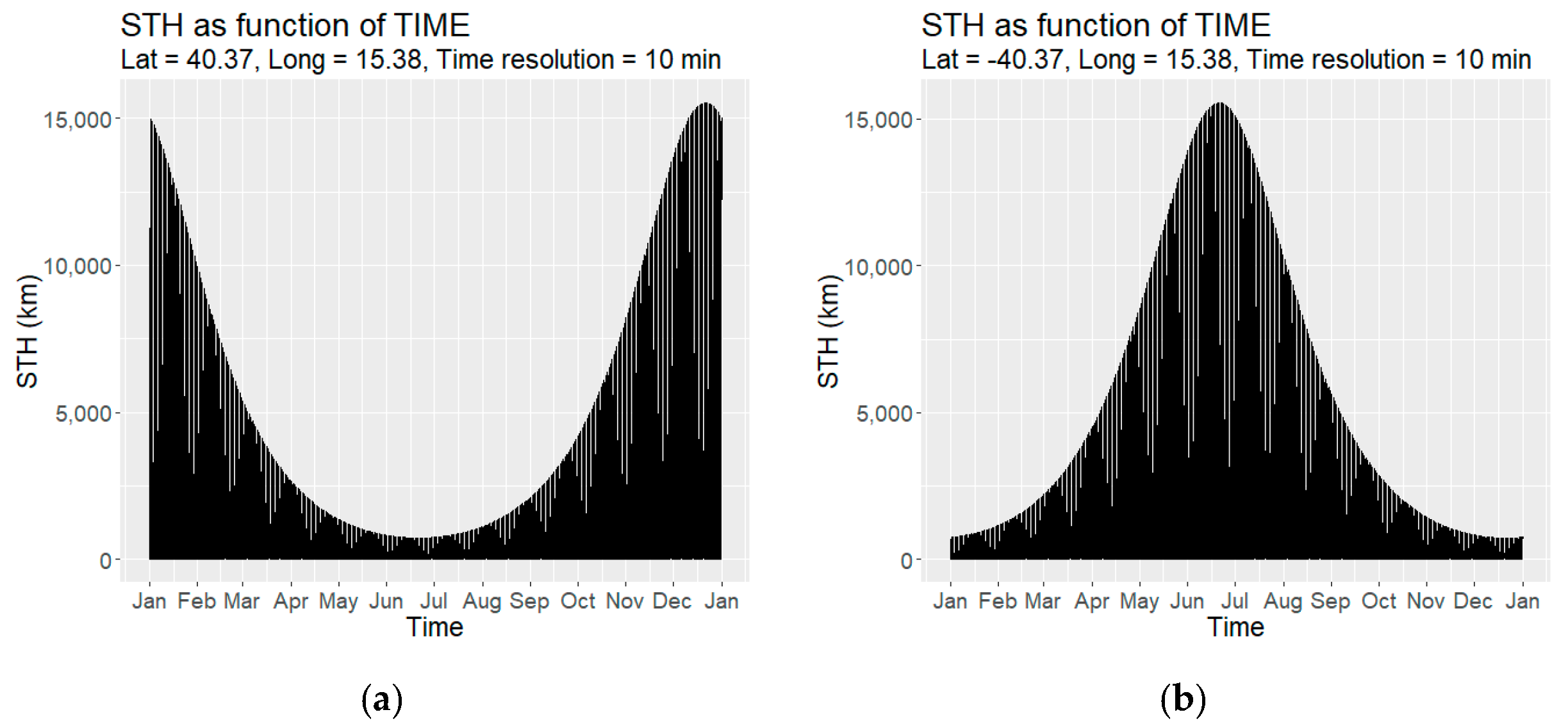
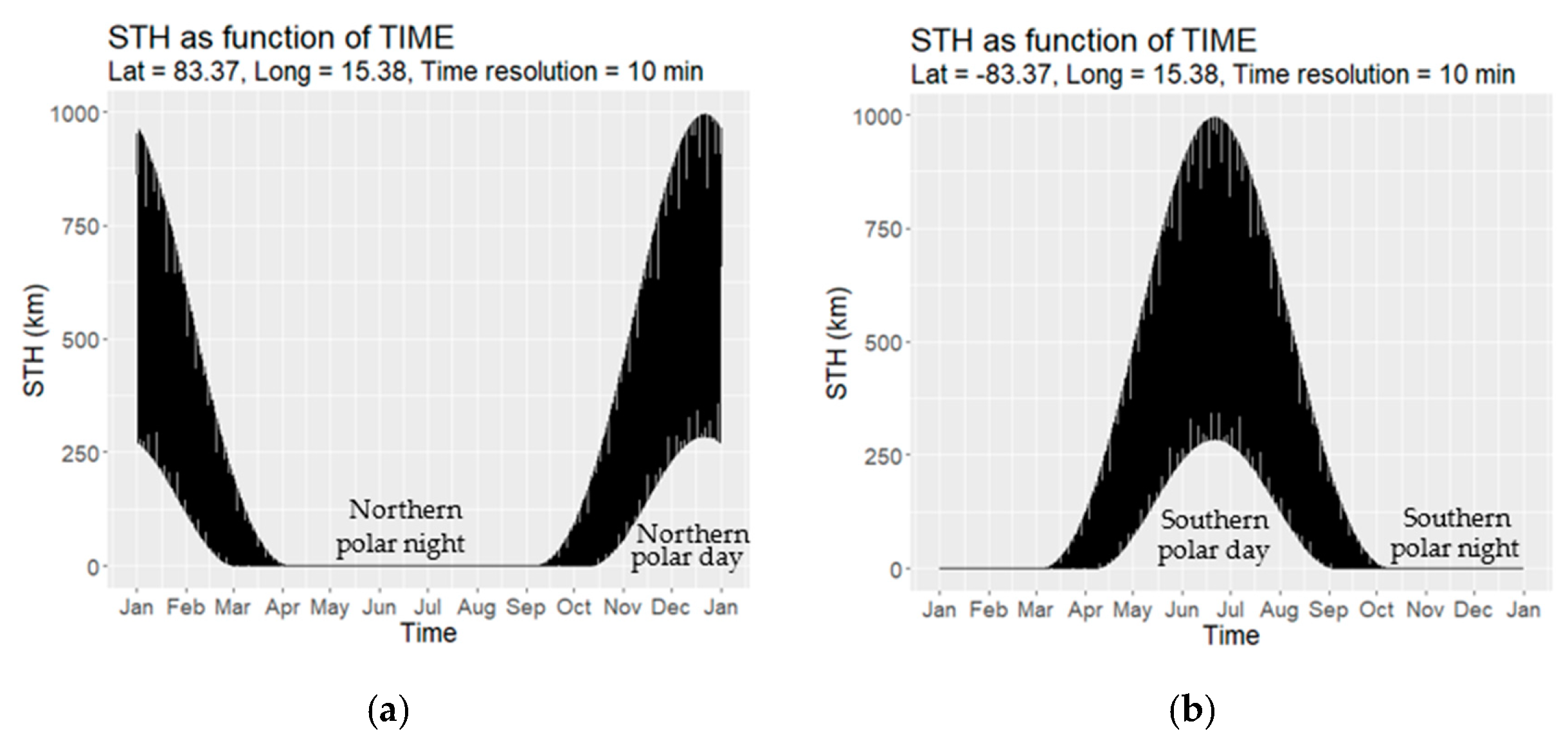
3.1. STH as Function of Time
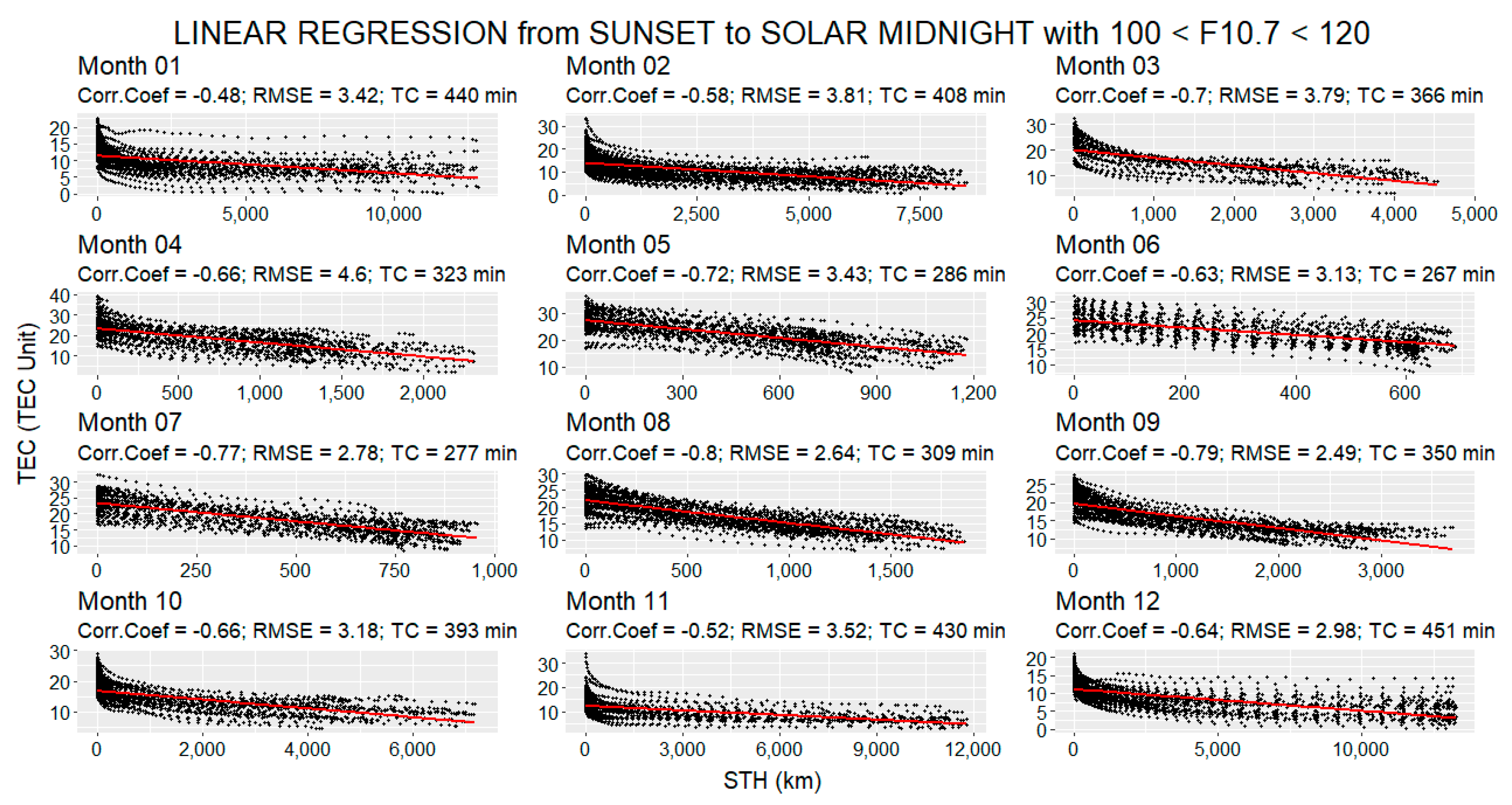
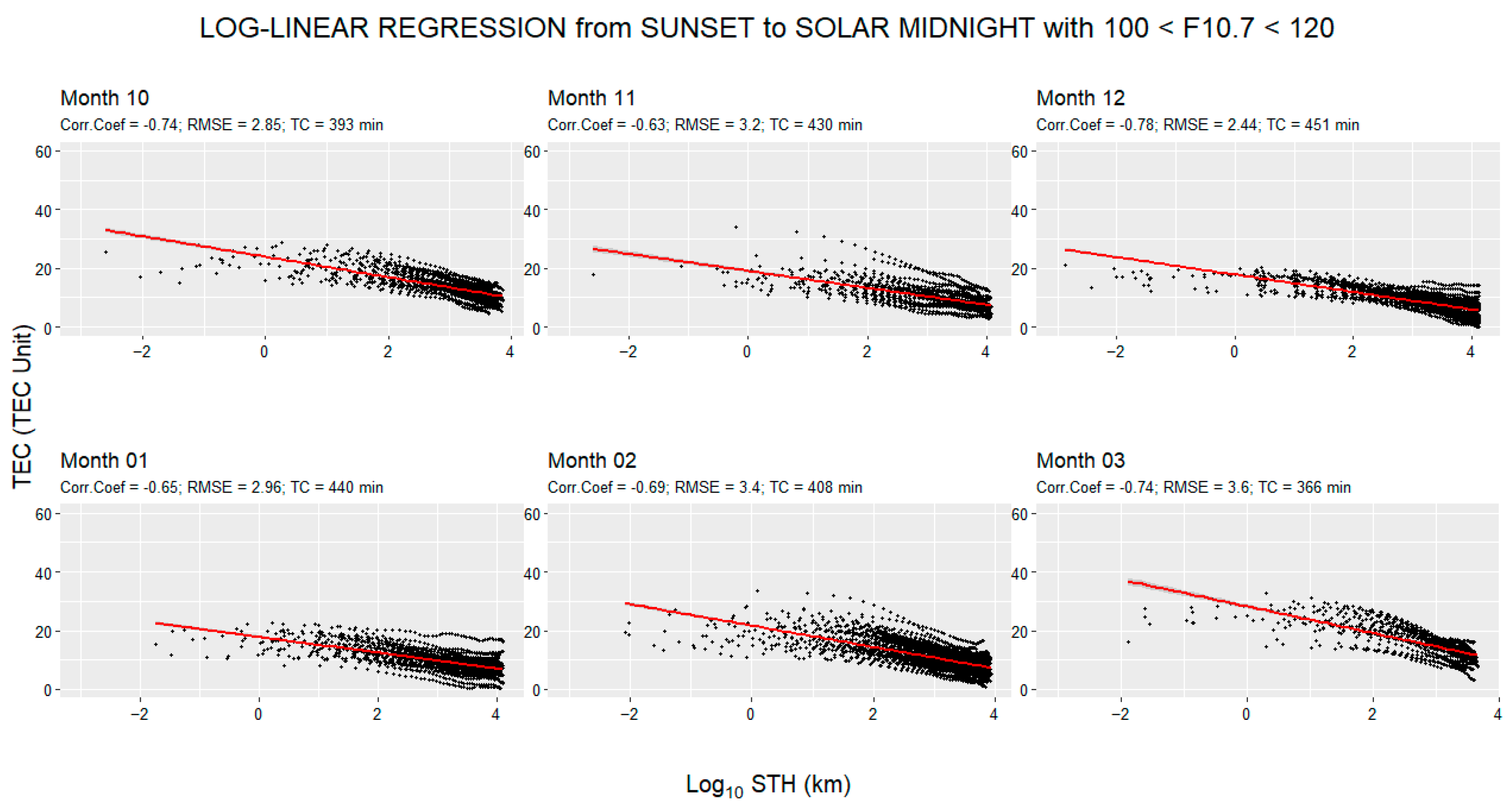
3.2. STH–TEC Correlation Analysis
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beer, T. Supersonic Generation of Atmospheric Waves. Nature 1973, 242, 34. [Google Scholar] [CrossRef]
- Dominici, P.; Bianchi, C.; Cander, L.; De Francheschi, G.; Scotto, C.; Zolesi, B. Preliminary results on the ionospheric structure at dawn time observed during HRIS campaigns. Ann. Geophys. 1994, 37, 71–76. [Google Scholar] [CrossRef]
- Vasilyev, V.P. Latitude location of the source of the ionospheric short-term terminator disturbances. Geomag. Aeron. 1996, 35, 589. [Google Scholar]
- Galushko, V.G.; Paznukhov, V.V.; Yampolski, Y.M.; Foster, J.C. Incoherent scatter radar observations of AGW/TID events generated by the moving solar terminator. Ann. Geophys. 1998, 16, 821–827. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Edemskiy, I.K.; Leonovich, A.S.; Leonovich, L.A.; Voeykov, S.V.; Yasyukevich, Y.V. MHD nature of night-time MSTIDs excited by the solar terminator. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- MacDougall, J.; Jayachandran, P. Solar terminator and auroral sources for traveling ionospheric disturbances in the midlatitude F region. J. Atmos. Sol. Terr. Phys. 2011, 73, 2437–2443. [Google Scholar] [CrossRef]
- Fowler, D.; Pilegaard, K.; Sutton, M.; Ambus, P.; Raivonen, M.; Duyzer, J.; Simpson, D.; Fagerli, H.; Fuzzi, S.; Schjoerring, J.; et al. Atmospheric composition change: Ecosystems–Atmosphere interactions. Atmos. Environ. 2009, 43, 5193–5267. [Google Scholar] [CrossRef]
- Karpov, I.V.; Bessarab, F.S. Model studying the effect of the solar terminator on the thermospheric parameters. Geomagn. Aeron. 2008, 48, 209–219. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Edemskiy, I.K.; Voeykov, S.V.; Yasyukevich, Y.V.; Zhivetiev, I.V. The first GPS-TEC imaging of the space structure of MS wave packets excited by the solar terminator. Ann. Geophys. 2009, 27, 1521–1525. [Google Scholar] [CrossRef]
- Bespalova, A.V.; Fedorenko, A.; Cheremnykh, O.; Zhuk, I. Satellite observations of wave disturbances caused by moving solar TERMINATOR. J. Atmos. Sol. Terr. Phys. 2016, 140, 79–85. [Google Scholar] [CrossRef]
- Pignalberi, A.; Habarulema, J.; Pezzopane, M.; Rizzi, R. On the Development of a Method for Updating an Empirical Climatological Ionospheric Model by Means of Assimilated vTEC Measurements from a GNSS Receiver Network. Space Weather 2019, 17, 1131–1164. [Google Scholar] [CrossRef] [Green Version]
- Verhulst, T.G.W.; Stankov, S.M. Height-dependent sunrise and sunset: Effects and implications of the varying times of occurrence for local ionospheric processes and modelling. Adv. Space Res. 2017, 60, 1797–1806. [Google Scholar] [CrossRef]
- Kintner, P.M.; Ledvina, B.M. The ionosphere, radio navigation, and global navigation satellite systems. Adv. Space Res. 2005, 35, 788–811. [Google Scholar] [CrossRef]
- Rocken, C.; Kuo, Y.H.; Schreiner, W.S.; Hunt, D.; Sokolovskiy, S.; McCormick, C. COSMIC System Description. Terr. Atmos. Ocean. Sci. 2000, 11, 21–52. [Google Scholar] [CrossRef] [Green Version]
- Hajj, G.A.; Lee, L.C.; Pi, X.; Romans, L.J.; Schreiner, W.S.; Straus, P.R.; Wang, C. COSMIC GPS Ionospheric Sensing and Space Weather. Terr. Atmos. Ocean. Sci. 2000, 11, 235–272. [Google Scholar] [CrossRef] [Green Version]
- Parrot, M. The micro-satellite DEMETER. J. Geodyn. 2002, 33, 535–541. [Google Scholar] [CrossRef]
- Tiwari, R.; Bhattacharya, S.; Purohit, P.K.; Gwal, A.K. Effect of TEC Variation on GPS Precise Point at Low Latitude. Open Atmos. Sci. J. 2009, 3, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Fayose, R.S.; Babatunde, R.; Oladosu, O.; Groves, K. Variation of Total Electron Content [TEC] and Their Effect on GNSS over Akure, Nigeria. Appl. Phys. Res. 2012, 4, 105. [Google Scholar] [CrossRef] [Green Version]
- Freund, F. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere—Atmosphere—Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Kuo, C.L.; Huba, J.D.; Joyce, G.; Lee, L.C. Ionosphere plasma bubbles and density variations induced by pre-earthquake rock currents and associated surface charges. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Kuo, C.L.; Lee, L.C.; Huba, J.D. An improved coupling model for the lithosphere-atmosphere-ionosphere system. J. Geophys. Res. Space Phys. 2014, 119, 3189–3205. [Google Scholar] [CrossRef]
- Yang, S.; Asano, T.; Hayakawa, M. Abnormal Gravity Wave Activity in the Stratosphere Prior to the 2016 Kumamoto Earthquakes. J. Geophys. Res. Space Phys. 2019, 124, 1410–1425. [Google Scholar] [CrossRef]
- Meeus, J. Astronomical Algorithms, 2nd ed.; Willmann-BeIl Inc.: Richmond, VA, USA, 1998. [Google Scholar]
- NOAA. Solar Calculation Details. Available online: https://www.esrl.noaa.gov/gmd/grad/solcalc/calcdetails.html (accessed on 8 April 2021).
- Astronomical Almanac for the Year 2010 and Its Companion the Astronomical Almanac Online. Available online: http://www.admiraltyshop.co.uk (accessed on 8 April 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: http://www.R-project.org/ (accessed on 8 April 2021).
- Eyelade, V.A.; Adewale, A.O.; Akala, A.O.; Bolaji, O.S.; Rabiu, A.B. Studying the variability in the diurnal and seasonal variations in GPS total electron content over Nigeria. Ann. Geophys. 2017, 35, 701–710. [Google Scholar] [CrossRef] [Green Version]
- Yuen, P.; Roelofs, T. Seasonal variations in ionospheric total electron content. J. Atmos. Sol. Terr. Phys. 1967, 29, 321–326. [Google Scholar] [CrossRef]
- Zhao, B.; Wan, W.; Liu, L.; Mao, T.; Ren, Z.; Wang, M.; Christensen, A.B. Features of annual and semiannual variations derived from the global ionospheric maps of total electron content. Ann. Geophys. 2007, 25, 2513–2527. [Google Scholar] [CrossRef] [Green Version]
- Tsai, H.-F.; Liu, J.-Y.; Tsai, W.-H.; Liu, C.-H.; Tseng, C.-L.; Wu, C.-C. Seasonal variations of the ionospheric total electron content in Asian equatorial anomaly regions. J. Geophys. Res. Space Phys. 2001, 106, 30363–30369. [Google Scholar] [CrossRef]
- Perevalova, N.; Polyakova, A.; Zalizovski, A. Diurnal variations of the total electron content under quiet helio-geomagnetic conditions. J. Atmos. Sol. Terr. Phys. 2010, 72, 997–1007. [Google Scholar] [CrossRef]
- IONOLAB. Available online: http://www.ionolab.org/index.php?page=ionolabtec&language=en (accessed on 9 February 2021).
- Sezen, U.; Arikan, F.; Arikan, O.; Ugurlu, O.; Sadeghimorad, A. Online, automatic, near-real time estimation of GPS-TEC: IONOLAB-TEC. Space Weather 2013, 11, 297–305. [Google Scholar] [CrossRef]
- Arikan, F.; Nayir, H.; Sezen, U.; Arikan, O. Estimation of single station interfrequency receiver bias using GPS-TEC. Radio Sci. 2008, 43, 4. [Google Scholar] [CrossRef]
- OMINWeb. Available online: https://omniweb.gsfc.nasa.gov/form/dx1.html (accessed on 8 April 2021).
| Solar Activity Level | Range 1 | Range 2 | Range 3 | Range 4 | Range 5 | Range 6 |
|---|---|---|---|---|---|---|
| F10.7 (s.f.u.) | 0–80 | 80–100 | 100–120 | 120–140 | 140–160 | 160–Inf. |
| Linear and Log-Linear TEC–STH Correlation Coefficients Comparison | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month | F10.7 < 80 | 80 < F10.7 < 100 | 100 < F10.7 < 120 | 120 < F10.7 < 140 | 140 < F10.7 < 160 | F10.7 > 160 | ||||||
| Lin | Log-Lin | Lin | Log-Lin | Lin | Log-Lin | Lin | Log-Lin | Lin | Log-Lin | Lin | Log-Lin | |
| 1 | −0.38 | −0.45 | −0.55 | –0.67 | –0.48 | –0.65 | –0.60 | –0.78 | –0.60 | –0.79 | –0.45 | –0.63 |
| 2 | –0.45 | –0.50 | –0.64 | –0.68 | –0.58 | –0.69 | –0.71 | –0.82 | –0.69 | –0.81 | –0.47 | –0.53 |
| 3 | –0.49 | –0.50 | –0.66 | –0.64 | –0.70 | –0.74 | –0.70 | –0.72 | –0.71 | –0.71 | –0.67 | –0.66 |
| 4 | –0.66 | –0.56 | –0.67 | –0.60 | –0.66 | –0.57 | –0.74 | –0.69 | –0.71 | –0.68 | –0.59 | –0.63 |
| 5 | –0.66 | –0.53 | –0.61 | –0.49 | –0.72 | –0.58 | –0.78 | –0.67 | –0.65 | –0.56 | –0.77 | –0.70 |
| 6 | –0.69 | –0.55 | –0.60 | –0.50 | –0.63 | –0.52 | –0.65 | –0.56 | –0.72 | –0.61 | –0.62 | –0.52 |
| 7 | –0.70 | –0.58 | –0.66 | –0.53 | –0.77 | –0.63 | –0.76 | –0.62 | –0.76 | –0.64 | –0.63 | –0.53 |
| 8 | –0.64 | –0.53 | –0.67 | –0.57 | –0.80 | –0.69 | –0.79 | –0.67 | –0.78 | –0.65 | –0.75 | –0.63 |
| 9 | –0.54 | –0.52 | –0.65 | –0.63 | –0.79 | –0.78 | –0.61 | –0.66 | –0.75 | –0.76 | –0.64 | –0.65 |
| 10 | –0.44 | –0.42 | –0.67 | –0.58 | –0.66 | –0.74 | –0.62 | –0.73 | –0.69 | –0.83 | –0.59 | –0.70 |
| 11 | –0.42 | –0.44 | –0.58 | –0.60 | –0.52 | –0.63 | –0.59 | –0.74 | –0.65 | –0.82 | –0.55 | –0.75 |
| 12 | –0.39 | –0.45 | –0.47 | –0.60 | –0.64 | –0.78 | –0.57 | –0.75 | –0.62 | –0.82 | –0.54 | –0.76 |
| Seasonal Means of The TEC–STH Correlation Coefficients | ||||||
|---|---|---|---|---|---|---|
| F10.7 < 80 | 80 < F10.7 < 100 | 100 < F10.7 < 120 | 120 < F10.7 < 140 | 140 < F10.7 < 160 | F10.7 > 160 | |
| Lin (May–Aug) | −0.67 | −0.64 | −0.73 | −0.74 | −0.73 | −0.69 |
| Log-Lin (Nov–Feb) | −0.46 | −0.64 | −0.69 | −0.77 | −0.81 | −0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colonna, R.; Tramutoli, V. A New Model of Solar Illumination of Earth’s Atmosphere during Night-Time. Earth 2021, 2, 191-207. https://doi.org/10.3390/earth2020012
Colonna R, Tramutoli V. A New Model of Solar Illumination of Earth’s Atmosphere during Night-Time. Earth. 2021; 2(2):191-207. https://doi.org/10.3390/earth2020012
Chicago/Turabian StyleColonna, Roberto, and Valerio Tramutoli. 2021. "A New Model of Solar Illumination of Earth’s Atmosphere during Night-Time" Earth 2, no. 2: 191-207. https://doi.org/10.3390/earth2020012
APA StyleColonna, R., & Tramutoli, V. (2021). A New Model of Solar Illumination of Earth’s Atmosphere during Night-Time. Earth, 2(2), 191-207. https://doi.org/10.3390/earth2020012







