A Review of Machine Learning Applications in Land Surface Modeling
Abstract
1. Introduction
2. LSMs: Importance, Then and Now
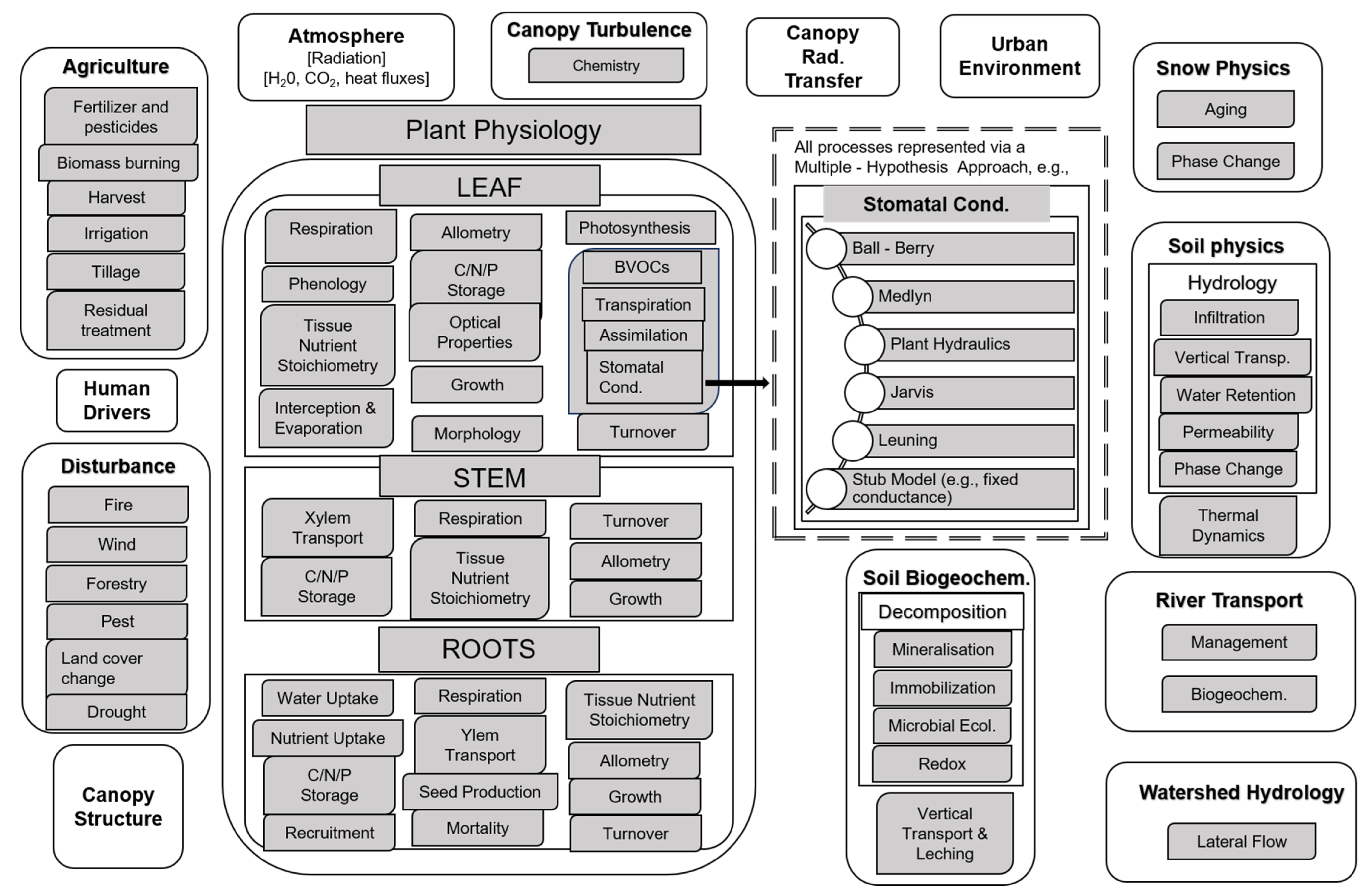
3. Complexity and Limitations of LSMs: Prospect of ML
4. Major Applications of Machine Learning in Land Surface Modeling
4.1. Estimation of Evapotranspiration
4.2. Parameter Estimation and Uncertainty Assessment
4.3. Crop Yield Prediction
4.4. Hybrid Simulation of Land-Surface Variables Other Than ET
4.5. Benchmarking the LSMs
5. Techniques of Machine Learning
5.1. Traditional ML Methods
Random Forests (RF)
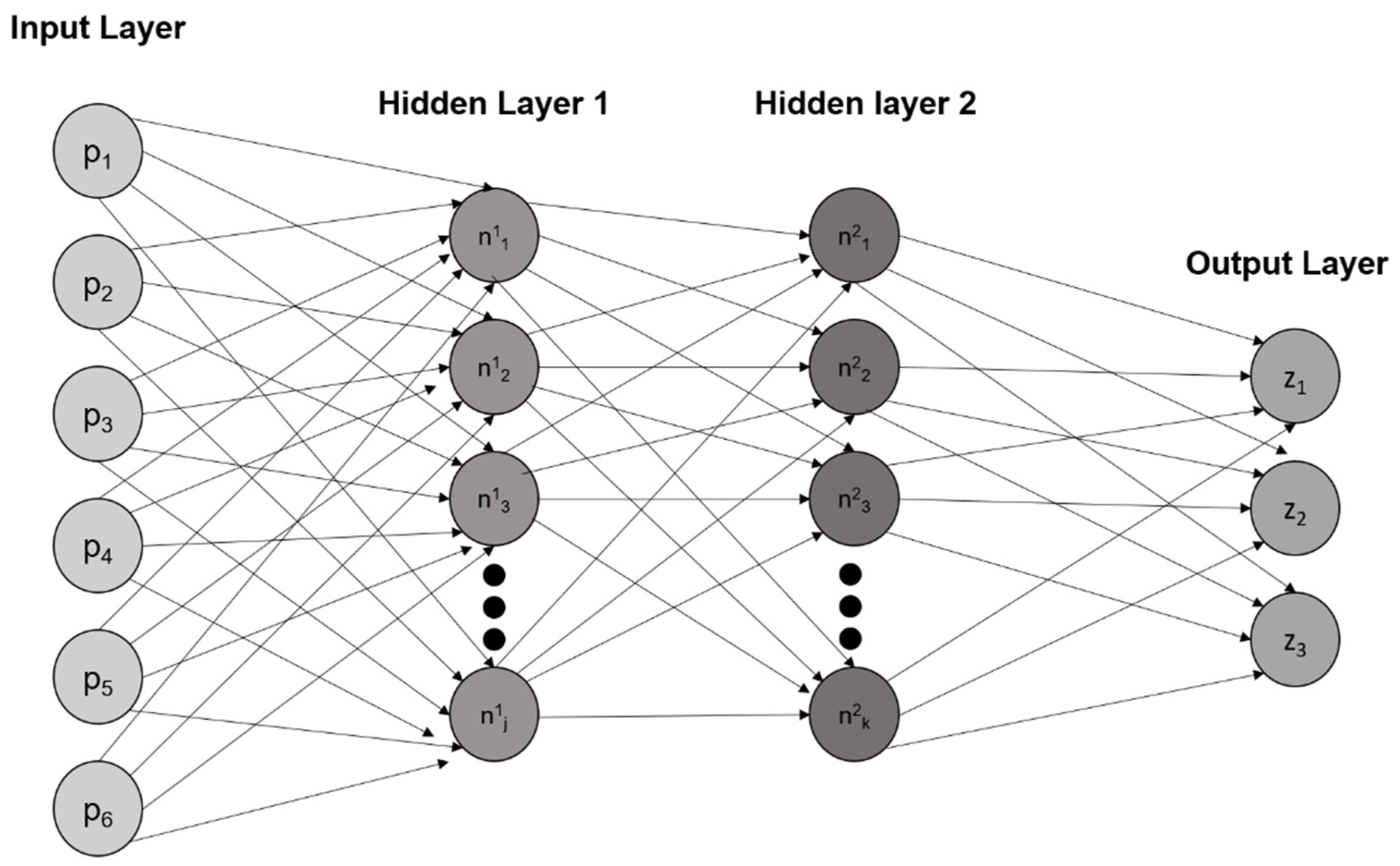
5.2. Deep Learning (DL) methods
Artificial Neural Networks (ANN)
6. Possible future directions
- ML techniques can be a suitable way to reduce the process complexity of the LSMs. Currently, the complex interactive processes of the terrestrial system and way they are represented in conventional LSMs makes them intractable. It is often difficult to assess the added value of a complex process given its cost of burdening the model. ML can help in this regard to take a modular approach, where modelers can represent a complex process in multiple ways and test the model performance easily. This will help in reducing the structural uncertainty of the models as well. The model intercomparison projects (e.g.; MsTMIP) are often constrained by the under-sampling of the potential range of model configurations. Such technique will also help us in collaborative development of the model, rather than adding processes on a specific need basis.
- Processes in the model which have little physics knowledge or complex calculation, but more data availability, could be replaced by a ML-based surrogate. As mentioned in Section 4.4, there have been some attempts to predict important land surface properties by a hybrid modeling approach, but we are still lacking in exploring some of the more fundamental variables which can be easily provided by ML applications as the amount of observations increase in recent days. For example, hydrology, phenology and snow cover fraction. Hydrologic observations are increasing all over the globe with advanced velocimetry techniques and phenology is easily obtained now from satellite remote sensing data. Improving these components leveraging ML will help upgrade the overall LSM performance.
- Parametric uncertainty can be investigated, and parameters can be better optimized following Dagon et al. [55]. However, we need to consider longer data records (now possible with the availability of computing resources) and more output variables. Good quality globally gridded observations are now available. For example, Atmospheric CO2 from National Oceanic and Atmospheric Administration (NOAA), Commonwealth Scientific and Industrial Research Organisation (CSIRO), gridded FLUXNET from Max Planck Institute for Biogeochemistry (MPI-BCG), river flow (GRDC), albedo (MODIS), and so on (ILAMB project, etc.).
- Data assimilation is proved to be an important tool to improve model simulations at different earth system modeling applications [80,81]; and advancement in ML can further enhance that. Conventional data assimilation methods include Kalman filter and variational approaches. These methods have underlying assumptions of normality, Markovian processes, zero error covariance and similar ML algorithms, being completely data-driven, may improve the assimilation in terms of speed, accuracy, and efficiency.
- There are several avenues for better crop yield prediction. Soil hydrology related variables such as soil moisture or drought indices (obtained from either remote sensing, in-situ measurements, or process-based models) can further improve the ML predictions on crop yield. Precision agriculture is another advanced recent agricultural technology which includes sensors, robotics, and AI to assemble ‘big data’ which can further be processed with ML models to develop a sustainable agricultural practice with enhanced yield. We can use such data and the extracted information to assess the yield variability among regions to make informed decisions [82]. As such, the yield stability maps, included in the landscape, can provide information about environment friendly areas and constant low yield areas. We should focus on intensifying the high yield areas sustainably. On the other hand, low yield zones can be improved by perennial bioenergy crops and recycling of plant available nutrients.
- Interpretability of ML models [83] has potential to reveal some of the hidden links and physics between different parts of the terrestrial hydrology. Relative importance of the predictors to predict a specific outcome could be more rigorously analyzed for similar interpretations.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huntingford, C.; Jeffers, E.S.; Bonsall, M.B.; Christensen, H.M.; Lees, T.; Yang, H. Machine learning and artificial intelligence to aid climate change research and preparedness. Environ. Res. Lett. 2019, 14, 124007. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, L.; Leung, H.; Wang, J. A deep-learning based precipitation forecasting approach using multiple environmental factors. In 2017 IEEE International Congress on Big Data (BigData Congress); IEEE: New York, NY, USA, 2017; pp. 193–200. [Google Scholar] [CrossRef]
- Shen, C. A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Schmidt, L.; Heße, F.; Attinger, S.; Kumar, R. Challenges in applying machine learning models for hydrological inference: A case study for flooding events across Germany. Water Resour. Res. 2020, 56, e2019WR025924. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Long, Y.; Gong, Y.; Xiao, Z.; Liu, Q. Accurate object localization in remote sensing images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2486–2498. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, Z.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Dirmeyer, P.A.; Koster, R.D.; Sud, Y.C.; Bonan, G.; Oleson, K.W.; Chan, E.; Verseghy, D.; Cox, P.; Gordon, C.T.; et al. GLACE: The Global Land Atmosphere Coupling Experiment. 2. Analysis. J. Hydrometeor. 2006, 7, 611–625. [Google Scholar] [CrossRef]
- Dirmeyer, A.P.; Schlosser, C.A.; Brubaker, K.L. Precipitation, recycling and land memory: An integrated analysis. J. Hydrometeor. 2009, 10, 278–288. [Google Scholar] [CrossRef]
- Abramowitz, G.; Leuning, R.; Clark, M.; Pitman, A. Evaluating the Performance of Land Surface Models. J. Clim. 2008, 21, 5468–5481. [Google Scholar] [CrossRef]
- Fisher, R.A.; Koven, C.D. Perspectives on the future of land surface models and the challenges of representing complex terrestrial systems. J. Adv. Model. Earth Syst. 2020, 12, e2018MS001453. [Google Scholar] [CrossRef]
- Richardson, L.F. Weather prediction by numerical process Cambridge University Press. Q. J. Royal Meteorol. Soc. 1922, 48, 282–284. [Google Scholar] [CrossRef]
- Charney, J.G.; Quirk, W.J.; Chow, S.H.; Kornfield, J. A comparative study of the effects of albedo change on drought in semiarid regions. J. Atmos. Sci. 1977, 34, 1366–1385. [Google Scholar] [CrossRef]
- Matthews, E. Global vegetation and land use: New high-resolution data bases for climate studies. J. Clim. Appl. Meteorol. 1983, 22, 474–487. [Google Scholar] [CrossRef]
- Nicholson, S.E. Land surface-atmosphere interaction: Physical processes and surface changes and their impact. Prog. Phys. Geogr. 1988, 12, 36–65. [Google Scholar] [CrossRef]
- Garratt, J.R. Sensitivity of Climate Simulations to Land-Surface and Atmospheric Boundary-Layer Treatments-A Review. J. Clim. 1993, 6, 419–448. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J.; Higgins, R.W.; Van den Dool, H.M. Observational evidence that soil moisture variations affect precipitation. Geophys. Res. Lett. 2003, 30, 1241. [Google Scholar] [CrossRef]
- Dirmeyer, P.; Randal, A.; Koster, D.; Guo, Z. Do Global Models Properly Represent the Feedback between Land and Atmosphere? J. Hydrometeorol. 2006, 7, 1177–1198. Available online: http://www.jstor.org/stable/24910939 (accessed on 25 November 2020). [CrossRef]
- Seneviratne, S.I.; Thierry, C.; Edouard, L.D.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, J.A. Investigating soil moisture–climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Sellers, P.J.; Mintz, Y.; Sud, Y.C.; Dalcher, A. A simple biosphere model (SIB) for use within general circulation models. J. Atmos. Sci. 1986, 43, 505–531. [Google Scholar] [CrossRef]
- De Kauwe, M.G.; Kala, J.; Lin, Y.-S.; Pitman, A.J.; Medlyn, B.E.; Duursma, R.A.; Abramowitz, G.; Wang, Y.-P.; Miralles, D.G. A test of an optimal stomatal conductance scheme within the CABLE land surface model. Geosci. Mod. Dev. 2015, 8, 431–452. [Google Scholar] [CrossRef]
- Ding, R.; Kang, S.; Du, T.; Hao, X.; Zhang, Y. Scaling Up Stomatal Conductance from Leaf to Canopy Using a Dual-Leaf Model for Estimating Crop Evapotranspiration. PLoS ONE 2014, 9, e95584. [Google Scholar] [CrossRef]
- Liang, X.; Wood, E.F.; Lettenmaier, D.P. Surface soil moisture parameterization of the VIC-2L model: Evaluation and modification. Global Planet. Chang. 1996, 13, 195–206. [Google Scholar] [CrossRef]
- Takata, K.; Emori, S.; Watanabe, T. Development of the minimal advanced treatments of surface interaction and runoff. Glob. Planet. Chang. 2003, 38, 209–222. [Google Scholar] [CrossRef]
- Chen, F.; Xie, Z. Effects of crop growth and development on regional climate: A case study over East Asian monsoon area. Clim. Dyn. 2012, 38, 2291–2305. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Brye, K.R. Integrated BIosphere Simulator (IBIS) Yield and Nitrate Loss Predictions for Wisconsin Maize Receiving Varied Amounts of Nitrogen Fertilizer. J. Environ. Qual. 2003, 32. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Yates, D.N.; Nagai, H.; LeMone, M.A.; Ikeda, K.; Grossman, R.L. Land surface heterogeneity in the cooperative atmosphere surface exchange study (CASES-97). Part I: Comparing modeled surface flux maps with surface-flux tower and aircraft measure-ments. J. Hydrometeorol. 2003, 4, 196–218. [Google Scholar] [CrossRef]
- Dickinson, R.E.; Shaikh, M.; Bryant, R.; Graumlich, L. Interactive canopies for a climate model. J. Clim. 1998, 11, 2823–2836. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Bras, R.L.; Vivoni, E.R. Vegetation-hydrology dynamics in complex terrain of semiarid areas: 2. Energy-water con-trols of vegetation spatiotemporal dynamics and topographic niches of favorability. Water Resour. Res. 2008, 44, 1–20. [Google Scholar] [CrossRef]
- Lipson, M.; Hart, M.; Thatcher, M. Efficiently modelling urban heat storage: An interface conduction scheme in an urban land surface model (aTEB v2.0). Geosci. Model Dev. 2017, 10, 991–1007. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Fisher, R.A.; Koven, C.D.; Oleson, K.W.; Swenson, S.C.; Bonan, G.; Collier, N.; Ghimire, B.; van Kampenhout, L.; Kennedy, D.; et al. The Community Land Model Version 5: Description of new features, benchmarking, and impact of forcing uncertainty. J. Adv. Model. Earth Syst. 2017, 11, 245–4287. [Google Scholar] [CrossRef]
- Decharme, B.; Delire, C.; Minvielle, M.; Colin, J.; Vergnes, J.; Alias, A.; Saint-Martin, D.; Séférian, R.; Sénési, S.; Voldoire, A. Recent changes in the ISBA-CTRIP land surface system for use in the CNRM-CM6 climate model and in global off-line hydrological applications. J. Adv. Model. Earth Syst. 2019, 11, 1207–1252. [Google Scholar] [CrossRef]
- Fisher, R.A.; Koven, C.D.; Anderegg, W.R.; Christoffersen, B.O.; Dietze, M.C.; Farrior, C.E.; Holm, J.A.; Hurtt, G.C.; Knox, R.G.; Lawrence, P.J.; et al. Vegetation demo-graphics in Earth System Models: A review of progress and priorities. Glob. Chang. Biol. 2018, 24, 35–54. [Google Scholar] [CrossRef] [PubMed]
- Miguez-Macho, G.; Fan, Y.; Weaver, C.P.; Walko, R.; Robock, A. Incorporating water table dynamics in climate modeling: 2. For-mulation, validation, and soil moisture simulation. J. Geophys. Res. 2007, 112, D13108. [Google Scholar] [CrossRef]
- Yao, Q.; Li, Z.; Song, Y.; Wright, S.J.; Guo, X.; Tringe, S.G.; Tfaily, M.M.; Paša-Tolić, L.; Hazen, T.C.; Turner, B.L.; et al. Community proteogenomics reveals the systemic impact of phosphorus availability on microbial functions in tropical soil. Nat. Ecol. Evol. 2018, 2, 499–509. [Google Scholar] [CrossRef] [PubMed]
- Boone, A.; Samuelsson, P.; Gollvik, S.; Napoly, A.; Jarlan, L.; Brun, E.; Decharme, B. The interactions between soil-biosphere-atmosphere land surface model with a multi-energy balance (ISBA-MEB) option in SURFEXv8-Part 1: Model description. Geosci. Model Dev. 2017, 10. [Google Scholar] [CrossRef]
- Nabel, J.E.M.S.; Naudts, K.; Pongratz, J. Accounting for forest age in the tile-based dynamic global vegetation model JSBACH4 (4.20p7; git feature/forests)–A land surface model for the ICON-ESM. Geosci. Model Dev. 2020, 13, 185–200. [Google Scholar] [CrossRef]
- Wiltshire, A.J.; Duran Rojas, M.C.; Edwards, J.M.; Gedney, N.; Harper, A.B.; Hartley, A.J.; Hendry, M.A.; Robertson, E.; Smout-Day, K. JULES-GL7: The Global Land configuration of the Joint UK Land Environment Simulator version 7.0 and 7.2. Geosci. Model Dev. 2020, 13, 483–505. [Google Scholar] [CrossRef]
- Smith, B.; Samuelsson, P.; Wramneby, A.; Rummukainen, M. A model of the coupled dynamics of climate, vegetation and terrestrial ecosystem biogeochemistry for regional applications. Tellus A 2010, 63, 87–106. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (NoahMP): 1. Model description and evaluation with localscale measurements. J. Geophys. Res. 2011, 116, D12109. [Google Scholar] [CrossRef]
- Jones, C.G.; Lawton, J.H.; Shachak, M. Organisms as ecosystem engineers. JSTOR 1994, 69, 373–386. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; Fang, B.; Konings, A.G.; Aires, F.; Green, J.K.; Kolassa, J.; Miralles, D.; Prigent, C.; Gentine, P. Water, Energy, and Carbon with Artificial Neural Networks (WECANN): A statistically based estimate of global surface turbulent fluxes and gross primary productivity using solar induced uorescence. Biogeosciences 2017, 14, 4101–4124. Available online: https://bg.copernicus.org/articles/14/4101/2017/ (accessed on 6 February 2021). [CrossRef] [PubMed]
- Bourras, D.; Eymard, L.; Liu, W.T. A neural network to estimate the latent heat flux over oceans from satellite observations. Int. Remote Sens. J. 2002, 23, 2405–2424. [Google Scholar] [CrossRef]
- Feng, Y.; Peng, Y.; Cui, N.; Gong, D.; Zhang, K. Modeling reference evapotranspiration using extreme learning machine and generalized regression neural network only with temperature data. Comput. Electron. Agric. 2017, 136, 71–78. [Google Scholar] [CrossRef]
- Gocic, M.; Petković, D.; Shamshirband, S.; Kamsin, A. Comparative analysis of reference evapotranspiration equations modelling by extreme learning machine. Comput. Electron. Agric. 2016, 127, 56–63. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Tang, D.; Feng, Y.; Gong, D.; Hao, W.; Cui, N. Evaluation of artificial intelligence models for actual crop evapotranspiration modeling in mulched and non-mulched maize croplands. Comput. Electron. Agric. 2018, 152, 375–384. [Google Scholar] [CrossRef]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef]
- Zhao, W.L.; Gentine, P.; Reichstein, M.; Zhang, Y.; Zhou, S.; Wen, Y.; Lin, C.; Li, X.; Qiu, G.Y. Physics constrained machine learning of evapotranspiration. Geophys. Res. Lett. 2019, 46, 14496–14507. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Pan, N.; Tian, H.; Friedlingstein, P.; Sitch, S.; Shi, H.; Arora, V.K.; Haverd, V.; Jain, A.K.; Kato, E. Evaluation of global terrestrial evapotranspiration by state- of-the-art approaches in remote sensing, machine learning, and land surface models. Hydrol. Earth Syst. Sci. Discuss 2019, 1–51. [Google Scholar] [CrossRef]
- Chaney, N.W.; Herman, J.D.; Ek, M.B.; Wood, E.F. Deriving global parameter estimates for the Noah land surface model using FLUXNET and machine learning. J. Geophys. Res. Atmos. 2016, 121, 13218–13235. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Sawada, Y. Machine Learning Accelerates Parameter Optimization and Uncertainty Assessment of a Land Surface Model. J. Geophys. Res. Atmos. 2020. [Google Scholar] [CrossRef]
- Dagon, K.; Sanderson, B.M.; Fisher, R.A.; Lawrence, D.M. A machine learning approach to emulation and biophysical parameter estimation with the Community Land Model, version 5. Adv. Stat. Clim. Meteorol. Oceanogr. 2020, 6, 223–244. [Google Scholar] [CrossRef]
- Everingham, Y.; Sexton, J.; Skocaj, D.; Inman-Bamber, G. Accurate prediction of sugarcane yield using a random forest algorithm. Agron. Sustain. Dev. 2016, 36, 27. [Google Scholar] [CrossRef]
- Feng, P.; Wang, B.; Liu, D.; Waters, C.; Xiao, D.; Shi, L.; Yu, Q. Dynamic wheat yield forecasts are improved by a hybrid approach using a biophysical model and machine learning technique. Agric. Forest Meteorol. 2020, 285–286, 107922, ISSN 0168-1923. [Google Scholar] [CrossRef]
- Schlund, M.; Eyring, V.; Camps-Valls, G.; Friedlingstein, P.; Gentine, P.; Reichstein, M. Constraining uncertainty in projected gross primary production with machine learning. J. Geophys. Res. Biogeosci. 2020, 125, e2019JG005619. [Google Scholar] [CrossRef]
- Christian, F.; Baklanov, A.; Balkovič, J.; Skalsky, R.; Khabarov, N.; Obersteiner, M. Spatio-temporal downscaling of gridded crop model yield estimates based on machine learning. Agric. Forest Meteorol. 2019, 264, 1–15. [Google Scholar] [CrossRef]
- Shahhosseini, M.; Guiping Hu, S. Archontoulis and Isaiah Huber. Coupling Machine Learning and Crop Modeling Improves Crop Yield Prediction in the US Corn Belt. arXiv Preprint 2020, arXiv:abs/2008.04060. [Google Scholar]
- Pelissier, C.; Frame, J.; Nearing, G. Combining parametric land surface models with machine learning. arXiv Preprint 2020, arXiv:abs/2002.06141. [Google Scholar]
- Leufen, L.H.; Schädler, G. Calculating the Turbulent Fluxes in The Atmospheric Surface Layer with Neural Networks. Geosci. Model Dev. 2019, 12, 2033–2047. [Google Scholar] [CrossRef]
- Gentine, P.; Pritchard, M.; Rasp, S.; Reinaudi, G.; Yacalis, G. Could machine learning break the convection parameterization deadlock? Geophys. Res. Lett. 2018, 45, 5742–5751. [Google Scholar] [CrossRef]
- Rasp, S.; Pritchard, M.S.; Gentine, P. Deep learning to represent sub-grid processes in climate models. Proc. Natl. Acad. Sci. USA 2018, 39, 9684–9689. [Google Scholar] [CrossRef] [PubMed]
- Huntzinger, D.N.; Schwalm, C.R.; Wei, Y.; Cook, R.B.; Michalak, A.M.; Schaefer, K.; Jacobson, A.R.; Arain, M.A.; Ciais, P.; Fisher, J.B.; et al. NACP MsTMIP: Global 0.5-deg Terrestrial Biosphere Model Outputs (Version 1) in Standard Format; ORNL DAAC: Oak Ridge, TN, USA, 2016. [Google Scholar] [CrossRef]
- Schwalm, C.R.; Schaefer, K.; Fisher, J.B.; Huntzinger, D.; Elshorbany, Y.; Fang, Y.; Hayes, D.; Jafarov, E.; Michalak, A.M.; Piper, M. Divergence in land surface modeling: Linking spread to structure. Environ. Res. Commun. 2019, 1, 111004. [Google Scholar] [CrossRef]
- Sreepathi, S.; Xu, M.; Collier, N.; Kumar, J.; Mao, J.; Hoffman, F.M. Land Model Testbed: Accelerating Development, Benchmarking and Analysis of Land Surface Models. OSFHOME 2020. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef]
- Ren, Y.Z.; Xia, K.W.; Wang, Y.; Shi, J. Application on Network Traffic Prediction Based on Least Squares Support Vector Machine. Appl. Mech. Mater. 2010, 20–23, 364–369. [Google Scholar] [CrossRef]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Alonso Fernández, J.R.; García Nieto, P.J.; Díaz Muñiz, C.; Álvarez Antón, J.C. Modeling eutrophication and risk prevention in a reservoir in the Northwest of Spain by using multivariate adaptive regression splines analysis. Ecol. Eng. 2014, 68, 80–89. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Joshi, D.R.; Clay, D.E.; Henebry, G.M. Characterizing land cover/land use from multiple years of Landsat and MODIS time series: A novel approach using land surface phenology modeling and random forest classifier. Remote Sens. Environ. 2018, 111017. [Google Scholar] [CrossRef]
- Constantin, I.; Lungu, M.L.; Panaitescu, L.; Ilie, M.; Simulating Lungu, D.; Nita, S. Simulating for predicting the hourly dew point temperature using artificial neural networks. J. Environ. Prot. Ecol. 2014, 15, 1101–1109. Available online: https://www.researchgate.net/publication/285526297_Simulating_for_predicting_the_hourly_dew_point_temperature_using_artificial_neural_networks (accessed on 11 March 2021).
- Park, Y.-S.; Lek, S. Artificial Neural Networks: Multilayer Perceptron for Ecological Modeling. Dev. Environ. Model. 2016, 28, 123–140. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C.; Kifer, D.; Yang, X. Prolongation of SMAP to Spatiotemporally Seamless Coverage of Continental, U.S. Using a Deep Learning Neural Network. Geophys. Res. Lett. 2017, 44, 11030–11039. [Google Scholar] [CrossRef]
- Rahmani, F.; Lawson, K.; Ouyang, W.; Appling, A.; Oliver, S.; Shen, C. Exploring the exceptional performance of a deep learning stream temperature model and the value of streamflow data. Environ. Res. Lett. 2021. [Google Scholar] [CrossRef]
- Li, Y.; Ryu, D.; Western, A.W.; Wang, Q. Assimilation of stream discharge for flood forecasting. Updating a semidistributed model with an integrated data assimilation scheme. Water Resour. Res. 2015. [Google Scholar] [CrossRef]
- Pal, S.; Dominguez, F.; Dillon, M.E.; Alvarez, J.; Garcia, C.M.; Nesbitt, S.W.; Gochis, D. Hydrometeorological Observations and Modeling of an Extreme Rainfall Event using WRF and WRF-Hydro during the RELAMPAGO Field Campaign in Argentina. J. Hydrometeor. 2021, 22, 331–351. [Google Scholar] [CrossRef]
- Basso, B.; Antle, J. Digital agriculture to design sustainable agricultural systems. Nat. Sustain. 2020, 3, 254–256. [Google Scholar] [CrossRef]
- Kohlbrenner, M.; Bauer, A.; Nakajima, S.; Binder, A.; Samek, W.; Lapuschkin, S. Towards best practice in explaining neural network decisions with LRP. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; Available online: https://arxiv.org/abs/1910.09840 (accessed on 6 February 2021).
| ML Algorithm | Category | Purpose | Reference |
|---|---|---|---|
| Feedforward ANN | Traditional | Provide monthly estimates of GPP, LH and SH at a global scale | [42] |
| ELM and GRNN | Obtain ETo from temperature data in southwest China | [44] | |
| RT, Bagging, RF and SVM | Provide ET estimates in central Florida | [46] | |
| SVM and GANN | Provide crop ET estimates in China | [47] | |
| RF, RT, KRR, RS, ANN | Provide CO2, LH, SH, Rn at multiple sites globally | [48] | |
| Extra-Trees | Obtain global parameter estimates for Noah land model | [52] | |
| MCMC | Parameter optimization of land model | [54] | |
| RF | Improving regional crop yield prediction | [56,57,59,60] | |
| GBRT | Constrain uncertainty in GPP estimates | [58] | |
| DL-ANN | Deep learning | Obtain LH estimates over ocean | [43] |
| DL-ANN | Constructing physics-constrained ML model | [49] | |
| DL-ANN | Constructing emulators for land modeling | [55] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, S.; Sharma, P. A Review of Machine Learning Applications in Land Surface Modeling. Earth 2021, 2, 174-190. https://doi.org/10.3390/earth2010011
Pal S, Sharma P. A Review of Machine Learning Applications in Land Surface Modeling. Earth. 2021; 2(1):174-190. https://doi.org/10.3390/earth2010011
Chicago/Turabian StylePal, Sujan, and Prateek Sharma. 2021. "A Review of Machine Learning Applications in Land Surface Modeling" Earth 2, no. 1: 174-190. https://doi.org/10.3390/earth2010011
APA StylePal, S., & Sharma, P. (2021). A Review of Machine Learning Applications in Land Surface Modeling. Earth, 2(1), 174-190. https://doi.org/10.3390/earth2010011






