Lie Optimal Solutions of Heat Transfer in a Liquid Film over an Unsteady Stretching Surface with Viscous Dissipation and an External Magnetic Field ^†

Abstract

A lie point symmetry analysis of flow and heat transfer under the influence of an external magnetic field and viscous dissipation was previously conducted using a couple of lie point symmetries of the model. In this article, we construct a one-dimensional optimal system for the flow model to extend the previous analysis. This optimal system reveals all the solvable classes of the flow model by deducing similarity transformations, reducing flow equations, and solving the obtained equations analytically. A general class of solutions that encompasses all the previously known lie similarity solutions is provided here.

1. Introduction

Heat transfer in liquid films governs numerous engineering, industrial, and biomedical applications under multiple physical conditions. There are many products and operations like chemical reactors, heat exchangers, and biomedical devices which depend on predicting precise flow dynamics. Therefore, one finds an extensive treatment of these kinds of problems in the literature. All such studies depend on the solution of the underlying system of nonlinear partial differential equations (PDEs), while exact solution schemes are not available for most of these systems. Similarity transformations are designed to reduce the flow PDEs to ordinary differential equations (ODEs) by reducing the independent as well as the dependent variables of the flow equations. These reduced ODEs are further solved using analytic and numerical approximation solution procedures. These solutions lead to flow and heat transfer profiling through graphs of the obtained analytic and approximate solutions.

Flow dynamics have been investigated by imposing a magnetohydrodynamic (MHD) condition on the flow and heat transfer; for example, in [1], the homotopy analysis method is applied to investigate a similar flow. The MHD natural convection flow of a nanofluid over a linear porous stretching sheet was studied in [2] using lie symmetry group transformation under the influence of thermal stratification. In [3], a partial slip condition was implemented to conduct a similar study, while for a stagnation-point MHD, convective and viscoelastic flow under the effect of slip velocity was studied in [4] to investigate the impact of heat generation/absorption and variable diffusivity. The thermal variable conductivity of the fluid was coupled with thermal radiation on an MHD flow in [5], which examined its impact on the flow dynamics of a Casson fluid that was observed to significantly influence flow and heat transfer. In [6], a symmetry approach was employed on viscous MHD flow along with heat transfer on a stretching sheet. In this study, thermal conductivity, viscosity, and the magnetic field were shown to influence the flow. By considering flow on an exponentially permeable stretching surface, [7] investigated heat and mass transfer. On a semi-infinite stretching surface, the influence of a magnetic field on fluid flow was presented in [8] using lie symmetry group analysis. In [9], an investigation of concentration flux depending on radiative Casson MHD flow with Arrhenius activation energy was carried out by employing homotopy analysis with an evolutionary algorithm.

The lie symmetry method is a proven useful algebraic tool that generates the similarity transformations applied to reduce the dependent and independent variables of the corresponding flow PDEs. In numerous attempts similarity transformations are obtained using scaling-type transformations only. However, the use of such transformations, unlike lie, does not guarantee the invariance of both the flow PDEs and associated boundary/initial conditions. Five-dimensional lie symmetry algebra was derived for the PDEs of flow and heat transfer on a stretching sheet under the influence of magnetic field and viscous dissipation in [10]. This flow model includes the influence of unsteadiness, which makes it more realistic in applications encompassing polymer processing to industrial cooling. Furthermore, the magnetic field is imposed in the momentum equation here, which alters the flow as well as the transfer of heat. Lastly, in the energy equation, viscous dissipation is introduced, which incorporates internal heating due to fluid viscosity. The inclusion of the time-dependent unsteadiness, magnetic field, and viscous dissipation makes the model more comprehensive compared to the classical flow equations without these physical constraints. Solutions of this model claim more control over the flow and heat transfer through the physical parameters imposed by the unsteadiness, magnetic field, and viscous dissipation. However, it further complicates the study of the corresponding flow and heat transfer. As the approaches developed to deal with these flow equations often map the PDEs of the flow model to ODEs, the additional nonlinear/linear terms have to be rederived and implemented. For example, in [10], a couple of lie symmetries out of five existing symmetry generators were used to construct lie similarity transformations, and linked reduced forms were unraveled and solved using the homotropy analysis method. We consider the same fluid flow model and the corresponding symmetries here to deduce an optimal system of one-dimensional lie subalgebras, which leads towards a complete invariant characterization of the invariant similarity solutions. Though solutions in [10] have already been presented, they were not claimed to be a complete set of solutions, i.e., there does not exist any other solution except that presented in the cited work. The existence of the complete invariant set of solutions for the considered flow is ensured through the construction of the previously mentioned optimal system, which we pursue in this study. We have found that solutions corresponding to the constructed optimal system present similar flow dynamics as in [10]. Velocity and temperature profiles are constructed using the homotropy analysis method. The impact of the physical parameters on flow dynamics is presented graphically and tabulated in the subsequent sections. The obtained analytic solutions have also been verified through the finite difference method by deducing the numerical solutions. We have found a good agreement between the numerical and analytic similarity solutions obtained here.

2. Derivation of Lie Point Symmetries and Invariants for Flow Model

The two-dimensional boundary layer equations under the influence of the external magnetic field and viscous dissipation, as given in [11], reads as follows:

$${\displaystyle \frac{\partial u}{\partial x}} +{\displaystyle \frac{\partial v}{\partial y}} = 0$$

(1)

$${\displaystyle \frac{\partial u}{\partial t}}+u{\displaystyle \frac{\partial u}{\partial x}} +v{\displaystyle \frac{\partial u}{\partial y}}-\nu \left({\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}\right)+{\displaystyle \frac{\sigma B^2}{\rho }}u=0$$

(2)

$${\displaystyle \frac{\partial T}{\partial t}}+u{\displaystyle \frac{\partial T}{\partial x}}+v{\displaystyle \frac{\partial T}{\partial y}}-{\displaystyle \frac{\kappa }{\rho Cp}}\left({\displaystyle \frac{{\partial }^{2}T}{\partial y^2}}\right)-{\displaystyle \frac{\mu }{\rho Cp}}{\left({\displaystyle \frac{\partial u}{\partial y}}\right)}^2=0$$

(3)

along with the conditions

$$y=0, u=U\left(x, t\right), v=0, T=T_s\left(x, t\right)$$

(4)

$$y=h\left(t\right), u_y=T_y=0,v=h_t={\displaystyle \frac{dh}{dt}}$$

(5)

where $u$ and $v$ are the velocities in two spatial directions, $T$ is the temperature, $\nu$ is the kinetic viscosity, $B$ is the magnetic field parameter, $\sigma$ is the electrical conductivity, $\rho$ is the density, $\mu$ is the dynamic viscosity, $\kappa$ is the thermal conductivity, and $c_p$ is the specific heat. Furthermore, at $y=0$, i.e., at the surface of the fluid, the velocities are as follows: $u=U(x,t)$ and $v=0$, respectively, and the temperature reads as $T=T_s(x,t)$. For the free surface of the fluid, i.e., $y=h\left(t\right)$, the variations in $u$ velocity and temperature vanish in the $y$ direction.

Similarity transformations for the above flow model were driven by the lie symmetries in [10] and employed to reduce the dependent and independent variables of the above system of PDEs along with the boundary condition. The same results are also obtained through the stream function by considering

$$\eta ={\displaystyle \frac{y}{\beta }}\sqrt{{\displaystyle \frac{b}{\nu \left(1-\alpha t\right)}}} , f\left(\eta \right)={\displaystyle \frac{\psi \left(x, y, t\right)}{x\sqrt{\frac{b\nu }{1-\alpha t}}}} ,\theta \left(\eta \right)={\displaystyle \frac{T_0-T\left(x, y, t\right)}{T_{ref}\left(\frac{b{x}^2}{2\nu }\right){\left(1-\alpha t\right)}^{\frac{3}{2}}}}$$

(6)

which further extends to

$$u={\displaystyle \frac{\partial \psi }{\partial y}}={\displaystyle \frac{bx}{1-\alpha t}}{f}^{\prime },v=-{\displaystyle \frac{\partial \psi }{\partial x}}=-\beta \sqrt{{\displaystyle \frac{b\nu }{1-\alpha t}}}f$$

(7)

This transformation maps the boundary layer equation to the system of ODEs

$$f^{‴}+\gamma f^{\prime 2}+\gamma \left({\displaystyle \frac{S\eta }{2}}-f\right)f^{″}+\gamma \left(S-Mn\right)f^{\prime }=0$$

(8)

$${\mathit{Pr}}^{-1}{\theta }^{″}+2\gamma \left(S+f^{\prime }\right)\theta +\gamma \left({\displaystyle \frac{S\eta }{2}}-f\right){\theta }^{\prime }+Ec{f}^{″2}=0$$

(9)

and conditions

$$f\left(0\right)=0, f^{\prime }\left(0\right)=1, \theta \left(0\right)=1, f\left(1\right)={\displaystyle \frac{S}{2}}, f″\left(1\right)=0, \theta \prime \left(1\right)=0$$

(10)

where $h(t) = \beta \sqrt{{\displaystyle \frac{\nu \left(1-\alpha t\right)}{b}}}$ with a dimensionless constant $\beta$, $Mn={\displaystyle \frac{\sigma B_0^2}{b\rho }}$ is the magnetic parameter, $Ec={\displaystyle \frac{U^2}{C_p{(T}_s-T_0)}}$ is the Eckert number, and $Pr={\displaystyle \frac{\nu \rho C_p}{\kappa }}$ is the Prandtl number. A lie point symmetry for the system of PDEs (1)–(3) that must also leave the conditions (4) and (5) in the invariant form is written as

$$\begin{array}{c}\mathbf{X}={\xi }_k{\displaystyle \frac{\partial }{\partial {\psi }_k}}+{\varphi }_k{\displaystyle \frac{\partial }{\partial {\zeta }_k}}, k=1, 2, 3 \end{array}$$

(11)

$${\mathbf{X}}^{\left[2\right]}={\mathbf{X}}^{\left[1\right]}+{\varphi }_k^t{\displaystyle \frac{\partial }{\partial {\zeta }_{k,t}}}+{\varphi }_k^x{\displaystyle \frac{\partial }{\partial {\zeta }_{k,x}}}+{\varphi }_k^y{\displaystyle \frac{\partial }{\partial {\zeta }_{k,y}}}+{\varphi }_k^{tt}{\displaystyle \frac{\partial }{\partial {\zeta }_{k,tt}}}+{\varphi }_k^{xx}{\displaystyle \frac{\partial }{\partial {\zeta }_{k,xx}}}+{\varphi }_k^{yy}{\displaystyle \frac{\partial }{\partial {\zeta }_{k,yy}}}$$

(12)

with the extension coefficients obtainable from

$${\varphi }_k^n=D_n{\varphi }_k-{\zeta }_{k,t}{D}_n\left({\xi }_1\right)-{\zeta }_{k,x}{D}_n\left({\xi }_2\right)-{\zeta }_{k,y}{D}_n\left({\xi }_3\right); n \in \left\{t, x, y\right\}, k=1, 2, 3$$

(13)

and

$$\begin{array}{l}{\Phi }_k^{tt}=D_t{\varphi }_k^t-{\zeta }_{k,tt}{D}_t({\xi }_1)-{\zeta }_{k,tx}{D}_t({\xi }_2)-{\zeta }_{k,ty}{D}_t({\xi }_3)\\ {\Phi }_k^{xx}=D_x{\varphi }_k^x-{\zeta }_{k,tx}{D}_x\left({\xi }_1\right)-{\zeta }_{k,xx}{D}_x\left({\xi }_2\right)-{\zeta }_{k,xy}{D}_x\left({\xi }_3\right) \\ {\Phi }_k^{yy}=D_y{\varphi }_k^y-{\zeta }_{k,ty}{D}_y\left({\xi }_1\right)-{\zeta }_{k,yx}{D}_y\left({\xi }_2\right)-{\zeta }_{k,yy}{D}_y\left({\xi }_3\right) m=1, 2, 3.\end{array}$$

(14)

The above expressions contain the total derivative operator, which in expanded form reads as $D_n={\displaystyle \frac{\partial }{\partial n}}+{\zeta }_{k,n}{\displaystyle \frac{\partial }{\partial k}} +{\zeta }_{k,nn}{\displaystyle \frac{\partial }{\partial k,n}} + \dots , n\in \left\{t, x, y\right\}$, where the summation is over repeated indices.

The derivation of the infinitesimal coordinates of the symmetry generator (14) involves the application of ${\mathbf{X}}^{\left[2\right]}$ on each equation of system (1)–(3) through an invariance criterion of the following form ${\mathbf{X}}^{\left[2\right]}{\left.\left({\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}\right)\right|}_{{\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}=0}=0,$ solving the resulting linear PDEs provides the following symmetries:

$${\mathbf{X}}_1={\displaystyle \frac{\partial }{\partial x}} , {\mathbf{X}}_2={\displaystyle \frac{\partial }{\partial T}} , {\mathbf{X}}_3=x{\displaystyle \frac{\partial }{\partial x}}+u{\displaystyle \frac{\partial }{\partial u}}+2T{\displaystyle \frac{\partial }{\partial T}} , {\mathbf{X}}_4=t{\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{y}{2}}{\displaystyle \frac{\partial }{\partial y}}-u{\displaystyle \frac{\partial }{\partial u}}-{\displaystyle \frac{v}{2}}{\displaystyle \frac{\partial }{\partial v}}-2T{\displaystyle \frac{\partial }{\partial T}}$$

$${\mathbf{X}}_5=t^{1-{\displaystyle \frac{\sigma B_o^2}{\rho {\alpha }^2}}}{\displaystyle \frac{\partial }{\partial x}}+{\displaystyle \frac{\rho {\alpha }^2-\sigma B{o}^2}{\rho {\alpha }^{2}t}}{t}^{1-{\displaystyle \frac{\sigma B_o^2}{\rho {\alpha }^2}}}{\displaystyle \frac{\partial }{\partial u}}$$

(15)

A complete procedure to obtain lie point symmetries of PDEs is given in [12].

Likewise, we have followed the procedure given in [13,14,15] to construct a one-dimensional optimal system of subalgebras for the symmetry generators given in

Table 1. Symmetries and invariants.

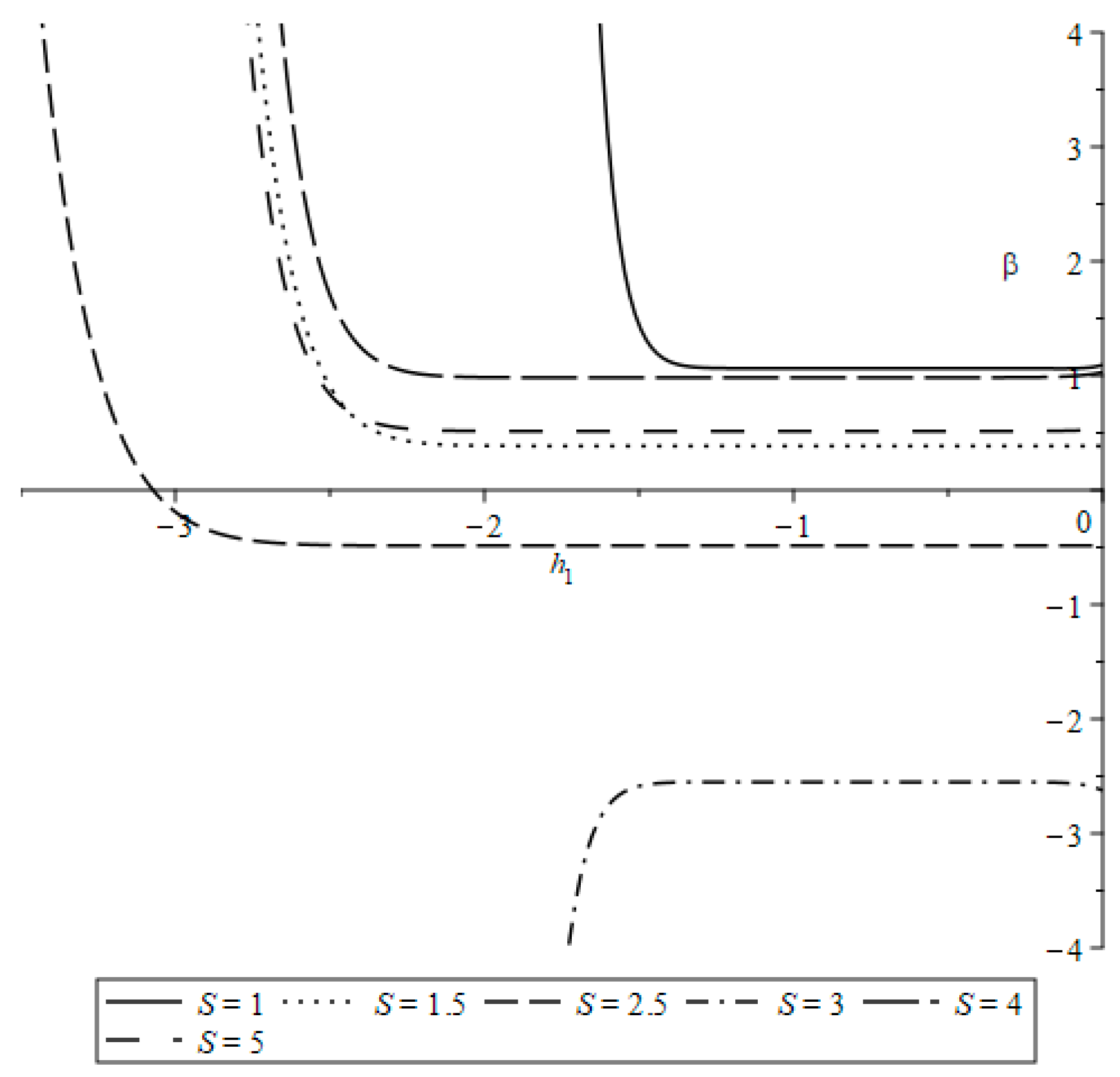
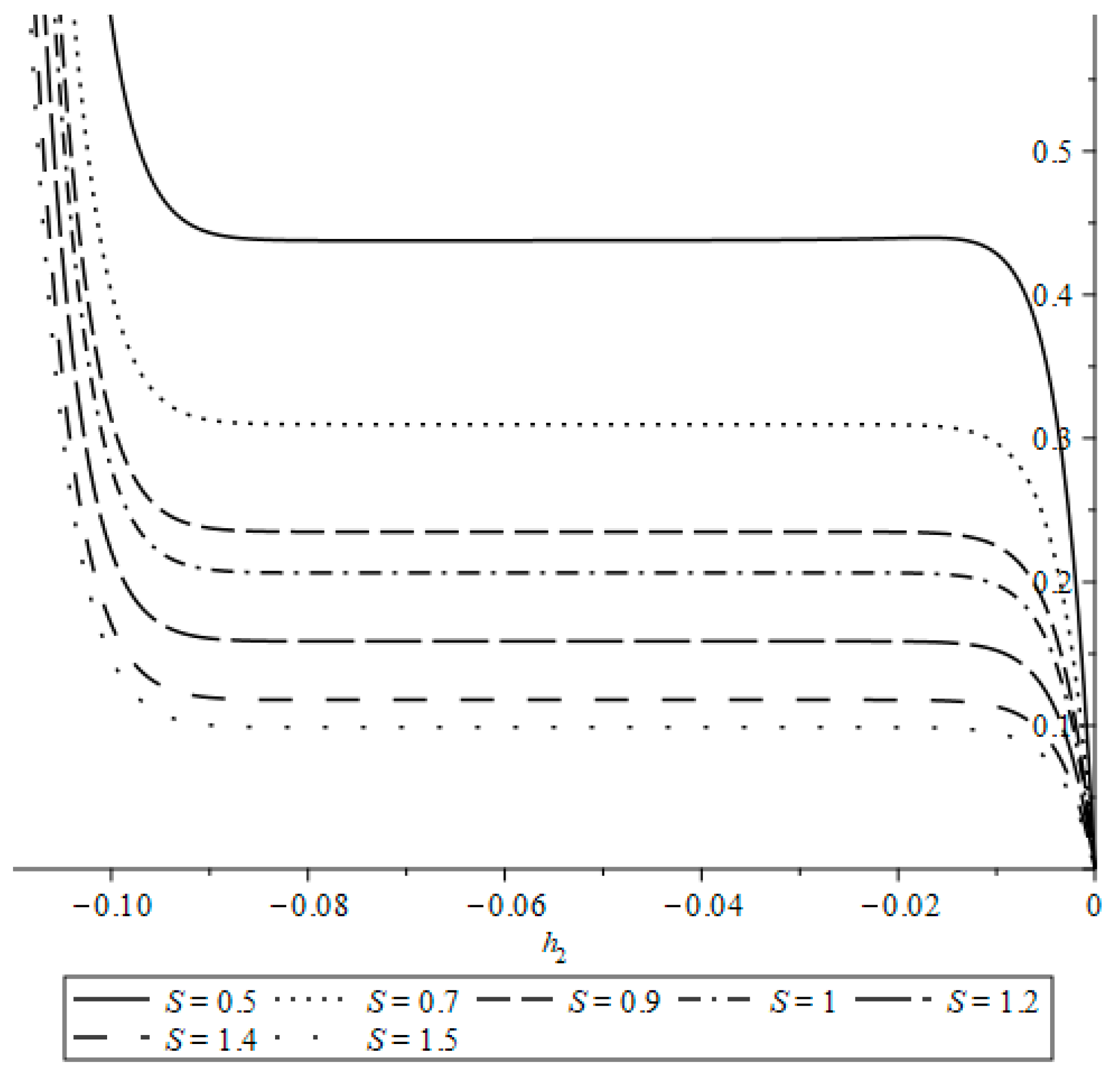
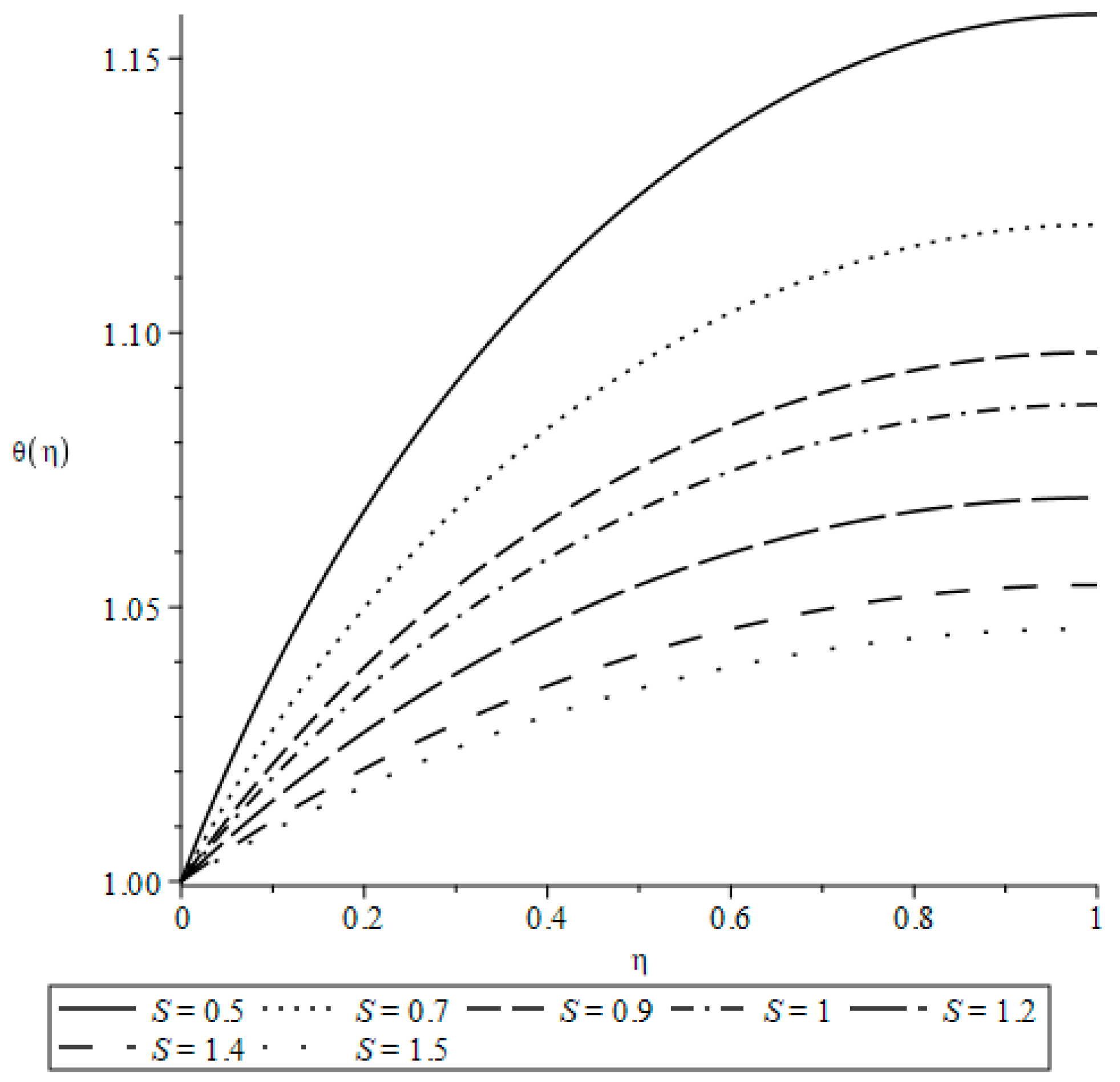
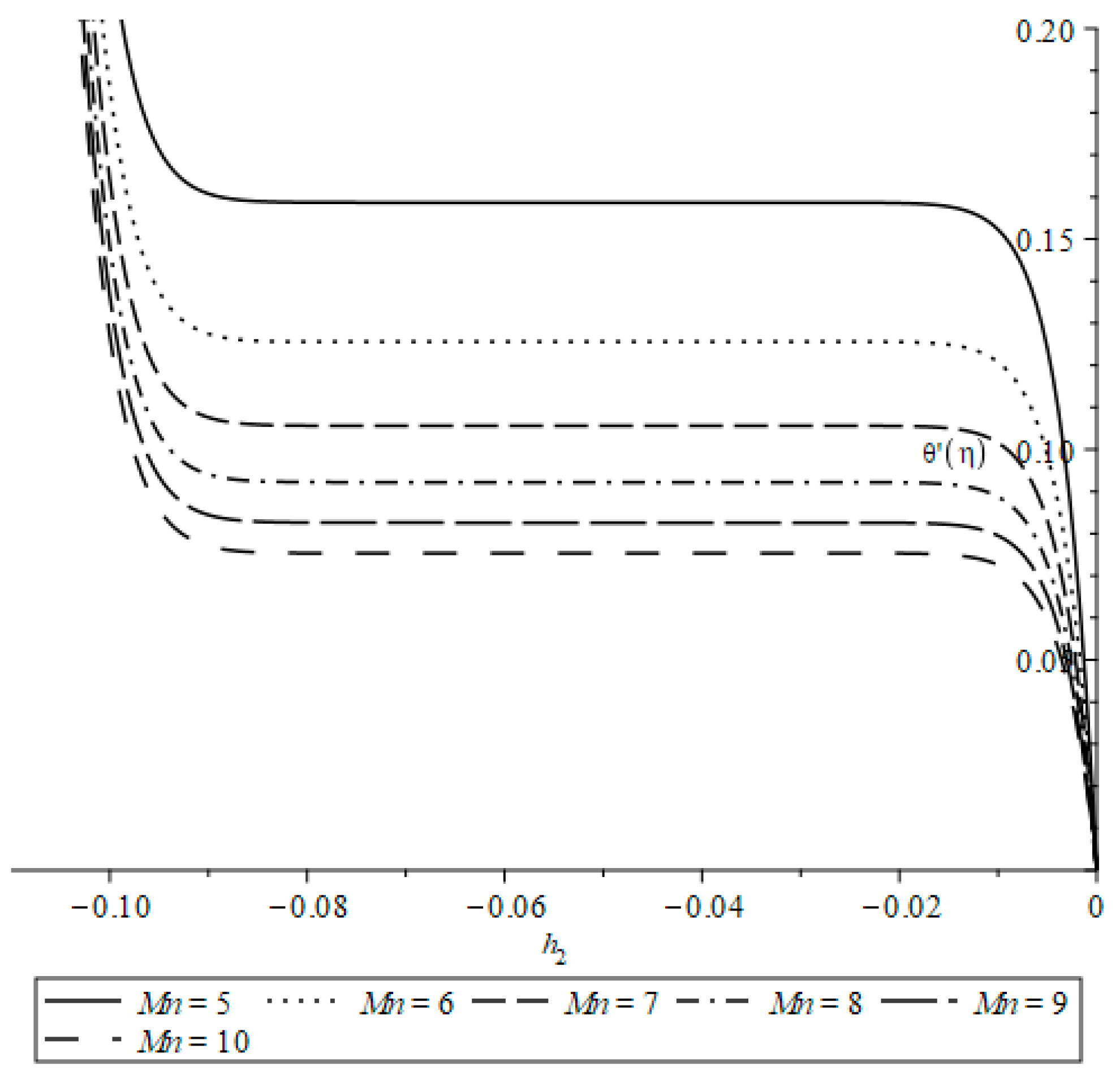
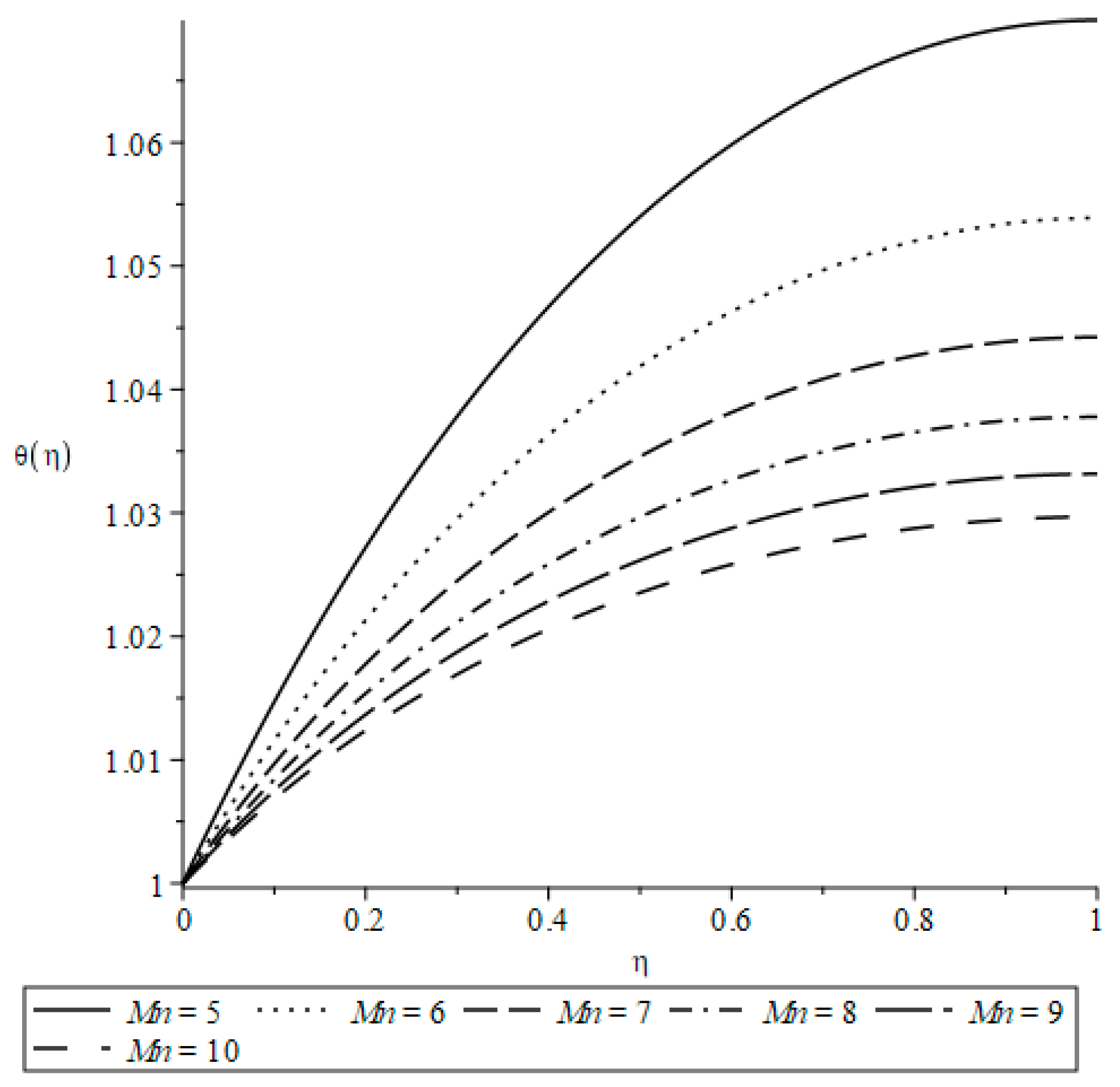
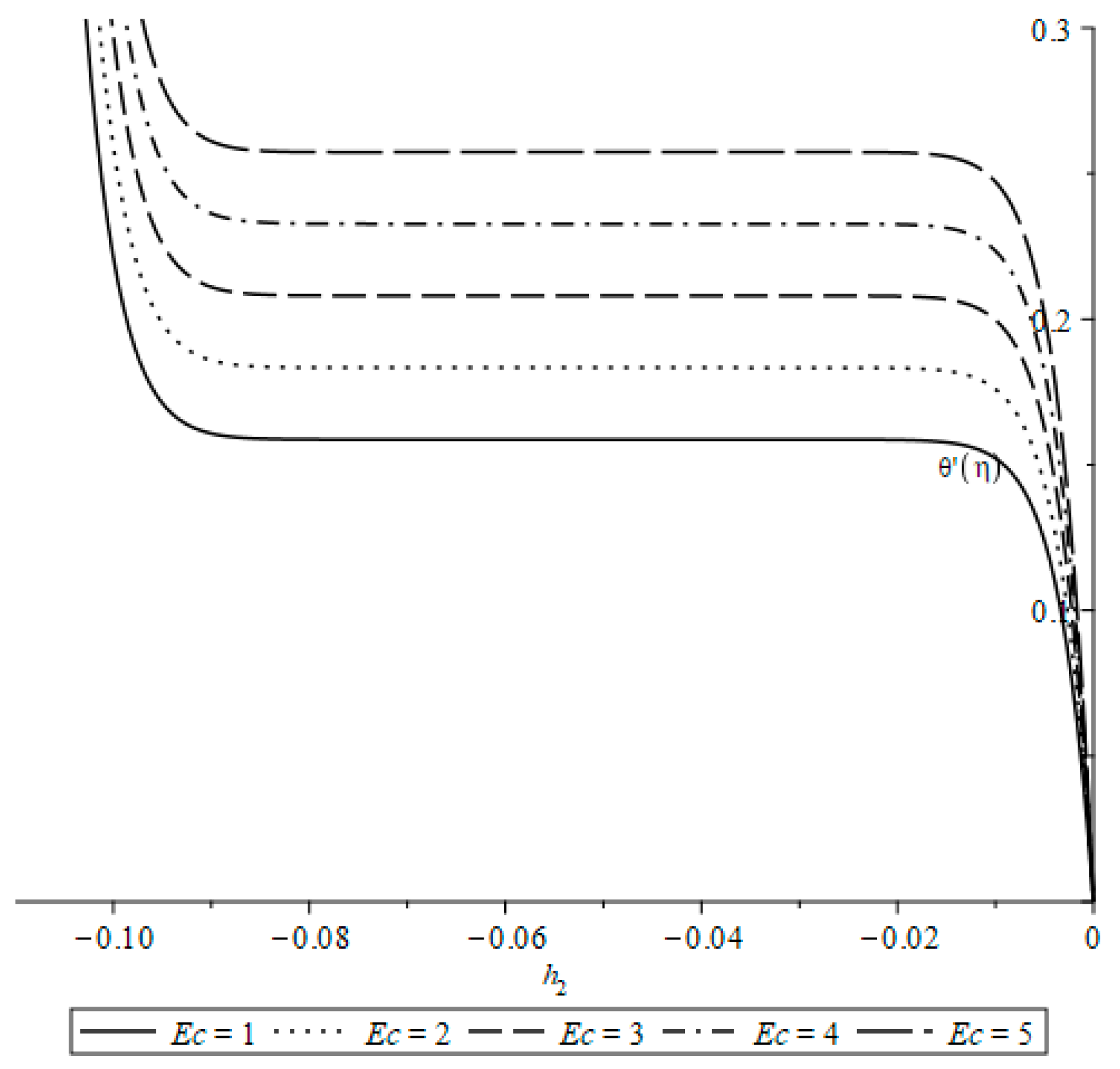
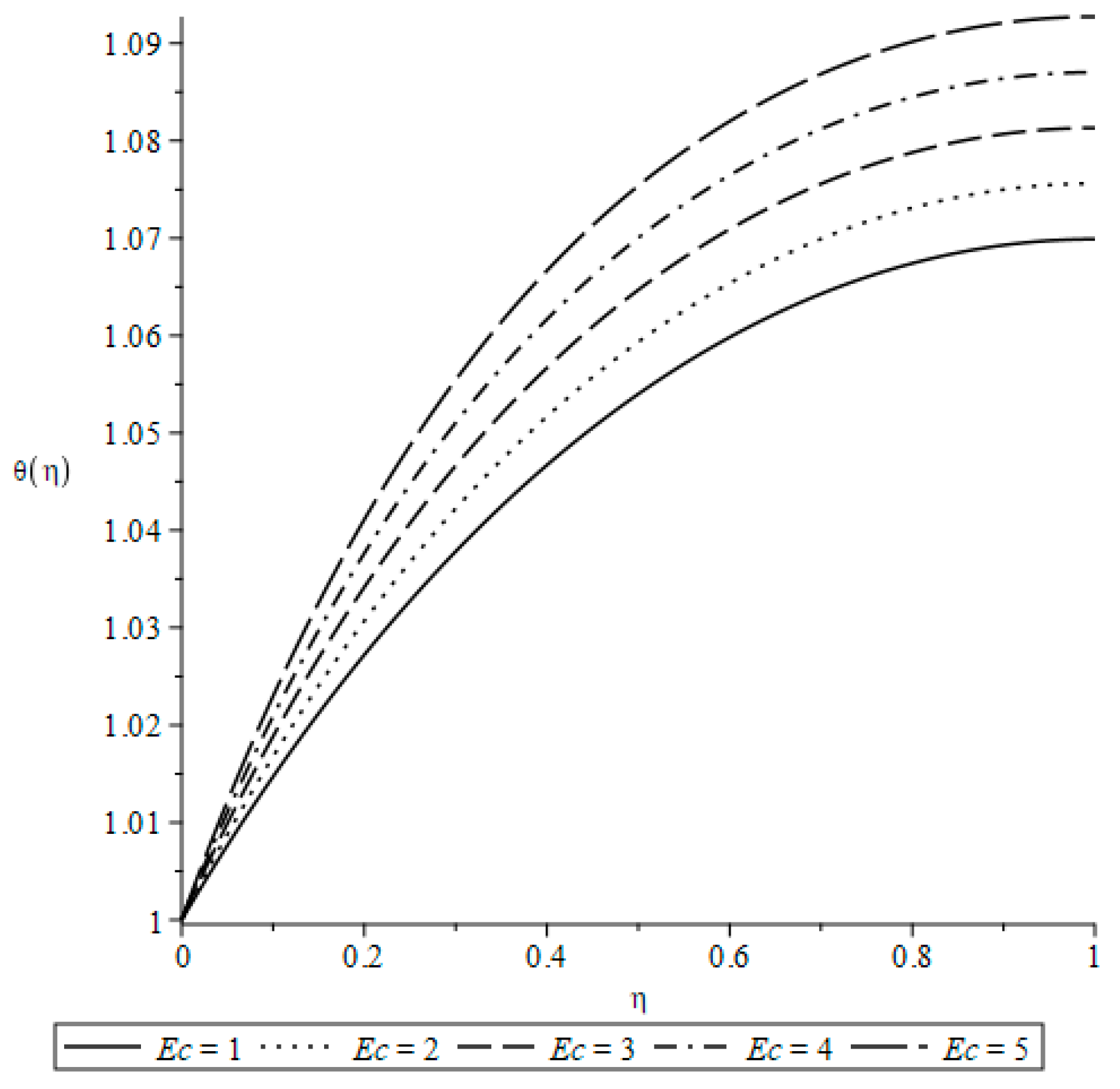
Case	Symmetry	Invariants
1	${\mathbf{X}}_3+{\alpha \mathbf{X}}_4$	$t{x}^{-\alpha },y{x}^{-{\displaystyle \frac{\alpha }{2}}}, u{x}^{\alpha -1},v{x}^{{\displaystyle \frac{\alpha }{2}}},x^{2\left(\alpha -1\right)}T$
2	${\mathbf{X}}_4+{\alpha \mathbf{X}}_1$	$t{e}^{-{\displaystyle \frac{x}{\alpha }}},y{e}^{-{\displaystyle \frac{x}{2\alpha }}},{ue}^{{\displaystyle \frac{x}{\alpha }}},v{e}^{{\displaystyle \frac{x}{2\alpha }}},{Te}^{{\displaystyle \frac{2x}{\alpha }}}$
3	${\mathbf{X}}_3$	$t,y,{\displaystyle \frac{u}{x}},v,{\displaystyle \frac{T}{x^2}}$
4	${{\mathrm{C}}_1\mathbf{X}}_1+{{\mathrm{C}}_2\mathbf{X}}_2+{\mathrm{C}}_3{\mathbf{X}}_3+{{\mathrm{C}}_4\mathbf{X}}_4$	$t,y,{\displaystyle \frac{u}{x}},v,{\displaystyle \frac{T}{x^2}}$

. In the subsequent sections, we perform reductions in the flow PDEs (1)–(3) and the associated conditions (4) and (5) using the linear combination in case 4, as it seems to be the most general form of the subalgebras provided by the optimal system derived above. By following the procedure given in [10], one arrives at the following similarity transformations corresponding to the linear combination of case 4:

$$y=\beta \sqrt{{\displaystyle \frac{\alpha vt}{b}}}\eta , u=-{\displaystyle \frac{bx}{\alpha t}}{f}^{\prime }, v=\beta \sqrt{{\displaystyle \frac{vb}{\alpha t}}}f, T={\displaystyle \frac{x^2}{t^2}}\theta$$

(16)

3. Results and Discussion (Homotopy Analytic Solutions)

The HAM has been implemented in numerous studies conducted to investigate flow dynamics [1,9,16,17,18,19,20]. Firstly, in this approach, one constructs the zero-order initial functions

$$f_0\left(\eta \right)=\eta +3{\displaystyle \frac{\left(S-2\right)}{4}} {\eta }^2-{\displaystyle \frac{\left(S-2\right)}{4}}{\eta }^3, {\theta }_0\left(\eta \right)=1$$

(17)

which approximate the solution of the reduced system of ODEs. The above functions are derived using associated boundary conditions. These functions are used in the deformation equations which are finally integrated to generate analytic solutions for $f\left(\eta \right)$ and $\theta \left(\eta \right)$. In the subsequent part of this section, we present the findings of this study in the form of graphs and tables to summarize the influences of the physical parameters on the flow dynamics.

Table 2. Variation in film thickness $\beta$ with unsteadiness $S$ and magnetic parameter $Mn.$

$\mathit{M}\mathit{n}$	$\mathit{S}=0.5$	$\mathit{S}=0.7$	$\mathit{S}=0.9$	$\mathit{S}=1.0$	$\mathit{S}=1.2$	$\mathit{S}=1.4$	$\mathit{S}=1.5$
$5$	$4.200727$	$2.157636$	$1.317824$	$1.064351$	$0.715314$	$0.479888$	$0.385409$
$6$	$3.330918$	$1.700584$	$1.028113$	$0.824712$	$0.544815$	$0.357457$	$0.283289$
$7$	$2.760233$	$1.403570$	$0.842920$	$0.673206$	$0.439966$	$0.284801$	$0.223951$
$8$	$2.356749$	$1.194989$	$0.714297$	$0.568748$	$0.368965$	$0.236693$	$0.185165$
$9$	$2.039973$	$1.040425$	$0.619749$	$0.492360$	$0.317699$	$0.202489$	$0.157832$
$10$	$1.809418$	$0.921291$	$0.547313$	$0.434067$	$0.278943$	$0.176923$	$0.137530$

presents film thicknesses by varying the unsteadiness and magnetic parameters. A decrease in film thickness is observed due to increments in the magnetic parameter, while a decreasing trend is evident from this table due to an increase in the unsteadiness parameter. The unsteadiness and magnetic parameters are shown to significantly impact the liquid film thickness, as was expected to be an influence in this case. The unsteadiness parameter appears in the velocity boundary condition, which varies over time; hence, the value of $\beta$ determines whether the stretching rate is increasing or decreasing with the passage of time. An increase in magnetic field strength is usually expected to increase film thickness, while in Table 2, we observe the opposite behavior due to interactions between the viscous dissipation and Joule heating associated with the magnetic field, resulting in a thinner liquid film.

In

Table 3. Variation in $f\prime \left(\eta \right)$ and $\theta \left(\eta \right)$ with $S$, $Mn$, and $Pr.$

$\mathit{M}\mathit{n}$	$\mathit{f}\mathbf{\prime }\left(1\right)$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.05$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.06$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.07$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.08$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.09$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.1$
$\mathit{S}\mathbf{=}\mathbf{0.5}$
$5$	$0.026523$	$1.157968$	$1.193940$	$1.231595$	$1.271069$	$1.312505$	$1.355506$
$7.5$	$0.032626$	$1.096385$	$1.117178$	$1.138560$	$1.160520$	$1.183095$	$1.206315$
$10$	$0.034214$	$1.071482$	$1.086595$	$1.101988$	$1.117675$	$1.133670$	$1.149983$
$\mathit{S}\mathbf{=}\mathbf{1.5}$
$5$	$0.629464$	$1.046026$	$1.055634$	$1.065383$	$1.075275$	$1.085315$	$1.095504$
$7.5$	$0.630354$	$1.024864$	$1.029950$	$1.035074$	$1.040237$	$1.045440$	$1.050682$
$10$	$0.630669$	$1.017481$	$1.021032$	$1.024601$	$1.028187$	$1.031792$	$1.035416$

, we present the variation in the velocity and temperature distribution, which shows that the velocity of the fluid increases with the magnetic as well as the unsteadiness parameter, while opposite trends are recorded for the temperature distribution. Usually, with a strong magnetic field, the velocity is expected to experience a resistive force, which however may convert into an opposite trend due to a redistribution of the momentum that happens because of the interaction of the magnetic field with the unsteadiness. A decrease in the fluid temperature is observed due to the increase in the fluid velocity that triggers the cooling of the liquid film. This table also highlights the influence of the Prandtl number on the temperature distribution, which implies that increasing the Prandtl number gives rise to temperature distribution. This increase is due to the dominance of the momentum diffusivity. Figure 1 sketches temperature profiles for different values of the magnetic parameter and the unsteadiness parameter. Likewise, in the remaining tables and figures, we provide the influences of the physical parameters on the flow dynamics.

Both

Table 4. Variation in $\theta \left(\eta \right)$ with $S$, $Mn$, and $Pr$for $S=0.5.$

$\mathit{E}\mathit{c}$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.05$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.06$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.07$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.08$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.09$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.1$
$\mathit{M}\mathit{n}\mathbf{=}\mathbf{5.0}$
$\mathbf{1}$	$1.157968$	$1.193940$	$1.231595$	$1.271069$	$1.312505$	$1.355506$
$\mathbf{3}$	$1.186461$	$1.229036$	$1.273689$	$1.320542$	$1.369785$	$1.421655$
$\mathbf{5}$	$1.215068$	$1.264189$	$1.315801$	$1.370025$	$1.427070$	$1.487212$
$\mathit{M}\mathit{n}\mathbf{=}\mathbf{10.0}$
$\mathbf{1}$	$1.071482$	$1.086595$	$1.101988$	$1.117675$	$1.133670$	$1.149983$
$\mathbf{3}$	$1.097523$	$1.118149$	$1.139200$	$1.160679$	$1.182592$	$1.204958$
$\mathbf{5}$	$1.123410$	$1.149688$	$1.176407$	$1.203679$	$1.231512$	$1.259933$

and

Table 5. Variation in $\theta \left(\eta \right)$ with $S$, $Mn$, and $Pr.$

$\mathit{E}\mathit{c}$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.05$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.06$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.07$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.08$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.09$	$\mathit{\theta }\left(1\right)$ $\mathit{P}\mathit{r}=0.1$
$\mathit{M}\mathit{n}\mathbf{=}\mathbf{5.0}$
$\mathbf{1}$	$1.046026$	$1.055634$	$1.065383$	$1.075275$	$1.085315$	$1.095504$
$\mathbf{3}$	$1.050679$	$1.061263$	$1.072002$	$1.082903$	$1.093967$	$1.105198$
$\mathbf{5}$	$1.055332$	$1.066890$	$1.078622$	$1.090531$	$1.102619$	$1.114891$
$\mathit{M}\mathit{n}\mathbf{=}\mathbf{10.0}$
$\mathbf{1}$	$1.017481$	$1.021032$	$1.024601$	$1.028187$	$1.031792$	$1.035416$
$\mathbf{3}$	$1.021958$	$1.026418$	$1.030902$	$1.035409$	$1.039940$	$1.044495$
$\mathbf{5}$	$1.026433$	$1.031804$	$1.037203$	$1.042631$	$1.048088$	$1.053575$

are given to compare the temperature profiles for different values of the unsteadiness parameter $S.$ In these tables, an increase in the Eckert number causes an increase in the temperature profiles due to the enhancement in the viscous dissipation.

The HAM requires $h$curves to draw convergent solution regions. In Figure 2, these curves are drawn to identify the region where convergent solutions for the velocity of the fluid can be constructed, while in Figure 3, velocity profiles are drawn for suitable values of the $h$ curves. Likewise, in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, the $h$ curves and corresponding temperature profiles can be seen under the influence of the variation in the unsteadiness magnetic field and the Eckert number. Comments on these trends have already been given when these values were tabulated in Table 3, Table 4 and Table 5.

4. Conclusions

In this article, we considered flow and heat transfer under the influence of viscous dissipation and a magnetic field. To conduct this study, we used the lie symmetry method to derive lie point symmetries for the flow equations, constructing a one-dimensional optimal system of subalgebras, invariants, and corresponding similarity transformations. We utilized these transformations to perform a reduction in the dependent and independent variables of the flow differential equations, which helped us to reduce the flow PDEs to ODEs. For the resulting ODEs, we used an analytic solution procedure known as the homotopy analysis method. We applied it to construct the analytic solutions that are presented with the help of graphs and tables. The lie algebra we used in this article has not been employed previously. The results obtained here are in agreement with the results already obtained for this flow, as the systems of ODEs we derived is the same system deduced in earlier studies.