Investigating Mesh Sensitivity in Linear and Non-Linear Buckling Analysis of Composite Cylindrical Shells †
Abstract
1. Introduction
2. Methodology
2.1. Model Description
2.2. Modeling
2.3. Meshing
2.4. Setting up Steps
2.5. Application of Loads and Boundary Conditions
2.6. Analysis
3. Results
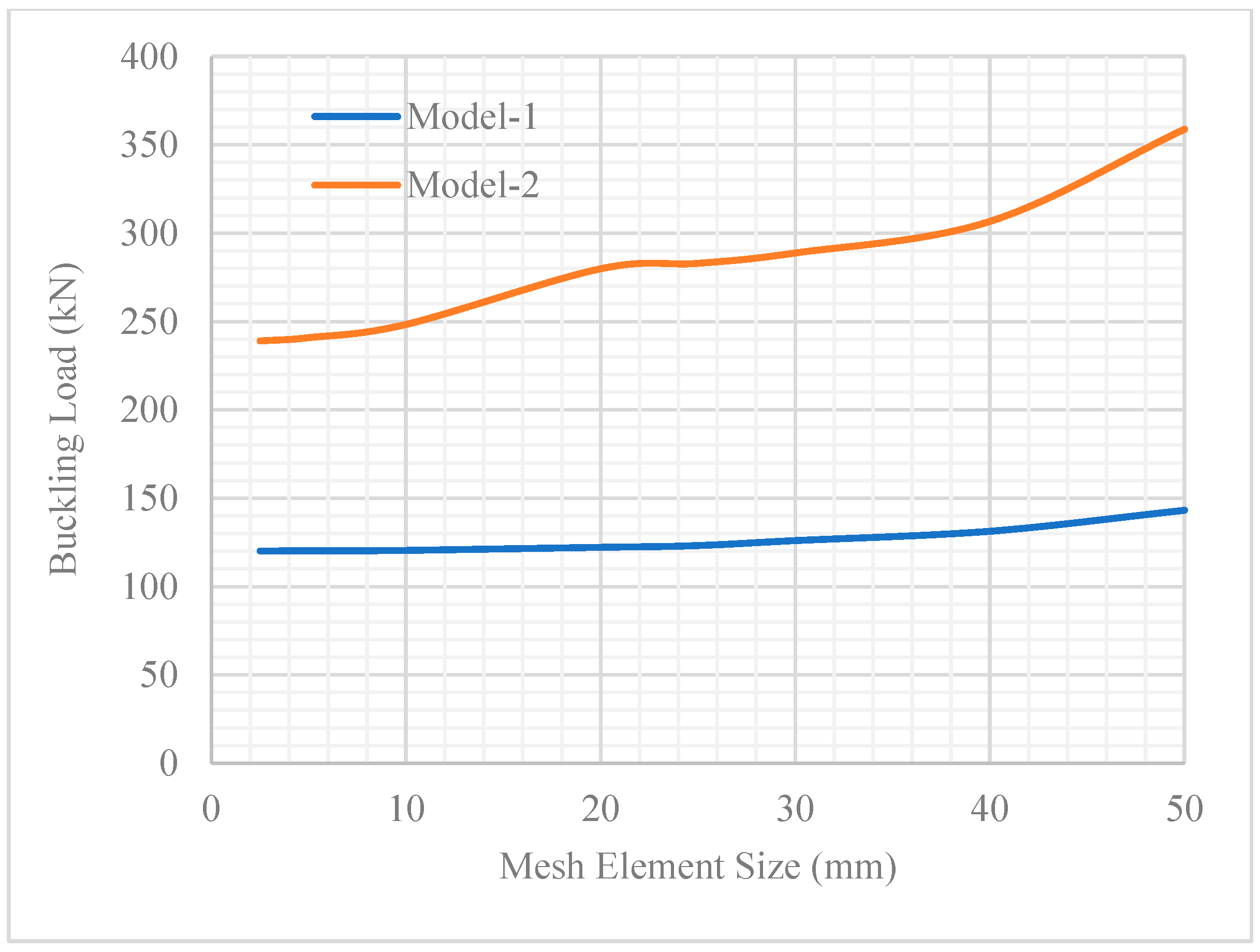
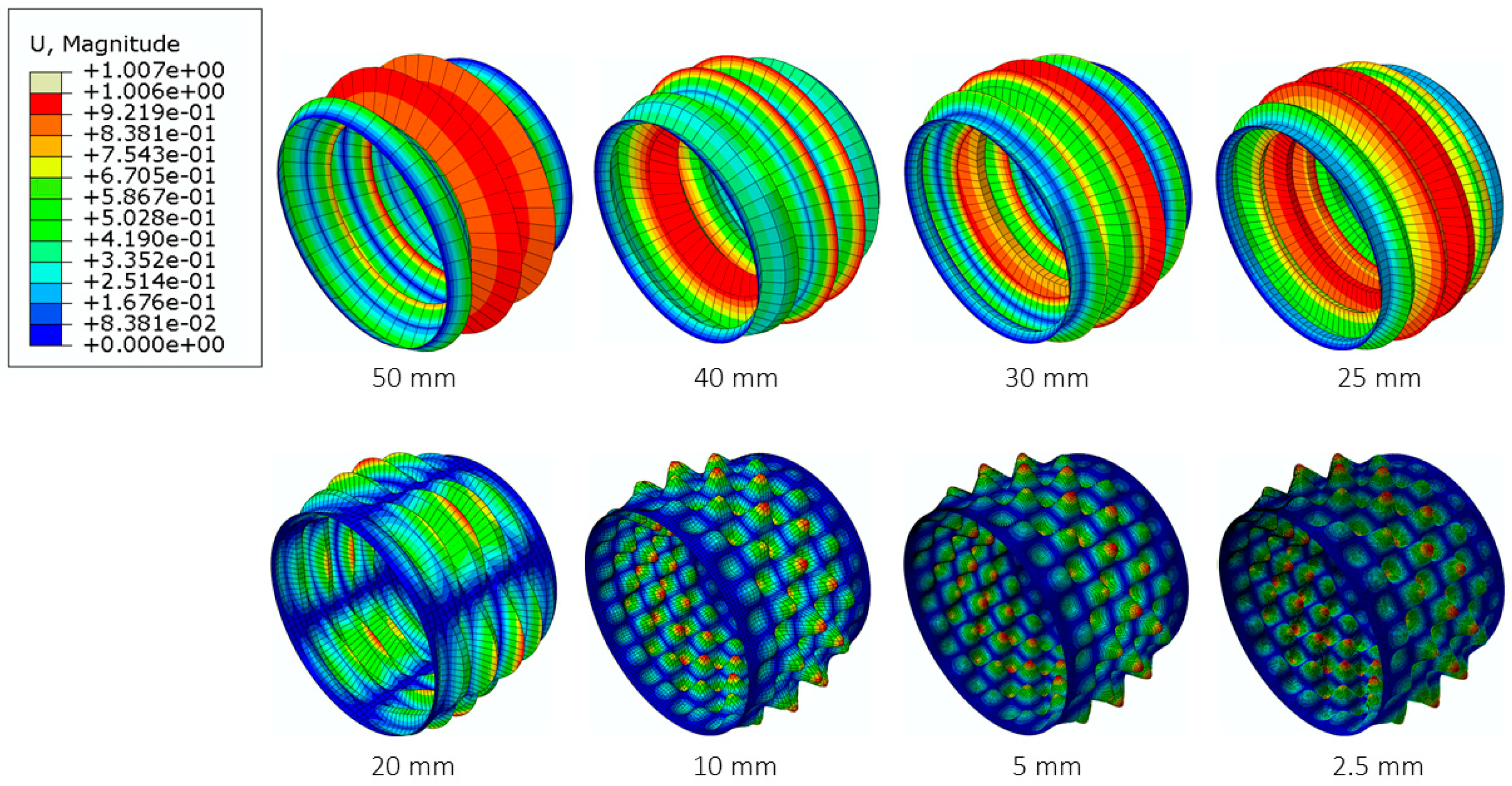
3.1. Linear Results
3.1.1. Model-1 (Linear Analysis)
3.1.2. Model-2 (Linear Analysis)
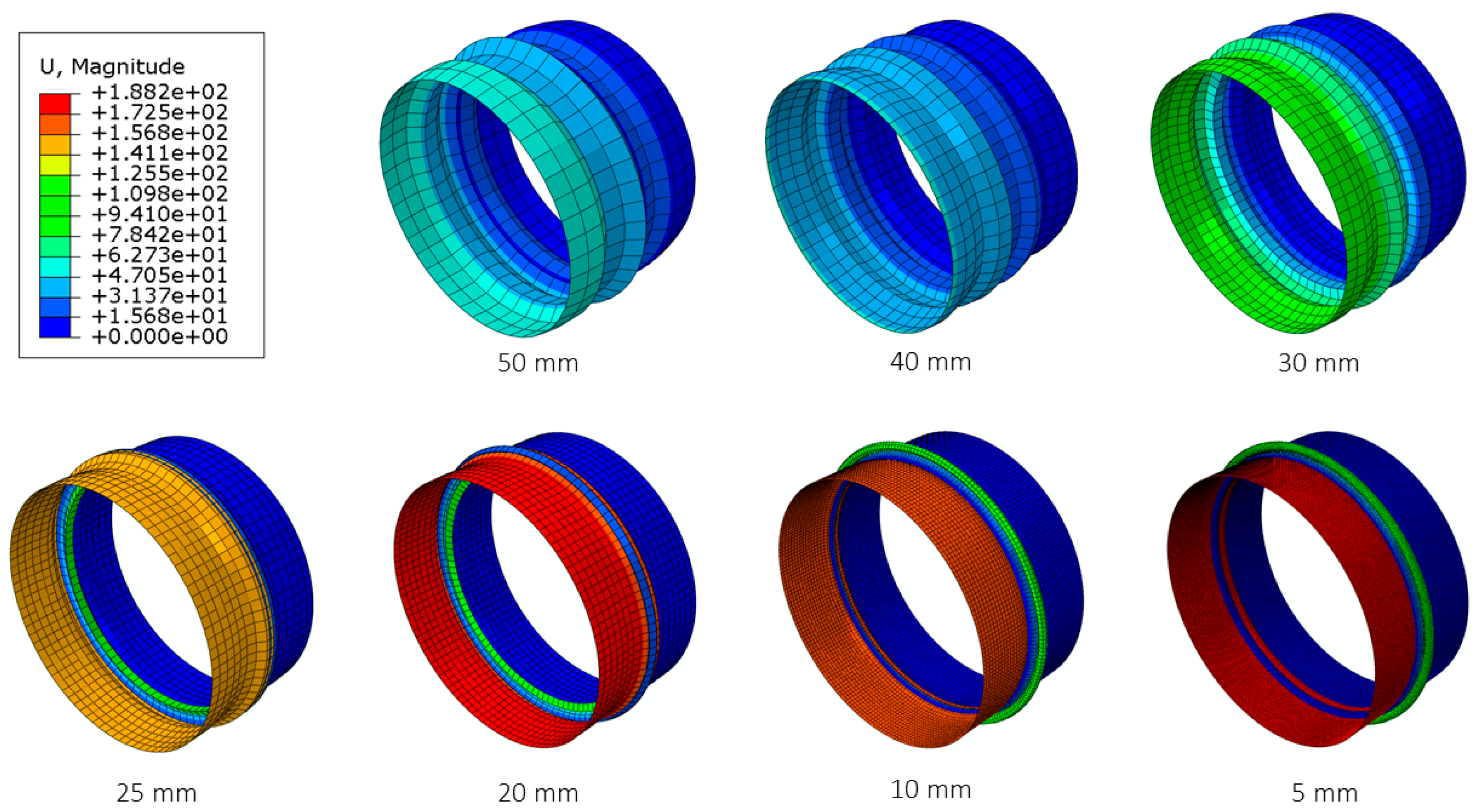
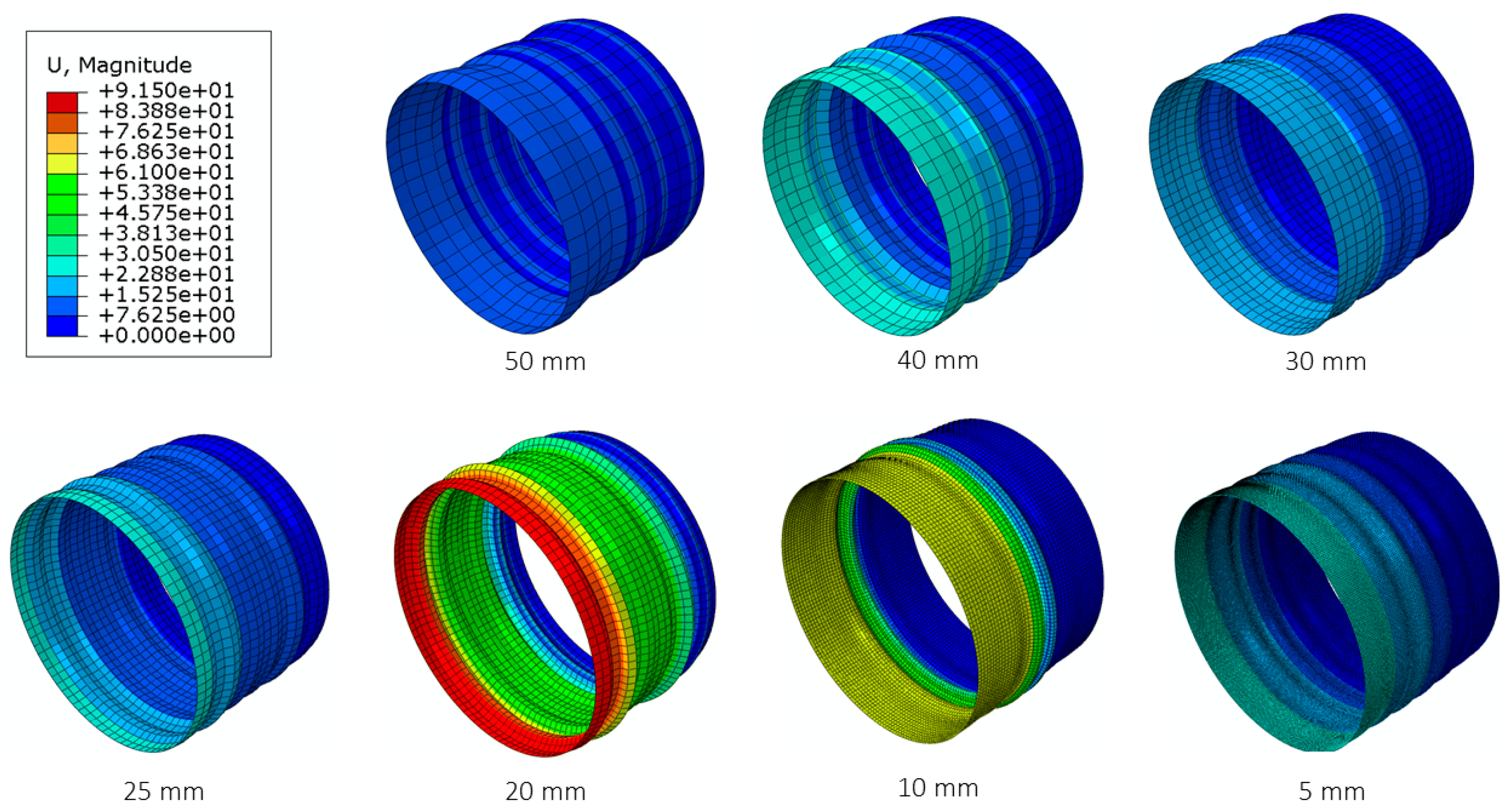
3.2. Non-Linear Results
3.2.1. Model-1 (Non-Linear Analysis)
3.2.2. Model-2 (Non-Linear Analysis)
4. Discussion
4.1. Comparison of Numerical Results
4.1.1. Model-1
4.1.2. Model-2
4.2. Error Analysis
4.3. Comparison with Analytical and Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thompson, J.M.T. Advances in shell buckling: Theory and experiments. Int. J. Bifurc. Chaos 2015, 25, 1530001. [Google Scholar] [CrossRef]
- Tsien, H.-S. A Theory for the Buckling of Thin Shells. J. Aeronaut. Sci. 1942, 9, 373–384. [Google Scholar] [CrossRef]
- Teng, J.G. Buckling of Thin Shells: Recent Advances and Trends. Appl. Mech. Rev. 1996, 49, 263–274. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C. Mechanical characterization of carbon fiber-reinforced plastic specimens for aerospace applications. In Mechanical and Physical Testing of Biocomposites, Fibre-Reinforced Composites and Hybrid Composites; Woodhead Publishing: Cambridge, UK, 2019; pp. 387–407. [Google Scholar]
- Mandal, P.; Calladine, C. Buckling of thin cylindrical shells under axial compression. Int. J. Solids Struct. 2000, 37, 4509–4525. [Google Scholar] [CrossRef]
- Khayal, O.E.S. Literature review on imperfection of composite laminated plates. J. Microsc. Ultrastruct. 2017, 5, 119–122. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhao, Q.; Qiao, P. A Critical Review on Buckling and Post-Buckling Analysis of Composite Structures. Front. Aerosp. Eng. 2013, 2, 157–168. (In English) [Google Scholar]
- Mugahed Amran, Y.H.; Alyousef, R.; Rashid, R.S.M.; Alabduljabbar, H.; Hung, C.-C. Properties and applications of FRP in strengthening RC structures: A review. Structures 2018, 16, 208–238. [Google Scholar] [CrossRef]
- Singh, S.K.; Chakrabarti, A. Buckling analysis of laminated composite plates using an efficient C0 FE model. Lat. Am. J. Solids Struct. 2012, 9, 1–13. [Google Scholar] [CrossRef]
- Dubey, R.K. Report on studying the effect of mesh density on finite element analysis and establish an optimal mesh density for finite element analysis of a bridge deck under the effect of self-weight and vehicular dynamic load. Int. J. Adv. Res. Ideas Innov. Technol. 2018, 9, 1–9. [Google Scholar]
- Zhuang, Z.; Liu, Z.; Cheng, B.; Liao, J. Extended Finite Element Method: Tsinghua University Press Computational Mechanics Series; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Liu, Y.; Glass, G. Effects of mesh density on finite element analysis. In Proceedings of the SAE 2013 World Congress & Exhibition Location, Detroit, MI, USA, 8 April 2013. SAE Technical Paper, 0148-7191. [Google Scholar] [CrossRef]
- Ghavidel, A.; Mousavi, S.R.; Rashki, M. The Effect of FEM Mesh Density on the Failure Probability Analysis of Structures. KSCE J. Civ. Eng. 2018, 22, 2370–2383. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, Y.; Zhou, L.; Zhang, J. Buckling characteristics of carbon fiber composite/aluminium alloy combined cylindrical shells under external hydrostatic pressure. Int. J. Press. Vessel. Pip. 2024, 208, 105125. [Google Scholar] [CrossRef]
- Choudhary, P.K. Optimal design of composite cylindrical shells subject to compression buckling strength. Multidiscip. Model. Mater. Struct. 2023, 19, 829–847. [Google Scholar] [CrossRef]
- Taraghi, P.; Zirakian, T.; Karampour, H. Parametric study on buckling stability of CFRP-strengthened cylindrical shells subjected to uniform external pressure. Thin-Walled Struct. 2021, 161, 107411. [Google Scholar] [CrossRef]
- Bisagni, C. Experimental Buckling of Thin Composite Cylinders in Compression. AIAA J. 1999, 37, 276–278. [Google Scholar] [CrossRef]
- Tahir, Z.U.R.; Mandal, P. Effect of asymmetric meshing on the buckling behavior of composite shells under axial compression. Int. J. Comput. Methods Eng. Sci. Mech. 2017, 18, 47–63. [Google Scholar] [CrossRef]




| Parameter | Values |
|---|---|
| Elastic Modulus E11 (MPa) | 52,000 |
| Elastic Modulus E22 (MPa) | 52,000 |
| Shear Modulus G12 (MPa) | 2350 |
| Poisson’s Ratio | 0.302 |
| Length (mm) | 520 |
| Diameter (mm) | 700 |
| Overall Thickness (mm) | 1.32 |
| Single Layer Thickness (mm) | 0.33 |
| Compressive Load (N) | 1 |
| Mesh Size (mm) | Buckling Load for Model-1 (N) | Buckling Load for Model-2 (N) |
|---|---|---|
| 50 | 143,222 | 358,851 |
| 40 | 131,368 | 306,694 |
| 30 | 126,116 | 288,828 |
| 25 | 123,236 | 282,976 |
| 20 | 122,318 | 279,925 |
| 10 | 120,551 | 248,417 |
| 5 | 120,297 | 240,911 |
| 2.5 | 120,236 | 239,080 |
| Mesh Size (mm) | Buckling Load for Model-1 (N) | Buckling Load for Model-2 (N) |
|---|---|---|
| 50 | 145,654 | 601,515 |
| 40 | 130,251 | 309,081 |
| 30 | 123,267 | 308,041 |
| 25 | 122,242 | 317,257 |
| 20 | 121,940 | 301,875 |
| 10 | 119,269 | 274,945 |
| 5 | 118,842 | 274,858 |
| Mesh Size (mm) | %Error for Linear Analysis (Model-1) | %Error for Non-Linear Analysis (Model-1) | %Error for Linear Analysis (Model-2) | %Error for Non-Linear Analysis (Model-2) |
|---|---|---|---|---|
| 50 | 20.78 | 22.83 | 49.52 | 150.63 |
| 40 | 10.78 | 9.84 | 27.79 | 28.78 |
| 30 | 6.36 | 3.95 | 20.34 | 28.35 |
| 25 | 3.93 | 3.09 | 17.91 | 32.19 |
| 20 | 3.15 | 2.83 | 16.64 | 25.78 |
| 10 | 1.66 | 0.58 | 3.51 | 14.56 |
| 5 | 1.45 | 0.22 | 0.38 | 14.52 |
| 2.5 | 1.4 | - | 0.38 | - |
| Experiment No. | Buckling Load for Model-1 (N) | Buckling Load for Model-2 (N) |
|---|---|---|
| 1 | 120,236 | 172,877 |
| 2 | 116,454 | 151,618 |
| 3 | 102,447 | 155,676 |
| 4 | 112,632 | 164,702 |
| Average | 112,942 | 161,218 |
| Result Type | Buckling Load for Model-1 (N) | Buckling Load for Model-2 (N) |
|---|---|---|
| Numerical Linear (Mesh size 5 mm) | 120,297 | 240,911 |
| Numerical Linear (Mesh size 2.5 mm) | 120,236 | 239,080 |
| Numerical Non-Linear (Mesh size 10 mm) | 119,269 | 274,945 |
| Numerical Non-Linear (Mesh size 5 mm) | 118,842 | 274,858 |
| Average Experimental | 112,942 | 161,218 |
| Analytical | 118,580 | 240,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatha, S.K.; Ali, M.S.; Butt, M.N.; Usman, M. Investigating Mesh Sensitivity in Linear and Non-Linear Buckling Analysis of Composite Cylindrical Shells. Mater. Proc. 2025, 23, 8. https://doi.org/10.3390/materproc2025023008
Chatha SK, Ali MS, Butt MN, Usman M. Investigating Mesh Sensitivity in Linear and Non-Linear Buckling Analysis of Composite Cylindrical Shells. Materials Proceedings. 2025; 23(1):8. https://doi.org/10.3390/materproc2025023008
Chicago/Turabian StyleChatha, Shahmeer Khalid, Muhammad Sher Ali, Muhammad Noman Butt, and Muhammad Usman. 2025. "Investigating Mesh Sensitivity in Linear and Non-Linear Buckling Analysis of Composite Cylindrical Shells" Materials Proceedings 23, no. 1: 8. https://doi.org/10.3390/materproc2025023008
APA StyleChatha, S. K., Ali, M. S., Butt, M. N., & Usman, M. (2025). Investigating Mesh Sensitivity in Linear and Non-Linear Buckling Analysis of Composite Cylindrical Shells. Materials Proceedings, 23(1), 8. https://doi.org/10.3390/materproc2025023008




