Comparative Study of Conical and Cylindrical Basins for Gravitational Water Vortex Turbines †
Abstract
1. Introduction
2. Working Model
2.1. Configurations of Basins
2.2. Conical and Cylindrical Basin
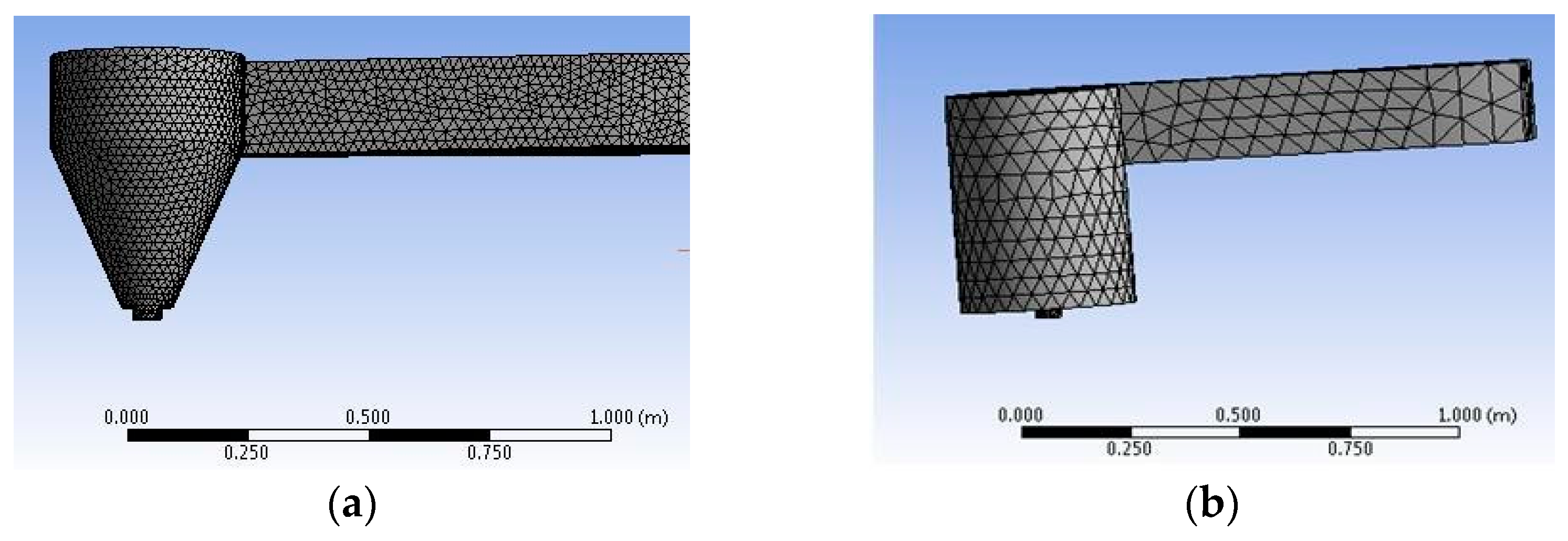
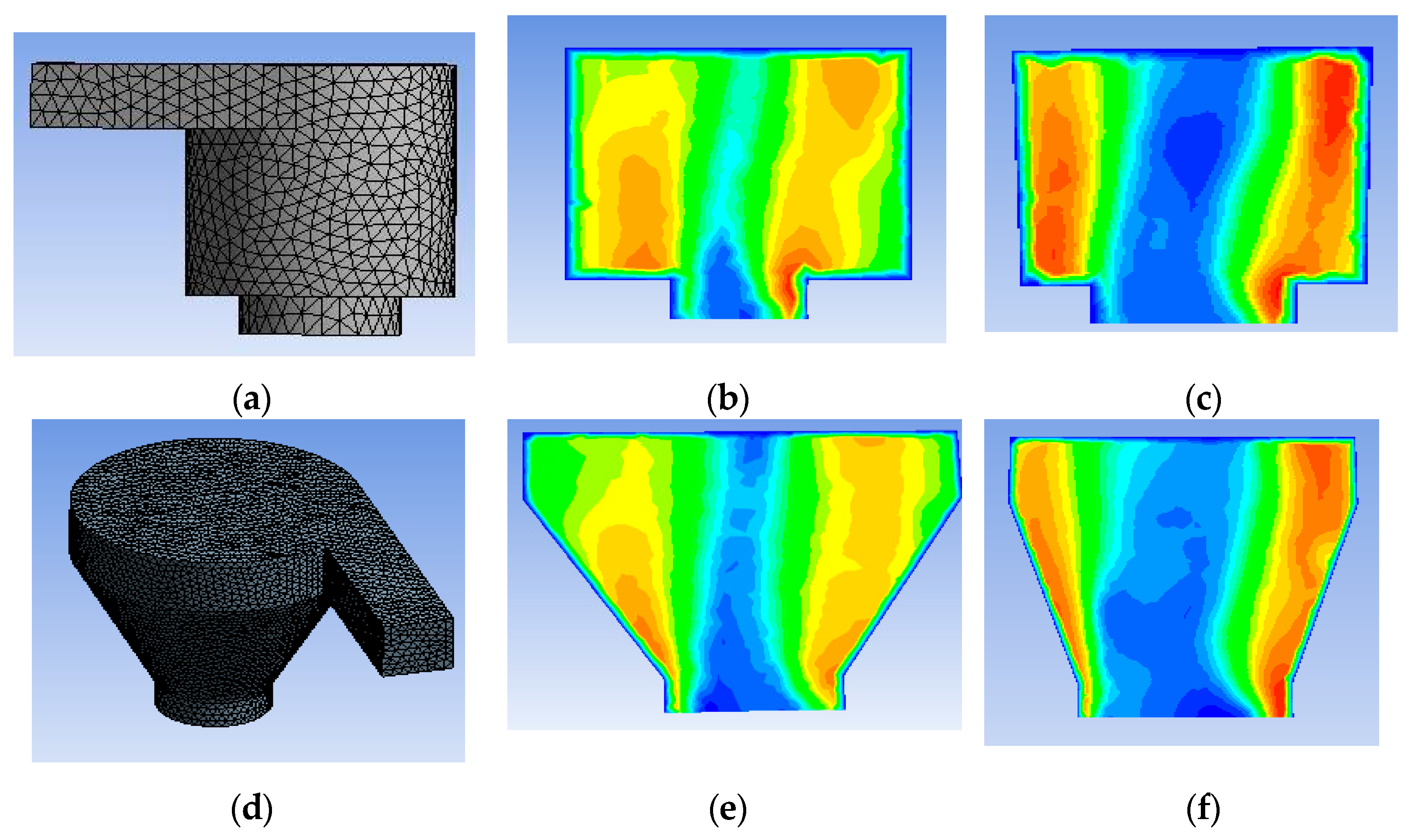
2.3. Model Development and Simulation Procedure
Initial Flow Condition for Conical and Cylindrical Basin
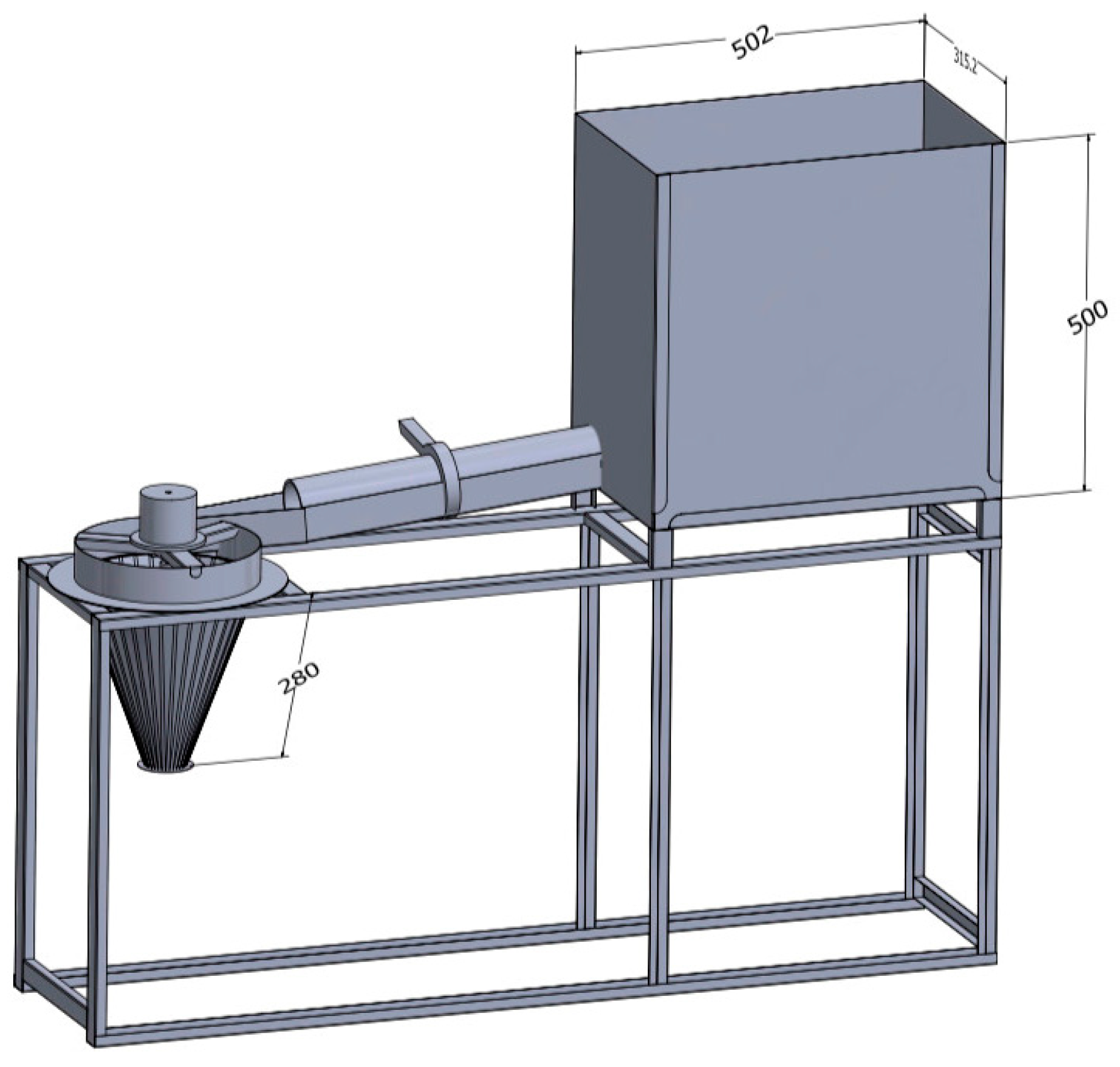
3. Experimental Setup
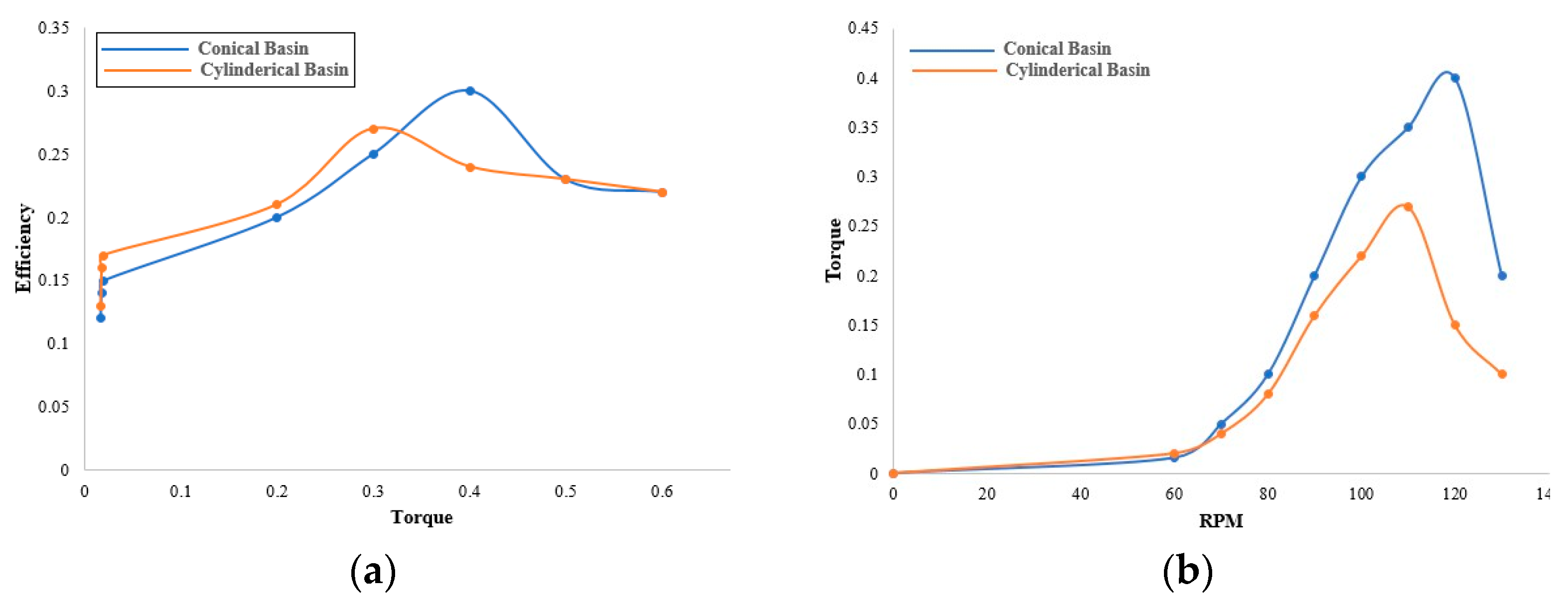
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dhakal, R.; Chaulagain, R.K.; Bajracharya, T.; Shrestha, S. Economic Feasibility Study of Gravitational Water Vortex Power Plant for the Rural Electrification of Low Head Region of Nepal and Its Comparative Study with Other Low Head Power Plant. In Proceedings of the 11th International Conference ASIAN Community Knowledge Networks for the Economy, Society, Culture, and Environmental Stability, Kathmandu, Nepal, 30 March–3 April 2015. [Google Scholar]
- Date, A.; Akbarzadeh, A. Design and cost analysis of low head simple reaction hydro turbine for Remote Area Power Supply. J. Renew. Energy 2009, 34, 409–415. [Google Scholar] [CrossRef]
- Arantes, C.C.; Fitzgerald, D.B.; Hoeinghaus, D.J.; Winemiller, K.O. Impacts of hydroelectric dams on fishes and fisheries in tropical rivers through the lens of functional traits. Curr. Opin. Environ. Sustain. 2019, 37, 28–40. [Google Scholar] [CrossRef]
- Sopian, K.; Ali, B.; Asim, N. Strategies for renewable energy applications in the Organization of Islamic Conference (OIC) countries. Renew. Renew. Sustain. Energy Rev. 2011, 15, 4706–4725. [Google Scholar] [CrossRef]
- Rahman, M.M.; Tan, J.H.; Fadzlita, M.T.; Muzammil, A.W.K. A review on the development of gravitational water vortex power plant as alternative renewable energy resources. In Proceedings of the International Conference on Materials Technology and Energy, Curtin University, Miri, Malaysia, 20–21 April 2017. [Google Scholar]
- Dhakal, S.; Nakarmi, S.; Pun, P.; Thapa, A.B.; Bajracharya, T.R. Development and testing of runner and conical basin for Gravitational Water Vortex Power Plant. J. Eng. Educ. 2014, 10, 140–148. [Google Scholar] [CrossRef]
- Power, C.; McNabola, A.; Coughlan, P. A parametric experimental investigation of the operating conditions of gravitational vortex hydropower (GVHP). J. Clean Energy Technol. 2015, 4, 112–119. [Google Scholar] [CrossRef]
- Zotlöterer, Smart Energy Systems. Available online: http://www.zotloeterer.com/welcome/gravitation-water-vortex-power-plants/zotloeterer-turbine/ (accessed on 13 September 2023).
- Wanchat, S.; Suntivarkon, R. Preliminary design of a vortex pool for electrical generation. Adv. Sci. Lett. 2012, 13, 173–177. [Google Scholar] [CrossRef]
- Paish, O. Small hydro power: Technology and current status. Renew. Sustain. Energy Rev. 2002, 6, 537–556. [Google Scholar] [CrossRef]
- Ali, M.H. Experimental comparison study for Savonius wind turbine of two & three blades at low wind speed. Int. J. Sci. Eng. 2013, 3, 2978–2986. [Google Scholar]
- Nishi, Y.; Inagaki, T. Performance and flow field of a gravitation vortex type water turbine. Int. J. Rotating Mach. 2017, 2017, 2610508. [Google Scholar] [CrossRef]
- Shabara, H.M.; Yaakob, O.B.; Ahmed, Y.M.; Elbatran, A.H. CFD simulation of water gravitation vortex pool flow for mini hydropower plants. J. Teknol. 2015, 74, 77–78. [Google Scholar] [CrossRef]
- Gheorghe-Marius, M.; Tudor, S. Energy capture in the gravitational vortex water flow. J. Mar. Technol. Environ. 2013, 1, 89. [Google Scholar]
- Kueh, T.C.; Beh, S.L.; Ooi, Y.S.; Rilling, D.G. Experimental study to the influences of rotational speed and blade shape on water vortex turbine performance. J. Phys. Conf. Ser. 2017, 822, 012066. [Google Scholar] [CrossRef]
- Wanchat, S.; Suntivarakorn, R.; Wanchat, S.; Tonmit, K.; Kayanyiem, P. A parametric study of a gravitation vortex power plant. Adv. Mater. Res. 2013, 805–806, 811–817. [Google Scholar] [CrossRef]
| Models | Elements | Nodes | Basin Diameter (mm) | Outlet Diameter (mm) | Height (mm) | Outlet Flow Velocity (m/s) |
|---|---|---|---|---|---|---|
| 1 | 24440 | 4762 | 1000 | 400 | 900 | 4.907 |
| 2 | 25083 | 4874 | 1000 | 500 | 900 | 3.99 |
| 3 | 24805 | 4838 | 1000 | 600 | 900 | 4.37 |
| Models | Elements | Nodes | Basin Diameter (mm) | Outlet Diameter (mm) | Height (mm) | Outlet Flow Velocity (m/s) |
|---|---|---|---|---|---|---|
| 1 | 86608 | 17250 | 1000 | 400 | 900 | 6.74 |
| 2 | 91707 | 17909 | 1000 | 500 | 900 | 3.93 |
| 3 | 96944 | 18891 | 1000 | 600 | 900 | 4.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zafar, U.; Javid, W.; Jamil, F.; Iqbal, S.; Ahmed, S.; Aziz, A.; Mehmood, T. Comparative Study of Conical and Cylindrical Basins for Gravitational Water Vortex Turbines. Mater. Proc. 2024, 17, 30. https://doi.org/10.3390/materproc2024017030
Zafar U, Javid W, Jamil F, Iqbal S, Ahmed S, Aziz A, Mehmood T. Comparative Study of Conical and Cylindrical Basins for Gravitational Water Vortex Turbines. Materials Proceedings. 2024; 17(1):30. https://doi.org/10.3390/materproc2024017030
Chicago/Turabian StyleZafar, Usman, Waqas Javid, Furqan Jamil, Shahid Iqbal, Sikander Ahmed, Abdul Aziz, and Tayyab Mehmood. 2024. "Comparative Study of Conical and Cylindrical Basins for Gravitational Water Vortex Turbines" Materials Proceedings 17, no. 1: 30. https://doi.org/10.3390/materproc2024017030
APA StyleZafar, U., Javid, W., Jamil, F., Iqbal, S., Ahmed, S., Aziz, A., & Mehmood, T. (2024). Comparative Study of Conical and Cylindrical Basins for Gravitational Water Vortex Turbines. Materials Proceedings, 17(1), 30. https://doi.org/10.3390/materproc2024017030






