Efficient Detection of Galileo SAS Sequences Using E6-B Aiding ^†

Abstract

Galileo Signal Authentication Service (SAS) is an assisted signal authentication capability under development by Galileo, designed to enhance the robustness of the European Global Navigation Satellite System (GNSS) against malicious attacks like spoofing. It operates by providing information about some fragments of the unknown spreading codes in the E6-C signal. Unlike other approaches, Galileo SAS uniquely employs Timed Efficient Stream Loss-tolerant Authentication (TESLA) keys provided by Open Service Navigation Message Authentication (OSNMA) in the E1-B signal for decryption, avoiding the need for key storage in potentially compromised receivers. The encrypted fragments are made available to the receivers before the broadcast of the E6-C signal, along with their broadcast time. However, if the receiver lacks an accurate time reference, searching for these fragments—which typically last for milliseconds and have periodicities extending to several seconds—can become impractical. In such cases, the probability of detection is severely diminished due to the excessively large search space that results. To mitigate this, initial estimates for the code phase delay and Doppler frequency can be obtained from the E1-B signal. Nevertheless, the alignment between E1-B and E6-C is not perfect, largely due to the intrinsic inter-frequency biases they exhibit. To mitigate this issue, we can leverage auxiliary signals like E6-B, processed by High Accuracy Service (HAS)-compatible receivers. This is a logical choice as E6-B shares the same carrier frequency as E6-C. This could help in obtaining more precise estimates of the location of the encrypted fragments and improving the probability of detection, resulting in enhanced robustness for the SAS authentication process. This paper presents a comparison of uncertainties associated with the use of the E1-B and E6-B signals, based on real data samples obtained with a custom-built Galileo SAS evaluation platform based on Software Defined Radio (SDR) boards. The results show the benefits of including E6-B in SAS processing, with minimal implementation cost.

1. Introduction

Spoofing represents a significant concern within satellite navigation, as it can manipulate the location information of any GNSS receiver. The recent launch of OSNMA [1], provided free of charge by Galileo, has emerged as a pivotal development in this domain by offering authentication of the navigation message. To complement this encryption at data (symbol) level, Galileo is currently testing a new service known as SAS, a proposal of CAS (Commercial Authentication Service) aimed at providing protection at signal (chip) level. For this purpose, SAS is based on the E6-C Galileo signal, whose spreading codes are anticipated to be encrypted soon. Galileo SAS was previously known as Galileo ACAS (Assisted CAS).

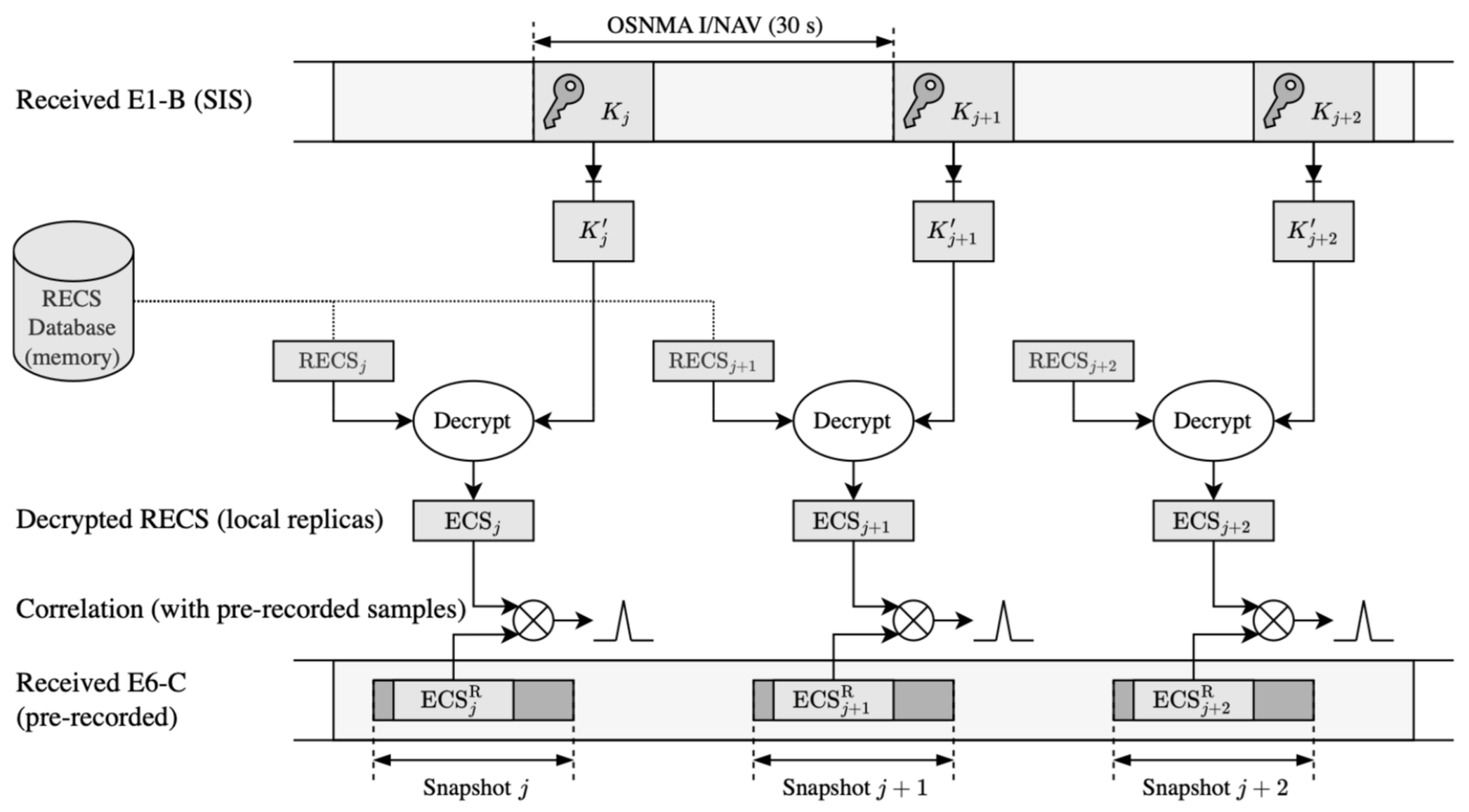
The operation of Galileo SAS, detailed in [2], can be divided into two parts. From the system side, segments of the encrypted E6-C, called Encrypted Code Sequences (ECS), are re-encrypted using TESLA keys from OSNMA in the E1-B signal. These Re-Encrypted Code Sequences (RECSs), along with other information needed for PVT computation, are stored on a public server like the GNSS Service Center (GSC) before the Galileo signals are broadcast.

On the receiver side, the user downloads the necessary RECS files from the server to operate autonomously for a desired period. When the E6-C signal is broadcast, the receiver captures a snapshot around the expected ECS time, which can be determined from the RECS file headers. Once the TESLA key is released in the E1-B signal, it is used to decrypt the RECS and obtain the ECS, which serves as a local replica for correlating with the recorded E6 samples. If the ECS is detected during acquisition, the user can authenticate the received signal if certain conditions are met [2]. Figure 1 shows the receiver’s side of the SAS operation.

This approach facilitates the computation of an authenticated PVT without modifying Galileo’s current signal plan or requiring the receiver to store any secret key [3]. However, as discussed in [4], providing only specific fragments of the E6-C signal to the receiver requires optimizing the detection of the ECS. Given the non-repeating nature of the encrypted E6-C signal, the search for a small fragment—RECS are expected to last only a few milliseconds—within large snapshots could result in poor detection capabilities.

Having an accurate time reference to align the broadcast time of the ECS/RECS with the samples recorded by the receiver allows for minimizing the snapshot size. Without such precision, the snapshot duration must be extended to account for time reference uncertainty [4]. To avoid reliance solely on the receiver clock, the nominal operating mode of SAS is expected to use the E1-B signal to infer an accurate time reference, as this signal is already used to obtain the required TESLA keys. This can be achieved by using PVT computed from the E1-B signal or from the transmit GST contained in E1-B samples [5]. This method assumes the E1-B signal is trustworthy; however, in the event of a spoofing attack that compromises this assumption, additional safeguards must be considered, as analyzed in [6].

The E1-B signal is also employed in the proposed SAS authentication process [2]. This mechanism uses the trusted ranging signal (E6-C) as an anchor for another signal from the same satellite (E1-B for the SAS nominal mode). If the difference between the measurements to the anchor and the other signal falls below a predefined threshold, an unauthenticated measurement may be deemed trustworthy and usable for PVT [7].

However, the alignment between the E1-B and E6-C components is not perfect, primarily due to inter-frequency biases. Consequently, using the E6-B signal instead of, or in addition to, the E1-B signal for SAS could help to reduce the authentication threshold and yield more precise estimates. This aspect is further analyzed in Section 2.

Nevertheless, the use of E6 extends beyond refining the authentication process. It could also be used to obtain a sufficiently accurate time reference using the E6 snapshot recorded by the receiver, provided that the required TESLA keys for decrypting the RECS can be accessed through an alternative channel (e.g., a remote server). This approach would permit the avoidance of processing the E1-B signal, enabling the use of simpler, single-frequency receivers for Galileo SAS. The E6-B assisted snapshot mode for SAS is analyzed in Section 3.

The results that support the preceding analysis are detailed in Section 4, using real data snapshots acquired via a custom-built evaluation platform for Galileo SAS, which is described in [8]. Finally, the paper’s conclusions are presented in Section 5.

2. Detecting Galileo SAS Sequences Using Handover from E6-B

The non-repeating nature of E6-C has important implications for the receiver. Without further assistance, the acquisition search space could be prohibitively large. This is why, in SAS, the use of an auxiliary signal is assumed, which helps to reduce this search space. The natural choice for this auxiliary signal is the E1-B component, as it is the signal that provides the TESLA keys required for the RECS decryption. Indeed, the Galileo SAS specification outlines the corresponding E1-E6 BGD files, which are made available at the GSC along with the companion RECS files. These resources can be effectively leveraged by the receiver.

Therefore, in a nominal Galileo CAS operation, the receiver would take advantage of the measurements provided by E1-B—specifically, the code phase delay and the Doppler frequency, denoted ${\tau }_{\mathrm{E}1\mathrm{B}}$ and $f_{\mathrm{E}1\mathrm{B}}$, respectively—to derive the measurement estimates for E6-C, denoted ${\widehat{\tau }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}$ and ${\widehat{f}}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}$, respectively. These estimates can be obtained by adding the corresponding offsets between E1-B and E6-C signals:

$${\widehat{\tau }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}={\tau }_{\mathrm{E}1\mathrm{B}}+{\widehat{\delta }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}$$

(1)

$${\widehat{f}}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}=f_{\mathrm{E}1\mathrm{B}}+{\widehat{∆f}}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}$$

(2)

The difference in Doppler frequency measurements between the two bands is mainly determined by the ratio of their carrier frequencies, denoted $f_{c,i}$ for the $i$-th band [4]:

$${\widehat{∆f}}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}=f_{\mathrm{E}1\mathrm{B}}\left({\displaystyle \frac{f_{c,\mathrm{E}6}}{f_{c,\mathrm{E}1}}}-1\right)$$

(3)

The offset in code phase measurements between the two bands has three main contributors: satellites bias or Broadcast Group Delay (BGD), ionospheric effect, and hardware bias, denoted ${\widehat{\delta }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}^{\mathrm{BGD}}$, ${\widehat{\delta }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}^{\mathrm{iono}}$, and ${\widehat{\delta }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}^{\mathrm{HWB}}$, respectively. This offset can be expressed as [2]:

$${\widehat{\delta }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}={\widehat{\delta }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}^{\mathrm{BGD}}+{\widehat{\delta }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}^{\mathrm{iono}}+{\widehat{\delta }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}^{\mathrm{HWB}}$$

(4)

Notably, the ionosphere also affects frequency estimation, as specified in (3), but this impact depends on the rate of change of TEC over time, not its absolute value [4].

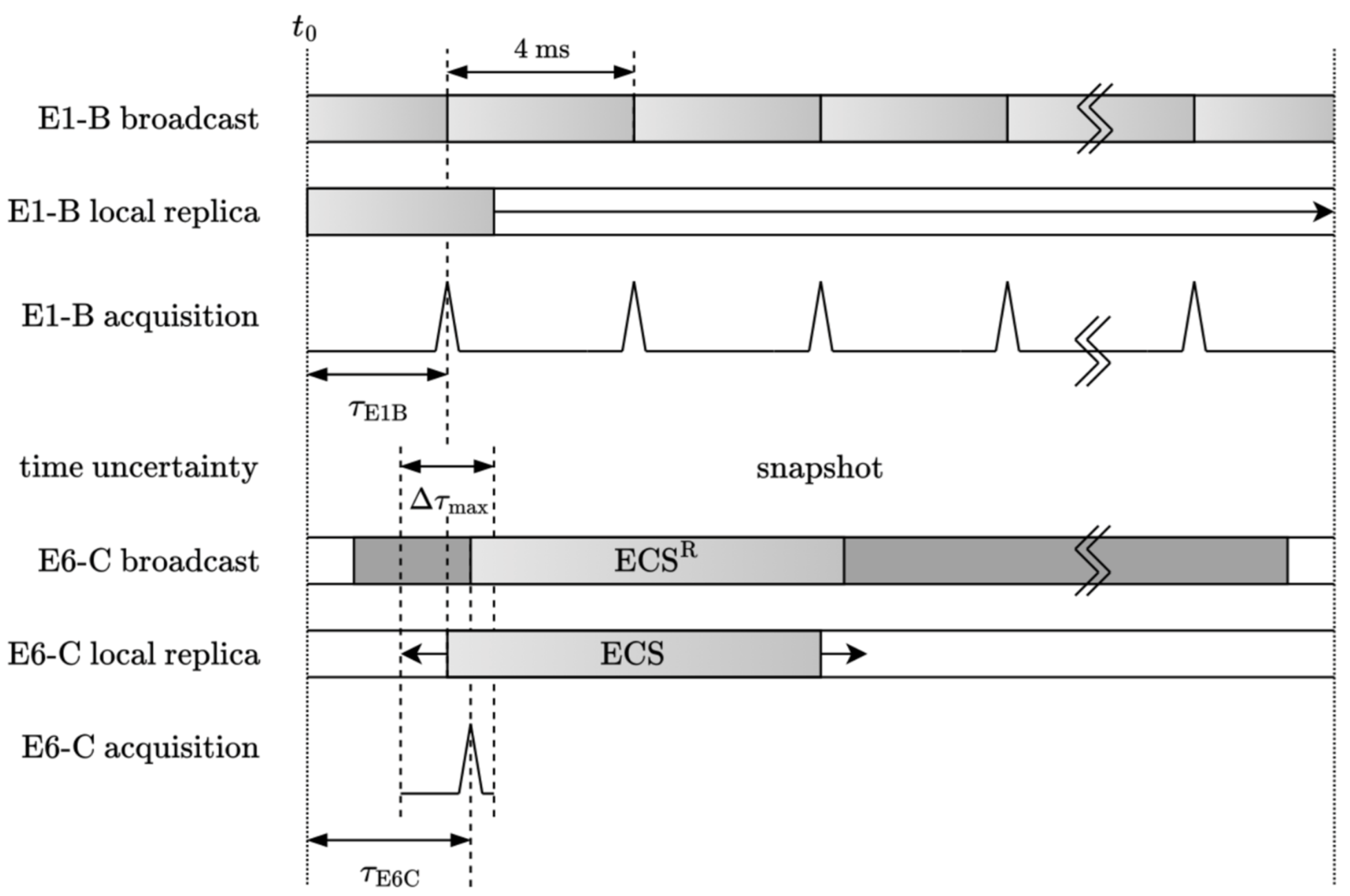
In an ideal scenario, transitioning from the E1-B to the E6-C provides the receiver with the exact location of the ECS^R in the recorded snapshot. However, in practice, due to the ionospheric and multipath effects, in addition to the potential errors in the previous estimates, the receiver must account for an uncertainty. This will define the search space for the Cross Ambiguity Function (CAF) during the acquisition. The number of search cells will be the product of the cells needed for both the code phase delay and Doppler frequency.

Nevertheless, the Doppler search can generally be avoided, and using the Doppler bin provided by the E1-B measurement should suffice. This results in computing only a limited number of cells in the time domain due to code phase delay uncertainty, denoted ${∆\tau }_{\max }$. An example is shown in Figure 2 for the case of the code phase delay measurements.

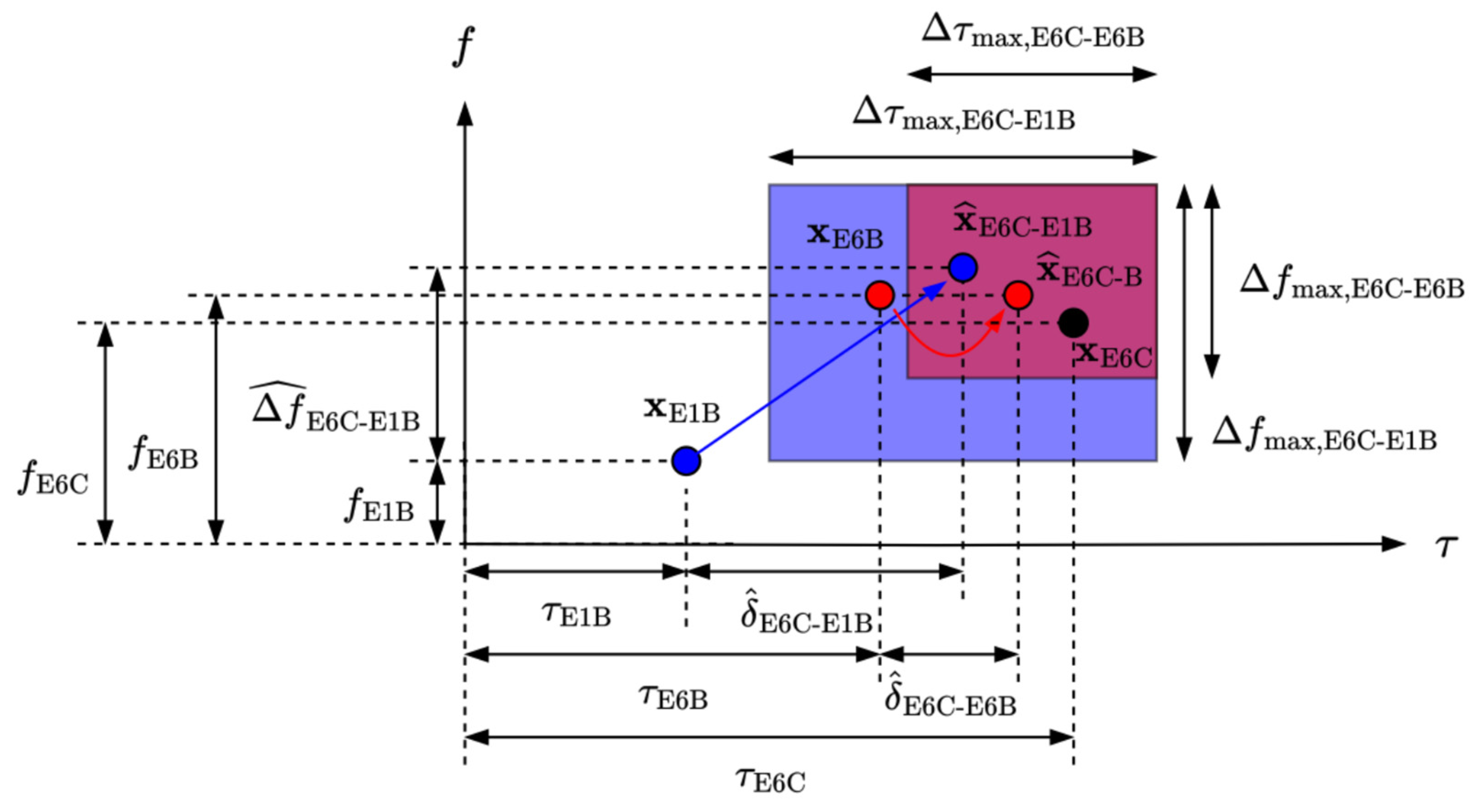
Using the E6-B component as the auxiliary signal further reduces the uncertainty associated with E6-C measurements. This does not require additional hardware within the receiver, as E6-B shares the same frequency as E6-C. The main advantage of using E6-B over E1-B is that a handover from E6-B does not involve any inter-frequency biases, leading to more precise estimates, particularly in relation to the ionosphere contributions. This is depicted in Figure 3. Indeed, the term $∆f_{\max ,\mathrm{E}6\mathrm{C}-\mathrm{E}6\mathrm{B}}$ can be neglected in practice, as differences, if any, are likely only due to different processing of different of the E6-C and E6-B.

The accuracy of these estimates has a direct impact on the authentication mechanism used in the nominal operating mode of Galileo SAS. Specifically, the measurement is considered authenticated only if the difference between the code phase delay measured on E6-C and the code phase delay estimated for E6-C from E1-B is lower than a predefined threshold, denoted ${\gamma }_{\mathrm{auth}}$ [2]. The same applies for the code phase estimated from E6-B:

$$\left|{\tau }_{\mathrm{E}6\mathrm{C}}-{\widehat{\tau }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}1\mathrm{B}}\right|\le {\gamma }_{\mathrm{auth}}\to \mathrm{measurement} \mathrm{authenticated}$$

(5)

$$\left|{\tau }_{\mathrm{E}6\mathrm{C}}-{\widehat{\tau }}_{\mathrm{E}6\mathrm{C}\text{-}\mathrm{E}6\mathrm{B}}\right|\le {\gamma }_{\mathrm{auth}}^{\prime }\to \mathrm{measurement} \mathrm{authenticated}$$

(6)

Since the threshold depends on the characterization of the error contributions in the estimation process, it becomes evident that using an estimate of E6-C from E6-B could facilitate a reduction in the threshold (${\gamma }_{\mathrm{auth}}^{\prime }\le {\gamma }_{\mathrm{auth}}$), thereby enhancing the authentication mechanism. 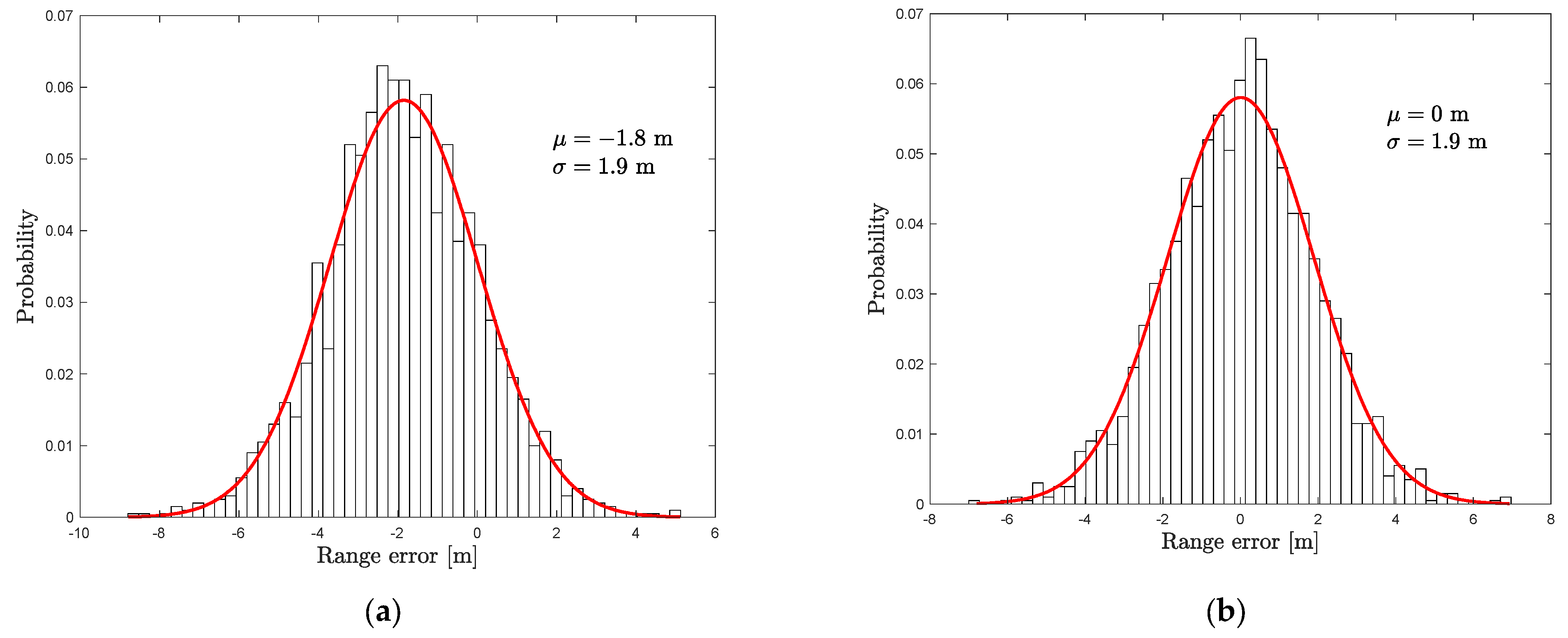A comparison of the code phase delays estimated from E1-B and E6-B is presented in Section 4. The results provided corroborate the analysis discussed previously.

3. Snapshot Positioning Using E6-B

The main goal of SAS is to authenticate the PVT, but the specific method of obtaining this PVT will vary depending on the receiver’s implementation. In the nominal operating mode of SAS, the E1-B signal can be used to obtain the PVT, which could subsequently be authenticated with E6-C if the corresponding ECS is found where expected. Such an approach could yield high accuracy in position determination, as the receiver will be tracking the E1-B signal. However, this method requires the use of dual-frequency receivers that process both E1-B and E6-C signals and account for the inter-frequency biases between them to accurately estimate the code phase delay and Doppler frequency, as discussed in Section 2.

However, single-frequency SAS receivers can be considered if the E6-B signal is used instead of E1-B. In this approach, it is assumed that the TESLA keys required to decrypt the RECS are provided through alternative means (i.e., remote server) rather than through processing E1-B. With this setup, the receiver relies on the snapshot of E6 samples it records to compute the PVT, as this snapshot contains both E6-B and E6-C components.

Snapshot positioning entails certain nuances compared to the conventional “acquisition and tracking” approach, such as peak interpolation and block-wise implementation. For more details, see Chapter 9 of [9]. The accuracy of the PVT derived from the snapshot largely depends on the snapshot size and the carrier bandwidth, which, for E6-B, is substantial—approximately 10 MHz two-sided bandwidth for the main lobe.

3.1. E6 Snapshot Size

The size of the E6 snapshot is critical for the accuracy of snapshot-based positioning in Galileo SAS. This size is mainly influenced by two factors: the RECS configuration and the accuracy of the time reference available at the receiver. According to the latest Galileo SAS specification [10], RECS parameters affecting snapshot size include the number of satellites being tracked and the chosen randomization settings. Since RECS are provided per satellite, more satellites require a larger snapshot size to account for variations in propagation delays and satellite clock offsets. For Galileo, propagation delays span about 20 ms. Depending on randomization parameters, the ECS may be transmitted at the specified broadcast time or delayed by a few milliseconds. Considering these factors, snapshot sizes typically range from 25 to 150 ms.

Table 1. Examples of snapshot sizes for different SAS configurations. The definition of the parameters RAND and KDI can be found in the latest Galileo SAS specification published (v1.2) [10].

RECS Length	RAND	KDI	Snapshot Length
4 ms	0	0	~25 ms
4 ms	0	2	~50 ms
16 ms	1	0	~100 ms
16 ms	1	2	~150 ms

illustrates snapshot sizes for various SAS configurations.

3.2. Comparison of E1-B Tracking with E6-B Snapshot Acquisition Accuracy

Depending on receiver processing, the accuracy from the limited E6-B snapshot samples may be lower than that from continuous E1-B signal tracking. However, from an SAS perspective, the accuracy provided by E6-B snapshot acquisition may be sufficient for many applications, where an authenticated solution is more important than precise PVT.

Next, we provide a preliminary analysis of the expected accuracies from both approaches. For continuous tracking of the E1-B signal, we refer to the simplified model in (7). The selected parameters are typical for a conventional commercial receiver: 0.1 chips for early-late spacing, 40 dB-Hz of $C/N_0$, and 1 Hz for DLL bandwidth (see Chapter 4 of [9]). The $K$ factor measures the sharpness of the correlation curve relative to a Binary Pulse Shift Keying (BPSK) signal. For Binary Offset Carrier (BOC) (1,1) processing of E1-B, this factor is three. The chip period $T_c$ is about 1 µs for E1-B [11], with $c$ representing the speed of light. A refined model is discussed in Chapter 5 of [12], which offers a general expression for the thermal noise code tracking jitter for a noncoherent Delay Lock Loop (DLL) discriminator.

$${\sigma }_{\mathrm{DLL}}\approx c{T}_c\sqrt{{\displaystyle \frac{B_{\mathrm{D}\mathrm{L}\mathrm{L}} d_{\mathrm{E}-\mathrm{L}}}{2 KC/N_0}}}\approx 0.5 [\mathrm{m}]$$

(7)

For snapshot acquisition on E6-B, the Cramér–Rao Lower Bound (CRLB) for time delay estimation can be applied (see Chapter 3 of [13]). This sets a lower bound for the variance of time delay using Maximum Likelihood Estimation (MLE), which is equivalent to the estimation of the code phase delay by comparing the received signal with all possible delay values during the receiver’s acquisition stage. This bound depends on the Signal-to-Noise (SNR) ratio at the correlator’s output, given by the $\mathrm{C}/{\mathrm{N}}_0$, the coherent integration time used for the correlation ($T_{\mathrm{int}}$), and the quadratic mean square bandwidth (Gabor or Mean Square bandwidth, $B_{\mathrm{ms}}$). Thus, the ranging accuracy for snapshot positioning can be expressed as:

$${\sigma }_{\mathrm{snp}}\ge c\sqrt{{\displaystyle \frac{1 }{2 C/N_0 T_{\mathrm{int}} B_{\mathrm{ms}} }}} [\mathrm{m}]$$

(8)

Alternative approaches can be considered to derive specific expressions of the CRLB for the GNSS signals (see Appendix D of [14]).

Table 2. Maximum code phase delay accuracies attainable for various E6 snapshot sizes.

Snapshot Size	C/N0	Accuracy (σsnp)
25 ms	45 dB-Hz	0.7 m
25 ms	40 dB-Hz	1.3 m
50 ms	40 dB-Hz	0.9 m
100 ms	40 dB-Hz	0.6 m
100 ms	35 dB-Hz	1.1 m
150 ms	35 dB-Hz	0.9 m

shows the achievable accuracies for different combinations of snapshot sizes and $C/N_0$’s ratios, assuming a 10 MHz receiver bandwidth that enables the capture of the entire main lobe of the E6-B signal spectrum.

In the absence of data symbols, non-coherent integration is required for E6-B, resulting in some square losses compared to coherent integration. However, these losses are negligible for the $C/N_0$ values in this analysis and primarily affect indoor scenarios. Nonetheless, the accuracy remains comparable to that of a DLL, mainly due to the high Gabor bandwidth of the E6-B signal.

4. Results

4.1. Evaluation Platform and Test Samples

To support the theoretical analysis presented in previous sections, we next provide results using real data samples obtained with a custom-built evaluation platform designed specifically for Galileo SAS. This platform employs bladeRF Software-Defined Radio (SDR) boards from Nuand, specifically the micro 2.0 xA4/xA5 models, which meet the specifications necessary to evaluate the SAS performance. A comprehensive description of this platform can be found in [8]. The real datasets used in this study comprise two snapshots of samples (E1 + E6) recorded synchronously with the evaluation platform. The recording spot was a rural area located near Girona, Spain, at a latitude of 41°59′35″ N (41.9932) and a longitude of 2°47′43″ E (2.7954). Two datasets are used in this paper, as shown in

Table 3. Information about the real datasets used in the paper.

Dataset ID	Recording Date/Time	Duration	Sampling Rate
D1	22 February 2023 17:24 (GMT)	10 s	60 MHz
D2	14 April 2023 14:21 (GMT)	3.2 s	20 MHz

.

4.2. E6-C vs. E6-B Code Phase Delay Comparison

The initial results analyze the alignment of code phase delays, which is crucial for the Galileo SAS nominal operating mode. This alignment reduces the acquisition search space and affects the authentication process. The dataset used (D1) was collected in a clear-sky scenario with an estimated $\mathrm{C}/{\mathrm{N}}_0$ of at least 45 dB-Hz. Snapshots from the SDR platform are processed with a custom MATLAB R2024b simulator to obtain estimates for E6-C and the auxiliary signal (E1-B or E6-B). The snapshots are segmented into smaller chunks for individual processing, where acquisition is performed for the required RECS length to obtain code phase delay and Doppler frequency estimates. These estimates are averaged for statistical analysis. Here, 10 s snapshots are divided into 2000 chunks of 4 ms each.

Since the E6-C signal is currently broadcast unencrypted, the dataset snapshots capture the existing periodic pilot open signal, which consists of 1 ms primary spreading codes tiered with a known 100-symbol, 1 ms secondary code [15]. Therefore, it is necessary to emulate the RECS. This is performed by first acquiring the secondary code on E6-C to determine the Secondary Code Index (SCI) for each satellite. Then, a conventional acquisition method is used, coherently integrating the required 1 ms primary spreading codes to obtain the desired RECS length, set to 4 ms, which has been shown to provide high detection probabilities in most clear-sky scenarios [16].

The results are shown in Figure 4, showing the code phase delay differences between E6-C and E1-B (a) and between E6-C and E6-B (b). As expected, the distributions exhibit a Gaussian-like shape, with variance related to the sample’s thermal noise. For E6-C vs. E1-B, the Gaussian is non-centered due to inter-frequency biases, while for E6-C vs. E6-B, there is no bias. A Gaussian curve (in red) is fitted to the experimental data (in blue) to interpolate the mean and standard deviation for each case.

4.3. E6-B Snapshot Code Phase Delay Estimation

The subsequent results focus on estimating the ranging accuracy from processing snapshots of E6-B samples. The dataset used (D2) was recorded under clear-sky conditions with the antenna covered by concrete blocks to simulate different $C/N_0$ levels. As in Section 4.2, the snapshots are processed with a custom MATLAB simulator, but, in this case, they are divided into smaller segments of the required sizes, as shown in Table 2.

For each segmented snapshot, the code phase delay is estimated. As expected, owing to the Doppler frequency effect, the code phase delay estimates exhibit a linear trend over time. This trend line is subtracted from the estimates to obtain an estimation of the ranging accuracy by estimating the standard deviation of the interpolated Gaussian distribution.

The results are shown in Figure 5. The standard deviations estimated for ranging accuracy are consistent with the CRLBs in Table 2. The slight discrepancies may arise from factors like non-ideal filters in the SDRs or the method used to estimate ranging accuracy, achieved by removing the trend line from the code phase delay estimates, which may not precisely reflect the disparity between the estimated and true measurements.

5. Conclusions

Galileo SAS offers an effective method for authenticating ranging signals by encrypting the E6-C signal. A key feature is the use of an auxiliary signal to speed up RECS detection, crucial for SAS’s nominal operation. While the E1-B signal remains the default choice, adding signals like E6-B could enhance future SAS receivers’ robustness without adding significant complexity. The E6-B signal, already present in the samples that receivers must record, also avoids inter-frequency biases, offering a way to improve SAS authentication.

The results of this study, based on real data samples, highlight the advantages of using E6-B for SAS as an additional verification layer and for receivers relying solely on the E6 signal, provided TESLA keys are accessible through alternative channels instead of the E1-B signal. E6-B could also aid Vestigial Signal Search (VSS) techniques crucial for detecting spoofed signals during attacks. Further research is needed to explore the potential benefits of integrating E6-B, ensuring SAS remains secure and reliable against evolving threats.