Quadrotor Trajectory Tracking Under Wind Disturbance Using Backstepping Control Based on Different Optimization Techniques †
Abstract
1. Introduction
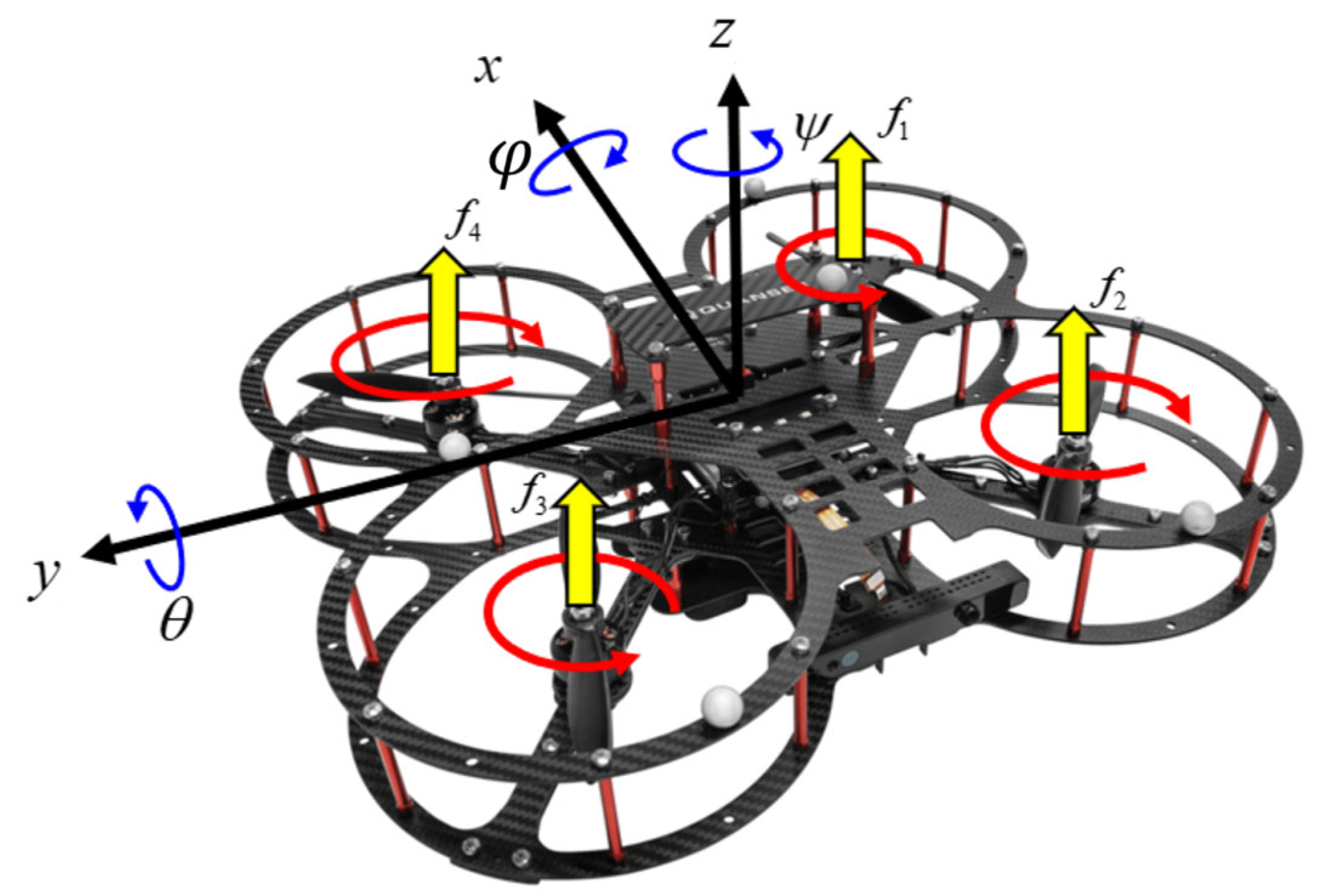
2. Quadrotor Modeling
3. Assumptions
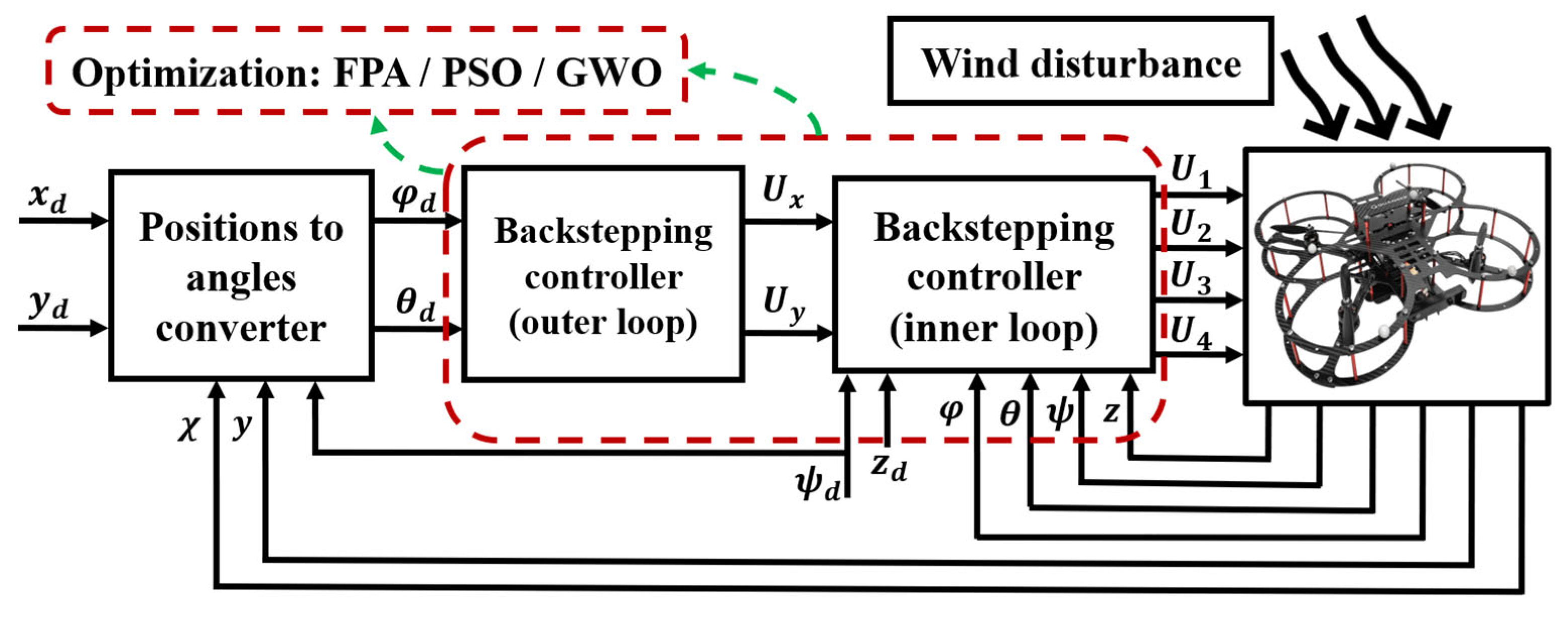
4. Control Method
5. Proposed Controller’s Optimization
5.1. Flower Pollination Algorithm FPA
5.2. Gray Wolf Optimization GWO
5.3. Particle Swarm Optimization PSO
6. Results and Discussion
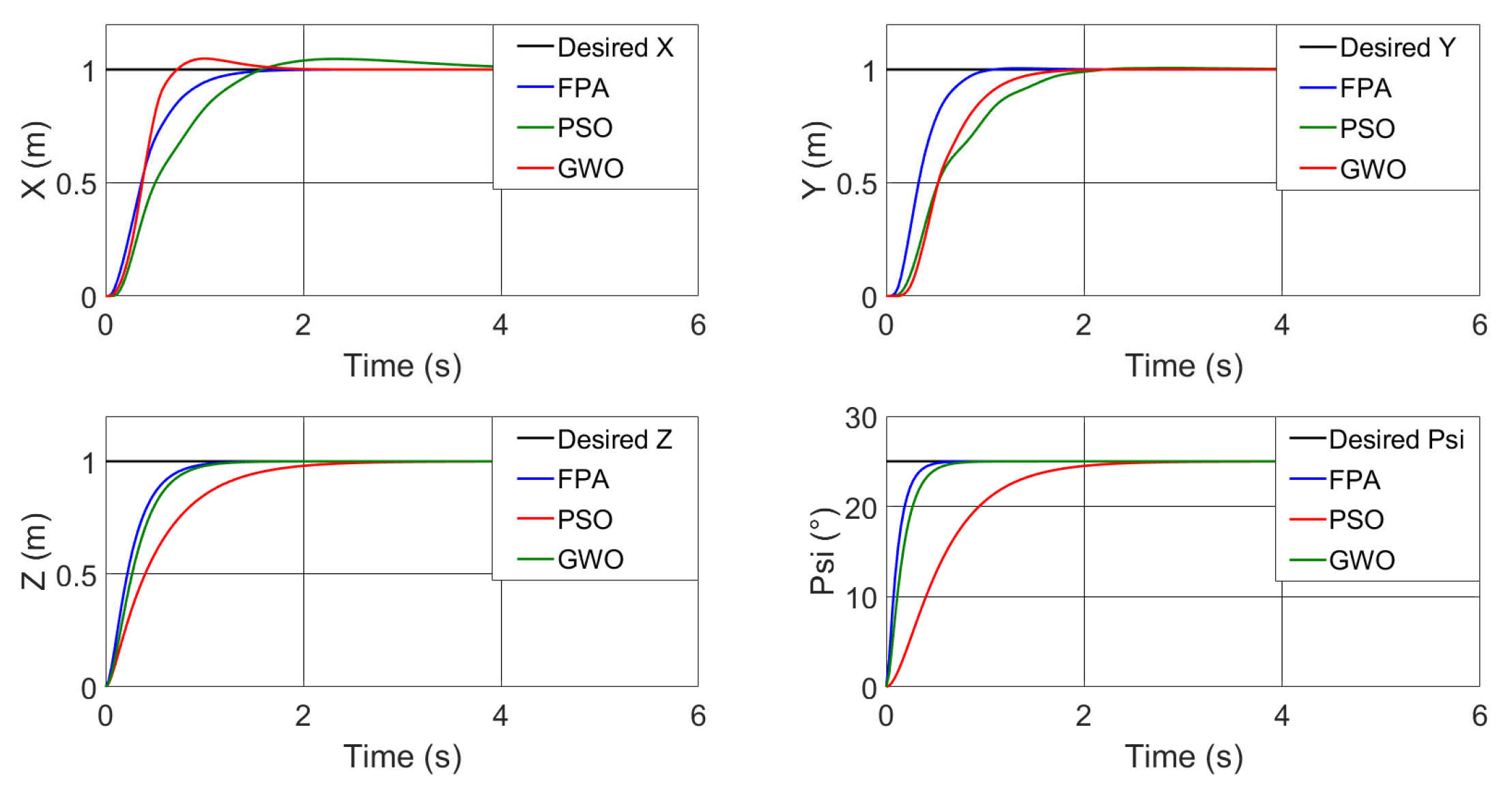
6.1. Step Response
6.2. Comparison
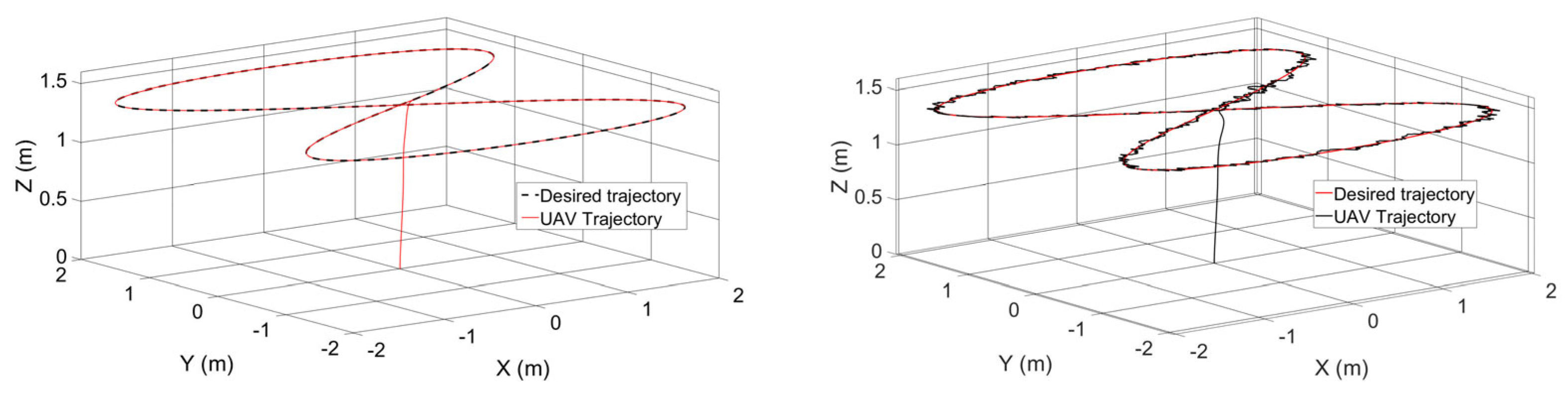
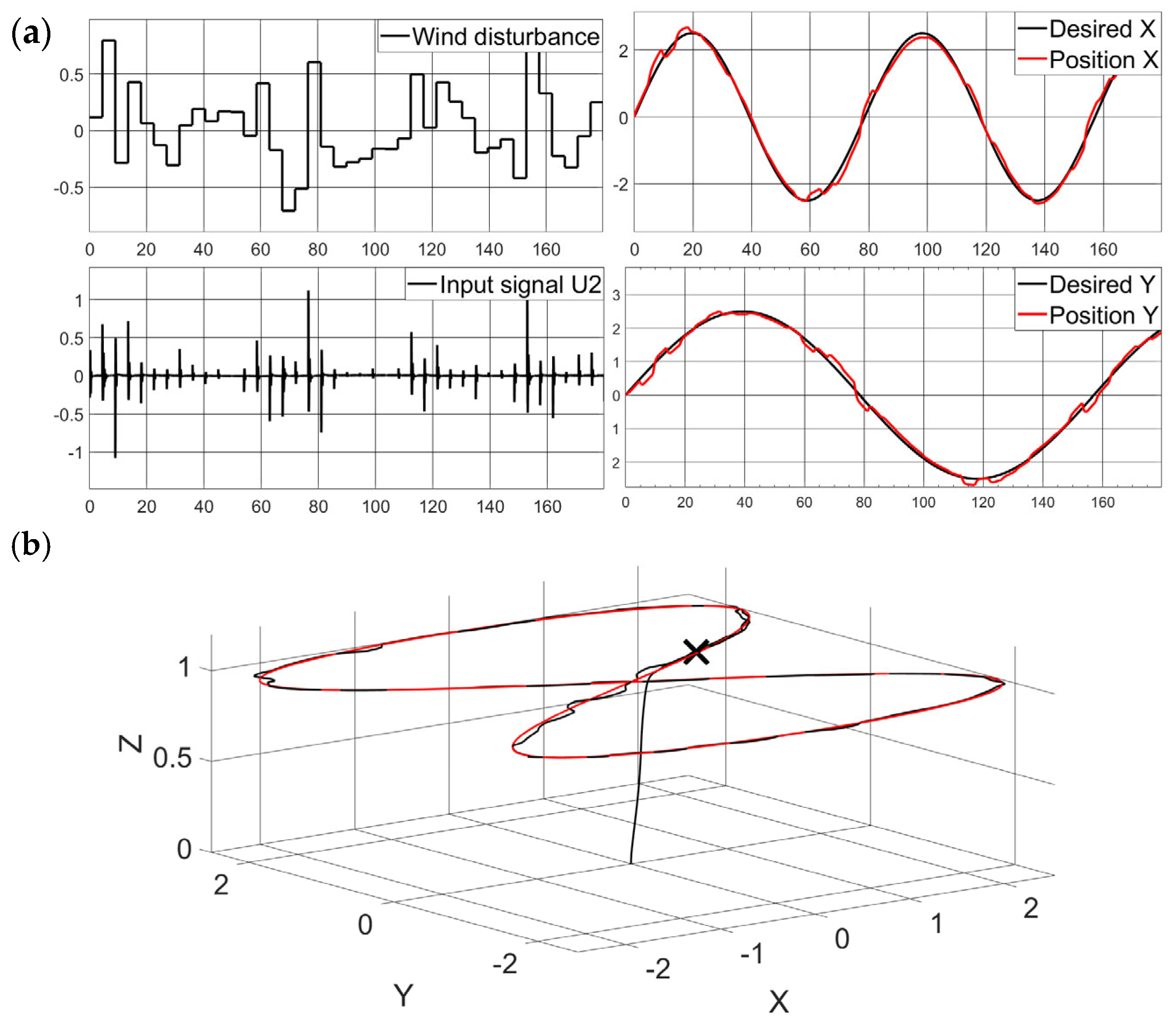
6.3. Trajectory Tracking and Robustness Test
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y. Modelling and simulation of quadcopter UAV based on PID control. Appl. Comput. Eng. 2024, 75, 2721–2755. [Google Scholar] [CrossRef]
- Ghiloubi, I.B.; Abdou, L.; Lahmar, O.; Dahnoun, I. 3 DOF Quanser’s Quadrotor control using LQR based on PSO, FPA & ACO with input saturation. In Proceedings of the 2023 IEEE 11th International Conference on Systems and Control (ICSC), Sousse, Tunisia, 18–20 December 2023. [Google Scholar] [CrossRef]
- Dong, J. Performance comparison and analysis of traditional PID and fuzzy PID control applied to UAV. J. Phys. Conf. Ser. 2023, 2649, 012001. [Google Scholar] [CrossRef]
- Sang, H.; Zheng, F.; Huang, F.; Zhang, S. Quadrotor UAV Trajectory Tracking Control Based on Adaptive Non-singular Terminal Sliding Mode. J. Electr. Syst. 2024, 20, 929–939. [Google Scholar] [CrossRef]
- Zhou, R. Research on High-precision Algorithm for Flight Attitude Evaluation of Quadrotor Aircraft. Trans. Comput. Sci. Intell. Syst. Res. 2024, 8, 29–34. [Google Scholar] [CrossRef]
- Ud Din, A.F.; Mir, I.; Gul, F.; Mir, S.; Saeed, N.; Althobaiti, T.; Abbas, S.M.; Abualigah, L. Deep Reinforcement Learning for Integrated Non-Linear Control of Autonomous UAVs. Processes 2022, 10, 1307. [Google Scholar] [CrossRef]
- Mien, T.; Tu, T.; Vo, V.-A. Cascade PID control for altitude and angular position stabilization of 6-DOF UAV quadcopter. Int. J. Robot. Control Syst. 2024, 4, 814–831. [Google Scholar] [CrossRef]
- Leitão, D.; Cunha, R.; Lemos, J. Adaptive Control of Quadrotors in Uncertain Environments. Eng 2024, 5, 544–561. [Google Scholar] [CrossRef]
- Wang, B.; Yan, Y.; Xiong, X.; Han, Q.; Li, Z. Attitude Control of Small Fixed−Wing UAV Based on Sliding Mode and Linear Active Disturbance Rejection Control. Drones 2024, 8, 318. [Google Scholar] [CrossRef]
- Darwito, P. Control System for Quadcopter UAV based SMC-RBFNN with External Disturbance. E3S Web Conf. 2024, 482, 03004. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, F.; Sui, S.; Yi, Z.; Chen, K. Enhancing Quadrotor Control Robustness with Multi-Proportional–Integral–Derivative Self-Attention-Guided Deep Reinforcement Learning. Drones 2024, 8, 315. [Google Scholar] [CrossRef]
- Karahan, M. Nonlinear Modelling and Robust Backstepping Control of a Quadcopter in Aggressive Maneuvering. Stud. Inform. Control 2024, 33, 29–38. [Google Scholar] [CrossRef]
- Boubakir, A.; Souanef, T.; Labiod, S.; Whidborne, J. A Robust Adaptive PID-like Controller for Quadrotor Unmanned Aerial Vehicle Systems. Aerospace 2024, 11, 980. [Google Scholar] [CrossRef]
- Maaruf, M.; Abubakar, A.; Gulzar, M. Adaptive backstepping and sliding mode control of a quadrotor. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 630. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, Y.; Muhammad Usman, S.; Yan, Y.; Wang, J.; Yang, L.; Yan, F.; Yan, L. Deep Reinforcement Learning-Based Wind Disturbance Rejection Control Strategy for UAV. Drones 2024, 8, 632. [Google Scholar] [CrossRef]
- Ramirez-Neria, M.; Luviano-Juárez, A.; González-Sierra, J.; Ramírez-Juárez, R.; Aguerrebere, J.; Hernandez-Martinez, E. Active Disturbance Rejection Control for the Trajectory Tracking of a Quadrotor. Actuators 2024, 13, 340. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, D. Nonlinear Adaptive Control Design for Quadrotor UAV Transportation System. Drones 2024, 8, 420. [Google Scholar] [CrossRef]
- Abdussamad, M.F.; Abubakar, S.I.; Lawal, M.I.; Mukhtar, I.B.; Muhammad, A.B. Adaptive Control of Quadrotor with Neural disturbance Estimator. Glob. J. Res. Eng. Comput. Sci. 2024, 4, 88–101. [Google Scholar] [CrossRef]
- Lone, A.; Zhu, Q.; Nemati, H.; Mercorelli, P. Dynamic Inversion-Enhanced U-Control of Quadrotor Trajectory Tracking. Drones 2024, 8, 599. [Google Scholar] [CrossRef]
- He, X. A review of research on the control of quadrotor UAVs based on deep learning PID algorithm. Appl. Comput. Eng. 2024, 45, 129–133. [Google Scholar] [CrossRef]
- Al-Husnawy, T.; Al-Ghanimi, A. A review of control methods for quadrotor UAV. Kufa J. Eng. 2024, 15, 98–124. [Google Scholar] [CrossRef]
- Nguyen, V.-C.; Nguyen, M.; Tran, H.; Mien, T.; La, H.; Nguyen, H. Trajectory Tracking Control for a Quadcopter under External Disturbances. Eng. Technol. Appl. Sci. Res. 2024, 14, 17620–17628. [Google Scholar] [CrossRef]
- Qi, Z. On the use of PID control to improve the stability of the quad-rotor UAV. Appl. Comput. Eng. 2024, 49, 31–36. [Google Scholar] [CrossRef]
- Oh, Y.; Lee, M.; Moon, J. Koopman-Based Control System for Quadrotors in Noisy Environments. IEEE Access 2024, 12, 71675–71684. [Google Scholar] [CrossRef]
- Hasseni, S.-E.-I.; Abdou, L.; Glida, H. Parameters tuning of a quadrotor PID controllers by using nature-inspired algorithms. Evol. Intell. 2021, 14, 61–73. [Google Scholar] [CrossRef]
- Kidambi, G.K.; Annamalai, A.; Sahu, R.; Kumar, P. Nonlinear robust adaptive control for quadrotors under actuator faults and gyroscopic effects. Aerosp. Sci. Technol. 2023, 142, 108223. [Google Scholar] [CrossRef]
- Rao, S.S.; Krishnakumar, R.; Sundar, R. Adaptive super-twisting control for quadrotor trajectory tracking with external disturbances. ISA Trans. 2023, 141, 382–395. [Google Scholar] [CrossRef]
- Huang, H.; Wu, Q.; Song, S.; Yuan, Z. Deep adaptive trajectory tracking control for quadrotors using reinforcement learning. In IEEE Transactions on Neural Networks and Learning Systems; Early Access; IEEE Xplore: Piscataway, NJ, USA, 2023. [Google Scholar]
- Oniz, Y. Trajectory Control of Quadrotors via Spiking Neural Networks. Electronics 2024, 13, 3319. [Google Scholar] [CrossRef]
- Kazim, M.; Sim, H.; Shin, G.; Hwang, H.; Kim, K.K.K. Aggressive Trajectory Tracking for Nano Quadrotors Using Embedded Nonlinear Model Predictive Control. In Intelligent Autonomous Systems 18; Lee, S.G., An, J., Chong, N.Y., Strand, M., Kim, J.H., Eds.; Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2024; Volume 795, pp. 317–332. [Google Scholar] [CrossRef]
- Ullah, S.; Alghamdi, H.; Algethami, A.A.; Alghamdi, B.; Hafeez, G. Robust control design of under-actuated nonlinear systems: Quadcopter unmanned aerial vehicles with integral backstepping integral terminal fractional-order sliding mode. Fractal Fract. 2024, 8, 412. [Google Scholar] [CrossRef]
- Alghamdi, H.; Khan, T.A.; Hua, L.-G.; Hafeez, G.; Khan, I.; Ullah, S.; Khan, F.A. A novel intelligent optimal control methodology for energy balancing of microgrids with renewable energy and storage batteries. J. Energy Storage 2024, 90, 111657. [Google Scholar] [CrossRef]
- Irfan, S.; Zhao, L.; Ullah, S.; Javaid, U.; Iqbal, J. Differentiator- and observer-based feedback linearized advanced nonlinear control strategies for an unmanned aerial vehicle system. Drones 2024, 8, 527. [Google Scholar] [CrossRef]
- Abitha, A.M. Modelling of quad-rotor dynamics and Hardware-in-the-Loop simulation. Int. J. Eng. Technol. 2024, 13, 349–359. [Google Scholar]
- Ghiloubi, I.B.; Abdou, L.; Lahmar, O. Adjusted linear quadratic regulator-proportional-derivative control of Quanser’s three degrees of freedom helicopter based on flower pollination algorithm under external disturbances. IAES Int. J. Robot. Autom. 2024, 13, 432–433. [Google Scholar] [CrossRef]
- Ghiloubi, I.B.; Abdou, L.; Lahmar, O. PD-LQR control of 3DOF helicopter using FPA optimization. In Proceedings of the 2023 International Conference on Control, Automation and Diagnosis (ICCAD), Rome, Italy, 10–12 May 2023. [Google Scholar] [CrossRef]
| Algorithm | Population | Iterations | Key Parameters |
|---|---|---|---|
| PSO | 50 | 12 | Inertia weight Cognitive constant |
| FPA | 70 | 12 | Switching probability Lévy flight coefficient |
| GWO | 50 | 15 | Coefficient of decreasing from 2 to 0 |
| Parameter | Symbol | Value |
|---|---|---|
| Inertia on axis | 0.0038 | |
| Inertia on axis | 0.0038 | |
| Inertia on axis | 0.0071 | |
| Gravitational constant | 9.81 | |
| Quadcopter’s mass | 0.486 | |
| The distance between each rotor and the quadcopter’s center | 0.25 | |
| Aerodynamic drag coefficient on axis | 0.0056 | |
| Aerodynamic drag coefficient on axis | 0.0056 | |
| Aerodynamic drag coefficient on axis | 0.0064 |
| Obtained Gains | GWO | PSO | FPA |
|---|---|---|---|
| Performances | OverShoot (%) | Settling Time (s) | Steady Error (m or °) |
|---|---|---|---|
| Control based on FPA | |||
| Control based on GWO | |||
| Control based on PSO |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghiloubi, I.B.; Abdou, L.; Lahmar, O.; Drid, A.H. Quadrotor Trajectory Tracking Under Wind Disturbance Using Backstepping Control Based on Different Optimization Techniques. Eng. Proc. 2025, 87, 93. https://doi.org/10.3390/engproc2025087093
Ghiloubi IB, Abdou L, Lahmar O, Drid AH. Quadrotor Trajectory Tracking Under Wind Disturbance Using Backstepping Control Based on Different Optimization Techniques. Engineering Proceedings. 2025; 87(1):93. https://doi.org/10.3390/engproc2025087093
Chicago/Turabian StyleGhiloubi, Imam Barket, Latifa Abdou, Oussama Lahmar, and Abdel Hakim Drid. 2025. "Quadrotor Trajectory Tracking Under Wind Disturbance Using Backstepping Control Based on Different Optimization Techniques" Engineering Proceedings 87, no. 1: 93. https://doi.org/10.3390/engproc2025087093
APA StyleGhiloubi, I. B., Abdou, L., Lahmar, O., & Drid, A. H. (2025). Quadrotor Trajectory Tracking Under Wind Disturbance Using Backstepping Control Based on Different Optimization Techniques. Engineering Proceedings, 87(1), 93. https://doi.org/10.3390/engproc2025087093







