A Comparative Study of Vibrations in Front Suspension Components Using Bushings Made from Different Materials ^†

Abstract

The design of the suspension system affects handling and stability, vibrations of the steered wheels, vehicle ride comfort, and tyre tread wear. One of the most important vibration parameters is acceleration; high acceleration values can have an adverse effect on both the driver and passengers, as well as on the components of the vehicle’s suspension and handling. This paper presents the results of the effects of acceleration on the components of a front-independent MacPherson suspension system. Data on the accelerations were obtained from theoretical and experimental studies. A simulation study was conducted, taking into account the elastic and damping characteristics of the elastic components. The experimental study was conducted under laboratory conditions by using a suspension tester, BEISSBARTH, and a measuring system developed with LabVIEW 2021 SP1 and MATLAB R2022b software. The experiments were conducted with different tyre pressures and by using bushings made from different materials. The experimental tests were conducted with two rubber bushings within the mounting of the arm, as well as a rubber bushing and a polyurethane bushing. The experimental results were compared and analyzed. Two theoretical models were considered: one is a mathematical model, and the other is a simulation model which uses the finite element method. Numerical dynamic analysis of the suspension was performed using the SolidWorks 2023.

1. Introduction

The vibrations of vehicles, and especially the suspension systems, are of interest to researchers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. Vibrations and their amplitudes are important in the design of the suspension system and its components, as well as in determining their technical condition [6,16,17]. Finding the optimal suspension system design is a difficult task for designers, as vibrations are inevitable and affect its performance.

In [1,2,3,4,5,8,10,11,12], the authors investigated the vibrations of a quarter car suspension system through mathematical modelling and conducted simulation studies on developed models of two and three degrees of freedom (2DOF and 3DOF) using Matlab software. Other authors investigated the propagation of vibrations on the driver and passenger seats and suspension components under laboratory conditions and road tests and by developing additional systems for measuring vibration parameters [7,8,14,15,16,17]. The test stands to evaluate the effectiveness of shock absorbers in vehicles, and were carried out under laboratory conditions. Vibration studies of various types of quarter car suspension systems are increasingly being conducted using the finite element method FEM, as well as using developed CAD models. Various analyses are performed with simulation software products, such as Abaqus, SolidWorks, Ansys, ADAMS, etc. [1,6,9,10,14,15,16].

Polyurethane bushings are also offered and applied in the vehicle’s suspension, instead of the traditional rubber ones. In [18], polyurethane bushings for suspension arms were designed and simulated with SolidWorks.

The purpose of the publication is to determine the vibration accelerations in MacPherson-type suspension components of a passenger car using bushings made from different materials at different tyre pressures. A geometric model of a quarter car suspension is proposed, and the accelerations of two suspension components are determined using the finite element method depicted by the SolidWorks program. The simulation modeling was performed using the stiffness characteristics of the tyre at pressures of 0.22 MPa, and the suspension and the stiffnesses of a polyurethane bushing and rubber bushing, respectively, mounted on the arm. The simulation was performed for part of the duration of the experiment. Accelerations were experimentally determined and compared using bushings made from different materials. The measuring system developed and described in [19,20] was used, including hardware and software parts. The LabVIEW virtual measuring instrument was used, along with a MATLAB script, and the kinematic disturbance was generated under laboratory conditions by using a suspension tester—BEISSBARTH SA640.

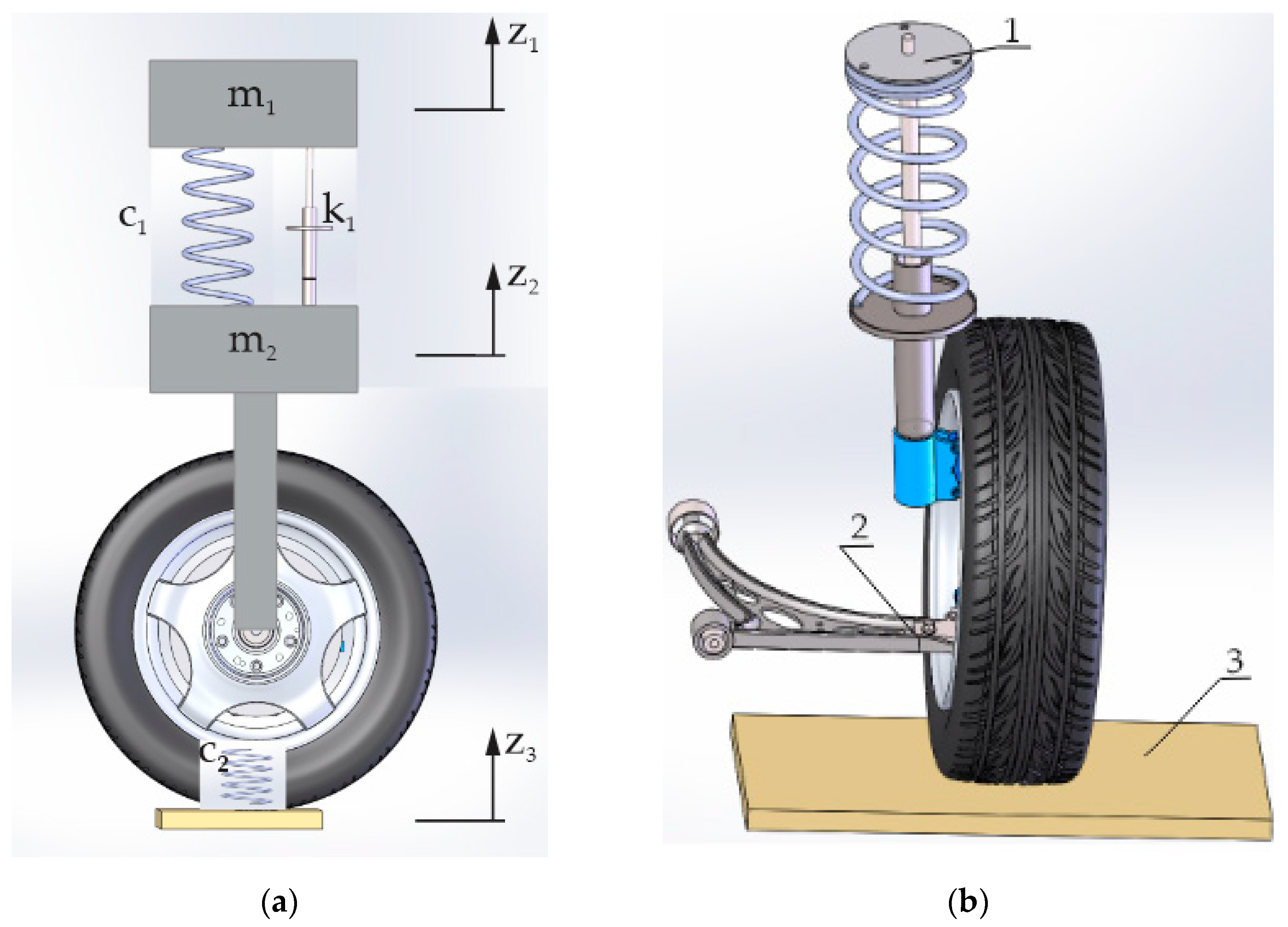
2. Materials and Methods

One of the vibration parameters measured is the vibration acceleration, which affects ride comfort and can be determined using numerical methods and by conducting experimental studies.

Two theoretical models are considered: one is a mathematical model, and the other is a simulation model which uses the finite element method.

Figure 1a depicts a scheme of a quarter car suspension system model of two degrees of freedom. The mathematical model of suspension is described by the following equations [11]:

m₁∙ z₁ + k₁∙(z₁ − z₂) + c₁∙(z₁ − z₂) = 0

(1)

m₂∙ z₂ − k₁∙(z₁−z₂) − c₁∙(z₁ − z₂) + c₂∙(z₂ − z₃) = 0

(2)

where m₁ is the sprung mass; m₂ is the unsprung mass; c₁, c₂ are the spring and the tyre elastic coefficients, respectively; k₁ is the damper coefficient; z₁, z₂ and z₃ are the displacements of the sprung mass, unsprung mass and the displacement of the platform.

The external excitation for the suspension system is varied in terms of vertical direction by a suspension tester. The driven platform of the tester performs a reciprocating motion in a vertical direction, and the displacement, velocity and acceleration can be described by the following equation [8]:

z₃ = A∙sin(ωt) = A∙sin(2πft)

(3)

z₃ = 2ωAcos(ωt) = 2πf A∙cos(2πft)

(4)

z₃ = −4ω²Asin(ωt) = −4π²f²∙A∙sin(2πft)

(5)

where A is the amplitude of the platform, A = ±6 mm; f is the frequency, and t is the time.

Figure 1b depicts a 3D model of a quarter car MacPherson suspension, along with the measuring points of vibration on the suspension and platform of the suspension tester. Vibration measurement points are presented in Figure 1b, and they are as follows: sensor 1 on the body of the strut, sensor 2 on the control arm, and sensor 3 on the platform of the suspension tester. The model was created using SolidWorks. The main parameters required to develop a three-dimensional geometric (3D) model of the quarter car suspension as a prototype is the same as that depicted in [20].

To perform the numerical dynamic study, SolidWorks Simulation software was used, and the model was simplified. The suspension components, supports and connections and others necessary conditions in the simulation model are presented in [20]. The static deformation characteristics of the rubber bushing, polyurethane bushing and the spring stiffness were presented in another publication by the authors [21,22]. The radial stiffness of the tyre with dimension 205/55R16 was obtained experimentally. The experiments were conducted using the laboratory setup of the flat bed tyre testing machine [20]. The damper coefficient of the shock absorber and other necessary parameters needed to perform the analysis are as depicted in [3,8].

The arm is made of cast steel according to EN 10293 [23], and the other suspension components are made of alloy steel according to EN 10250-3 [24]. The material properties are shown in

Table 1. Material properties.

Parameters	Arm	Hub, Shrut, Knuckle, Joint
Density [kg/m3]	7300	7700
Elastic modulus [N/mm2]	190,000	210,000
Poisson’s ratio	0.26	0.28

.

The input parameter of the simulation is a harmonic representation of acceleration and time in sensor 3, mounted in the platform, and the accelerations are measured while operating a suspension tester.

Numerical dynamic analysis of the suspension was performed, and three-dimensional blended curvature-based mesh was generated. The mesh includes 379,444 nodes and 233,669 elements. Figure 2 presents the mesh.

Experimental studies were conducted with the developed system described in [19,20]. The system is characterized by high measurement accuracy, the relatively small size and low mass of the sensors, the possibility of external generation of the vibrations (external disturbing impact for the suspension system), and ease of operation. The system allows measurements both in laboratory conditions (by artificially creating an external disturbing impact) and in road conditions.

The main goal of the experimental study was to determine and analyze the accelerations of the suspension components using different bushings and different tyre pressures. An Audi passenger car was used for the experiment, as described in [20]. The experiment was conducted in the following sequence:

-

The car is placed on the suspension tester; initially, the arm is with the original bushings;

-

The sensors of the measuring system are installed;

-

The wheels of the front axle are positioned on the tester platforms;

-

The test is started;

-

The accelerations are measured on the platform, on the arm and on the body of the strut, and this is carried out several times for different tyre pressures;

-

After replacing one of the rubber bushings in the arm with a polyurethane one, the measurements are repeated under the same conditions and in the same sequence.

The results of the experiments were recorded. The recorded acceleration data for both variants were processed and visualized using a script file developed in the Matlab program.

3. Results and Discussion

Figure 3a illustrates the experimental results of the static vertical load from the radial displacement of the tyre during loading and unloading at different pressures. The results presented in Figure 3a at tyre pressures of 0.20, 0.25 and 0.30 Mpa are offset from zero for better visualization. Figure 3b presents the results for the static stiffness characteristic in the radial direction at different tyre pressures. The stiffness was obtained by linear approximation, and it is presented in Figure 3b. The radial tyre stiffness at a pressure of 0.22 Mpa is obtained at 179,161 N/m.

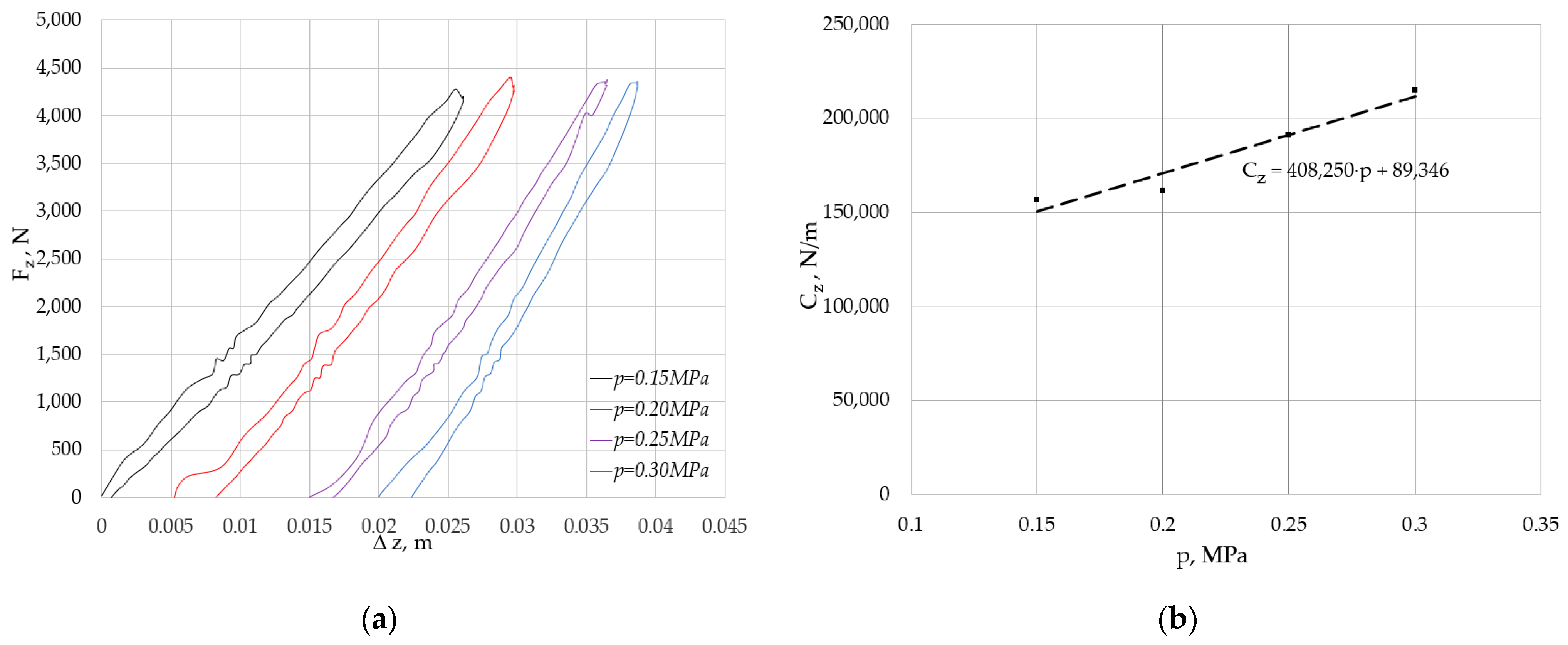
3.1. Simulation Results

Figure 4 presents the obtained results of the accelerations at sensors 1 and 2 from the conducted numerical study using polyurethane and rubber bushings. The presented results are set in the time period of the experiment from 5.5 s to 8.2 s.

3.2. Experimental Results

The results of the experimental studies are presented in the sequential tests performed, using two (both) rubber bushings (case I) and using a rubber bushing and polyurethane bushing (case II) mounted on the arm, respectively.

Figure 5 and Figure 6 present the results obtained for the accelerations of sensor 1 mounted on the body of the strut, and the accelerations of sensor 2 mounted on the arm at different tyre pressures, respectively. The tyre pressures are 0.18, 0.20, 0.22 and 0.25 MPa.

In Figure 5 and Figure 6, the time represented on the horizontal axis starts from 4 s, after the start of the external disturbance, and it increases to 15 s, in order to better visualize the obtained results. The black line represents the acceleration when using two rubber bushings; the red line represents the acceleration when using a rubber bushing and a polyurethane bushing.

From the presented graphic dependencies of the acceleration, it can be seen that when using a polyurethane bushing and a rubber bushing, the damping occurs faster than when using two rubber bushings.

Table 2. Comparison of FEM and experimental results.

Parameter	Theoretical (FEM)	Experimental
Max. acceleration sensor 1, [m/s2]	2.8	3.6
Max. acceleration sensor 2, [m/s2]	25.3	25

presents the maximum acceleration results of sensors 1 and 2 obtained by FEM and by experiment, respectively. The maximum acceleration of sensor 1 is about 7.7 s; for sensor 2, this is about 6.7 s.

4. Conclusions

The present study allows us to make the following conclusions:

-

The acceleration results of sensors 1 and 2 obtained using numerical analysis have comparable values to those obtained from the experiment, and the results by FEA can be used to refine the methodology.

-

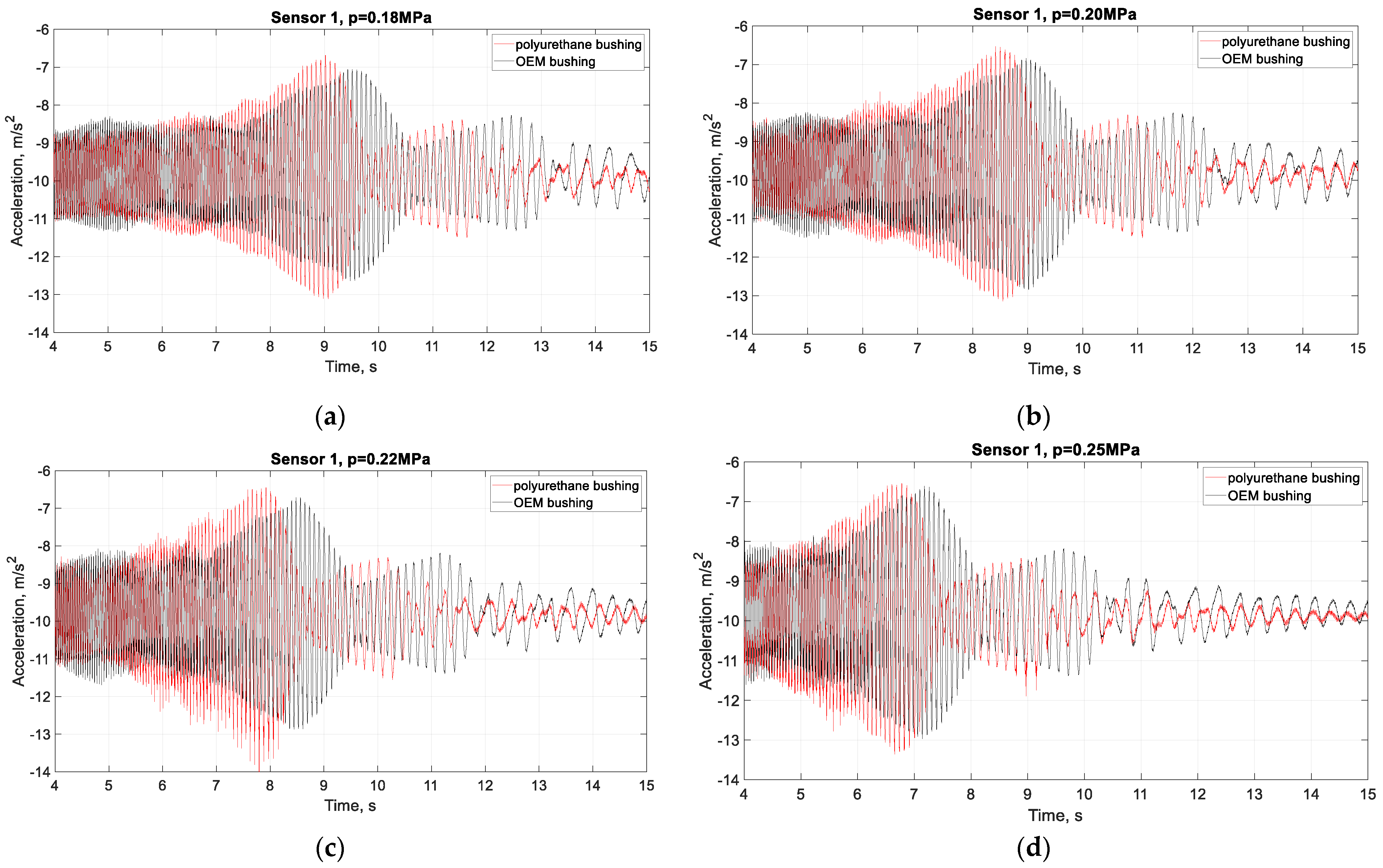
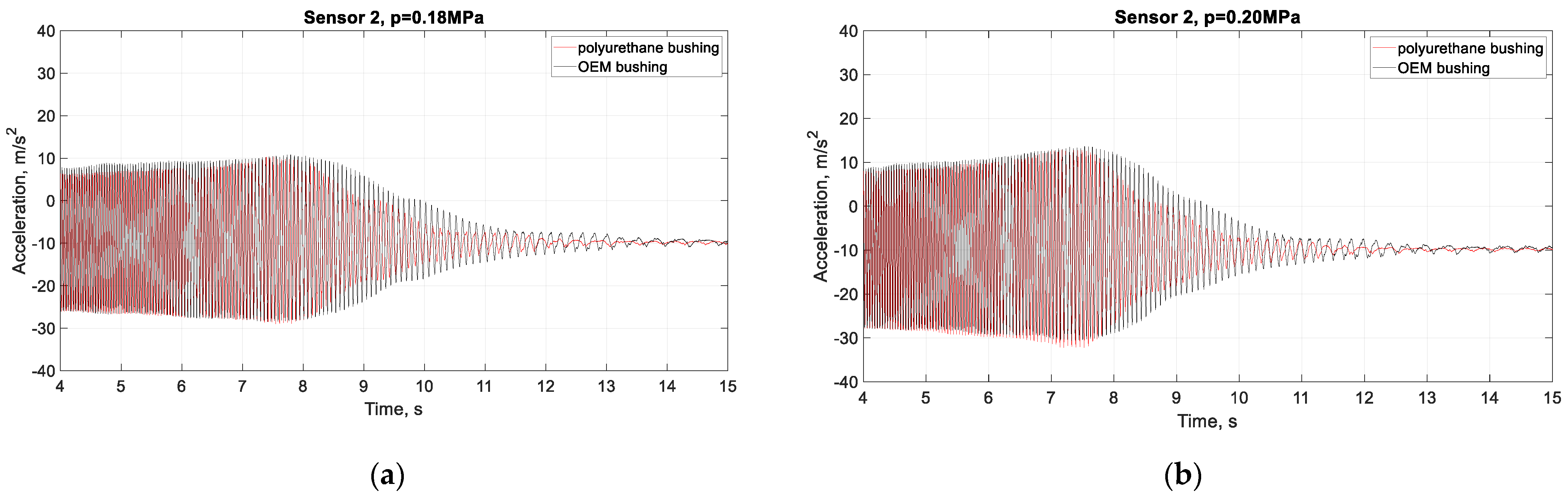
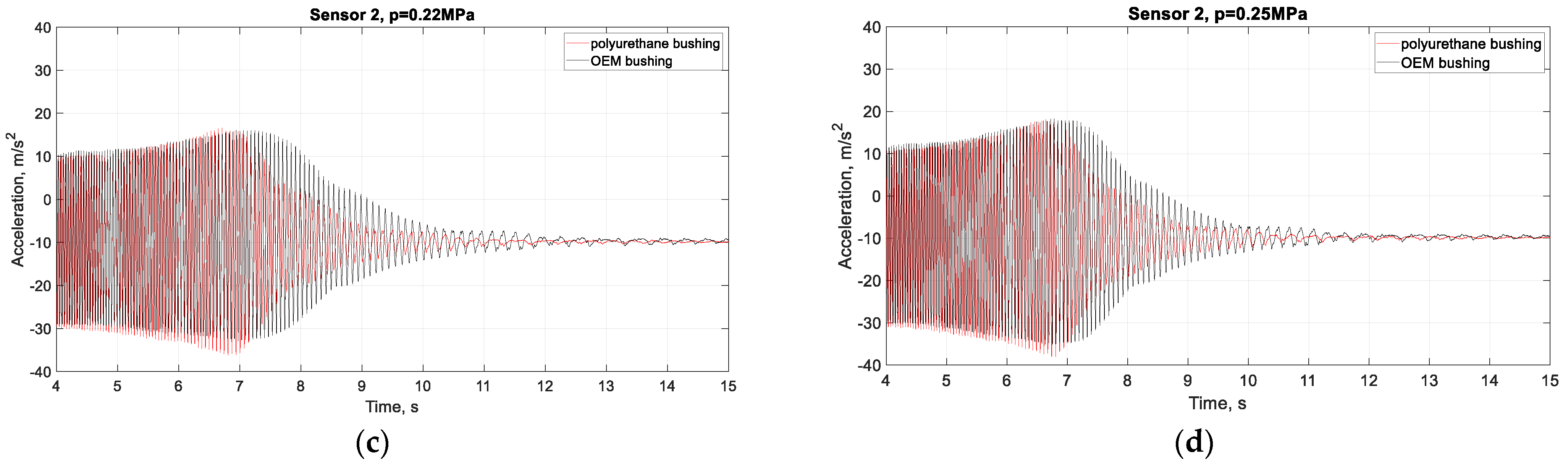
The maximum acceleration value of sensor 1, mounted on the body of the strut, is around 3 m/s² at tyre pressures of 0.22MPa when the rubber bushings are mounted in the arm. When rubber bushing and polyurethane bushing are used, the acceleration is around 3.6 m/s² at tyre pressures of 0.22 MPa.

-

The amplitude of the acceleration values of sensors 1 and 2 increases with increasing tyre pressure.

-

A significant difference in values and type of the accelerations curve is observed in sensor 1, mounted on the body of the strut.

-

The obtained acceleration values on the body of the suspension strut are comparable to those obtained in other publications [7,8].

-

After replacing one of the rubber bushings on the arm with a polyurethane one, damping occurs faster, which is a prerequisite for slower wear, and therefore for greater durability and endurance under higher loads. This is due to the different material properties of the polyurethane and rubber.