Cascade Control Based on Sliding Mode for Trajectory Tracking of Mobile Robot Formation ^†

Abstract

An innovative cascade control strategy is presented in this work, based on sliding mode control (SMC) for trajectory tracking of the formation of mobile robots. The proposed strategy was compared with five alternative control approaches: PID control, inverse dynamics, and other SMC-based structures. The objective was to evaluate the most effective control technique by analyzing the integral of squared error (ISE) index. Additionally, robustness tests were carried out by varying the parameters of the dynamic model of the mobile robot and analyzing the response of the controllers to perturbations in the modeling. The results show that the PD-SMCV controller provides the best performance in trajectory tracking and robustness against disturbances, demonstrating significant superiority over the evaluated methods for maintaining a stable mobile robot formation under dynamic conditions.

1. Introduction

Nowadays, with the development of technology and the increased use of robotic systems, the need to control multiple robots to perform a cooperative task in formation has increased, with the objective that all robots execute different tasks such as cargo transportation and navigation, among others [1,2,3]. The design and evaluation of controllers for robotic formation have been a subject of interest by researchers. Several studies have been conducted, as in [4], which presents a leader–follower robot formation system, employing a fully actuated system (FAS) method to improve stability and convergence by eliminating uncertainties and handling disturbances. In [5], formation control using a null space-based sliding mode control (NSB-SMC) is discussed, which improves robustness in environments with static and dynamic obstacles. On the other hand, for uncertainty and disturbance handling, an adaptive SMC is proposed in [6] to improve the accuracy, stability, and convergence of tracking errors under different conditions, and in [7], this type of controller is applied to sliding steering mobile robots (SSMRs) used in various mobile robotic systems with different morphologies that do not have steerable wheels.

Other techniques, such as the stage-by-stage evolutionary fuzzy obstacle boundary following (OBF) control of the three robots proposed in [8], were implemented through a cooperative behavioral supervisor to coordinate the learned OBF behavior, while [9] introduces fuzzy logic to replace switching control in traditional sliding mode control (SMC). Models such as Markov have also been employed within robot formation; for example, [10] proposes a static controller for multi-agent systems with Markovian topologies, ensuring stability in the face of imperfect information. Furthermore, [11] investigates tracking protocols with variable delays, while [12] presents a fault-tolerant approach for mobile manipulators. These works highlight the robustness of Markov models in complex environments.

In robot formation, the leader–follower system is employed, where the leader robot sets the trajectory and the followers adjust their positions accordingly [13,14]. This setup can facilitate coordination but also introduces vulnerabilities to possible leader failures. In [15], the author describes a multi-leader scheme, using an optimization method for the leaders and an SMC-like controller for the followers. The SMC can be combined with other types of control such as fuzzy control, which reduces the chattering present in the SMC, as demonstrated in [16]. When integrated with a PD control, it achieves a combination of the simplicity of the PD control and the robustness of the SMC, decreasing the chattering present in the SMC control studied in [17].

In the present work, in contrast to the literature reviewed on leader–follower robot-based formation control using traditional controllers, which focused on a single control strategy, a novel approach is proposed by implementing a cascade control strategy for mobile robot formation control. This strategy takes advantage of different controllers and is compared with five different control schemes, allowing the evaluation of the system behavior in the outer loop for the formation control and in the inner loop for the dynamic compensation of the robots. In addition, by working with the dynamic model of mobile robots, factors such as inertia, external forces, and interactions with the environment are taken into account to predict how the robot will behave in different conditions, allowing more precise control, improving stability, maneuverability, and response to system perturbations.

This work is organized as follows: Section 2 presents the dynamic model of the three mobile robots performing the formation and the formation system model; Section 3 details the design of the formation controllers: (i) PD without dynamic compensation (PD), (ii) PD with dynamic compensation (PD-DI), (iii) PD with dynamic sliding mode controller (PD-SMCV), (iv) SMC without dynamic compensation (SMC), and (v) SMC with dynamic sliding mode controller (SMC-SMCV); Section 4 describes the simulation tests and results. The stability analysis, discussion, and comparison of all the implemented controllers are presented by obtaining the integral of squared error (ISE) index, which helps to verify and evaluate the best controller for this application. Finally, Section 6 provides the conclusions of this work.

2. Modeling

2.1. Kinematic and Dynamic Model of the Mobile Robot

The real operation of a mobile robot can be represented by different mathematical models, starting with the kinematic model, which represents more simply the operation of the robot, since it does not consider friction forces or physical disturbances. The kinematic model is defined by the following:

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\psi }\end{array}\right]=\left[\begin{array}{c}cos\psi \hspace{1em}-a sin\psi \\ sin\psi \hspace{1em}a cos\psi \\ 0\hspace{1em}1\end{array}\right]\left[\begin{array}{c}u\\ \omega \end{array}\right]$$

(1)

where $\psi$ is the orientation of the robot, $\omega$ is the angular velocity of the robot, $u$ is the linear velocity of the mobile robot, $\dot{x}$ is the component of the velocity in $x$, $\dot{y}$ is the component of the velocity in $y$, $\dot{\psi }$ is the angular velocity, and $a$ is the distance between the point of interest $(x, y)$ from the axis joining the wheels.

On the other hand, the dynamic model of the robot can also be used, which considers factors such as friction forces, masses, dimensions, etc. This model is closer to the actual operation of the robot. The dynamic model is defined in [18].

2.2. Mobile Robot Formation Model

The objective of the proposed formation is based on the fact that three mobile robots $\mathcal{R}\{r_1, r_2, r_3\}$ will form a geometrical figure, in this case, a triangle, as shown in Figure 1. $(x_c, y_c)$ follows a proposed trajectory, and it also controls the formation variables, i.e., the distances between the leader robot and the other two robots.

Figure 1. Formation diagram of three mobile robots $r_1, r_2$, and $r_3.$

In the diagram, $(x_c, y_c)$ is the position of the centroid of the formation in the world coordinate frame {W}; $d_1$ is the distance between $r_1$ and $r_2$; $d_2$ is the distance between $r_1$ and $r_3$; $d_3$ is the distance between $r_2$ and $r_3$; $\beta$ is the angle opposite to the segment $d_3$; and $\theta$ is the formation pose angle with respect to $\left\{W\right\}$. On the other hand, the control of the pose variables seeks to achieve trajectory tracking based on the calculation of the centroid of the geometric figure established in the algorithm.

The formation model of the mobile robot system is given in [19]:

$$\dot{h}=J_{R}U$$

(2)

where $\dot{h}={\left[\dot{x_1} \dot{y_1}\dot{{ x}_2}\dot{ y_2 }\dot{x_3} \dot{y_3}\right]}^T$ are the variations of the robot positions in the formation; $U={\left[u_1 {\omega }_1 u_{2 }{\omega }_2 u_3 {\omega }_3\right]}^T$ are the velocities of the robots in the formation; and $J_R$ is the Jacobian of the rotational arrays for the three-robot system. To determine the model in formation variables [19], the geometry or shape of the formation is described by $q_f={\left[d_1 d_2 \beta \right]}^T,$ and the posture geometry is given by $q_p={\left[x_c y_c \theta \right]}^T$, mathematically defined in (3).

$$q_p=\left[\begin{array}{c}\hfill {\displaystyle \frac{x_1+x_2+x_3}{3}}\hfill \\ \hfill {\displaystyle \frac{y_1+y_2+y_3}{3}}\hfill \\ \mathit{atan}\left({\displaystyle \frac{\frac{2}{3}{x}_1-\frac{1}{3}\left(x_2+x_3\right)}{\frac{2}{3}{y}_1-\frac{1}{3}\left(y_2+y_3\right)}}\right)\end{array}\right]\hspace{1em}{q}_f=\left[\begin{array}{c}\sqrt{{\left(x_1-x_3\right)}^2+{\left(y_1-y_3\right)}^2}\\ \sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}\\ \mathit{acos}\left({\displaystyle \frac{{d_1}^2+{d_2}^2-{d_3}^2}{2d_1{d}_2}}\right)\end{array}\right]$$

(3)

The relationship of the robot’s velocity to the formation variables can be expressed as follows:

$$\dot{q}={JJ}_{R}U$$

(4)

where $J$ is the formation Jacobian matrix and $\dot{q}={\left[q_f q_p\right]}^T$ represents the derivative of the shape and pose variables of the given formation.

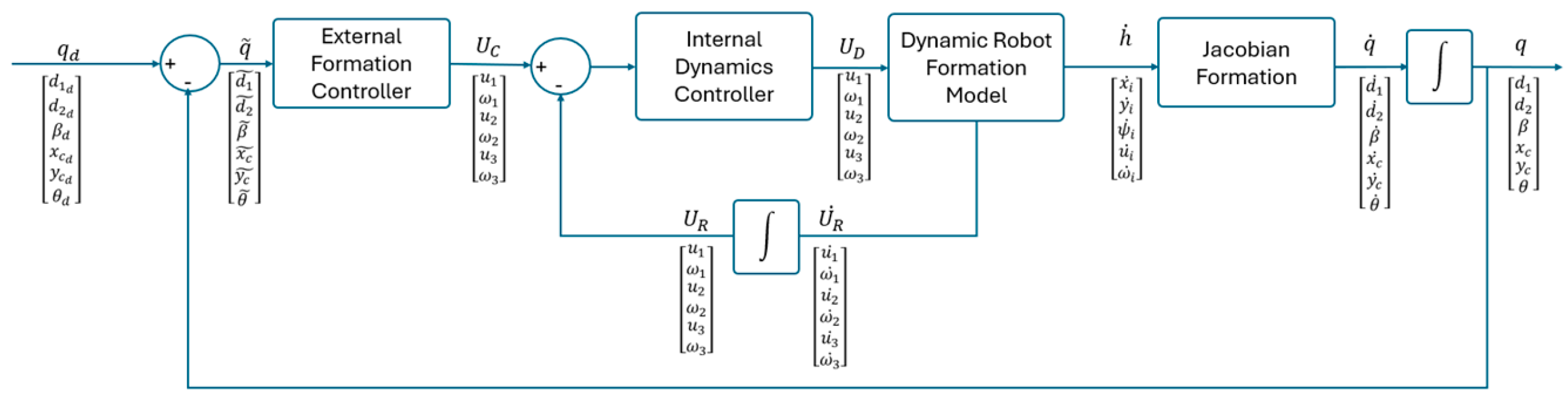
3. Controllers

This section details the five different cascade controllers that were developed. The outer controller is responsible for managing the formation, while the inner controller handles the robot’s dynamic compensation. The developed controllers are (i) PD formation controller without dynamic compensation (PD); (ii) SMC formation controller without dynamic compensation; (iii) PD formation controller with dynamic compensation (PD-DI); (iv) PD formation controller with dynamic sliding mode control (PD-SMCV); and (v) sliding mode formation control with dynamic sliding mode dynamic compensation (SMC-SMCV). Figure 2 shows the control diagram without dynamic compensation, which includes only the outer controller scheme. This scheme is used for the PD and SMC formation controllers. Additionally, Figure 3 shows the control diagram for both formation and dynamic compensation control, using a cascade controller configuration. This scheme is employed by the PD-DI, PD-SMCV, and SMC-SMCV controllers.

Figure 2. Formation control scheme without dynamic compensation.

Figure 3. Formation cascade control scheme with dynamic compensation.

3.1. PD Formation Controller without Dynamic Compensation (PD)

Based on the scheme shown in Figure 2, the PD formation controller without dynamic compensation employs the following control law [20]:

$$U_c={\left(J{J}_R\right)}^{-1}(\dot{q_d}+k_1\tilde{q})$$

(5)

where $\tilde{q}=q_d-q$ is the formation error variable; $k_1$ is a positive constant; and ${\dot{q}}_d$ is the derivative of the desired formation reference.

3.2. SMC Formation Controller without Dynamic Compensation

The SMC control law is defined by the following:

$$u_{smc}=u_{ac}+u_{dc}$$

(6)

where $u_{ac}$ corresponds to the continuous part of the control law; $u_{dc}$ is the discontinuous part of the control law, where each part is defined as follows:

$$u_{ac}={\left(J{J}_R\right)}^{-1}\left({\dot{q}}_d+{\displaystyle \frac{{\lambda }_{iF}}{{\lambda }_{pF}}}\tilde{q}\right) ;\hspace{1em}{u}_{dc}={\left(J{J}_R\right)}^{-1}{\displaystyle \frac{{\delta }_c}{{\lambda }_{pF}}}{\displaystyle \frac{s}{\left|s\right|+0.5}}$$

(7)

To obtain the continuous part, a sliding mode surface $s$ is defined as follows:

$$s={\lambda }_{pF}\tilde{q}+{\lambda }_{iF}\int \tilde{q}$$

(8)

where ${\lambda }_{iF}, {\lambda }_{pF}$ are the constants that correspond to the integral and proportional parts of the surface, respectively, and ${\delta }_c$ is a positive constant. For this controller, the control diagram shown in Figure 2 is employed, where the formation control is defined by the SMC controller [5].

3.3. PD Formation Controller with Dynamic Compensation (PD-DI)

This controller uses the cascade controller scheme shown in Figure 3, where the outer formation control is given by (5), while the inner control for dynamic compensation is defined as [21]:

$$u_{DI}=M\sigma +\eta$$

(9)

where $M$ is a diagonal matrix formed by the values ${\varphi }_1$ y ${\varphi }_2$, while $\eta$ is given by the following:

$$\eta =\left[\begin{array}{cccccc}0& 0& {\omega }_{ref}^2& u_{ref}& 0& 0\\ 0& 0& 0& 0& u_{ref}{\omega }_{ref}& {\omega }_{ref}\end{array}\right]$$

(10)

where $\varphi ={\left[\begin{array}{cccccc}{\varphi }_1& {\varphi }_2& {\varphi }_3& {\varphi }_4& {\varphi }_5& {\varphi }_6\end{array}\right]}^T$ is a vector formed by parameters that describe the dynamic behavior of the robot. Their values are as follows [18]: ${\varphi }_1=0.4072,{ \varphi }_2=0.2937,{ \varphi }_3=-0.0287,{ \varphi }_4=0.9979,{ \varphi }_5=-0.0004, \mathrm{a}\mathrm{n}\mathrm{d} {\varphi }_6=0.9865$. Lastly, $\sigma$:

$$\sigma ={\dot{U}}_c+Q_{D}tanh\left(\tilde{v}\right)$$

(11)

Here, $\tilde{v}=[U_c-U_r]$ represents the angular and linear speed error, with $U_r$ being the robot’s angular and linear velocity and $U_c$ being the output of the outer control loop.

3.4. PD Formation Controller with Dynamic Sliding Mode Control (PD-SMCV)

The inner loop controller for PD-SMCV control is given by the following:

$$u_{smcV}=u_{aV}+u_{dV}$$

(12)

The sliding mode surface $s$ is defined by the following:

$$s={\lambda }_{pV} \tilde{p}+{\lambda }_{iV}\int \tilde{p}$$

(13)

By differentiating (13), we obtain the following:

$$\dot{s}={\lambda }_{pV }\dot{\tilde{p}}+{\lambda }_{iV }\tilde{p}$$

(14)

where $\dot{\tilde{p}}={\dot{U}}_c-{\dot{U}}_r$, ${\dot{U}}_r$ is the derivative of the angular and linear velocity of the robot, and $U_c$ is the derivative of the output of the outer control loop. For the system to remain in the sliding mode surface $s$, it is required that $\dot{s}=0$. To obtain $u_{av}$, it is considered that $u_{dV}=0$; hence, in a closed loop, $u_{smcV}=u_{aV}$. By solving (16), the following expression is obtained:

$$u_{aV}=M\left({\displaystyle \frac{{\lambda }_{iV}}{{\lambda }_{pV}}}\tilde{p}+{\dot{U}}_c\right)+\eta$$

(15)

To obtain $u_{dV}$, the Lyapunov candidate $V={\displaystyle \frac{1}{2}}{s}^{T}s$ is defined. Thus, the derivative of $V$ is given by $\dot{V}=s^T\dot{s}$. In a closed loop, $u_{smcV}=U_r$. By substituting (12), (14), and (15) into $\dot{V}$, the following expression is obtained:

$$\dot{V}=s^T(-{\lambda }_{pV}{M}^{-1}{u}_{dV})$$

(16)

Thus, $u_{dV}$ is defined by the following:

$$u_{dV}=\left({\lambda }_{pV}{M}^{-1}\right)k_V sig\left(s\right);k_V>0$$

(17)

Substituting (17) into (16), it is verified that $\dot{V}<0$, ensuring that $s\to 0$ as $t\to \infty$. Analyzing (13) at $s=0$ and considering that the surface is defined by a first-degree polynomial function, it is determined that $\tilde{p}\to 0$ when ${\displaystyle \frac{{\lambda }_{iV}}{{\lambda }_{pV}}}>0$.

3.5. Sliding Mode Formation Control with Dynamic Sliding Mode Dynamic Compensation (SMC-SMCV)

For this controller, the scheme shown in Figure 3 is used. The outer formation control is defined by the SMC controller described in Section 3.2, while the inner control loop is managed by a controller defined as SMCV, which is given by the SMS controller in Section 3.4.

3.6. Stability Analysis of the PD Formation Controller with Dynamic Compensation (PD-DI)

For the stability analysis of the cascade system, the following Lyapunov is used:

$$V_C={\displaystyle \frac{1}{2}}{\tilde{v}}^T\tilde{v}+{\displaystyle \frac{1}{2}}{\tilde{q}}^T\tilde{q}$$

(18)

From this, the following is derived:

$${\dot{V}}_C={\tilde{v}}^T\dot{\tilde{v}}+{\tilde{q}}^T\dot{\tilde{q}}$$

(19)

The definition of errors is replaced as follows:

$${\dot{V}}_C={\tilde{v}}^T({\dot{U}}_c-{\dot{U}}_r)+{\tilde{q}}^T({\dot{q}}_d-\dot{q})$$

(20)

In a closed loop, replacing (5) and (9) in (20) and developing the expression, the following is obtained:

$${\dot{V}}_C=-{\tilde{v}}^T{Q}_{D}tanh\left(\tilde{v}\right)-{\tilde{q}}^T{k}_1\tilde{q}$$

(21)

It is shown that ${\dot{V}}_C<0$ whereby $\tilde{v}\to 0 and \tilde{q}\to 0$ with $t\to \infty$ are verified.

3.7. Stability Analysis of the PD Formation Controller with Dynamic Sliding Mode Control (PD-SMCV)

For the stability analysis of the cascaded system, we employed the Lyapunov (18), (19), and (20) in a closed loop and replaced (5), (15), and (17) in (20); it was shown that $s\to 0$ with $t\to \infty$, and after developing the expression, the following is obtained:

$${\dot{V}}_C=-{\tilde{v}}^T{Q}_{D}tanh\left(\tilde{v}\right)-{\tilde{q}}^T{\displaystyle \frac{{\lambda }_{iF}}{{\lambda }_{pF}}}\tilde{q}$$

(22)

It is shown that ${\dot{V}}_C<0$ whereby $\tilde{v}\to 0 \mathrm{a}\mathrm{n}\mathrm{d} \tilde{q}\to 0$ with $t\to \infty$ are verified.

3.8. Stability Analysis of the Sliding Mode Formation Control with Dynamic Sliding Mode Dynamic Compensation (SMC-SMCV)

For the stability analysis of the cascade system, the following Lyapunov is used:

$$V_C={\displaystyle \frac{1}{2}}{\tilde{p}}^T\tilde{p}+{\displaystyle \frac{1}{2}}{\tilde{q}}^T\tilde{q}$$

(23)

By differentiating it in a closed loop and replacing (7), (15), and (17) in (23), it is also shown that $s\to 0$ with $t\to \infty$, and after developing the expression, the following is obtained:

$${\dot{V}}_C=-{\tilde{p}}^T{\displaystyle \frac{{\lambda }_{iV}}{{\lambda }_{pV}}}\tilde{p}-{\tilde{q}}^T{\displaystyle \frac{{\lambda }_{iF}}{{\lambda }_{pF}}}\tilde{q}$$

(24)

It is shown that ${\dot{V}}_C<0$ whereby $\tilde{p}\to 0 \mathrm{a}\mathrm{n}\mathrm{d} \tilde{q}\to 0$ with $t\to \infty$ are verified.

4. Results

To evaluate the trajectory tracking of the formation of the three mobile robots using the five proposed control techniques, two experiments were conducted: Experiment 1: trajectory tracking of the formation of the robots with the five proposed controllers without perturbations; and Experiment 2: trajectory tracking of the formation of robots with the five proposed controllers with perturbations, to evaluate the robustness. The methodology implemented to define the parameters of the controllers was to select small initial values for the controllers to avoid abrupt control actions. The constants were assumed to have the following values ${\lambda }_{pF}={\lambda }_{iF}={\lambda }_{pV}={\lambda }_{iV}={\delta }_C=k_V=0.1$,$Q_D=\left[10; 01\right], \mathrm{a}\mathrm{n}\mathrm{d} k_1=\left[11111\right]$. For each controller, the parameters were modified according to the error curves obtained, and the integral of squared error (ISE) value was calculated. For the smallest ISE values, the following parameters were obtained: PD formation controller: diagonal 6 × 6 matrix $k_1$ with values $\left[11251\right]$; SMC formation controller: ${\lambda }_{pF}=1$, ${\lambda }_{iF}=1$, and ${\delta }_C=0.6$; dynamic compensation controller: diagonal 2 × 2 matrix $Q_D={\left[70;07\right]}_{2x2}$; and SMCV controller: ${\lambda }_{pV}=1$, ${\lambda }_{iV}=1$, and $k_V=1.5$. The parameters of the trajectory used in the tests were $x_d\left(t\right)=1+10 cos\left(0.01t\right)$ and $y_d\left(t\right)=1+10 sin\left(0.01t\right)$.

4.1. Experiment 1: Path Following without Disturbance

This experiment had a duration of 50 s. Figure 4 shows the pose and shape errors. Analyzing the results, the controller with the best performance (faster stabilization) was the PD-SMCV controller, which implemented PD formation control and SMC dynamic compensation. It can also be observed that controllers with SMC formation control exhibited oscillatory and abrupt variations in error, resulting in longer settling times.

Figure 4. Formation errors.

Figure 5 shows the trajectory followed by the centroid of the triangle formation of the robots. For the trajectory, a circle with a radius of 10 m was set. In this graph, it can be observed that the PD, PD-DI, and PD-SMC controllers describe a smoother path with less oscillation and similar settling times. The SMC and SMC-SMCV controllers resulted in a rougher response, with a more pronounced overshoot at the start of the path. Analyzing this figure, it can be observed that, consistent with the error analysis, the SMC-SMCV controller provided a smoother response with a shorter settling time.

Figure 5. Centroid formation trajectory (Without Disturbance).

4.2. Experiment 2: Path Following Applying Dynamic Disturbance

From $t=50 \mathrm{s}$ onwards, a disturbance was introduced to evaluate the robustness of the controllers. This disturbance was meant to simulate an external force that alters the dynamic behavior of the robots, affecting the path-following capabilities of the controllers. To modify the dynamic properties of the robot model, the parameters were multiplied by a constant $k=15$.

Figure 6 shows the formation errors. In this experiment, it can be observed that the PD-SMCV controller resulted in lower errors and faster settling times, indicating that this controller better corrected the dynamic perturbations of the system compared to the other controllers, which exhibited higher errors. The PD-SMCV controller presented errors of less than 0.5 m for the centroid positions, while the PD controller, which lacked dynamic compensation, resulted in errors greater than 6 [m] for the centroid position. In contrast, the PD-DI, SMC, and SMC-SMCV controllers presented errors of less than 2 m. Additionally, it can be observed that controllers implementing the SMC formation control exhibited significantly higher errors and oscillations in the formation variables $\theta , d_1$, and $\beta$. Figure 7 shows the centroid formation trajectory. It is observed that most of the controllers exhibited a significant deviation between the path followed and the reference, except for the PD-SMCV controller, which effectively corrected the disturbance and aligned closely with the reference.

Figure 6. Formation errors.

Figure 7. Centroid formation trajectory (With Disturbance).

5. Discussion

Based on the results in Table 1 and Table 2, it is determined that the PD-DI and PD-SMCV controllers resulted in a more robust performance in following the desired trajectory and maintaining the specified formation. These controllers have lower ISE values, indicating reduced error and higher accuracy in formation control. In addition, the SMC-SMCV controller showed poor performance in all experiments analyzed, worsening especially when larger perturbations were applied to the dynamic parameters. This indicates that, although SMC controllers are useful due to their robustness, combining SMC controllers for formation control (outer loop) and dynamic compensation (inner loop) may be disadvantageous. Finally, based on the obtained plots and ISE values, the controller with the best results was the PD-SMCV controller.

Table 1. ISE for each controller in the path following of the formation without disturbance.

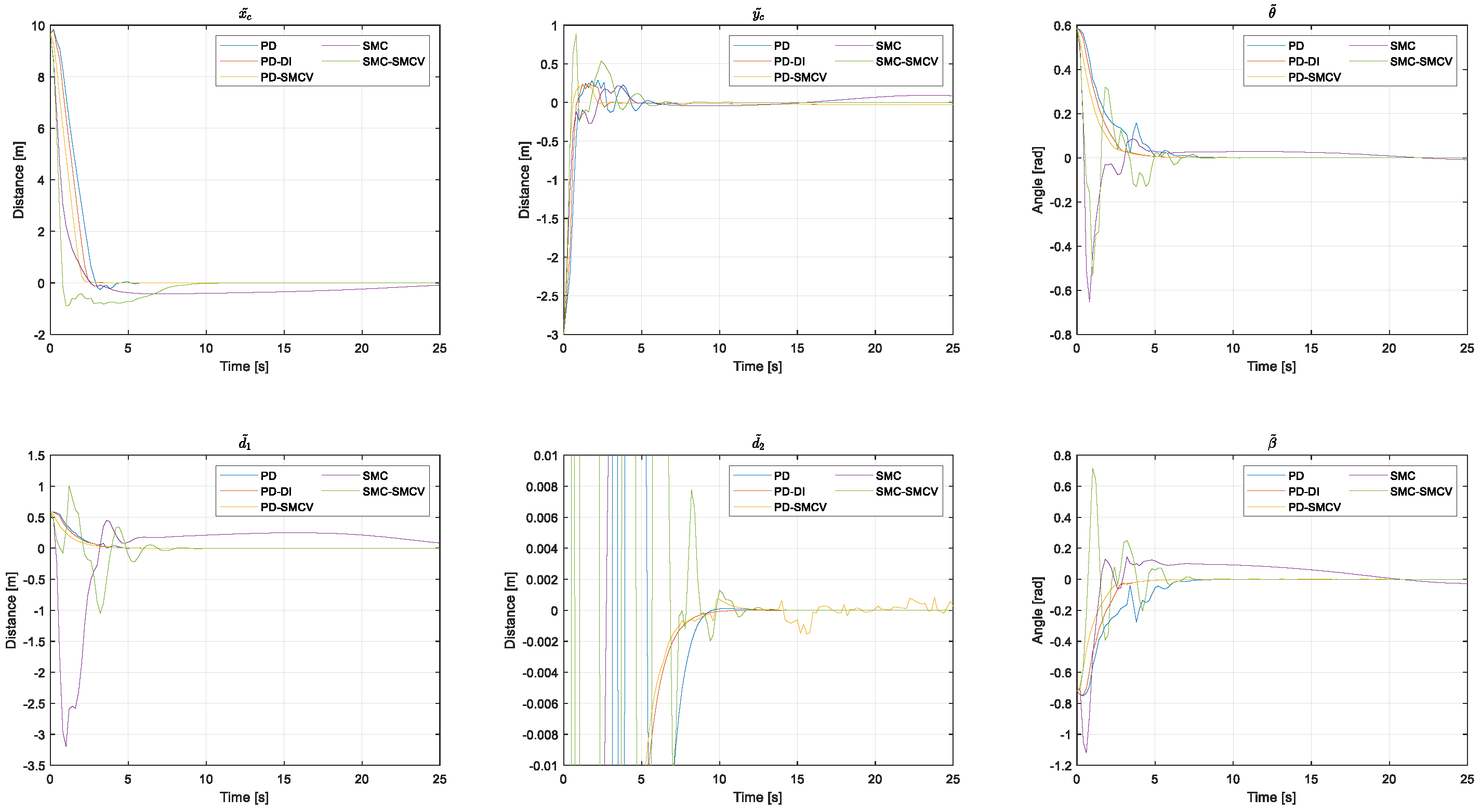
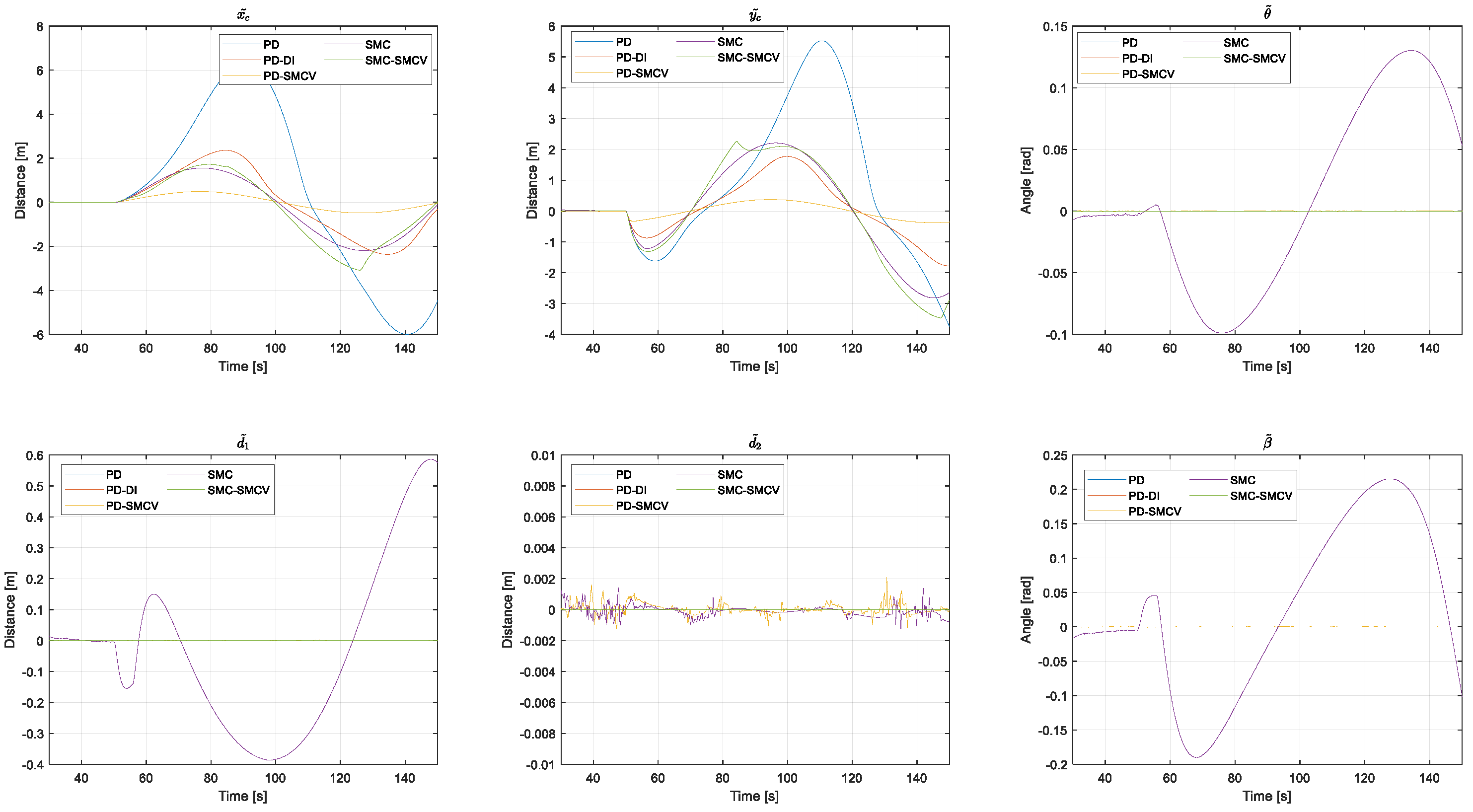
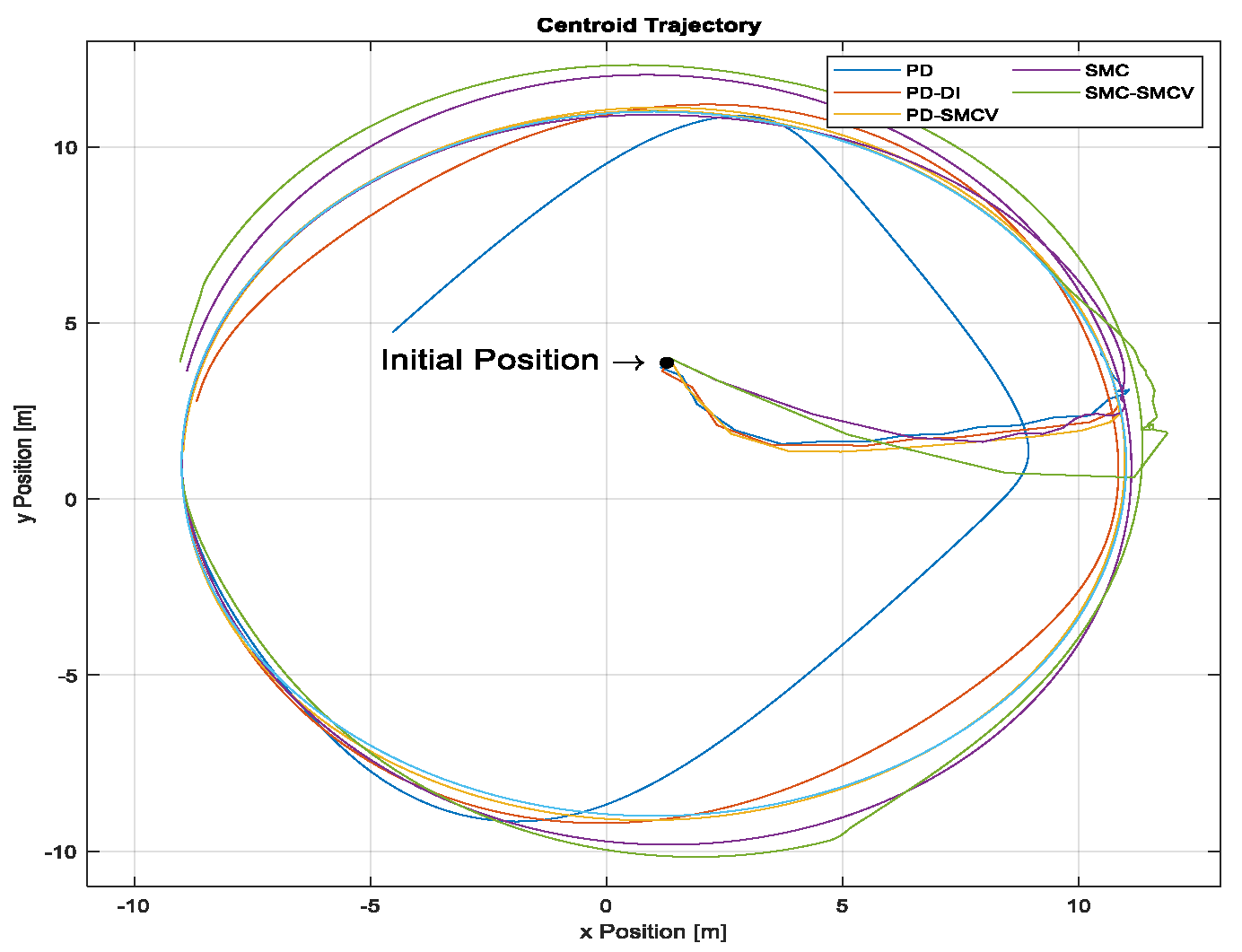
PD	0.536	2.034	0.719	207.505	10.258	0.453
PD-DI	0.361	1.770	0.617	187.605	7.691	0.319
PD-SMCV	0.481	1.358	1.104	156.313	6.212	0.480
SMC	0.476	1.960	0.479	38.100	4.479	0.727
SMC–SMCV	6.195	1.377	1.494	44.890	4.940	0.599

Table 2. ISE for each controller in the path following of the formation with disturbance.

Controller	${\tilde{\mathit{d}}}_1$	${\tilde{\mathit{d}}}_2$	$\tilde{\mathit{\beta }}$	${\tilde{\mathit{x}}}_{\mathit{c}}$	${\tilde{\mathit{y}}}_{\mathit{c}}$	$\tilde{\mathit{\theta }}$
PD	0.3726	2.0811	0.7767	1.80E+03	708.0329	0.3766
PD-DI	0.3307	1.8614	0.5798	328.021	99.8266	0.2986
PD-SMCV	0.211	1.93	0.3269	79.8945	8.5865	0.2118
SMC	20.4928	1.4243	2.8142	221.6967	269.3052	0.9635
SMC–SMCV	1.3112	1.5882	0.557	275.4384	335.2991	0.271

6. Conclusions

Based on the results of the experiments performed, the PD-SMCV controller demonstrated the best performance compared to the other controllers without disturbance. In the robustness test with the introduction of a disturbance, the controllers without dynamic compensation did not perform well. Although the SMC controller lacked dynamic compensation control, it showed remarkable robustness, outperforming the PD controller. According to ISE indicators, the PD-SMCV controller, which combined PD forming control with SMCV dynamic compensation for the inner loop, not only quickly reduced the error in forming variables, but also maintained stable and accurate robot forming in the presence of disturbances. In summary, the PD-SMCV controller excels in its ability to deliver superior performance in robotic formation trajectory tracking and disturbance management, reaffirming its effectiveness by combining advanced control techniques with dynamic compensation.