The Development and Evaluation of a High-Frequency Toroidal Transformer for Solid-State Transformer Applications †
Abstract
:1. Introduction
2. Design and Analysis Procedure
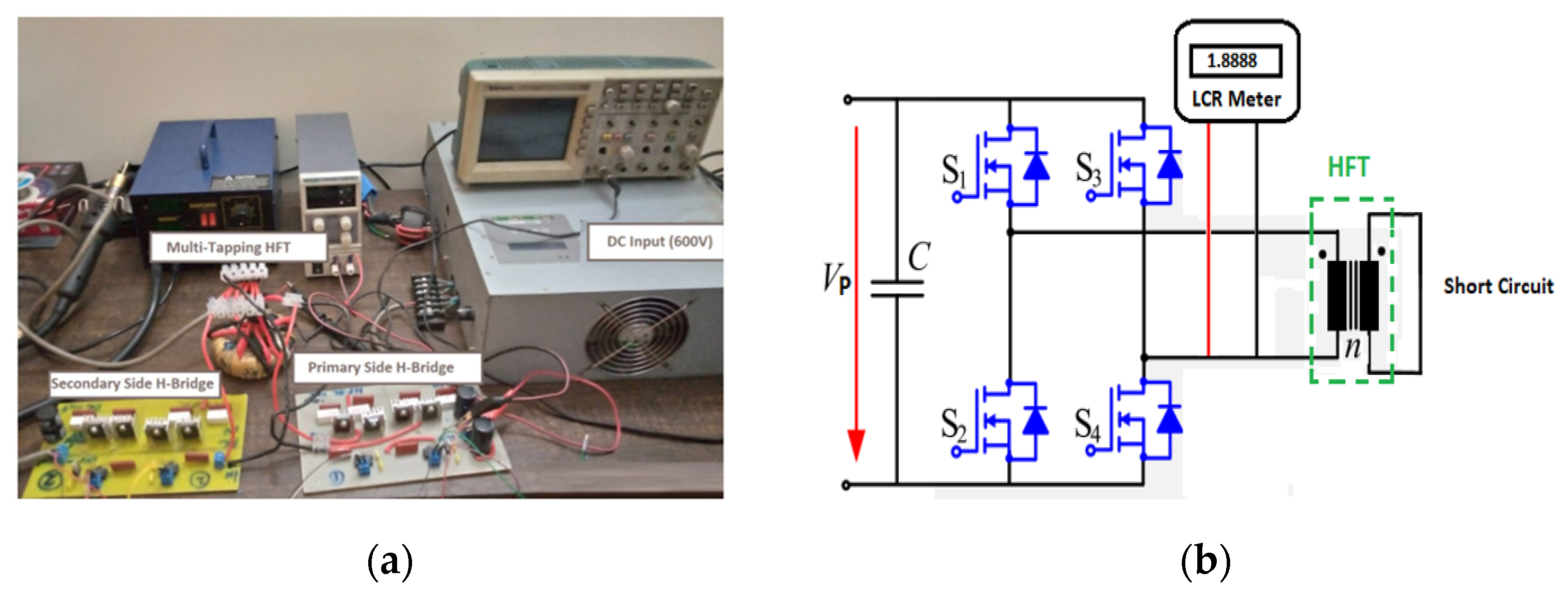
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Amini, M.; Almassalkhi, M. Trading off robustness and performance in receding horizon control with uncertain energy resources. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Saadatmand, S.; Shamsi, P. Adaptive critic design-based reinforcement learning approach in controlling virtual inertia-based grid-connected inverters. Int. J. Electr. Power Energy Syst. 2021, 127, 106657. [Google Scholar] [CrossRef]
- Rhaman, M.; Matin, M.; Hossain, M. Ferromagnetic, electric, and ferroelectric properties of samarium and cobalt co-doped bismuth ferrite nanoparticles. J. Phys. Chem. Solids 2020, 147, 109607. [Google Scholar] [CrossRef]
- Imaoka, J.; Okamoto, K.; Shoyama, M. Modeling, magnetic design, simulation methods, and experimental evaluation of various powder cores used in power converters considering their dc superimposition characteristics. IEEE Trans. Power Electron. 2019, 34, 9033–9051. [Google Scholar] [CrossRef]
- Ahmed, S.; Chang, K.-C.; Nguyen, T.-T.; Chu, K.-C.; Chang, F.-H.; Wang, H.-C. Interleaved DC/DC Boost Converter for Hybrid Electric and Electrical Vehicles; Springer: Cham, Switzerland, 2021; pp. 708–716. [Google Scholar]
- Nan, X.; Sullivan, C.R. An equivalent complex permeability model for Litz-wire windings. IEEE Trans. Ind. Appl. 2009, 45, 854–860. [Google Scholar] [CrossRef]
| Test Cases | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Core Material | Ferrite | Iron-Powdered Alloy (MPP) | Amorphas (Microlite) |
| Optimal Flux Density (Tesla) | 0.25 | 0.9 | 0.7 |
| Dimension (OD, ID, H) | |||
| Number of Turns (Primary, Secondary) | 100, 50 | 100, 50 | 100, 50 |
| Wire Gauge (Primary, Secondary) | 21, 21 | 21, 21 | 21, 21 |
| Numbers of Strands (Primary, Secondary) | 5, 3 | 5, 3 | 5, 3 |
| Voltage (Primary, Secondary) | 600, 300 | 600, 300 | 600, 300 |
| Frequency (kHz) | 10 | 10 | 10 |
| Windings Configuration | Core Material | Magnetizing Inductance | Leakage Inductance | ||
|---|---|---|---|---|---|
| Primary | Secondary | Primary | Secondary | ||
| Winding | Winding | Winding | Winding | ||
| Round Wire | Ferrite | 47.3 | 11.5 | 89.00 | 24.20 |
| Microlite | 34.7 | 8.32 | 191.2 | 127.7 | |
| MPP | 33.1 | 8.91 | 191.1 | 126.4 | |
| Twisted Wire (isolated strands) | Ferrite | 46.1 | 11.1 | 69.00 | 14.00 |
| Microlite | 35.3 | 8.31 | 189.2 | 119.7 | |
| MPP | 34.7 | 9.12 | 191.1 | 120.4 | |
| LITZ wire | Ferrite | 47.9 | 10.9 | 61.00 | 12.10 |
| Microlite | 34.9 | 8.12 | 181.2 | 117.1 | |
| MPP | 34.8 | 9.01 | 181.9 | 117.9 | |
| Parameters | Unit | 10 kHz | 50 kHz | ||
|---|---|---|---|---|---|
| Simulation | Experimental | Simulation | Experimental | ||
| Inductance (Primary) | 46.1 | 46.5 | 40.5 | 42.9 | |
| Inductance (Secondary) | 11.1 | 11.3 | 9.70 | 9.95 | |
| Leakage Inductance (Primary) | 69.0 | 70.2 | 1.0 | 1.18 | |
| Leakage Inductance (Secondary) | 14.1 | 14.8 | 4.00 | 4.73 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakoor, A.; Haq, A.U.; Iqbal, T. The Development and Evaluation of a High-Frequency Toroidal Transformer for Solid-State Transformer Applications. Eng. Proc. 2023, 45, 11. https://doi.org/10.3390/engproc2023045011
Shakoor A, Haq AU, Iqbal T. The Development and Evaluation of a High-Frequency Toroidal Transformer for Solid-State Transformer Applications. Engineering Proceedings. 2023; 45(1):11. https://doi.org/10.3390/engproc2023045011
Chicago/Turabian StyleShakoor, Abdul, Azhar Ul Haq, and Taosif Iqbal. 2023. "The Development and Evaluation of a High-Frequency Toroidal Transformer for Solid-State Transformer Applications" Engineering Proceedings 45, no. 1: 11. https://doi.org/10.3390/engproc2023045011
APA StyleShakoor, A., Haq, A. U., & Iqbal, T. (2023). The Development and Evaluation of a High-Frequency Toroidal Transformer for Solid-State Transformer Applications. Engineering Proceedings, 45(1), 11. https://doi.org/10.3390/engproc2023045011






