Abstract
The problem of anomaly detection in time series has recently received much attention, but in most practical applications, labels for normal and anomalous data are not available. Furthermore, reasons for anomalous results must often be determined. In this paper, we propose a new anomaly detection method based on the expectation–maximization algorithm, which learns the probabilistic behavior of local patterns inherent in time series in an unsupervised manner. The proposed method is simple yet enables anomaly detection with accuracy comparable with that of the conventional method. In addition, the representation of local patterns based on probabilistic models provides new insight that can be used to determine reasons for anomaly detection decisions.
1. Introduction
Time series data, including sensor data in factories, are continuously collected in a variety of areas. One of the important applications for analyzing such data is anomaly detection. However, there are two major challenges in the actual implementation of automatic time series anomaly detection systems. First, it is often difficult to obtain labeled data for anomalies, so the data must be treated as unsupervised data, assuming that the majority of the data are normal. The other challenge is that the maintainability and reliability of anomaly detection systems often require a transparent anomaly detection model and interpretability of the output. These requirements make it necessary to use simple models, but this gives rise to a trade-off between model simplicity and anomaly detection performance. Therefore, a new anomaly detection method is needed that is interpretable without compromising anomaly detection performance.
One of the promising methods for solving these problems is OCLTS (One Class Time Seires Shapelets) [1]. OCLTS applies important subsequences in time series data, called shapelets, to enable unsupervised anomaly detection and to provide the specific parts of the time series that are the reason for the anomaly detection. However, OCLTS has several difficulties. First, the anomaly score is based on complex correlations between local patterns, so there is no direct correspondence between the anomaly score and the location in the time series that is the reason for the anomaly. In addition, the shapelets learned by OCLTS tend to take the average shape of similar time series. For example, consider the pattern shown in Figure 1a,b, in which a single concave point appears in a rightward sloping waveform. The position of the concavity is different in Figure 1a,b, but when such a pattern is the learning target, shapelets tends to have an average waveform, as shown in Figure 1c, and the concavity feature becomes unclear. In this case, it is difficult to identify the basis of the anomaly from the anomalous waveform with no concavity.
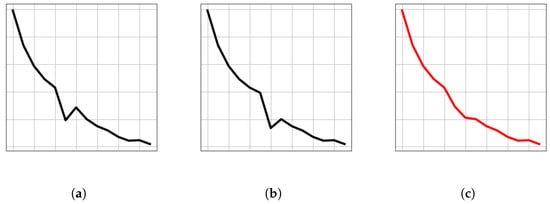
Figure 1.
Examples of similar subsequences (a,b) and the average subsequence of these subsequences (c).
In this paper, we propose a method for time series representation learning and anomaly detection based on a novel learning procedure inspired by the subsequence-based feature transformation used in OCLTS. In the proposed method, there is one-to-one correspondence between the anomaly score and the local pattern representation, and the location of the time series for the cause of the anomaly becomes clearer. By stochastically modeling the subsequences, the proposed method provides another insight into the difference between anomalous and normal patterns, which is different from traditional shapelets-based methods. Despite the simplicity of the proposed method, experiments using public datasets show that it can detect anomalies with accuracy comparable to that of OCLTS.
2. Related Work
One of the most successful data mining methods for time series data analysis in recent years is a method based on representations of subsequences called shapelets, which classify time series data according to differences in subsequences rather than the entire time series. The original method [2] searched for the most different subsequences among classes and performed classification based on decision trees, but in [3,4], classification performance was greatly improved by combining advanced machine learning models with feature transformations that treat shapelets as feature transformation parameters. Shapelets can be applied not only to time series classification problems, but also to time series clustering [5,6] and approximation of DTW (Dynamic Time Warping) [7]. OCLTS [1], the method most closely related to this paper, extends shapelets to the anomaly detection problem. In that method, multiple shapelets are used for approximation over the entire time series, and the time series is converted to a vector. A one-class SVM [8] model is defined with transformed vectors as input, and the shapelet shape and one-class SVM model parameters are learned simultaneously using the gradient method. The feature transformation of time series data using shapelets proposed in OCLTS is very promising because of its extensibility in various ways in time series data analysis based on subsequences. In this paper, we propose a simpler algorithm for learning local patterns based on this feature transformation.
A time series data classification method called LOGIC [9] has been studied for the probabilistic representation of local patterns in time series. In LOGIC, local patterns based on multiple subsequences inherent in a set of time series are modeled by Gaussian process regression and mapped to a feature space of dimension equal to the number of models by using the likelihood of each model. By using the mapped features as input data for various machine learning classifiers, such as random forests, time series classification can be performed with accuracy comparable to that of state-of-the-art time series classification methods. This method showed promising results for modeling the probabilistic behavior of local patterns and for potentially representing times series based on the likelihood of features. However, LOGIC targets time series classification, which is a different problem from the one addressed in this paper. In addition, this method learns and evaluates subsequences obtained by fixing the position of time series segmentation, and does not take into account the case where the position of subsequence patterns shifts. In this paper, when learning or evaluating a subsequence, the starting position of the subsequence is searched for according to the input time series data.
3. Preliminaries
3.1. Notation
3.1.1. Time Series Data
Let denote a set of N normal time series data of length Q. Let for the nth time series data.
3.1.2. Time Series Subsequence
Let of a time series denote the subsequence of length L starting at position j, where .
3.2. LOPAS Transform
In this section, we describe a method for transforming time series data into feature vectors using local patterns. This was proposed in OCLTS as a feature transform using shapelets. Here we describe a generalized version of the transformation using any local patterns, including shapelets. Because it was not named in [1], we call it LOPAS (Local Patterns-based Similarity) transform.
Let M be a model for which the similarity to subsequences can be defined. For a set containing K models M, denote the kth model by . In [1], the model corresponds to a shapelet, and in our proposed method, described in Section 4, the model corresponds to a multivariate Gaussian distribution. The similarity between a model M and a subsequence is denoted by . In [1], the distance between the shapelet and the subsequence is defined as the dissimilarity; in our proposed method, the log-likelihood is defined as the similarity.
In the LOPAS transform, the K models and the nth time series are taken as input. A subsequence on corresponds to any of for , based on the similarity . A K-dimensional vector is output as the feature.
The intuitive explanation is that each model in is assumed to represent a subsequence, and the whole time series is approximated by the subsequences. In the approximation, while allowing for overlap, the positions on are slid so that there are no gaps, and the model and its position are searched for the position that best approximates the subsequences on . Here, is the number of slides on , in other words, the number of models used to approximate . The model number that maximizes the similarity for the th slide and its position are given as follows:
The set of in Equation (1) is denoted by
Because models are slid with no gaps, increases between as increases by 1 for . Note that never exceeds J. The number of slides depends on the set of models and the time series .
Once is determined, a K-dimensional feature vector is calculated based on the following equation.
where is the set of in satisfying . That is,
The LOPAS transform is the above procedure for transforming time series data to features .
3.3. Assignment Factor
Another way to look at the LOPAS transformation is to consider that the subsequence used in the transformation to the features is assigned to the model . Other subsequences are considered not to be assigned to any model. Here, we introduce an assignment factor r and define if a subsequence is assigned to the kth model and otherwise. This is expressed mathematically as follows.
4. Proposed Method
In this section, we describe time series local patterns for anomaly detection and propose a learning method for them. We named these patterns LOPAD (Local Patterns for Anomaly Detection). We describe the basic idea of local patterns in Section 4.1 and explain how they are learned in Section 4.2. In Section 4.3, we describe how to evaluate anomaly scores of time series data using LOPAD.
4.1. Basic Concept
The proposed method learns a set of multivariate Gaussian distributions that represent a sufficient variety of local patterns in the context of the LOPAS transformation inherent in a set T of normal time series. For diagnostics, the LOPAS transformation is applied to the time series data to be diagnosed using the set of models. The time series data are considered anomalous if any of the subsequences deviates significantly from the normal pattern, and the anomaly is detected by calculating the anomaly score based on the similarity at that time. The anomalous subsequence is output as the reason for the anomaly detection. Furthermore, because the model uses a multivariate Gaussian distribution to model the pattern of subsequences, it can provide the probabilistic pattern with a confidence interval.
Specifically, instead of the shapelets used in OCLTS for the LOPAS transformation, K multivariate Gaussian distributions of dimension L are retained. The mean and covariance matrix parameters of the kth Gaussian distribution are denoted by , where are the parameters of the kth Gaussian distribution. The parameters of are estimated from the set of similar subsequences, and is considered to have a distribution of waveforms with similar patterns. The set of similar subsequences is the set of all local patterns in the normal time series dataset T that satisfy the assignment factor as described in Definition 4. In other words, the set of local patterns defined as
contains the samples for estimating the parameters of the model . Put another way, the local patterns assignment procedure in the LOPAS transformation yields K clusters of patterns. The model represents the probability distribution of the clusters.
Furthermore, the similarity between and the subsequence is defined as the log-likelihood
where
However, for optimal assignment, an appropriate must be obtained but this requires that appropriate clusters be obtained. In the next section, we describe the objective function and the learning method for optimizing these parameters.
4.2. Learning Method
The proposed method aims to obtain multiple multivariate Gaussian models that represent all local patterns inherent in normal time series data. Specifically, the models are obtained by the following two procedures:
- Assign subsequence to clusters by LOPAS transformation.
- Obtain a Gaussian model for each cluster.
These can be formulated as follows:
This objective function can be optimized by using the expectation–maximization algorithm, which has long been used in K-means clustering and other methods. First, each parameter in the models is fixed and the assignment factor r is obtained. Second, the parameters of the multivariate Gaussian model corresponding to each cluster are updated by fixing r. By repeating these two procedures until the objective function converges, we obtain a set of multivariate Gaussian models that represent the various subsequence patterns inherent in a set of normal time series data.
Specifically, a model set consisting of K Gaussian distributions initialized with appropriate parameters is prepared. Using the procedure in Equation (4), we calculate the assignment factor r for each K and obtain the set of assigned subsequences . Next, using as input, we estimate the mean parameter and the covariance matrix parameter of the model for each k. To estimate the mean parameter and covariance matrix parameter of the Gaussian distribution, any method can be used, such as maximum likelihood estimation.
The parameters are updated using the obtained and . As described above, representing various subsequence patterns is obtained by repeating the two steps of (1) subsequence assignment and (2) parameter updating until the termination condition is satisfied.
The above algorithm is summarized in Algorithm 1.
| Algorithm 1 Algorithm of the proposed method |
|
4.3. Evaluation Method
Each model in obtained by training represents subsequence patterns inherent in normal data. Therefore, when the LOPAS transformation is applied to time series data, the likelihood of each model should be large for normal time series data. Conversely, anomalous data will result in a small likelihood for one or more of the models. Therefore, the smallest of the K-dimensional feature vectors obtained by the LOPAS transformation is adopted as the degree of normality of the time series data. In other words, if represents the K-dimensional features obtained by the LOPAS transformation for time series data , the anomaly score is given by the following formula.
The subsequence with the maximum anomaly can be regarded as the local pattern that most greatly differs from the normal pattern in the time series data. Let denote the model that has the maximum anomaly score and denote the corresponding subsequence. Let be the ith value of . The possible values of are considered to follow a Gaussian distribution , conditioned by the points other than in in . Therefore, by obtaining the conditional distribution at all points of i and visualizing the range of
for each point, we can analyze the difference between the normal subsequence pattern and the anomalous waveform (where C is an arbitrary constant).
5. Experiment and Evaluation
5.1. Accuracy in the UCR Dataset
We evaluate the proposed method on some data from the UCR dataset [10]. For the experiment, the class with the largest number of data, defined originally as “Train” in the dataset, was assumed as the normal class and was used as training data. The data for the other classes were used as validation data. In the data defined originally as “Test”, data with the same class as the training data were taken as the normal class, and data with other classes were taken as the anomalous class. The training data were used for training, and the anomaly score was calculated for each of the normal and anomalous data in the test data, and the area under the curve (AUC) was calculated for evaluation.
The initial parameters of were set by estimating the Gaussian mixture model with K mixed models for all subsequences of length L in the time series dataset T, and the parameters of each model were used as initial parameters. Other hyperparameters were set using validation data from among the number of models and subsequence length .
The experimental results are shown in Table 1. The proposed method detected anomalies with the same accuracy as OCLTS. Note, however, that OCLTS uses a highly non-linear transformation based on a kernel method to calculate the anomaly, whereas the proposed method uses a simple method to calculate the anomaly.

Table 1.
Comparison of AUC in UCR time series data.
5.2. Visualization Evaluation Using Current Data
In this experiment, we used a dataset of solenoid current measurements called NASA Shuttle Valve Data [11]. As a preprocessing step, data were sampled every 100 points from the original time series of length 20,000 to make a time series of length 200. The time series is scaled so that the minimum and maximum values are [0, 1]. In the dataset, the seven time series shown in Figure 2 are taken as normal data, and the models are trained with the proposed method and OCLTS, respectively. After a certain period of time with noisy steady current in the first half of the time series, the data enters a phase in which the current rises. During the rise phase, the current temporarily drops during the rise, but soon rises and enters the steady current phase, where the current remains high. The current then enters a descending phase, rising temporarily during the descending phase, but eventually decreasing to near the initial current value. Normal data tend to differ in the timing and magnitude of the temporary drops or rises during the rise and fall phases. For the anomaly data, the time series data shown in Figure 3 are used. These data do not show a temporary drop in the current value during the rise phase. The proposed method and OCLTS were applied to these data to diagnose and visualize the anomaly.

Figure 2.
Seven time series of current measurements in NASA Shuttle Valve Data used as training data.
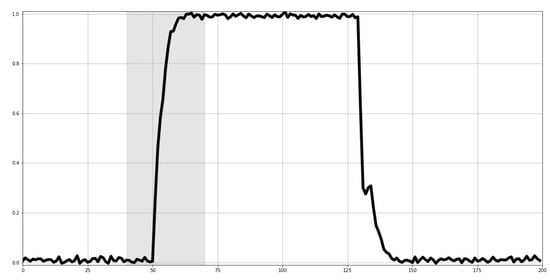
Figure 3.
Anomaly data in NASA Shuttle Valve Data. The current rise phase is highlighted, which is different from the pattern of normal data.
First, the results of the OCLTS visualization are shown in Figure 4. The black line is the original time series, and the upward phase showing the anomaly pattern is enlarged. The red line shows the shapelet obtained by training in OCLTS. The learned shapelet appears to be the average pattern of the training data. In the training data, the position of the temporary dip in the ascending phase varies, and as a result of learning the average pattern, the temporary dip disappears in the learned pattern. The visualization results of the proposed method are shown in Figure 5, where the normal pattern region is obtained as in Formula (11). The normal pattern region obtained using the proposed method shows a distorted region with repeated unevenness, and the original time series (black line) is found to be out of the normal region. This implies that the proposed method’s normal pattern contains some kind of uneven waveform in the ascending phase. Thus, the proposed method provides insight into the behavior of patterns based on subsequences, which is difficult to achieve with conventional shapelets.
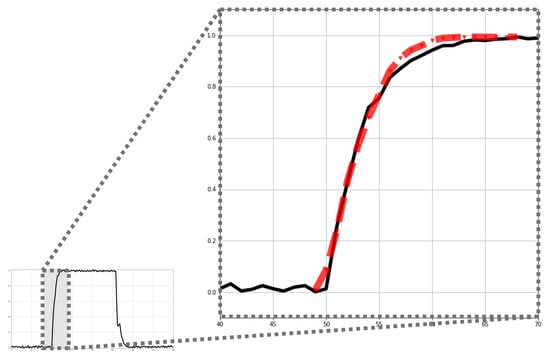
Figure 4.
Results of visualization analysis using OCLTS. The black line represents the time series data and the red line represents the shapelet obtained by training.

Figure 5.
Results of visualization analysis using LOPAD (proposed). The black line is the time series data, and the pink area indicates the normal pattern.
5.3. Limitations of Our Method
The above results demonstrate that our proposed method is effective in anomaly detection in various domains of data. However, we should mention that there may be situations where our proposed method fails. First, our proposed method is designed to identify anomalies primarily based on the most irregular subsequence and is unable to consider correlations between subsequences. In such cases, it is necessary to employ OCLTS, which can capture complex correlations between subsequences that cannot be resolved due to its kernel method. Furthermore, both the proposed method and OCLTS generate features from time series data using the LOPAS transform, they cannot model in which the training data do not have roughly similar shapes.
6. Conclusions
In this paper, we proposed a representation learning method based on the probabilistic behavior of subsequences for anomaly detection in time series. Experiments confirmed that the proposed method has anomaly detection performance comparable to that of the conventional method OCLTS, but with a more transparent anomaly calculation procedure. Furthermore, the probabilistic modeling of subsequence patterns provides insight into the reason why anomaly detection differs from OCLTS.
Author Contributions
Conceptualization, K.K., A.Y. and K.U.; methodology, K.K.; software, K.K. and A.Y.; validation, K.K.; writing—original draft preparation, K.K.; writing—review and editing, A.Y. and K.U.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study applied open access dataset [10,11].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yamaguchi, A.; Nishikawa, T. One-class learning time-series shapelets. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 2365–2372. [Google Scholar]
- Ye, L.; Keogh, E. Time series shapelets: A new primitive for data mining. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 947–956. [Google Scholar]
- Grabocka, J.; Schilling, N.; Wistuba, M.; Schmidt-Thieme, L. Learning time-series shapelets. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 392–401. [Google Scholar]
- Lines, J.; Davis, L.M.; Hills, J.; Bagnall, A. A shapelet transform for time series classification. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12 August 2012; pp. 289–297. [Google Scholar]
- Zakaria, J.; Mueen, A.; Keogh, E. Clustering time series using unsupervised-shapelets. In Proceedings of the 2012 IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 785–794. [Google Scholar]
- Zhang, Q.; Wu, J.; Yang, H.; Tian, Y.; Zhang, C. Unsupervised feature learning from time series. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 2322–2328. [Google Scholar]
- Lods, A.; Malinowski, S.; Tavenard, R.; Amsaleg, L. Learning DTW-preserving shapelets. In Proceedings of the Advances in Intelligent Data Analysis XVI: 16th International Symposium, IDA 2017, London, UK, 26–28 October 2017; pp. 198–209. [Google Scholar]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Berns, F.; Hüwel, J.D.; Beecks, C. LOGIC: Probabilistic Machine Learning for Time Series Classification. In Proceedings of the 2021 IEEE International Conference on Data Mining (ICDM), Auckland, New Zealand, 7–10 December 2021; pp. 1000–1005. [Google Scholar]
- Dau, H.A.; Bagnall, A.; Kamgar, K.; Yeh, C.C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Keogh, E. The UCR time series archive. IEEE/CAA J. Autom. Sin. 2019, 6, 1293–1305. [Google Scholar] [CrossRef]
- Ferrell, B.; Santuro, S. NASA Shuttle Valve Data. Available online: http://www.cs.fit.edu/~pkc/nasa/data/ (accessed on 1 February 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).