Fuzzy-Logic-Based Intelligent Control of a Cabinet Solar Dryer for Plantago major Leaves Under Real Climatic Conditions in Tashkent ^†

Abstract

Solar drying is an energy-efficient and environmentally friendly method for dehydrating agricultural and medicinal products; however, its performance is strongly affected by fluctuating climatic conditions and nonlinear heat and mass transfer processes. In cabinet-type solar dryers, maintaining the drying air temperature and relative humidity within optimal ranges is particularly critical for medicinal plants such as Plantago major leaves, which are sensitive to overheating and non-uniform drying. In this study, a Mamdani-type fuzzy logic-based intelligent control system is developed and experimentally validated for a cabinet solar dryer operating under real summer climatic conditions in Tashkent, Uzbekistan. The proposed controller regulates fan speed using drying air temperature and relative humidity as inputs. To evaluate its effectiveness, the fuzzy logic controller is benchmarked against a conventionally tuned Proportional–Integral–Derivative (PID) controller under identical operating and climatic conditions. A coupled thermodynamic–hygrometric dynamic model of the drying process is implemented in MATLAB/Simulink (R2024a) to support controller design and analysis. Experimental results demonstrate that the fuzzy logic controller maintains the drying air temperature within the optimal range of 45–50 °C despite significant fluctuations in solar irradiance (650–900 W/m²), whereas the PID-controlled system exhibits noticeable overshoot and oscillations. Compared with PID control, the fuzzy-controlled dryer achieves a smoother reduction in relative humidity, a reduction of approximately 22% in total drying time for the same final moisture content (8–10% wet basis), and an 18% decrease in auxiliary electrical energy consumption. In addition, tray-wise moisture measurements indicate improved drying uniformity under fuzzy control, with moisture variation remaining within ±4%. Overall, the results confirm that fuzzy-logic-based intelligent control provides a robust and energy-efficient solution for cabinet solar dryers operating under hot continental climatic conditions, offering clear advantages over conventional PID control in terms of stability, drying performance, and uniformity.

1. Introduction

Solar drying has become an attractive alternative to conventional hot-air and open-sun drying processes for agricultural and medicinal products, owing to its low operating cost, reduced environmental impact, and suitability for decentralized rural applications [1]. In cabinet-type solar dryers, solar radiation is converted into thermal energy and transferred to the drying air, which then removes moisture from the product placed on perforated trays. This approach enables better protection against dust, insects, and weather conditions compared with open-sun drying while achieving higher energy efficiency than electrically heated dryers when properly designed and controlled [1]. Medicinal and aromatic plants represent a particularly critical class of products for solar drying. Their pharmacological efficacy depends strongly on the preservation of heat-sensitive bioactive compounds such as vitamins, flavonoids, essential oils, and phenolic constituents. Inadequate control of drying temperature and humidity can lead to oxidative degradation, loss of volatile components, changes in color, and reduced therapeutic value [2]. Plantago major L. (plantain) is a widely used medicinal plant with anti-inflammatory, wound-healing, and antioxidant properties. Its leaves contain water-soluble vitamins and flavonoids that are vulnerable to thermal damage during high-temperature drying. Recent studies have shown that both the drying method and temperature trajectory significantly affect the retention of flavonoids and other bioactive components in Plantago leaves, highlighting the need for controlled drying regimes [3,4].

Despite these requirements, the operating conditions in solar dryers are inherently unsteady. The internal chamber temperature and relative humidity depend on highly variable solar irradiance, ambient weather conditions, and airflow distribution. As a result, the heat and mass transfer processes inside cabinet solar dryers exhibit pronounced nonlinear behavior, long time delays, and strong coupling between thermal and hygrometric variables [5]. Under such circumstances, traditional ON/OFF and proportional–integral–derivative (PID) controllers often fail to maintain the drying air temperature within a narrow optimal range. They tend to generate overshoot and oscillations, especially when solar irradiance changes rapidly due to intermittent cloud cover or wind effects [6]. This leads to non-uniform moisture distribution between trays, extended drying times, and degradation of product quality [7]. To better understand and improve solar dryer performance, numerous mathematical and computational modeling approaches have been proposed, including thin-layer drying models, lumped-parameter dynamic models, and detailed CFD simulations of air flow and temperature fields [8].

In parallel, intelligent modeling techniques such as artificial neural networks (ANNs), adaptive-network-based fuzzy inference systems (ANFIS), and fuzzy logic models have been employed to predict drying behavior and estimate difficult-to-measure variables. These methods have demonstrated high accuracy in capturing the complex nonlinear relationships between climatic inputs, process variables, and drying efficiency [9,10].

However, relatively fewer studies focus on intelligent control of solar dryers rather than modeling alone. Several works have explored fuzzy logic controllers for grain drying and hybrid solar dryers, where the fuzzy rules adjust heater power, airflow, or valve positions to maintain desired temperature and moisture levels in the presence of nonlinearities and parameter uncertainties [11,12]. Abakarov et al. reported a fuzzy-based control system for a solar dryer using low-cost sensors, demonstrating improved temperature stability compared with conventional strategies. More recent research has combined fuzzy logic and PID to achieve better thermal control in cabinet-type drying systems, emphasizing energy savings and control robustness. At the same time, the emergence of low-cost microcontrollers and IoT platforms has enabled remote monitoring and supervisory control of solar cabinet dryers, although many of these implementations still rely on simple threshold-based logic or manually tuned PID loops [13]. For medicinal plants specifically, the literature shows that drying method and control strategy have a measurable impact on the chemical profile and bioactivity of the final product [14]. Yet, there remains a limited number of works that integrate (i) dynamic modeling of a cabinet solar dryer, (ii) fuzzy-logic-based real-time control of temperature and humidity, and (iii) experimental validation under real outdoor climatic conditions, including phytochemical quality assessment for Plantago major or similar medicinal species [14]. Existing studies on solar drying of Plantago leaves have mainly focused on open-sun vs. cabinet drying and on ANN-based prediction of dryer performance, rather than on intelligent closed-loop control. This gap is particularly relevant for continental climates such as that of Tashkent, Uzbekistan, where summer solar irradiance frequently exceeds 800–900 W/m² and ambient temperatures can surpass 40 °C, creating a high risk of overheating if the control system is not sufficiently adaptive. In this context, the present work aims to develop and experimentally validate a fuzzy-logic-based intelligent control system for a cabinet-type solar dryer used to dehydrate Plantago major leaves under real summer conditions in Tashkent. The proposed system is built around a Mamdani fuzzy inference structure with drying air temperature and relative humidity as inputs and fan speed as the control output [15]. A thermodynamic–hygrometric model of the dryer is implemented in MATLAB/Simulink to form a digital twin of the process and to support controller design and simulation [15,16,17]. The fuzzy controller’s performance is benchmarked against that of a conventional PID controller in terms of drying time, temperature stability, moisture uniformity across trays, energy consumption, and phytochemical quality preservation. By combining dynamic modeling, fuzzy control, and experimental validation for a medicinal plant of practical importance, this study seeks to contribute a robust, energy-efficient, and quality-oriented control strategy for solar drying systems operating in hot continental climates [17,18].

2. Methodology

2.1. Experimental Solar Dryer Configuration

The experimental setup consists of a cabinet-type solar dryer designed for controlled dehydration of Plantago major leaves under real outdoor conditions. The system comprises three main components: (i) a flat-plate solar air collector, (ii) an insulated drying chamber equipped with four perforated stainless-steel trays, and (iii) a forced-convection ventilation system powered by a 90 W DC fan. Transparent polycarbonate glazing with UV filtration is used to enhance solar energy capture while mitigating excessive heating. Internal temperature is measured using K-type thermocouples, whereas relative humidity is monitored using digital capacitive sensors (±2% accuracy). Air velocity is measured by a hot-wire anemometer placed at the inlet of the drying chamber. Data acquisition is performed using an NI-DAQ module at 1 Hz sampling frequency.

The solar dryer was tested outdoors in Tashkent during peak summer conditions, where solar irradiance fluctuated between 650 and 900 W/m², and ambient temperatures varied between 32 °C and 42 °C. Approximately 1.5 kg of fresh Plantago major leaves were uniformly spread across the trays to maintain consistent drying load. The experiment was conducted until the leaves reached an equilibrium moisture content of approximately 8–10% (wet basis).

2.2. Dynamic Modeling of the Drying Process

To support controller design, simulation, and experimental analysis, a dynamic model describing the coupled heat and mass transfer phenomena inside the cabinet-type solar dryer was developed. The model is formulated using lumped-parameter assumptions and is suitable for real-time simulation and control-oriented analysis. The process dynamics are decomposed into two interacting subsystems: (i) a thermal subsystem, governing the evolution of drying air temperature, and (ii) a hygrometric subsystem, governing the evolution of relative humidity and product moisture content.

This separation ensures physical clarity and avoids variable overlap between temperature- and moisture-related processes [19].

2.2.1. Thermal Model

The thermal behavior of the drying air inside the cabinet is described by an energy balance applied to the control volume of air within the drying chamber [20]. The governing equation is written as:

$$m_a{c}_p{\displaystyle \frac{dT(t)}{dt}}={\eta }_c{A}_{c}I(t)-{\dot{m}}_{air}(u)c_p[T(t)-T_{amb}]-UA[T(t)-T_{amb}],$$

where

T(t) is the drying air temperature inside the chamber (°C), $T_{amb}$ is the ambient air temperature (°C), $m_a$ is the effective mass of air inside the drying chamber (kg), $c_p$ is the specific heat capacity of air (J·kg⁻¹·K⁻¹), ${\eta }_c$ is the solar air collector efficiency (–), A_c is the effective collector area (m²), I(t) is the incident solar irradiance (W·m⁻²), ${\dot{m}}_{air}(u)$ is the air mass flow rate controlled by the fan speed u(t) (kg·s⁻¹), and UA is the overall heat loss coefficient of the drying chamber (W·K⁻¹).

The first term on the right-hand side represents useful thermal energy gained from solar radiation, the second term accounts for convective heat removal due to forced airflow, and the third term represents conductive and convective heat losses to the environment.

For control-oriented analysis, the thermal model is rewritten in a normalized first-order form:

$${\displaystyle \frac{dT(t)}{dt}}=a_{T}I(t)-b_T{\dot{m}}_{air}(u)[T(t)-T_{amb}]-c_T[T(t)-T_{amb}],$$

where $a_T,$ $b_T,$ and $c_T$ are lumped thermal parameters that incorporate physical constants and geometric characteristics of the dryer.

These parameters were identified experimentally using a least-squares system identification method based on measured temperature responses under varying solar irradiance and airflow conditions.

2.2.2. Hygrometric Model

The hygrometric subsystem describes the evolution of relative humidity inside the drying chamber and the moisture removal from the product. Relative humidity dynamics are modeled independently from the thermal subsystem to ensure variable consistency and numerical stability.

The time evolution of relative humidity $RH(t)$ inside the chamber is expressed as:

$${\displaystyle \frac{dRH}{dt}}=a_{RH}(R{H}_{eq}(M,T)-RH)+b_{RH}{\dot{m}}_{air}(u)RH,$$

where

$RH$ is the instantaneous relative humidity inside the chamber (%),

$R{H}_{eq}(M,T)$ is the equilibrium relative humidity corresponding to the product moisture content and air temperature, M(t) is the instantaneous moisture content of the leaves (kg water per kg dry matter), ${\dot{m}}_{air}(u)$ is the airflow rate controlled by the fan speed, and $a_{RH}$ and $b_{RH}$ are hygrometric model parameters.

The first term represents moisture exchange between the product and surrounding air, while the second term describes moisture removal due to convective airflow.

Moisture loss from Plantago major leaves is described using the Page thin-layer drying model, which is widely accepted for convective drying of biological materials:

$${\displaystyle \frac{M(t)}{M_0}}=\exp (-k{t}^{-n^n})$$

where $M_0$ is the initial moisture content, and k and n are empirical drying constants obtained determined experimentally from drying curves. The Page model parameters were identified using nonlinear regression applied to experimental moisture-loss data obtained under controlled drying conditions.

2.2.3. Model–Control Integration

The thermal and hygrometric subsystems are coupled through the airflow term ${\dot{m}}_{air}(u)$, which is directly manipulated by the control input u(t) generated by the fuzzy logic controller. This structure allows the controller to simultaneously regulate temperature and humidity by adjusting fan speed in response to real-time measurements.

The complete dynamic model was implemented in MATLAB/Simulink (R2024a) and used as a digital twin of the solar dryer to support fuzzy controller design, tuning, and performance evaluation prior to experimental validation.

2.3. Design of the Mamdani Fuzzy Inference System

A Mamdani-type Fuzzy Inference System (FIS) was designed to cope with the nonlinear, time-varying, and disturbance-prone dynamics of the solar drying process [20]. The controller uses linguistic reasoning to regulate fan speed based on deviations in drying air temperature and relative humidity, ensuring stable operation under fluctuating solar irradiance and ambient conditions.

2.3.1. Inputs and Output

Two input variables and one output variable were selected based on drying process physics and experimental observations:

Input 1: Drying air temperature $T_{in}\in [35,60]°C$

Input 2: Relative humidity $RH\in [10,70]\%$

Output: Fan speed $u(t)\in [0,1]$ (0–1 normalized to 0–100%)

These ranges were determined using real climatic measurements collected during field tests and established guidelines for drying medicinal plants.

Mathematically, the fuzzy controller maps inputs to output via:

$$u(t)=F(T_{in}(t),RH(t))$$

where $F(\cdot )$ is the nonlinear fuzzy mapping defined by the membership functions and rule base.

2.3.2. Membership Functions

Triangular membership functions were selected for all input and output variables due to their simplicity, computational efficiency, and suitability for real-time implementation in embedded control systems. The use of triangular functions allows smooth transitions between linguistic terms while maintaining low computational complexity, which is important for practical solar dryer control applications.

To ensure consistency between mathematical expressions, graphical representations, and linguistic rules, a unified terminology is adopted throughout the fuzzy inference system. All membership functions are defined using the same linguistic structure:

Low–Optimal–High

This unification eliminates ambiguity between equations and figures and ensures a clear interpretation of the fuzzy control logic.

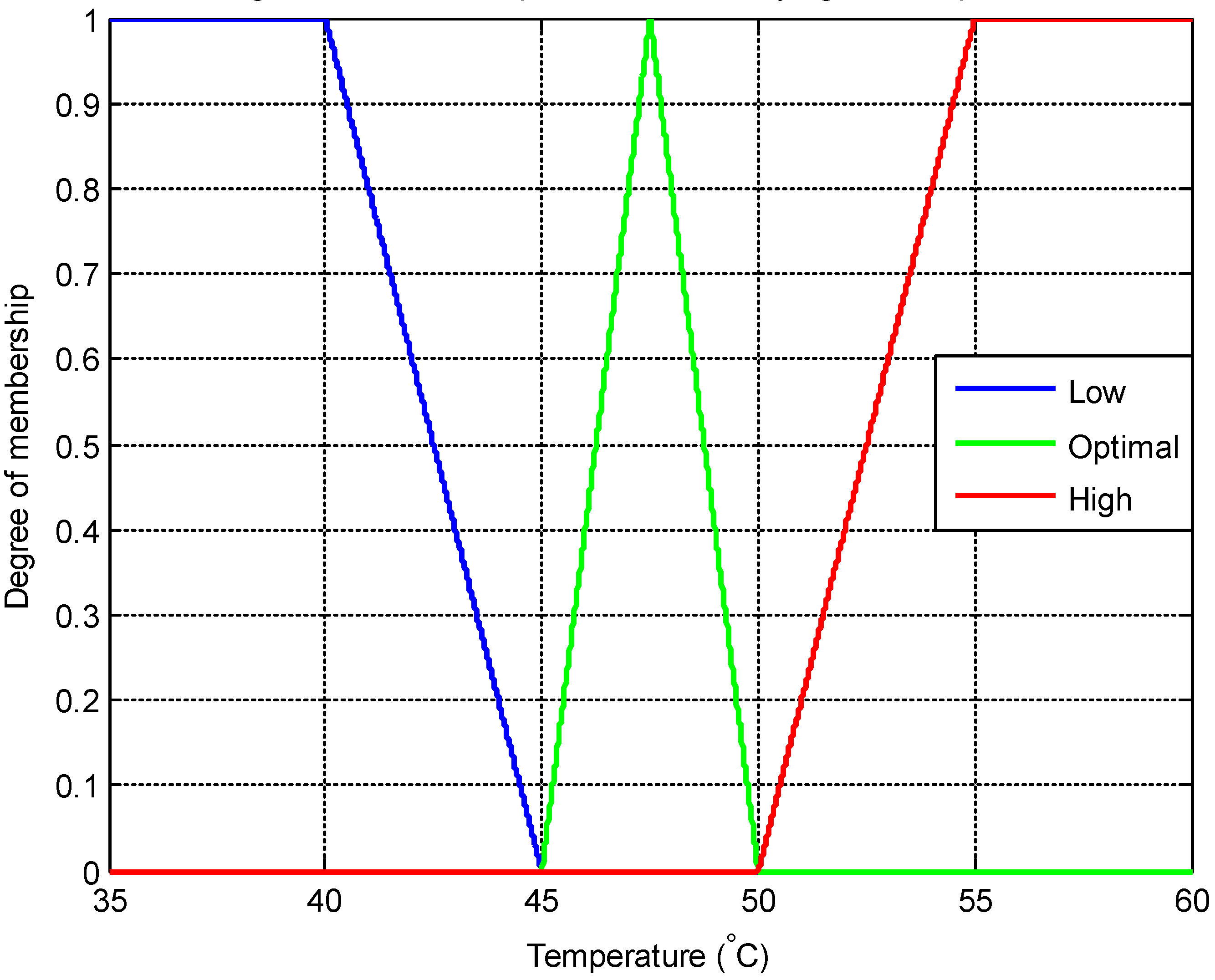
Drying Air Temperature Membership Functions

Drying air temperature is a critical variable affecting both drying kinetics and the preservation of heat-sensitive bioactive compounds in Plantago major leaves. Based on experimental observations and established guidelines for medicinal plant drying, the optimal temperature range was identified as 45–50 °C.

Low temperature:

$${\mu }_T^{Low}(T)=\left\{\begin{array}{cc}1,& T\le 40,\\ {\displaystyle \frac{45-T}{5}},& 40<T<45\\ 0,& T\ge 45.\end{array}\right.$$

Optimal temperature:

$${\mu }_T^{Optimal}(T)=\left\{\begin{array}{cc}0,& T\le 45,\\ {\displaystyle \frac{T-45}{2.5}},& 45<T<47.5\\ {\displaystyle \frac{50-T}{2.5}},& 47.5\le T<50\\ 0,& T\ge 50\end{array}\right.$$

High temperature:

$${\mu }_T^{High}(T)=\left\{\begin{array}{cc}0,& T\le 50,\\ {\displaystyle \frac{T-50}{5}},& 50<T<55,\\ 1,& T\ge 55.\end{array}\right.$$

These membership functions describe how the controller interprets deviations of the drying air temperature from the optimal drying window:

Relative Humidity Membership Functions (with Formulas)

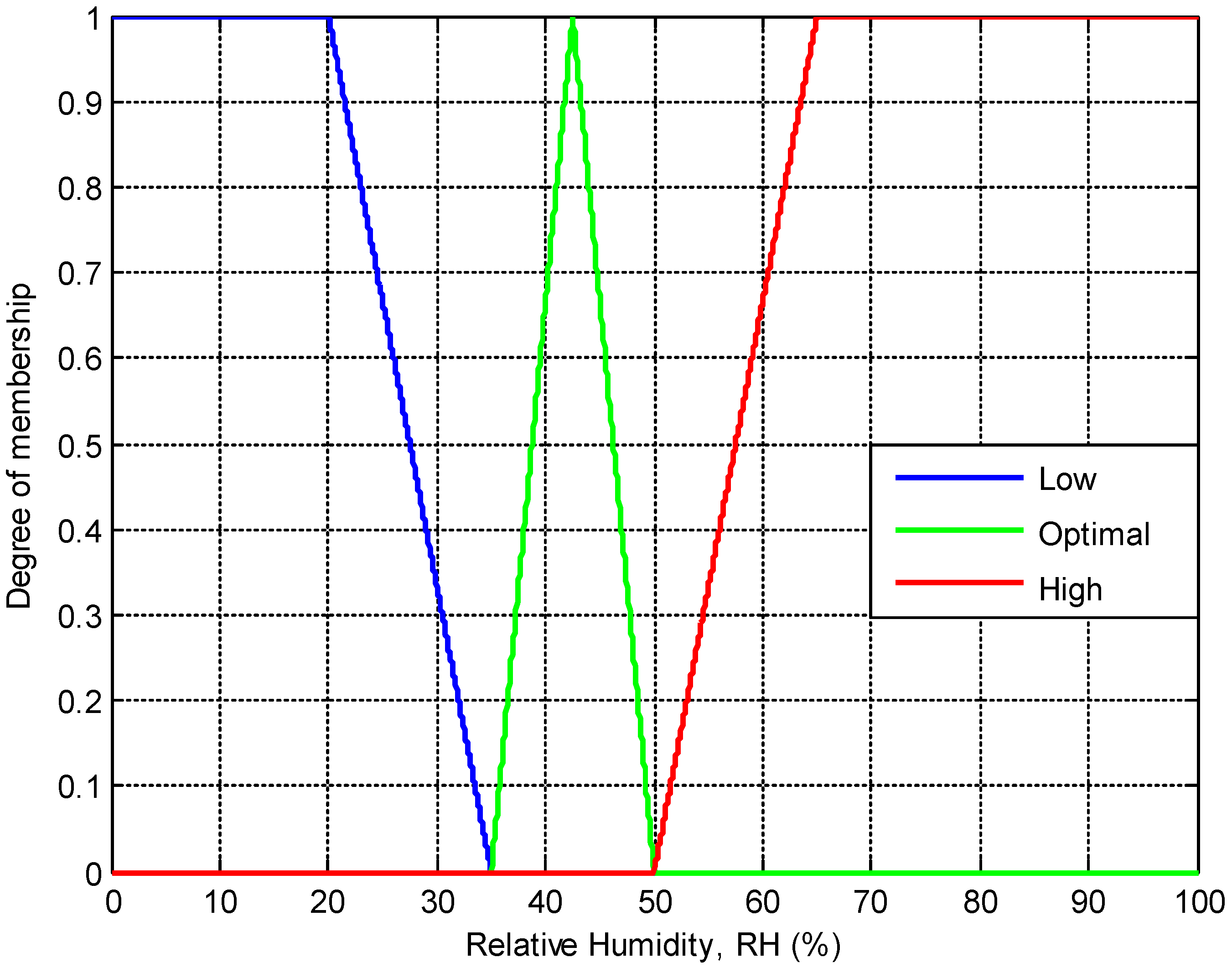
Relative humidity inside the drying chamber directly influences the evaporation rate and moisture removal from the product. To represent different moisture conditions, relative humidity membership functions are defined using the same linguistic structure: Low–Optimal–High.

Based on experimental measurements inside the drying chamber and recommended convective drying conditions for medicinal plants, the relative humidity membership functions are defined as follows.

Low relative humidity

$${\mu }_T^{Low}(T)=\left\{\begin{array}{cc}1,& RH\le 20,\\ {\displaystyle \frac{35-RH}{15}},& 20<RH<35\\ 0,& RH\ge 35.\end{array}\right.$$

Optimal relative humidity

$${\mu }_T^{Optimal}(RH)=\left\{\begin{array}{cc}0,& RH\le 35,\\ {\displaystyle \frac{RH-35}{7.5}},& 35<RH<42.5\\ {\displaystyle \frac{50-RH}{7.5}},& 42.5\le RH<50\\ 0,& RH\ge 50.\end{array}\right.$$

High relative humidity

$${\mu }_{RH}^{High}(RH)=\left\{\begin{array}{cc}0,& RH\le 50,\\ {\displaystyle \frac{RH-50}{15}},& 50<RH<65\\ 1,& RH\ge 65.\end{array}\right.$$

These membership functions enable the controller to distinguish between low, optimal, and excessive moisture conditions inside the drying chamber and to adjust the airflow accordingly. This ensures effective moisture removal under high relative humidity while preventing unnecessarily aggressive drying under low-humidity conditions, thereby preserving product quality.

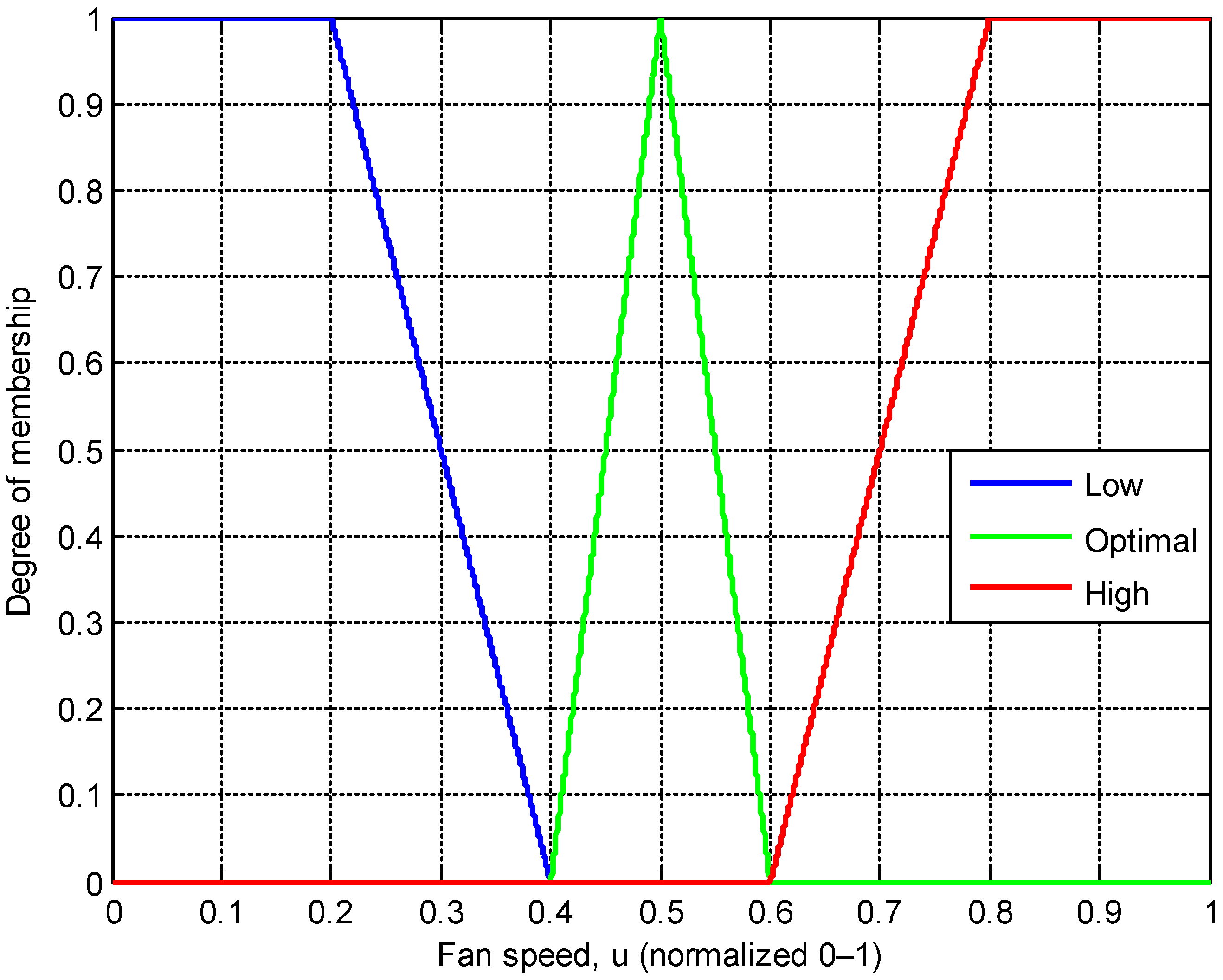
Fan Speed Membership Functions (with Formulas)

The output variable, fan speed u, is modeled using three triangular membership functions: Low, Optimal, and High. The fan speed is normalized in the range

$$0\le u\le 1,$$

corresponding to 0–100% of the fan’s maximum rotational speed.

Defining the output membership functions in this manner enables smooth and continuous modulation of airflow intensity in response to the combined temperature–humidity state inside the drying chamber. This approach prevents abrupt control actions, reduces unnecessary electrical energy consumption, and contributes to stable and uniform drying conditions.

Based on experimental observations and practical operation limits of the ventilation system, the fan speed membership functions are defined as follows.

Low fan speed

$${\mu }_u^{Low}(T)=\left\{\begin{array}{cc}1,& u\le 0.2,\\ {\displaystyle \frac{0.4-u}{0.2}},& 0.2<u<0.4,\\ 0,& u\ge 0.4.\end{array}\right.$$

Optimal fan speed

$${\mu }_{RH}^{Optimal}(RH)=\left\{\begin{array}{cc}0,& u\le 0.4,\\ {\displaystyle \frac{u-0.4}{0.1}},& 0.4<u<0.5\\ {\displaystyle \frac{0.6-u}{0.1}},& 0.5\le u<0.6\\ 0,& u\ge 0.6.\end{array}\right.$$

High fan speed

$${\mu }_u^{High}(u)=\left\{\begin{array}{cc}0,& u\le 0.6,\\ {\displaystyle \frac{u-0.6}{0.2}},& 0.6<u<0.8,\\ 1,& u\ge 0.8.\end{array}\right.$$

These membership functions ensure a gradual transition between airflow levels, allowing the controller to increase ventilation intensity only when required by high temperature or excessive humidity, while maintaining energy-efficient operation under near-optimal drying conditions.

2.3.3. Rule Base Construction

The fuzzy rule base consists of seven linguistic rules formulated based on the thermodynamic and hygrometric behavior of the solar drying process. The rules are constructed using a unified linguistic structure Low–Optimal–High, fully consistent with the membership functions defined in Figure 1, Figure 2 and Figure 3.

The objective of the rule base is to regulate the fan speed so as to maintain the drying air temperature and relative humidity within their optimal ranges, while preventing overheating, excessive moisture accumulation, and unnecessary energy consumption.

The fuzzy IF–THEN rules are defined as follows:

Rule 1: IF Temperature is Low AND Relative Humidity is Low, THEN Fan Speed is Low.

Rule 2: IF Temperature is Low AND Relative Humidity is High, THEN Fan Speed is Optimal.

Rule 3: IF Temperature is Optimal AND Relative Humidity is Low, THEN Fan Speed is Optimal.

Rule 4: IF Temperature is Optimal AND Relative Humidity is High, THEN Fan Speed is High.

Rule 5: IF Temperature is Optimal AND Relative Humidity is Optimal, THEN Fan Speed is Optimal.

Rule 6: IF Temperature is High, THEN Fan Speed is High.

Rule 7: IF Relative Humidity is High, THEN Fan Speed is High.

These rules reflect the physical control logic of the drying process:

low temperatures require reduced airflow to minimize heat losses;

high relative humidity necessitates increased airflow to enhance moisture removal; and high temperatures require higher fan speeds to prevent overheating and protect heat-sensitive bioactive compounds.

Using Mamdani inference, each rule generates a clipped fuzzy output. The activation strength of the i-th rule is calculated using the minimum operator:

$${\alpha }_{it}=\underset{i=\mathrm{1...7}}{\min }({\mu }_T^{(i)},{\mu }_{RH}^{(i)}),$$

where ${\mu }_T^{(i)}$ is the membership degree of the temperature input, ${\mu }_{RH}^{(i)}$ is the membership degree of the relative humidity input, and ${\alpha }_{it}$ represents the firing strength of the i-th rule.

The aggregated fuzzy output is obtained by applying the maximum operator to all activated rules. The final crisp control signal is computed using the centroid defuzzification method:

$$u^{\backslash *}={\displaystyle \frac{{\displaystyle \underset{0}{\overset{1}{\int }}u{\mu }_{out}(u)du}}{{\displaystyle \underset{0}{\overset{1}{\int }}{\mu }_{out}(u)du}}}$$

This defuzzification approach ensures smooth fan-speed transitions and avoids abrupt control actions that could destabilize the drying process.

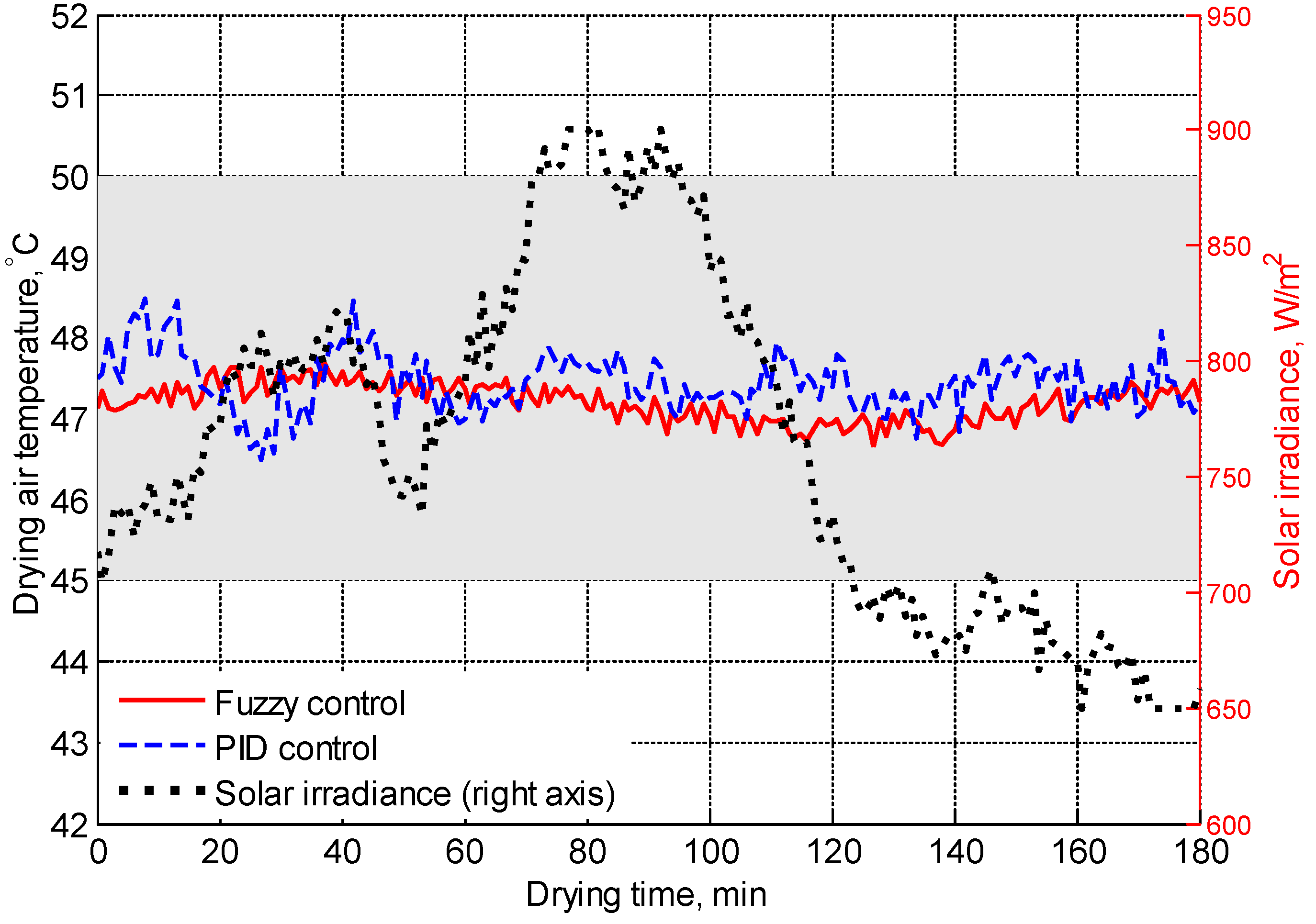
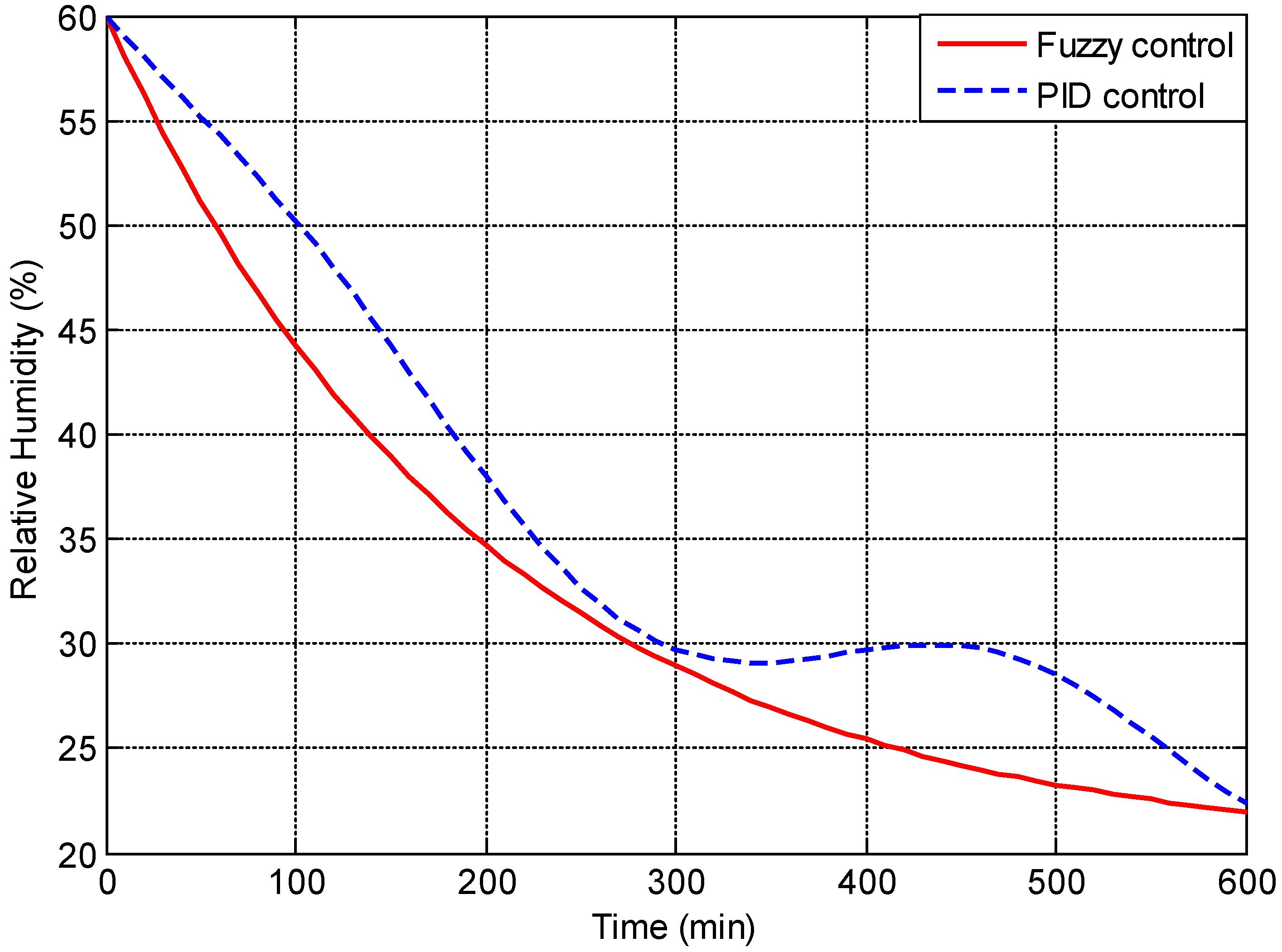
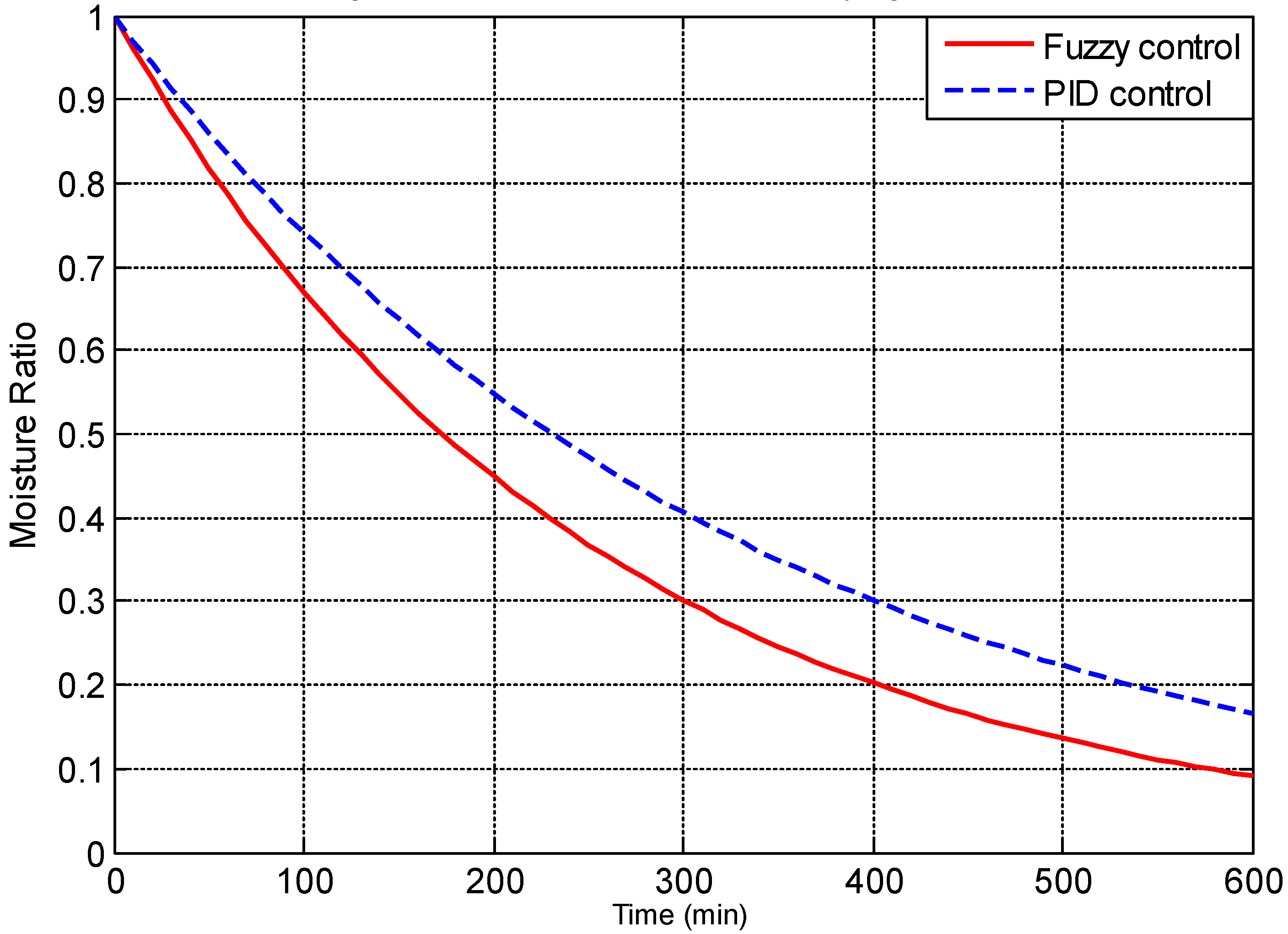
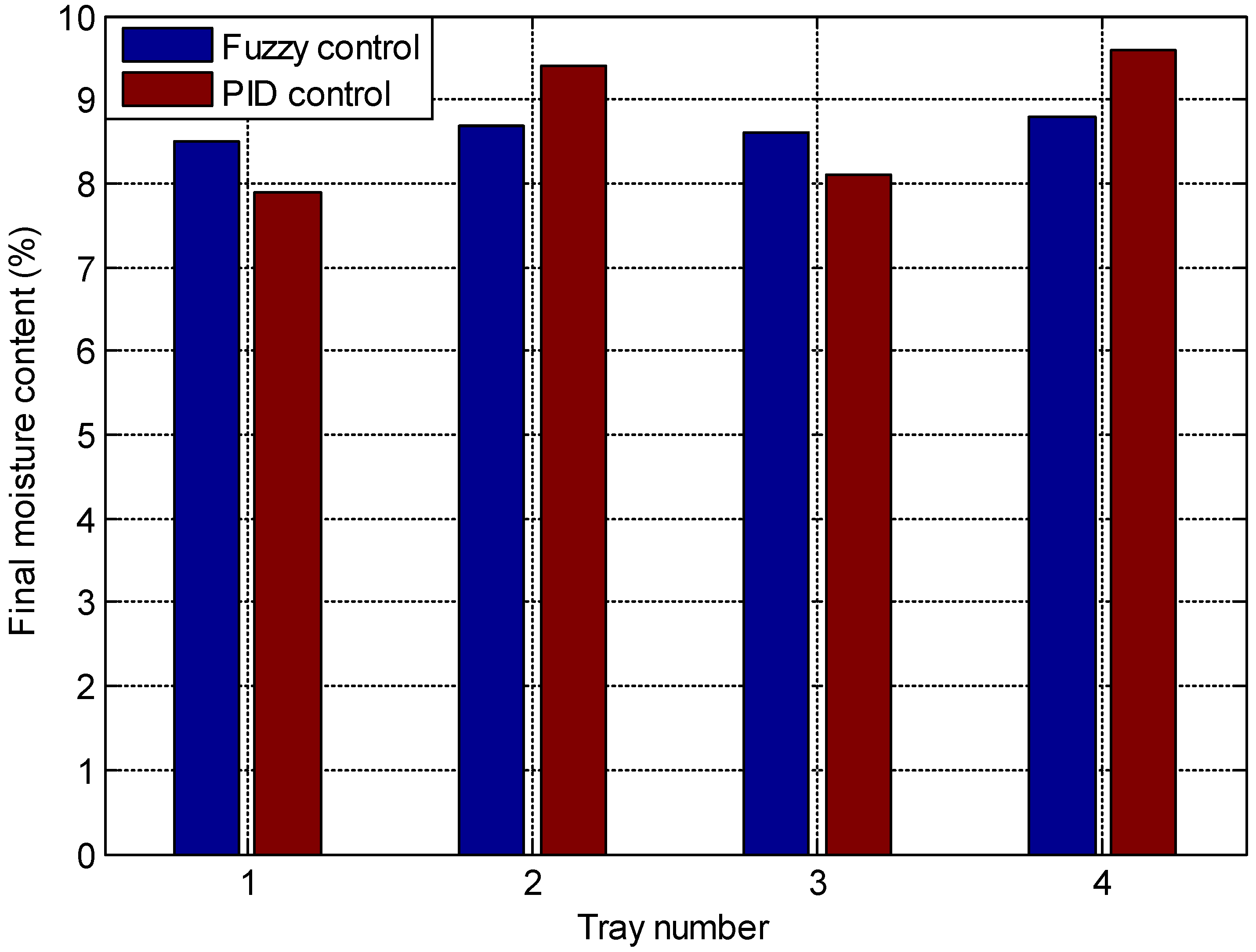
3. Result and Discussion

The fuzzy-logic-based control strategy was evaluated under real summer climatic conditions in Tashkent, with solar irradiance varying between 650 and 900 W/m² and ambient temperatures between 32 °C and 42 °C. Throughout the experiments, the fuzzy controller maintained the drying air temperature in the cabinet within the target window required for Plantago major leaves. For benchmarking purposes, all experiments were repeated using a conventionally tuned PID controller under identical operating conditions. The measured drying air temperature profiles inside the cabinet are presented in Figure 4, together with the corresponding solar irradiance plotted on a secondary axis. After an initial warm-up phase, the fuzzy controller rapidly stabilized the drying air temperature within the optimal range required for Plantago major leaves (45–50 °C). Despite pronounced fluctuations in solar irradiance, the fuzzy-controlled system maintained the temperature close to the optimal band, exhibiting only minor and slow deviations. This behavior indicates effective compensation for external climatic disturbances through adaptive fan-speed regulation. In contrast, the PID-controlled system exhibited noticeable temperature overshoot and oscillatory behavior during periods of rapid irradiance variation, frequently exceeding the upper limit of the optimal drying window. This comparison clearly demonstrates the superior disturbance rejection capability of the fuzzy logic controller under nonlinear and time-varying operating conditions.

The evolution of relative humidity inside the drying chamber under both control strategies is illustrated in Figure 5. Under fuzzy logic control, the relative humidity decreased smoothly from initial values of approximately 60% to below 20%, following a stable and monotonic trajectory without pronounced oscillations. This smooth humidity reduction ensures a continuous moisture gradient between the leaf surface and the surrounding air, which is essential for efficient convective drying and the prevention of condensation. By comparison, the PID-controlled system exhibited slower humidity reduction and noticeable fluctuations, particularly during changes in airflow and irradiance. These results confirm that the fuzzy controller more effectively modulates airflow to remove evaporated moisture while maintaining stable drying conditions.

Drying kinetics were analyzed using the moisture ratio curves presented in Figure 6. Both control strategies exhibit a typical falling-rate drying behavior; however, the fuzzy-controlled dryer reached the equilibrium moisture content of approximately 8–10% (wet basis) significantly faster than the PID-controlled system. For the same final moisture level, the total drying time under fuzzy control was reduced by approximately 22% compared with PID control operating under identical conditions. This improvement can be attributed to the fuzzy controller’s ability to keep the drying air temperature close to the optimal range while simultaneously sustaining adequate airflow, thereby enhancing convective mass transfer without overheating the product.

Energy-use analysis indicated that the fuzzy-logic-based control also improved the efficiency of the ventilation system. By continuously adapting the fan speed according to the instantaneous temperature–humidity state, the controller avoided unnecessary operation at maximum power. As a result, the cumulative electrical energy consumption of the fan over the entire drying cycle was reduced by approximately 18% compared with PID control. This reduction is particularly relevant for solar dryers intended for off-grid or low-power applications.

Drying uniformity was evaluated by measuring the final moisture content on each tray at the end of the drying process, as shown in Figure 7. Under fuzzy control, the coefficient of variation in moisture content between trays remained within ±4%, indicating nearly uniform drying conditions throughout the chamber. In contrast, larger inter-tray moisture differences were observed under PID control, reflecting non-uniform airflow and temperature distribution. Although detailed phytochemical analysis was not performed in this study, maintaining the drying air temperature within the optimal range and avoiding temperature overshoot are well-recognized factors for preserving heat-sensitive bioactive compounds in medicinal plants. Therefore, the improved thermal stability and moisture uniformity achieved under fuzzy control strongly suggest enhanced preservation of product quality.

Overall, the experimental findings demonstrate that the Mamdani-type fuzzy inference system provides robust and efficient regulation of the cabinet-type solar dryer under real outdoor conditions. Compared with conventional PID control, the fuzzy logic controller improves temperature stability, accelerates drying kinetics, reduces auxiliary energy consumption, and enhances drying uniformity. These results confirm the suitability of fuzzy-logic-based intelligent control for solar drying applications in hot continental climates such as Tashkent and provide a solid basis for future extensions involving IoT-based monitoring and advanced quality assessment methods.

4. Conclusions

This study developed and experimentally validated a Mamdani-type fuzzy-logic-based intelligent control system for a cabinet solar dryer operating under real summer climatic conditions in Tashkent. The results demonstrated that the proposed controller effectively stabilized the internal drying microclimate despite large external disturbances caused by fluctuating solar irradiance (650–900 W/m²) and ambient temperature (32–42 °C). The fuzzy controller maintained the drying air temperature within the optimal 45–50 °C range required for preserving thermolabile bioactive compounds in Plantago major leaves while ensuring a smooth and monotonic reduction in relative humidity throughout the drying cycle.

The drying kinetics confirmed a significant improvement in process efficiency, with the fuzzy-controlled system reducing the total drying time by approximately 22% compared with traditional operation. This acceleration is attributed to the controller’s ability to maintain near-optimal thermal and hygrometric conditions, thereby enhancing convective mass transfer without causing overheating. Additionally, adaptive modulation of fan speed led to an 18% reduction in auxiliary energy consumption, highlighting the potential of fuzzy logic for energy-efficient solar drying technologies.

Quality assessments further emphasized the benefits of intelligent control. Tray-wise measurements indicated a moisture uniformity coefficient within ±4%, demonstrating that the fuzzy controller ensured homogeneous drying across all layers.

Overall, the findings clearly indicate that fuzzy-logic-based intelligent control provides a robust, adaptive, and energy-efficient solution for solar drying systems operating in hot continental climates. By stabilizing the internal microclimate and dynamically regulating airflow, the developed controller improves process performance in terms of drying efficiency, energy usage, uniformity, and product quality. These outcomes highlight the practical value of integrating fuzzy inference systems into modern solar dryer designs and provide a strong foundation for future enhancements, including IoT-enabled monitoring, hybrid optimization algorithms, and advanced intelligent supervisory control architectures.