Next Article in Journal
Fuzzy-Logic-Based Intelligent Control of a Cabinet Solar Dryer for Plantago major Leaves Under Real Climatic Conditions in Tashkent
Previous Article in Journal
Application of Artificial Intelligence in Maintenance as an Important Factor of Corporate Business Strategy
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Engineering Proceedings
Volume 124
Issue 1
10.3390/engproc2026124010
engproc-logo
Submit to this Journal
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Proceeding Paper

Impact of Operating Conditions on the Reliability of SRAM-Based Physical Unclonable Functions (PUFs) †

by
Marco Grossi
*,
Martin Omaña
,
Simone Bisi
,
Cecilia Metra
and
Andrea Acquaviva
Department of Electrical Energy and Information Engineering “Guglielmo Marconi” (DEI), University of Bologna, 40136 Bologna, Italy
*
Author to whom correspondence should be addressed.
†
Presented at the 6th International Electronic Conference on Applied Sciences, 9–11 December 2025; Available online: https://sciforum.net/event/ASEC2025.
Eng. Proc. 2026, 124(1), 10; https://doi.org/10.3390/engproc2026124010
Published: 27 January 2026
(This article belongs to the Proceedings of The 6th International Electronic Conference on Applied Sciences)
Browse Figures
Versions Notes

Abstract

Wireless sensor systems can collect and share a large amount of data for different kinds of applications, but are also vulnerable to cyberattacks. The impact of cyberattacks on systems’ confidentiality, integrity, and availability can be mitigated by using authentication procedures and cryptographic algorithms. Authentication passwords and cryptographic keys may be stored in a non-volatile memory, which may be easily tampered with. Alternately, Physical Unclonable Functions (PUFs) can be adopted. They generate a chip’s unique fingerprint, by exploiting the randomness of process parameters’ variations occurring during chip fabrication, thus constituting a more secure alternative to the adoption of non-volatile memories for password storage. PUF reliability is of primary concern to guarantee a system’s availability. In this paper, the reliability of a Static Random Access Memory (SRAM)-based PUF implemented by a standard 32 nm CMOS technology is investigated, as a function of different operating conditions, such as noise, power supply voltage, and temperature, and considering different values of transistor conduction threshold voltages. The achieved results will show that transistor threshold voltage and noise are the operating conditions mostly affecting PUF reliability, while the impact of temperature variations is lower, and that of power supply variations is negligible.

1. Introduction

Merging computing devices, sensors, actuators, and network connectivity has led to the development of wireless sensor systems [1,2,3,4,5,6,7]. As known, such systems are vulnerable to cyberattacks, with potential threats in terms of data confidentiality (e.g., confidential data stolen by malicious attackers), system integrity (e.g., due to data manipulation), and system availability (e.g., because of denial of service based cyberattacks). As an example, firewalls and packet sniffers can be effectively adopted to inspect the traffic among nodes and detect potential anomalies due to cyberattacks [8,9,10,11]. Wireless sensor systems are usually built using low-cost microcontrollers as computing devices. They present low power consumption, but feature a limited computational ability. Therefore, lightweight authentication procedures and cryptography algorithms, that do not demand high performance computing, have to be implemented [12,13,14,15]. Moreover, authentication passwords and cryptographic keys need to be stored in non-volatile memories on the device. Since these memories are vulnerable to hacking attacks, their content may be disclosed, with serious security threats.
A more secure alternative to passwords’ storage in non-volatile memories is represented by the use of Physical Unclonable Function (PUF) architectures. They exploit the randomness of process parameter variations occurring during chip fabrication to make the chip generate a unique fingerprint [16]. Different PUF architectures have been proposed in the literature so far, such as Arbiter PUFs [17,18], ring oscillator (RO) PUFs [19,20], Static Random Access Memory (SRAM) PUFs [21,22], as well as other PUF devices reusing portions of a microcontroller, or FPGA, to generate the unique fingerprint [23,24].
As known [25], SRAM PUF architectures are widely adopted in wireless sensor systems. However, as highlighted in [26,27,28,29], SRAM-based PUFs suffer from reliability issues, mainly due to noise [30], and variations in temperature and power supply voltage. Moreover, as known [31,32], ageing phenomena, mainly Bias Temperature Instability (BTI) and Hot Carrier Injection (HCI), may also impact PUF reliability.
The reliability of SRAM-based PUFs has been investigated in some papers (e.g., those in [26,27,28,29]), some of which also proposed solutions to improve the reliability of SRAM-based PUFs (e.g., those in [26,29]). In particular, in [26], the authors analyse the impact of temperature and power supply voltage variations on the reliability of an SRAM-based PUF implemented by 90 nm CMOS technology. Then they propose a strategy enabling the selection of the most reliable SRAM cells of an array to be adopted to implement the PUF. In [27], the authors analyse the impact of temperature and power supply voltage variations on the reliability of an SRAM-based PUF device implemented by 65 nm CMOS technology. In [28], the authors analyse the reliability of SRAM-based PUFs in the presence of process parameter variations occurring during fabrication, as well as variations in temperature and power supply voltage. In [29], the authors evaluate the reliability of an SRAM PUF under variations in temperature and power supply voltage. Then, they propose a design strategy to improve the reliability of SRAM-based PUFs that operate with very low values of power supply voltage.
Different from previous studies in [26,27,28,29], in this paper we perform a comparative analysis of the impact on the reliability of SRAM-based PUFs of temperature variations only, of power supply voltage variations only, and of different noise levels (possibly affecting the internal nodes of the SRAM cells), all of them in the presence of variations in transistors’ conduction threshold, which, in [33], has been proven to be the parameter mostly influencing SRAM cells’ stability (which is an essential requirement for PUF adoption in security applications) over all parameters possibly varying during fabrication. In particular, we considered the case of an SRAM PUF implemented by 32 nm CMOS technology.
Our performed analyses have shown that noise results in a significant reduction in PUF reliability, while variations in temperature and power supply voltage cause a limited, or negligible, reduction in PUF reliability. Therefore, our analyses highlight that effective solutions aiming at increasing SRAM-based PUF reliability should mainly address the impact of noise on reliability.
The paper is organised as follows. In Section 2, we present the working principle of an SRAM-based PUF. In Section 3, we analyse how noise, as well as variations in temperature and power supply voltage impact the value stored by an SRAM cell after start-up, considering different values of transistor conduction threshold voltages. In Section 4, we analyse the reliability of SRAM-based PUFs. Finally, conclusive remarks are presented in Section 5.

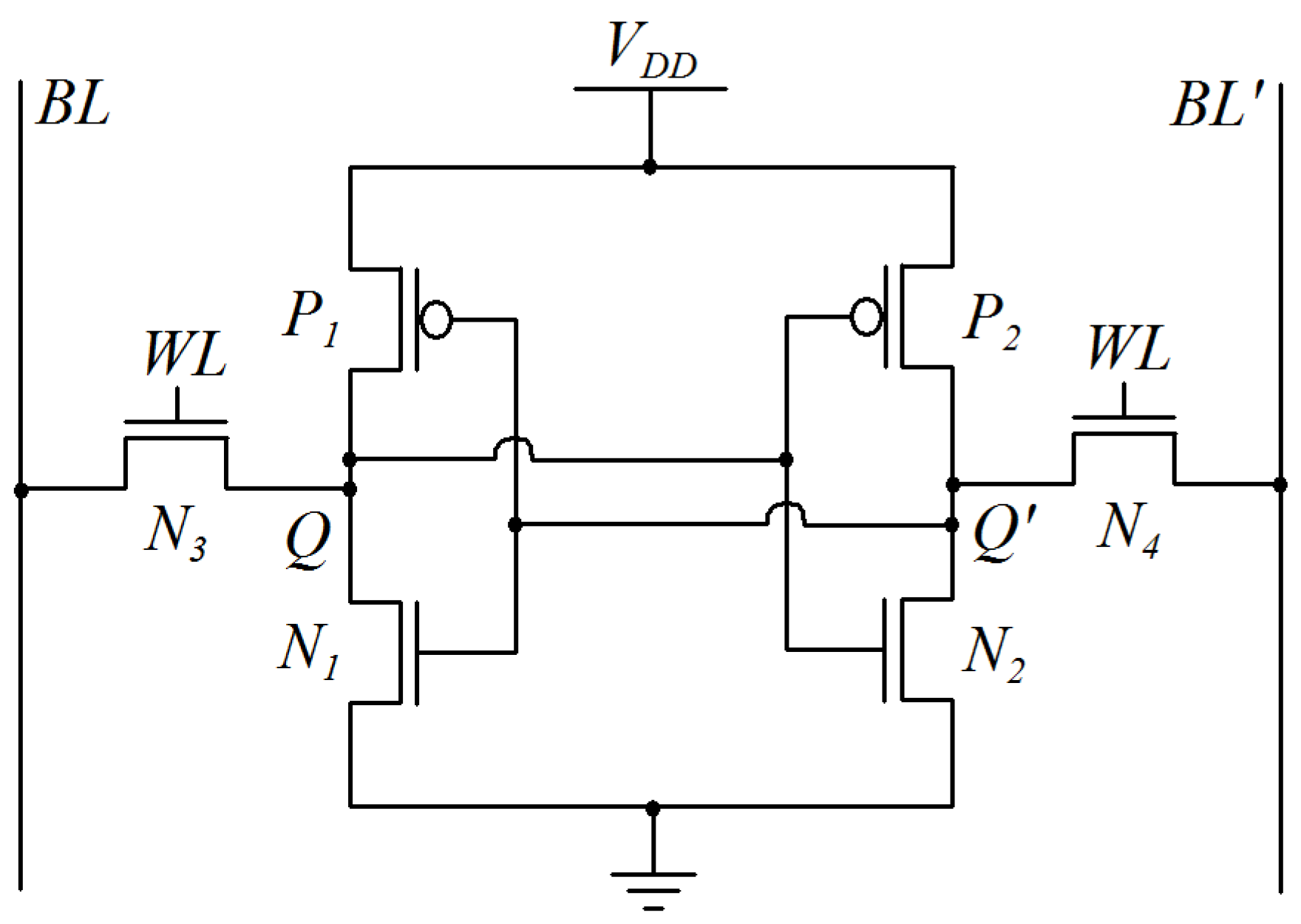
2. SRAM PUF Device

As known [33], an SRAM-based PUF generates a unique response, based on the outputs that SRAM cells feature at power-on which, in turn, depend on SRAM cells’ electrical parameters that may vary due to process parameter variations occurring during fabrication.
A schematic representation of a traditional six-transistor single SRAM cell is shown in Figure 1. Transistors N1 and N2 are the nMOS pull-down devices, while transistors P1 and P2 are the pMOS pull-up devices of the cell. Transistors N3 and N4 are nMOS access transistors that enable data transfer during read/write operations. During both read and write operations, the word line is asserted (WL = 1). This way, during a read operation, the stored data are transferred from the cell to the bit lines (i.e., Q is connected to BL and Q′ is connected to BL′). Instead, during a write operation, the data present on the bit lines are written into the SRAM cell.
Each time the SRAM cell is powered on (i.e., when the power supply VDD switches from 0 V to the nominal value), the initial value of the cell (i.e., the voltage value at node Q) switches to a value that depends on the mismatch between the values of the parameters of the transistors composing the SRAM cell, that are due to process parameter variations occurring at fabrication, and that are different from cell to cell. In order to be reliable, the initial value stored in each cell should be the same each time the cell is powered on. However, due to the presence of noise, as well as temperature and power supply voltage variations, SRAM cells may not always present the same initial value at power-on, thus impacting PUF reliability [26,27,28,29].
For each SRAM cell, we can define the probability PQ that the initial value (at power-on) of its internal node Q presents a binary value 1. Based on the value of such a probability, the SRAM cells of an array can be divided into two different groups: (1) stable cells, that feature a value of PQ equal (or very close) to either 1 or 0; (2) unstable cells, that feature a value of PQ between 0 and 1.
In order to maximise its reliability, an SRAM-based PUF should generate its response from stable cells only. In fact, if the PUF response is derived from SRAM cells with low stability (i.e., cells featuring a value of PQ between 0 and 1), then responses to the same challenge generated at different times are likely to be different, with consequent negative impact on the PUF reliability. However, this can seriously reduce PUF efficiency, since unstable cells may constitute a non-negligible portion of the entire array. For example, in [34], it is shown that up to 30% of SRAM cells in an array can be unstable. Moreover, stable cells can become unstable when voltage and temperature conditions change [30].

3. Analysis of SRAM Cell Stability

In this section, the SRAM cell presented in Figure 1 has been simulated using LTSpice [35], considering its implementation by a standard 32 nm CMOS technology. The considered nominal values of transistors’ parameters are L = 32 nm, Wn = 32 nm, Wp = 64 nm, VTn = 493 mV, VTp = −491 mV. In addition, we considered VDD = 1.0 V, T = 27 °C and the presence of noise with a nominal peak-to-peak amplitude VPP,noise = 20 mV, which has been simulated by adding a random noise source to node Q′.
As for variations in process parameters, we considered those of the conduction threshold voltage only, which, in [33], has been proven to be the dominant parameter. For simplicity, we initially considered such variations only for one transistor of the SRAM cell, as an example for transistor P1. The performed analyses enabled to identify which operating condition, among temperature, power supply voltage, and noise has the highest impact on PUF reliability. Simulations were then performed considering variations in the conduction threshold of all transistors of the SRAM cell and the operating conditions that have been found to have the dominant effect on PUF reliability.
Moreover, we evaluated the probability that an SRAM cell stores a logic 1 at node Q at power-on (PQ) by performing electrical-level simulations of an SRAM cell. In particular, by means of simulations, we evaluated the logic value given at node Q each time the cell is powered on, after a previous switching off of the power supply voltage. This was performed by simulating 100 consecutive power-off and power-on cycles. The value of PQ was obtained by simply counting the number of times it is Q = 1.
These simulations were performed in the presence of (A) different values of VPP,noise (and nominal temperature and power supply voltage); (B) temperature variations (with nominal value of noise level and power supply voltage); (C) power supply voltage variations (with nominal values of noise level and temperature). The achieved results are reported in Section 3.1, Section 3.2, and Section 3.3, respectively.

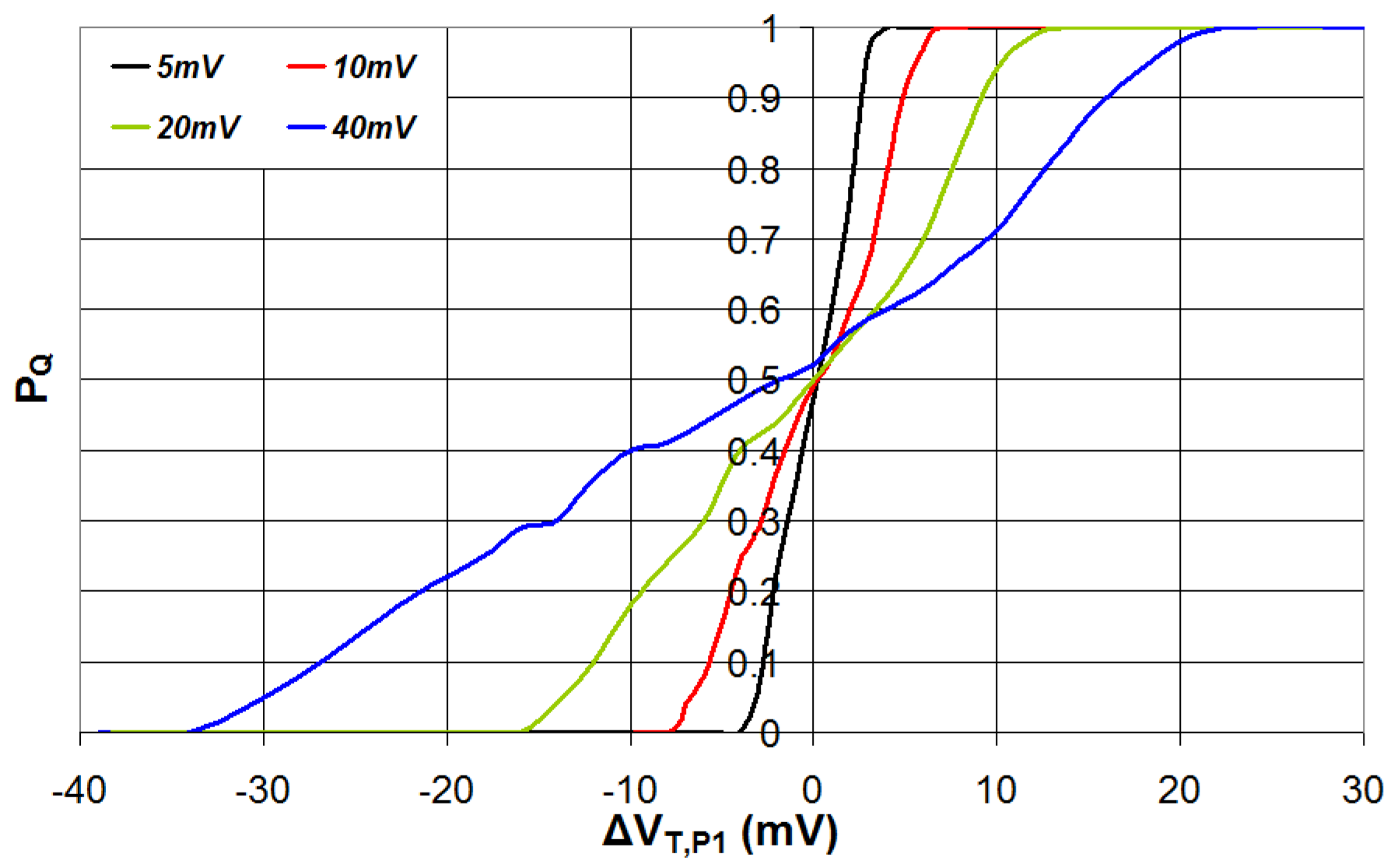
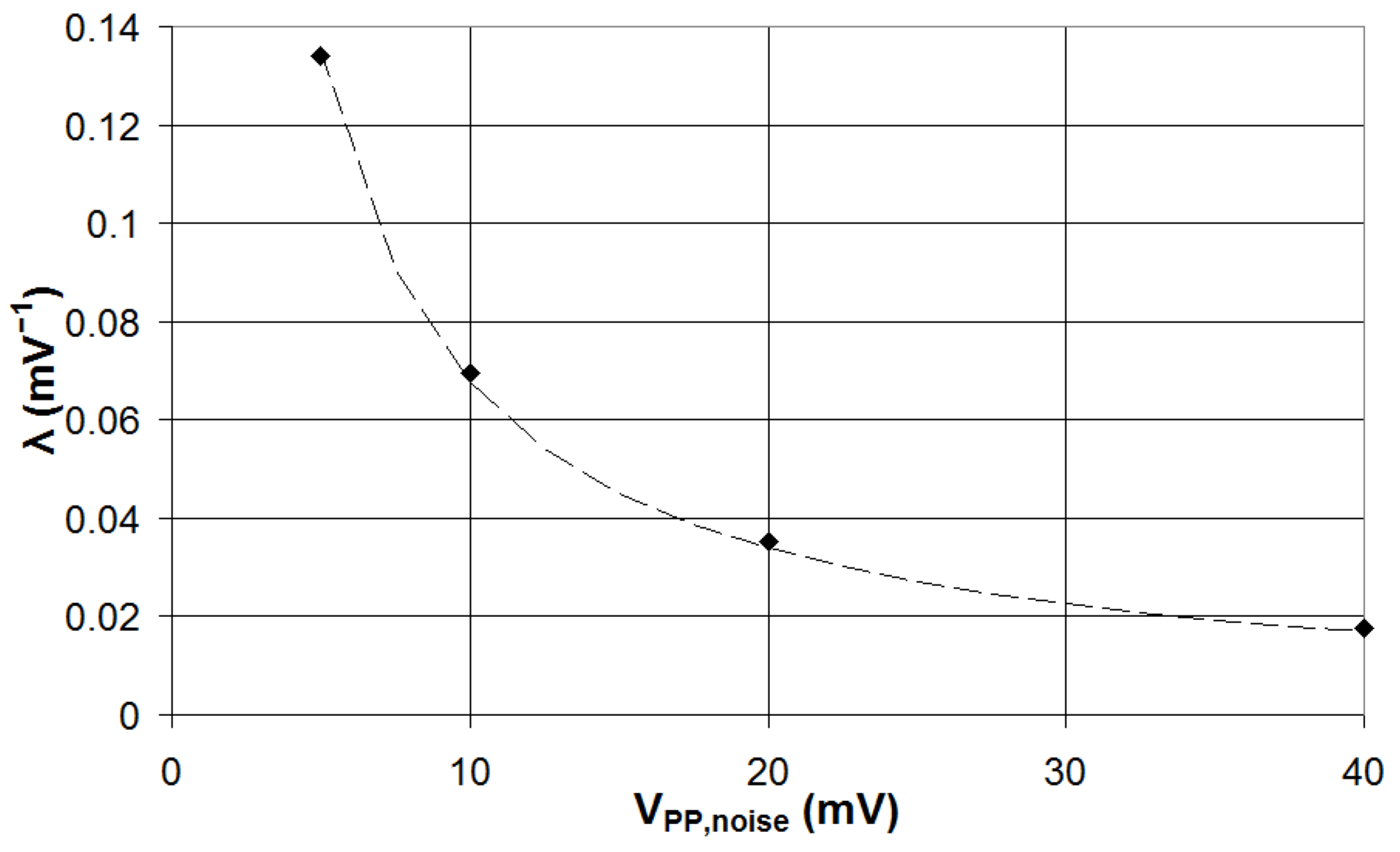
3.1. Impact of the Electrical Noise

The impact of noise has been evaluated by calculating PQ as a function of variations in the values of the threshold voltage of transistor P1 (ΔVT,P1), for four different values of VPP,noise: 5 mV, 10 mV, 20 mV, and 40 mV. The obtained results are presented in Figure 2.
As can be seen, for the four considered VPP,noise values, PQ presents a quasi-linear dependence on ΔVT,P1 (with a slope hereinafter indicated by λ), and saturates at 0 and 1 at different ΔVT,P1 values, which depend on VPP,noise. In particular, the lower the VPP,noise value is, the higher the slope of the quasi-linear function is, thus the lower the value of ΔVT,P1 at which PQ saturates, so that the SRAM stability is higher. Therefore, Figure 2 shows that, an increase in VPP,noise results in a significant reduction in the stability of SRAM cells.
In more detail, we have estimated the λ of the quasi-linear portions of the characteristics in Figure 2 by performing a linear regression of the PQ values calculated starting from simulation results. Figure 3 reports such λ values as a function of the value of VPP,noise (where the four points in the curve represent the four values of VPP,noise considered in Figure 2). As can be seen from Figure 3, λ decreases as a hyperbolic function of VPP,noise. This confirms that relatively small values of noise can significantly affect the stability of SRAM cells. As an example, we can observe that an increase in VPP,noise from 5 mV to 10 mV results in a reduction in λ of approximately 48%.

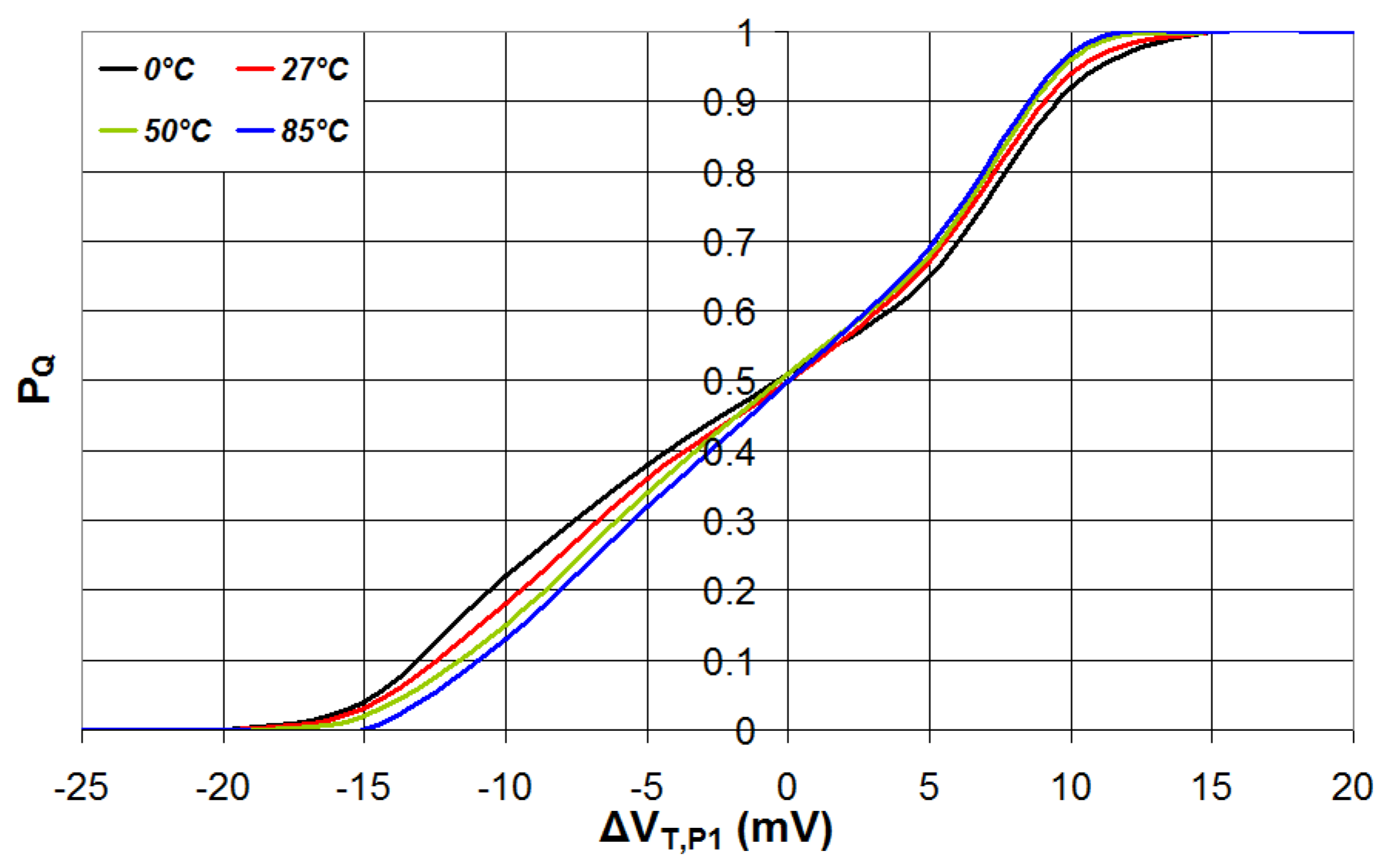
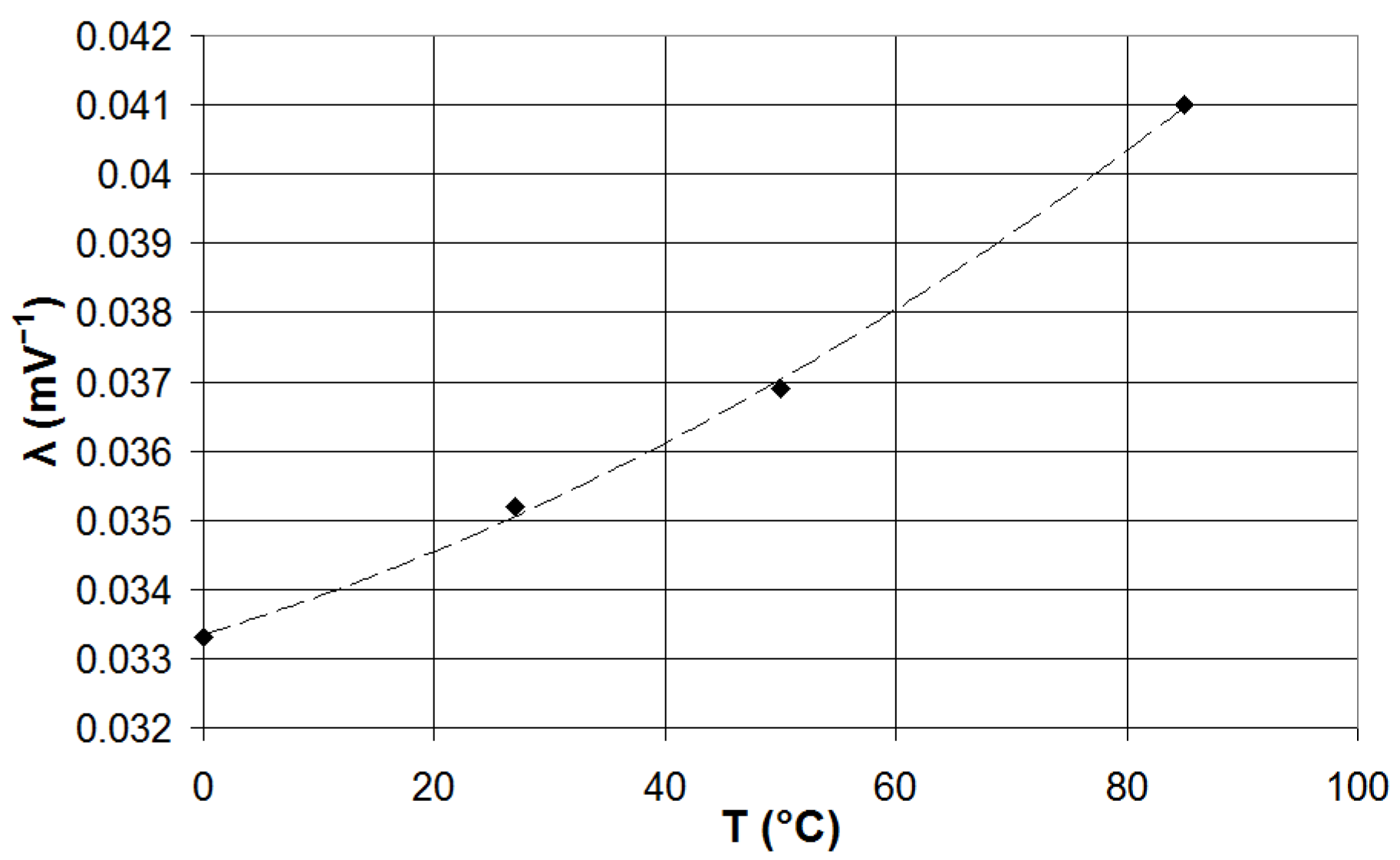
3.2. Impact of Temperature Variations

The impact of temperature variations has been evaluated by calculating the probability PQ as a function of the threshold voltage variation in transistor P1 (ΔVT,P1), for the case of four different values of operating temperature (T): 0 °C, 27 °C, 50 °C, and 85 °C. The obtained results are reported in Figure 4. As before, we have estimated the λ of the quasi-linear portions of the characteristics in Figure 4 by performing a linear regression of the PQ values calculated starting from simulation results.
As can be seen, PQ presents again a quasi-linear dependence on ΔVT,P1, but the λ of the quasi-linear portions of the characteristics obtained for the four considered temperatures are very similar to each other, thus showing that the stability of the SRAM cell is less dependent on temperature variations than on VPP,noise (as shown in the previous Figure 2).
Figure 5 reports the values of λ as a function of the operating temperature (where the four points in the curve represent the four temperature values in Figure 4). As can be seen, the value of λ increases with temperature, following a quadratic function, thus showing that the stability of SRAM cells increases with temperature increase. However, comparing the results in Figure 5 with those in Figure 3, we can observe that the change in λ as a function of temperature is smaller than the change in λ as a function of noise. As an example, from Figure 3 we can see that a noise (VPP,noise) varying from 5 mV to 40 mV results in a λ change of approximately 650%. Instead, from Figure 5 we can see that a temperature variation between 0 °C and 85 °C results in a λ change from 0.0333 mV−1 to 0.041 mV−1, with a variation of approximately 23%.

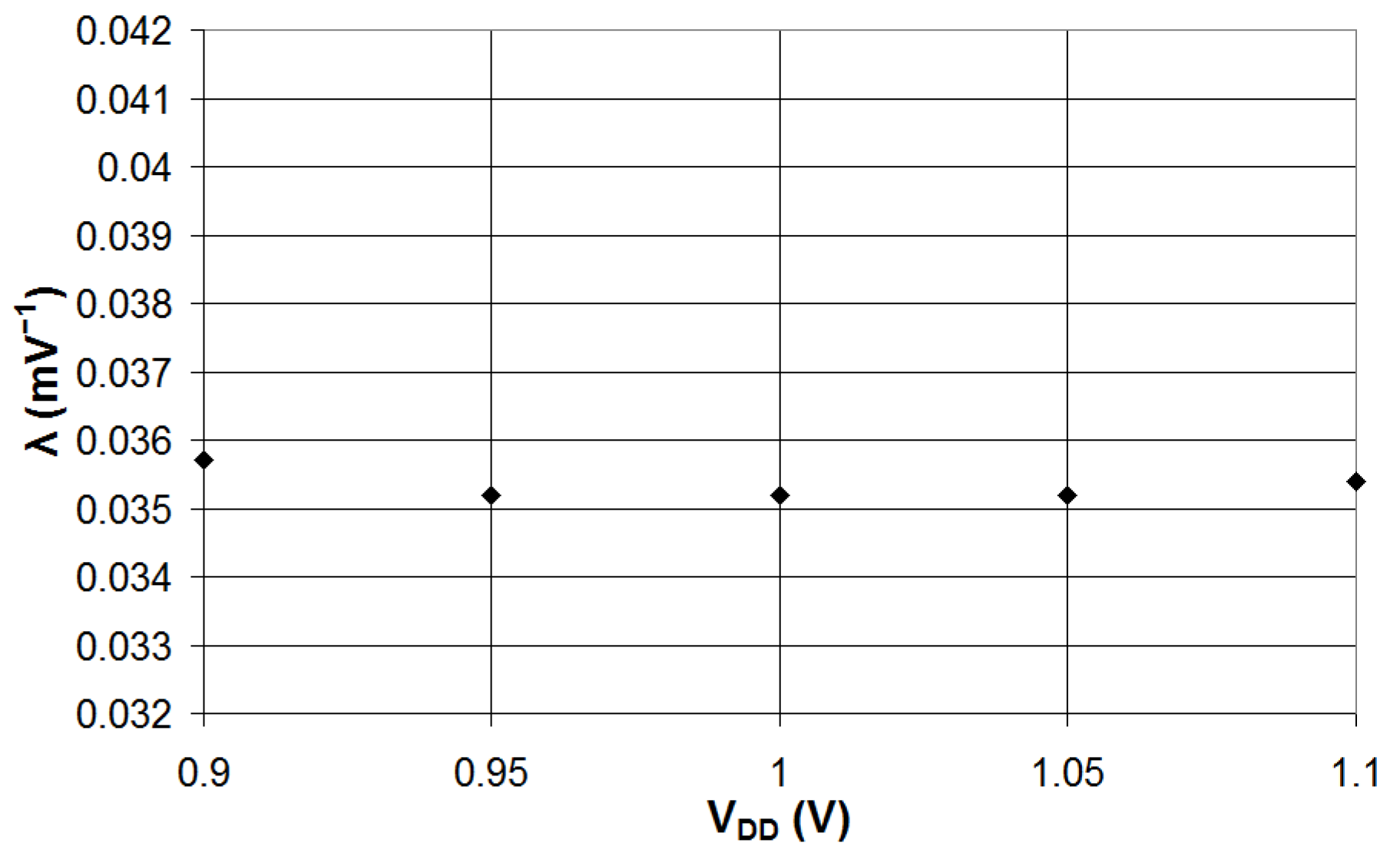
3.3. Impact of Power Supply Voltage Variations

The impact of power supply voltage variations has been evaluated by calculating PQ as a function of the threshold voltage variation in transistor P1 (ΔVT,P1), for the case of five different values of VDD: 0.9 V, 0.95 V, 1.0 V, 1.05 V, and 1.1 V. The obtained results are presented in Figure 6. As before, we have estimated the λ of the quasi-linear portions of the characteristics in Figure 6 by performing a linear regression of the PQ values calculated starting from simulation results.
As can be seen from Figure 6a, PQ presents again a quasi-linear dependence on ΔVT,P1 but, in this case, the λ values of the quasi-linear portions of the characteristics obtained for the five considered power supply voltage values are almost the same, thus showing that the stability of the SRAM cell is almost independent of the power supply voltage value. In fact, as can be seen from Figure 6b, the maximum variation in PQ (ΔPQ) among the considered power supply voltage is never higher than 0.01.
Figure 7 reports the values of λ as a function of power supply voltage values.
As can be seen from Figure 7, the impact of power supply variations on the value of λ is negligible, thus showing that the stability of SRAM cells depends minimally on power supply variations. As an example, for a power supply variation between 0.9 V and 1.1 V, the value of λ changes from 0.0352 mV−1 to 0.0357 mV−1, resulting in a λ change of approximately 1.42% only.

4. Analysis of SRAM-Based PUF Reliability

In this section, we evaluate the PUF reliability considering an SRAM-based PUF implemented by means of an SRAM array of 250 cells. The cell array has been implemented considering again 32 nm CMOS technology, and with the same transistor parameter variations, random noise source, and temperature and power supply voltage variations considered in the previous Section 3.
We have evaluated the reliability (R) of an SRAM-based PUF considering the typical PUF reliability metric [36], with an optimal value of 100%. It is given by
R = 100 · 1 − 1 n r e p · ∑ j = 1 n r e p H D R i , R i , j n b i t , C R P
where nrep is the number of times the PUF response is evaluated (1000 in our analysis) for each applied PUF input challenge (10,000 input challenges in our analysis), and nbit,CRP is the number of bits in the PUF response (64 bits in our analysis). Moreover, Ri represents the PUF response to a challenge Ci under nominal operating conditions, while Ri,j represents the PUF response to the same challenge Ci during one of the nrep tests (with operating conditions different from the nominal one and the presence of noise). In addition, HD(Ri, Ri,j) is the Hamming distance between responses Ri and Ri,j, that is the number of bits in which the two responses differ.
In particular, in Section 4.1, we evaluate the reliability of the considered SRAM-based PUF considering threshold voltage variations on transistor P1 (Figure 1) only.
Then, in Section 4.2, we evaluate the reliability of the considered SRAM-based PUF considering the more general case in which all transistors of the SRAM cells present random variations in their threshold voltage.

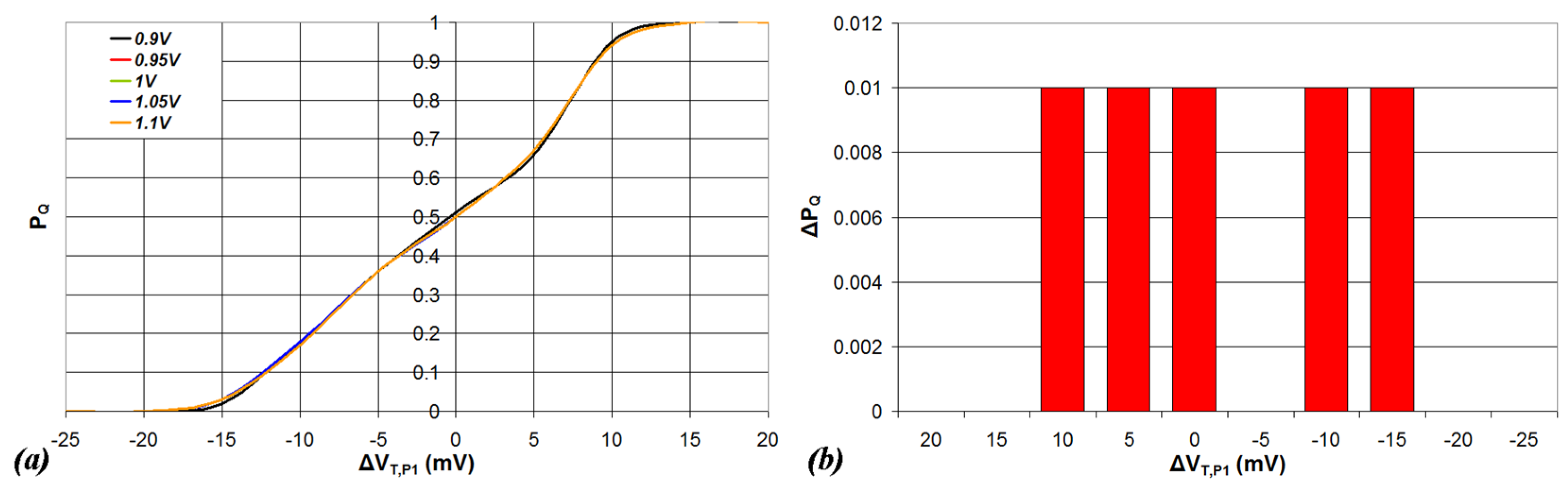
4.1. Impact of Transistor P1 Threshold Voltage Variations

In this subsection, we evaluate the reliability of the considered SRAM PUF for the case of variations in the conduction threshold voltage of transistor P1 of the cells (Figure 1).
In particular, we evaluate the reliability of the PUF by considering four different scenarios: (1) variations in the threshold voltage distribution of transistor P1 for the SRAM cells, with nominal values of noise level, temperature, and power supply voltage; (2) variations in the noise level, with nominal values of the threshold voltage distribution of transistor P1 for the SRAM cells, temperature, and power supply voltage; (3) variations in temperature, with nominal values of the threshold voltage distribution of transistor P1 for the SRAM cells, level of noise, and power supply voltage; (4) variations in power supply voltage, with nominal values of the threshold voltage distribution of transistor P1 for the SRAM cells, level of noise, and temperature.
As for the first scenario, we considered different values of threshold voltages for transistor P1 (VT,P1) of the SRAM cells, that have been derived considering a threshold voltage variation with a Gaussian distribution, with a mean value of −491 mV and four different values for the standard deviation σ: 8 mV, 16 mV, 25 mV, 34 mV. In addition, we considered a noise with VPP,noise = 20 mV, a nominal temperature T = 27 °C, and a nominal power supply voltage VDD = 1.0 V.
For this case, the achieved values of reliability are R = 64.41% for the case of σ = 8 mV, R = 79.67% for the case of σ = 16 mV, R = 84.03% for the case of σ = 25 mV, and R = 90.02% for the case of σ = 34 mV. As expected, reliability increases with the increase in the standard deviation of the VT,P1 distribution.
As for the second scenario, we considered a noise with the following VPP,noise values: 5 mV, 10 mV, 20 mV, and 40 mV. In addition, we considered a distribution of the P1 threshold voltage with a mean value of −491 mV and a standard deviation σ = 16 mV, a nominal temperature T = 27 °C, and a nominal power supply VDD = 1.0 V.
For this case, the achieved values of reliability are R = 94.76% for the case of VPP,noise = 5 mV, R = 89.17% for the case of VPP,noise = 10 mV, R = 79.67% for the case of VPP,noise = 20 mV, and R = 64.50% for the case of VPP,noise = 40 mV. As can be seen, and as expected, reliability increases with the decrease in values of VPP,noise.
As for the third scenario, we considered the following four temperature values: 0 °C, 27 °C, 50 °C, and 85 °C. In addition, we considered a distribution of the P1 threshold voltage with a mean value of −491 mV and a standard deviation σ = 16 mV, a noise with VPP,noise = 20 mV, and a nominal power supply VDD = 1.0 V.
For this case, the achieved values of reliability are R = 78.54% for the case of T = 0 °C, R = 79.67% for the case of T = 27 °C, R = 80.52% for the case of T = 50 °C, and R = 82.51% for the case of T = 85 °C. We can observe that reliability slightly increases with the increase in the temperature value.
As for the fourth scenario, we considered the following five power supply voltage values: 0.9 V, 0.95 V, 1.0 V, 1.05 V, and 1.1 V. In addition, we considered a distribution of the P1 threshold voltage with a mean value of −491 mV and a standard deviation σ = 16 mV, a noise with VPP,noise = 20 mV, and a nominal temperature T = 27 °C.
For this last case, the achieved values of reliability are R = 79.91% for the case of VDD = 0.9 V, R = 79.66% for the case of VDD = 0.95 V, R = 79.67% for the case of VDD = 1.0 V, R = 79.68% for the case of VDD = 1.05 V, and R = 79.73% for the case of VDD = 1.1 V. We can observe that the reliability of the PUF is almost unaffected by the values of VDD.

4.2. Impact of Threshold Voltage Variations on All Transistors

We evaluated the reliability of the considered SRAM-based PUF considering the more general case in which all transistors of the SRAM cells present random variations in their threshold voltage.
The PUF reliability has been evaluated considering variations in threshold voltage of all transistors of the SRAM cell, with a Gaussian distribution with a mean value of 493 mV for nMOS and of −491 mV for pMOS, and standard deviation σ = 16 mV. In addition, we considered a noise with VPP,noise = 20 mV, a constant temperature T = 27 °C, and a constant power supply VDD = 1.0 V.
The obtained PUF reliability is R = 89.39%. We can notice that this value is higher than the corresponding value obtained in case of variations in threshold voltage of transistor P1 only (case 1 in the previous Section 4.1, with R = 79.67%).

5. Conclusions

In this paper, the reliability of an SRAM-based PUF implemented by a standard 32 nm CMOS technology was investigated as a function of different operating conditions, such as variations in temperature and power supply voltage, and presence of noise, considering also different values of transistor conduction threshold voltages. The PUF reliability was evaluated by LTSpice circuit-level simulations. The achieved results have shown that noise plays a major role in the value of PUF reliability, while the impact of temperature variations is lower, and the impact of power supply variations is negligible.

Author Contributions

Conceptualization, M.G. and M.O.; methodology, M.G. and M.O.; software, M.G. and M.O.; validation, S.B., M.G. and M.O.; formal analysis, S.B., M.G. and M.O.; investigation, S.B., M.G. and M.O.; resources, M.G. and M.O.; data curation, S.B., M.G. and M.O.; writing—original draft preparation, M.G.; writing—review and editing, M.G., C.M. and M.O.; supervision, C.M. and A.A.; project administration, C.M. and A.A.; funding acquisition, C.M. and A.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the European Union—NextGenerationEU under the National Recovery and Resilience Plan (PNRR)—Mission 4 Education and research—Component 2 From research to business—Investment 1.3, Notice D.D. 341 of 15/03/2022, from title: SEcurity and RIghts in the CyberSpace, proposal code PE0000014—CUP J33C22002810001.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Choudhary, V.; Guha, P.; Pau, G.; Mishra, S. An overview of smart agriculture using internet of things (IoT) and web services. Environ. Sustain. Indic. 2025, 26, 100607. [Google Scholar] [CrossRef]
  2. Bhuiyan, M.N.; Rahman, M.M.; Billah, M.M.; Saha, D. Internet of things (IoT): A review of its enabling technologies in healthcare applications, standards protocols, security, and market opportunities. IEEE Internet Things J. 2021, 8, 10474–10498. [Google Scholar] [CrossRef]
  3. Jamshed, M.A.; Ali, K.; Abbasi, Q.H.; Imran, M.A.; Ur-Rehman, M. Challenges, applications, and future of wireless sensors in Internet of Things: A review. IEEE Sens. J. 2022, 22, 5482–5494. [Google Scholar] [CrossRef]
  4. Grossi, M.; Valli, E.; Glicerina, V.T.; Rocculi, P.; Toschi, T.G.; Riccò, B. Optical determination of solid fat content in fats and oils: Effects of wavelength on estimated accuracy. Eur. J. Lipid Sci. Technol. 2022, 124, 2100071. [Google Scholar] [CrossRef]
  5. Hosseini, S.N.; Akram, M.M.; Das, P.S.; Lazarjan, V.K.; Tremblay, D.M.; Moineau, S.; Messaddeq, Y.; Gosselin, B. Multimodal CMOS Biosensor for Microbial Growth Monitoring. IEEE Sens. J. 2023, 23, 14670–14684. [Google Scholar] [CrossRef]
  6. Vela, L.M.; Kwon, H.; Rutkove, S.B.; Sanchez, B. Standalone IoT bioimpedance device supporting real-time online data access. IEEE Internet Things J. 2019, 6, 9545–9554. [Google Scholar] [CrossRef]
  7. Qiu, C.; Wu, F.; Han, W.; Yuce, M.R. A wearable bioimpedance chest patch for real-time ambulatory respiratory monitoring. IEEE Trans. Biomed. Eng. 2022, 69, 2970–2981. [Google Scholar] [CrossRef] [PubMed]
  8. Grossi, M.; Alfonsi, F.; Prandini, M.; Gabrielli, A. Increasing the Security of Network Data Transmission with a Configurable Hardware Firewall Based on Field Programmable Gate Arrays. Future Internet 2024, 16, 303. [Google Scholar] [CrossRef]
  9. Li, J.; Fan, Y.; Bian, X.; Yuan, Q. Online/offline MA-CP-ABE with cryptographic reverse firewalls for IoT. Entropy 2023, 25, 616. [Google Scholar] [CrossRef] [PubMed]
  10. Sha, K.; Yang, T.A.; Wei, W.; Davari, S. A survey of edge computing-based designs for IoT security. Digit. Commun. Netw. 2020, 6, 195–202. [Google Scholar] [CrossRef]
  11. Grossi, M.; Alfonsi, F.; Prandini, M.; Gabrielli, A. A Highly Configurable Packet Sniffer Based on Field-Programmable Gate Arrays for Network Security Applications. Electronics 2023, 12, 4412. [Google Scholar] [CrossRef]
  12. Oh, J.; Yu, S.; Lee, J.; Son, S.; Kim, M.; Park, Y. A secure and lightweight authentication protocol for IoT-based smart homes. Sensors 2021, 21, 1488. [Google Scholar] [CrossRef]
  13. Saqib, M.; Jasra, B.; Moon, A.H. A lightweight three factor authentication framework for IoT based critical applications. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 6925–6937. [Google Scholar]
  14. Thakor, V.A.; Razzaque, M.A.; Khandaker, M.R. Lightweight cryptography algorithms for resource-constrained IoT devices: A review, comparison and research opportunities. IEEE Access 2021, 9, 28177–28193. [Google Scholar]
  15. Fotovvat, A.; Rahman, G.M.; Vedaei, S.S.; Wahid, K.A. Comparative performance analysis of lightweight cryptography algorithms for IoT sensor nodes. IEEE Internet Things J. 2020, 8, 8279–8290. [Google Scholar] [CrossRef]
  16. Gao, Y.; Al-Sarawi, S.F.; Abbott, D. Physical unclonable functions. Nat. Electron. 2020, 3, 81–91. [Google Scholar] [CrossRef]
  17. Hemavathy, S.; Bhaaskaran, V.K. Arbiter puf—A review of design, composition, and security aspects. IEEE Access 2023, 11, 33979–34004. [Google Scholar] [CrossRef]
  18. He, Z.; Chen, W.; Zhang, L.; Chi, G.; Gao, Q.; Harn, L. A highly reliable arbiter PUF with improved uniqueness in FPGA implementation using bit-self-test. IEEE Access 2020, 8, 181751–181762. [Google Scholar] [CrossRef]
  19. Omaña, M.; Grossi, M.; Rossi, D.; Metra, C. Aging resilient ring oscillators for reliable Physically Unclonable Functions (PUFs). Microelectron. Reliab. 2024, 162, 115520. [Google Scholar] [CrossRef]
  20. Deng, D.; Hou, S.; Wang, Z.; Guo, Y. Configurable ring oscillator PUF using hybrid logic gates. IEEE Access 2020, 8, 161427–161437. [Google Scholar] [CrossRef]
  21. Baek, S.; Yu, G.H.; Kim, J.; Ngo, C.T.; Eshraghian, J.K.; Hong, J.P. A reconfigurable SRAM based CMOS PUF with challenge to response pairs. IEEE Access 2021, 9, 79947–79960. [Google Scholar] [CrossRef]
  22. Lu, L.; Kim, T.T.H. A high reliable SRAM-based PUF with enhanced challenge-response space. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 589–593. [Google Scholar] [CrossRef]
  23. Grossi, M.; Omaña, M.; Acquaviva, C.M.A. Novel Physical Unclonable Function Implementation for Microcontrollers and Field Programmable Gate Arrays. IEEE Access 2025, 13, 55970–55983. [Google Scholar] [CrossRef]
  24. Grossi, M.; Omaña, M. Feasibility of Physical Unclonable Function (PUF) implementation using the pull-up/pull-down resistances integrated in microcontrollers GPIO. AEU-Int. J. Electron. Commun. 2025, 202, 156053. [Google Scholar] [CrossRef]
  25. Barbareschi, M.; Cirillo, F.; Esposito, C. SRAM-PUF Authentication Schemes Empowered with Blockchain on Resource-Constrained Microcontrollers. In Proceedings of the IEEE 27th International Symposium on Real-Time Distributed Computing (ISORC), Tunis, Tunisia, 22–25 May 2024; pp. 1–10. [Google Scholar]
  26. Baturone, I.; Prada-Delgado, M.A.; Eiroa, S. Improved generation of identifiers, secret keys, and random numbers from SRAMs. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2653–2668. [Google Scholar] [CrossRef]
  27. Miller, A.; Shifman, Y.; Weizman, Y.; Keren, O.; Shor, J. A highly reliable SRAM PUF with a capacitive preselection mechanism and pre-ECC BER of 7.4 E-10. In Proceedings of the 2019 IEEE Custom Integrated Circuits Conference (CICC), Austin, TX, USA, 14–17 April 2019; pp. 1–4. [Google Scholar]
  28. Cortez, M.; Dargar, A.; Hamdioui, S.; Schrijen, G.J. Modeling SRAM start-up behavior for physical unclonable functions. In Proceedings of the 2012 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFT), Austin, TX, USA, 3–5 October 2012; pp. 1–6. [Google Scholar]
  29. Golanbari, M.S.; Kiamehr, S.; Bishnoi, R.; Tahoori, M.B. Reliable memory PUF design for low-power applications. In Proceedings of the 19th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 13–14 March 2018; pp. 207–213. [Google Scholar]
  30. Holcomb, D.E.; Burleson, W.P.; Fu, K. Power-up SRAM state as an identifying fingerprint and source of true random numbers. IEEE Trans. Comput. 2008, 58, 1198–1210. [Google Scholar] [CrossRef]
  31. Maes, R.; Van Der Leest, V. Countering the effects of silicon aging on SRAM PUFs. In Proceedings of the 2014 IEEE International symposium on hardware-oriented security and trust (HOST), Arlington, VA, USA, 6–7 May 2014; pp. 148–153. [Google Scholar]
  32. Bhatta, N.P.; Singh, H.; Ghimire, A.; Amsaad, F. Analyzing aging effects on SRAM PUFs: Implications for security and reliability. J. Hardw. Syst. Secur. 2024, 8, 174–186. [Google Scholar] [CrossRef]
  33. Alheyasat, A.; Torrens, G.; Bota, S.; Alorda, B. Selection of SRAM cells to improve reliable PUF implementation using cell mismatch metric. In Proceedings of the IEEE XXXV Conference on Design of Circuits and Integrated Systems (DCIS), Segovia, Spain, 18–20 November 2020; pp. 1–6. [Google Scholar]
  34. Mathew, S.K.; Satpathy, S.K.; Anders, M.A.; Kaul, H.; Hsu, S.K.; Agarwal, A.; Chen, G.K.; Parker, R.J.; Krishnamurthy, R.K.; De, V. A 0.19 pJ/b PVT-variation-tolerant hybrid physically unclonable function circuit for 100% stable secure key generation in 22nm CMOS. In Proceedings of the 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 278–279. [Google Scholar]
  35. LTSpice Simulator. Available online: https://www.analog.com/en/resources/design-tools-and-calculators/ltspice-simulator.html (accessed on 30 October 2025).
  36. Maiti, A.; Gunreddy, V.; Schaumont, P. A systematic method to evaluate and compare the performance of physical unclonable functions. In Embedded Systems Design with FPGAs; Springer: New York, NY, USA, 2013; pp. 245–267. [Google Scholar]
Engproc 124 00010 g001
Figure 1. Schematic of a traditional six-transistor SRAM cell.
Figure 1. Schematic of a traditional six-transistor SRAM cell.
Engproc 124 00010 g001
Engproc 124 00010 g002
Figure 2. Simulation results showing values of PQ as a function of threshold voltage variations in transistor P1, for different values of VPP,noise.
Figure 2. Simulation results showing values of PQ as a function of threshold voltage variations in transistor P1, for different values of VPP,noise.
Engproc 124 00010 g002
Engproc 124 00010 g003
Figure 3. Calculated values of the slope (λ) of the quasi-linear dependence of PQ on ΔVT,P1, as a function of VPP,noise.
Figure 3. Calculated values of the slope (λ) of the quasi-linear dependence of PQ on ΔVT,P1, as a function of VPP,noise.
Engproc 124 00010 g003
Engproc 124 00010 g004
Figure 4. Simulation results showing values of PQ as a function of threshold voltage variations in transistor P1, for different values of temperature T.
Figure 4. Simulation results showing values of PQ as a function of threshold voltage variations in transistor P1, for different values of temperature T.
Engproc 124 00010 g004
Engproc 124 00010 g005
Figure 5. Calculated values of the slope (λ) of the quasi-linear dependence of PQ on ΔVT,P1, as a function of temperature T.
Figure 5. Calculated values of the slope (λ) of the quasi-linear dependence of PQ on ΔVT,P1, as a function of temperature T.
Engproc 124 00010 g005
Engproc 124 00010 g006
Figure 6. Simulation results showing (a) the values of PQ as a function of threshold voltage variations in transistor P1, for different values of power supply voltage; (b) the maximum variation in PQ (ΔPQ) among the considered power supply voltages.
Figure 6. Simulation results showing (a) the values of PQ as a function of threshold voltage variations in transistor P1, for different values of power supply voltage; (b) the maximum variation in PQ (ΔPQ) among the considered power supply voltages.
Engproc 124 00010 g006
Engproc 124 00010 g007
Figure 7. Calculated values of the slope (λ) of the quasi-linear dependence of PQ on ΔVT,P1, as a function of power supply voltage values.
Figure 7. Calculated values of the slope (λ) of the quasi-linear dependence of PQ on ΔVT,P1, as a function of power supply voltage values.
Engproc 124 00010 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Grossi, M.; Omaña, M.; Bisi, S.; Metra, C.; Acquaviva, A. Impact of Operating Conditions on the Reliability of SRAM-Based Physical Unclonable Functions (PUFs). Eng. Proc. 2026, 124, 10. https://doi.org/10.3390/engproc2026124010

AMA Style

Grossi M, Omaña M, Bisi S, Metra C, Acquaviva A. Impact of Operating Conditions on the Reliability of SRAM-Based Physical Unclonable Functions (PUFs). Engineering Proceedings. 2026; 124(1):10. https://doi.org/10.3390/engproc2026124010

Chicago/Turabian Style

Grossi, Marco, Martin Omaña, Simone Bisi, Cecilia Metra, and Andrea Acquaviva. 2026. "Impact of Operating Conditions on the Reliability of SRAM-Based Physical Unclonable Functions (PUFs)" Engineering Proceedings 124, no. 1: 10. https://doi.org/10.3390/engproc2026124010

APA Style

Grossi, M., Omaña, M., Bisi, S., Metra, C., & Acquaviva, A. (2026). Impact of Operating Conditions on the Reliability of SRAM-Based Physical Unclonable Functions (PUFs). Engineering Proceedings, 124(1), 10. https://doi.org/10.3390/engproc2026124010

Article Metrics

Back to TopTop