Robust Control Design for an Off-Board EV Charger Considering Grid Impedance Variation ^†

Abstract

Grid impedance variation has the possibility of leading to voltage oscillation and control instability, which poses a serious problem to electric vehicle (EV) charger design. In response to this problem, this paper proposes a robust control approach that is capable of dealing with grid impedance variation and system uncertainties. The proposed dual-loop control strategy is composed of an outer-loop proportional–integral (PI) controller and an inner-loop robust state feedback controller with integral action. The benefits of control are maximized according to linear matrix inequality (LMI) techniques. This paper aims to address the effects of grid impedance variation by including the uncertainty model considering the potential varying parameters in the control design process. Additionally, the uncertainty model considers sixteen possible sets, which are described by variations in the four most important parameters: grid impedance, grid resistance, filter impedance, and filter resistance. The simulations suggest that the proposed controller maintains stable current regulation for uncertainty factors as high as γ = 3.3, where all closed-loop poles remain within the unit circle. For all the tested uncertainty levels, the grid-current tracks the reference of 10 A with a faster settling time at γ = 1.1 and no overshoot for higher uncertainty levels.

1. Introduction

The increased need for electric vehicles (EVs) has placed significant pressure on the establishment of robust and effective EV charging stations. Ensuring that grid-connected EV chargers are stable and function optimally under poor conditions, like fluctuations in the grid impedance, is one of the most critical technical challenges. Grid impedance fluctuations are common in real power distribution networks due to effects like line impedance variations, varied load patterns, and switching operations [1]. These changes can cause voltage oscillations, decrease control performance, and even generate system instability if not corrected.

Previous control approaches, such as proportional–integral (PI) control [2], are extensively used on power electronic systems due to simplicity and effectiveness in regular operation modes. These methods are generally based upon fixed parameters, therefore susceptible to loss in performance when they face parameter drifts and external disturbances. In grid-connected electric vehicle (EV) chargers, the grid impedance may vary significantly due to the effects of load switching, network reconfiguration, and the integration of distributed energy resources. Such variation may cause voltage oscillation and control instability not addressed by traditional controllers. As charging infrastructure for electric vehicles becomes more widespread and embedded within more sophisticated and dynamic power grids, the limitations of traditional control solutions become ever more apparent. Therefore, a more resilient and dynamic control solution is required.

Among the robust methods, sliding mode control (SMC) has demonstrated strong robustness properties, particularly for systems with matched uncertainties. Nevertheless, SMC often suffers from chattering, which can excite high-frequency components in the system and potentially damage power electronic switches. Adaptive control techniques have also been explored, enabling real-time adjustment of controller parameters, but these often require persistent excitation conditions and can be complex to implement. More recently, Model Predictive Control (MPC) [3,4] has been applied to EV chargers, offering predictive optimization capabilities, but MPC requires high computational resources and accurate prediction models, which may not be ideal for fast sampling applications.

To overcome the limitations of the above methods, linear matrix inequality (LMI)-based robust control has emerged as a powerful alternative. LMIs allow the robust control problem to be framed as a convex optimization problem, offering global optimality and tractability. Notably, in [5], an LMI-based H_∞ controller was developed to regulate inverter output voltage under varying loads. In [6,7], LMI-based control was proposed for power inverters, achieving robust tracking performance in the presence of system uncertainty. Similarly, observer-based approaches integrated with LMIs, as seen in [8], help handle state estimation in uncertain systems. Predictive methods in [9] and robust pole placement in [10] further confirm the utility of LMIs in power electronics control design.

Accounting for the uncertain impedance or unexpected grid has been emphasized in previously published works as a way to keep the inverter operation stable. Robust optimal control methods have been applied to single-phase grid-tied inverters [11] by explicitly modeling impedance variations, while sudden grid and system uncertainties are handled by LMI-based predictive control in LCL-filtered inverters [12]. These studies emphasize that control strategies must be designed to remain reliable under fluctuating grid conditions. In this context, this work extends the robust LMI-based design to off-board EV chargers by considering structured variations in grid impedance, grid resistance, and filter parameters to ensure resilient performance under practical grid uncertainties.

Despite these advances, few studies explicitly address the robust control of off-board EV chargers under grid impedance variation as a critical issue in fast-charging environments where grid conditions can fluctuate unpredictably. Most existing works either assume constant grid impedance or consider uncertainty in a general, non-structured form without modeling its specific influence on system dynamics. This paper aims to address the effects of grid impedance variation by including the uncertainty model, considering these parameters in the control design process. This proposed dual-loop control strategy is composed of an outer-loop proportional–integral (PI) controller and an inner-loop robust state feedback controller with integral action. The benefits of control are maximized according to LMI techniques.

2. Charger Modeling Considering Grid Impedance Variation

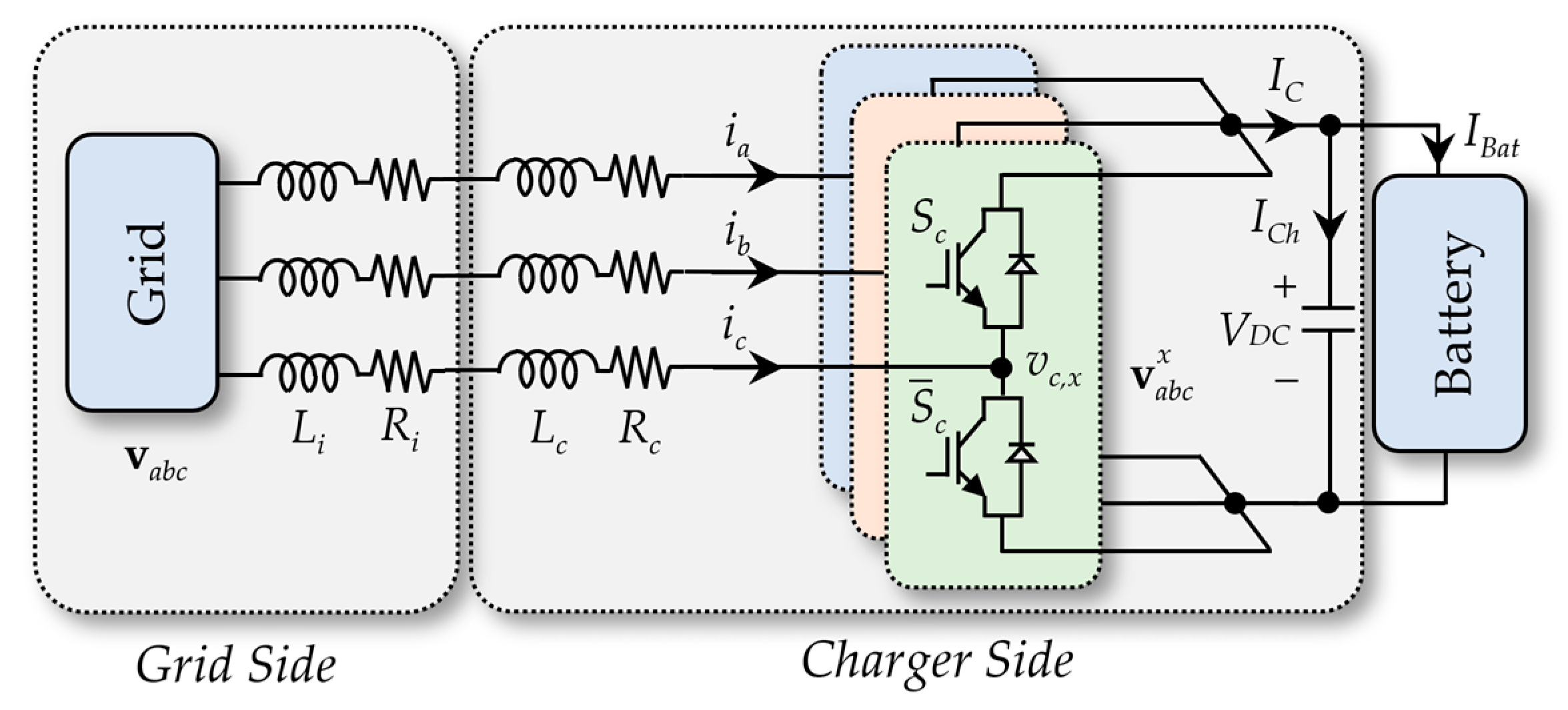
Figure 1 illustrates the configuration of the proposed bidirectional charger, which explicitly takes grid impedance into account. The characteristic equations governing the system dynamics in the time domain can be derived as follows.

$$v_{abc}(t)-(L_i+L_c){\displaystyle \frac{d{i}_{abc}(t)}{dt}}-(R_i+R_c)i_{abc}(t)-v_{abc}^x(t)=0$$

(1)

Accordingly, the equation above is mathematically equivalent to:

$${\displaystyle \frac{d{i}_{abc}(t)}{dt}}={\displaystyle \frac{v_{abc}(t)}{L_t}}-{\displaystyle \frac{R_t}{L_t}}{i}_{abc}(t)-{\displaystyle \frac{v_{abc}^x(t)}{L_t}}$$

(2)

where $i_{abc}=\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]$, $v_{abc}=\left[\begin{array}{c}{v}_a\\ v_b\\ v_c\end{array}\right]$, $v_{abc}^x=\left[\begin{array}{c}{v}_{a,x}\\ v_{b,x}\\ v_{c,x}\end{array}\right]$, $L_t=L_i+L_c$, $R_t=R_i+R_c$. $v_{abc}$ is voltage source vector in the abc-frame, $i_{abc}$ denotes current vector in abc-frame, $v_{abc}^x$ is the switching voltage of the converter, $L_i$ is grid inductance, $R_i$ is grid resistance, $L_c$ represents the inductance of the converter’s filter, and $R_c$ denotes filter’s resistance.

The AC-DC converter’s characteristic can be converted to the dq-frame as follows:

$${\dot{i}}_{dq}(t)=\left[\begin{array}{cc}{R}_t/L_t& \omega \\ \omega & R_t/L_t\end{array}\right]i_{dq}(t)+\left[\begin{array}{cc}-1/2L_t& 0\\ 0& -1/2L_t\end{array}\right]V_{DC}u(t)+\left[\begin{array}{c}{v}_d(t)\\ v_q(t)\end{array}\right]$$

(3)

Additionally, the relationship between abc-signals and dq-signals can be found as follows:

$$i_{dq}(t)={\displaystyle \frac{2}{3}}X(t)i_{abc}(t)$$

(4)

$$v_{dq}(t)={\displaystyle \frac{2}{3}}X(t)v_{abc}(t)$$

(5)

$$u(t)={\displaystyle \frac{2}{3}}X(t)v_{abc}^x(t)$$

(6)

$$X(t)=\left[\begin{array}{ccc}\cos (\omega t)& \cos (\omega t-2\pi /3)& \cos (\omega t+2\pi /3)\\ -\sin (\omega t)& -\sin (\omega t-2\pi /3)& -\sin (\omega t+2\pi /3)\end{array}\right]$$

(7)

The system Equation (3) can be converted to dq-frame discrete time model with sampling interval $T_s$ as

$$x(k+1)=Ax(k)+B{V}_{DC}u(k)+D(k)$$

(8)

where $D(k)=\left[\begin{array}{c}{T}_s{v}_d(k)\\ T_s{v}_q(k)\end{array}\right]$, $u(k)=\left[\begin{array}{c}{v}_d^x (k)\\ v_q^x (k)\end{array}\right]$, $x(k)=\left[\begin{array}{c}{i}_d(k) \\ i_q(k)\end{array}\right]$, $B=\left[\begin{array}{cc}-T_s/2L_t& 0\\ 0& -T_s/2L_t\end{array}\right]$, $A=\left[\begin{array}{cc}1-(R_t{T}_s/L_t)& \omega T_s\\ \omega T_s& 1-(R_t{T}_s/L_t)\end{array}\right]$, x denotes the current vector in the dq-frame, $T_s$ represents a sampling instance, $\omega$ denotes angular frequency, $u$ is the control input in the dq-frame, D represents the discrete-time voltage source in the dq-frame.

3. Uncertainty Models and Control Design

In the design of control systems for off-board EV chargers, maintaining stable and accurate operation under grid-connected conditions is a critical challenge, especially when grid impedance is uncertain or varies with time and location. These variations introduce significant uncertainty into the system dynamics, which can adversely affect control performance and system reliability. To address this issue, an uncertainty model is developed to characterize the effect of grid impedance fluctuation on the charger dynamics. This model serves as a basis for the subsequent design of an LMI-based robust control strategy, ensuring that the system maintains stability and desired performance across a range of grid conditions. The uncertainty is structured in a form compatible with LMI formulations, allowing systematic controller synthesis under worst-case scenarios. It is assumed that the inductance L and resistance R are subject to parametric variations within the following ranges:

$${\mathsf{\gamma }}^{-1}{R}_i<R_i<\mathsf{\gamma }{R}_i$$

(9)

$${\mathsf{\gamma }}^{-1}{L}_i<L_i<\mathsf{\gamma }{L}_i$$

(10)

$${\mathsf{\gamma }}^{-1}{R}_c<R_c<\mathsf{\gamma }{R}_c$$

(11)

$${\mathsf{\gamma }}^{-1}{L}_c<L_c<\mathsf{\gamma }{L}_c$$

(12)

Due to the variation in grid impedance, specifically in inductance L and resistance R the system matrices A and B are not fixed but vary within certain limits. To handle this uncertainty range γ(>1), the system is represented using a polytopic model, where matrices A and B are assumed to lie within a set formed by a convex combination of several known vertex systems. Each vertex corresponds to a specific combination of the minimum and maximum values of L and R. This can be written as follows:

$$(A, B)\in \mathrm{Co}\{(A_1, B_1),(A_2, B_2),\dots (A_{16}, B_{16})\}$$

(13)

Here, Co stands for the convex hull, and the set contains all possible combinations of A and B that result from the range of L and R. This polytopic form is suitable for designing robust controllers using LMIs.

The control law used in this proposed method is described below:

$$\left\{\begin{array}{l}i(k)=i(k-1)-e(k-1)\\ u(k)=K_{1}x(k)+K_{2}i(k)\end{array}\right.$$

(14)

where $i\in {\Re }^{2\times 1}$ represents the integral element, $e\in {\Re }^{2\times 1}$ is the error between the grid current and the control reference, $u\in {\Re }^{2\times 1}$ denotes the control input, $K_1\in {\Re }^{2\times 2}$ is the state feedback gain vector, $K_2\in {\Re }^{2\times 2}$ represents the integral control gain vector, and $x\in {\Re }^{2\times 1}$ is the system state. To determine the control gain vector $K_1$ and $K_2$, an LMI-based optimization method is utilized with the sixteen possible matrices of $(A, B)$. The process of this gain realization can be performed following the previous studies such as [13,14,15].

4. Simulation Results

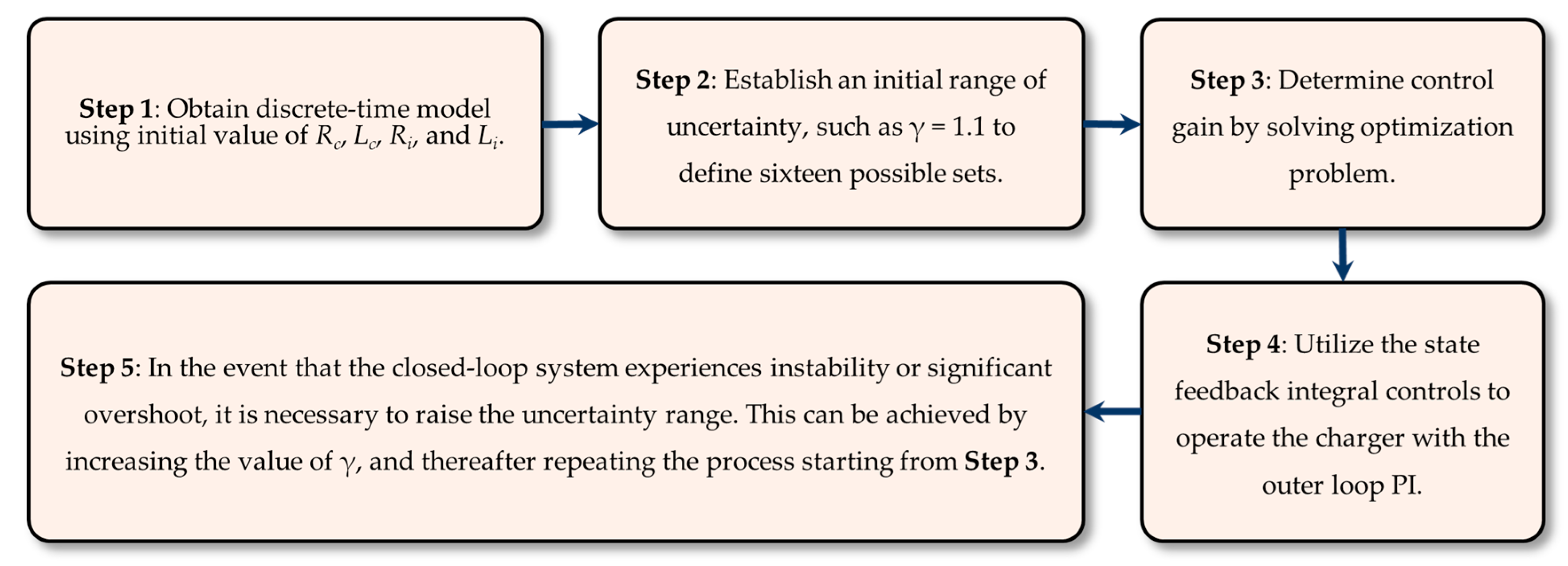
The implementation of the proposed control algorithm begins by deriving a discrete-time model of the system using the initial parameters $R_c$, $L_c$, $R_i$, and $L_i$. An initial uncertainty range is then defined using a factor such as $\mathsf{\gamma }=1.1$, which generates sixteen possible parameter sets to account for variations in the system. Based on these models, optimal control gain is obtained by solving an optimization problem to ensure robust and stable performance. The resulting control gain is applied through state feedback with integral control, while an outer-loop PI controller is used to regulate the charging process. If instability or overshoot occurs, the uncertainty range is increased by raising $\gamma$, and the optimization process is repeated until satisfactory performance is achieved. The summary of this proposed control can be found in Figure 2.

The control gain was derived using MATLAB R2021a in conjunction with the YALMIP toolbox to perform the LMI-based optimization. Subsequently, the obtained gain was implemented in an m-file for the application of state feedback integral control. The simulation parameters utilized in this study are listed in

Table 1. System parameters.

Description	Symbol	Value
Converter-side inductance	Lc	2.5 mH
Converter-side resistance	Rc	0.1 Ω
Grid-side inductance	Li	3.4 mH
Grid-side resistance	Ri	0.1 Ω
Grid-phase voltage (max)	vabc	310 V
Sampling interval	Ts	100 µs

.

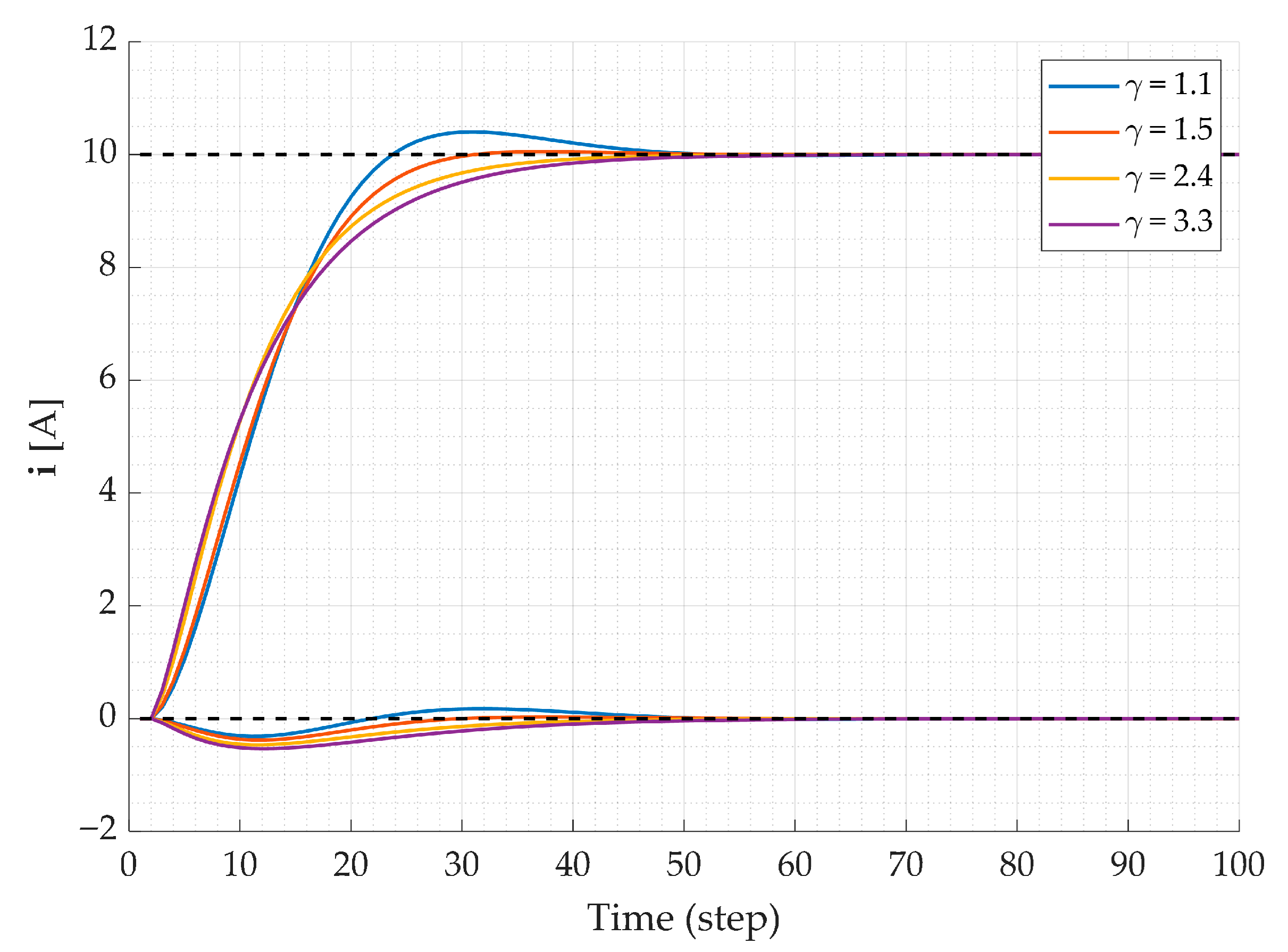
The horizontal axis in Figure 3 is expressed in simulation steps. Since the sampling interval T_s = 100 μs, each step is equal to 100 µs. Therefore, 100 steps represent a total simulation time of 0.01 s. The grid current behavior of a three-phase charger under different uncertainty levels is presented in Figure 3, where the parameter γ represents the range of uncertainty. The plotted curves correspond to γ values of 1.1, 1.5, 2.4, and 3.3, capturing the influence of grid impedance variations. Across all cases, the current responses converge to the steady-state reference of 10 A, confirming that the proposed control approach ensures precise current regulation even under uncertainty. When γ = 1.1, the system reaches the reference faster and shows a slight overshoot. In contrast, as γ increases—reflecting higher uncertainty and impedance variation—the transient response becomes slower, and the overshoot diminishes, suggesting enhanced damping and robustness. In summary, the results demonstrate that the controller maintains stable grid current performance across varying uncertainty levels, achieving reliable tracking and strong stability.

Figure 4 shows the locations of the closed-loop poles for the three-phase charger system under different uncertainty levels, represented by the parameter γ. For all simulated values of γ (1.1, 1.5, 2.4, and 3.3), the poles remain within the unit circle, confirming that the closed-loop system is stable. As γ increases—indicating greater system uncertainty and variations in grid impedance—the poles move slightly toward the origin. This shift reflects a more damped response and reduced oscillatory behavior.

The simulation results suggest that the proposed LMI-based robust control strategy can provide stable current regulation and enhanced damping against grid impedance uncertainties. The controller tracks accurately for uncertainty levels as large as γ = 3.3, and all the simulated closed-loop poles lie within the unit circle. This promises a possibility of robust operation under fluctuating grid conditions. These results are, however, limited to simulation only, and real-life factors such as measurement noise, device non-idealities, and unmodeled dynamics might affect performance. Hence, the real-time hardware implementation for experimental validation and the extension of the uncertainty model to account for grid frequency variations and voltage harmonic distortion should be part of future work. Further development of an adaptive or learning-based robust control method would also lead to better performance under rapidly changing grid conditions.

5. Conclusions

This paper presented a robust control strategy for a single-stage three-phase AC/DC EV charger to effectively address grid impedance variation and system uncertainties. The proposed dual-loop control structure, consisting of an outer-loop PI controller and an inner-loop robust state feedback controller optimized using LMI techniques, demonstrated strong stability and accurate current regulation under varying operating conditions. Simulation results confirmed that the grid current maintained precise tracking of the reference value with minimal steady-state error, while all closed-loop poles remained within the unit circle across different uncertainty levels, ensuring robust stability. As the uncertainty increased, the system exhibited enhanced damping and reduced oscillations, highlighting its resilience and improved transient behavior. Overall, the LMI-based robust control method achieved superior performance compared to conventional PI control, offering better disturbance rejection, faster response, and greater robustness, making it a reliable and efficient solution for modern EV charger applications. Future studies may focus on implementing the proposed controller in real-time hardware for experimental validation and extending the uncertainty model to include grid frequency variations and harmonic distortion. Further performance improvement under fast-changing grid conditions could also be achieved by deeper studies on adaptive or learning-based robust control.