Impact of Lewis Number on Natural Convection with Double Diffusion in a Square Cavity Filled with Non-Newtonian Fluid with Viscosity Varying with Temperature †
Abstract
1. Introduction
2. Mathematical Formulation
Equations Governing Convection Accompanied by Their Boundary Conditions
3. Numerical Method
4. Results and Discussion
4.1. Validation of the Numerical Code
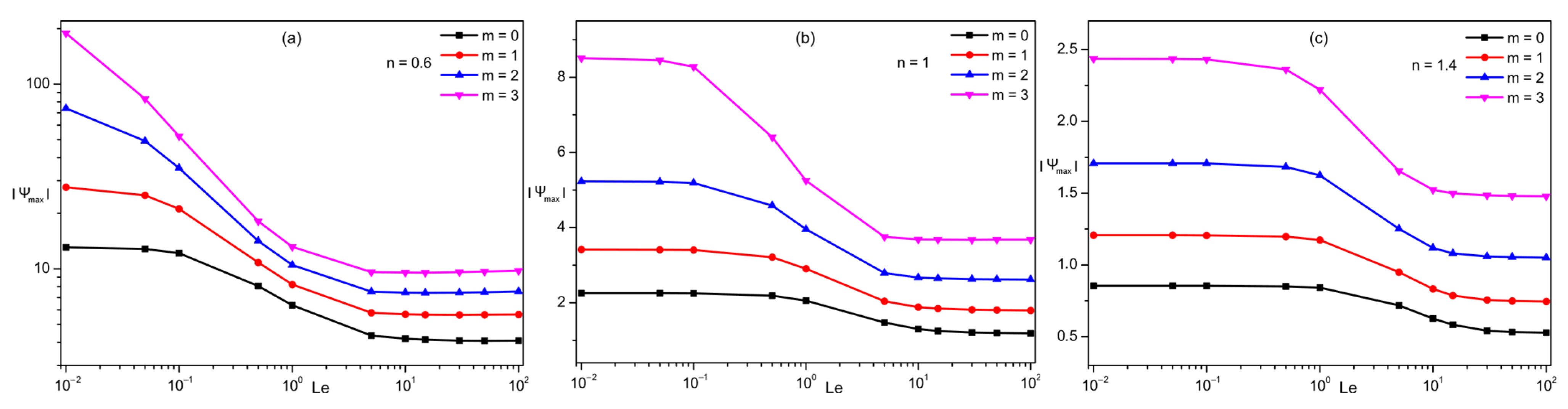
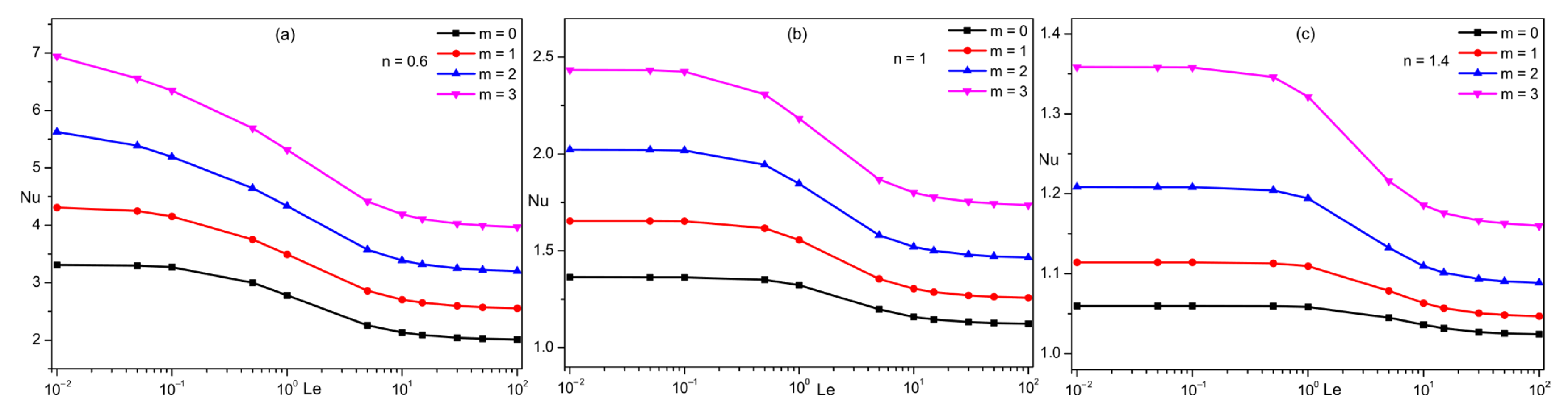
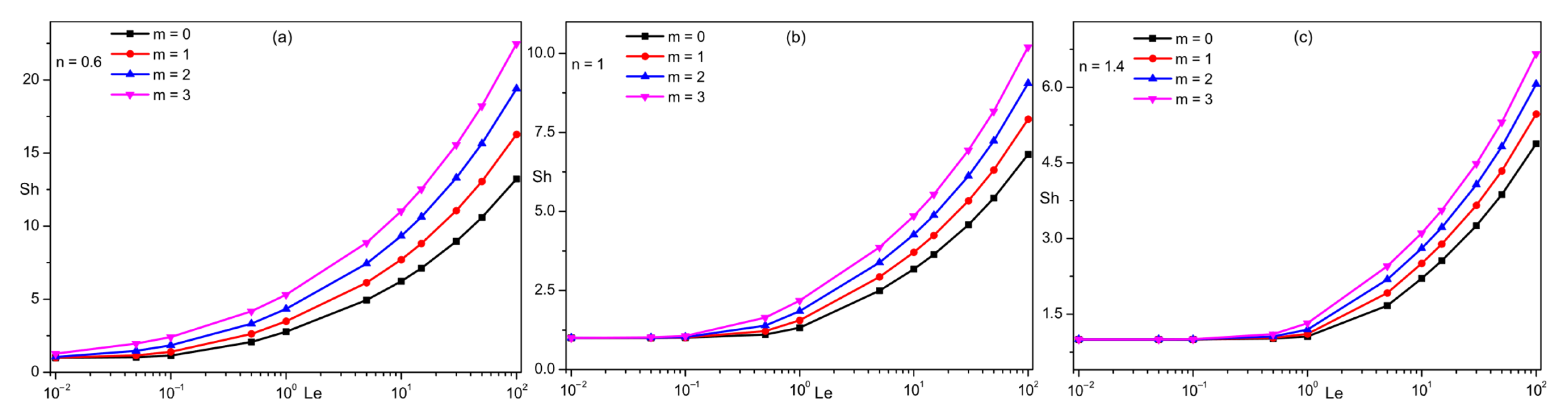
4.2. Lewis Number Effect
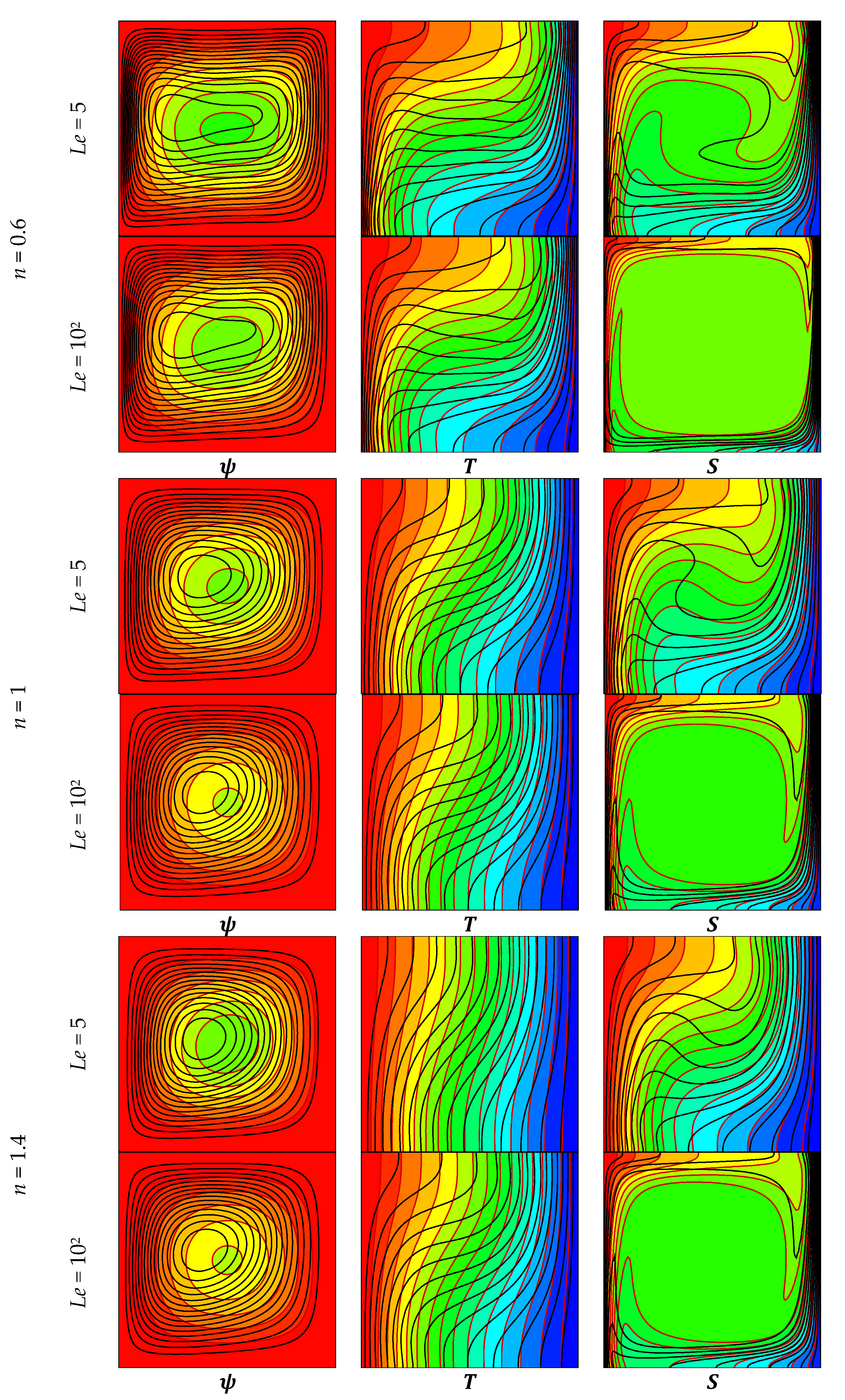
4.3. Analysis of Flow Fields, Isotherms, and Isoconcentrations
5. Conclusions
- The high Lewis number enhances mass transfer and reduces heat transfer and flow intensity, and this effect is amplified by increased thermo-dependence (high values of (m)).
- Variations according to (n) show that the flow intensity and heat and mass transfer increase with decreasing n.
- The increase in the thermo-dependence parameter (m) improves the flow intensity and heat and mass transfer due to the decrease in the apparent viscosity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kousksou, T.; Arid, A.; Majid, J.; Zeraouli, Y. Numerical Modeling of Double-Diffusive Convection in Ice Slurry Storage Tank. Int. J. Refrig. 2010, 33, 1550–1558. [Google Scholar] [CrossRef]
- Ali, I.; Saleem, M.T. Applications of Orthogonal Polynomials in Simulations of Mass Transfer Diffusion Equation Arising in Food Engineering. Symmetry 2023, 15, 527. [Google Scholar] [CrossRef]
- Kim, J.; Kang, Y.T.; Choi, C.K. Soret and Dufour Effects on Convective Instabilities in Binary Nanofluids for Absorption Application. Int. J. Refrig. 2007, 30, 323–328. [Google Scholar] [CrossRef]
- Bush, M.B. Applications in Non-Newtonian Fluid Mechanics. In Viscous Flow Applications; Springer: Berlin/Heidelberg, Germany, 1989; pp. 134–160. [Google Scholar]
- Tsilingiris, P.T. The Application and Experimental Validation of a Heat and Mass Transfer Analogy Model for the Prediction of Mass Transfer in Solar Distillation Systems. Appl. Therm. Eng. 2013, 50, 422–428. [Google Scholar] [CrossRef]
- Baïri, A.; Zarco-Pernia, E.; García de María, J.-M. A Review on Natural Convection in Enclosures for Engineering Applications. The Particular Case of the Parallelogrammic Diode Cavity. Appl. Therm. Eng. 2014, 63, 304–322. [Google Scholar] [CrossRef]
- Buchberg, H.; Catton, I.; Edwards, D.K. Natural Convection in Enclosed Spaces—A Review of Application to Solar Energy Collection. J. Heat. Transf. 1976, 98, 182–188. [Google Scholar] [CrossRef]
- Davaille, A.; Jaupart, C. Onset of Thermal Convection in Fluids with Temperature-dependent Viscosity: Application to the Oceanic Mantle. J. Geophys. Res. Solid. Earth 1994, 99, 19853–19866. [Google Scholar] [CrossRef]
- Sivaraj, R.; Banerjee, S. Transport Properties of Non-Newtonian Nanofluids and Applications. Eur. Phys. J. Spec. Top. 2021, 230, 1167–1171. [Google Scholar] [CrossRef]
- Onken, R.; Brambilla, E. Double Diffusion in the Mediterranean Sea: Observation and Parameterization of Salt Finger Convection. J. Geophys. Res. Ocean. 2003, 108, 1–12. [Google Scholar] [CrossRef]
- More, R.; Balasubramanian, S. Mixing Dynamics in Double-Diffusive Convective Stratified Fluid Layers. Curr. Sci. 2018, 114, 1953. [Google Scholar] [CrossRef]
- Javaheri, M.; Abedi, J.; Hassanzadeh, H. Linear Stability Analysis of Double-Diffusive Convection in Porous Media, with Application to Geological Storage of CO2. Transp. Porous Media 2010, 84, 441–456. [Google Scholar] [CrossRef]
- Saleem, K.B.; Koufi, L.; Alshara, A.K.; Kolsi, L. Double-Diffusive Natural Convection in a Solar Distiller with External Fluid Stream Cooling. Int. J. Mech. Sci. 2020, 181, 105728. [Google Scholar] [CrossRef]
- Islam, A.W.; Lashgari, H.R.; Sephernoori, K. Double Diffusive Natural Convection of CO2 in a Brine Saturated Geothermal Reservoir: Study of Non-Modal Growth of Perturbations and Heterogeneity Effects. Geothermics 2014, 51, 325–336. [Google Scholar] [CrossRef]
- Kolsi, L.; Hussain, S.; Ghachem, K.; Jamal, M.; Maatki, C. Double Diffusive Natural Convection in a Square Cavity Filled with a Porous Media and a Power Law Fluid Separated by a Wavy Interface. Mathematics 2022, 10, 1060. [Google Scholar] [CrossRef]
- Nag, P.; Molla, M.M. Non-Newtonian Effect on Double Diffusive Natural Convection of Nanofluid within a Square Cavity. AIP Conf. Proc. 2021, 2324, 050030. [Google Scholar] [CrossRef]
- Nag, P.; Molla, M.M. Double-Diffusive Natural Convection of Non-Newtonian Nanofluid Considering Thermal Dispersion of Nanoparticles in a Vertical Wavy Enclosure. AIP Adv. 2021, 11, 095219. [Google Scholar] [CrossRef]
- Daghab, H.; Kaddiri, M.; Lamsaadi, M.; Raghay, S.; Arroub, I.; Erritali, I. Free Convection of Thermodependent Non-Newtonian Fluids in a Square Enclosure Partially Heated at One Side. Numer. Heat. Transf. A Appl. 2023, 86, 1927–1950. [Google Scholar] [CrossRef]
- Rahmoun, M.; Makayssi, T.; El hadoui, B.; Lamsaadi, M. Lewis Number’s Effect on Natural Double Diffusive Convection of Thermo-Dependent Non-Newtonian Carreau-Yasuda Liquids in a Square Enclosure. In Proceedings of the Fifteen International Conference on Thermal Engineering: Theory and Applications, Tashkent, Uzbekistan, 28 May–1 June 2024; pp. 1–3. [Google Scholar]
- El hadoui, B.; Kaddiri, M. Double Diffusive Natural Convection with Variable Properties of Nanofluid Using Lattice Boltzmann Method. In Advances in Thermal Science and Energy; Springer Nature: Cham, Switzerland, 2024; pp. 22–32. [Google Scholar]
- Astanina, M.S.; Sheremet, M.A.; Umavathi, J.C. Unsteady Natural Convection with Temperature-Dependent Viscosity in a Square Cavity Filled with a Porous Medium. Transp. Porous Media 2015, 110, 113–126. [Google Scholar] [CrossRef]
- Dumoulin, C.; Doin, M.; Fleitout, L. Heat Transport in Stagnant Lid Convection with Temperature- and Pressure-dependent Newtonian or Non-Newtonian Rheology. J. Geophys. Res. Solid. Earth 1999, 104, 12759–12777. [Google Scholar] [CrossRef]
- Ramamurthy, T.; Krishnan, S. Importance of Temperature-Dependent Non-Newtonian Fluid in Conventional Thermal Processing. J. Therm. Sci. Eng. Appl. 2022, 15, 1–21. [Google Scholar] [CrossRef]
- Larbi, A.O.; Rebhi, R.; Rahal, S.; Lorenzini, G.; Maamar, L.; Menni, Y.; Ahmad, H. Impact of Non-Newtonian Fluids’ Rheological Behavior on Double- Diffusive Natural Convection in an Inclined Square Porous Layer. J. Adv. Res. Fluid. Mech. Therm. Sci. 2022, 99, 17–47. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Saha, B.C.; Pal, D. Magnetohydrodynamic Double-Diffusive Natural Convection for Nanofluid within a Trapezoidal Enclosure. Comput. Appl. Math. 2018, 37, 6132–6151. [Google Scholar] [CrossRef]
- Foruzan Nia, M.; Gandjalikhan Nassab, S.A. Thermohydrodynamic Characteristics of Combined Double-Diffusive Radiation Convection Heat Transfer in a Cavity. Comptes Rendus. Mécanique 2019, 347, 406–422. [Google Scholar] [CrossRef]
- Kumar, S.B.N.; Shivakumara, I.S.; Shankar, B.M. Linear and Weakly Nonlinear Double-Diffusive Magnetoconvection in a Non-Newtonian Fluid Layer. Microgravity Sci. Technol. 2020, 32, 629–646. [Google Scholar] [CrossRef]
- Moufekkir, F.; Moussaoui, M.A.; Mezrhab, A.; Bouzidi, M.; Lemonnier, D. Combined Double-Diffusive Convection and Radiation in a Square Enclosure Filled with Semitransparent Fluid. Comput. Fluids 2012, 69, 172–178. [Google Scholar] [CrossRef]
- Teamah, M.A.; El-Maghlany, W.M. Numerical Simulation of Double-Diffusive Mixed Convective Flow in Rectangular Enclosure with Insulated Moving Lid. Int. J. Therm. Sci. 2010, 49, 1625–1638. [Google Scholar] [CrossRef]
- Abidi, A.; Borjini, M.N. Effects of Microstructure on Three-Dimensional Double-Diffusive Natural Convection Flow of Micropolar Fluid. Heat. Transf. Eng. 2020, 41, 361–376. [Google Scholar] [CrossRef]
- Ghenai, C.; Mudunuri, A.; Lin, C.X.; Ebadian, M.A. Double-Diffusive Convection during Solidification of a Metal Analog System (NH4Cl–H2O) in a Differentially Heated Cavity. Exp. Therm. Fluid. Sci. 2003, 28, 23–35. [Google Scholar] [CrossRef]
- Tizakast, Y.; Kaddiri, M.; Lamsaadi, M. Rayleigh-Bénard Double-Diffusive Mixed Convection in Two-Dimensional Rectangular Cavities Filled with Non-Newtonian Fluids. Int. J. Mech. Sci. 2022, 227, 107448. [Google Scholar] [CrossRef]
- Tizakast, Y.; Kaddiri, M.; Lamsaadi, M. Double-Diffusive Mixed Convection in Rectangular Cavities Filled with Non-Newtonian Fluids. Int. J. Mech. Sci. 2021, 208, 106667. [Google Scholar] [CrossRef]
- Erritali, I.; Kaddiri, M.; Arroub, I.; Daghab, H. Heat Transfer and Mixed Convection Flow of Non-Newtonian Thermo-Dependent Power Law Fluids with Thermal Radiation Effect. Int. J. Heat. Technol. 2022, 40, 1175–1185. [Google Scholar] [CrossRef]
- Nouri, R.; Kaddiri, M.; Tizakast, Y.; Daghab, H. Non-Newtonian Natural Convection in a Square Box Submitted to Horizontal Heat Flux and Magnetic Field. Therm. Sci. 2024, 28, 3049–3061. [Google Scholar] [CrossRef]
- Bihiche, K.; Lamsaadi, M.; El hadoui, B.; Tizakast, Y. Double-Diffusive Natural Convection of Power-Law Fluids in an Inclined Square Cavity with Soret Effect. Numer. Heat. Transf. A Appl. 2025, 1–26. [Google Scholar] [CrossRef]
- El Hadoui, B.; Ighris, Y.; Kaddiri, M.; Baliti, J. Thermal Management and Heat Transfer Enhancement through Heatlines Visualization in a Moving-Wall Chamber: Effects of Shear, Heater Geometry, and Nanoparticle Suspension. Int. J. Therm. Sci. 2025, 217, 110098. [Google Scholar] [CrossRef]
- Lamsaadi, M.; Naïmi, M.; Hasnaoui, M. Natural Convection Heat Transfer in Shallow Horizontal Rectangular Enclosures Uniformly Heated from the Side and Filled with Non-Newtonian Power Law Fluids. Energy Convers. Manag. 2006, 47, 2535–2551. [Google Scholar] [CrossRef]
- El Hadoui, B.; Kaddiri, M.; Lamsaadi, M.; El Harfi, H. Effect of the Thermal Rayleigh Number on Natural Double Diffusive Convection in Shallow Rectangular Cavities Filled with Nanofluids. AIP Conf. Proc. 2023, 2761, 040002. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018; ISBN 9781315275130. [Google Scholar]
- El Hadoui, B.; Kaddiri, M. Comparing Two Numerical Methods in the Case of Aiding and Opposing Natural Double Diffusion in a Square Enclosure. In Proceedings of the 2024 4th International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), FEZ, Morocco, 16–17 May 2024; pp. 1–5. [Google Scholar]
- Wang, J.; Wang, D.; Lallemand, P.; Luo, L.-S. Lattice Boltzmann Simulations of Thermal Convective Flows in Two Dimensions. Comput. Math. Appl. 2013, 65, 262–286. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Zheng, C. A Coupled Lattice BGK Model for the Boussinesq Equations. Int. J. Numer. Methods Fluids 2002, 39, 325–342. [Google Scholar] [CrossRef]

| Wang et al. [42] | Guo et al. [43] | Present Work | |
| Ra | Nu | ||
| 103 | 1.117 | 1.116 | 1.118 |
| 104 | 2.247 | 2.247 | 2.247 |
| 105 | 4.551 | 4.534 | 4.538 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmoun, M.; El hadoui, B.; Makayssi, T.; Lamsaadi, M. Impact of Lewis Number on Natural Convection with Double Diffusion in a Square Cavity Filled with Non-Newtonian Fluid with Viscosity Varying with Temperature. Eng. Proc. 2025, 111, 33. https://doi.org/10.3390/engproc2025111033
Rahmoun M, El hadoui B, Makayssi T, Lamsaadi M. Impact of Lewis Number on Natural Convection with Double Diffusion in a Square Cavity Filled with Non-Newtonian Fluid with Viscosity Varying with Temperature. Engineering Proceedings. 2025; 111(1):33. https://doi.org/10.3390/engproc2025111033
Chicago/Turabian StyleRahmoun, Mohamed, Bilal El hadoui, Taoufik Makayssi, and Mohamed Lamsaadi. 2025. "Impact of Lewis Number on Natural Convection with Double Diffusion in a Square Cavity Filled with Non-Newtonian Fluid with Viscosity Varying with Temperature" Engineering Proceedings 111, no. 1: 33. https://doi.org/10.3390/engproc2025111033
APA StyleRahmoun, M., El hadoui, B., Makayssi, T., & Lamsaadi, M. (2025). Impact of Lewis Number on Natural Convection with Double Diffusion in a Square Cavity Filled with Non-Newtonian Fluid with Viscosity Varying with Temperature. Engineering Proceedings, 111(1), 33. https://doi.org/10.3390/engproc2025111033






