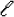Theoretical and Experimental Research on Centrifugal Casting of Short and Long Castings †
Abstract
1. Introduction
2. Methodology and Methods
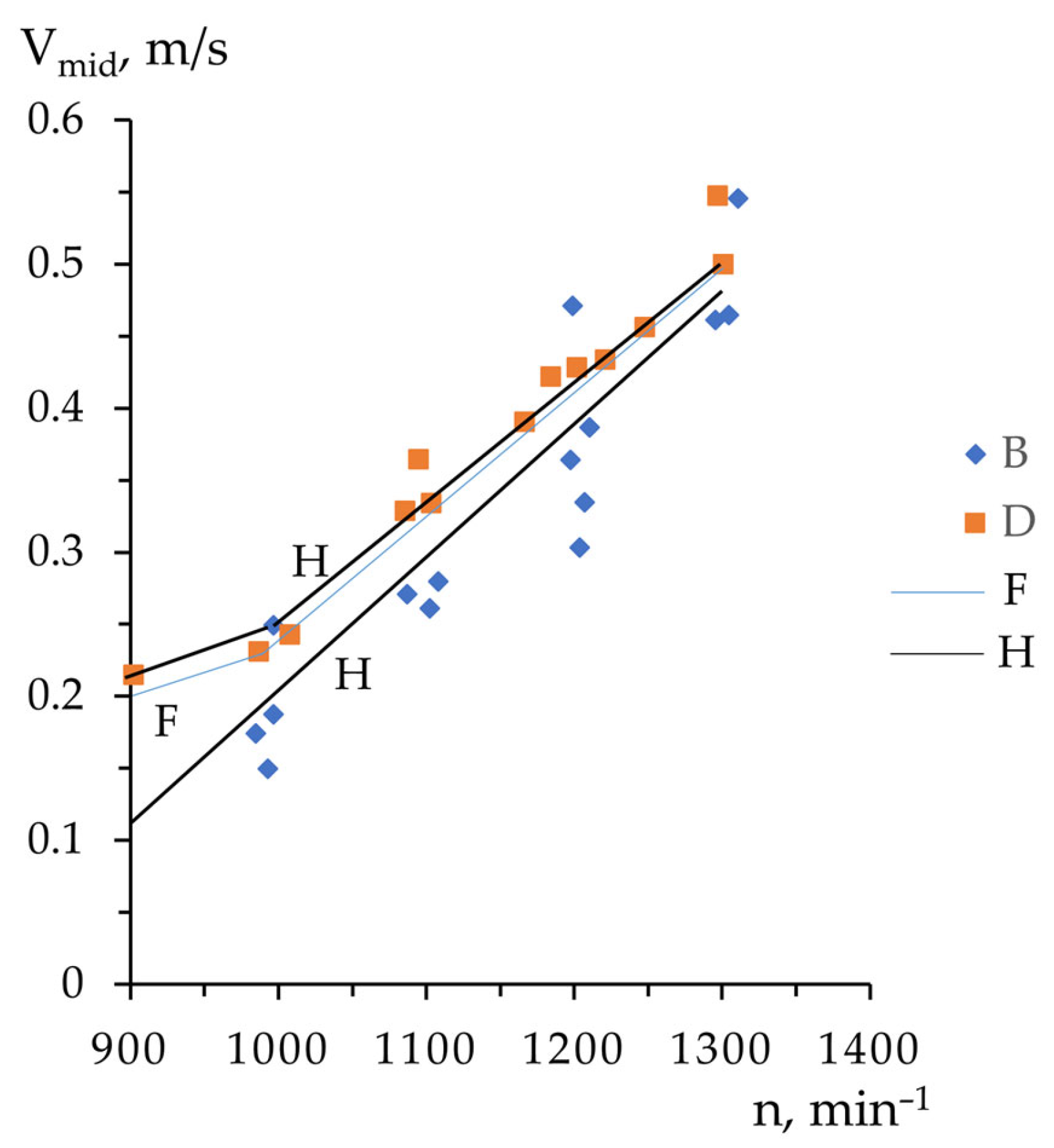
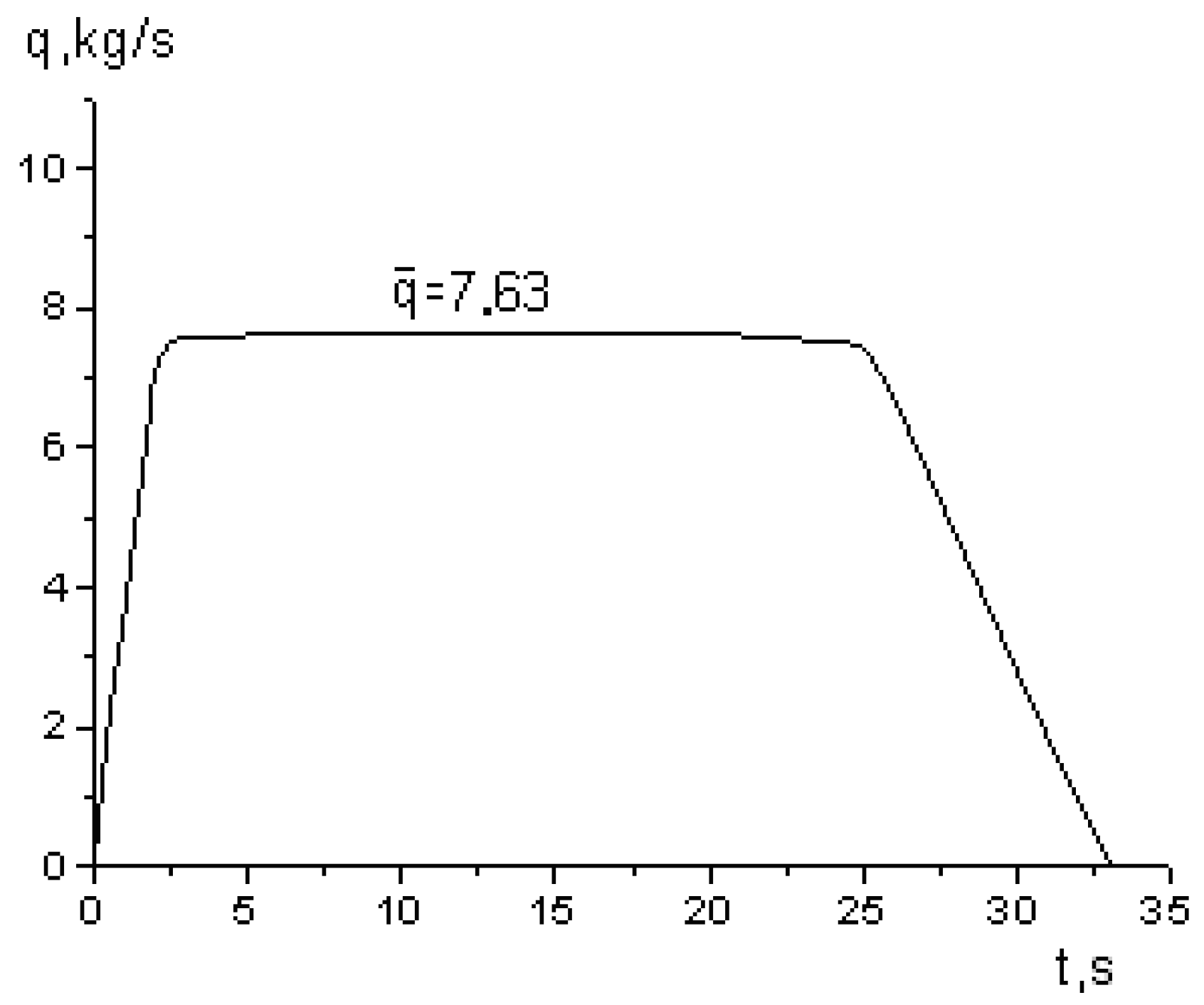
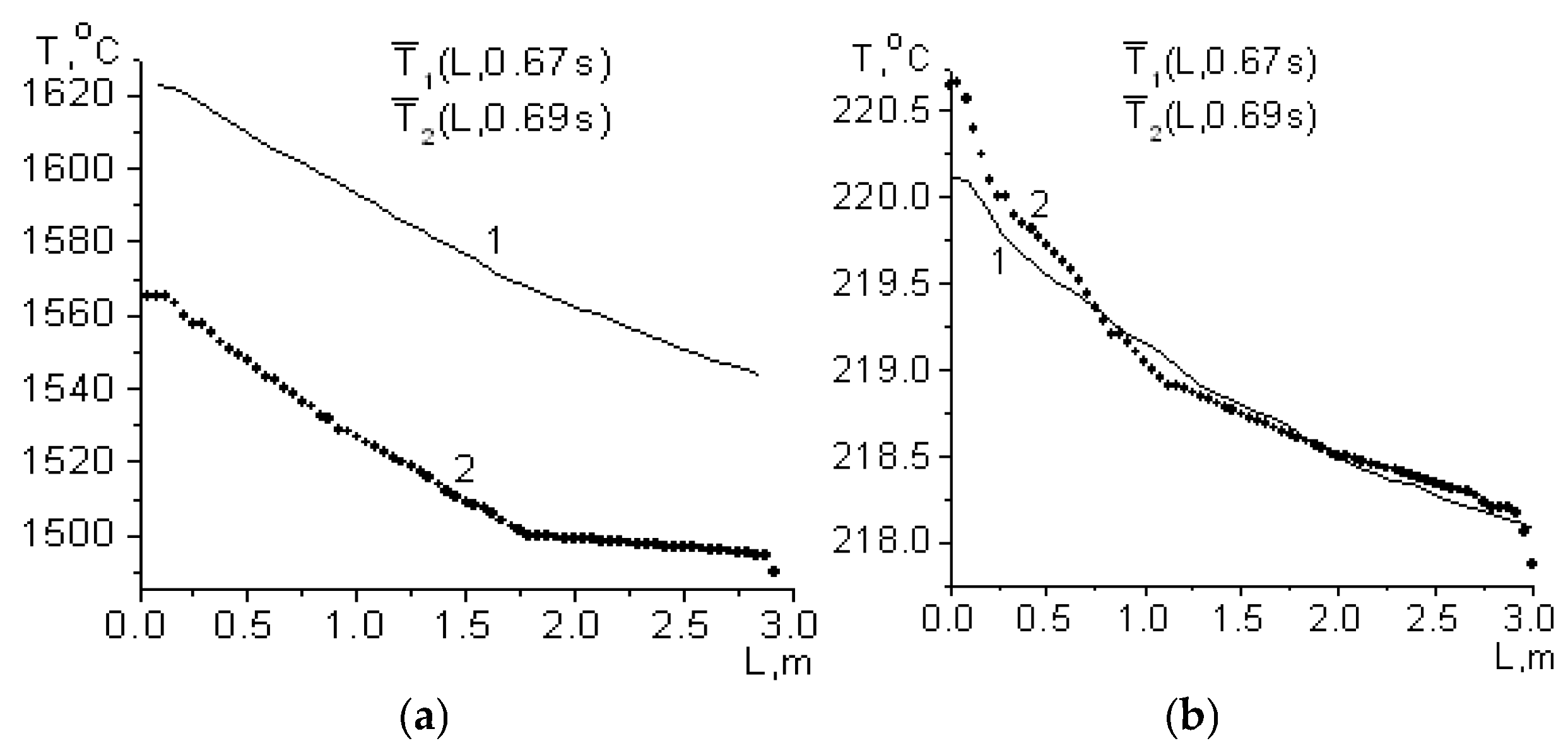
3. Results
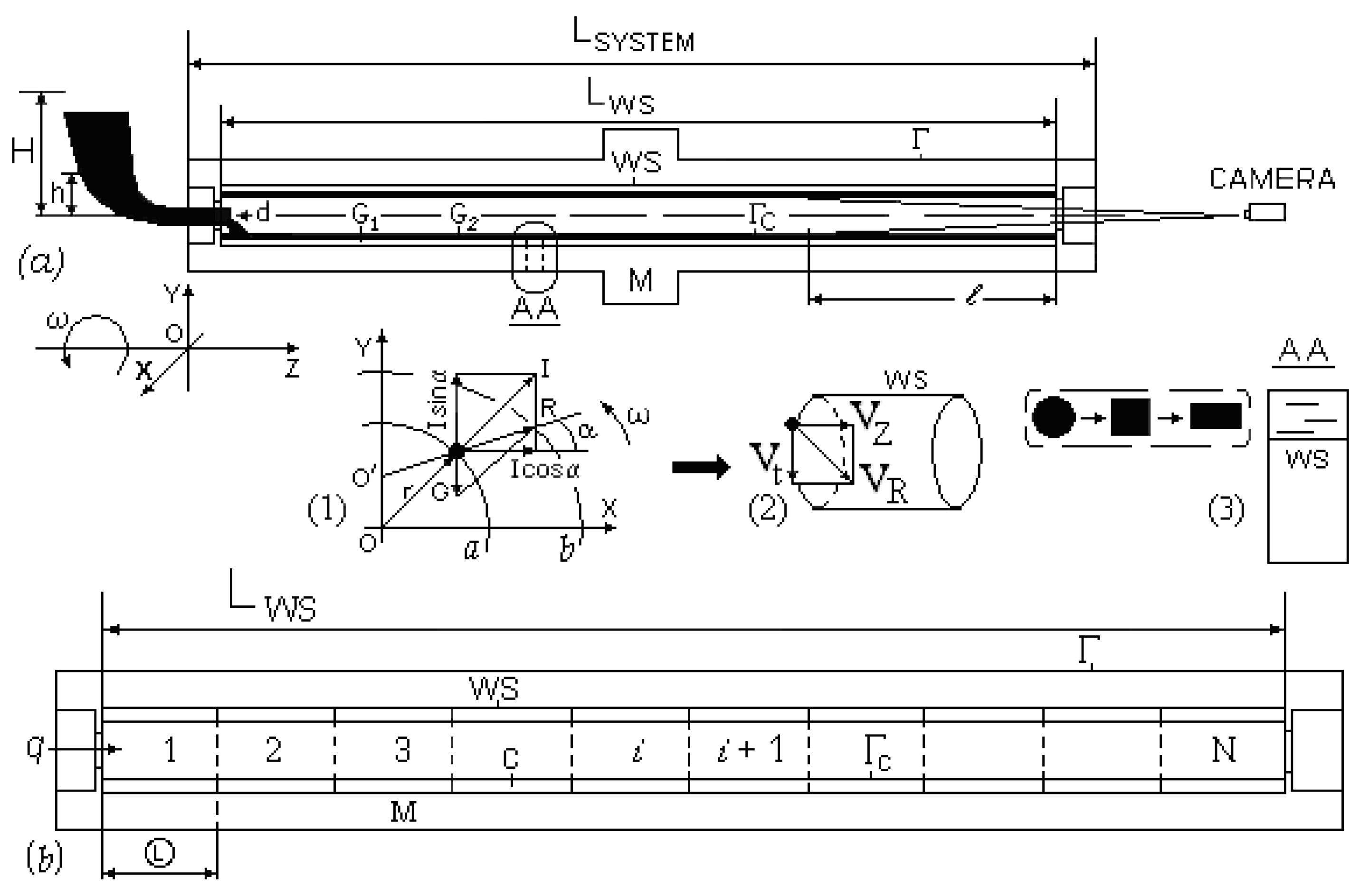
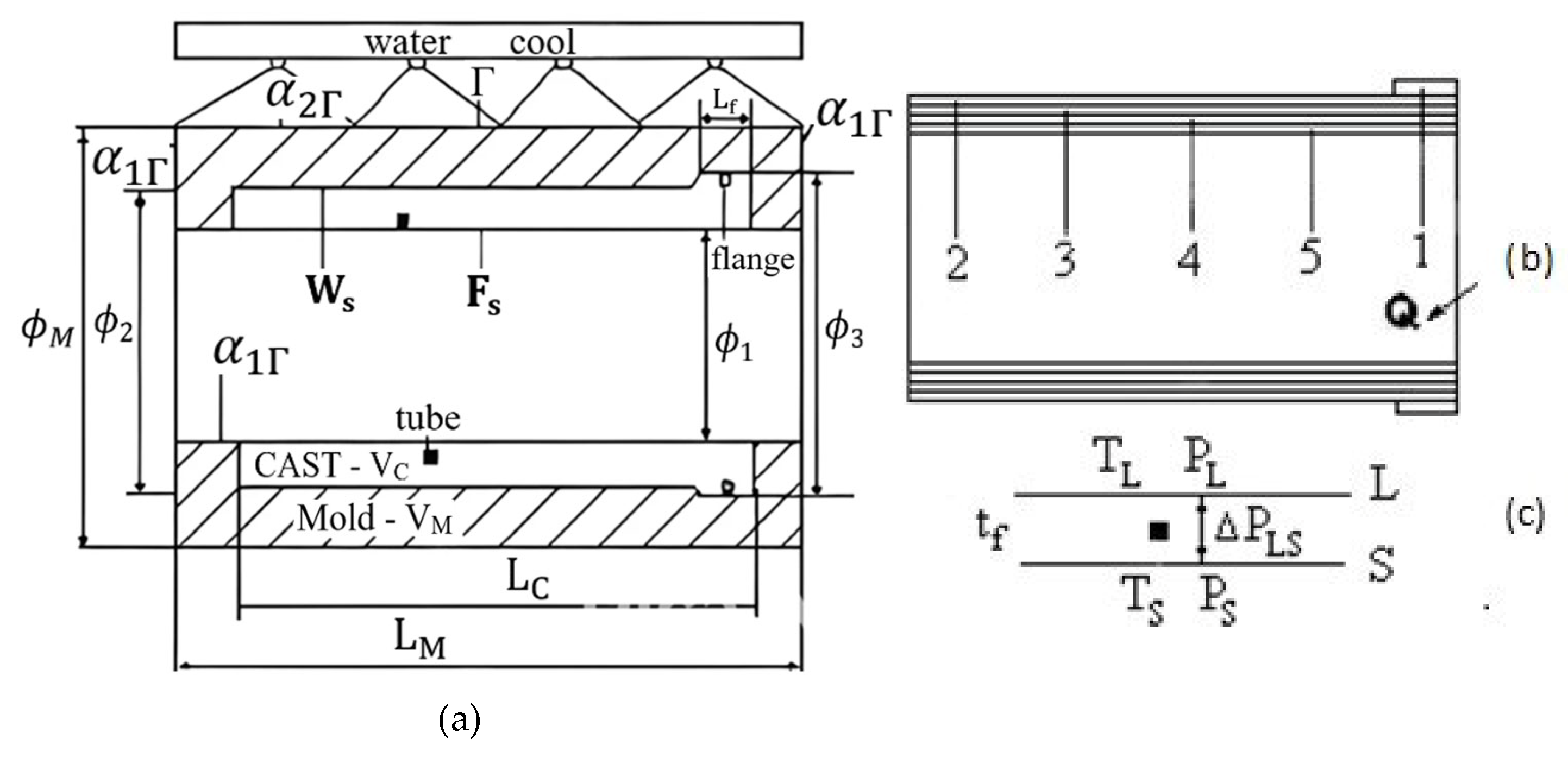
3.1. Scheme for Mathematical Modeling of Centrifugal Casting of Short Castings
- (a)
- Geometric dimensions: L—lengths; φ—diameters; Γ, Ws—outer and working surface of the mold; Fs—free surface of the casting, where heat transfer is neglected, cooled with a water shower; α1Γ and α2Γ—mold–environment heat transfer coefficients;
,
—volumes for evaluating the conditions of the structure-formation at a flange and pipe.
- (b)
- Dividing the cast into five volumes to assess the filling.
- (c)
- tf—local solidification time: residence time of a considered volume of the casting in the two-phase zone; TL, TS—isothermal liquidus and solidus surfaces; ΔPLS—difference between the pressures for two opposite points of TL and TS.
3.2. Scheme for Mathematical Modeling of Centrifugal Casting of Long Castings
- Cooling after the end of filling;
- Filming of air release at the hot end;
- Cooling after the end of filling.
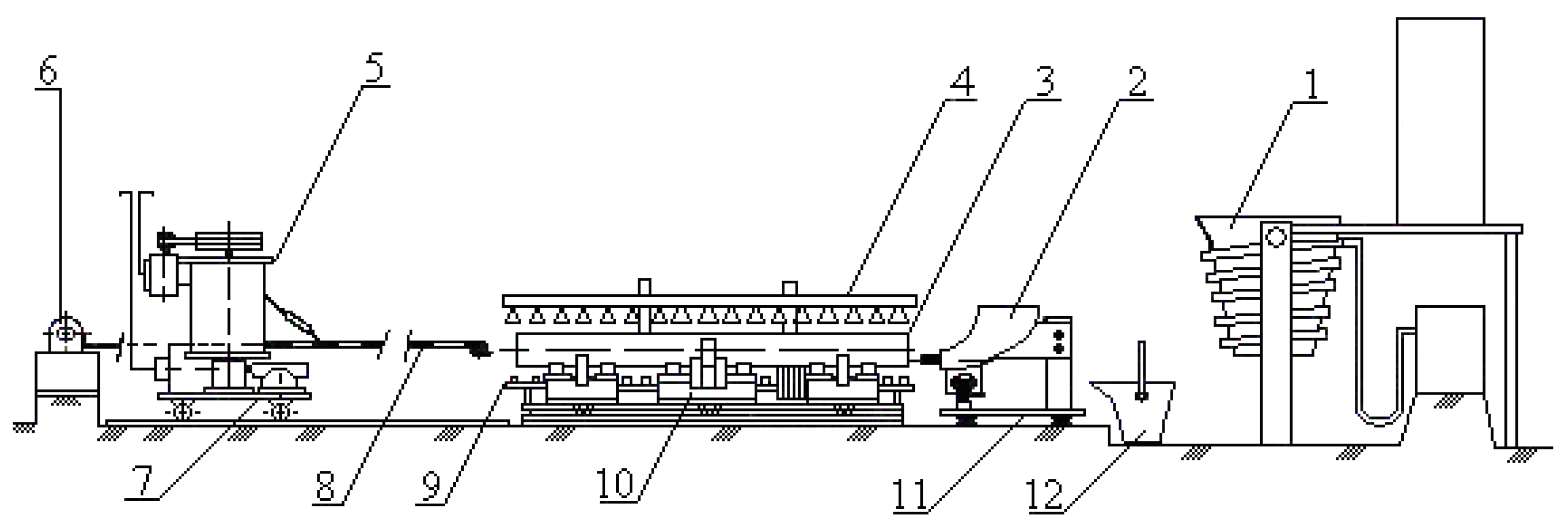
- (a)
- Casting C—before filling (
) and casting C—after filling (
) with weights of layers, respectively, G1 and G2; H—pouring height; h—height of the melt in the runner with a clear open diameter (d); LSYSTEM—length of BTS; LWS—length of work surface;
– (WS) invisible part of the camera; —imaginary section from OTC micromodel of Stefan-Schwartz task, according to [1]; OXYZ—coordinate system; ω—angular velocity of rotation; (1)—force field on a single particle of liquid metal in the cross section OXY; I—centrifugal force; G—weight force; R—resultant force; a—cylindrical surface shaped by equal pressure of the force field and the working surface (WS); OO/—eccentricity due to applied forces along the horizontal axis of rotation; b—oval surface described by the tip of the force vector R; (2)—velocity field of the molten metal particle; Vt—tangential, VZ—axis, and VR—resultant speed; (3) geometric model of liquid drop spillage with micromodel of Stefan-Schwartz task, according to [16,17].
- (b)
- Geometric idea for the mathematical modeling of the process of forming the first layer of molten metal, where q—flow rate, M—shape, and C—casting, composed of N volume elements of equal length
.
4. Discussion
5. Conclusions
- New data were obtained on the movement of the melt front along the axis of molding, as well as the release of gases at the hot end of the mold;
- Data were obtained on the transient processes (initial and final) during melt pouring;
- A generalized mathematical model was created in the dynamic system casting—the mold;
- Optimal parameters were experimentally obtained in centrifugal casting with a horizontal axis of short and long castings and evaluated using the created mathematical model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tsvetnenko, K.U. Theoretical Foundations for Calculating the Rotation Speed of a Mold During Centrifugal Casting of Pipes; Metallurgy Publishing House: Kharkov, Ukraine, 1961; Volume VNITI, Issue 4. [Google Scholar]
- Oyewole, A.; Sunday, A.M. Design and fabrication of a centrifugal casting machine. Int. J. Eng. Sci. Technol. 2011, 3, 8204–8210. [Google Scholar]
- Zagorski, R.; Sleziona, J. Pouring mould during centrifugal casting process. Arch. Mater. Sci. Eng. 2007, 28, 441–444. [Google Scholar]
- Madhusudhan, S.N.; Kumar, G.; Mukunda, P. Experimental study on rate of solidification of centrifugal casting. Int. J. Mech. Mater. Eng. 2010, 5, 101–105. [Google Scholar]
- Bushev, S. Thermodynamic systems for heat treatment. In Proceedings of the II International Conference, Metal Science, New Materials, Hydro and Aerodynamics, Sofia, Bulgaria, 31 May–1 June 2012. [Google Scholar]
- Bushev, S.; Dimitrov, M.; Stoychev, N. Processes of martensite type phase transition of low rate. Nucleation kinetics models. In Proceedings of the National Conference with International Participation, Material Science and New Materials, Sofia, Bulgaria, 4–5 December 2008; pp. 288–293. [Google Scholar]
- Valkov, V.; Georgiev, I.; Bushev, S.; Dimitrov, M.; Stoichev, N. Mathematical Modeling. In Proceedings of the Anniversary Scientifically Conference International Participation MTF 2007, Sozopol, Bulgaria, 14–16 September; Volume 1, p. 9499.
- Georgiev, I.; Stanev, S.; Velikov, A. Centrifugal casting of nitrogen alloy billets with industrial application. In Scientific Notices of NTSM. Collection of Reports, International Conference, Days of Non-Destructive Testing 2012; British Institute of Non-Destructive Testing: Northampton, UK, 2012; Volume XX, pp. 183–186. [Google Scholar]
- Georgiev, I.; Valkov, V. Centrifugal casting of two-layer cast iron castings with a wear-resistant layer of ductile iron. In Scientific notices of NTSM, Collection of Reports. International Conference, Days of Non-Destructive Testing 2013; British Institute of Non-Destructive Testing: Northampton, UK, 2013; Volume XXI, pp. 428–431. [Google Scholar]
- Bushev, S.; Georgiev, I.; Valkov, V. Analysis of Vertical Axis Centrifugal Casting Technology for Bimetal Casting. Comptes Rendus L’académie Bulg. Sci. 2010, 63, 1117–1122. [Google Scholar]
- Daming, X.; Qingmei, Y.; Xin, L.; Geying, A. Mold filling behavior of melts with different viscosity under centrifugal force field. J. Mater. Sci. Technol. 2009, 18, 149–151. [Google Scholar]
- Barron, M.A. Analysis of molten metal distribution in the mold of a horizontal centrifugal casting. Open J. Apllied Sci. 2020, 10, 444–454. [Google Scholar] [CrossRef]
- Ebhota, W.S.; Karun, A.S.; Inambao, F.L. Centrifugal casting technique baseline knowledge, application, and processing parameters. Int. J. Mater. Res. 2016, 107, 1–10. [Google Scholar] [CrossRef]
- Mohapatra, S.; Sarangi, H. Effect of processing factors on the characteristics of centrifugal casting. EDP Sci. 2020, 7, 26. [Google Scholar] [CrossRef]
- Ivanov, P. Structural researching of the inner, primary supporting layer from ductile cast iron with a bimetallic roller shell with high—chrome material used as an external (working) layer, during a centrifugal casting method of production with a vertical axis. Int. J. Sci. Tech. Innov. Ind. Mach. Technol. Mater. 2022, 16, 41–43. [Google Scholar]
- Ivanov, P.; Georgiev, I.; Velikov, A. Structural investigation of high- chromium material used as an external, working layer of a bimetallic mill roller. ETR 2021, 1, 91–94. [Google Scholar] [CrossRef]
- Velikov, A.; Ivanov, P.; Georgiev, I. Structural Investigation of the Intermediate Layer in a Bimetal Mill Roller Produced by the Method of Vertical Axis Centrifugal Casting. ETR 2021, 1, 255–258. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velikov, A.; Georgiev, I.; Krastev, B.; Petrov, K. Theoretical and Experimental Research on Centrifugal Casting of Short and Long Castings. Eng. Proc. 2025, 100, 58. https://doi.org/10.3390/engproc2025100058
Velikov A, Georgiev I, Krastev B, Petrov K. Theoretical and Experimental Research on Centrifugal Casting of Short and Long Castings. Engineering Proceedings. 2025; 100(1):58. https://doi.org/10.3390/engproc2025100058
Chicago/Turabian StyleVelikov, Angel, Ivan Georgiev, Boyko Krastev, and Krum Petrov. 2025. "Theoretical and Experimental Research on Centrifugal Casting of Short and Long Castings" Engineering Proceedings 100, no. 1: 58. https://doi.org/10.3390/engproc2025100058
APA StyleVelikov, A., Georgiev, I., Krastev, B., & Petrov, K. (2025). Theoretical and Experimental Research on Centrifugal Casting of Short and Long Castings. Engineering Proceedings, 100(1), 58. https://doi.org/10.3390/engproc2025100058