Abstract
The thermodynamics of protein–ligand interactions seems to be associated with a narrow range of Gibbs free energy. As a consequence, a linear enthalpy–entropy relationship showing an apparent enthalpy–entropy compensation (EEC) is frequently associated with protein–ligand interactions. When looking for the most negative values of ∆H to gain affinity, the entropy compensation gives rise to a barely noticeable increase in affinity, therefore negatively affecting the design and discovery of new and more efficient drugs capable of binding protein targets with a higher affinity. Originally attributed to experimental errors, compensation between ∆H and T∆S values is an observable fact, although its molecular origin has remained obscure and controversial. The thermodynamic parameters of a protein–ligand interaction can be interpreted in terms of the changes in molecular weak interactions as well as in vibrational, rotational, and translational energy levels. However, a molecular explanation to an EEC rendering a linear enthalpy–entropy relationship is still lacking. Herein, we show the results of a data search of ∆G values of 3025 protein–ligand interactions and 2558 “in vivo” ligand concentrations from the Protein Data Bank database and the Metabolome Database (2020). These results suggest that the EEC may be plausibly explained as a consequence of the narrow range of ∆G associated with protein–ligand interactions. The Gaussian distribution of the ∆G values matches very well with that of ligands. These results suggest the hypothesis that the set of ∆G values for the protein–ligand interactions is the result of the evolution of proteins. The conformation versatility of present proteins and the exchange of thousands (even millions) of minute amounts of energy with the environment may have functioned as a homeostatic mechanism to make the ∆G of proteins adaptive to changes in the availability of ligands and therefore achieve the maximum regulatory capacity of the protein function. Finally, plausible strategies to avoid the EEC consequences are suggested.
1. Introduction
A linear enthalpy–entropy relationship is frequently associated with thermodynamic protein–ligand interactions [1,2,3,4,5,6,7,8]. When the reaction enthalpy values, ∆H°, associated with any particular set of ligand–protein interactions are plotted against the corresponding changes in entropy values, T∆S°, a straight line with a slope close to 1 is usually obtained. The phenomenon is particularly relevant in studies concerned with the design and discovering of new drugs, either by computational docking simulations or by microcalorimetry experiments. Isothermal Titration Calorimetry renders useful ∆H° values in ligand optimization experiments. ∆H° values can be obtained from a panel of ligands composed of modified forms of a lead compound; the more negative values of ∆H° are then expected to yield information about the more favorable chemical modification to gain a higher affinity for the protein target. It is, however, frequently observed that whenever a structural ligand modification causes a more negative (favorable) ∆H° value to form the ligand–protein complex, a more negative (unfavorable) T∆S° value is obtained, therefore yielding no appreciable increase in the affinity (as measured by ∆G°) to form the ligand–protein complex.
Indeed, this apparent compensation between ∆H° and T∆S° is always observed in thermodynamic studies concerning the binding of a group of structurally related ligands to a particular biological macromolecule. But it also is observed in the binding of unrelated ligands to dissimilar macromolecules. Particularly interesting is the report by Olsson et al. [9] that 171 protein–ligand interactions concerning 32 proteins display a clearly linear enthalpy–entropy relationship. Most interesting is the observation that this behavior concerning the apparent compensation between ∆H° and T∆S° associated with protein–ligand interactions does not seem to be followed by simple chemical reactions.
Results such as those of Olsson et al. [9] reporting a linear enthalpy–entropy relationship for protein–ligand interactions could originally have been attributed to experimental errors in the ∆H measurements, since most of the ∆H° values were obtained from Van’t Hoff studies of equilibrium constants as a function of temperature. The development of ITC microcalorimeters, however, allows measuring enthalpy values with a precision high enough to discard experimental errors. The apparent enthalpy–entropy compensation (EEC) is an observable fact, although its molecular origin still remains controversial and hard to understand [6,8,10]. Herein, we want to present a plausible explanation to unveil its origin within the framework of contributing to those studies concerned with the design and discovery of new drugs having a higher affinity for their targets.
2. Methods
The set of 2558 metabolite concentrations was built by selecting all data obtained from the Metabolome Database (2020) (Wishart et al., 2022) [11] from human fluids, including blood, saliva, cerebrospinal fluid, breast milk, and amniotic fluid, which were detected and quantified. The data of affinities of protein–ligand interactions expressed as ∆G° (kJ/mol) were obtained from the 2020 version of the Protein Data Bank database (Wang et al., 2004) [12]. The survey of data corresponds to the period 2010–2020 and included 3025 values.
3. Results
3.1. Protein–Ligand Interactions
Part A of Figure 1 shows the plot of calorimetric ∆H° values vs. T∆S° for 42 examples of protein–ligand interactions extracted from different studies involving unrelated ligands and dissimilar proteins (Table 1, references [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]). The plot shows the kind of behavior usually denoted as an enthalpy–entropy compensation (EEC). This type of behavior has been repeatedly reported for more than fifty years in many experiments closely associated with protein–ligand interactions in water solution [6,7,8,10,31,32,33,34,35,36]. As can be observed in part B of the same figure, it is accompanied by the lack of correlation of ∆H° vs. ∆G°, which is, in turn, usually found in chemical transformations, mostly in gaseous phase, and having a simple stoichiometry similar to that of a simple protein–ligand interaction.
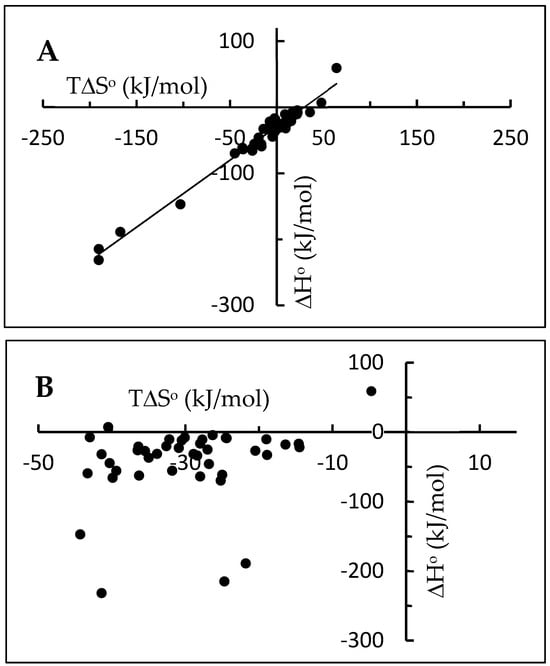
Figure 1.
Enthalpy–entropy (A) and enthalpy–free energy (B) correlations for some protein–ligand interactions.

Table 1.
Protein–ligand interactions included in Figure 1.
The linear relationship between ∆H° and T∆S° shown in part A of Figure 1 leads to an approximately constant value of ∆G° of about −30 kJ/mol. On the other hand, the ∆H° and T∆S° values included in the same figure are within the ranges of −232 kJ/mol to 59.2 kJ/mol and −190 kJ/mol to 64 kJ/mol, respectively. Relationships between ∆H° and T∆S° similar to the one shown here in Figure 1A have been repeatedly observed during the last decades [6,7,8,9,32,33,34], frequently displaying ∆G° values around −35 kJ/mol. Particularly interesting are the results obtained by Olsson et al. [9] from a survey of 171 protein–ligand interactions, rendering a similar approximate constant value of ∆G° and similar large ranges of ∆H° and T∆S° values. It is worth noting here the similarity between this range of ∆G° values found for protein–ligand interactions and the ranges of ∆G° values reported for the protein unfolding, which are typically between −20 and −60 kJ/mol [37,38].
In order to verify the possible general nature of the frequently found value of around −35 kJ for ∆G° of protein–ligand interactions, we made a scrutiny of more than three thousand values in the 2020 version of the Protein Data Bank database [12]. Figure 2 shows the normal distribution corresponding to the ∆G° values for a set of 3025 protein–ligand affinities. The average value obtained for ∆G° was −36.5 kJ/mol. As deduced from the standard deviation, about 70% of the cases are in between −46 and −26 kJ/mol. According to these data, any large enough set of protein–ligand interactions will probably display the kind of linear relationship shown in part A of Figure 1 whenever ∆H° and T∆S° values are of the same order of magnitude or greater than that of ∆G°.
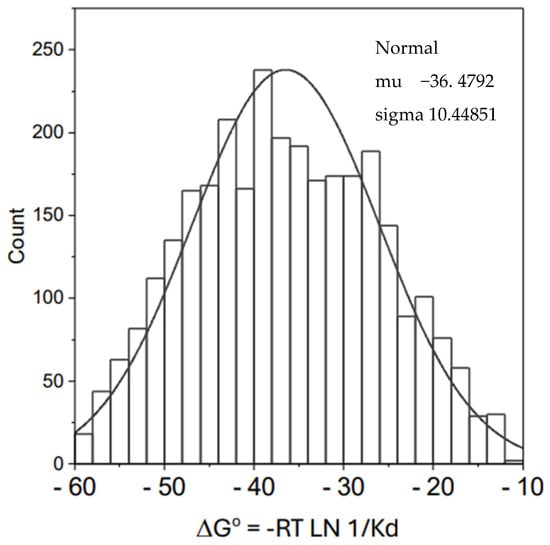
Figure 2.
Normal distribution for affinities of protein–ligand interactions expressed as DG° (kJ/mol). The data were obtained from the 2020 version of the Protein Data Bank Database. The survey of data correspond to the period 2010–2020 and included 3025 values.
The apparent compensation between ∆H° and T∆S° has usually been observed in thermodynamic studies about the binding of a group of structurally related ligands to a particular biological macromolecule. Within that context, the apparent enthalpy–entropy compensation (EEC) might be understood as a natural mechanism to restore the original protein structure after the attempt to change it to improve the affinity for a ligand. However, it is observed within any set of unrelated proteins and ligands. In addition, as derived from the statistical result of 3025 protein–ligand affinities, this apparent EEC seems to be a consequence of the narrow range of ∆G° values displayed by protein–ligand interactions around the particular value of −36.5 kJ/mol. Taking into consideration that the bond energy of a hydrogen bond—or any other weak interaction—is about −10 to −20 kJ/mol, the energy difference between a protein–ligand complex and the free protein plus the free ligand must be equivalent to the change in a small amount of energy.
3.2. Ligand Concentrations “In Vivo”
In addition to the information concerning the energy involved in the protein–ligand interaction, the ∆G° value may also contain valuable information relative to the functionality of the protein–ligand interaction within the context of metabolic regulation. The following equation may represent the simplest model for a protein–ligand interaction:
where P, L, and PL represent protein, ligand, and the protein–ligand complex, respectively. The equilibrium constant for the complex formation is defined by the following:
P + L = PL
K ≡ [PL]/[P] [L]
The corresponding protein saturation fraction, Y, for this simple model is defined as shown below:
Y ≡ [PL]/[P] total = [PL]/([P] + [PL])
After substituting (2) into (3) and solving for Y, we have
Y = [L]/(1/K + [L])
Solving for the ligand concentration, L0.5, in equilibrium with a fractional saturation, Y = 0.5, from Equation (4), we can obtain
where Kd is the dissociation constant of the protein–ligand complex, PL. Using the equation ∆G° = −RTlnK, we obtain finally
L0.5 = 1/K = Kd
∆G° = 2.3RTlogL0.5
According to the average values of ∆G° (−36.5 kJ/mol) and the standard deviation obtained from the normal distribution in Figure 2, the corresponding values for L0.5 must be within a micromolar range.
Taking logarithms in (4), and solving for Y, we obtain
Figure 3 shows the fractional saturation, Y, as a function of log [L]/Kd, according to Equation (7). As can be observed in this figure, a ligand concentration close to the value of Kd = L0.5 corresponds to 50% of protein saturated by the ligand. This is the inflection point of the curve. Minor changes in ligand concentration around the L0.5 value can induce major changes in the fractional saturation of the protein. It is the point of maximal sensitivity of response to changes in the inputs—the ligand concentration—coming from the protein environment. According to Equation (6), the most relevant meaning of ∆G°, from the point of view of functionality, is probably that its value determines the concentration of the ligand displaying the maximal regulatory sensitivity of the protein–ligand interaction.
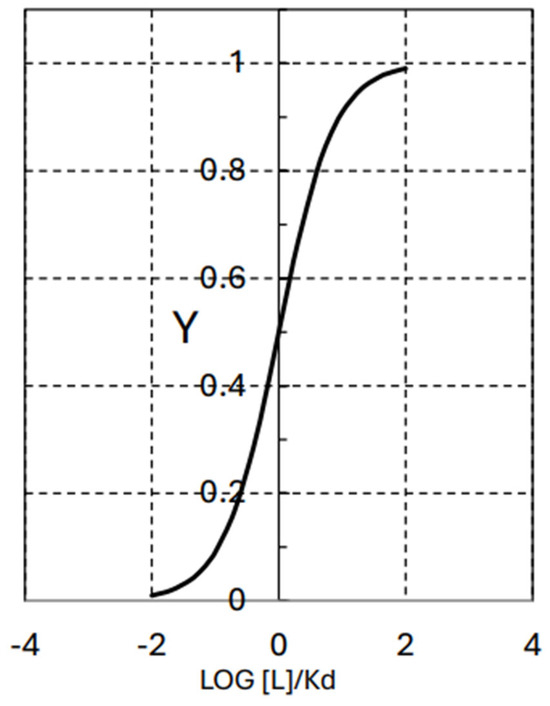
Figure 3.
The fractional protein saturation, Y, as a function of LOG [L]/Kd. Following Equation (6), [L] stands for the ligand concentration and Kd (Kd = L0.5) stands for the dissociation constant of the protein–ligand complex.
We have conducted a search of concentration of ligands, using the Metabolome Database [11] in order to obtain information about the in vivo concentration of ligands from different human sources. Figure 4 shows the normal distribution of 2558 ligands. The ligand concentration data have been transformed to chemical potential by the use of an analogous formula to Equation (6): −RT ln 1/[L], where L corresponds to the different concentration values found in the base. The result would be an energy value equivalent to the ∆G° of a hypothetical protein–ligand interaction in which L would be L0.5. As can be observed, the ligand concentrations transformed to chemical potential have a normal distribution with practically the same average value for the energy and standard deviation (−35.0 kJ/mol, SD 8.9) than the corresponding values for the normal distribution of protein affinities shown in Figure 2 (−36.5 kJ/mol, SD 10.4). Figure 5 shows the corresponding Gaussian curves for both data collection.
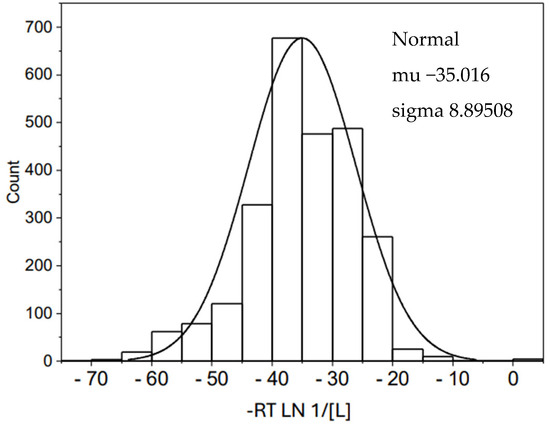
Figure 4.
Normal distribution for human metabolites. The set of data was obtained from the Metabolome Database (2020) and contains 2558 elements from human fluids, including blood, saliva, cerebrospinal fluid, breast milk, and amniotic fluid. All the data were expressed as chemical potential, according to the expression DG° = −RT LN 1/[L].
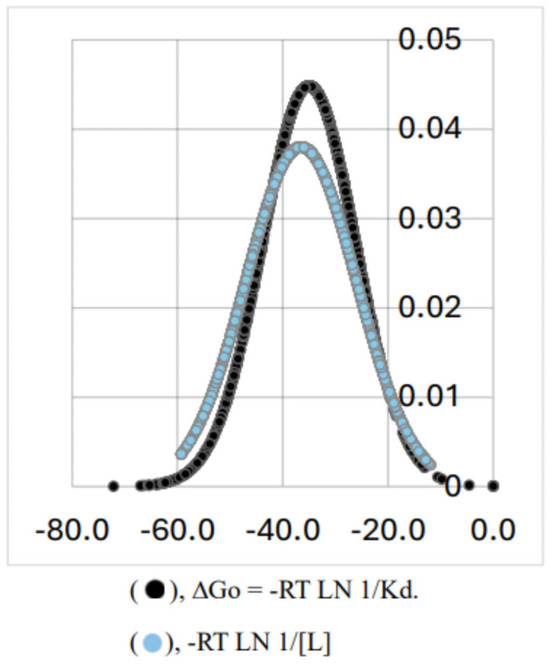
The Gaussian distribution of more than three thousand protein–ligand affinities renders a narrow range of ∆G° values. The known ranges of ∆H° and T∆S° values are larger than that of ∆G° (see, for example, the data included in Table 1, the data of Olsson et al. [9], and most of the data included in those reports about EEC). Therefore, and just from a phenomenological point of view, the narrow range of small ∆G° values may explain the frequently observed linear relationship between ∆H° and T∆S°. On the other hand, the scrutiny of the apparently unrelated 2588 “in vivo” concentrations of putative ligands renders, after translated to chemical potential as shown in Equation (6), practically the same Gaussian distribution as that shown by the set of ∆G° values (Figure 5). This empirical concordance suggested to us the hypothesis that the particularly narrow set of ∆G° values for protein–ligand interactions is the result of the evolution of proteins over millions of years to make them adaptative to changes in the availability of ligands. Indeed, this adaptative mechanism requires a hypothetical thermodynamic pathway that we will try to explain:
4. Discussion
The calorimetric enthalpy of a protein–ligand interaction at constant pressure can be expressed in molecular terms:
∆H° = (ΣUe)° + ∆Us° + p∆V
∆Us° + p∆V is by definition ∆Hs°; then, Equation (8) becomes:
∆H° = (ΣUe)° + ∆Hs°
(ΣUe)° stands for the stoichiometric sum of the electronic energies of the protein, ligand, and protein–ligand complex. Protein–ligand interactions do not usually involve changes in energy associated with covalent bonds. Therefore, (ΣUe)° includes all kind of weak interactions such as those derived from salt bridges, Cation-Π or Van der Waals forces, and all intramolecular and intermolecular hydrogen bonds that are broken and formed as a consequence of the complex formation. An important contribution to (ΣUe)° in protein–ligand interactions is the energy derived from changes in the water molecules reorganization. An enormous number of water–protein, water–ligand, water–complex, and water–water hydrogen bonds have to be involved in the water molecules’ reorganization. All these weak interactions play in protein–ligand interactions the role played by covalent bonds in keeping the electronic ground state of chemicals participating in a chemical transformation at room temperature.
Coming back to Equation (8), ∆Us° stands for the stoichiometric sums of vibrational rotational and translational energy values, ΣUv + ΣUr + ΣUt, corresponding to the protein, ligand, and protein–ligand complex. We have grouped ΣUv + ΣUr + ΣUt in the term ∆Us° because, according to the Boltzmann distribution law, at room temperature, the differences in energy values between different quantum levels of vibration, rotation, and translation energy is small enough to allow for a significant occupation of the different energy levels, therefore contributing to the change in the number of quantum states (or configurations) and therefore to the entropy change associated with the formation of the protein–ligand complex.
Following the Gibbs free energy definition, G ≡ U + pV − TS, the value of ∆G, at constant values of pressure and temperature will be given, under standard conditions, by the following:
∆G° = ∆H° − T∆S°
The substitution of Equation (9) into (10) yields
∆G° = (ΣUe)° + ∆Hs° − T∆S°
The difference between the two last terms in Equation (11), ∆Hs° − T∆S°, is the change in Gibbs free energy with respect to the lowest electronic levels of the protein, ligand, and protein–ligand complex, ∆Gs°. On the other hand, (ΣUe)° is the stoichiometric sum of the lowest electronic levels of the protein, ligand, and protein–ligand complex. Finally, after defining ∆Gs° ≡ ∆Hs° − T∆S°, we have
∆G° = (ΣUe)° + ∆Gs°
Equations (9) and (12) may help to follow the hypothesis most frequently used to provide a theoretical basis for EEC. Concisely, the idea that governs most research on EEC is that whenever (ΣUe)° is negative as a consequence of weak interactions tightening the PL complex, the vibrational and rotational quantum energy levels of the complex become more spaced, therefore contributing to an increase in ∆Gs°. The constraints imposed by the weak interactions that stabilize the complex would induce a better defined conformation and more spaced energy levels, therefore reducing the population of energy levels with the consequent decrease of entropy [10]. The negative value of (ΣUe)° would thus be partially compensated by the positive value of ∆Gs°.
In his 1995 paper [10], Dunitz maintains that, for biological reasons, ∆G° has to remain approximately constant; therefore, any change in ∆H° has to be balanced by the corresponding change in T∆S°. He uses a simple model consisting of a water molecule bonded to a very large molecule and a Morse potential to obtain ∆H° and the corresponding T∆S°; both of them as negative values. For energy values corresponding to covalent bonds, the ∆H° value is much higher (negative) than the also negative value of T∆S°. In this case, no enthalpy–entropy compensation would be found for the simple model. However, for a ∆H° value of −5 kcal/mol, which is very close to that of a hydrogen bond, the corresponding value of T∆S° was −4.5 kcal/mol, therefore obtaining the enthalpy–entropy compensation. A similar result to that of Dunitz is obtained by Yu, Privalov and Hodges [39] for the theoretical evaluation of the enthalpic and entropic contribution of translational and rotational contribution to molecular association in water solution. They obtain an enthalpic contribution of about −4.5 RT and an almost compensating T∆S° value of −5 RT.
The examples included in Figure 1 agree with this simple model. According to Equations (9) and (12), ∆G° and ∆H° share the term (ΣUe)°. When high-energy interactions (for example, covalent bonds) participate in the transformation, as is the case in chemical reactions, particularly in the absence of water, no enthalpy–entropy compensation is generally observed. On the contrary, (ΣUe)° is then such a high contribution that it makes T∆S° so small (as the difference between two small numbers, ∆Gs° and ∆Hs°) that a linear relationship of ∆H° vs. ∆G° can be clearly observed. The theoretical calculations of Dunitz provide theoretical support to the empirical observation mentioned above that the narrow range of small ∆G° values may explain the frequently observed linear relationship between ∆H° and T∆S°. However, the changes in T∆S° observed in those examples of Table 1 or those reported by Olsson et al. [9] seem to be too high and even positive to be explained by the protein conformation triggered by the weak interactions involved in the protein–ligand interaction.
In addition to the changes in protein conformation triggered by the weak interactions involved in the protein–ligand interaction, changes in the extent of hydration may have, as pointed out many years ago by Lumry and Rajender [40], an essential role in conforming EEC. The presence of water in protein–ligand interactions means that protein and ligand must be considered as a highly hydrated polymer interacting with an also highly hydrated ligand to form a complex surrounded by hydration spheres. An enormous number of water–protein, water–ligand, water–complex, and water–water hydrogen bonds have to be involved in the water molecules reorganization.
Water reorganization and the possible hydrophobic effect closely associated with it may play a decisive role in EEC. The formation of a protein–ligand complex in an aqueous media can produce a diminution of the volume excluded to water, the extent of which will depend on the amount of molecular surface involved in the complex formation. This diminution of excluded volume is associated with an increase of volume available to the water molecules, therefore giving place to an increase in the translational entropy of water [41,42]. It has been discussed by Dragan et al. [33] that this increase of entropy (about 6.5 kJ/mol) might compensate for the enthalpy to yield a very small value of ∆G°, under the assumption of an ice-like structure for tightly bound water, suggesting that the large amount of energy involved in the reorganization of water may provide the most important energetic contribution to EEC.
In a recent paper, Chen and Wang [8] use two oppositely charged polymers as models to study the interaction by molecular dynamics simulation. They conclude that enthalpy and entropy changes from water reorganization may be the major contribution to the free energy change in the binding and that both enthalpy and entropy compensate for each other. They discuss, however, that the model used is simple and that it requires hundreds of calculations of that kind to study EEC in biomolecular interactions, although it is currently beyond our computational resources.
One of the main drawbacks in studies concerning structure-based drug design is the linear relationship between ∆H° and T∆S° derived from the small value of ∆G° for the protein–ligand interactions. This apparent EEC is probably unavoidable when working with protein–ligand interactions. However, although unavoidable, it might be ignored. A good strategy may be to focus directly on more negative values of ∆G°.
A promising strategy to overcome the EEC compensation would be to look for ligand modifications that may promote salt bridges or hydrogen bonds with the protein, particularly with ligands with a high contact surface. This might produce a more negative value of (ΣUe)° and also a positive value of T∆S° [33] if the hydrophobic effect is high enough to compensate decreases in the conformational entropy. A particularly interesting case is that of the streptavidin–biotin interaction. It is probably one of the strongest protein–ligand interactions in the absence of covalent bonds, displaying a ∆G° close to −76 kJ/mol. This high affinity value derives from many weak interactions, including hydrophobic effects, van der Waals forces, and seven hydrogen bonds [43]. A double mutation of the protein S45A/D128A produces a strong decrease of affinity to about −34 kJ/mol, without hardly affecting the entropy contribution, which remains essentially constat at about −26 kJ/mol of T∆S°. Looking at the experiment in the opposite direction, the double mutation would render essentially the protein with the same capacity to bind biotin but with a much higher affinity, due to a much more negative value of (ΣUe)°, after probably increasing the number of hydrogen bonds without affecting the entropy change. On the other hand, this almost null entropy change might be due to the absence of conformational changes and hydrophobic effect or to an unpredictable compensation between conformational (negative) and hydrophobic (positive) entropy changes.
Although ∆G° can be obtained from ∆H° and T∆S°, its value only depends on the physical nature of the system: volume and molecular properties of reactants and products. These physical properties determine the electronic, vibrational, rotational, and translational quantum-energy level values. ITC experiments render very precise values of ∆H° but also can yield the equilibrium constant and ∆G° with the same precision. Therefore, instead of looking for the most negative value of ∆H°, it would probably be better to look directly for the most negative value of ∆G°, which directly supplies the most favorable chemical modification to gain a higher affinity for the protein.
5. Conclusions
According to Equation (12), ∆G° may have two components: first, the stoichiometric sum of the weak interactions taking place upon the complex formation, (ΣUe)°. Among them, there are the vast number of water molecules breaking and forming hydrogen bonds to form the hydration sphere (or spheres) of the complex and also those derived from the hydrophobic effect; secondly, the stoichiometric sum of the vast number of vibration, rotation, and translational energy levels occurring upon the complex formation, ∆Gs°. There are many ways to explain how EEC may occur as a natural effect by using classical and statistical thermodynamics. Even molecular dynamics calculations can be made with simple model systems. However, we think that we are still very far from explaining why the particular set of ∆G° values and the almost perfect match between the two Gaussian distributions of 2558 “in vivo” metabolite concentrations and more than three thousands ∆G° values of protein–ligand interactions.
We suggest the hypothesis that the particularly narrow set of ∆G° values for protein–ligand interactions is the result of the evolution of proteins. The vast number of small energy contributions, of both negative and positive sign, may have acted over millions of years, following the thermodynamic pathways described above, as a homeostatic mechanism to make proteins adaptative to changes in the availability of ligands in order to achieve the maximum regulatory capacity of the protein function. Therefore, the EEC might be the general evolutive mechanism to produce the present functional proteins.
EEC is probably unavoidable when working with protein–ligand interactions. A good strategy to avoid its undesirable consequences may be to focus directly on more negative values of ∆G°. However, although unavoidable, it might be ignored. ITC experiments directly render the equilibrium constant and ∆G° for the protein–ligand interaction studied. This suggests that instead of looking for the most negative value of ∆H°, it would probably be more profitable to look directly for the most negative value of ∆G°, which directly would lead to the most favorable chemical modifications to gain a higher affinity for the protein target. On the other hand, a strategy to overcome the EEC would be to look for ligand modifications that may promote salt bridges or hydrogen bonds [33], inducing negative values of (ΣUe)° and large contact surfaces leading to positive changes of hydrophobic entropy.
Author Contributions
Conceptualization, J.S.J.; methodology, J.S.J.; data curation, M.J.B. and J.S.J.; writing, J.S.J. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support has been provided by Ministerio de Ciencia e Innovación. Project PRPPID2021-123859OB-I00.
Data Availability Statement
All data and its sources are included in the Methods section and references.
Acknowledgments
The authors thank Jesús Ávila for inviting us to this contribution to Biophysica.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lumry, R. Uses of enthalpy-entropy compensation in protein research. Biophys. Chem. 2003, 105, 545–557. [Google Scholar] [CrossRef]
- Cooper, A. Thermodynamic analysis of biomolecular interactions. Curr. Opin. Chem. Biol. 1999, 3, 557–563. [Google Scholar] [CrossRef]
- Sharp, K. Entropy-Enthalpy compensation: Fact or artifact? Protein Sci. 2001, 10, 661–667. [Google Scholar] [CrossRef]
- Martin, S.F.; Clements, J.H. Correlating Structure and Energetics in Protein-Ligand Interactions: Paradigms and Paradoxes. Annu. Rev. Biochem. 2013, 82, 267–293. [Google Scholar] [CrossRef]
- Pan, A.; Kar, T.; Rakshit, A.K.; Moulik, S.P. Enthalpy–Entropy Compensation (EEC) Effect: Decisive Role of Free Energy. J. Phys. Chem. B 2016, 120, 10531–10539. [Google Scholar] [CrossRef]
- Fox, J.M.; Zhao, M.; Fink, M.J.; Kang, K.; Whitesides, G.M. The Molecular Origin of Enthalpy/Entropy Compensation in Biomolecular Recognition. Annu. Rev. Biophys. 2018, 47, 223–250. [Google Scholar] [CrossRef]
- Peccati, F.; Jiménez-Osés, G. Enthalpy–Entropy Compensation in Biomolecular Recognition: A Computational Perspective. ACS Omega 2021, 6, 11122–11130. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Z.-G. Using Implicit-Solvent Potentials to Extract Water Contributions to Enthalpy-Entropy Compensation in Biomolecular Associations. J. Phys. Chem. B 2023, 127, 6825–6832. [Google Scholar] [CrossRef]
- Olsson, T.S.G.; Ladbury, J.E.; Pitt, W.R.; Williams, M.A. Extent of enthalpy–entropy compensation in protein–ligand interactions. Protein Sci. 2011, 20, 1607–1618. [Google Scholar] [CrossRef]
- Dunitz, J.D. Win some, lose some: Enthalpy-entropy compensation in weak intermolecular interactions. Chem. Biol. 1995, 2, 709–712. [Google Scholar] [CrossRef]
- Wishart, D.S.; Guo, A.; Oler, E.; Wang, F.; Anjum, A.; Peters, H.; Dizon, R.; Sayeeda, Z.; Tian, S.; Lee, B.L.; et al. the Human Metabolome Database for 2022. Nucleic Acids Res. 2022, 50, D622–D631. [Google Scholar] [CrossRef]
- Wang, R.; Fang, X.; Lu, Y.; Wang, S. The PDB bind Database for Protein-Ligand Complexes with known Three-Dimensional Structures. J. Med. Chem. 2004, 47, 2977–2980. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, B.; Zheng, H.; Zhuang, C.; Li, X.; Lu, X.; Quan, C.; Dong, Y.; Zheng, Z.; Xiu, Z. Trivaric acid, a new inhibitor of PTP1b with potent beneficial effect on diabetes. Life Sci. 2017, 169, 52–64. [Google Scholar] [CrossRef]
- Ylilauri, M.; Mattila, E.; Nurminen, E.M.; Käpylä, J.; Niinivehmas, S.P.; Määttä, J.A.; Pentikäinen, U.; Ivaska, J.; Pentikäinen, O.T. Molecular mechanism of T-cell protein tyrosine phosphatase (TCPTP) activation by mitoxantrone. Biochim. Et Biophys. Acta 2013, 1834, 1988–1997. [Google Scholar] [CrossRef]
- Aggarwal, S.; Tanwar, N.; Singh, A.; Munde, M. Formation of Protamine and Zn–Insulin Assembly: Exploring Biophysical Consequences. ACS Omega 2022, 7, 41044–41057. [Google Scholar] [CrossRef]
- Crisalli, A.M.; Cai, A.; Cho, B.P. Probing the Interactions of Perfluorocarboxylic Acids of Various Chain Lengths with Human Serum Albumin: Calorimetric and Spectroscopic Investigations. Chem. Res. Toxicol. 2023, 36, 703–713. [Google Scholar] [CrossRef]
- Ueda, I.; Yamanaka, M. Titration calorimetry of anesthetic-protein interaction: Negative enthalpy of binding and anesthetic potency. Biophys. J. 1997, 72, 1812–1817. [Google Scholar] [CrossRef]
- Hinz, H.J.; Steininger, G.; Schmid, F.; Jaenide, R. Studies on an energy structure-function relationship of dehydrogenases. II. Calorimetric investigations on the interaction of coenzyme fragments with pig skeletal muscle lactate dehydrogenase. FEBS Lett. 1978, 87, 83–86. [Google Scholar] [CrossRef]
- Mateo, P.L.; Baron, C.; Lopez-Mayorga, O.; Jimenez, J.S.; Cortijo, M. AMP and IMP binding to glycogen phosphorylase b. A calorimetric and equilibrium dialysis study. J. Biol. Chem. 1984, 259, 9384–9389. [Google Scholar] [CrossRef]
- Camero, S.; Benítez, M.J.; Cuadros, R.; Hernández, F.; Ávila, J.; Jiménez, J.S. Thermodynamics of the Interaction between Alzheimer’s Disease Related Tau Protein and DNA. PLoS ONE 2014, 9, e104690. [Google Scholar] [CrossRef]
- Fukada, H.; Sturtevant, J.M.; Quiocho, F.A. Thermodynamics of the binding of L-arabinose and of D-galactose to the L-arabinose-binding protein of Escherichia coli. J. Biol. Chem. 1983, 258, 13193–13198. [Google Scholar] [CrossRef]
- Paketurytė, V.; Linkuvienė, V.; Krainer, G.; Chen, W.-Y.; Matulis, D. Repeatability, precision, and accuracy of the enthalpies and Gibbs energies of a protein-ligand binding reaction measured by isothermal titration calorimetry. Eur. Biophys. J. 2019, 48, 139–152. [Google Scholar] [CrossRef]
- Shi, J.-H.; Lou, Y.-Y.; Zhou, K.-L.; Pan, D.-Q. Elucidation of intermolecular interaction of bovine serum albumin with Fenhexamid: A biophysical prospect. J. Photochem. Photobiol. B Biol. 2018, 180, 125–133. [Google Scholar] [CrossRef]
- Sohrabi, Y.; Panahi-Azar, V.; Barzegar, A.; Dolatabadi, J.E.N.; Dehghan, P. Spectroscopic, thermodynamic and molecular docking studies of bovine serum albumin interaction with ascorbyl palmitate food additive. BioImpacts 2017, 7, 241–246. [Google Scholar] [CrossRef]
- Sobhany, M.; Negishi, M. Characterization of specific donor binding to α1,4Nacteylhexosaminyltransferase EXTL2 using Isothermal Titration Calorimetry. Methods Enzymol. 2006, 416, 3–12. [Google Scholar] [CrossRef]
- Clarke, C.; Woods, R.J.; Gluska, J.; Cooper, A.; Nutley, M.A.; Boons, G.-J. Involvement of Water in Carbohydrate-Protein Binding. J. Am. Chem. Soc. 2001, 123, 12238–12247. [Google Scholar] [CrossRef]
- Hamilton, P.D.; Andley, U.P. In vitro interactions of histones and α-crystallin. Biochem. Biophys. Rep. 2018, 15, 7–12. [Google Scholar] [CrossRef]
- Timmer, C.M.; Michmerhuizen, N.L.; Witte, A.B.; Van Winkle, M.; Zhou, D.; Sinniah, K. An Isothermal Titration and Differential Scanning Calorimetry Study of the G-Quadruplex DNA–Insulin Interaction. J. Phys. Chem. B 2014, 118, 1784–1790. [Google Scholar] [CrossRef]
- Honnappa, S.; Cutting, B.; Jahnke, W.; Seelig, J.; Steinmetz, M.O. Thermodynamics of the Op18/Stathmin-Tubulin Interaction. J. Biol. Chem. 2003, 278, 38926–38934. [Google Scholar] [CrossRef][Green Version]
- Danesh, N.; Sedighi, Z.N.; Beigoli, S.; Sharifi-Rad, A.; Saberi, M.R.; Chamani, J. Determining the binding site and binding affinity of estradiol to human serum albumin and holo-transferrin: Fluorescence spectroscopic, isothermal titration calorimetry and molecular modeling approaches. J. Biomol. Struct. Dyn. 2018, 36, 1747–1763. [Google Scholar] [CrossRef]
- Khrapunov, S. The Enthalpy-entropy Compensation Phenomenon. Limitations for the Use of Some Basic Thermodynamic Equations. Curr. Protein Pept. Sci. 2018, 19, 1088–1091. [Google Scholar] [CrossRef]
- Cornish-Bowden, A. Enthalpy-entropy compensation and the isokinetic temperature in enzyme catalysis. J. Biosci. 2017, 42, 665–670. [Google Scholar] [CrossRef]
- Dragan, A.I.; Read, C.M.; Crane-Robinson, C. Enthalpy-entropy compensation: The role of solvation. Eur. Biophys. J. 2017, 46, 301–308. [Google Scholar] [CrossRef]
- Huang, R.; Lau, B.L. Biomolecule–nanoparticle interactions: Elucidation of the thermodynamics by isothermal titration calorimetry. Biochim. Et Biophys. Acta 2016, 1860, 945–956. [Google Scholar] [CrossRef]
- Kragelj, J.; Orand, T.; Delaforge, E.; Tengo, L.; Blackledge, M.; Palencia, A.; Jensen, M.R. Enthalpy-Entropy Compensation in the Promiscuous Interaction of an Intrinsically Disordered Protein with Homologous Protein Partners. Biomolecules 2021, 11, 1204. [Google Scholar] [CrossRef]
- Cavalcanti, I.D.L.; Junior, F.H.X.; Magalhães, N.S.S.; Nogueira, M.C.d.B.L. Isothermal titration calorimetry (ITC) as a promising tool in pharmaceutical nanotechnology. Int. J. Pharm. 2023, 641, 123063. [Google Scholar] [CrossRef]
- Sánchez-Ruiz, J.M. Differential scanning calorimetry of proteins. Subcell. Biochem. 1995, 24, 133–176. [Google Scholar] [CrossRef]
- Liu, L.; Yang, C.; Guo, Q.-X. A study on the enthalpy-entropy compensation in protein unfolding. Biophys. Chem. 2000, 84, 239–251. [Google Scholar] [CrossRef]
- Yu, Y.B.; Privalov, P.L.; Hodges, R.S. Contribution of Translational and Rotational Motions to Molecular Association in Aqueous Solution. Biophys. J. 2001, 81, 1632–1642. [Google Scholar] [CrossRef]
- Lumry, R.; Rajender, S. Enthalpy-entropy compensation phenomena in water solutions of proteins and small molecules: A ubiquitous properly of water. Biopolym. 1970, 9, 1125–1227. [Google Scholar] [CrossRef]
- Harano, Y.; Kinoshita, M. Translational-Entropy Gain of Solvent upon Protein Folding. Biophys. J. 2005, 89, 2701–2710. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, M. Importance of Translational Entropy of Water in Biological Self-Assembly Processes like Protein Folding. Int. J. Mol. Sci. 2009, 10, 1064–1080. [Google Scholar] [CrossRef] [PubMed]
- Hyre, D.E.; Le Trong, I.; Merritt, E.A.; Eccleston, J.F.; Green, N.M.; Stenkamp, R.E.; Stayton, P.S. Cooperative hydrogen bond interactions in the streptavidin-biotin system. Protein Sci. 2006, 15, 459–467. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).