Simulation of the Influence of Braking System Damage on Vehicle Driving Safety

Abstract

This article presents an analysis of the effects of braking system damage on the course of the vehicle collision and driving safety. Research was conducted using simulation methods in the V-SIM 7.0 environment, analysing the collision between a car and a truck at three speeds—50, 60, and 70 km/h—under the assumption of a braking system malfunction in the car. The obtained results showed that as the speed of the truck increased, the total kinetic energy of the system nearly doubled, resulting in deformation of the vehicle’s body front of up to 0.6 m. The maximum force acting on the car decreased with increasing speed, which was due to the change in the point of impact. The recorded acceleration values of the car indicate a moderate level of overloads, which should not cause serious injuries to the passengers but do suggest significant stress on the vehicle’s load-bearing structure. The research may serve as a foundation for further work on braking system diagnostics, the development of friction materials, and the modelling of energy absorption processes in collisions involving vehicles of varying mass and geometry.

1. Introduction

Road safety is one of the most significant issues in modern transportation, both from the perspective of vehicle engineering and the protection of human life. With the continuous development of the automotive industry and the dynamic increase in the number of vehicles on the roads, the risk of road incidents caused by technical failures is also on the rise. Among all vehicle systems, the braking system plays a particularly crucial role in ensuring safety, as that system enables the driver to effectively reduce the speed of the vehicle or bring it to a controlled stop, regardless of road or weather conditions.

Alongside the steering and suspension systems, the braking system is one of the key components that directly affect a vehicle’s active safety [1,2,3]. Even partial damage to one of the system’s components, such as leakage in the hydraulic lines, wear of brake pads or discs, the malfunction of the brake master cylinder, or locking of a single wheel, may lead to a significant reduction in braking efficiency, loss of vehicle stability, or even complete loss of control over the vehicle’s trajectory. As a result, braking system defects are among the most hazardous failures occurring in motor vehicles. The decision to address the topic of the influence of braking system damage on driving safety stems from the growing need to analyse and assess the hazards associated with vehicle operation. Statistical data obtained from police reports and road safety organizations clearly indicate that technical failures constitute a significant share of the causes of road accidents. Among these, braking system defects are particularly dangerous, as they directly impair the driver’s ability to stop the vehicle in an emergency situation.

Although the braking system plays a crucial role in the safe and smooth operation of a vehicle, that system has not received sufficient attention; consequently, brake failures remain under-represented in road safety analyses. The current body of literature on accidents linked to braking system failures is limited [4].

In real-world vehicle operation, situations frequently occur in which the driver is unaware of the progressive wear or partial malfunction of braking system components. Symptoms such as uneven braking, vehicle pulling to one side, or an increased braking distance may be ignored, which—during a sudden road incident—significantly increases the risk of a collision. Therefore, the analysis of how specific types of braking system damage affect vehicle behaviour is of great importance both for technical diagnostics and for driver education.

Traditional braking system test methods, based on road or bench tests, are costly, time-consuming, and involve a level of risk. In many cases, recreating emergency situations under real-world conditions is virtually impossible due to the safety hazards posed to test participants. The use of simulation environments such as V-Sim eliminates these limitations, allowing for the analysis of even the most dangerous scenarios in a completely safe and repeatable way.

In the relevant literature, the importance of computer simulations as a tool supporting vehicle design and safety assessment is increasingly emphasised. Such simulations enable not only the analysis of failure consequences but also the testing of various design solutions and braking system control strategies. The results of such studies provide valuable information both for structural designers and engineers involved in the development of active safety systems, and for institutions engaged in traffic accident analysis or driver training in response to technical failures.

The subject of this research therefore carries both scientific and practical significance. From a scientific standpoint, this article contributes to a deeper understanding of vehicle dynamics under braking system failure conditions. From a practical perspective, the paper delivers insights that may contribute to improvements in road safety through the development of advanced diagnostic and preventive maintenance systems.

The braking system degradation mechanisms presented in the article, particularly hydraulic failures, are directly reflected in the simulation scenario, in which the loss of braking effectiveness leads to a collision between two vehicles.

2. Operational Conditions and Examples of Braking System Damage

Braking is quite a complex process, often influenced and constrained by a variety of factors [5]. The proper operation of a braking system depends on numerous factors, including the mechanical design, operational parameters, environmental conditions, and the quality of the materials used [6].

Braking systems operate under extreme conditions, which involve high temperatures, significant contact pressures, variable dynamic loads, and aggressive corrosive environments. These factors make the tribological phenomena occurring during braking particularly complex [7].

In a vehicle, the braking system slows down or completely stops the vehicle by converting its kinetic energy into thermal energy. Brake pads are an essential component of the vehicle’s braking system, generating the friction required to stop or reduce the vehicle’s motion [8]. During braking, the rapid interaction between the brake pad and the disc generates high temperatures, requiring the brake pad to quickly absorb heat to withstand high temperatures without wear [9]. Under typical conditions, these temperatures can reach 200–400 °C, while during intensive braking or prolonged downhill driving, they may rise to 700–800 °C. Such temperatures place significant stress on friction materials and metallic structural components, leading to changes in their physical properties, to the development of thermal stresses, and, consequently, to accelerated wear. The most advanced brake discs are made of ceramic materials and carbon composites, making them resistant to temperatures up to 1000 °C. However, due to their higher cost, these discs are primarily used in racing cars and high-performance vehicles [10]. As demonstrated in the studies by Mohammadnejad et al. [11], repeated heating and cooling cycles of the brake disc lead to the initiation of thermal cracks and deformation of the operating surfaces.

The operational conditions of a braking system are largely influenced by vehicle speed, driver behaviour, and environmental conditions. In cars and trucks used in urban traffic, the braking system is subjected to frequent, short braking cycles, which cause repetitive temperature fluctuations and gradual wear of the friction surfaces. The purpose of [12] was to determine the efficiency of a vehicle’s braking system depending on the vehicle mass, driving speed, distance travelled, and braking time, based on experimental tests conducted both at standstill and in real road traffic, in accordance with road safety regulations. The experimental tests showed that recommendations regarding the replacement intervals for brake pads and discs do not align with their actual wear patterns.

The operational environment also has a significant impact on the performance of the braking system. Under humid conditions or in areas with high dust or salt exposure, accelerated corrosion of the braking system’s metallic components can occur. This corrosion may restrict the movement of brake pads and pistons, leading to uneven wear of the friction linings and a reduction in braking efficiency. Research presented in [13] demonstrated that corrosion products and iron oxide particles generated through wear and oxidation of friction materials can additionally act abrasively, thus increasing the degradation rate of the operating surfaces. In [14], the results of research on the wear of brake pads containing copper and those without that chemical element were presented. The results indicate that copper-free brake pads exhibit a coefficient of friction comparable to that of copper-containing pads. All three types of friction materials produce similar wear as that of the brake disc. Copper-free brake pads generate more airborne particulate matter than copper-containing pads.

In addition to environmental factors, thermal and hydraulic operational conditions play a critical role in braking system performance. In hydraulic braking systems, the key component is the brake fluid, which transmits pressure from the brake pedal to the pistons in the calipers. Brake fluids are hygroscopic, meaning that they absorb moisture from the surrounding environment. An increase in water content lowers the fluid’s boiling point and raises the risk of vapour bubble formation during intensive braking. This phenomenon can result in reduced braking efficiency due to the compressibility of gas in the system.

Attention should also be paid to the importance of pressure distribution on the friction surfaces. Uneven contact between the brake disc and pad can lead to localised thermal overloads, hotspot overheating of the material, and disc deformation. As a result, vibration and noise phenomena occur, which not only reduce driving comfort but also accelerate fatigue processes in the material structure.

The issue of wear in braking system components is significant both from the perspective of travel safety and system design [15], which is why numerous scientific studies have been conducted and their results published in various papers. Barros et al. attempted to describe the sequence of events (cause–effect) leading to a shift from moderate to severe wear of brake friction materials. Those authors found out that a critical tensile strength exists, which leads to the destruction of the contact layers (of the secondary type), resulting in direct contact between metallic fibres and the tribofilm deposited on the disc surface. Subsequently, the tribofilm is gradually removed during braking, thus increasing the wear rate of the tribological pair. This behaviour was explained using Mohr’s circle, where the high contact pressure applied in experiments exceeded the maximum tensile strength of the contact plateau [16]. In addition to the studies mentioned above, other publications have examined factors contributing to braking system degradation.

In [17], a literature review on brake pad wear processes in motor vehicles was presented. The study included the results of research on the influence of material hardness and surface roughness on the wear rate. Factors affecting the wear coefficient were also analysed, including chemical affinity between materials, surface quality, thermoelastic instability of materials, and the environment.

All of the operational conditions and factors mentioned above can ultimately lead to the damage or wear of braking system components. Below, examples of braking system damage are presented which, if not addressed in a timely manner, can lead to a road situation, the consequences of which will depend on the prevailing road conditions at the time.

•

Brake disc cracking. Brake disc cracks often become initiated under conditions of extreme thermal or mechanical load. The initiation of cracks can be described using a model of thermal stress resulting from rapid heating followed by subsequent cooling of the disc. This process generates alternating stresses that may exceed the material’s yield strength or cause localised fatigue of the material. Once initiated, cracks propagate under the influence of subsequent braking cycles. Research conducted by the authors of [18] demonstrated that small cracks do not affect the migration of hot spots, as the hot spot moves above the crack. However, when the crack reaches a critical length, heat becomes concentrated within the crack, accelerating its growth and thereby reducing the service life of the disc.

•

Surface wear and the degradation of the disc material. In parallel with cracking, the disc surface undergoes intensive abrasion and oxidation. The authors of [19] analysed a grey cast iron disc, demonstrating that tribo-oxidation processes and thermal cracking interact in the mechanism of disc surface degradation.

•

Geometric deformations. Brake discs may undergo permanent geometric deformations as a result of cyclical heating and cooling (volume changes, thermal expansion) as well as mechanical loads from friction and caliper forces. These deformations result in damped residual stresses, uneven wear, disc run-out, and increased vibrations. Deformation can lead to localised increases in pressure on the friction lining, thereby accelerating surface wear or initiating additional cracks.

•

Friction wear of the disc-pad pair. Friction elements are subject to wear due to cyclical friction. The loss of friction material leads, among other effects, to changes in the contact geometry and an increase in local temperature.

•

Corrosion and seizure of moving components. Corrosion of the disc surface, brake pad guides, or caliper pistons reduces the efficiency of the self-adjustment mechanism and leads to seizures or single-side friction.

•

Hydraulic and operational damage. Leaks in brake lines, degradation of brake fluid, and air entrapment can indirectly contribute to the wear and deterioration of friction components.

Figure 1 illustrates examples of braking system component damage, observed at a diagnostic station during technical inspections. Long-term observations of customer vehicles at the diagnostic station indicate that brake disc cracking is the most prevalent issue.

Drivers were often unaware of the damage and continued to operate their vehicles until the next technical inspection, which led to the development of additional fatigue cracks. Fortunately, no complete disc cracking occurred, avoiding potential road accidents caused by impaired braking performance. These vehicles were not allowed to continue operation until the cracked or otherwise damaged discs were replaced.

Given the critical importance of braking systems, particularly brake discs, continuous improvement efforts are being made to reduce wear [20]. Nevertheless, numerous operational issues with disc brakes persist, requiring further understanding and resolution. Extensive research is being conducted on these topics, and various methods have been proposed to mitigate or prevent these issues [21]. For example, Cai et al. modified the disc surface morphology to promote the formation of an adhesive layer during the slide motion, thereby protecting the disc from wear. They proposed a locking surface prepared through a Plasma Electrolytic Aluminising (PEA) process. Results indicated that brake discs treated with PEA exhibited minimal wear due to the thin protective layer formed by the transfer of the pad material onto the PEA-treated cast iron [22].

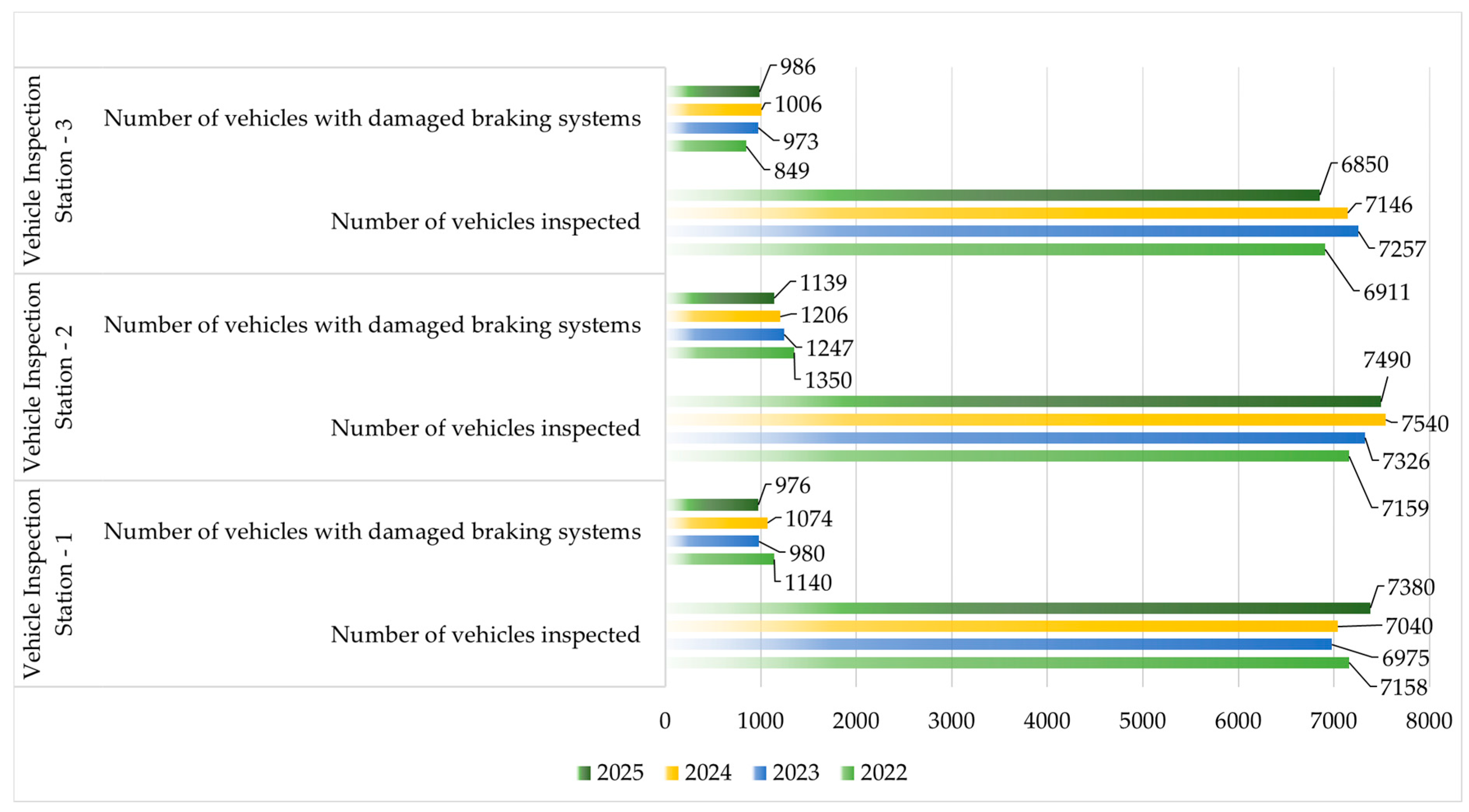
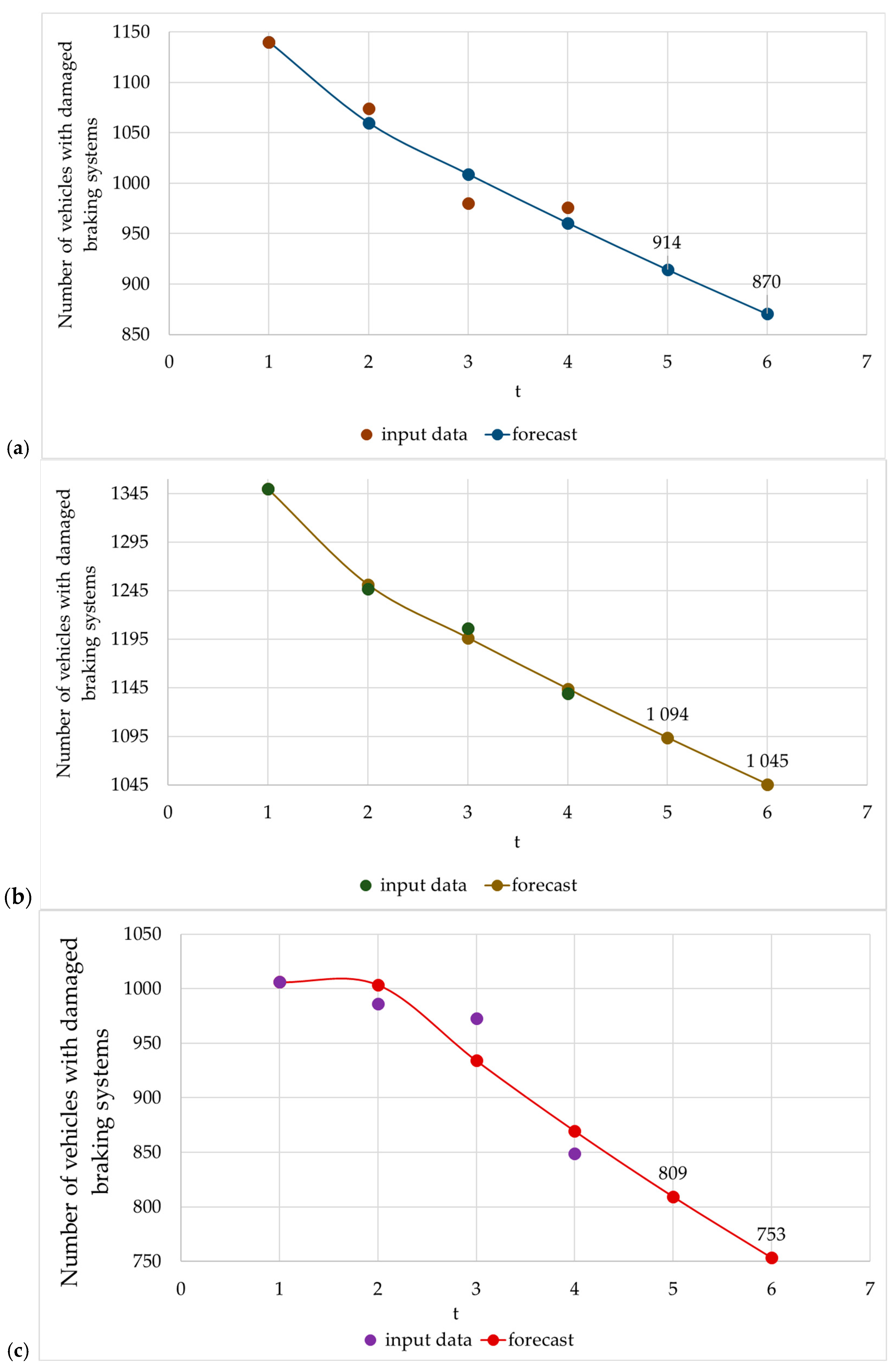
3. Analysis and Forecast of the Number of Vehicles with Damaged Braking Systems

The occurrence of braking system damage in vehicles operating daily on public roads is confirmed by statistical data collected from three regional vehicle inspection stations. The stations are located within the Małopolskie Region (Poland). The analysis of braking system damage identified during periodic technical inspections constitutes a key element in assessing the overall road traffic safety level.

In this item, an analysis is conducted using data obtained from three vehicle inspection stations covering the years 2022–2025 (Figure 2), with particular focus on the number of vehicles in which braking system damage was detected and their proportion relative to the total number of inspections carried out. This analysis provides a direct foundation for further prognostic studies employing grey systems theory.

Any irregularity within the braking system was recorded as damage, ranging from worn brake pads to cracked brake discs and incorrect hydraulic system pressure.

Across all analysed years, the number of vehicles undergoing periodic technical inspections at the various stations remained at a broadly comparable level, with only moderate year-to-year fluctuations. The results indicate that the instances of braking system damage represent a significant operational issue, the scale and dynamics of which vary between the analysed vehicle inspection stations.

For Vehicle Inspection Station 1, the proportion of vehicles with unoperational braking systems amounted to approximately 15.9% in 2022, 14.1% in 2023, 15.3% in 2024, and 13.2% in 2025 of all vehicles inspected at that station. An overall downward trend in the proportion of defects is therefore evident, despite a temporary increase in 2024, which may indicate an improvement in the technical condition of vehicles or greater effectiveness of corrective maintenance actions following earlier unfavourable inspection outcomes.

Vehicle Inspection Station 2 is characterised by the highest number of vehicles processed. The proportion of identified instances of braking system damage remained at approximately 18.9% in 2022, 17.0% in 2023, 16.0% in 2024, and 15.2% in 2025. In contrast to Station 1, a clear and almost linear downward trend is observed here in both absolute and relative terms, which may point to a systematic improvement in vehicle operational quality.

For Vehicle Inspection Station 3, the number of vehicles with damaged braking systems amounted to approximately 12.3% in 2022, 13.4% in 2023, 14.1% in 2024, and 14.4% in 2025. In this case, an upward trend in the proportion of defects is observed, despite a relatively stable number of inspections, which may indicate progressive technical wear of vehicles operated in the given region or reduced effectiveness of routine servicing and maintenance.

Data obtained from the regional vehicle inspection stations were used to forecast the number of identified instances of braking system damage over the subsequent two years. For this purpose, a grey system model was applied.

The essence of grey modelling lies in describing the behaviour of a real-world observed system, represented by the forecast (endogenous) variable: $x^{\left(0\right)} \left(k\right)$, where $k=1,2,\dots ,n$ through the set of explanatory variables representing factors that determine the state of the forecast variable.

The grey system theory model is defined by the differential Equation (1). The formulation of the following expressions and equations is based on works [23,24].

$${\displaystyle \frac{{dX}^1\left(t\right)}{dt}}+a{X}^{\left(1\right)}\left(t\right)=u$$

(1)

The parameters $a$ and $u$ are determined by specifying the model $X^{\left(1\right)}\left(k\right)$, which is expressed as the sum of the input quantities of the models $X^{\left(0\right)}\left(t\right)$ for i = 1, 2, …, k (2).

$$X^{\left(n\right)}\left(k\right)={\sum }_{i=1}^k{X}^{\left(n-1\right)}\left(i\right)$$

(2)

The grey system model is constructed using data obtained from observations, and its response takes the form of prediction Equation (3).

$$X^{\left(1\right)}\left(t+1\right)=\left(X^{\left(1\right)}\left(0\right)-{\displaystyle \frac{u}{a}}\right)·e^{-at}+{\displaystyle \frac{u}{a}}$$

(3)

Parameters $a$ and $u$ are determined from Equation (4).

$$\widehat{a}={(a,u)}^T={\left(B^{T}B\right)}^{-1}{B}^T{Y}_n$$

(4)

where $B$ and $Y_n$ are determined from formulae (5) and (6).

$$\left[\begin{array}{cc}-{\displaystyle \frac{1}{2}}\left[X^{\left(1\right)}\left(1\right)+X^{\left(1\right)}\left(2\right)\right]& 1\\ -{\displaystyle \frac{1}{2}}\left[X^{\left(1\right)}\left(2\right)+X^{\left(1\right)}\left(3\right)\right]& 1\\ \dots & \dots \\ \dots & \dots \\ \dots & \dots \\ -{\displaystyle \frac{1}{2}}\left[X^{\left(1\right)}\left(n-1\right)+X^{\left(1\right)}\left(n\right)\right]& 1\end{array}\right]$$

(5)

$$Y_n={\left[\begin{array}{ccc}{X}^{\left(0\right)}\left(2\right)& X^{\left(0\right)}\left(3\right)& X^{\left(0\right)}\left(n\right)\end{array}\right]}^T$$

(6)

The projected data are calculated using formula (7):

$${\widehat{X}}^{\left(0\right)}\left(t+1\right)=\left[X^{\left(0\right)}\left(1\right)-{\displaystyle \frac{u}{a}}\right]·e^{-a(t-1)}·\left(e^{-1}-1\right)$$

(7)

By using input data from regional vehicle inspection stations and the above formulae, the following forecasts were obtained:

Regional Vehicle Inspection Station—1

$${\widehat{X}}^{\left(0\right)}\left(t+1\right)=1059.89204·e^{-0.049234(t-1)}$$

Regional Vehicle Inspection Station—2

$${\widehat{X}}^{\left(0\right)}\left(t+1\right)=1251.32344·e^{-0.044930(t-1)}$$

Regional Vehicle Inspection Station—3

$${\widehat{X}}^{\left(0\right)}\left(t+1\right)=1003.55894·e^{-0.07173(t-1)}$$

Figure 3 presents the projected number of vehicles with damaged braking systems over the next two years.

From the perspective of road safety, the most critical values are those representing the number of vehicles with damaged braking systems over the forthcoming two-year period. The forecasting results indicate further changes in the number of instances of braking system damage across all three analysed stations, with the nature of these changes being consistent with trends observed in historical data. In each case, the model predicts a continuation of the downward trend, although its intensity varies between stations, reflecting differences in local operational conditions.

For Vehicle Inspection Station 1, the projected values for the next two years indicate a continued, moderate decline in the number of instances of braking system damage. The rate of this decline is relatively gradual, suggesting a gradual stabilisation of the technical condition of vehicles serviced by this station. A reduction in the instances of damage of approximately 4.8% per year is forecast. This represents a moderate decline, indicating a stable but gradual improvement in the technical condition of vehicles. This means that while there is potential for further reduction in defects, the easiest-to-eliminate malfunctions have largely been addressed in previous years.

For Vehicle Inspection Station 2, which recorded the highest number of the instances of damage during the baseline period, the forecast for the next two years also points to a significant reduction in the number of malfunctions. The percentage decrease is expected to remain around 4.4%. Thus, the forecast anticipates a relatively steady rate of defect reduction, which may reflect a consistent improvement in vehicle maintenance standards and a gradual replacement of the most heavily worn-out vehicles.

It should be emphasised, however, that despite a similar percentage decline, the absolute scale of the problem remains greater, meaning that Station 2 will continue to represent an area of elevated technical risk, albeit gradually decreasing.

For Vehicle Inspection Station 3, the model predicts the largest relative reduction in the number of instances of damage over the forecast two-year period, marking a clear reversal of the previously observed upward trend. The forecast indicates an annual decline of approximately 6.9%. This outcome may suggest that the adverse conditions observed during the baseline period were temporary, resulting from accumulated wear within a specific group of vehicles, which were subsequently repaired or withdrawn from service in the following years.

Analysing the forecast values for all three stations collectively, it can be concluded that the grey system theory model indicates an overall improvement in the technical condition of braking systems over the short term. The projected decrease in the number of defects over the next two years may contribute to a reduced risk of road incidents resulting from a braking system malfunction. It should also be noted that even the forecast minimum values remain at a level that cannot be considered negligible from a road safety perspective. This means that technical inspections and preventive measures will continue to play a key role in limiting the number of vehicles failing to meet safety requirements.

To illustrate the consequences of braking system damage for road safety, the following sections present a simulation of a traffic accident caused by a malfunction in the braking system of a single vehicle.

4. Simulation Conditions

The simulation involved two vehicles: a truck with a semitrailer, travelling at speeds ranging from 50 to 70 km/h, and a car, which was moving at 50 km/h immediately before the collision.

The simulation assumed that both vehicles were occupied solely by their drivers, with the truck carrying a cargo load of 25,000 kg. Detailed vehicle characteristics and a description of the traffic environment are presented later in this chapter.

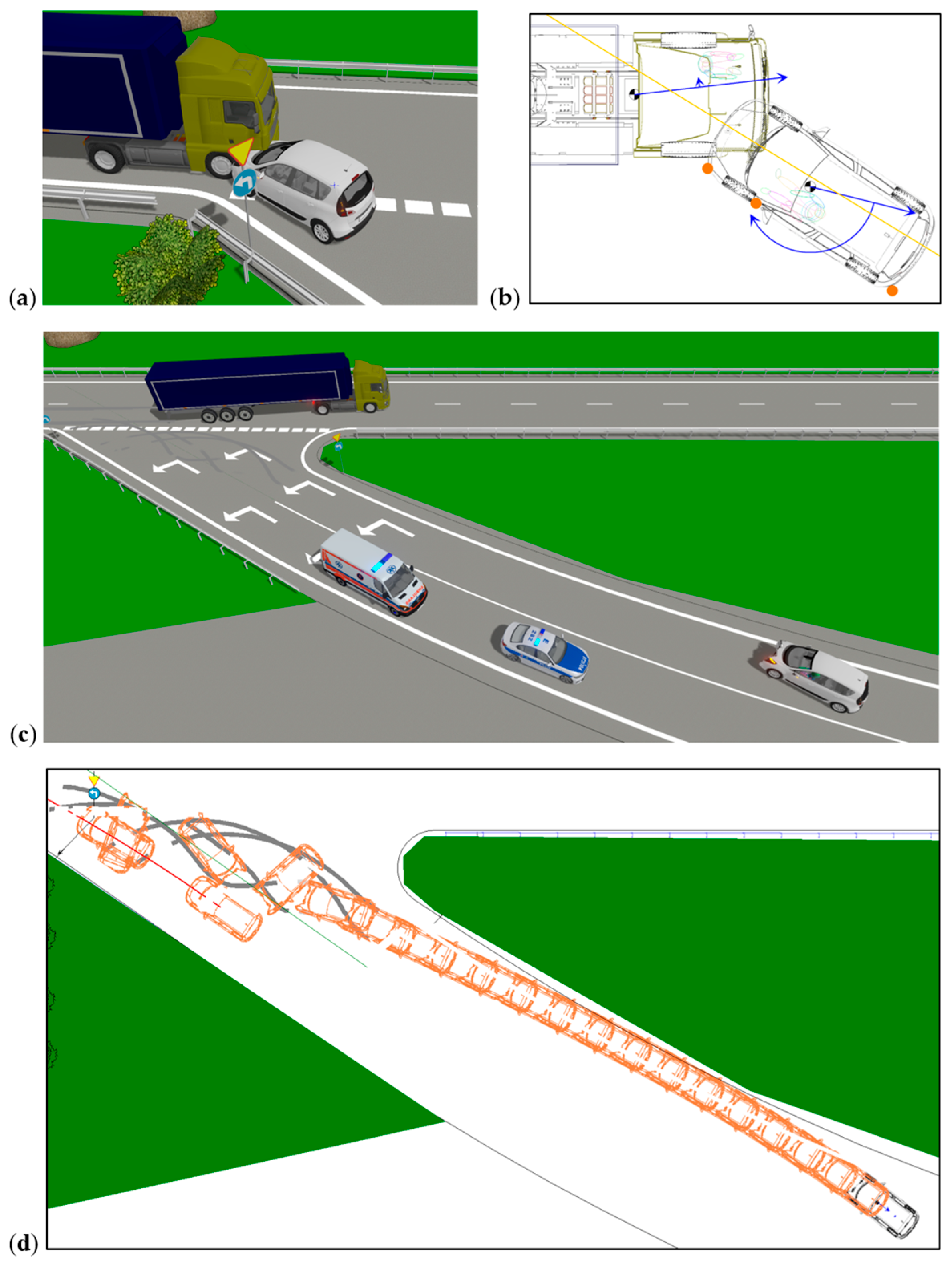
4.1. Road Incident Simulation Software

The road incident simulation was performed using V-SIM 7.0 software, licensed by CYBID sp. z o.o. sp. k., based in Kraków, Poland. V-SIM is an advanced simulation programme designed for road incident reconstruction. The software integrates sophisticated physics and numerical modelling in a 3D environment, and accounts for interactions within the Human-Environment-Vehicle system. The programme enables analysis of vehicle motion and collisions, including knocking down a pedestrian, cyclist, or scooter rider, as well as the driver’s and the passenger’s behaviour. The realistic representation of the traffic environment is supported by compatibility with multiple data formats, built-in drawing tools, and extensive libraries of 2D and 3D graphic objects.

4.2. Vehicle Characteristics

Below are the basic technical specifications of the vehicles involved in the road incident. These data were obtained using the V-SIM 7.0 software.

Truck with a semitrailer (Figure 4a):

•

Truck: length × width × height: 5875 × 2490 × 3530 mm,

•

Semitrailer: length × width × height: 13,950 × 2550 × 3970 mm

•

Number of axles: the truck: 2, the semitrailer: 3

•

Truck: kerb weight: 6568 kg, gross vehicle weight rating: 18,000 kg,

•

Semitrailer: kerb weight: 6200 kg, gross vehicle weight rating: 35,000 kg,

•

Maximum engine power of the truck: 324 kW at 1900 rpm,

•

Efficiency of the correctly operating service brake *: the truck: 108 kN, the semitrailer: 210 kN

* Braking efficiency is determined by an index that is the ratio of braking force to the force resulting from the vehicle’s permissible gross vehicle weight.

Car (Figure 4b):

•

Length × width × height: 4344 × 1845 × 1637 mm,

•

Number of axles: 2,

•

Wheelbase: 2702 mm,

•

First axle wheel track: 1545 mm, the second axle: 1547 mm,

•

Kerb weight: 1428 kg, gross vehicle weight rating: 1953 kg,

•

Maximum engine power: 103 kW at 6000 rpm,

•

Efficiency of the correctly operating service brake: 18.7 kN.

Figure 4. Silhouettes of the vehicles involved in the road incident simulation: (a) the truck with semitrailer; (b) the car.

Figure 4. Silhouettes of the vehicles involved in the road incident simulation: (a) the truck with semitrailer; (b) the car.

4.3. Traffic Environment

At the moment of the collision, road conditions were favourable. The sun was shining but did not cause glare. The road incident occurred on a dry asphalt surface with the following parameters:

•

Grip coefficient of adhesion—${\mu }_p=0.80$

•

Slide coefficient of adhesion—${\mu }_s=0.75$

•

Rolling resistance coefficient—$0.015$

The quality of the road surface at the collision site and its immediate surroundings was assessed as high. No ruts, surface defects, or other forms of road damage were noted.

The road incident occurred at a T-shaped junction, where the minor road intersects the major road at an angle of 35°. Safety barriers of type U-14a were installed along both shoulders in the vicinity of the junction. The traffic organization at the junction allows vehicles from the minor road to make only a left turn.

Prior to the road incident, the truck with a semitrailer was travelling along the major road in the lane adjacent to the minor road. There were no other vehicles on the same road at the time. The car was travelling on the minor road, turning left from the left lane. As the car approached the conditional stop line, unexpected damage occurred in the car braking system. Despite full depression of the brake pedal, the vehicle did not respond by decelerating. Most likely, the system was leaking, causing a brake fluid leak. As a result, the vehicle lost braking ability and all four wheels failed. The driver, surprised by the situation, did not attempt to use the additional brake.

The moment the car driver attempted to brake, the truck was located 16.25 m from the minor roadway axis. Meanwhile, the car was 8 m from the conditional stop line. Figure 5 illustrates the traffic environment and road conditions on the basis of which the vehicle collision was simulated.

5. Simulation Results

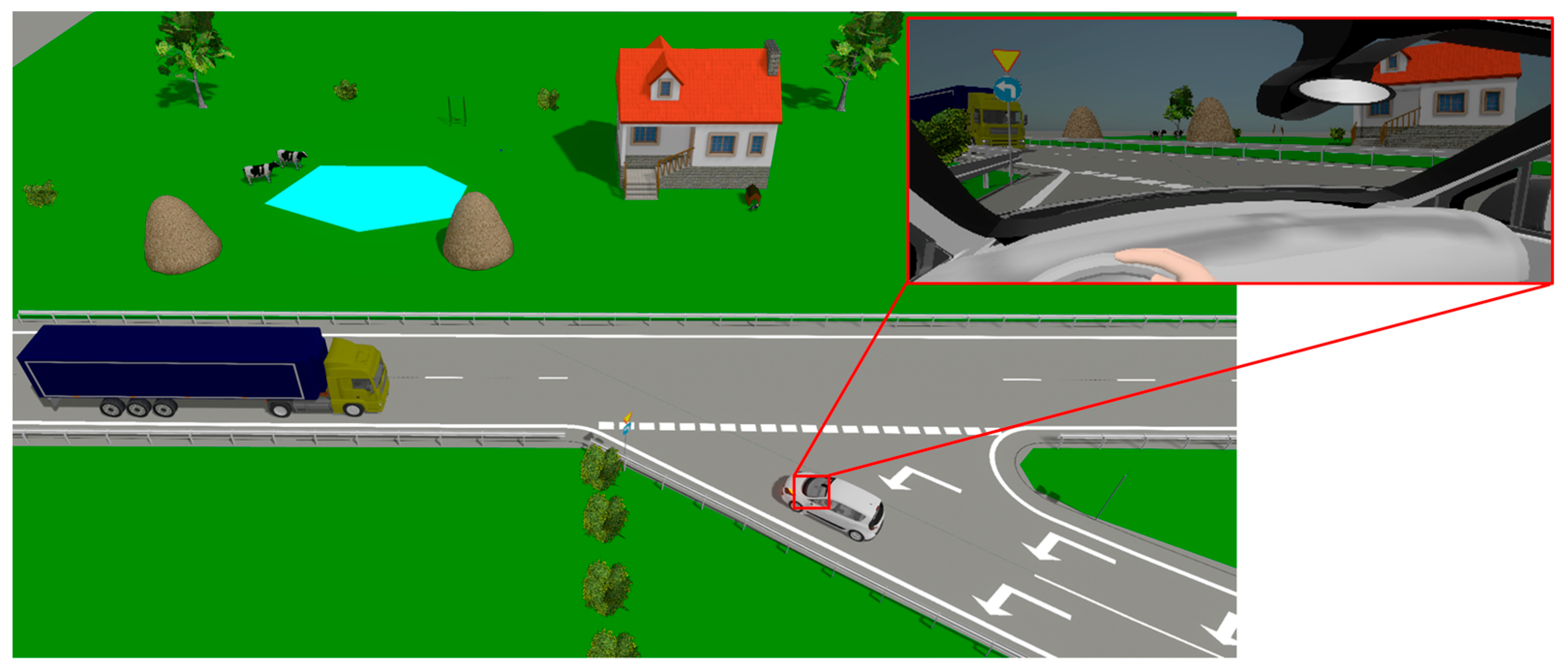
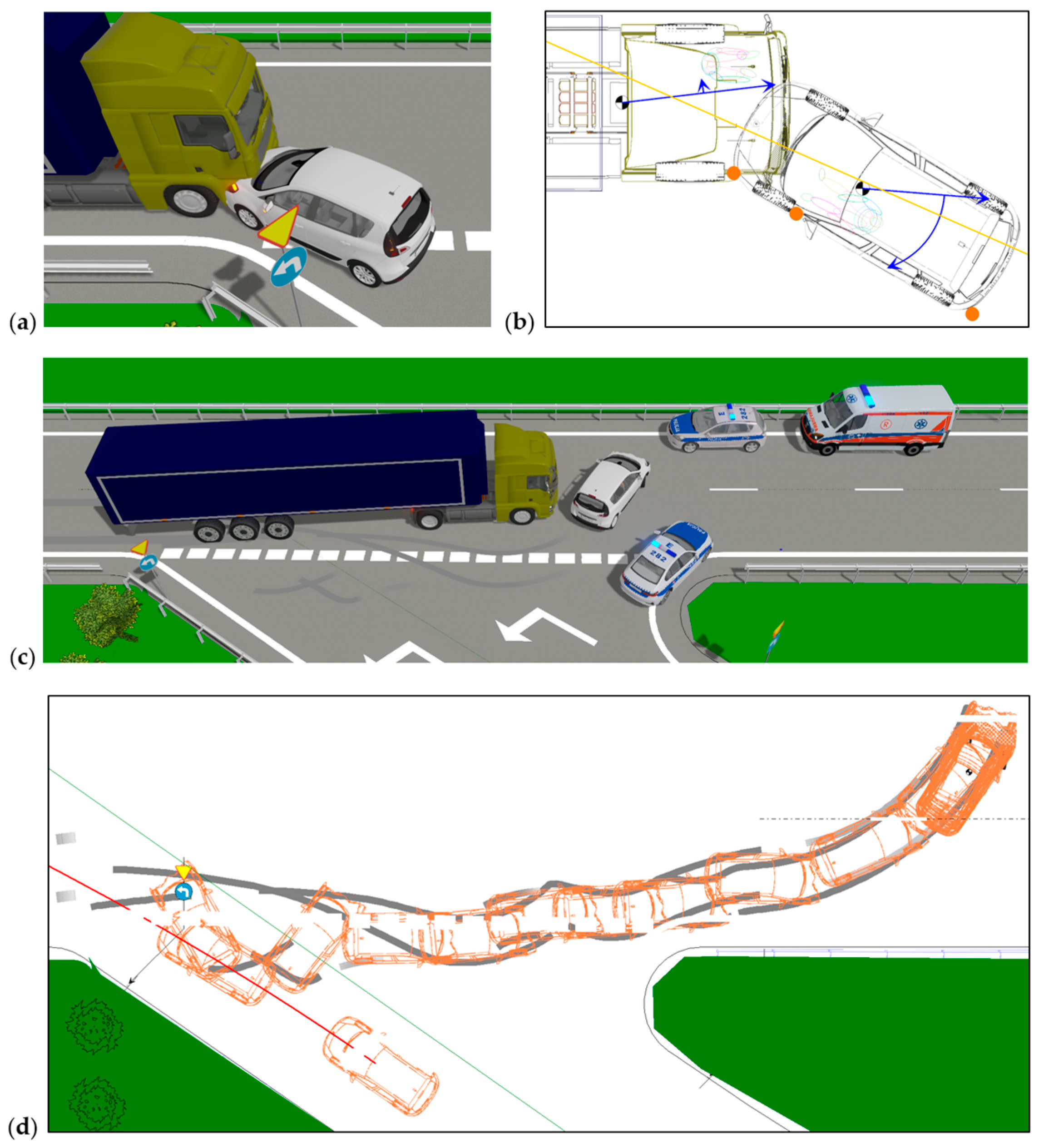
5.1. Post-Accident Vehicle Positions and Trajectories

This item presents the positions of the vehicles at the moment of collision as well as their post-accident locations after coming to a complete stop. Of particular interest is the post-accident behaviour of the car. In this case, the driver was unable to regain control of the vehicle, which came to a stop only after fully dissipating its kinetic energy. The truck driver, on the other hand, began braking after the collision and was able to bring the vehicle to a safe stop. Figure 6, Figure 7 and Figure 8 show the moment of the collision for truck speeds of 50 km/h, 60 km/h, and 70 km/h, as well as the post-accident positions of both vehicles and the post-accident trajectory of the car.

An analysis of the simulation results shows that, for all considered truck speeds, the nature of the collision remains similar. In each case, a frontal-side impact occurs, with only the collision parameters varying between simulations. The front section of the car sustained severe damage, which made the vehicle inoperable. In contrast, the truck suffered only minor damage and was able to continue its journey.

When the truck is travelling at 50 km/h, the collision occurs in such a way that the car strikes the truck with the car’s entire frontal section. As a result, the maximum overlapping volume of the vehicle silhouettes in this scenario is 0.59 m³. The simulation time from the moment the vehicles were in the positions shown in Figure 6 until the collision was 0.78 s, a very short interval for either driver to react. The collision caused a deformation depth of 518 mm in the car, affecting the entire front section of that vehicle, as illustrated in Figure 9a. The damage is therefore extensive and, as previously noted, disqualifies the vehicle from further independent operation. The truck sustained minor damage, with a maximum deformation depth of 186 mm.

In accident reconstruction analysis, one of the key parameters describing collision dynamics is the coefficient of restitution. It allows for a quantitative assessment of the extent to which a collision is elastic or plastic in nature. Knowledge of this parameter enables the calculation of vehicle speeds prior to the collision and the reconstruction of the course of the accident, both of which are crucial in judicial and expert analysis.

The coefficient of restitution determined by the V-SIM software for the case under analysis is 0.04. This indicates that the collision was almost completely inelastic. Nearly all kinetic energy along the collision axis was dissipated in the form of permanent plastic deformations, heat generation, vibrations and noise, as well as energy dispersion into secondary elements (e.g., fragments). Only 4% of the energy will be used for vehicle rebound motion, representing a very small amount of energy being recovered. The low value of the coefficient of restitution confirms a collision involving significant permanent deformations. Another piece of information that can be inferred from the obtained coefficient of restitution is that, following the collision, both vehicles likely moved in nearly the same direction and at similar speeds.

Another parameter used in accident reconstruction is the Equivalent Energy Speed (EES). This factor is applied in the analysis of vehicle body deformation and in the assessment of the course of the collision. The factor refers to the hypothetical speed at which a vehicle would have to impact a rigid, immovable barrier to produce the same level of structural deformation as is observed in the incident.

In the first analysed case, i.e., a collision with the truck travelling at 50 km/h, the following EES values were obtained: the truck—22.3 km/h, and the car—77.6 km/h. According to the above definition, these results indicate that the car sustained damage equivalent to impacting a rigid obstacle at nearly 78 km/h. The results for the truck can be interpreted in a similar way.

Based on these values, it is appropriate to conclude that the car absorbed significantly more deformation energy than the truck. This indicates that the car sustained significantly greater structural damage. Such a high EES value for the car suggests that the vehicle occupants suffered serious injuries. However, the actual severity of injuries to the travellers depends on the car’s crumple zone.

When the truck is travelling at 60 km/h, the collision occurs in a manner similar to the previous case. The car again strikes with its frontal section, but this time the impact occurs near the truck’s wheel. As a result, the maximum overlapping volume of the vehicle silhouettes is 0.56 m³. This value is slightly lower compared to the case where the truck speed was 50 km/h, which is due to the point of impact being located closer to the right corner of the truck’s side section. The collision caused a deformation depth of 635 mm in the car, affecting the entire front section of the vehicle, as illustrated in Figure 9b. The simulation time from the moment the vehicles were in the positions shown in Figure 5 until the moment of the collision was 0.71 s. As in the previous case, the truck sustained only minor damage, with a maximum deformation depth of 234 mm.

For the analysed scenario, the coefficient of restitution was again 0.04, indicating an almost completely inelastic collision. This value confirms the presence of significant plastic deformation in the car, rendering it inoperable.

The collision that occurred when the truck was travelling at 60 km/h resulted in increased EES values for both vehicles. The EES value for the car was 84.0 km/h, and for the truck—24.4 km/h. While the increase for the truck is relatively small, the car shows an increase of nearly 8 km/h compared to the previous case. Such an increase in the EES value may indicate more severe health consequences for the persons involved in the collision.

The final analysed case assumed a truck speed of 70 km/h. Given the vehicle’s full load and such a high speed, the consequences of the accident could be extremely severe.

The simulation showed that, in this scenario, the car struck the truck with the car right-front section. However, due to the truck’s higher speed, it had already travelled a greater distance from the assumed initial position, resulting in the car impacting the area near the truck’s wheel and cabin step. This configuration directly influenced the simulation results. In this case, the maximum overlapping volume of the vehicle silhouettes is 0.49 m³, indicating slightly less severe consequences of the accident for the car. Nevertheless, the vehicle still sustained major damage, as shown in Figure 9c, which renders it inoperable. A smaller maximum deformation depth of 605 mm was also recorded for the car. For the truck, however, this value increased to 420 mm.

In the analysed case, the coefficient of restitution also increased. The rise is insignificant as it is only by 0.03, and is 0.07 as well. This rise indicates that the impact partially involved the truck’s rubber components. Nevertheless, this value still corresponds to an almost completely inelastic collision and significant plastic deformation of the car body.

The Equivalent Energy Speed (EES) values obtained for the car were the same as in the case where the truck was travelling at 50 km/h, amounting to 77.6 km/h. For the truck, the EES is 39.9 km/h. Such an impact speed in the collision with the car will not result in major damage to the truck.

The post-impact trajectory of the car, however, varies considerably for each of the analysed truck speeds. First, the post-impact trajectory of the car after the collision with a truck travelling at 50 km/h will be analysed. The trajectory is graphically presented in Figure 6.

The impact force of 1483.1 kN, combined with the still-moving truck, caused the car to rotate clockwise and move along the main road parallel to the truck. The truck decelerated, preventing a secondary collision between the vehicles. The car then passed by the truck and collided with the safety barrier at an angle of 101.4° with a force of 238 kN. The accumulated kinetic energy of 0.3 kJ caused the car to rebound from the barrier and move backward until a complete stop. Figure 10 shows the post-accident speed variation of the car as a function of simulation time.

After the collision with the truck, the car rebounded and reversed at 35 km/h while simultaneously rotating. The car then continued along the main road at 20.77 km/h, gradually decelerating. After 4.41 s, the car collided with the safety barrier. At that moment, the car speed was 10.04 km/h and was further becoming lower. The rebound from the barrier occurred at 5.26 km/h. From that point, the car continued to decelerate until it came to a complete stop, which occurred at approximately 12 s during the simulation.

In the next simulation, the truck was travelling at 60 km/h. The post-accident trajectory of the car is presented in Figure 7. The impact force of the car against the truck in this case was 1473.5 kN. This value of the impact force is slightly lower than in the previously analysed case, which is due to the car striking partially against the truck’s tires. This contributed to a partial mitigation of the impact force.

After the collision, the car rebounded from the truck and almost immediately began to rotate clockwise. The car’s kinetic energy accumulated after the first rotation was 28.5 kJ. After completing the first rotation, the car started the second rotation. Upon reaching a rotation angle of 204.5 °, the car began reversing along the minor road (the one on which the car was originally located) in the right lane, maintaining this motion direction until kinetic energy was completely dissipated. The car moved very close to the road shoulder, and if safety barriers had been in place, a collision with them would have occurred. The car ultimately came to a stop near a ditch located beside the right shoulder of the road. Figure 11 shows the post-accident speed variation of the car as a function of simulation time.

After the collision with the truck, the car rebounded and almost immediately began its first rotation. At that moment, the car speed was 37.37 km/h. During the subsequent rotation, car speed decreased only slightly, reaching 34.70 km/h. After 2.28 s, the car began moving backward along the minor road. At that time, the car speed was 17.60 km/h. From that point onward, the car speed decreased linearly until the car came to a complete stop, which occurred at the thirteenth second of the simulation.

The last simulation assumed that the truck was travelling at 70 km/h. The post-accident trajectory of the car is presented in Figure 8. The impact force of the car against the truck in this case was 1335.5 kN. The force value for this simulation is the lowest of all. The explanation for this should be sought in the way in which the vehicles collided. The accident was of a frontal-side type. First, the car hit the truck with the car right side, rather than with the front part as in the previous cases. Second, the truck was moving at such a speed that it had partially entered the junction, causing the car to hit the front wheel of the truck with the car front. These two factors contributed to the reduced severity of the accident.

After the collision, the car makes a double rotation and strikes the safety barrier on the left side of the minor road with the car left rear part. The force with which the car hit the barrier was 170 kN, which resulted in the release of kinetic energy amounting to 17.3 kJ. The simulation time from the moment of the accident to the collision with the barrier was 2.4 s. After bouncing off the barrier, the car began to move forward across the road and then turned left. After this manoeuvre, the car continued moving forward in the right lane until its kinetic energy was completely dissipated. Figure 12 shows the post-accident speed variation of the car as a function of simulation time.

The traffic accident involving the vehicles occurred 0.66 s after the start of the simulation. As a result of the collision, the car lost its initial speed and began its first rotation clockwise at 37.944 km/h. This rotation ended after 1.15 s, at which point the next rotation commenced.

The accumulated kinetic energy caused the car to start a subsequent turn when its maximum linear speed was 35.892 km/h. Next, the car collided with a safety barrier at 19.620 km/h. This moment occurred 2.404 s after the start of the simulation. Such a speed caused an impact on the barrier with a force of 170 kN, corresponding to kinetic energy accumulation of 17.3 kJ. After rebounding from the barrier, the car moved at 6.264 km/h until coming to a complete stop in the eleventh second of the simulation.

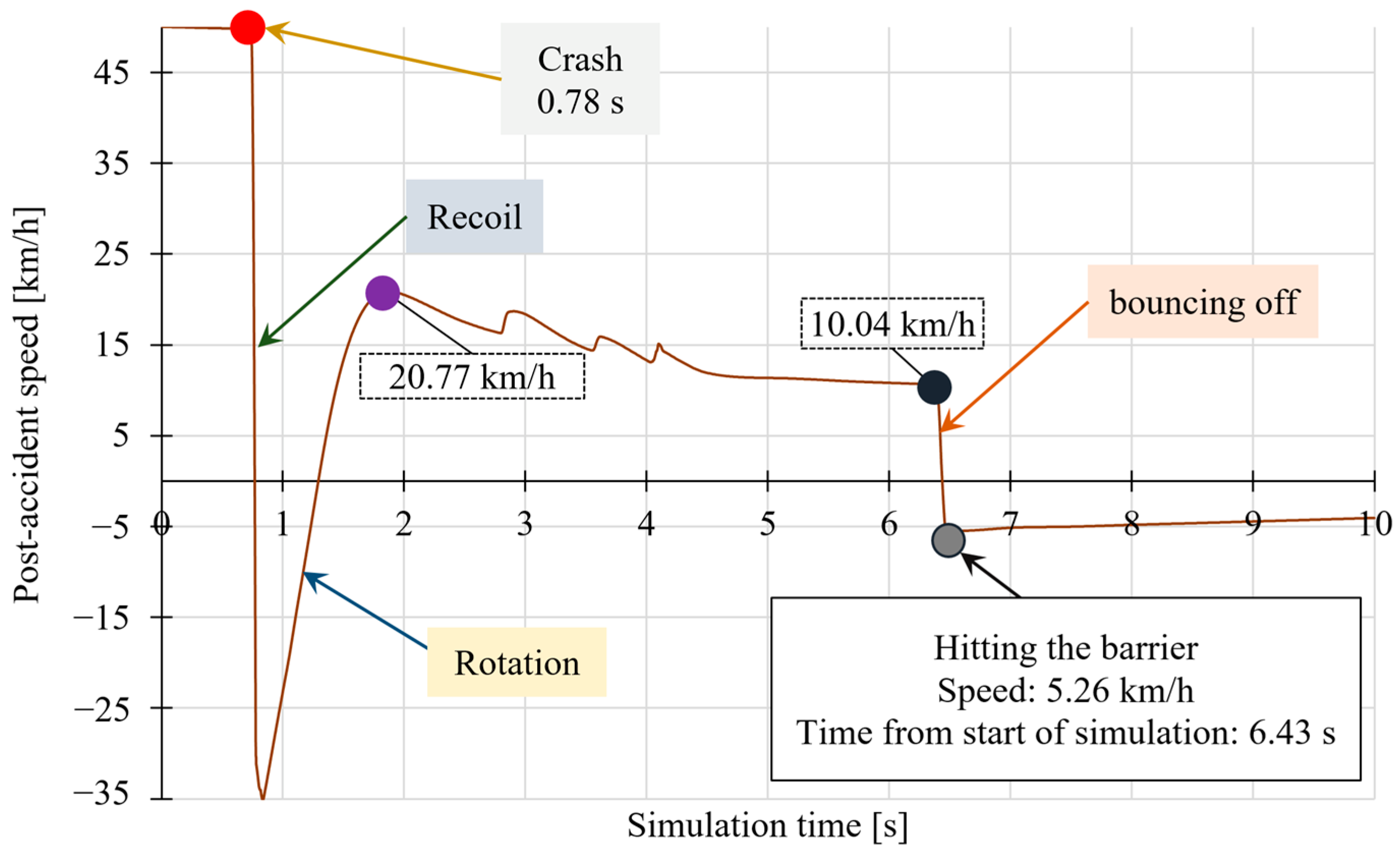
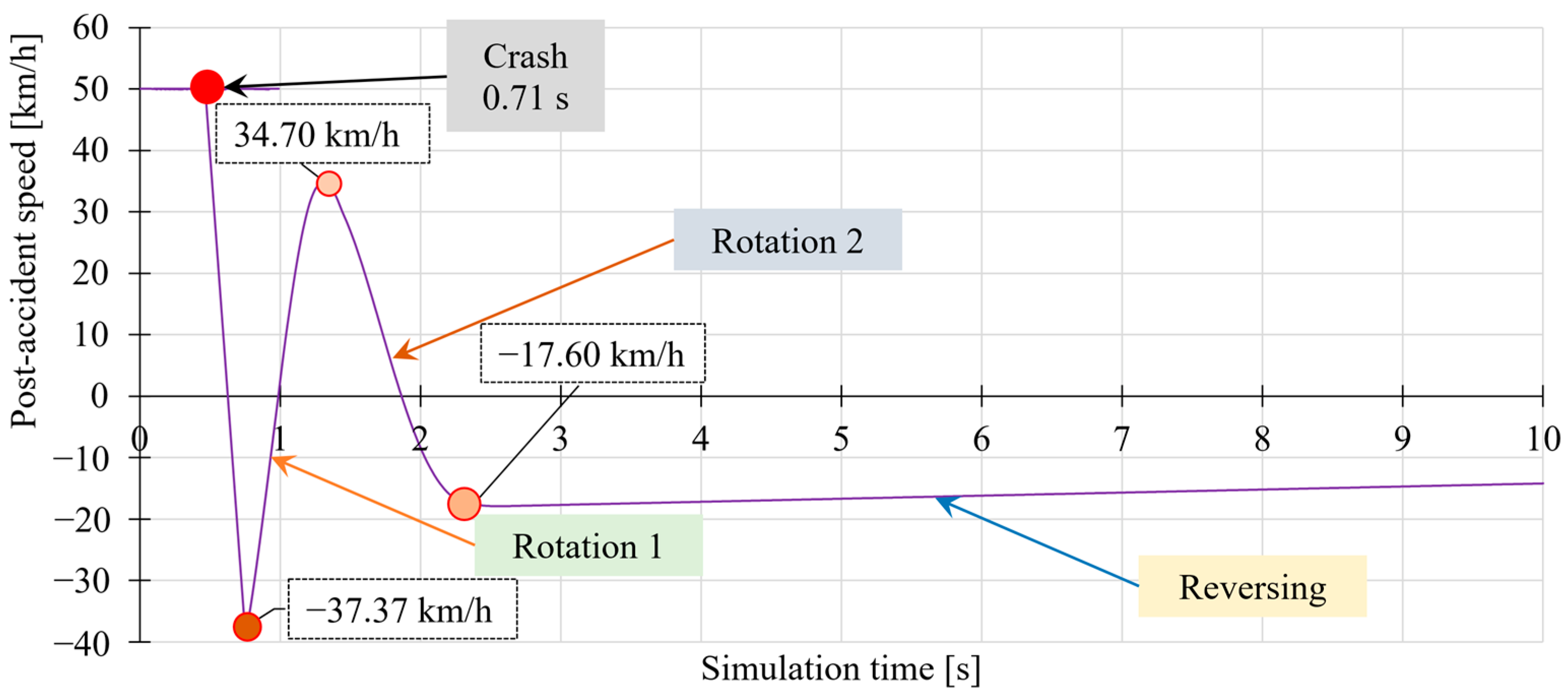
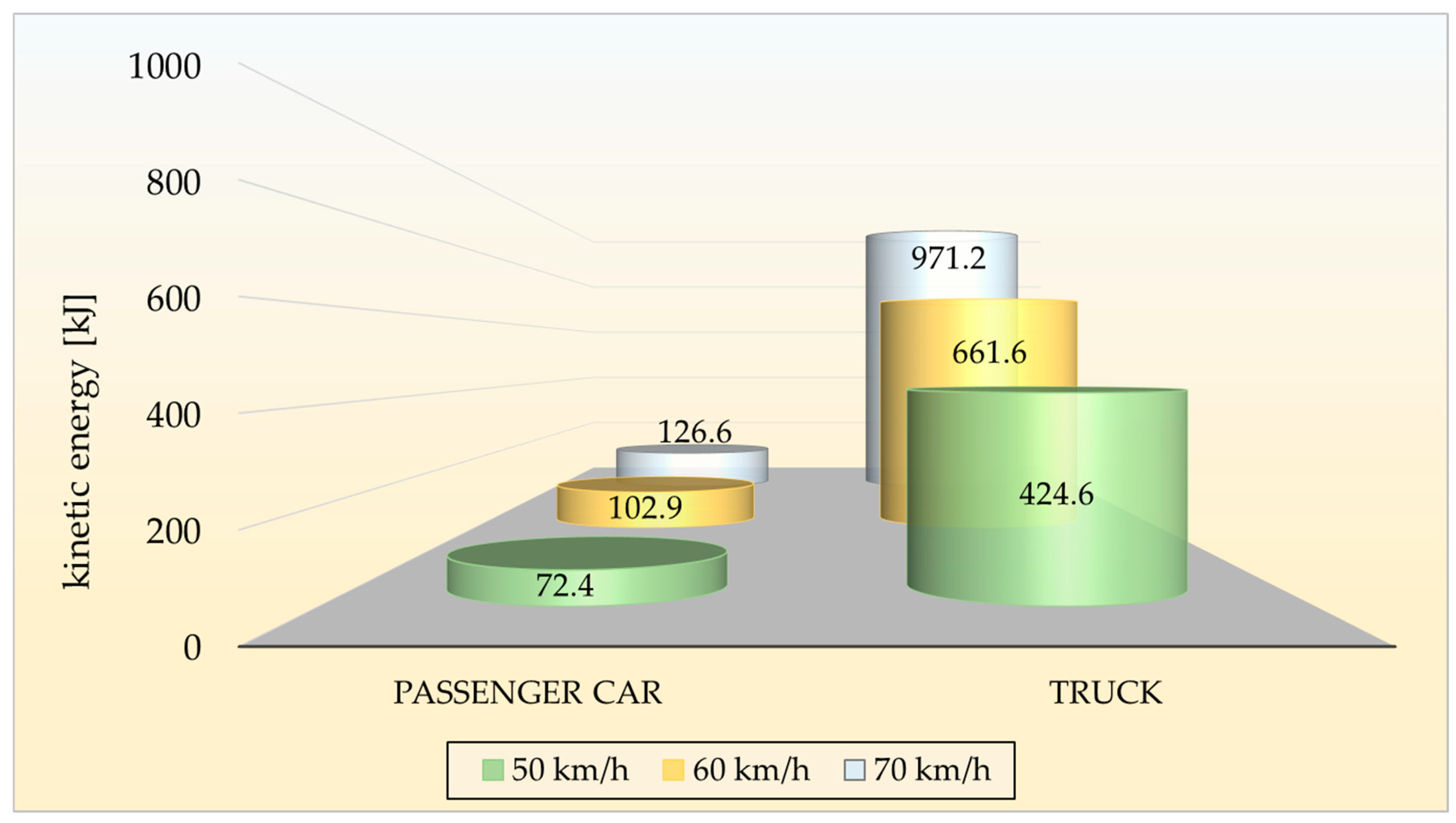
5.2. Kinetic Energy at the Moment of the Collision

During a vehicle collision, kinetic energy accumulated in the motion of the vehicles is rapidly transformed into other forms of energy—primarily the energy of plastic deformation of the structure, as well as thermal, acoustic, and vibrational energy. This phenomenon is one of the key aspects of passive safety analysis, as it determines the extent of vehicle body deformation and the magnitude of loads acting on the passengers.

According to the classical kinetic energy equation, kinetic energy increases proportionally to the square of speed. A twofold increase in speed therefore results in a fourfold increase in the energy that the vehicle’s structure and its components must dissipate during the collision. This non-linear relationship means that even a slight increase in pre-impact speed leads to a significant increase in impact energy and, consequently, a much greater potential for damage.

From an engineering standpoint, the analysis of the energy balance during a collision makes it possible not only to predict structural deformations but also to assess the efficiency of passive safety systems. Figure 13 presents the distribution of kinetic energy for both vehicles as a function of the truck’s speed.

An examination of the graph clearly confirms that, as the pre-impact speed increases, kinetic energy rises sharply and non-linearly, in accordance with the kinetic energy equation.

The data shown in the figure indicate that, for the car, the total increase in kinetic energy reaches approximately 75%, while for the truck this increase is close to 129%. Such a substantial difference in energy results in a significant increase in the load on the car structure, which—due to its considerably lower mass compared with the truck—absorbs the majority of plastic deformation energy.

It is appropriate to note that although the truck has higher total kinetic energy because of its mass, the truck’s structural deformation remains relatively limited. This energy is transferred to the lighter car, which in this system acts as the primary impact energy-absorbing element. This results in a considerable increase in the magnitude of the car body frontal crumple zone deformation and an increase in the overloads acting on the passengers.

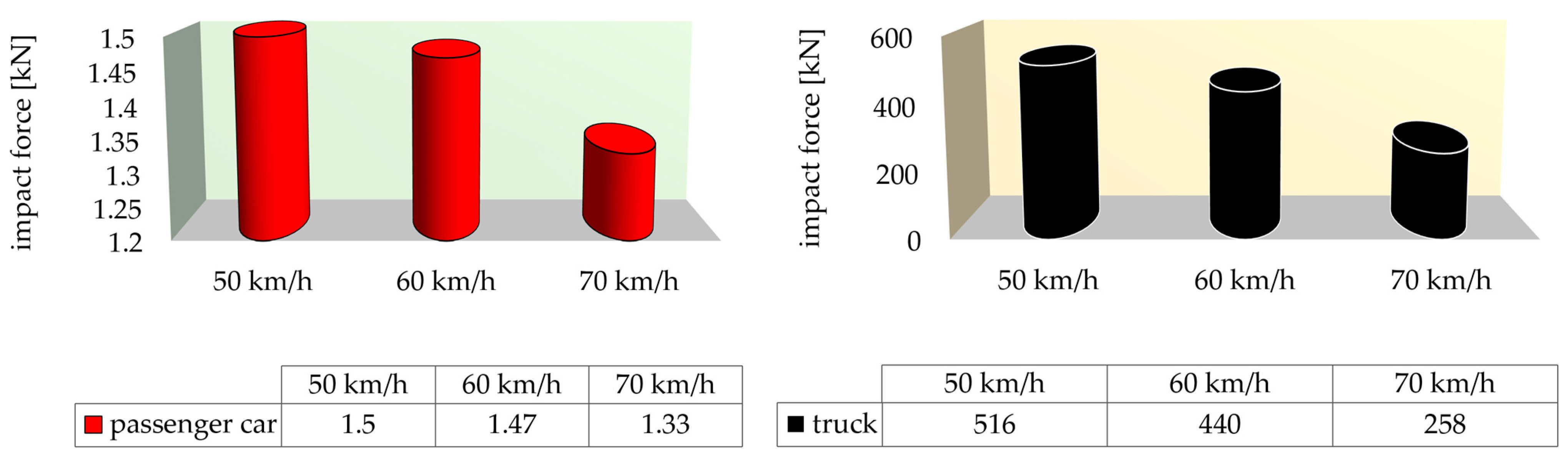
5.3. Resultant Force

During a vehicle collision, the interaction force at the moment of the collision is one of the key parameters describing the dynamics of the incident and its consequences. The magnitude of this force depends on the kinetic energy of the vehicles at the moment of contact, their masses, speed, and the characteristics of the vehicles’ structural deformation. The greater the kinetic energy at the moment of the collision, the higher the force acting at the contact point, and the greater the overloads transmitted to the load-bearing structure of the vehicle and its passengers.

In the context of the previous energy analyses, it can be stated that kinetic energy stored in the vehicle’s motion prior to the collision constitutes the source of work that is transformed, upon collision, into the force responsible for structural deformation. The magnitude of this force therefore depends directly on the degree to which kinetic energy is reduced during the braking phase. In the case of a malfunctioning braking system, where the vehicle fails to decelerate before impact, kinetic energy remains higher, and consequently the value of the force at the moment of contact increases.

Figure 14 presents the values of the force acting on the vehicles at the moment of the collision.

An analysis of the results indicates a decreasing trend in force values as the truck speed increases. Although this may seem contradictory to rising kinetic energy, the phenomenon is explained by the change in the location at which the car strikes the truck.

At lower speeds, the car hits the lower section of the truck’s frame rail, which is a structurally very rigid component. In such a case, the kinetic energy of the car is absorbed over a short time interval, generating higher impact force values. At 70 km/h, however, the trajectory of the car changes, and the impact occurs partially against the truck’s wheel, which is an elastic element capable of absorbing part of the energy through tire compression and suspension deformation. Longer contact between the vehicles and the lower stiffness of the impact location result in a reduced peak force value. This means that a larger portion of kinetic energy is dissipated over a longer time and distributed across a wider deformation zone. Additionally, the significant mass difference between the vehicles causes the truck to absorb only a fraction of the impulse, while most of the energy is taken up by the deformation of the car.

A comparison of both graphs shows that although the forces acting on the truck are several hundred times higher than those acting on the car, it is the lighter vehicle that experiences substantially greater deformation and acceleration. This outcome stems from the mass disparity between the vehicles as well as the specific nature of the contact during the collision.

5.4. Acceleration Acting on the Car

As part of the simulations, the accelerations acting on the car during frontal-side collisions with a truck travelling at different speeds were measured. The recorded acceleration values inside the car cabin are as follows:

•

for a truck speed of 50 km/h—0.64 G,

•

for a truck speed of 60 km/h—0.72 G,

•

for a truck speed of 70 km/h—0.50 G.

From a biomechanical perspective, the obtained results indicate relatively low dynamic loads acting on the passenger’s body.

An acceleration of 0.64 G falls within the range of a minor overload, which, according to [25], typically is not a cause of serious musculoskeletal injuries or internal organ damage. At a speed of 60 km/h, a slight increase in acceleration to 0.72 G is noted. Although this theoretically increases the risk of overload-related injuries, the values remain within human tolerance limits for short-duration forces acting along the human body’s longitudinal axis. In this type of collision, the presence of a side airbag and a properly designed headrest plays an important role, as both systems help limit head and neck motion, thereby reducing the risk of injury.

The decrease in acceleration to 0.50 G at the higher truck speed (70 km/h) may seem paradoxical; however, that decrease can be attributed to greater energy absorption through vehicle body deformation and to the dispersion of forces in the lateral and vertical directions. From an injury-risk perspective, an acceleration of 0.50 G is also classified as low. Typical injuries sustained by passengers at this level of acceleration are limited to minor soft-tissue trauma, bruising, or small contusions of the extremities, particularly when the seatbelt is not optimally positioned or when contact occurs with side vehicle body components.

6. Summary and Conclusions

The simulation studies enabled a comprehensive analysis of the influence of braking system damage on the course and consequences of a road incident involving a car and a truck. The results allowed for the assessment of the physical phenomena accompanying the collision, including the distribution of kinetic energy, impact forces, and the accelerations acting on the vehicles.

Braking system components, especially brake discs and pads, operate under extreme thermomechanical conditions, leading to fatigue phenomena, thermal cracking, and to the degradation of the friction material. Diagnostic observations confirmed the presence of real cracks in brake discs of vehicles operated in urban conditions, demonstrating the need for periodical inspection of the brakes’ technical condition.

The simulation results demonstrated that the collisions progressed in an almost completely inelastic manner, with the coefficient of restitution ranging from 0.04 to 0.07, which means that more than 90% of kinetic energy was dissipated through permanent deformation and heat. The car, being significantly lighter, absorbed the majority of that energy, which translated into a front-end deformation depth of up to 0.6 m.

The analysis of the acceleration acting on the car showed values between 0.50 and 0.72 G, falling within the range of low overloads that do not cause severe injuries to passengers. The decrease in impact force and acceleration at 70 km/h confirms that part of energy was dissipated within the elastic elements of the truck’s wheel system, which mitigated the peak force and overloads.

The simulations confirmed that braking system damage significantly increases the risk of a severe collision by reducing reaction time and preventing the effective reduction of kinetic energy prior to the collision. Even under favourable road conditions, a malfunctioning braking system prevents the car from avoiding a collision with the truck, with the car structure absorbing nearly all of the contact energy.

These findings are highly relevant both for the design of braking systems and friction materials with increased thermal resistance, as well as for preventive diagnostics. The results confirm the importance of implementing modern systems for monitoring brake component wear and educating drivers on recognizing the symptoms of partial brake malfunction.

The aim of this study was to analyse the influence of braking system damage on the course of a road collision involving a car and a truck, and to evaluate changes in kinetic energy, impact force, and acceleration at the moment of the collision. The results were obtained using computer simulations in the V-SIM 7.0 environment for three different truck speeds: 50, 60 and 70 km/h. The analysis allowed the following detailed conclusions to be drawn:

•

As the truck’s speed increased from 50 km/h to 70 km/h, the total kinetic energy of the system nearly doubled.

•

The kinetic energy of the car constituted a small percentage of the total energy of the system (below 15%); however, that vehicle absorbed over 80% of deformation energy, resulting in a front-end deformation of approximately 0.6 m.

•

An increase in speed by 20 km/h led to a rise in kinetic energy by approximately 96%, indicating a sharp increase in energy dissipated at the moment of the collision.

•

The coefficient of restitution of the collision ranged from 0.04 to 0.07, indicating an almost completely plastic nature of the collision. This means that nearly all of the kinetic energy was transformed into deformation and heat energy, with only a marginal portion recovered after rebounding.

•

At higher speeds, a decrease in acceleration values was observed, which confirms a “softer” course of the collision due to impact with an elastic item (the truck wheel).

•

The simulation results can serve as a basis for further research on modelling energy losses in collisions involving different vehicle geometries and structural materials.