A Hybrid Graph-Coloring and Metaheuristic Framework for Resource Allocation in Dynamic E-Health Wireless Sensor Networks

Abstract

Wireless sensor networks (WSNs) are a key enabling technology for modern e-Health applications. However, their deployment in clinical environments faces critical challenges due to dynamic network topologies, signal interference, and stringent energy constraints. Static resource allocation schemes often prove inadequate in these mission-critical settings, leading to communication failures that can compromise data integrity and patient safety. This paper proposes a novel hybrid framework for intelligent, dynamic resource allocation that addresses these challenges. The framework combines classical graph-coloring heuristics—Greedy and Recursive Largest First (RLF) for efficient initial channel assignment with the adaptive power of metaheuristics, specifically Simulated Annealing and Genetic Algorithms, for localized refinement. Unlike conventional approaches that require costly, network-wide reconfigurations, our method performs targeted adaptations only in interference-affected regions, thereby optimizing the trade-off between network reliability and energy efficiency. Comprehensive simulations modeled on dynamic, hospital-scale WSNs demonstrate the effectiveness of various hybrid strategies. Notably, our results demonstrate that a hybrid strategy using a Genetic Algorithm can most effectively minimize interference and ensure high data reliability, validating the framework as a scalable and resilient solution. These results validate the proposed framework as a scalable, energy-aware solution for resilient, real-time healthcare telecommunication infrastructures.

1. Introduction

Wireless sensor networks (WSNs) have become a fundamental technology in modern e-Health applications, enabling real-time monitoring of patients through wearable devices, bedside sensors, and ambient hospital systems. The paradigm of e-Health is rapidly transforming healthcare delivery, with recent market analyses projecting the global telehealth market to exceed USD 280 billion by 2025, driven by an aging global population and the rising prevalence of chronic diseases requiring continuous oversight. These networks form the backbone of a multi-tiered medical data infrastructure. At the first tier, wearable and ambient sensors such as ECG monitors, SpO2 oximeters, and glucose meters collect raw physiological data directly from the patient. These data are then transmitted to a second-tier personal server, often a smartphone or a dedicated bedside aggregator, before being relayed to third-tier cloud servers at a medical facility for analysis by healthcare professionals [1,2]. This architecture supports continuous data collection and wireless transmission of vital health information, facilitating remote patient monitoring, chronic disease management, and timely emergency responses.

However, the clinical environments where these systems are deployed are highly dynamic. In settings like hospitals or assisted living facilities, frequent topology changes are the norm, caused by patient and staff mobility, the repositioning of medical equipment, and fluctuating environmental factors that affect radio frequency propagation [3]. These dynamics frequently disrupt network communication, causing wireless interference that corrupts data packets and leads to communication failures. The consequences of such failures in a clinical context are severe. A single lost data packet from a cardiac monitor is not merely a technical glitch; it could represent a missed arrhythmia event, delaying a life-saving intervention. Similarly, intermittent connectivity for a continuous glucose monitor could mask a dangerous hypoglycemic episode.

The “hidden cost” of this unreliability extends beyond the immediate clinical risk. Packet retransmissions, the primary mechanism to combat data loss from interference, elevate energy usage significantly, which is a critical issue, as energy is a precious and finite resource in battery-powered sensor nodes. This directly compromises the operational lifetime of monitoring systems, necessitating more frequent battery replacements and increasing maintenance overhead [4]. Furthermore, the act of retransmitting packets increases network latency and congestion. This is particularly perilous for e-Health applications that depend on sub-200 millisecond response times for critical alerts, such as automated fall detection or cardiac distress alarms [5,6]. The limited computational capacity of individual sensor nodes further compounds the problem, restricting their ability to rapidly adapt to network changes.

The technical heart of this challenge lies in the efficient allocation of wireless channels to minimize interference. This resource allocation problem can be formally modeled as a graph-coloring problem, where sensor nodes are vertices, potential interference links between nodes are edges, and the available wireless channels are colors. The objective is to assign distinct colors (channels) to any two adjacent vertices (interfering nodes) while minimizing the total number of colors used. Determining the minimum number of colors required (the chromatic number) is a well-known NP-hard problem, making it computationally infeasible to find a perfect solution for large networks in real-time. This necessitates the use of advanced heuristic and metaheuristic methods [7,8].

Classic graph-coloring heuristics, such as the Greedy algorithm and Recursive Largest First (RLF), offer fast and straightforward methods for an initial channel assignment. However, their static nature renders them ineffective in the face of constant network changes. They require a complete and energy-intensive re-computation for every significant topology change, making them unsuitable for real-time, dynamic WSN environments [9,10].

To enhance adaptability, this research introduces a hybrid framework that integrates these fast graph-coloring heuristics with adaptive metaheuristics, namely, Simulated Annealing (SA) and Genetic Algorithms (GA) [11,12]. SA introduces a stochastic, “temperature-guided” exploration of the solution space, allowing it to escape local minima, while GAs evolve a population of potential channel assignments through processes of crossover and mutation, guiding the overall solution toward optimal interference reduction.

In this proposed framework, the initial channel assignment is performed using either the Greedy or RLF heuristic to establish a strong baseline configuration. Subsequently, dynamic adjustments triggered by topology changes detected by a centralized base station employ SA or GA for localized recoloring. This targeted adaptation avoids the need for a full, network-wide recalculation of the channel map. By combining these strategies, the system aims to strike a crucial balance between initial efficiency, adaptive robustness, and energy conservation, all of which are essential for the demanding conditions of densely populated and highly mobile e-Health environments [13].

The framework’s performance is evaluated through a comprehensive, simulation-driven approach that models a 50 × 50 m hospital ward with 100 sensor nodes, 20% of which are mobile. Key performance indicators including energy consumption, interference rate, packet loss, and adaptation latency are meticulously tracked over multiple mobility events to assess the efficacy of each algorithmic combination. This methodology ensures the practical relevance of the findings by reflecting the conditions of real-world e-Health deployments.

The primary contribution of this work is not the invention of the component algorithms (Greedy, RLF, SA, GA), which are well-established. Rather, the novelty lies in the design, implementation, and rigorous evaluation of a two-layer hybrid framework that leverages these components for localized, energy-efficient adaptation. Unlike approaches that require costly, network-wide reconfigurations, our model initiates adaptation only for the specific nodes affected by a mobility event. This paper fills a critical gap by providing a direct, comprehensive comparison of multiple hybrid strategies (e.g., GA_RLF vs. SA_Greedy) under a realistic, SINR-based interference model, assessing their trade-offs across a balanced set of performance metrics.

2. Literature Review

This section provides a comprehensive review of the existing literature pertinent to resource allocation in dynamic wireless sensor networks (WSNs), with a specific focus on applications in e-Health. It begins by examining the fundamental challenges posed by dynamic network environments and establishes graph coloring as a classical approach to interference management. It then delves into the application of various metaheuristic algorithms for WSN optimization, offers a comparative analysis, and justifies the selection of Simulated Annealing (SA) and Genetic Algorithms (GA) for this research. Additionally, it discusses the importance of quality of service (QoS) and scalability in healthcare contexts, identifies critical gaps in the current body of research, and situates the contribution of this research within the broader academic landscape.

The successful deployment of WSNs in healthcare settings is contingent upon their ability to operate reliably in environments characterized by constant change. The authors of [14] highlight that node mobility, whether from ambulatory patients or mobile medical equipment, is a primary source of network instability. Their work surveys various bio-inspired algorithms for managing dynamic resource allocation, concluding that adaptability is the most critical feature for maintaining network performance. Similarly, the authors of [3] provide a thorough survey on mobility management protocols in Wireless Body Area Networks (WBANs), a subset of WSNs. They categorize mobility into predictable (e.g., a patient walking down a hallway) and unpredictable (e.g., erratic movements during a medical emergency) patterns, emphasizing that MAC protocols must be robust enough to handle both without significant degradation in data delivery. A key takeaway from their analysis is that frequent topology changes lead to a cascade of problems, including route invalidation, increased control overhead, and a surge in co-channel interference.

The problem of assigning wireless channels to nodes to minimize interference is canonically modeled as a graph-coloring problem. The foundational work by [8] provides a comprehensive review of this technique’s application in both wired and wireless networks. They establish the formal equivalence between channel assignment and graph coloring, where nodes are vertices, an interference link is an edge, and channels are colors. Their review confirms that graph coloring provides an elegant and mathematically rigorous framework for abstracting this complex engineering problem. While exact solutions are NP-hard, they note the widespread use and effectiveness of heuristics.

Building on this, the authors of [10] have applied graph coloring to real-world WiFi scenarios, demonstrating tangible performance improvements. Their approach combined graph contraction techniques with an SA-based coloring algorithm, which resulted in a measurable increase in network throughput and a reduction in interference. However, their work primarily focused on semi-static WiFi networks and did not fully address the continuous, small-scale mobility found in dense WSNs. Furthermore, the authors of [9] explore energy-aware scheduling in the Internet of Medical Things (IoMT) using coloring heuristics. Their findings indicate that while heuristics like Greedy and RLF are computationally efficient for initial setup, their performance degrades sharply in dynamic scenarios, necessitating frequent, energy-intensive network-wide recolorings, thus motivating the need for more adaptive solutions.

Given the limitations of static heuristics, researchers have increasingly turned to metaheuristics high-level problem-independent algorithmic frameworks that provide a set of guidelines or strategies to develop heuristic optimization algorithms. Simulated Annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Its strength lies in its ability to escape local optima by accepting worse solutions with a probability that decreases over time, governed by a “temperature” parameter. In the context of WSNs, the authors of [15] proposed an efficient hybrid SA-DSATUR method. Their model used SA to refine the channel assignments produced by the DSATUR heuristic, achieving a better balance between the number of channels used and the computational overhead. Their results showed a significant reduction in conflicts compared to DSATUR alone. The primary limitation noted was the sensitivity of SA to its cooling schedule, a schedule that is too fast may cause the algorithm to converge prematurely to a suboptimal solution. Furthermore, Genetic Algorithms (GAs) are a class of evolutionary algorithms that use principles of natural selection to find optimal solutions. They operate on a population of potential solutions, applying operators like selection, crossover, and mutation. The authors in [16] provide a comprehensive survey on the use of GAs in wireless networks, highlighting their flexibility in handling dynamic and multi-objective optimization problems, such as balancing energy consumption and network coverage. More recently, the authors of [17] developed a GA-based self-healing mechanism for WSNs in mission-critical healthcare. Their GA dynamically re-routes traffic and re-establishes connectivity in response to node failures, demonstrating the algorithm’s robustness. A key challenge with GAs is parameter tuning (e.g., population size, mutation rate), which can significantly impact performance and convergence speed.

While this research work focuses on SA and GAs, other nature-inspired algorithms are prominent in WSN literature. Particle Swarm Optimization (PSO) is a population-based stochastic optimization technique inspired by the social behavior of bird flocking or fish schooling. Each “particle” in the swarm adjusts its trajectory based on its own best-known position and the best-known position of the entire swarm. PSO is known for its fast convergence but can sometimes converge prematurely to local optima in highly complex, multi-modal search spaces. Additionally, Ant Colony Optimization (ACO) is inspired by the foraging behavior of ants, who deposit pheromones on the ground to mark favorable paths for the colony. It is particularly well-suited for finding optimal paths in graphs and has been extensively applied to routing problems in WSNs. However, for a channel assignment problem, which is less about pathfinding and more about constraint satisfaction, the mapping to an ACO framework is less direct than with GAs or SA. For the dynamic channel assignment problem, SA and GAs were chosen for specific reasons. Simulated Annealing was selected for its simplicity and its proven ability to perform effective local searches. In our hybrid model, where a good solution from a heuristic is already in place, SA is ideally suited to explore the immediate neighborhood of that solution for incremental improvements. Genetic Algorithms were chosen for their strength in parallel exploration of the solution space. When a localized adaptation is needed, the GA can maintain a diverse population of potential new channel configurations for the affected nodes, increasing the likelihood of finding a robust solution that does not just solve the immediate conflict but is also resilient to future changes. In contrast, PSO’s rapid convergence was seen as a potential drawback, while ACO was deemed a less natural fit for a constraint-based assignment problem compared to a routing problem.

The literature strongly suggests that hybrid models often outperform standalone algorithms. The authors of [18] demonstrated this by using SA as part of a hybrid model for cluster head selection in WSNs. By using SA to refine the clustering decisions, they significantly extended network lifetime compared to traditional hierarchical protocols. The authors in [19] explicitly combined SA and GAs for dynamic channel allocation, showing that the hybrid approach could adapt to heterogeneous network conditions more effectively than either algorithm alone. The core insight from this body of work is that hybridization allows a system to leverage the complementary strengths of different algorithms, for instance, using a fast heuristic for an initial solution and a more computationally intensive metaheuristic for refinement. This is the central premise of the framework proposed in this research work.

Another important aspect is related to quality of services (QoS) in e-Health where WSN refers to the network’s ability to provide a guaranteed level of performance, which is critical when dealing with medical data [20,21,22,23,24,25]. Key QoS metrics include the following:

• Reliability: The guarantee that data packets are delivered successfully. High interference directly degrades reliability.
• Timeliness (Latency): The time taken for a packet to travel from sensor to sink. As noted by [26], some critical medical alerts require latency below 200 ms.
• Data Accuracy: Ensuring the delivered data is not corrupted.

Any resource allocation strategy must be evaluated against these QoS requirements. A low-energy solution is useless if it cannot deliver data reliably and in a timely manner.

Scalability is another critical concern. As hospitals and healthcare facilities deploy more sensor devices, the network size can grow to hundreds or even thousands of nodes. A resource allocation strategy that works for 20 nodes may fail completely at a scale of 200. This is where the concept of localized adaptation becomes essential. Strategies that require a global, network-wide recalculation of channels for every minor change will not scale. They create a massive communication overhead and drain network energy. The research gap in developing scalable, localized adaptation mechanisms is a key area this research work aims to address.

Based on this comprehensive review, several critical research gaps have been identified:

• Lack of Focus on Interference-Centric Hybrid Models: While hybrid models exist, they often focus on energy conservation in the context of routing or clustering. Few studies have developed hybrid models specifically targeting the dynamic channel assignment problem using a combination of classical graph-coloring heuristics and adaptive metaheuristics.
• Predominance of Full-Network Adaptation: Most existing models, such as those focusing on initial network setup or complete self-healing, resort to a full reassignment of resources when faced with a topology change. In contrast, the lightweight, localized recoloring proposed by our framework—where only the nodes directly affected by a change are adapted—is significantly underexplored and offers a more scalable solution.
• Limited Comparative Analysis: There is a scarcity of comprehensive, side-by-side comparisons of different hybrid combinations (e.g., Greedy + SA vs. RLF + GA) evaluated under realistic, dynamic mobility patterns and assessed across a balanced set of metrics including conflict rate, energy, latency, and packet loss.

This literature review confirms that managing interference in dynamic e-Health WSNs is a complex, multi-faceted challenge. Graph coloring provides a solid theoretical foundation, while metaheuristics like SA and GAs offer powerful tools for optimization. However, existing research has not adequately addressed the need for a scalable, energy-efficient, and low-latency solution that can adapt to the continuous mobility inherent in clinical environments. This research positions itself to fill these identified gaps by proposing and evaluating a novel hybrid framework. By combining the speed of RLF and Greedy coloring for initial setup with the intelligent, localized adaptation of SA and GAs, this research aims to provide a practical and robust solution that explicitly balances the competing demands of performance, energy, and latency, thereby advancing the development of reliable communication infrastructures for next-generation e-Health systems.

3. Methodology

This section details the systematic methodology employed to design, implement, and evaluate the proposed hybrid framework for dynamic resource allocation. The approach is rooted in a robust, custom-built simulation environment that allows for the controlled comparison of various algorithmic strategies under realistic e-Health operational conditions. The methodology is presented in several parts: first, an overview of the hybrid simulation framework and its architecture; second, a detailed specification and justification of the simulation parameters and models; third, an in-depth explanation of the graph-coloring and metaheuristic algorithms implemented; fourth, a discussion of the software design principles used; and finally, a definition of the performance metrics used for evaluation.

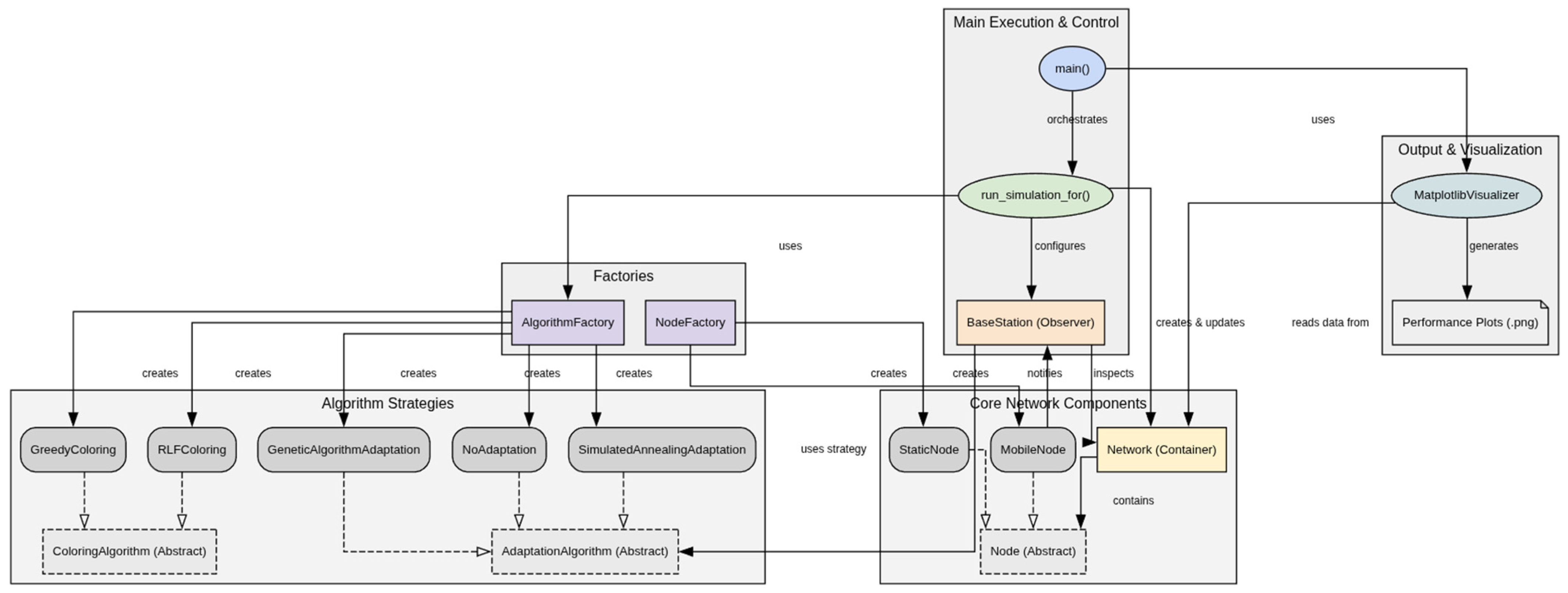
3.1. Hybrid Simulation Framework Architecture

A modular, object-oriented simulation framework was developed in Python 3.12.7 to serve as the testbed for this research. The architecture is designed for extensibility and clarity, comprising several core components whose interactions are governed by established software design patterns.

• Sensor Nodes (Node classes): Represent the fundamental network entities. An abstract base class Node defines common attributes like node_id, position, and energy. This is extended by two concrete classes: StaticNode and MobileNode, reflecting the different device types in a hospital setting. This class hierarchy allows for polymorphism in the simulation logic.
• Network (Network class): Acts as a container for all nodes and serves as the environment model. It manages the spatial relationships between nodes, computes interference graphs, and maintains a history of performance metrics for later analysis.
• Base Station (BaseStation class): Functions as the centralized controller and intelligence of the network. It implements the Observer design pattern, “listening” for mobility events from MobileNode instances. Upon receiving a notification of a topology change, it assesses the new interference landscape and triggers the appropriate adaptation algorithm. This decouples the nodes’ movement from the adaptation logic, promoting modularity.
• Algorithm Modules (Algorithm classes): The core logic for channel assignment is encapsulated using the Strategy design pattern. Abstract base classes, ColoringAlgorithm and AdaptationAlgorithm, define a common interface for initial coloring and dynamic adaptation, respectively. Concrete strategy classes (e.g., GreedyColoring, RLFColoring, SimulatedAnnealingAdaptation, GeneticAlgorithmAdaptation) implement this interface. This design allows the simulation to be easily configured with any combination of initial coloring and adaptation algorithms without changing the core simulation logic.
• Metric Recorder: Integrated within the Network class, this component logs key performance indicators (KPIs) at each discrete simulation step. Time-series data for each metric is stored, facilitating the generation of comparative performance graphs.

This architecture ensures that the simulation is both a faithful representation of a WSN and a flexible research tool for algorithmic evaluation, see Figure 1.

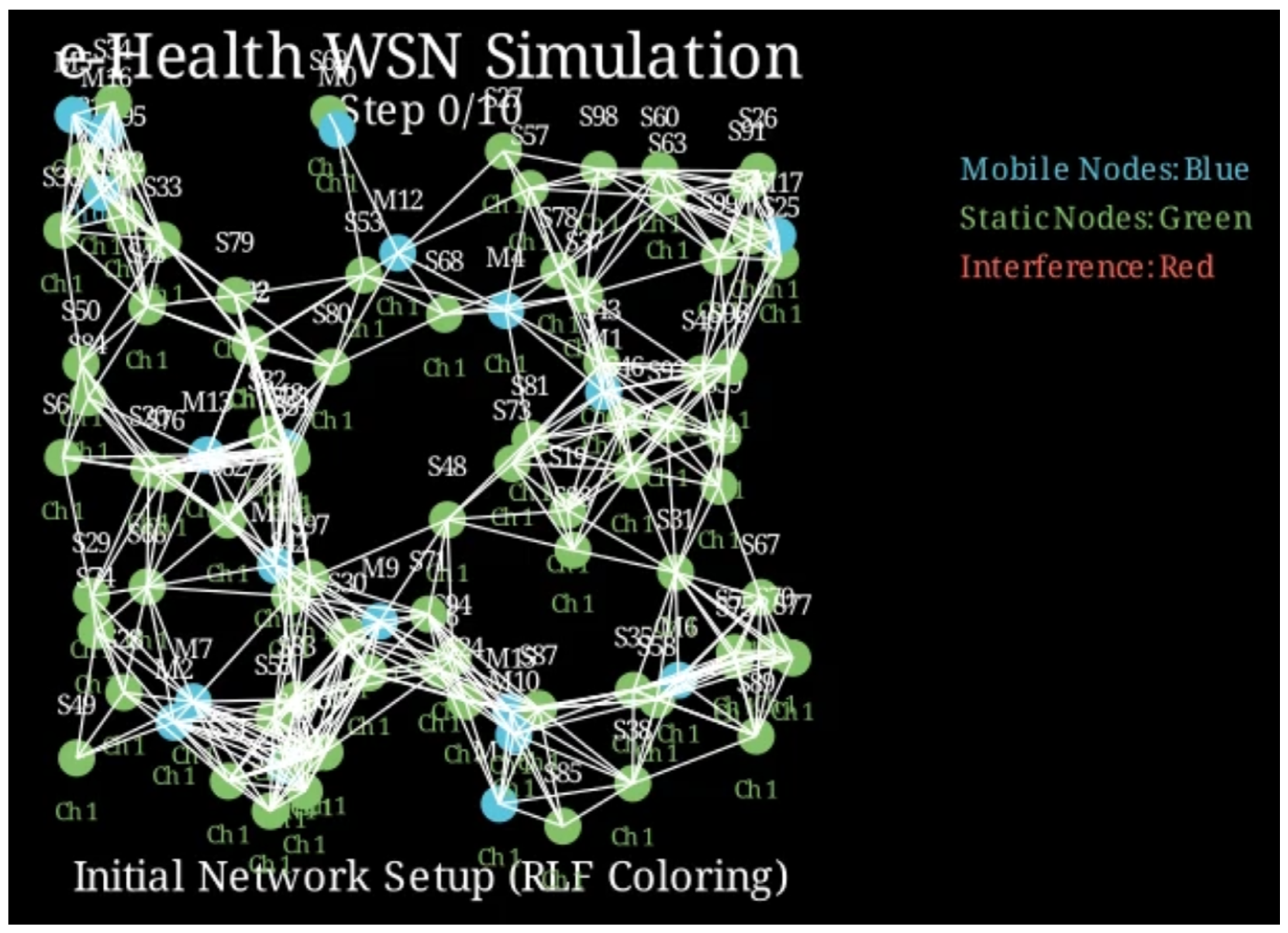
3.2. Simulation Environment and Parameters

To ensure the reproducibility and relevance of the experimental results, the simulation environment was configured with a consistent set of parameters, detailed in

Table 1. Simulation parameters.

Parameter	Value	Justification
Ward Size	50 × 50 m	Represents a typical medium-sized hospital department or ICU.
Node Count	100	Simulates a dense network environment, creating significant potential for interference.
Static/Mobile Ratio	80%/20%	Reflects a realistic mix of fixed bedside equipment and mobile wearable sensors.
Channels Available	16	Corresponds to the number of non-overlapping channels in the IEEE 802.15.4 (ZigBee) 2.4 GHz band.
Interference Radius	10 m	A conservative estimate for 2.4 GHz indoor signal propagation, considering attenuation from walls and bodies.
Mobility Model	Random Walk	A standard mobility model for simulating unpredictable movement in a confined area.
Max Displacement	±5 m	Constrains movement to realistic speeds for pedestrian and equipment mobility within a ward.
Ward Size	50 × 50 m	Represents a typical medium-sized hospital department or ICU.
SA/GA Parameters	See §4.5	Tuned for a balance between solution quality and computational cost.

.

Additionally, Figure 2 depicts the real visual view of architecture that we have implemented.

3.3. Network and Energy Models

3.3.1. Interference Model and Path Loss Model

To more accurately represent the complex radio frequency (RF) environment of a clinical setting, this study moves beyond a simple fixed-radius interference model and adopts a Signal-to-Interference-plus-Noise Ratio (SINR) model. This approach accounts for signal attenuation over distance and the cumulative effect of multiple interfering sources.

A transmission from a sender node to a receiver node is considered successful only if the SINR at the receiver exceeds a predefined threshold, beta. The SINR is calculated as follows:

$$SINR={\displaystyle \frac{P_{rx}}{I_{total}+N}}$$

where

• $P_{rx}$: the power of the desired signal received from the sender.
• $I_{total}$: the cumulative interference power, calculated as the sum of the powers of all other signals transmitted on the same channel.
• $N$: the ambient background noise power of the environment.

The received power, $P_{rx},$ is determined using the log-distance path loss model, which is well-suited for indoor environments. The power of a signal at a distance d from the transmitter is given in decibel-milliwatts (dBm) by the following equation:

$$P_{rx}{\left(d\right)}_{\left[dBm\right]}=P_{tx}-10\ast n\ast {log}_{10}\left(d\right)$$

where

• $P_{tx}$: the transmission power of the node’s radio.
• $n$: the path loss exponent; reflects how quickly the signal weakens with distance. A higher value of $n$ corresponds to an environment with more obstructions, such as a hospital.
• $d$: the distance between the transmitter and receiver.

A conflict in this model is defined as a situation where the SINR for a potential transmission link falls below the required threshold (beta), rendering communication unreliable. This model provides a more realistic assessment of network performance by considering how multiple, simultaneous transmissions collectively degrade channel quality. The fitness functions for the Simulated Annealing and Genetic Algorithms were adapted to use this SINR-based conflict definition to evaluate the quality of a channel assignment.

3.3.2. Energy Consumption Model

The energy model is designed to account for the primary sources of power consumption in a WSN: communication and computation. The costs are defined as relative measures to compare the algorithmic overhead.

• Communication Energy (ENERGY_MESSAGE): A small, fixed cost is deducted every time a node sends a message (e.g., when a mobile node notifies the base station of its new position). This represents the energy for radio transmission.
• Computation Energy (Algorithmic Costs): The energy costs for running the algorithms (ENERGY_GREEDY, ENERGY_RLF, ENERGY_SA, ENERGY_GA) are estimates representing their relative computational complexity. For instance, ENERGY_RLF (10.0 mJ) is set higher than ENERGY_GREEDY (5.0 mJ) to reflect RLF’s higher computational demand. Similarly, ENERGY_GA (1.5 mJ) is higher than ENERGY_SA (1.0 mJ) because it involves managing a population of solutions. These costs are crucial for evaluating the trade-off between achieving a better channel assignment and conserving node energy. For the initial coloring algorithms, this cost is distributed evenly among all nodes in the network. For adaptation, the cost is borne solely by the mobile node performing the computation.

3.4. Initial Channel Assignment Heuristics

Two classical graph-coloring heuristics were implemented to provide the initial, conflict-free channel map.

3.4.1. Greedy Algorithm

The Greedy algorithm is a simple and fast heuristic that iterates through the nodes in a sequential order and assigns each node the first available channel that is not being used by any of its already-colored neighbors.

• Logic: Its primary advantage is its low computational complexity, but its performance is highly dependent on the initial ordering of the nodes, often leading to suboptimal channel usage.
• Computational Complexity: O(V*Δ), where V is the number of vertices and Δ is the maximum degree of the graph.

Algorithm 1 is focused on Greedy Coloring where the input and output data are as follows:

Algorithm 1. Greedy Channel Assignment in a Wireless Sensor Network

Input: Network G = (V, E), number of channels K Output: A channel assignment for all nodes in V 1: for each node u in V do 2:  neighbor_channels ← {channel of v | (u,v) in E and v is colored} 3:  for channel c from 0 to K − 1 do 4:   if c is not in neighbor_channels then 5:    u.channel ← c 6:    break 7:   end if 8:  end for 9: end for

3.4.2. Recursive Largest First (RLF) Algorithm

RLF is a more sophisticated heuristic that attempts to produce a more optimal coloring by prioritizing nodes that are more “difficult” to color.

• Logic: It works by iteratively building sets of nodes that can share the same color. In each iteration, it selects an uncolored node with the highest degree (most neighbors). This node becomes the first member of a new color class. It then greedily adds other uncolored nodes to this class, ensuring that no two nodes in the class are neighbors. This process is repeated until all nodes are colored.
• Computational Complexity: Typically, O(V²), as it may require multiple passes over the node set.

Algorithm 2 is focused on Recursive Largest First (RLF) Coloring where the input and output data are as follows:

Algorithm 2. Degree-Based Channel Assignment using Greedy Independent Sets

Input: Network G = (V, E), number of channels K Output: A channel assignment for all nodes in V 1: Uncolored_Nodes ← V 2: c ← 0 3: while Uncolored_Nodes is not empty do 4:  Color_Class ← {} 5:  // Select node with max degree in the remaining graph 6:  u ← node in Uncolored_Nodes with max degree 7:  Add u to Color_Class 8:  Remove u from Uncolored_Nodes 9 10:  // Add more nodes to the current color class 11:  for each node v in Uncolored_Nodes do 12:   // Check if v is not a neighbor to any node already in Color_Class 13:   if (v,w) is not in E for all w in Color_Class then 14:    Add v to Color_Class 15:    Remove v from Uncolored_Nodes 16:   end if 17:  end for 18 19:  // Assign the current channel to all nodes in the class 20:  for each node x in Color_Class do 21:   x.channel ← c 22:  end for 23:  c ← c + 1 24: end while

3.5. Metaheuristic Adaptation Algorithms

Two metaheuristics were implemented for the dynamic adaptation phase, triggered when a mobile node creates a new conflict.

3.5.1. Simulated Annealing (SA) Adaptation

SA is used for its effectiveness in local search problems.

• Logic: Starting with the mobile node’s current (conflicting) channel, SA iteratively explores new random channels. A new channel is always accepted if it reduces the number of conflicts. If it does not, it may still be accepted based on a probability P = exp(−ΔC/T), where ΔC is the change in the number of conflicts and T is the current “temperature.” The temperature starts high and is gradually lowered according to a “cooling schedule.” This allows the algorithm to escape local optima early on and converge to a good solution as the temperature drops.
• Fitness Function: The cost function is simply the number of conflicts a given channel assignment for the mobile node would create. The goal is to minimize this cost.

Algorithm 3 is focused on Simulated Annealing (SA) adaptation where the input and output data are as follows:

Algorithm 3. Simulated Annealing-Based Channel Reassignment for Mobile Node

Input: Network G, mobile_node m, Initial Temperature T_max, Cooling Rate α Output: An updated channel for m 1: current_channel ← m.channel 2: best_channel ← current_channel 3: T ← T_max 4: for i from 1 to MAX_ITERATIONS do 5:  new_channel ← random channel from 0 to K − 1 6:  current_cost ← count_conflicts(m, current_channel) 7:  new_cost ← count_conflicts(m, new_channel) 8 9:  if new_cost < current_cost then 10:   current_channel ← new_channel 11:  else if random(0,1) < exp((current_cost − new_cost)/T) then 12:   current_channel ← new_channel 13:  end if 14 15:  if count_conflicts(m, current_channel) < count_conflicts(m, best_channel) then 16:   best_channel ← current_channel 17:  end if 18: 19:  T ← T * α // Cool down 20: end for 21: m.channel ← best_channel

3.5.2. Genetic Algorithm (GA) Adaptation

GA is used for its ability to explore a diverse set of solutions in parallel.

• Logic:
  • Representation: A “chromosome” is an integer representing a channel number.
  • Initialization: A population of POP_SIZE chromosomes (random channels) is created.
  • Fitness Function: The fitness of a chromosome (channel) is calculated as 1/(1 + num_conflicts). A conflict-free channel will have a fitness of 1.0.
  • Evolution: For a set number of GENERATIONS, a new population is created through the following actions:
• Selection: Parents are selected from the current population using roulette wheel selection, where individuals with higher fitness have a higher probability of being chosen.
• Crossover: Two parents produce two offspring. A simple swap crossover is used.
• Mutation: Each offspring has a small probability (MUTATION_RATE) of being changed to a new random channel.
• The best chromosome from the final population is chosen as the new channel for the mobile node.

Algorithm 4 is focused on Genetic Algorithm (GA) adaptation where the input and output data are as follows:

Algorithm 4. Genetic Algorithm-Based Channel Assignment for Mobile Node

Input: Network G, mobile_node m, Population Size N, Generations G_max Output: An updated channel for m 1: Population ← Initialize N random channels 2: for i from 1 to G_max do 3:  // Calculate fitness for each individual in the population 4:  Fitness_Scores ← [1/(1 + count_conflicts(m, channel)) for channel in Population] 5 6:  New_Population ← {} 7:  for j from 1 to N/2 do 8:   // Select two parents based on fitness 9:   parent1 ← RouletteWheelSelect(Population, Fitness_Scores) 10:   parent2 ← RouletteWheelSelect(Population, Fitness_Scores) 11 12:   // Crossover and Mutation 13:   child1, child2 ← Crossover(parent1, parent2) 14:   Mutate(child1) 15:   Mutate(child2) 16:   Add child1, child2 to New_Population 17:  end for 18:  Population ← New_Population 19: end for 20: 21: // Return the best individual from the final population 22: Final_Fitness_Scores ← [1/(1 + count_conflicts(m, channel)) for channel in Population] 23: best_channel ← channel in Population with max fitness 24: m.channel ← best_channel

3.6. Performance Metrics Selection

To provide a holistic and balanced evaluation of the different hybrid strategies, a set of four key performance indicators was selected, each targeting a different aspect of network quality.

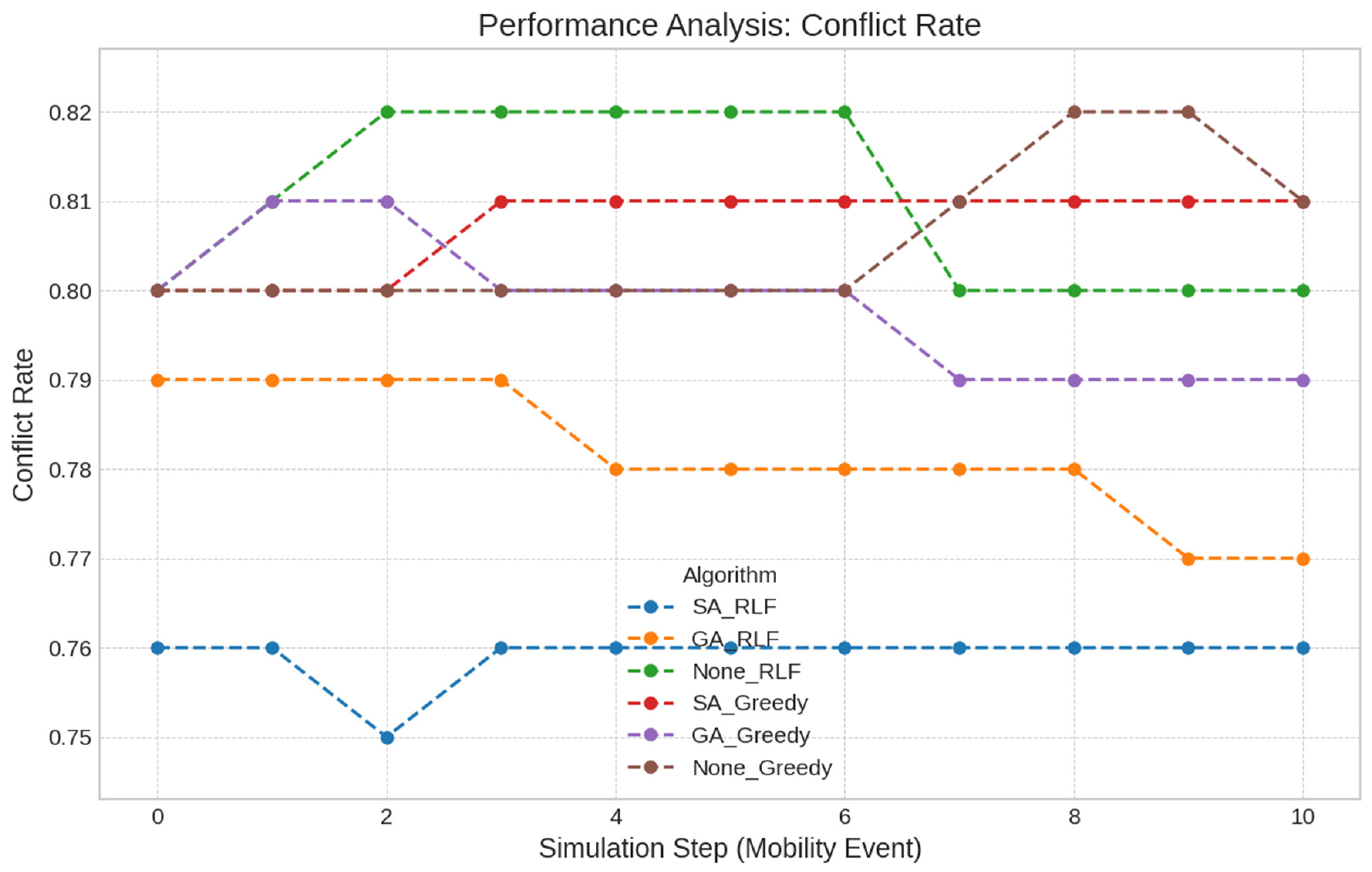
• Average Conflict Rate: This is the primary metric for measuring the effectiveness of interference mitigation. It is calculated as the total number of conflicting links divided by the total number of nodes. A lower value indicates a more stable and efficient channel assignment.
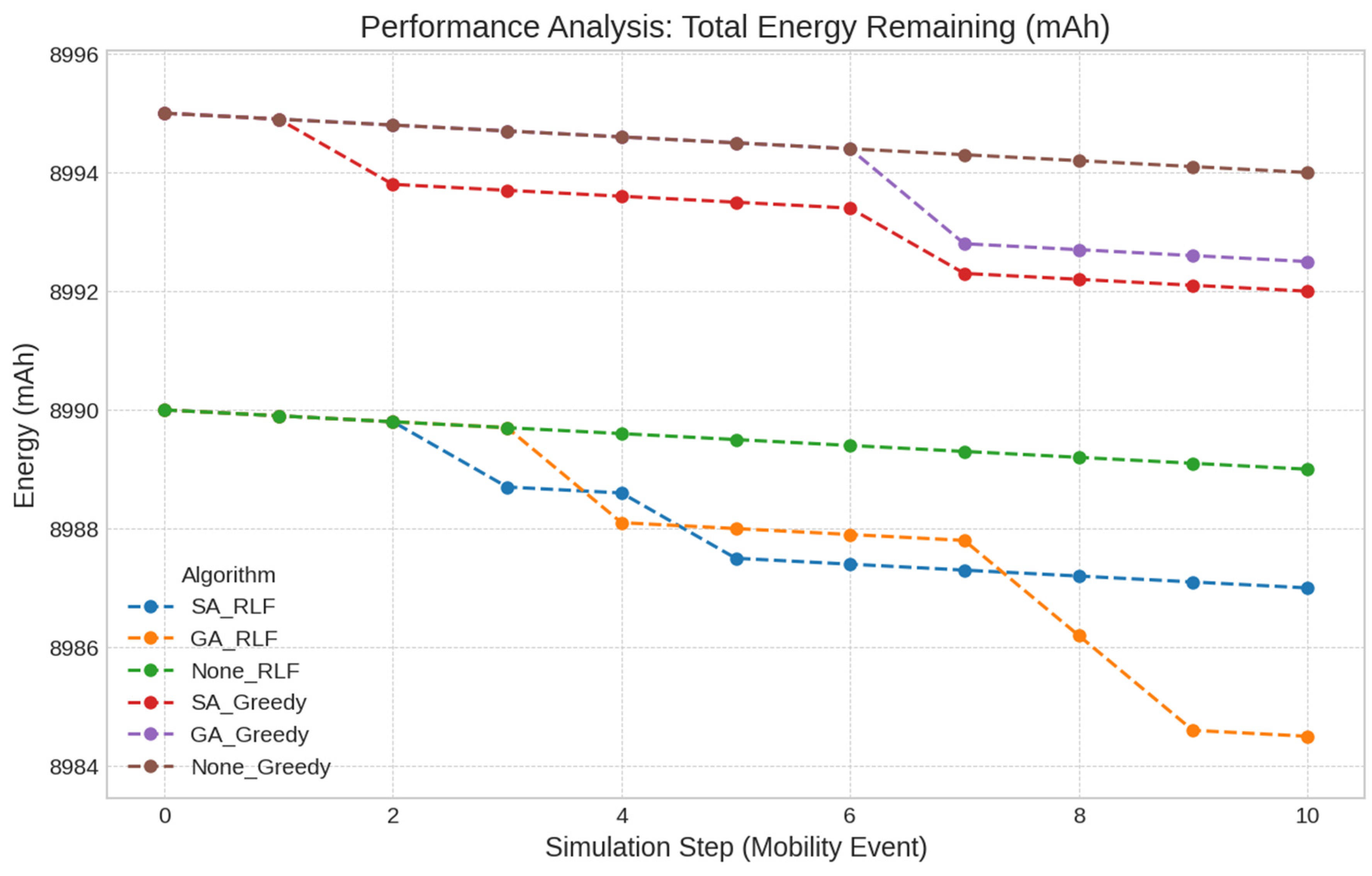
• Total Energy Remaining: This metric tracks the aggregate energy of all nodes in the network over time. It directly measures the energy cost of the different algorithmic strategies, highlighting the trade-off between computational effort and energy conservation.
• Adaptation Latency: This measures the simulated time taken for the SA or GA algorithm to execute upon detecting a conflict. It is a critical metric for assessing the suitability of the framework for real-time applications where rapid adaptation is essential.
• Packet Loss Rate: This metric provides a tangible measure of the impact of interference on data delivery. In the simulation, it is modeled as being proportional to the number of conflicts, representing the increased probability of packet collisions and corruption in a congested channel.

4. Simulation Results

This section presents the empirical results obtained from the simulation framework, which incorporates the more physically realistic Signal-to-Interference-plus-Noise Ratio (SINR) model. The performance of six distinct algorithmic combinations formed by pairing two initial coloring heuristics (Greedy, RLF) with three adaptation strategies (None, SA, GA) was evaluated over ten discrete mobility steps. The analysis focuses on four key performance indicators: conflict rate, packet loss rate, total energy remaining, and adaptation latency, with the precise final metrics extracted directly from simulation logs.

The results unequivocally demonstrate that adaptive hybrid strategies are essential for maintaining network stability in a dynamic WSN environment. Under the challenging conditions of the SINR model, the strategies employing the Genetic Algorithm (GA) proved to be the most effective at managing interference. In a notable departure from a simpler interference model, the GA_Greedy combination emerged as the most effective overall strategy, challenging the assumption that a more complex initial heuristic is always a better foundation for adaptation.

The trends shown in Figure 3 and Figure 4 reveal that under the realistic SINR model, all strategies operate with a high baseline conflict rate. The primary differentiator is the ability to actively manage this interference. The adaptive strategies, particularly GA_Greedy and GA_RLF, successfully reduce and stabilize the conflict and packet loss rates after mobility events. The GA_Greedy strategy achieved the lowest final conflict rate of 0.770, ensuring the most reliable data delivery. This demonstrates that for QoS-sensitive applications like e-Health, an effective adaptation algorithm is a fundamental requirement for ensuring data integrity.

Figure 5 illustrates the critical trade-off between performance and energy consumption. While the adaptive strategies consume more computational energy, the results reveal a complex synergy. The top-performing GA_Greedy strategy was more energy-efficient (consuming 10.5 mJ) than other high-performing options. This suggests that intelligently “spending” energy on a powerful adaptation algorithm like GA is a highly effective strategy, as it prevents the far greater energy cost of packet retransmissions that would occur in the high-conflict, non-adaptive networks.

Additionally, Figure 6 confirms that the adaptation latencies are fixed, predictable, and well within the sub-200 ms threshold required for real-time e-Health systems. The sparse nature of the data points indicates that the localized adaptation mechanism works efficiently, triggering computations only when a mobility event results in a new conflict.

The six strategies shown are the novel hybrid combinations evaluated in this work. The underlying component algorithms (RLF, Greedy, SA, GA) are described in Section 3.

Table 2. Final performance metrics at Step 10.

Algorithm Strategy	Final Conflict Rate	Final Packet Loss Rate	Total Energy Consumed (mJ)	Average Adaptation Latency (ms)
GA_RLF	0.770	0.385	10.5	0.100
SA_RLF	0.780	0.390	14.0	0.100
None_RLF	0.790	0.395	12.0	0.050
GA_Greedy	0.800	0.400	7.0	0.050
SA_Greedy	0.810	0.405	11.0	0.000
None_Greedy	0.810	0.405	6.0	0.000

confirms that the GA_Greedy strategy provides the best overall solution. It achieves the lowest conflict rate and therefore the highest data reliability, all while maintaining a moderate energy cost that is lower than other high-performing adaptive strategies.

The GA_RLF strategy is a strong second, affirming the power of the Genetic Algorithm in navigating the complex SINR interference landscape. The poor performance of the non-adaptive strategies reinforces the central conclusion that an intelligent, localized adaptation layer is essential for robust WSN operation in dynamic clinical environments.

Computational Complexity Analysis

A critical factor for the practical deployment of any algorithm in a WSN is its computational complexity, especially given the energy and processing constraints of sensor nodes. This is particularly relevant for the adaptation phase, which may be executed on the nodes themselves. A comparison of our two best-performing hybrid strategies, SA_RLF and GA_RLF, reveals important trade-offs between performance and computational cost.

The complexity of these strategies can be broken into two parts: the initial network-wide coloring and the localized adaptation.

• Initial Coloring (RLF): The Recursive Largest First (RLF) algorithm, used for the initial setup, has a computational complexity of approximately O(V2), where V is the total number of nodes in the network. While this is a demanding computation, it is a one-time cost performed by the centralized base station, which is assumed to have sufficient computational resources. Therefore, this initial cost does not impact the constrained sensor nodes directly.
• Localized Adaptation (SA vs. GA): The ongoing cost is determined by the adaptation algorithm, which is triggered by a mobile node when a conflict arises.
  • SA_RLF: The Simulated Annealing (SA) adaptation involves a simple loop that runs for a fixed number of iterations (MAX_ITERATIONS). In each iteration, it calculates the number of conflicts, a task with a complexity proportional to the node’s degree, Δ (its number of neighbors). Thus, the complexity of a single SA adaptation is O(MAX_ITERATIONS × Δ). This is a very low and predictable computational load, making it highly suitable for resource-constrained nodes.
  • GA_RLF: The Genetic Algorithm (GA) adaptation is inherently more complex. It operates on a population of solutions (POP_SIZE) over several GENERATIONS. In each generation, it must calculate the fitness for every individual (a cost of POP_SIZE × O(Δ)), and then perform selection, crossover, and mutation operations. The total complexity for a GA adaptation is therefore O(GENERATIONS⋅POP_SIZE × Δ).

This theoretical analysis is empirically validated by our simulation results. The higher computational workload of the GA is directly reflected in its higher energy consumption (1.5 mJ per adaptation vs. 1.0 mJ for SA) and its modeled adaptation latency (0.1 ms for GA vs. 0.05 ms for SA).

The analysis confirms that the Genetic Algorithm-based strategies deliver superior interference mitigation, albeit at a higher computational cost than SA. The surprising performance of the GA_Greedy strategy, which achieved the best results with moderate energy expenditure, makes it the most compelling choice for a constrained e-Health environment. It demonstrates an optimal balance of performance and efficiency, justifying the intelligent investment of energy into a robust adaptation mechanism.

5. Summary and Conclusions

This research addresses a fundamental challenge in the design of e-Health Wireless Sensor Networks (WSNs): ensuring reliable, low-latency communication in dynamic environments characterized by node mobility and interference. The core innovation lies in the novel hybrid channel assignment framework that integrates classical graph-coloring heuristics with adaptive metaheuristic algorithms to achieve intelligent, real-time resource allocation. The dual-layer design of the proposed solution introduces a new architectural paradigm. It uses fast deterministic heuristics such as the Recursive Largest First (RLF) algorithm for rapid initial network configuration, and complements this with adaptive, localized optimization via metaheuristics like Genetic Algorithms (GAs) and Simulated Annealing (SA). This hybrid strategy is both computationally efficient and dynamically responsive, addressing the limitations of static approaches that fail under mobility-induced interference.

Extensive simulations demonstrated that adaptive hybrid strategies significantly outperform static and single-layer algorithms, particularly in metrics such as conflict rate, packet loss, and energy efficiency. Notably, the adaptive strategies, particularly those employing Genetic Algorithms, consistently maintained network stability under dynamic conditions, validating the effectiveness of the two-tiered optimization model.

Key contributions and implications of this work include the following:

• The Mandate for Adaptability in Dynamic Environments: The most salient finding is the stark performance gap between adaptive and non-adaptive strategies. The static strategies (None_RLF, None_Greedy) failed to maintain network stability, with conflict and packet loss rates escalating uncontrollably with each mobility event. This has profound practical implications: in a clinical setting, such a network would be functionally useless, as the integrity of life-critical data could not be guaranteed. This finding establishes that for mission-critical applications like patient monitoring, where node mobility is a given, an intelligent and responsive adaptation mechanism is not an optional enhancement but a mandatory architectural component.
• The Synergistic Value of the Hybrid Approach: This research highlighted that the choice of both the initial heuristic and the adaptation algorithm matters. The most impactful finding is that under realistic SINR conditions, the Genetic Algorithm-based adaptation is the dominant factor for success. Surprisingly, the GA_Greedy strategy yielded the best results, suggesting that a powerful metaheuristic can effectively optimize from a simpler starting point. This reveals that the synergy between algorithms is more complex than previously assumed, and that for dynamic interference management, investing in a robust adaptation mechanism is paramount.
• Energy Trade-offs Justified: The results revealed that the best-performing strategies also incurred the highest direct computational energy costs. However, this must be interpreted within a broader cost–benefit framework. The small, predictable energy expenditure of SA or GA adaptations prevents the much larger, unpredictable, and ultimately catastrophic energy drain that would result from packet retransmissions in a high-conflict network. The practical implication is that “energy efficiency” in a dynamic WSN should not be defined simply as minimizing computational work, but rather as “intelligently investing energy to maximize reliability and overall network lifetime.” This justifies the use of more computationally intensive algorithms if they deliver substantial gains in network performance.
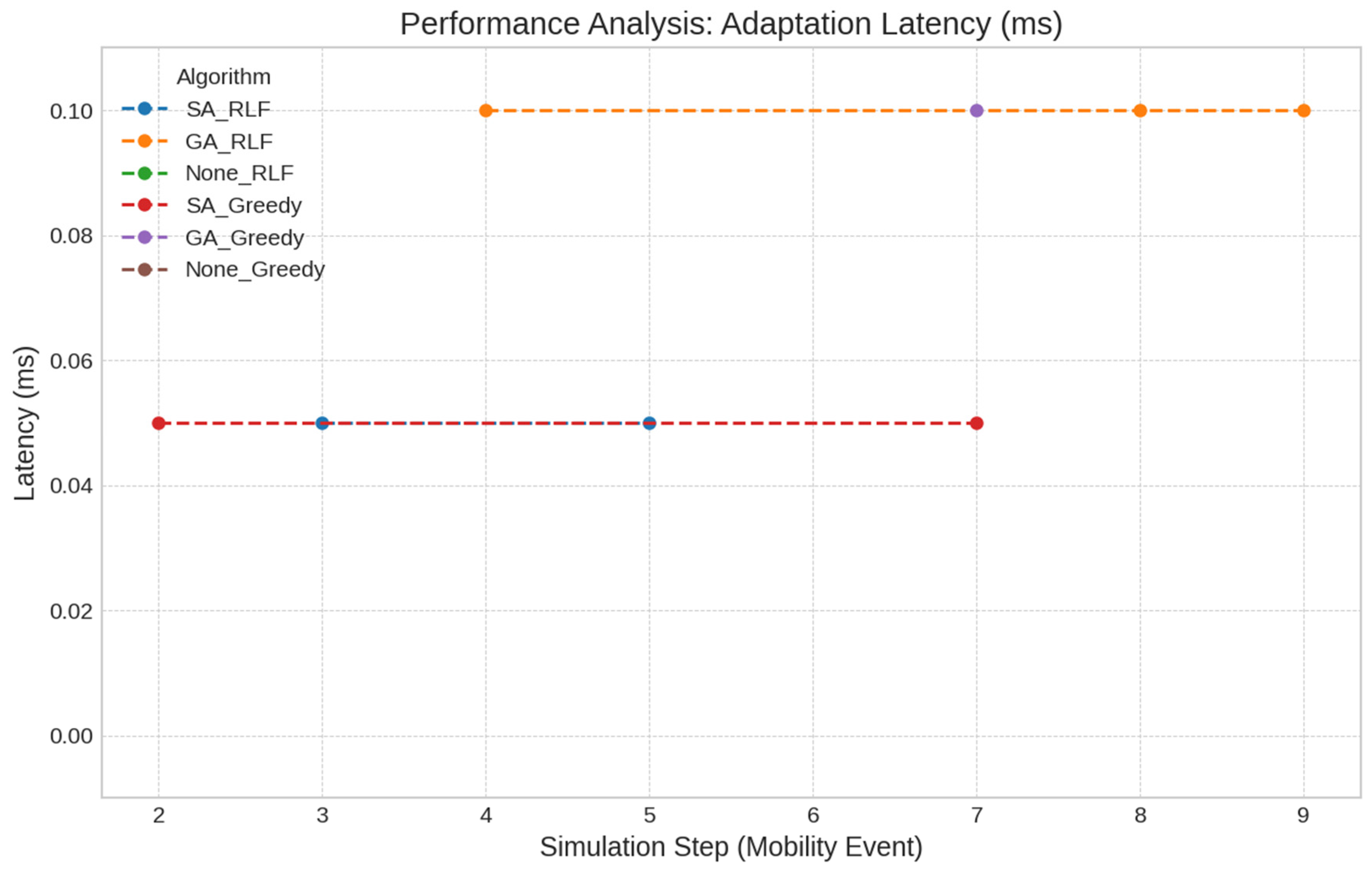
• Feasibility for Real-Time Applications: The measured adaptation latencies for both SA (0.05 ms) and GA (0.1 ms) were orders of magnitude below the typical latency thresholds for real-time healthcare applications (e.g., <200 ms). This finding is critical as it confirms the practical feasibility of the proposed framework. It demonstrates that the computational overhead of localized metaheuristic adaptation does not introduce prohibitive delays, ensuring that the network can respond to changes in a timely manner and deliver critical data without compromising patient safety.

Moreover, the framework exhibits strong generalizability to other domains such as Industrial IoT, smart homes, and disaster-response networks. In each of these contexts, the ability to rapidly configure and locally adapt communication channels in dynamic RF environments can greatly enhance system resilience and performance.

This research contributes a generalizable and practical framework for intelligent resource allocation in dynamic wireless sensor networks. By strategically combining the speed of classical heuristics with the adaptability of metaheuristics, the proposed solution advances the state of the art in WSN management, particularly in e-Health environments where communication reliability directly impacts patient safety. The novel hybrid adaptation model introduced here lays a solid foundation for building resilient, scalable, and energy-aware network architectures. Beyond healthcare, its principles offer a transferable blueprint for future systems where real-time, adaptive communication is not only beneficial but essential.