Control Algorithm for an Inverter-Based Virtual Synchronous Generator with Adjustable Inertia
Abstract
1. Introduction
- A Holistic PLL-less Control Architecture: A comprehensive control structure is proposed that joins synchronverter dynamics with a virtual impedance-based self-synchronization mechanism, eliminating the need for a dedicated Phase-Locked Loop (PLL). This inherently improves the controller’s robustness and stability margin, particularly under weak grid conditions, where PLLs are a known source of instability [19].
- Synergistic Integration of Dynamic Inertia: This demonstrates how an adjustable virtual inertia can be seamlessly incorporated into a PLL-less framework, allowing the system to dynamically modulate its inertial response to minimize frequency deviations (nadir/overshoot) and the Rate of Change of Frequency (RoCoF), without the stability constraints imposed by a traditional PLL.
- Improved Stability Margin and Computational Efficiency: The proposed controller achieves a superior stability margin by eliminating the adverse dynamics of the PLL. Furthermore, the direct emulation of the synchronous machine equations, without the computational overhead of a complex PLL algorithm, offers a pathway towards a more efficient implementation on digital signal processors (DSPs).
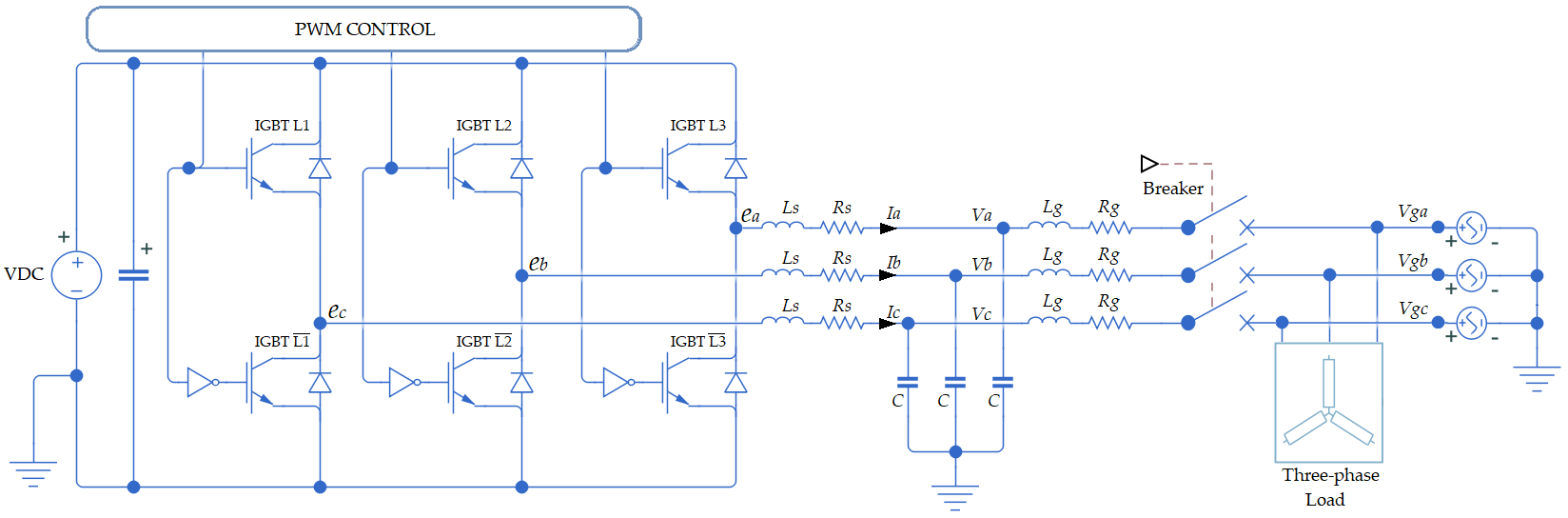
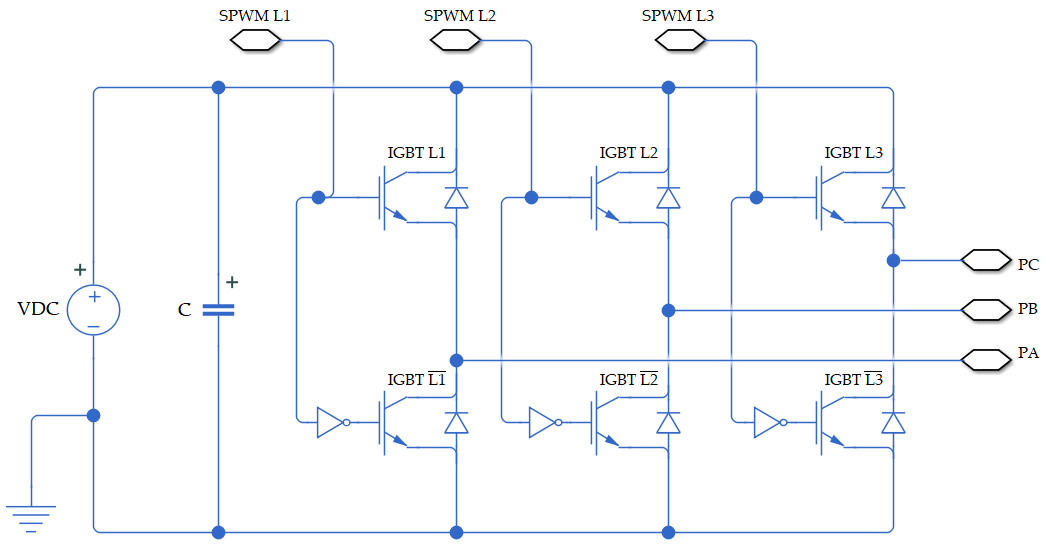
2. The System Under Study
3. Previous Works on VSM Derivations
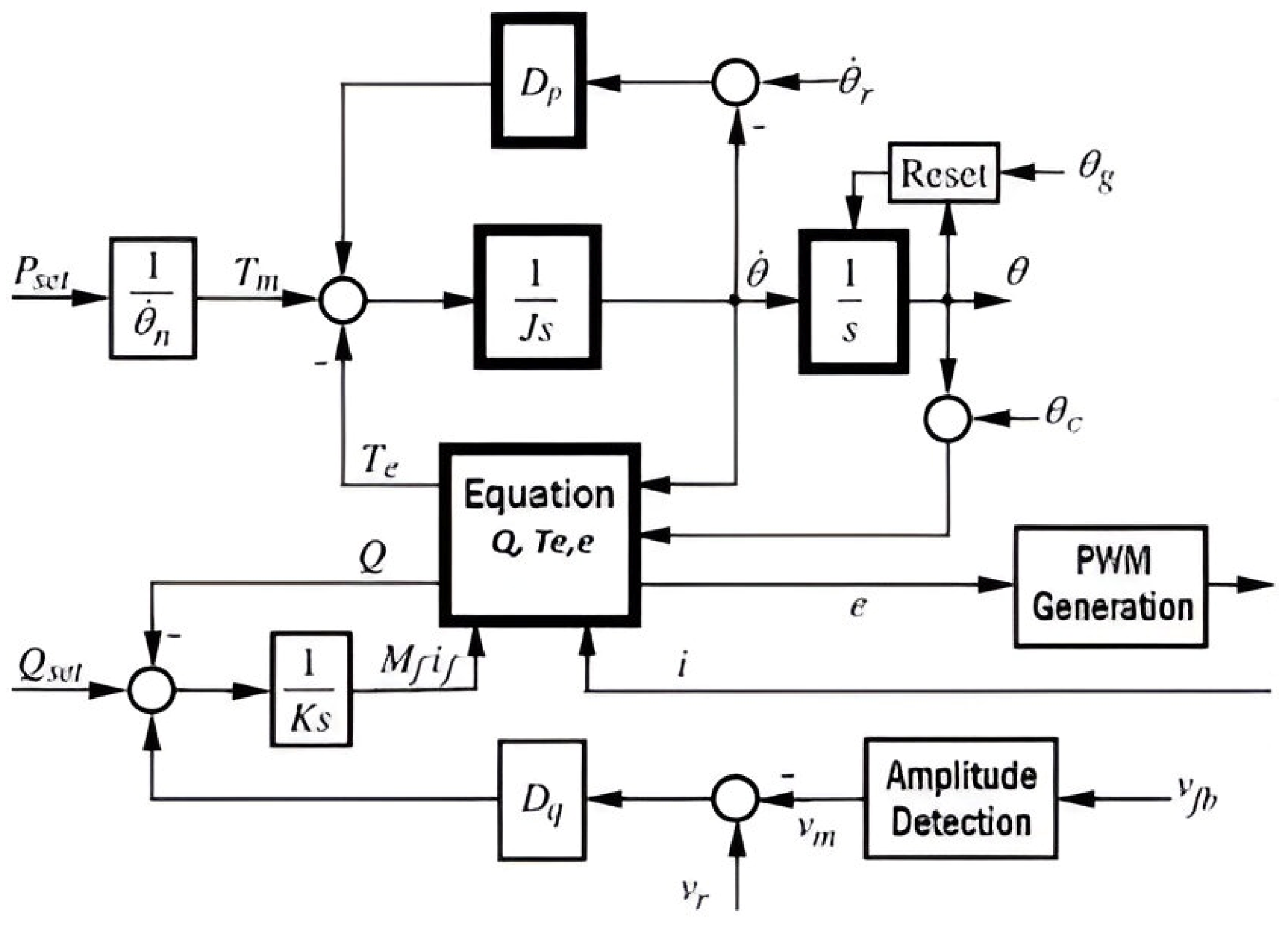
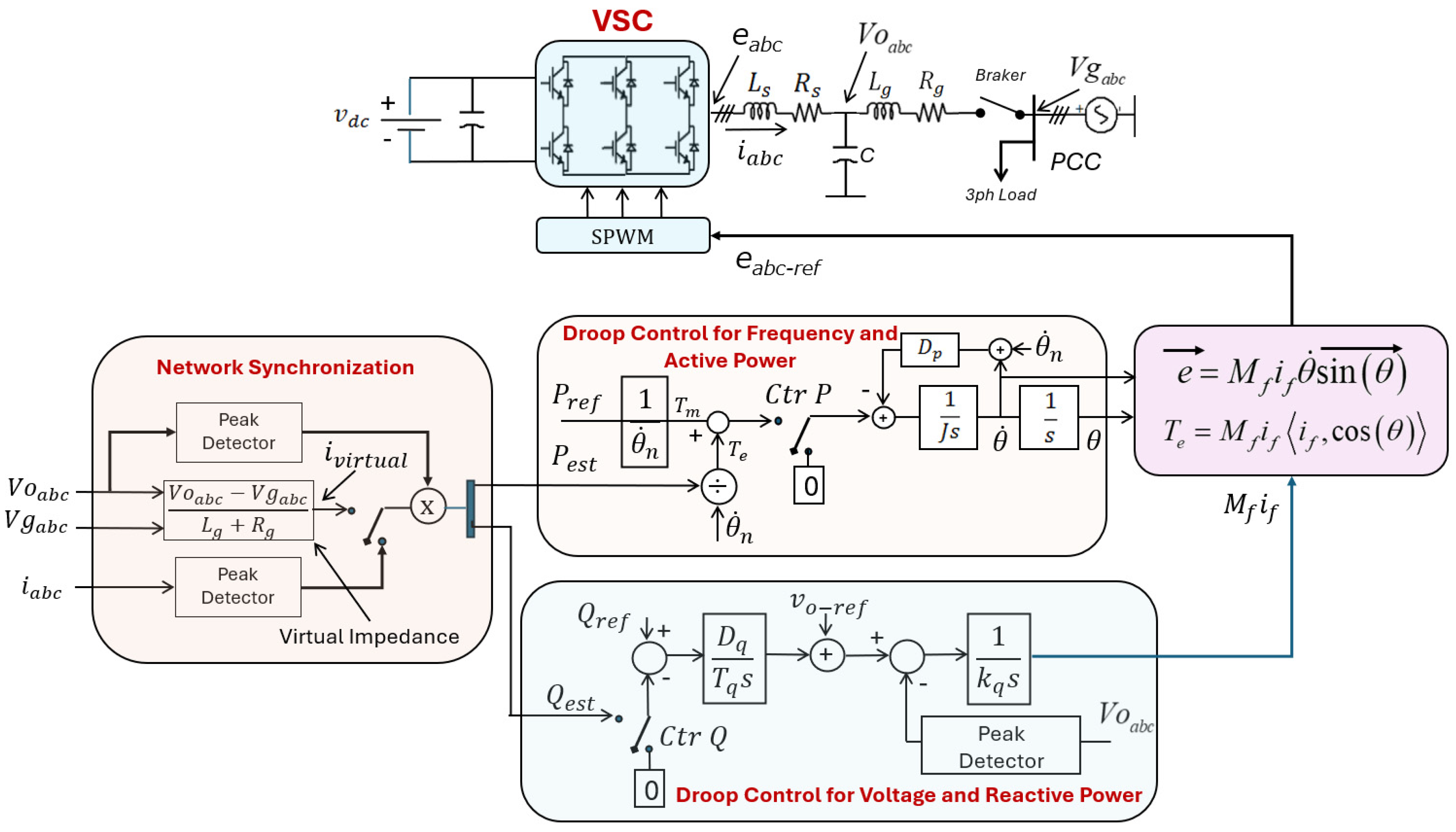
4. The Derived Algorithm
4.1. Droop Control for Frequency and Active Power
4.2. Droop Control for Voltage and Reactive Power
4.3. Control Loop for Grid Synchronization
- (a)
- The Ctr P and Ctr Q switches are initially set to use “0” as the reference. This configuration enables the Voltage Source Converter (VSC) to generate an output voltage, Vo, at a reference frequency (θn) and a reference magnitude (Vo-ref).
- (b)
- Subsequently, the switches are commutated to use Pest and Qest as the new references. This step is critical, as it utilizes the virtual impedance to synchronize the VSC’s frequency and voltage with the grid prior to connection, ensuring that the transient upon connection is minimal. The quality of the synchronization will depend on how accurately the values of Lg and Rg are determined in the real implementation.
- (c)
- During the synchronization process, the synchronization network must have the reference current iVirtual selected. The inverter’s connection to the grid is only established when the value of iVirtual approaches zero.
- (d)
- Once the VSC inverter is connected to the grid, the synchronization network’s switch selects the actual current being delivered by the inverter. This current, which should be very close to zero at the moment of connection, is then used to calculate the active and reactive power that the VSC supplies to the point of common coupling (PCC). At this stage, the power references, Pref and Qref, are set by the user or by another grid control algorithm.
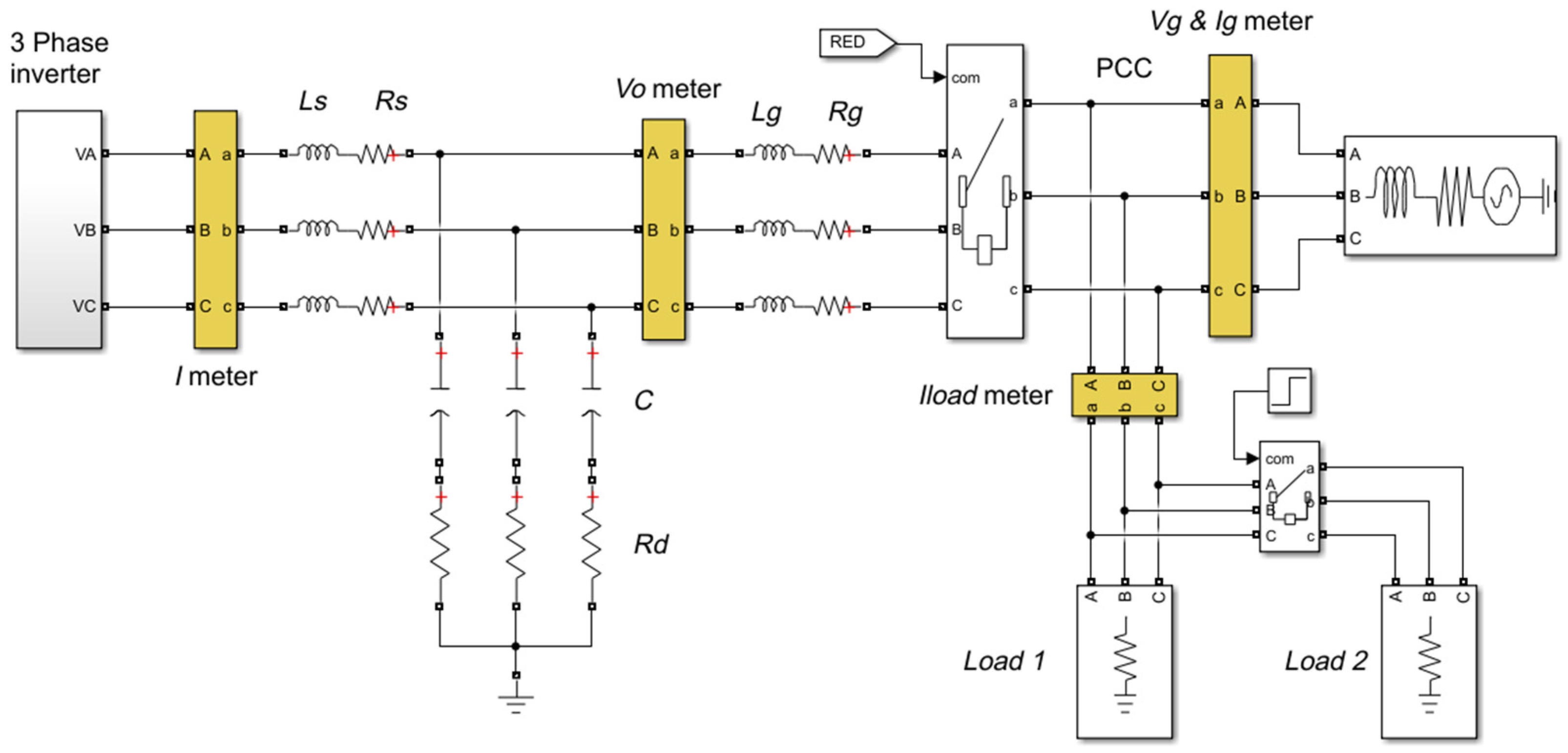
5. Simulation Results
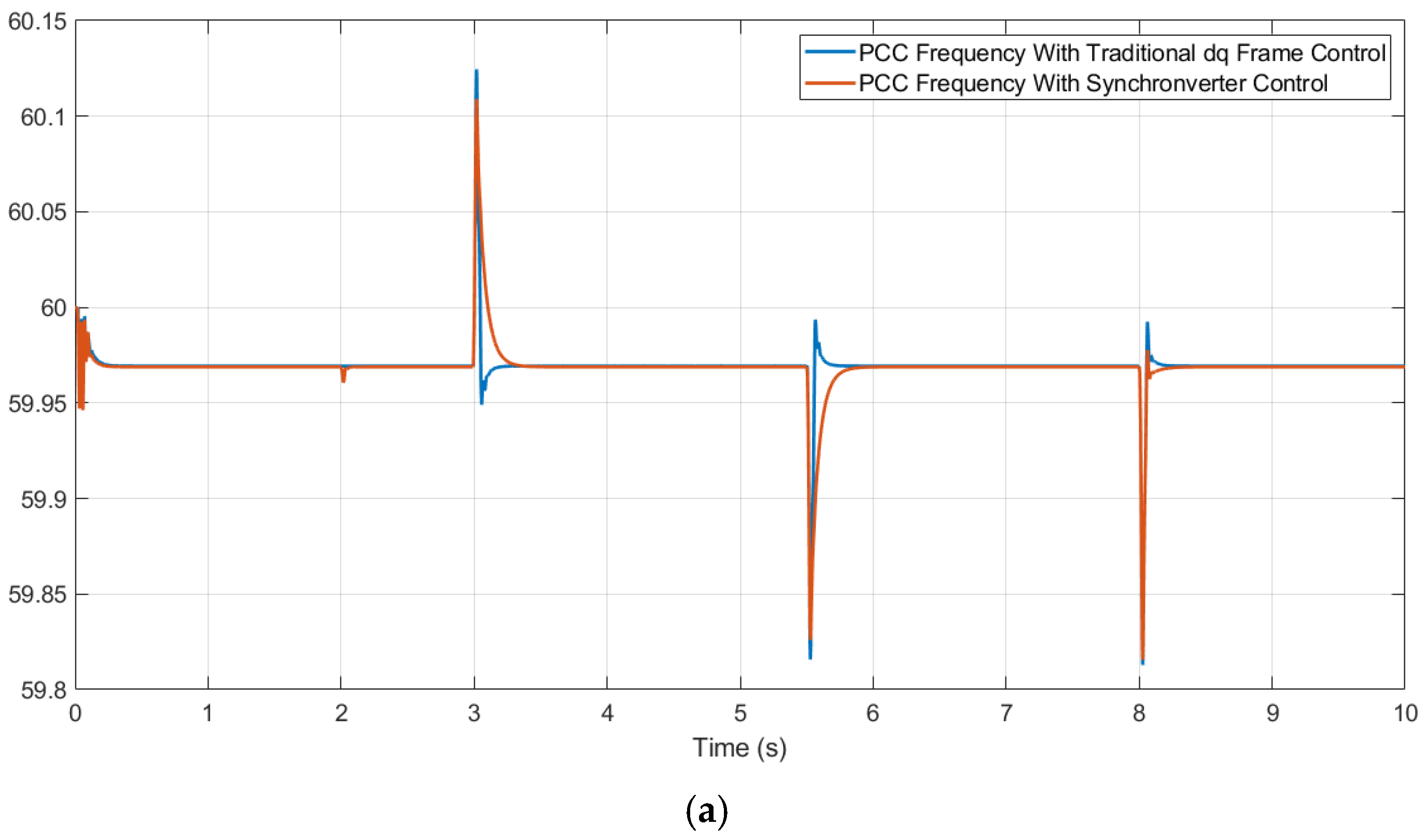
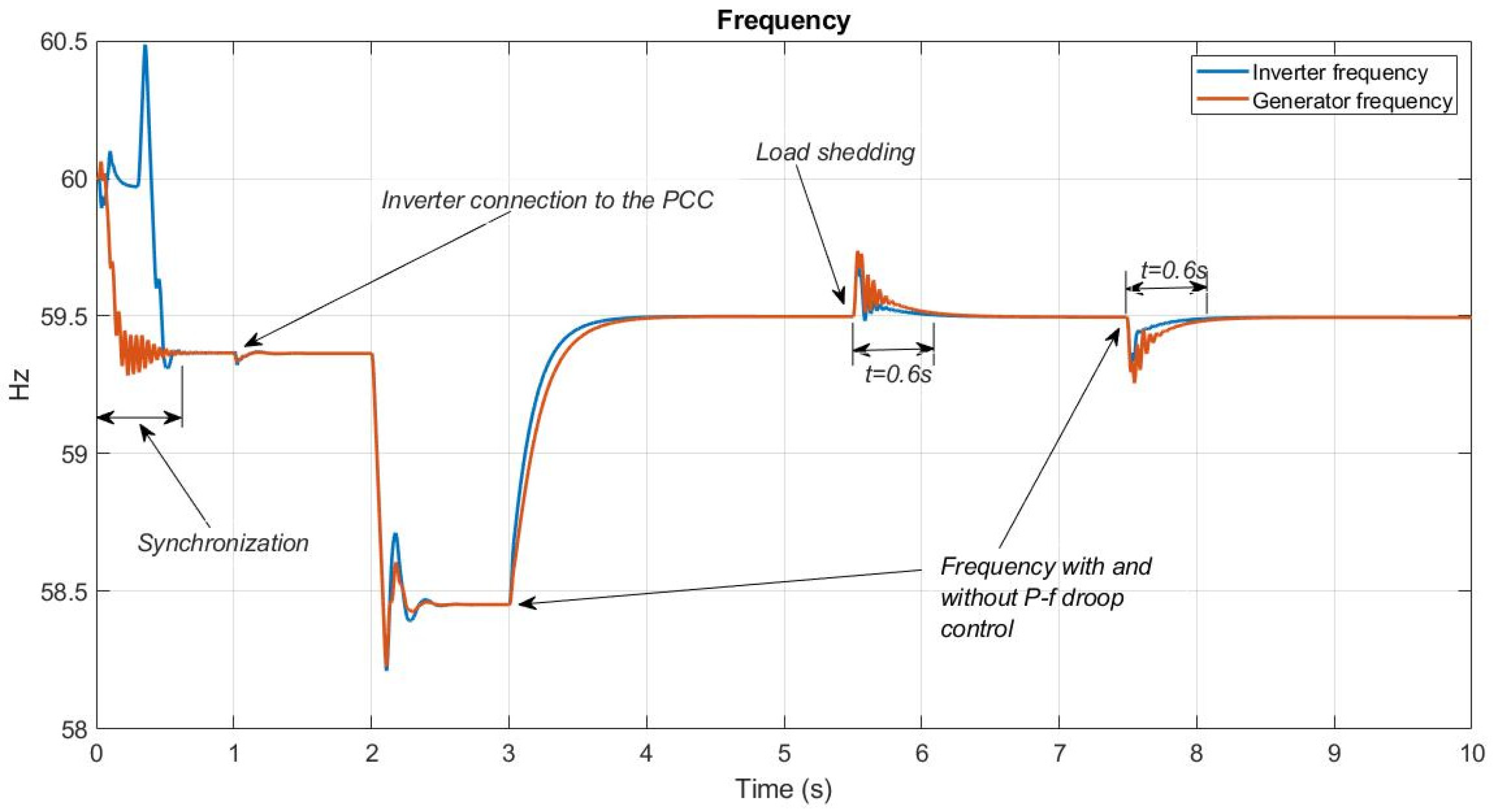
5.1. Frequency Response
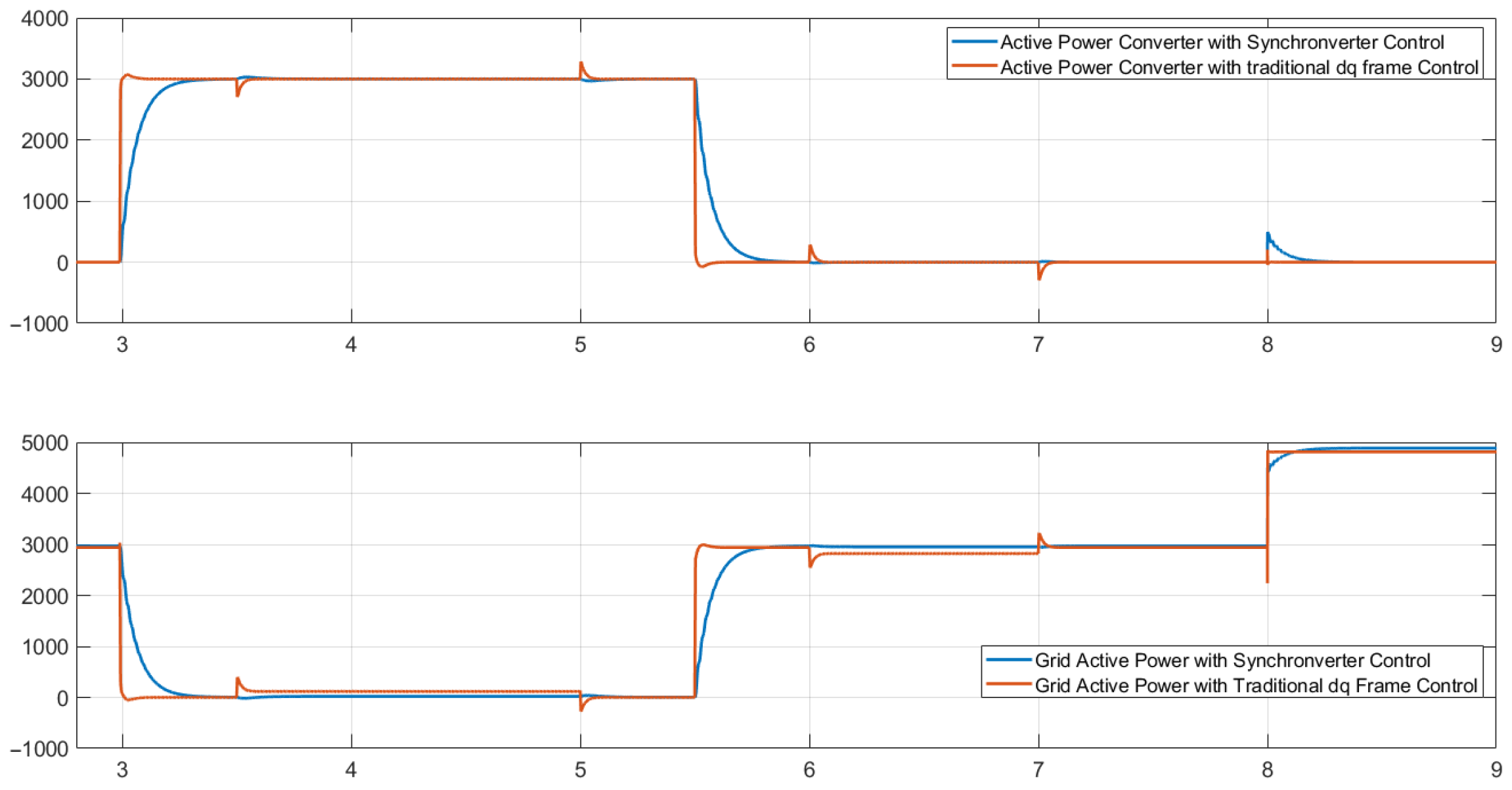
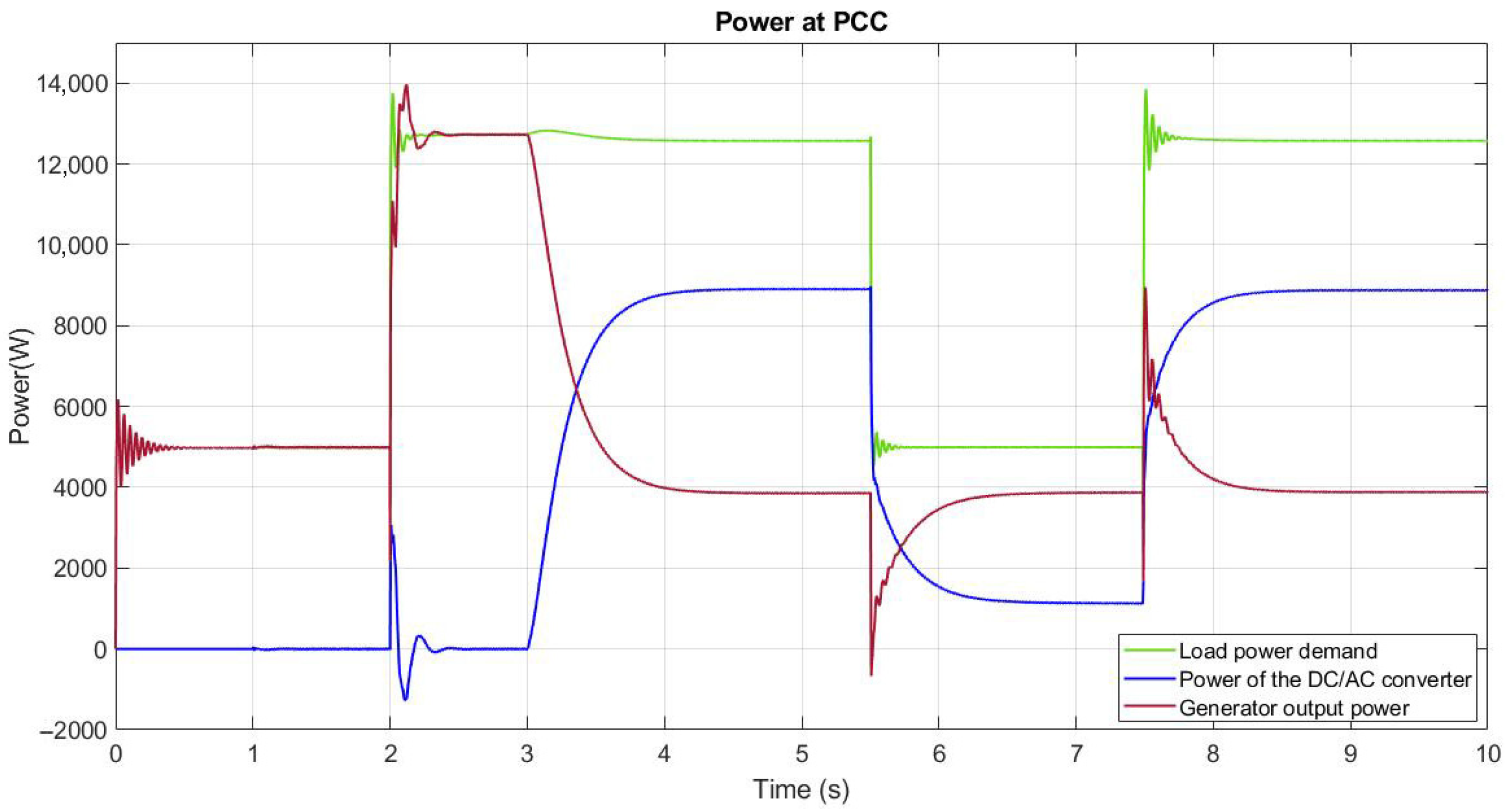
5.2. Active Power Transfer
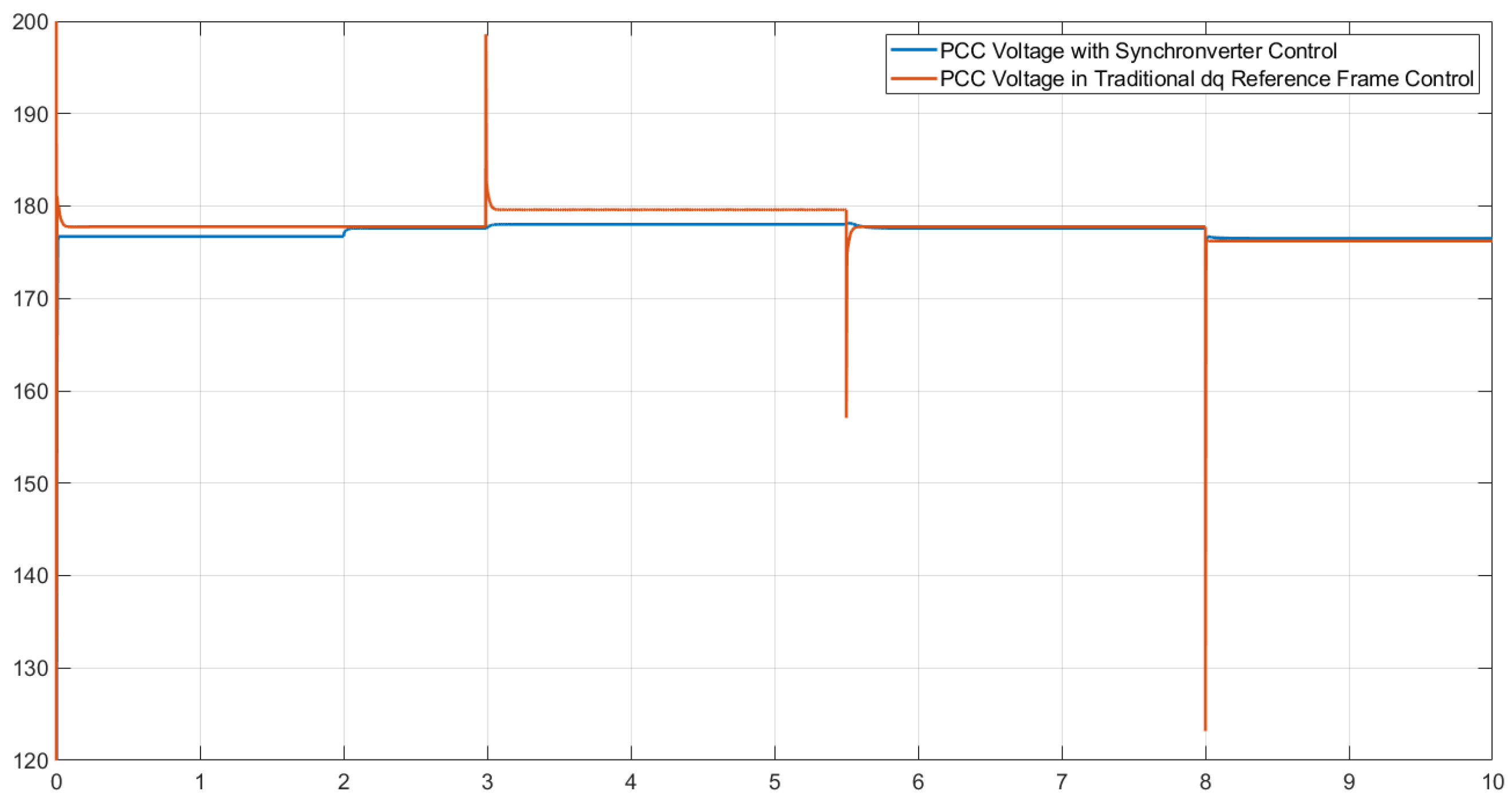
5.3. Voltage Regulation
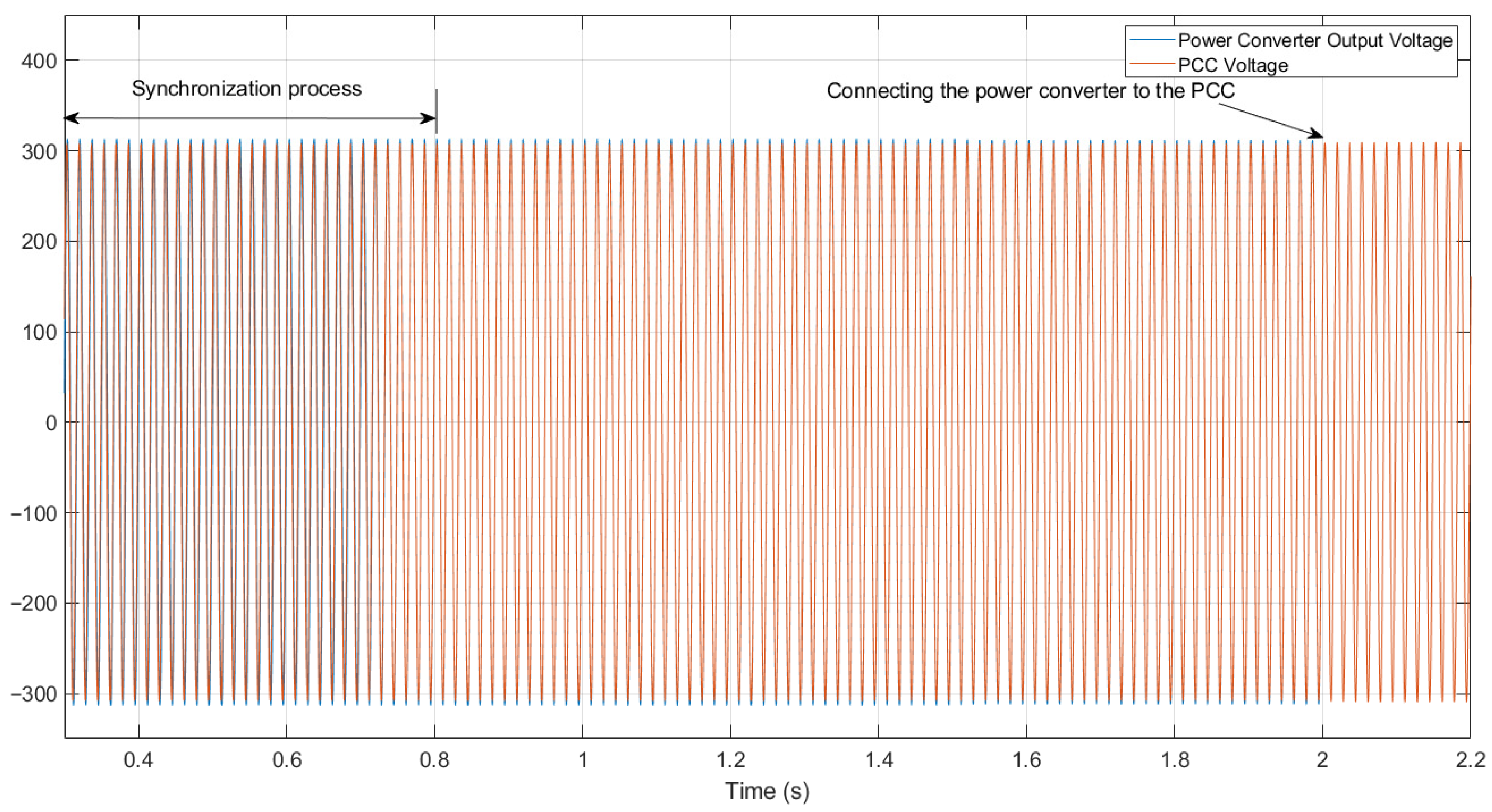
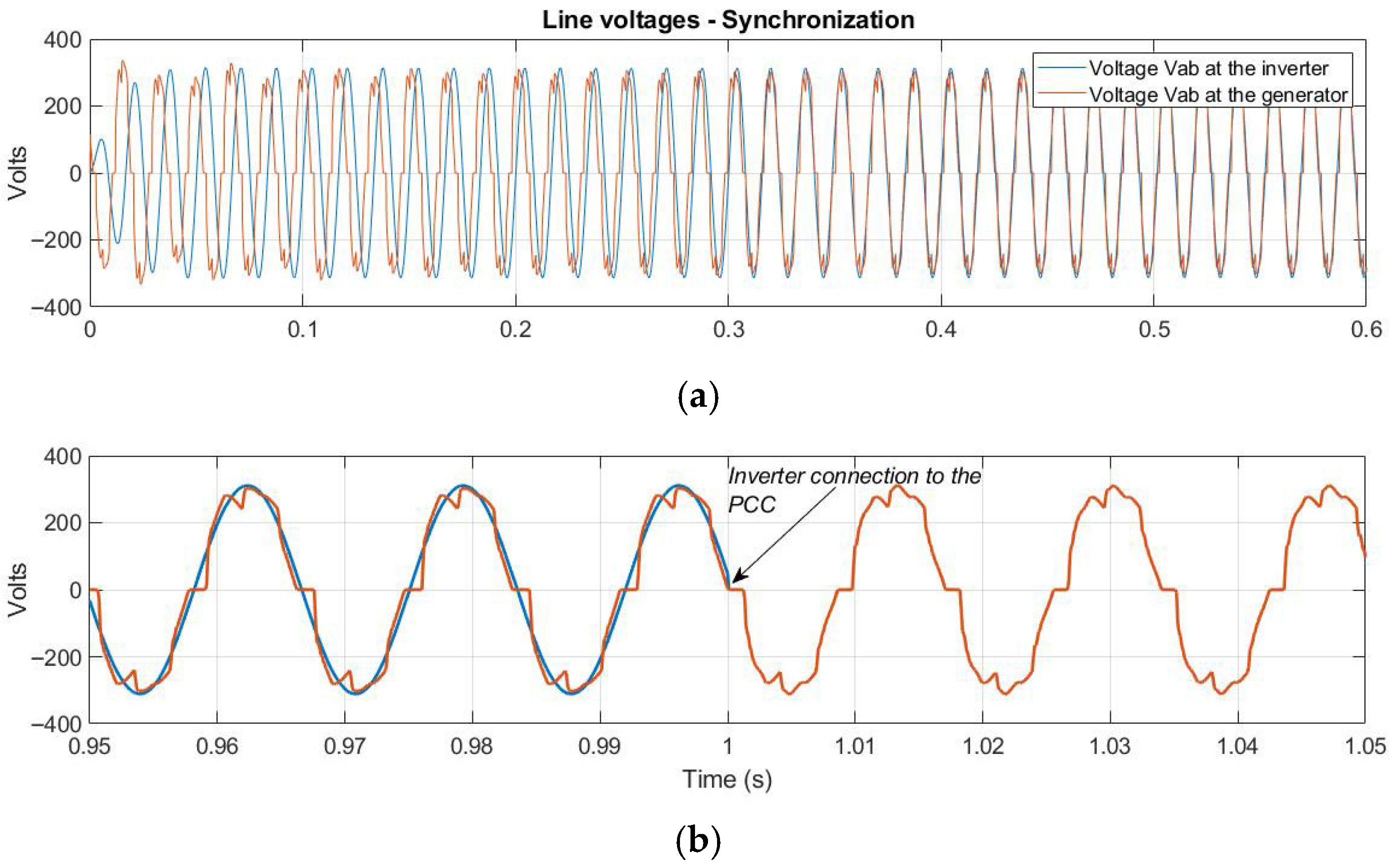
5.4. Synchronization Without PLL
5.5. Simulation of DC/AC Converter Under Weak Grid Conditions and Frequency Variation
- Grid synchronization of the DC/AC converter occurs at t = 0.4 s, and its connection to the grid is executed at t = 1 s. The connection is performed manually (Figure 11). This connection step can be automated, a task planned for future experiments.
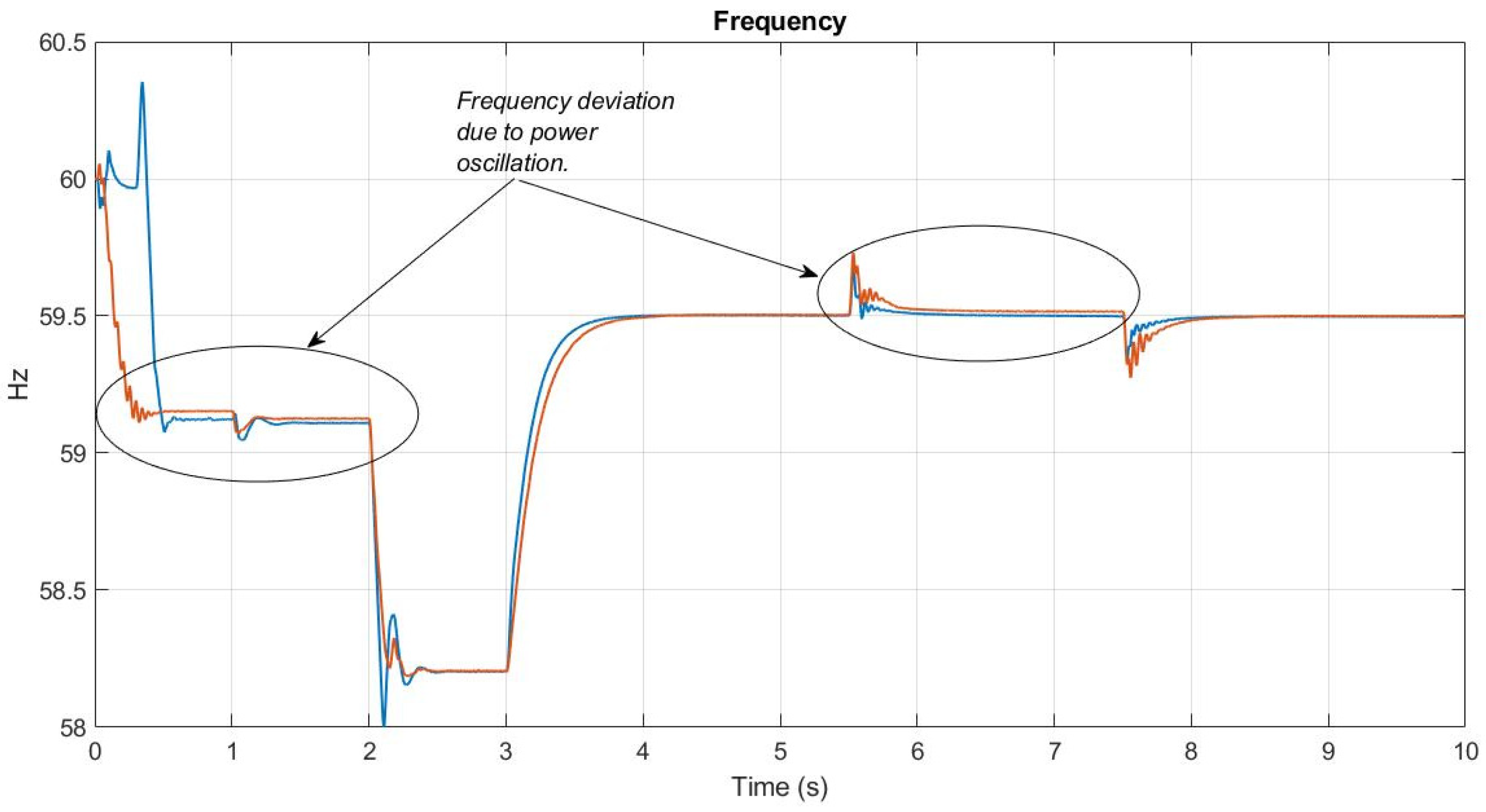
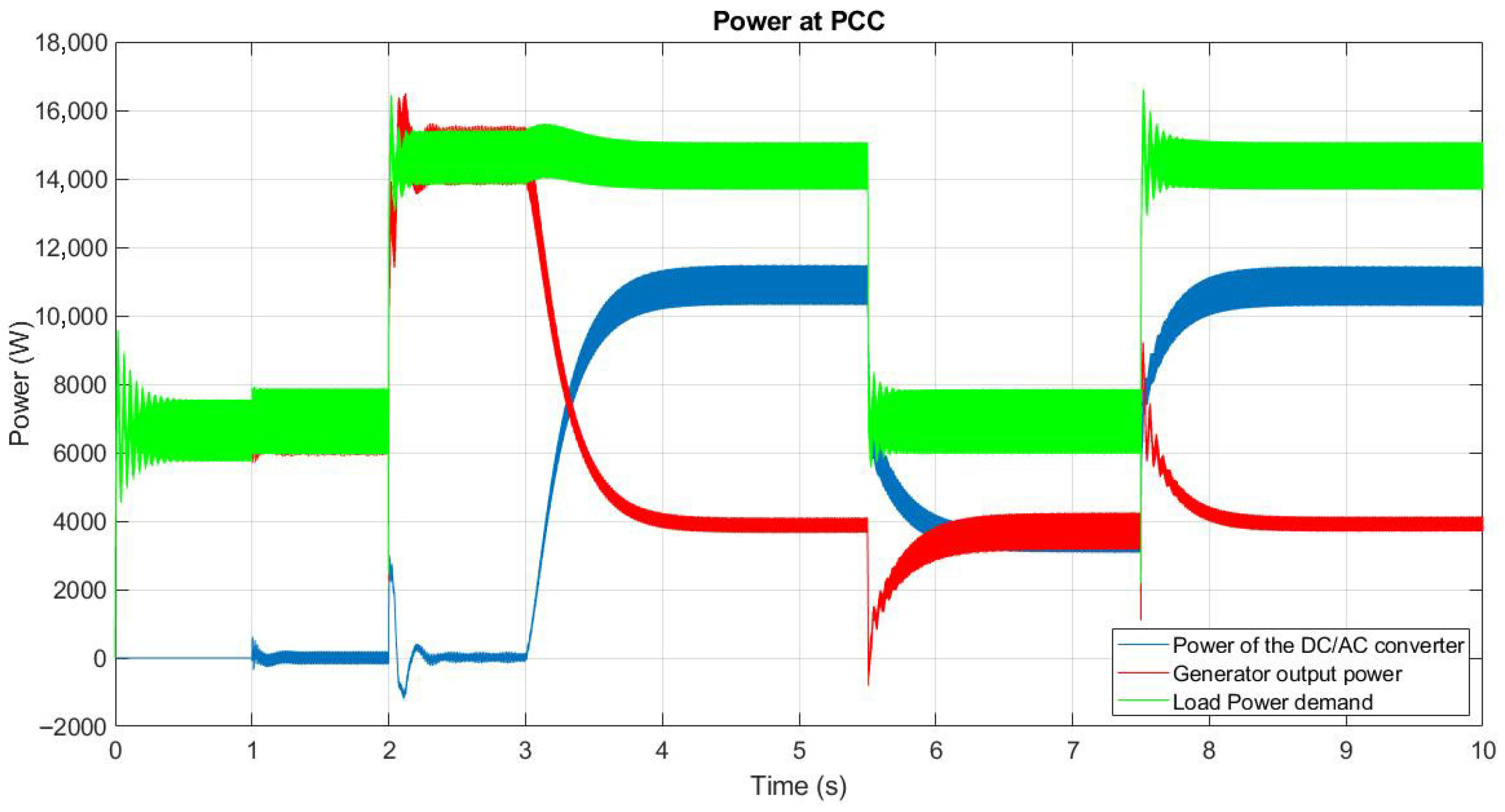
- A sudden load at the PCC at t = 2 s exceeds the generator’s nominal capacity (Figure 12—green line), forcing the frequency to drop below the 58.8 Hz limit established by the IEEE 1547-2018 standard. Figure 12 shows this frequency drop, and Figure 13 shows the increase in power delivered by the generation to the PCC, reaching approximately 13 kW (red line).
- The DC/AC converter with the synchronverter begins operation to restore the frequency to normal ranges. Here, the power contribution from each generation source is 8.9 kW from the DC/AC converter (Figure 13—blue line) and 3.86 kW from the generator connected to the PCC (Figure 13—red line). This corresponds to a slight drop in the load’s power, attributed to voltage regulation. Figure 12 shows the restoration of the PCC frequency to permissible operating levels (f = 59.5 Hz).
- Sudden load shedding occurs at t = 5.5 s to verify the frequency behavior and power sharing while the DC/AC converter is injecting power into the grid, prioritizing frequency regulation. The frequency remains constant after a short operating transient, which lasts 0.5 s and causes a frequency increase of 0.24 Hz without exceeding permissible limits (see Figure 12).
- The previously described sudden load event is repeated at 7.5 s, identical to the load applied at 2.5 s. This time, the test is performed with the synchronverter’s power droop control active in the DC/AC converter. This event is executed to verify the droop control’s operation in the converter, acting as an inertia compensator with a correction time of 0.6 s.
5.6. Simulation of DC/AC Converter Under Weak Grid Conditions and Non-Linear Load
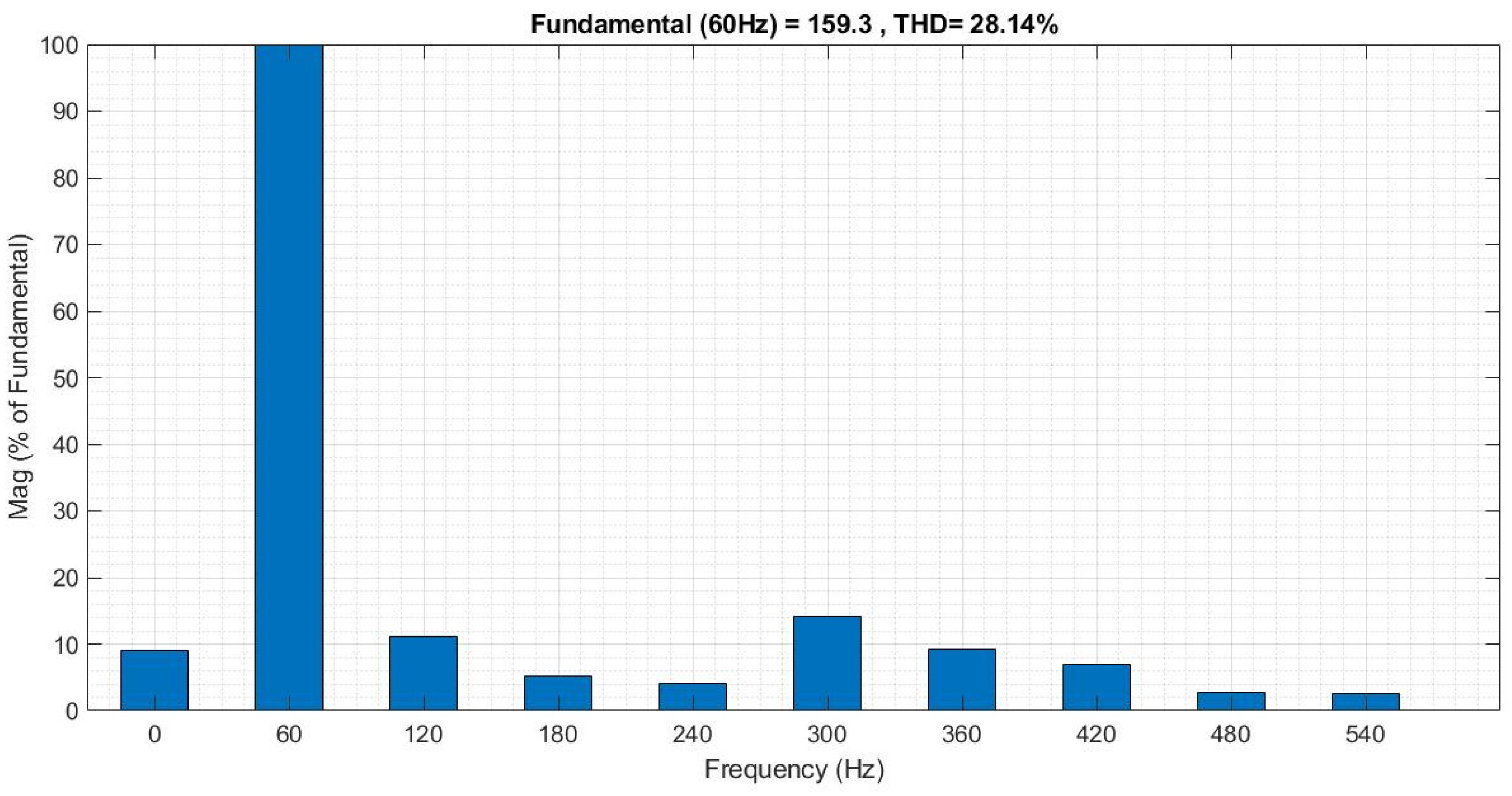
- Figure 14a shows the synchronization process of the DC/AC inverter’s waveform with the PCC signal, which contains harmonic content; synchronization is achieved at t = 0.4 s. Figure 14b shows the instant the inverter is connected to the PCC node, where the dominance of the node’s voltage is observed. Figure 15 displays the harmonic content of the voltage signal, which causes oscillations in the power exchanged between the converter and the grid and between the grid and the load. Despite the voltage’s harmonic content, synchronization is possible because the virtual impedance used in this process is equivalent to the coupling impedance (comprising Lg and Rg), which is small, thereby minimizing the power oscillations generated by voltage harmonics during synchronization. As a next step, the THD limit at which synchronization is no longer possible should be established, and the level of interaction and coupling between the power oscillations and the control loops must also be determined, as these topics are subjects for investigation and presentation in future work.
6. Conclusions
- Verify the real-time execution and computational feasibility of the PLL-less synchronverter algorithm integrated into a hardware controller.
- Evaluate the controller’s robustness against simulated sensor noise and parameter variations in the grid model.
- Quantify the impact of discrete-time implementation and processing delays on the system’s stability and dynamic response.
- Validate seamless synchronization and power transfer performance under various initially simulated testbeds, including voltage sags, frequency deviations, and phase jumps.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kundur, P.; Malik, O.P. Power System Stability and Control, 2nd ed.; McGraw-Hill: New York, NY, USA, 2022. [Google Scholar]
- Machowski, J.; Lubosny, Z.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control, 3rd ed.; John Wiley & Sons: Chichester, UK, 2020. [Google Scholar]
- Sáiz-Marín, E.; Zarei, M.E.; Medina, D.; Curbelo, Ó.; Babiano, A.M.; Berrueta, A.; Ursúa, A.; Sanchis, P. Doubly Fed Induction Generator Robust Design for Avoiding Converter-Driven Instability: Perspective. Energies 2025, 18, 2736. [Google Scholar] [CrossRef]
- Jansen, L.A.; Botha, M.G.; van Schoor, G.; Uren, K.R. Increasing Renewable Energy Penetration on Low-Voltage Networks: An Expert Knowledge Approach. Electricity 2024, 5, 804–825. [Google Scholar] [CrossRef]
- Nussipali, R.; Martyushev, N.V.; Malozyomov, B.V.; Konyukhov, V.Y.; Oparina, T.A.; Romanova, V.V.; Kononenko, R.V. Combined Power Generating Complex and Energy Storage System. Electricity 2024, 5, 931–946. [Google Scholar] [CrossRef]
- Fayek, H.H.; Rusu, E. Novel Combined Load Frequency Control and Automatic Voltage Regulation of a 100% Sustainable Energy Interconnected Microgrids. Sustainability 2022, 14, 9428. [Google Scholar] [CrossRef]
- Oshnoei, S.; Fathollahi, A.; Oshnoei, A.; Khooban, M.H. Microgrid Frequency Regulation Based on a Fractional Order Cascade Controller. Fractal Fract. 2023, 7, 343. [Google Scholar] [CrossRef]
- Li, T.; Wen, B.; Wang, H. A Self-Adaptive Damping Control Strategy of Virtual Synchronous Generator to Improve Frequency Stability. Processes 2020, 8, 291. [Google Scholar] [CrossRef]
- Liu, R.; Wang, S.; Liu, G.; Wen, S.; Zhang, J.; Ma, Y. An Improved Virtual Inertia Control Strategy for Low Voltage AC Microgrids with Hybrid Energy Storage Systems. Energies 2022, 15, 442. [Google Scholar] [CrossRef]
- Torres, E.; Sanchez, V.M.; Ramirez, J.M. Synchronverter Assessment for the Frequency Regulation of Control Areas Encompassing Renewable Distributed Generation. Int. J. Hydrogen Energy 2021, 46, 26138–26151. [Google Scholar] [CrossRef]
- Ramírez, J.M.; Montalvo, E.T.; Nuño, C.I. Modelling, Synchronisation, and Implementation of the Virtual Synchronous Generator: A Study of Its Reactive Power Handling. Electr. Eng. 2020, 102, 1605–1619. [Google Scholar] [CrossRef]
- Shadoul, M.; Ahshan, R.; AlAbri, R.S.; Al-Badi, A.; Albadi, M.; Jamil, M. A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications. Energies 2022, 15, 8406. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.-Y. Virtual Inertia-Based Inverters for Mitigating Frequency Instability in Grid-Connected Renewable Energy System: A Review. Appl. Sci. 2019, 9, 5300. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, Y.; Chen, Y.; Shi, J.; Yang, Y.; Li, W.; Li, K. A Cooperative Adaptive VSG Control Strategy Based on Virtual Inertia and Damping for Photovoltaic Storage System. Energies 2025, 18, 1505. [Google Scholar] [CrossRef]
- Youzhuo, Z.; Yutao, X.; Yekui, Y.; Long, H.; Yuqing, Y. Application of adaptive virtual synchronous generator based on improved active power loop in photovoltaic storage systems. Front. Energy Res. 2025, 12, 2024. [Google Scholar] [CrossRef]
- Gurski, E.; Kuiava, R.; Perez, F.; Benedito, R.A.S.; Damm, G. A Novel VSG with Adaptive Virtual Inertia and Adaptive Damping Coefficient to Improve Transient Frequency Response of Microgrids. Energies 2024, 17, 4370. [Google Scholar] [CrossRef]
- Younis, T.; Ismeil, M.; Hussain, E.K.; Orabi, M. Single-Phase Self-Synchronized Synchronverter with Current-Limiting Capability. In Proceedings of the 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 848–853. [Google Scholar]
- Huang, L.; Xin, H.; Dong, W.; Dörfler, F. Impacts of Grid Structure on PLL-Synchronization Stability of Converter-Integrated Power Systems. IFAC-PapersOnLine 2022, 55, 264–269. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, X.; Hu, C.; Xu, H.; Gu, J.; Cao, W. Self-tuning Virtual Synchronous Generator Control for Improving Frequency Stability in Autonomous Photovoltaic-Diesel Microgrids. J. Mod. Power Syst. Clean Energy 2019, 6, 482–494. [Google Scholar] [CrossRef]
- Xu, H.; Yu, C.; Liu, C. An Improved Virtual Inertia Algorithm of Virtual Synchronous Generator. J. Mod. Power Syst. Clean Energy 2020, 8, 2. [Google Scholar] [CrossRef]
- Meng, J.; Wang, Y.; Fu, C.; Wang, H. Adaptive Virtual Inertia Control of Distributed Generator for Dynamic Frequency Support in Microgrid. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–5. [Google Scholar]
- Ren, M.; Li, T.; Shi, K. Coordinated Control Strategy of Virtual Synchronous Generator Based on Adaptive Moment of Inertia and Virtual Impedance. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 99–110. [Google Scholar] [CrossRef]
- Meng, J.; Wang, Y.; Peng, J.; Xu, L.; Yin, J. Flexible Virtual Synchronous Generator Control for Distributed Generator with Adaptive Inertia. Electr. Power Compon. Syst. 2019, 47, 128–140. [Google Scholar] [CrossRef]
- Li, J.; Wen, B.; Wang, H. Adaptive Virtual Inertia Control Strategy of VSG for Micro-Grid Based on Improved Bang-Bang Control Strategy. IEEE Access 2019, 7, 39509–39514. [Google Scholar] [CrossRef]
- Venkatraman, A.; Markovic, U.; Shchetinin, D.; Vrettos, E.; Aristidou, P.; Hug, G. Improving Dynamic Performance of Low-Inertia Systems Through Eigensensitivity Optimization. IEEE Trans. Power Syst. 2021, 36, 4075–4088. [Google Scholar] [CrossRef]
- Zhang, C.; Dou, X.; Zhang, Z.; Lou, G.; Yang, F.; Li, G. Inertia-Enhanced Distributed Voltage and Frequency Control of Low-Inertia Microgrids. IEEE Trans. Power Syst. 2021, 36, 4270–4280. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, D.; Yin, S.; Lei, Y.; He, T. Improved Adaptive Inertia and Damping Coefficient Control Strategy of VSG Based on Optimal Damping Ratio. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 102–107. [Google Scholar]
- Fu, J.; Wen, G.; Yu, W.; Huang, T.; Yu, X. Consensus of Second-Order Multiagent Systems with Both Velocity and Input Constraints. IEEE Trans. Ind. Electron. 2019, 66, 7946–7955. [Google Scholar] [CrossRef]
- Tang, W.; Yuan, W.; Li, X.; Chen, L. Virtual Inertia Optimization for Microgrids with High Renewable Penetration Considering Frequency Stability Constraints. In Proceedings of the 2022 6th International Conference on Power and Energy Engineering (ICPEE), Shanghai, China, 25–27 November 2022; pp. 96–101. [Google Scholar]
- Poungdokmai, A.; Polmai, S. Stabilization of Power System Using Improved Virtual Inertia of Virtual Synchronous Generator. In Proceedings of the 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–5. [Google Scholar]
- Song, J.; Gao, X.; Sun, H.; Guo, W. Improved Virtual Inertia Damping Adaptive VDG Control Strategy for DC Microgrid Hybrid Energy Storage Converter. In Proceedings of the 4th International Conference on Electrical Engineering and Control Technologies (CEECT), Shanghai, China, 16–18 December 2022; pp. 1188–1192. [Google Scholar]
- Su, J.; Hong, Z.; Qing, W.; Liang, L.; Wenju, L.; Yuxiao, Y.; He, H. An Improving Planning Method for the Receiving-End System Considering Multiple Sources of Inertia Support. In Proceedings of the 5th International Conference on Power and Energy Applications (ICPEA), Guangzhou, China, 18–20 November 2022; pp. 452–458. [Google Scholar]
- Hasan, M.M.; Chowdhury, A.H. Droop Control Based Virtual Inertia Emulation for Stability Enhancement of a Microgrid System. In Proceedings of the 12th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 21–23 December 2022; pp. 224–227. [Google Scholar]
- Jithin, T.; Rajeev, T.; Jithin, S. Inertia Control of Hybrid AC/DC Microgrid Using Supercapacitors. In Proceedings of the 2022 Second International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 1–3 March 2022; pp. 1–4. [Google Scholar]
- Chen, S.; Zhang, X.; Wu, Y.; Zhu, Q.; Bao, C.; Zhan, X. Segmented Adaptive Control of Virtual Inertia for Virtual Synchronous Machines. In Proceedings of the 7th International Conference on Power and Renewable Energy (ICPRE 2022), Shanghai, China, 23–26 September 2022; pp. 176–181. [Google Scholar]
- Maaruf, M.; Ahmad, S.; Khalid, M. Improving the Frequency Response of High Renewable Penetrated Islanded Microgrids. In Proceedings of the 2022 IEEE PES 14th Asia-Pacific Power and Energy Engineering Conference (APPEEC), Melbourne, Australia, 20–23 November 2022; pp. 1–6. [Google Scholar]
- Nandi, R.; Tripathy, M.; Gupta, C.P. Adaptive Virtual Impedance Droop Control for AC Microgrid Based on Voltage and Current Deviations. In Proceedings of the 2022 IEEE Global Conference on Computing, Power and Communication Technologies (GlobConPT), New Delhi, India, 23–25 September 2022; pp. 1–6. [Google Scholar]
- Luo, C.; Chen, Y.; Xu, Y.; Wang, Z.; Li, Q. Transient Stability Analysis and Enhancement for VSG with Virtual Impedance-Based Current Limitation. In Proceedings of the 48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar]
- Huang, M.; Li, H. Disturbance Rejection Control of Grid-Forming Inverter for Line Impedance Parameter Perturbation in Weak Power Grid. Electronics 2024, 13, 1926. [Google Scholar] [CrossRef]
- Zhang, Y.; Mou, J.; Zhang, F.; Huang, N. Modeling and Stability Analysis Based on Internal Voltage Dynamics in Synchronverter. Electronics 2023, 12, 700. [Google Scholar] [CrossRef]
- NTC 1340; Electrotechnics. Rated Voltages and Frequencies in Electric Power Systems for Public Service Networks. ICONTEC: Bogota, Colombia, 2013.
- IEEE 1547-2003; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: New York, NY, USA, 2018.
- Dokus, M.; Mertens, A. On the Coupling of Power-Related and Inner Inverter Control Loops of Grid-Forming Converter Systems. IEEE Access 2021, 9, 16173–16192. [Google Scholar] [CrossRef]
- Wen, T.; Zhu, D.; Zou, X.; Jiang, B.; Peng, L.; Kang, Y. Power Coupling Mechanism Analysis and Improved Decoupling Control for Virtual Synchronous Generator. IEEE Trans. Power Electron. 2021, 36, 3028–3041. [Google Scholar] [CrossRef]
- Kumar, R.; Chaudhari, M.; Chaturvedi, P. Analysis of Synchronverter and PLL-Less Control for Three-Phase VSI in AC Microgrids. In Proceedings of the 2024 Third International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 18–20 January 2024; pp. 810–816. [Google Scholar] [CrossRef]



| Ref. | Year | Control Strategy | Analysis | Controller Function | Conclusion | Disadvantage | P+ | P− | T |
|---|---|---|---|---|---|---|---|---|---|
| [20] | 2019 | VSG droop with auto-tuning | Numerical and experimental | Reduces overshoot (+5) Regulates frequency (+4) | Reduces the ROCOF Reduces frequency deviation | Response capability directly depends on the number of batteries (−3) Islanded mode only (−2) | 9 | 5 | 4 |
| [21] | 2020 | VSG with droop control | Numerical and experimental | Reduces overshoot (+5) Regulates frequency (+4) | Significantly reduces response time by mitigating overshoot during active power injection | Only step response tested with fixed parameters Not evaluated with multiple generation sources Islanded mode only (−2) | 9 | 2 | 7 |
| [22] | 2021 | VSG with droop and current control | Numerical | Reduces overshoot (+5) Regulates frequency (+5) | Controls sudden frequency changes | Stabilization time greater than 10 s (−5) | 10 | 5 | 5 |
| [23] | 2021 | VSG with virtual impedance | Numerical | Reduces response time to a disturbance (+3) Mitigates overshoot (+5) | Very fast frequency response without offset | Control tested only for one generator and one load High computational cost (−3) | 8 | 3 | 5 |
| [24] | 2019 | VSG with droop for frequency and voltage | Numerical and experimental | Dynamic inertia is directly dependent on frequency (+4) Smooths the ROCOF (+3) Reduces overshoot (+5) | Mitigates the ROCOF Reduces overshoot | Significant computational burden (−3) Multiple nested control loops (−3) Very long stabilization time (15 s) (−5) Secondary-level control | 12 | 11 | 1 |
| [25] | 2019 | VSG with droop for frequency and voltage | Numerical | Controls overshoot (+5) Regulates voltage (+4) Grid connection support (+4) Regulates frequency (+4) | Fast response time Dynamic behavior Increases inertia Reduces the ROCOF Mitigates frequency nadir Very low complexity | Reactive power loop and voltage regulation not analyzed | 17 | 0 | 17 |
| [26] | 2021 | VSG with optimized dynamic virtual inertia and damping control | Numerical | Mitigates frequency nadir Reduces the ROCOF (+3) Reduces overshoot (+5) | Distributes inertia evenly across each microgrid node | Very high computational cost (−3) | 8 | 3 | 5 |
| [27] | 2021 | VSG with per-node droop control. Nearest node to node compensation. | Numerical and experimental | Mitigates the Rocof (+5) Mitigates RocoV. | Reduced battery implementation Uniform energy distribution among nodes | High computational cost (−3) High implementation cost due to communication equipment (−2) Secondary level control | 5 | 5 | 0 |
| [28] | 2022 | VSG with droop adapted according to damping coefficient | Numerical | Reduces overshoot (+5) Reduces response time(+3) | Coordinated inertia increase with damping coefficient | Stabilization time greater than 3 s (−5) | 8 | 5 | 3 |
| [29] | 2020 | Microgrid control using VSG based on graph theory | Numerical | Mitigates dependence on battery banks Regulates frequency (+4) Regulates voltage (+4) Mitigates power drop with energy from the nearest node. | Reduces implementation costs No need for external sources; self-managed via distributed generation | Secondary level control Response time greater than 3 s (−5) High computational cost (−3) | 8 | 8 | 0 |
| [30] | 2022 | VSG with optimization method | Numerical | Reduces frequency response time (+3) Reduces the ROCOF (+3) | Stabilization time below 1 s | Significant computational burden (−3) Difficult implementation (−2) | 6 | 5 | 1 |
| [31] | 2022 | VSG with virtual inertia and damping | Numerical and experimental | Reduces response time to small-scale frequency fluctuations (+3) | Reduces response time Increases inertia with the help of additional storage | Uncontrolled overshoot Fast frequency response, but with fluctuations; stabilization time exceeds 3 s (−5) | 11 | 5 | 6 |
| [32] | 2022 | VSG with increased damped inertia | Numerical | Reduces response time (+3) Reduces overshoot (+5) | Mitigates overshoot Improves response time | High cost due to batteries and supercapacitors (−2) | 8 | 2 | 6 |
| [33] | 2022 | VSG with PI and virtual inertia | Numerical | Reduces the ROCOF (+3) Decreases response time (+3) | Mitigates sudden frequency changes | Stabilization time greater than 1 s (−5) | 6 | 5 | 1 |
| [34] | 2022 | VSG with droop for frequency and voltage | Numerical | Compensates for active (+4) and reactive (+4) power variations Decreases the ROCOF (+3) | Increases inertia Response time under 1 s | Active power overshoot during frequency drops (−5) | 11 | 5 | 6 |
| [35] | 2022 | VGS with virtual inertia stored in supercapacitors | Numerical | Bidirectional control for the supercapacitor and compensate voltage imbalances (+1) Regulates voltage (+4) Regulates frequency (+4) Grid connection analysis (+4) | Increases inertia Reduces the number of electronic control components | High cost considering implementation with supercapacitors (−2) High computational cost (−3) | 13 | 5 | 8 |
| [36] | 2022 | VSG with segmented virtual inertia | Numerical | Improves reliability Reduces the ROCOF (+3) Improves response time (+3) | Decreases response time Controls overshoot | Significant computational burden (−3) | 6 | 3 | 3 |
| [37] | 2022 | VSG with virtual impedance control | Numerical | Reduces the ROCOF (+3) Enhanced response time (+3) Controlled overshoot (+5) | Distributes virtual inertia uniformly in the microgrid to respond faster to active power variations | Stabilization time greater than 6 s (−5) | 11 | 5 | 6 |
| [38] | 2022 | VSG with virtual impedance control | Numerical | Voltage imbalance reduction (+4) Harmonic distortion correction Frequency regulation (+4) Supports both linear and non-linear loads Stabilization time below 1 s (+3) Analyzed in grid-connected operation (+4) | Adapts impedance according to load behavior Few control elements required | High computational cost (−3) | 15 | 3 | 12 |
| [39] | 2022 | VSG with virtual impedance control | Numerical | Optimizes control parameters based on load variations Regulates frequency (+4) Regulates voltage (+4) Significantly reduced stabilization time (+3) | Reduces maximum transmission power Reduces transient stability margin Maintains voltage levels within established limits | Significantly increases overshoot compared to other control methods Complex implementation (−2) | 11 | 2 | 9 |
| [17] | 2024 | Novel VSG with Adaptive Virtual Inertia and Adaptive Damping Coefficient | Numerical | Reduce overshoot (+4) Regulate frequency (+4) Significantly reduced stabilization time (+3) | Improve the transient frequency response, | High computational cost (−3) Depends on a dispatchable power source for frequency support, (−3) | 11 | 6 | 5 |
| Parameter | Symbol | Description | Value | Unit |
|---|---|---|---|---|
| Power and Grid | ||||
| Nominal Power | Snom | Nominal apparent power of the inverter | 5000 | VA |
| Nominal Grid Freq. | fn | Nominal grid frequency | 60 | Hz |
| Nominal Grid Ang. Freq. | ωn | Nominal grid angular frequency (2π fn) | 377 | rad/s |
| Line-to-Line Voltage | VLL | RMS line-to-line grid voltage | 220 | V |
| DC Bus Voltage | VDC | Inverter DC link voltage | 500 | V |
| Active Power Loop | ||||
| Virtual Inertia | J | Moment of inertia of the virtual rotor | 0.00117 | kg·m2 |
| Freq. Droop Coeff. | Dp | Damping/droop coefficient for the P-ω loop | 0.703 | N·m·s/rad |
| Active Power Filter TC | Tf | Time constant of the active power measurement filter | 0.01 | s |
| Reactive Power Loop | ||||
| Voltage Droop Coeff. | Dq | Droop coefficient for the Q-V loop | 0.001 | V/VAR |
| Voltage Loop Integrator TC | Tq | Time constant of the reactive power integrator | 0.1 | s |
| Voltage Controller Gain | Kv | Proportional gain for internal voltage regulation | 1/377 | - |
| Synchronization | ||||
| Virtual Inductance | Lg | Inductive part of the virtual impedance | 1 | mH |
| Virtual Resistance | Rg | Resistive part of the virtual impedance | 0.1 | Ω |
| LCL Filter | ||||
| Inverter-Side Inductor | Ls | Inverter-side inductance of the LCL filter | 2 | mH |
| Inverter-Side Resistor | Rs | Resistive part of inductor at the inverter-side LCL filter | 0.1 | Ω |
| Grid-Side Inductor | Lg | Grid-side inductance of the LCL filter | 1 | mH |
| Grid-Side Resistor | Rg | Resistive part of inductor at the grid-side LCL filter | 0.1 | Ω |
| Filter Capacitor | C | Capacitance of the LCL filter | 10 | µF |
| Damping Resistor | Rd | Damping resistance in series with C (not shown in Figure 4) | 1 | Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villada-Leon, C.A.; Posada Contreras, J.; Rosas-Caro, J.C.; Núñez-Rodríguez, R.A.; Valencia, J.C.; Valdez-Resendiz, J.E. Control Algorithm for an Inverter-Based Virtual Synchronous Generator with Adjustable Inertia. Eng 2025, 6, 231. https://doi.org/10.3390/eng6090231
Villada-Leon CA, Posada Contreras J, Rosas-Caro JC, Núñez-Rodríguez RA, Valencia JC, Valdez-Resendiz JE. Control Algorithm for an Inverter-Based Virtual Synchronous Generator with Adjustable Inertia. Eng. 2025; 6(9):231. https://doi.org/10.3390/eng6090231
Chicago/Turabian StyleVillada-Leon, Christian A., Johnny Posada Contreras, Julio C. Rosas-Caro, Rafael A. Núñez-Rodríguez, Juan C. Valencia, and Jesus E. Valdez-Resendiz. 2025. "Control Algorithm for an Inverter-Based Virtual Synchronous Generator with Adjustable Inertia" Eng 6, no. 9: 231. https://doi.org/10.3390/eng6090231
APA StyleVillada-Leon, C. A., Posada Contreras, J., Rosas-Caro, J. C., Núñez-Rodríguez, R. A., Valencia, J. C., & Valdez-Resendiz, J. E. (2025). Control Algorithm for an Inverter-Based Virtual Synchronous Generator with Adjustable Inertia. Eng, 6(9), 231. https://doi.org/10.3390/eng6090231








