Numerical Analysis and Design of Hole and Electron Transport Layers in Lead-Free MASnIBr2 Perovskite Solar Cells
Abstract
1. Introduction
- Distinct Emphasis on MASnIBr2. While the majority of investigations into tin-based perovskites concentrate on MASnI3 or mixed halides (e.g., MASnIxBr3−x), our research specifically addresses MASnIBr2, a relatively underexplored yet promising material owing to its adjustable bandgap (1.75 eV) and superior stability in comparison to iodine-rich variants.
- Comprehensive parameter optimization. We concurrently optimize electron affinity, bandgap, thickness, and doping density for both the hole transport layer (HTL) and electron transport layer (ETL), demonstrating their interrelated impacts on device performance. This methodology extends the singular-parameter analyses commonly observed in the literature.
- Theoretical efficiency breakthrough. Our simulations attain a power conversion efficiency (PCE) of 20.42%, markedly surpassing prior experimental and simulation-derived results for MASnIBr2-based perovskite solar cells.
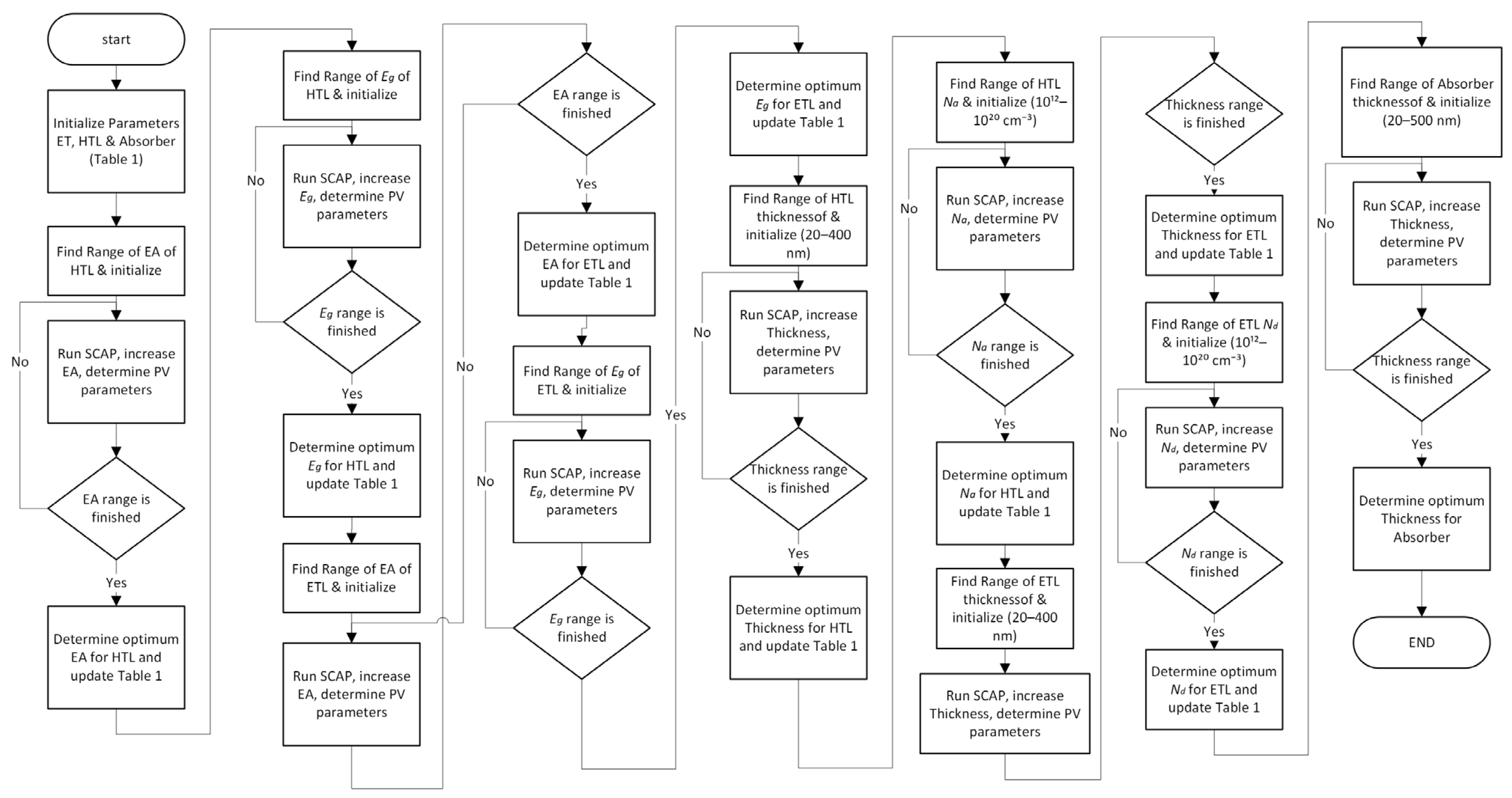
2. Approaches to Simulation and Physical Considerations
2.1. Models for Device Simulations
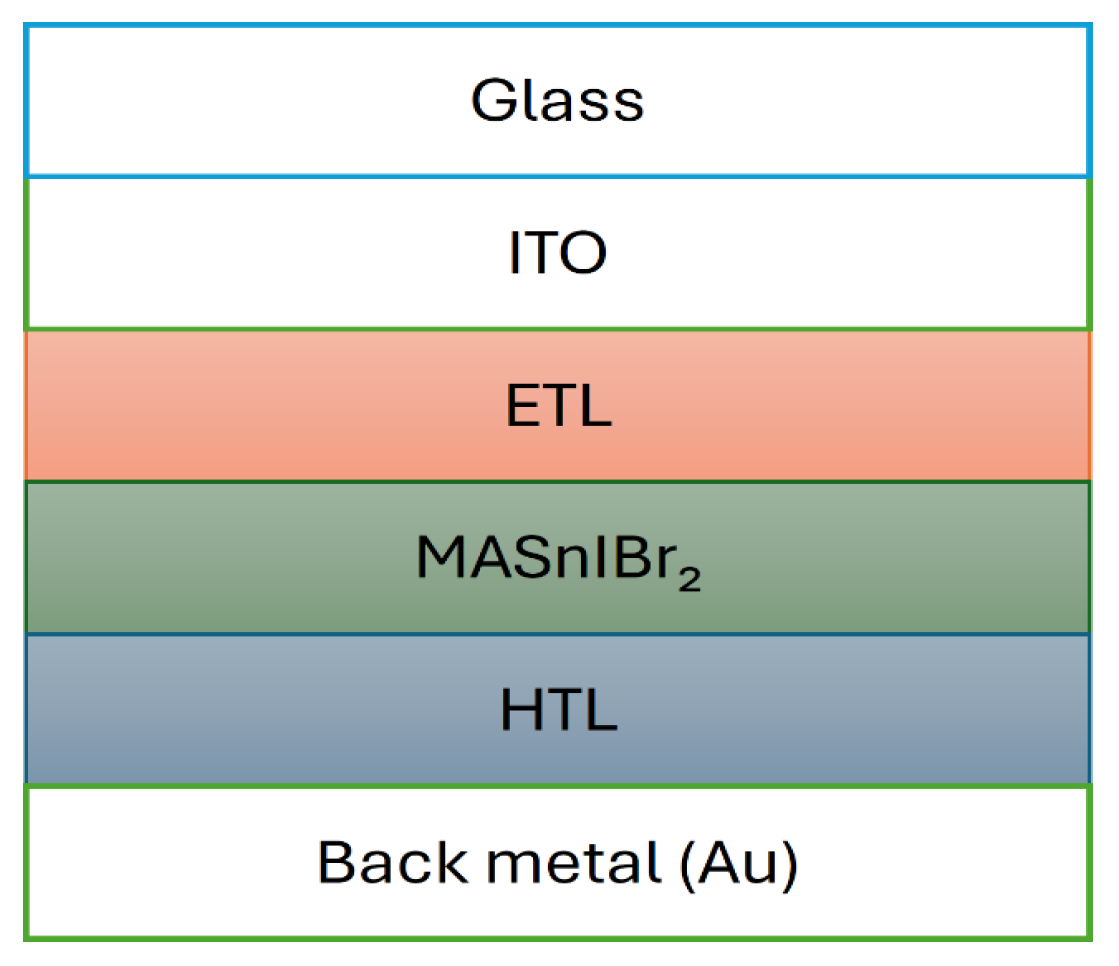
2.2. Proposed Solar Cell Design and Material Parameters
- Set values at random from the ranges given in Steps 1 and 2 for each of the parameters that were mentioned before.
- Obtain the maximum power conversion efficiency by simulating the hole transport layer to find its ideal EA. Refine the HTL electron affinity simulation parameter.
- Find the maximum power conversion efficiency by finding the optimal hole transport layer Eg. Set the simulation’s Eg parameter.
- Find the best electron transport layer EA that maximizes PCEs. Update the electron transport layer EA simulation parameter.
- Find the electron transport layer’s ideal Eg that maximizes PCEs. Update the electron transport layer Eg simulation parameter.
- Find the ideal hole transport layer thickness that maximizes PCEs. Update the thickness of the hole transport layer simulation parameter.
- Find the optimal hole transport layer Na that maximizes PCEs. Update the Na (hole transport layer) simulation parameter.
- Gain the maximum power conversion efficiency by finding the ideal thickness of the electron transport layer. Set the electron transport layer thickness parameter in the simulation.
- Obtain the maximum power conversion efficiency by finding the ideal electron transport layer Nd. Update the Nd (electron transport layer) simulation parameter.
- Under optimal conditions for the hole transport layer and the electron transport layer, find the MASnIBr2 thickness that maximizes PCEs.
- Simulate the photocurrent voltage characteristics of the fully optimized device structure.
- With an optimal hole transport layer and electron transport layer, find out the other responses of the optimized device. End the simulation.
3. Results and Discussion
3.1. Electron Affinity Optimization for the Hole Transport Layer
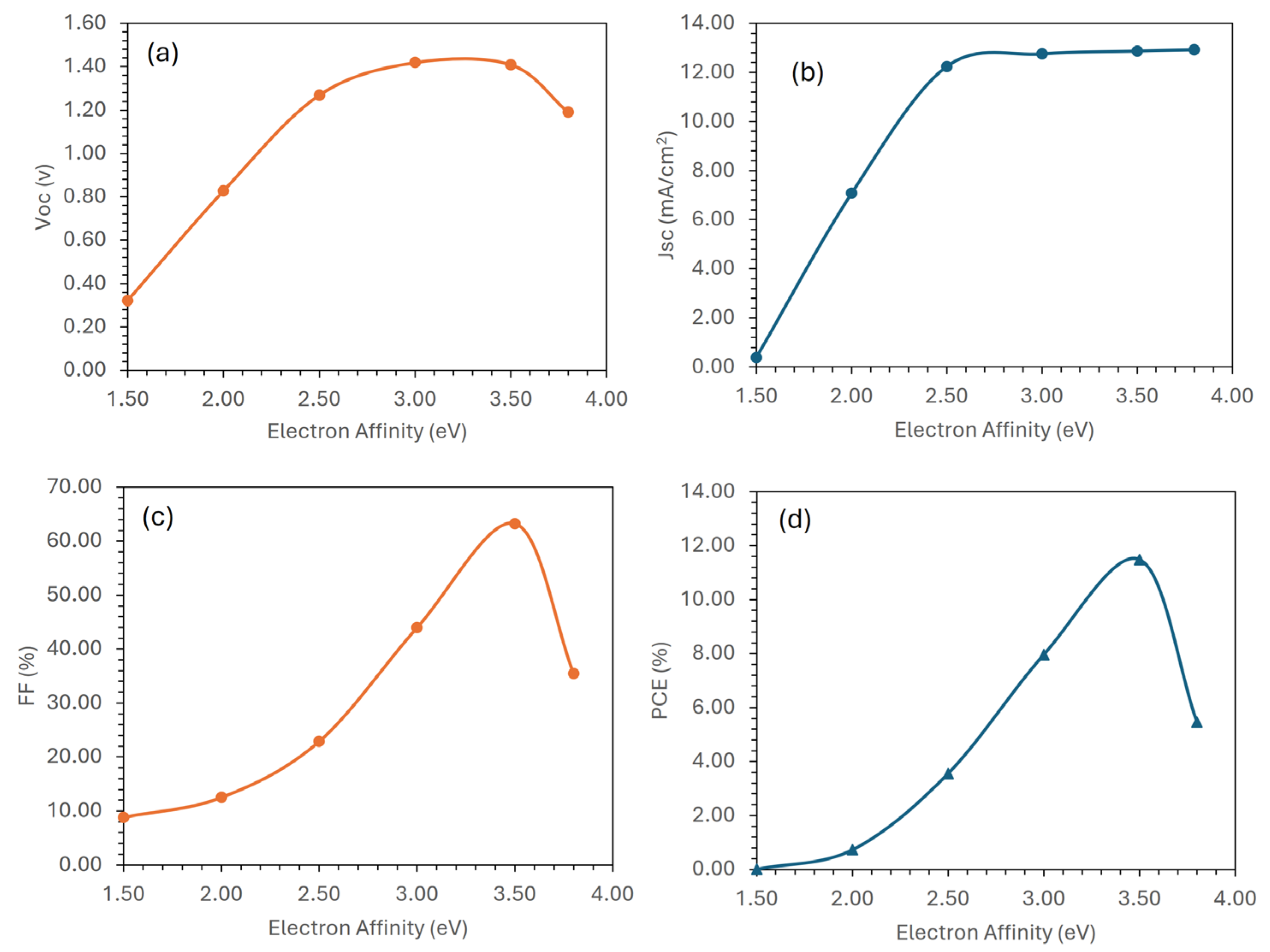
3.2. Energy Bandgap Optimization for the Hole Transport Layer
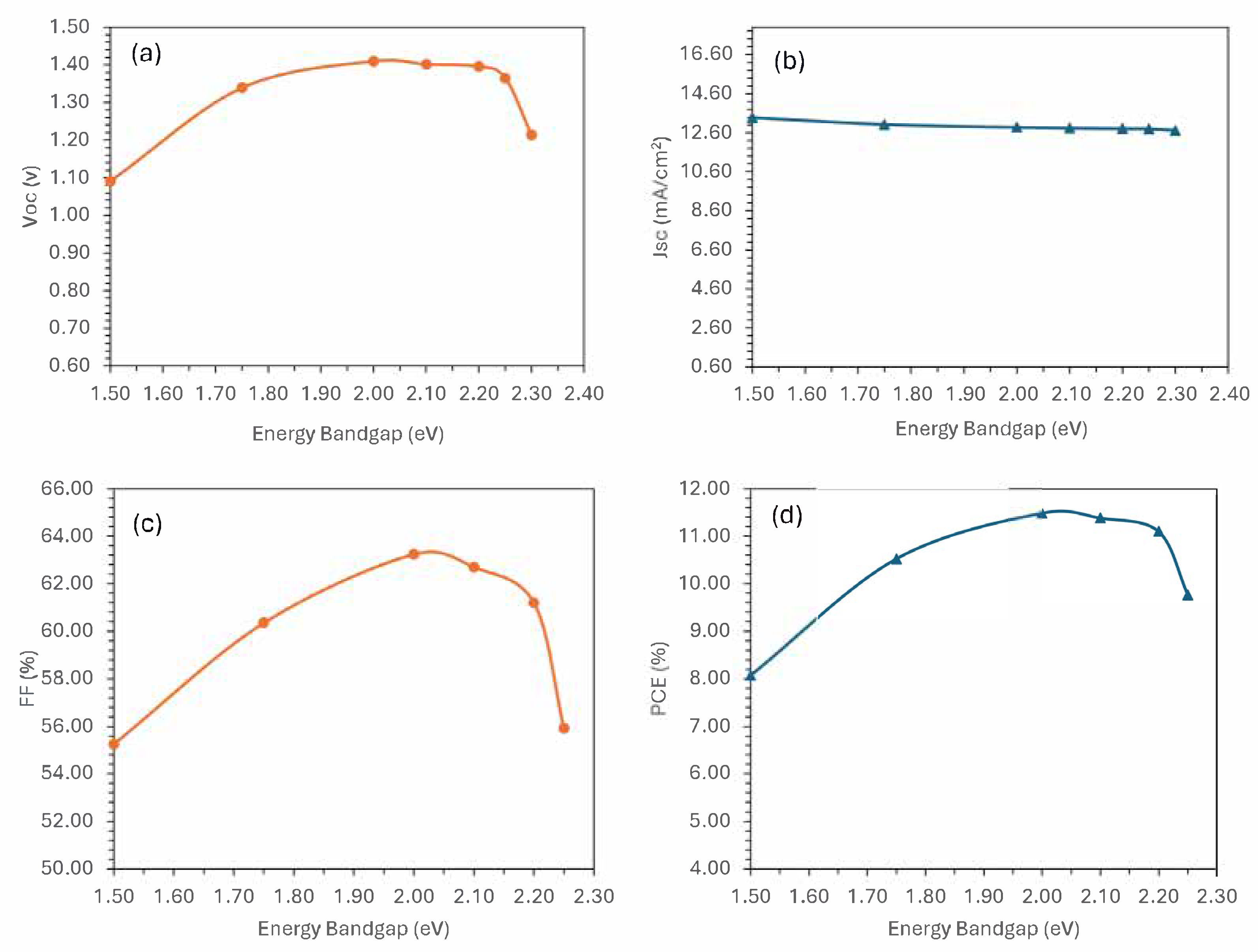
3.3. Electron Affinity Optimization for the Electron Transport Layer
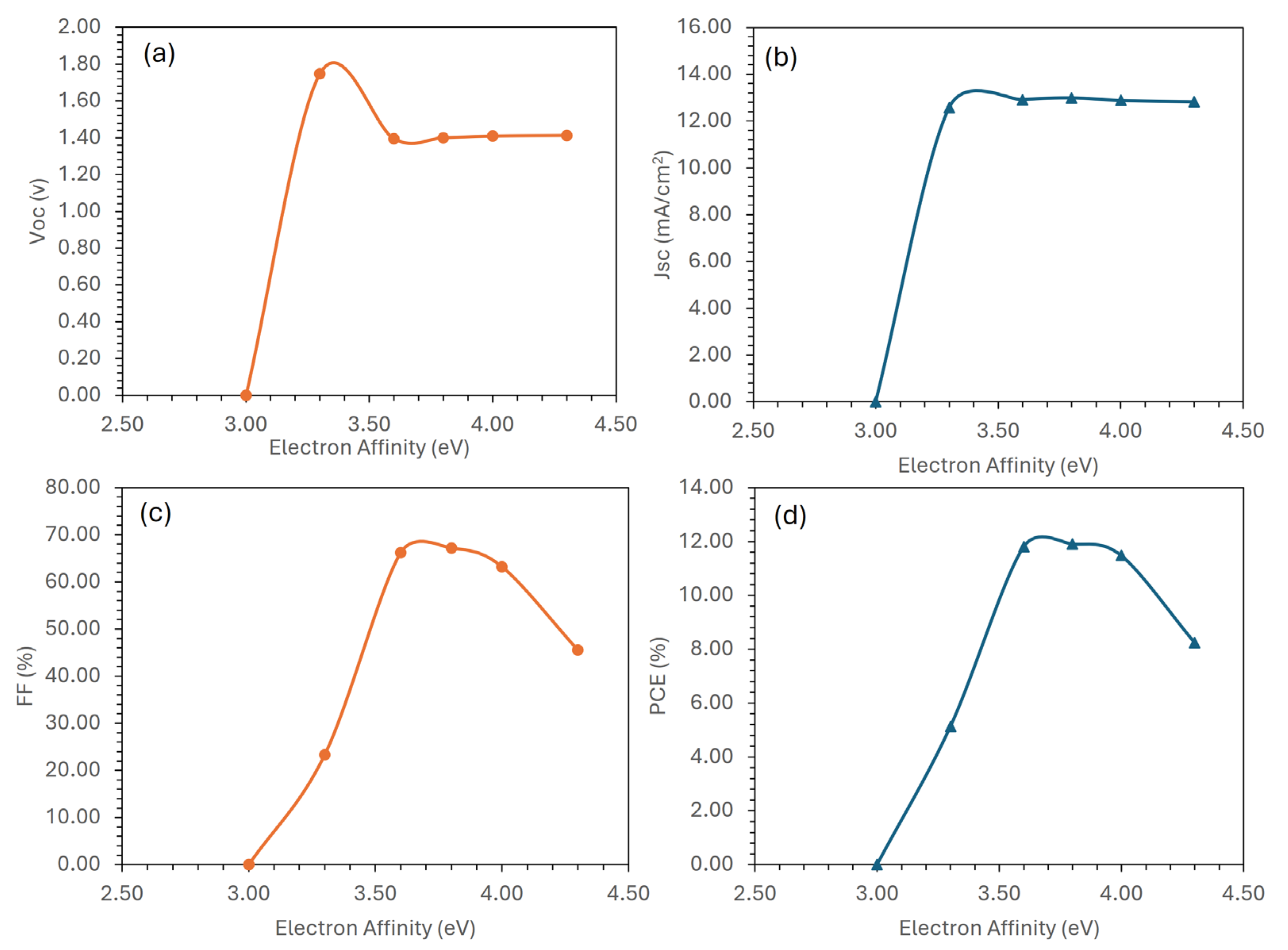
3.4. Energy Bandgap Optimization for the Electron Transport Layer

3.5. Thickness Optimization for the Hole Transport Layer
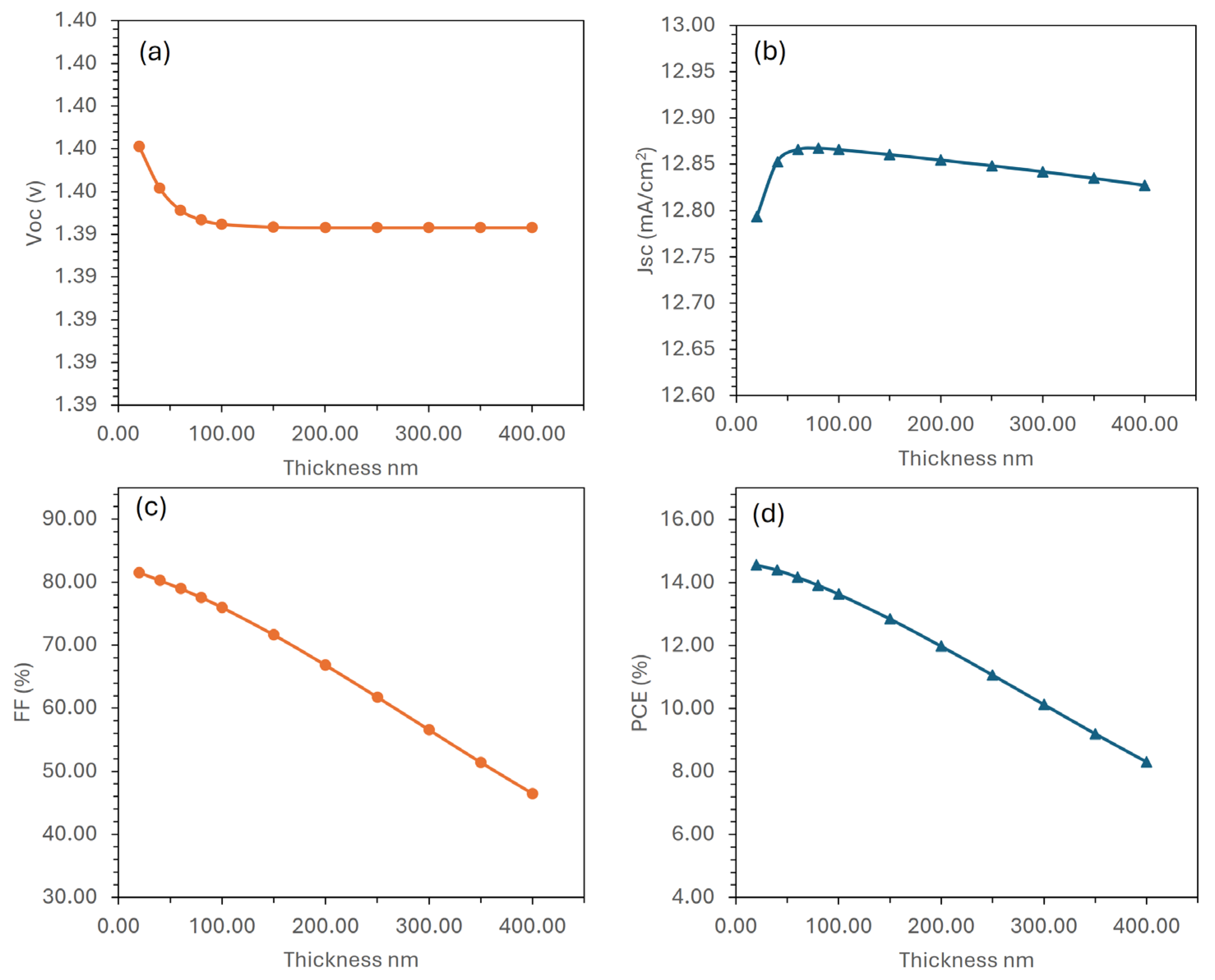
3.6. Doping Density Optimization for the Hole Transport Layer
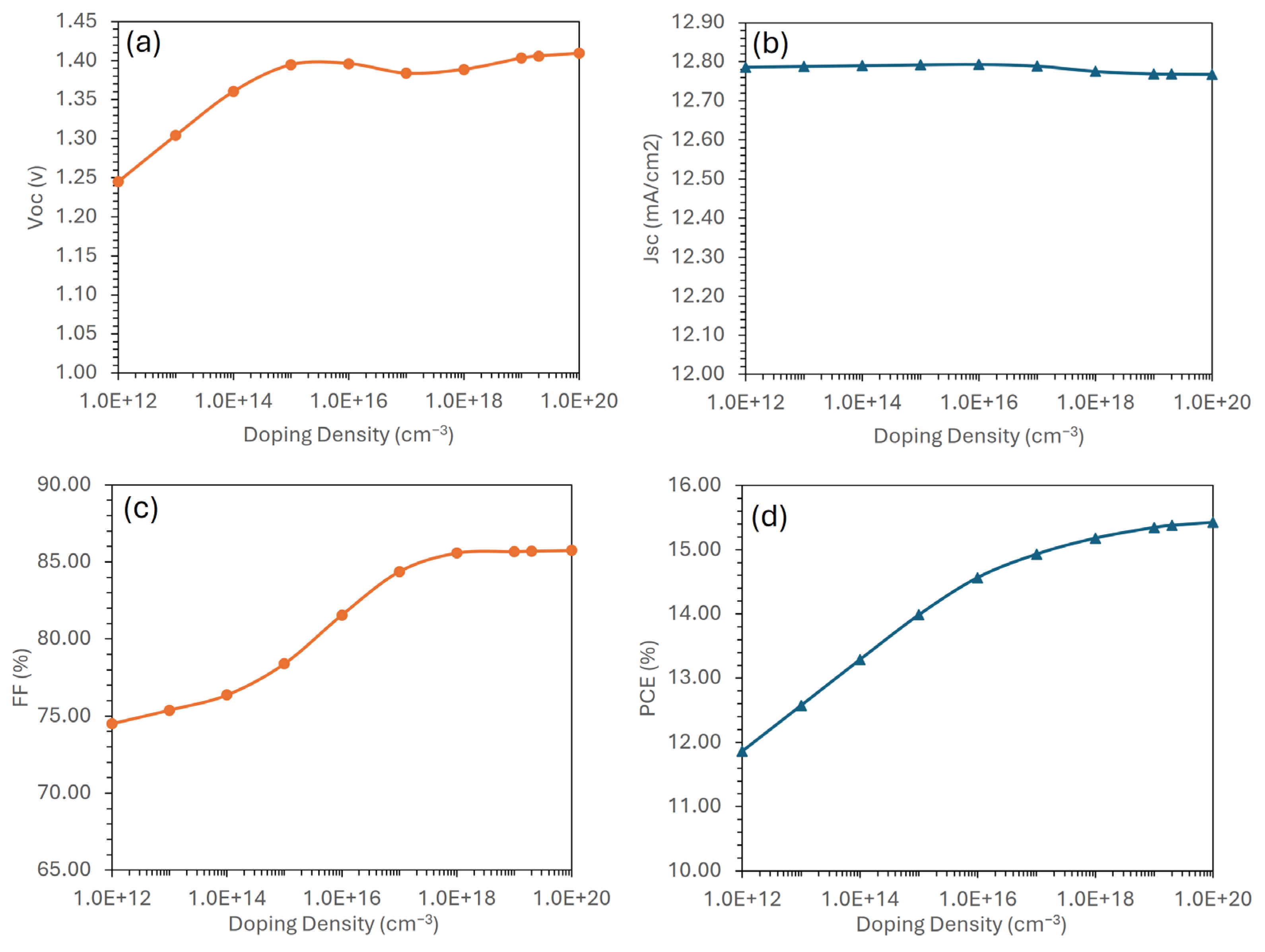
3.7. Thickness Optimization for the Electron Transport Layer

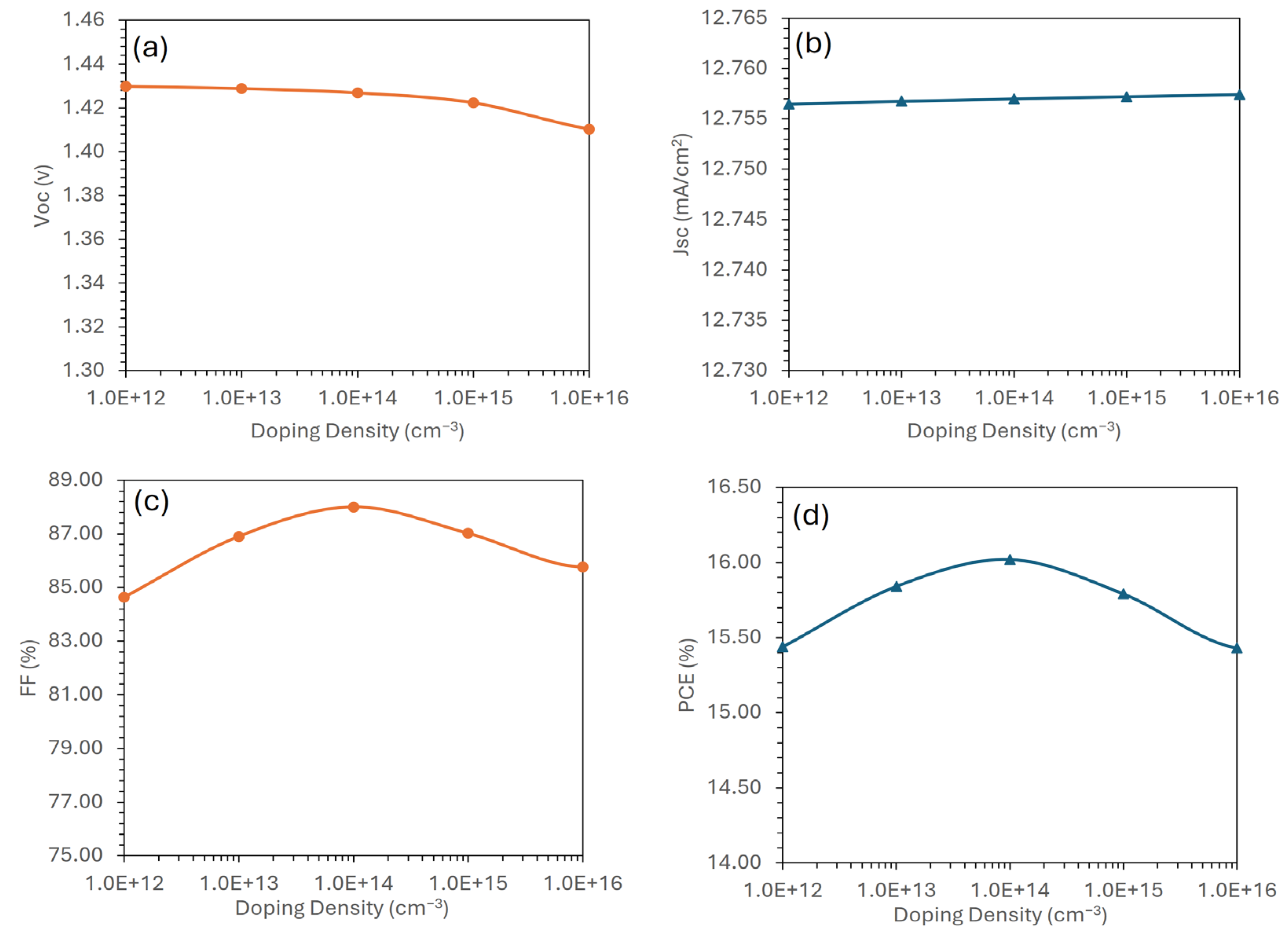
3.8. Doping Density Optimization for the Electron Transport Layer
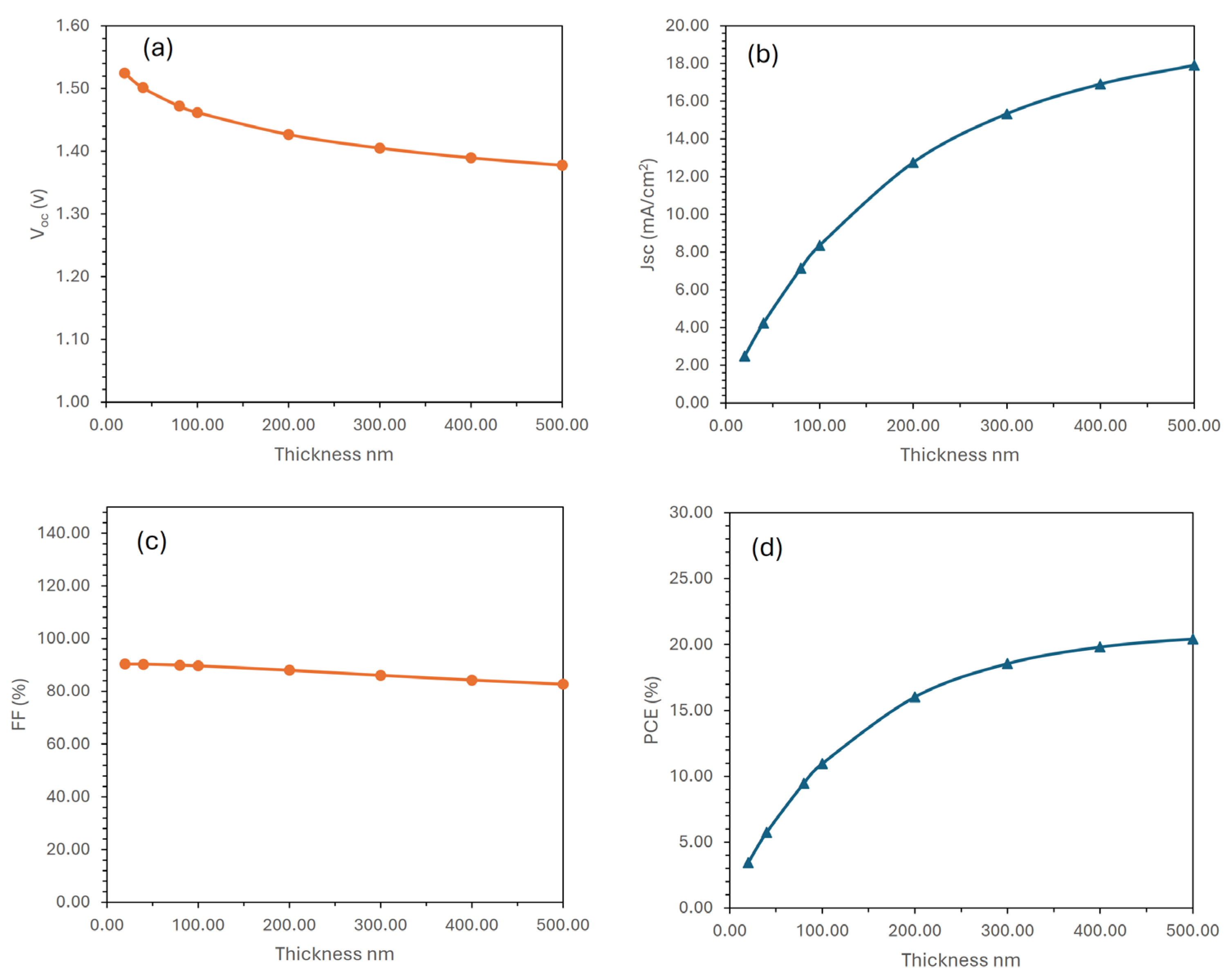
3.9. Thickness Optimization for the MASnIBr2 Absorber Layer
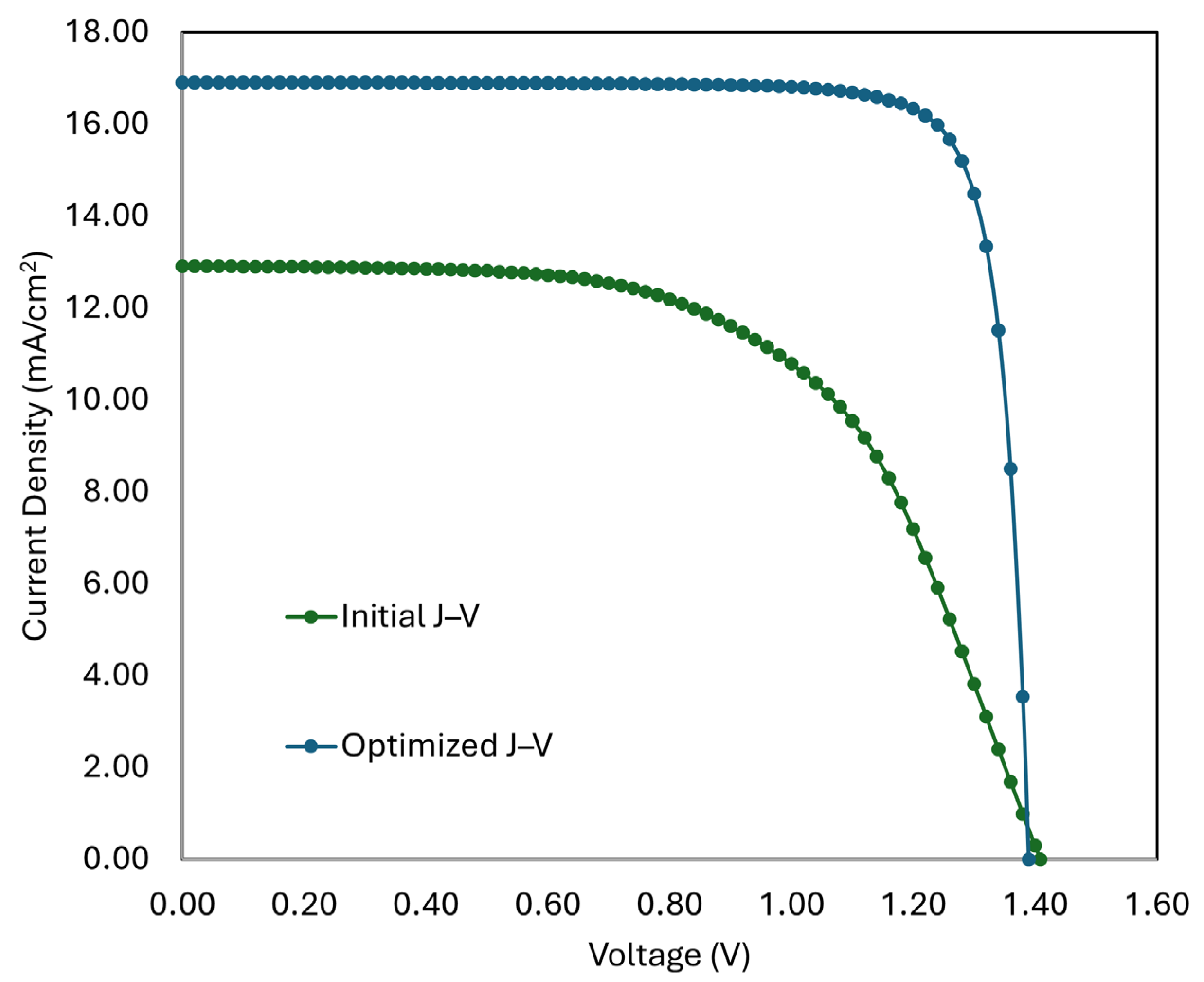
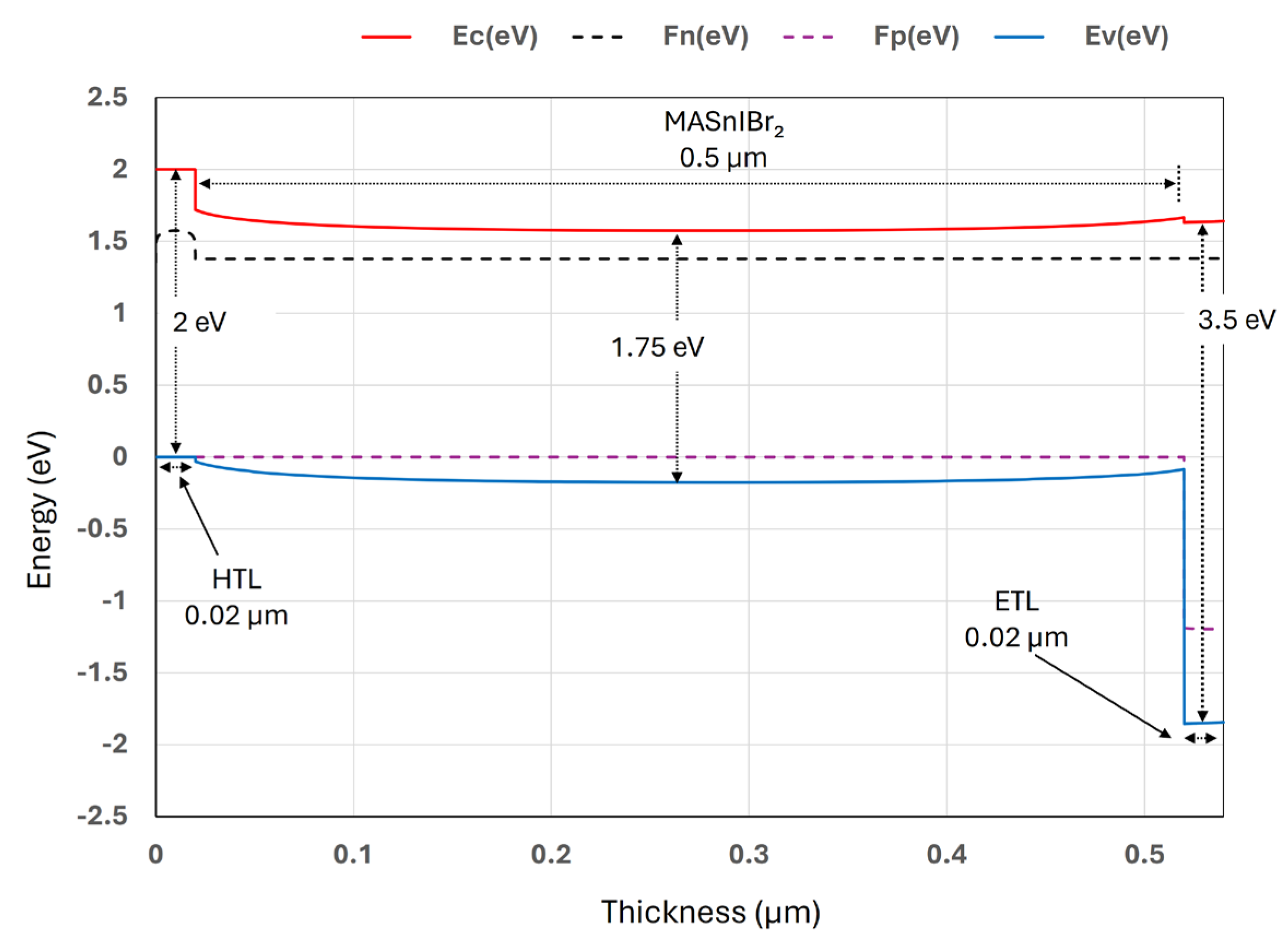
3.10. Performance Overview of the Optimized Perovskite Solar Cell
3.11. Impact of Defect Density on the Performance of the MASnIBr2 Absorber Layer
3.12. Comparison with Previous Results
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, M.; Akash; Tiwari, J.P. Solar Cells Based on Pb-Free and Perovskite-Inspired Materials: Futuristic of Perovskite Solar Cells. ACS Appl. Energy Mater. 2024, 7, 10212–10229. [Google Scholar] [CrossRef]
- Zhou, J.; Fu, S.; Zhou, S.; Huang, L.; Wang, C.; Guan, H.; Pu, D.; Cui, H.; Wang, C.; Wang, T.; et al. Mixed Tin-Lead Perovskites with Balanced Crystallization and Oxidation Barrier for All-Perovskite Tandem Solar Cells. Nat. Commun. 2024, 15, 2324. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Bie, T.; Yang, L.; Gao, Y.; Jin, X.; He, F.; Zheng, N.; Yu, Y.; Zhang, X. Over 21% Efficiency Stable 2D Perovskite Solar Cells. Adv. Mater. 2022, 34, 2107211. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Aydin, E.; Yin, J.; De Bastiani, M.; Isikgor, F.H.; Rehman, A.U.; Yengel, E.; Ugur, E.; Harrison, G.T.; Wang, M.; et al. 28.2%-Efficient, Outdoor-Stable Perovskite/Silicon Tandem Solar Cell. Joule 2021, 5, 3169–3186. [Google Scholar] [CrossRef]
- Ding, G.; Zheng, Y.; Xiao, X.; Cheng, H.; Zhang, G.; Shi, Y.; Shao, Y. Sustainable Development of Perovskite Solar Cells: Keeping a Balance between Toxicity and Efficiency. J. Mater. Chem. A 2022, 10, 8159–8171. [Google Scholar] [CrossRef]
- Zhang, W.; Cai, Y.; Liu, H.; Xia, Y.; Cui, J.; Shi, Y.; Chen, R.; Shi, T.; Wang, H.L. Organic-Free and Lead-Free Perovskite Solar Cells with Efficiency over 11%. Adv. Energy Mater. 2022, 12, 2202491. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Q.; Liu, Y.; Luo, W.; Guo, X.; Huang, Z.; Ting, H.; Sun, W.; Zhong, X.; Wei, S.; et al. The Dawn of Lead-Free Perovskite Solar Cell: Highly Stable Double Perovskite Cs2AgBiBr6 Film. Adv. Sci. 2018, 5, 1700759. [Google Scholar] [CrossRef]
- Bibi, A.; Lee, I.; Nah, Y.; Allam, O.; Kim, H.; Quan, L.N.; Tang, J.; Walsh, A.; Jang, S.S.; Sargent, E.H.; et al. Lead-Free Halide Double Perovskites: Toward Stable and Sustainable Optoelectronic Devices. Mater. Today 2021, 49, 123–144. [Google Scholar] [CrossRef]
- Ustinova, M.I.; Babenko, S.D.; Luchkin, S.Y.; Talalaev, F.S.; Anokhin, D.V.; Olthof, S.; Troshin, P.A. Correction: Experimental Evaluation of Indium(i) Iodide as a Lead-Free Perovskite-Inspired Material for Photovoltaic Applications. J. Mater. Chem. C Mater. 2023, 11, 2398. [Google Scholar] [CrossRef]
- Giustino, F.; Snaith, H.J. Toward Lead-Free Perovskite Solar Cells. ACS Energy Lett. 2016, 1, 1233–1240. [Google Scholar] [CrossRef]
- Mora-Herrera, D.; Pal, M. Path toward the Performance Upgrade of Lead-Free Perovskite Solar Cells Using Cu2ZnSn1- XGexS4as a Hole Transport Layer: A Theoretical Simulation Approach. J. Phys. Chem. C 2022, 126, 5847–5862. [Google Scholar] [CrossRef]
- Bello, O.O.; Emetere, M.E. Progress and Limitation of Lead-Free Inorganic Perovskites for Solar Cell Application. Sol. Energy 2022, 243, 370–380. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alahmadi, A.N.M. Design of Dopant and Lead-Free Novel Perovskite Solar Cell for 16.85% Efficiency. Polymers 2021, 13, 2110. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alahmadi, A.N.M.; Aljohani, A.J. Design of a Novel Lead-Free Perovskite Solar Cell for 17.83% Efficiency. IEEE Access 2021, 9, 54254–54263. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alahmadi, A.N.M.; Alshaikh, M.S. Lead-Free FACsSnI3 Based Perovskite Solar Cell: Designing Hole and Electron Transport Layer. Nanomaterials 2023, 13, 1524. [Google Scholar] [CrossRef] [PubMed]
- Al-Amri, A.M.; Cheng, B.; He, J.H. Perovskite Methylammonium Lead Trihalide Heterostructures: Progress and Challenges. IEEE Trans. Nanotechnol. 2019, 18, 1–12. [Google Scholar] [CrossRef]
- Treglia, A.; Ambrosio, F.; Martani, S.; Folpini, G.; Barker, A.J.; Albaqami, M.D.; De Angelis, F.; Poli, I.; Petrozza, A. Effect of Electronic Doping and Traps on Carrier Dynamics in Tin Halide Perovskites. Mater. Horiz. 2022, 9, 1763–1773. [Google Scholar] [CrossRef]
- Jokar, E.; Chien, C.H.; Tsai, C.M.; Fathi, A.; Diau, E.W.G. Robust Tin-Based Perovskite Solar Cells with Hybrid Organic Cations to Attain Efficiency Approaching 10%. Adv. Mater. 2019, 31, e1804835. [Google Scholar] [CrossRef]
- Ricciarelli, D.; Meggiolaro, D.; Ambrosio, F.; De Angelis, F. Instability of Tin Iodide Perovskites: Bulk p-Doping versus Surface Tin Oxidation. ACS Energy Lett. 2020, 5, 2787–2795. [Google Scholar] [CrossRef]
- Ke, W.; Stoumpos, C.C.; Kanatzidis, M.G. “Unleaded” Perovskites: Status Quo and Future Prospects of Tin-Based Perovskite Solar Cells. Adv. Mater. 2019, 31, e1803230. [Google Scholar] [CrossRef]
- Jin, Z.; Yu, B.B.; Liao, M.; Liu, D.; Xiu, J.; Zhang, Z.; Lifshitz, E.; Tang, J.; Song, H.; He, Z. Enhanced Efficiency and Stability in Sn-Based Perovskite Solar Cells with Secondary Crystallization Growth. J. Energy Chem. 2021, 54, 414–421. [Google Scholar] [CrossRef]
- Macdonald, T.J.; Lanzetta, L.; Liang, X.; Ding, D.; Haque, S.A. Engineering Stable Lead-Free Tin Halide Perovskite Solar Cells: Lessons from Materials Chemistry. Adv. Mater. 2023, 35, 2206684. [Google Scholar] [CrossRef] [PubMed]
- Solis, O.E.; Mínguez-Avellán, M.; Betancur, P.F.; Sánchez-Alarcón, R.I.; Rodriguez, I.; Martínez-Pastor, J.P.; Ripolles, T.S.; Abargues, R.; Boix, P.P. Adjusting the Crystallization of Tin Perovskites through Thiophene Additives for Improved Photovoltaic Stability. ACS Energy Lett. 2024, 9, 5288–5295. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Hu, W.; Liu, J.; Han, C.; Gao, Q.; Mei, A.; Zhou, Y.; Guo, F.; Han, H. Achievements, Challenges, and Future Prospects for Industrialization of Perovskite Solar Cells. Light. Sci. Appl. 2024, 13, 227. [Google Scholar] [CrossRef]
- Song, D.; Shin, S.W.; Wu, H.-P.; Diau, E.W.-G.; Correa-Baena, J.-P. Toward Maximizing Hole Selection with Self-Assembled Monolayers in Sn-Based Perovskite Solar Cells. ACS Energy Lett. 2025, 10, 1292–1312. [Google Scholar] [CrossRef]
- Shukla, A.; Khadka, D.B.; Li, C.; Rikukawa, M.; Takeoka, Y.; Sahara, R.; Yanagida, M.; Shirai, Y. Defect Mitigation via Fullerene-Based Functional Additives for Enhanced Efficiency and Stability in Tin Perovskite Solar Cells. J. Mater. Chem. A Mater. 2025, 13, 23487–23498. [Google Scholar] [CrossRef]
- Ke, W.; Kanatzidis, M.G. Prospects for Low-Toxicity Lead-Free Perovskite Solar Cells. Nat. Commun. 2019, 10, 965. [Google Scholar] [CrossRef]
- Wang, M.; Wang, W.; Ma, B.; Shen, W.; Liu, L.; Cao, K.; Chen, S.; Huang, W. Lead-Free Perovskite Materials for Solar Cells. Nano-Micro Letters. 2021, 13, 1–36. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.; Chen, X.; Zhang, L. High-Performance Flexible Lead-Free Perovskite Solar Cells Based on Tin-Halide Perovskite Films Doped by Reductant Metal Halide. Mater. Lett. 2022, 321, 132460. [Google Scholar] [CrossRef]
- Ozório, M.S.; Srikanth, M.; Besse, R.; Da Silva, J.L.F. The Role of the A-Cations in the Polymorphic Stability and Optoelectronic Properties of Lead-Free ASnI3perovskites. Phys. Chem. Chem. Phys. 2021, 23, 2286–2297. [Google Scholar] [CrossRef]
- Shi, T.; Zhang, H.S.; Meng, W.; Teng, Q.; Liu, M.; Yang, X.; Yan, Y.; Yip, H.L.; Zhao, Y.J. Effects of Organic Cations on the Defect Physics of Tin Halide Perovskites. J. Mater. Chem. A Mater. 2017, 5, 15124–15129. [Google Scholar] [CrossRef]
- Saski, M.; Prochowicz, D.; Marynowski, W.; Lewiński, J. Mechanosynthesis, Optical, and Morphological Properties of MA, FA, Cs-SnX3 (X = I, Br) and Phase-Pure Mixed-Halide MASnIxBr3–x Perovskites. Eur. J. Inorg. Chem. 2019, 2019, 2680–2684. [Google Scholar] [CrossRef]
- Şen, E.; Kaleli, M.; Aldemir, D.A.; Lapa, H.E. Investigation of MASnIxBr3−x (x = 3, 2, 1, 0) Perovskite Thin Films Produced by Ultrasonic Spray Pyrolysis Method. Arab. J. Sci. Eng. 2024, 49, 10085–10094. [Google Scholar] [CrossRef]
- Al Jame, H.; Sarker, S.; Islam, S.; Islam, T.; Rauf, A.; Ahsan, S.; Nishat, S.S.; Jani, R.; Shorowordi, K.; Carbonara, J.; et al. Supervised Machine Learning-Aided SCAPS-Based Quantitative Analysis for the Discovery of Optimum Bromine Doping in Methylammonium Tin-Based Perovskite (MASnI3–XBrx). ACS Appl. Mater. Interfaces 2022, 14, 502–516. [Google Scholar] [CrossRef]
- Chen, N.; Li, Y.; Lv, S.; Hu, L.; Lv, B.; Nie, Q.; Yan, B. Co-Treatment of an Inorganic Additive SnF2 and an Organic Additive P(VDF-TrFE) for Improving the Performances of MASnBr3 Films. Opt. Mater. 2024, 147, 114721. [Google Scholar] [CrossRef]
- Xiao, M.; Gu, S.; Zhu, P.; Tang, M.; Zhu, W.; Lin, R.; Chen, C.; Xu, W.; Yu, T.; Zhu, J. Tin-Based Perovskite with Improved Coverage and Crystallinity through Tin-Fluoride-Assisted Heterogeneous Nucleation. Adv. Opt. Mater. 2018, 6, 1700615. [Google Scholar] [CrossRef]
- Hao, F.; Stoumpos, C.C.; Cao, D.H.; Chang, R.P.H.; Kanatzidis, M.G. Lead-Free Solid-State Organic-Inorganic Halide Perovskite Solar Cells. Nat. Photonics 2014, 8, 489–494. [Google Scholar] [CrossRef]
- Nguyen, B.P.; Shin, D.; Jung, H.R.; Kim, J.; Nguyen, T.T.T.; Yoon, S.; Yi, Y.; Jo, W. Phase Formation and Local Charge Transport of Lead-Free CH3NH3Sn(I1−xBrx)3 (0 ≤ x ≤ 1)Perovskite Solar Cells Fabricated by Solvent Optimization. Sol. Energy 2019, 186, 136–144. [Google Scholar] [CrossRef]
- Abdelaziz, S.; Zekry, A.; Shaker, A.; Abouelatta, M. Investigation of Lead-Free MASnI3-MASnIBr2 Tandem Solar Cell: Numerical Simulation. Opt. Mater. 2022, 123, 111893. [Google Scholar] [CrossRef]
- Burgelman, M.; Nollet, P.; Degrave, S. Modelling Polycrystalline Semiconductor Solar Cells. Thin Solid Film. 2000, 361, 527–532. [Google Scholar] [CrossRef]
- Alahmadi, A.N.M. Design of an Efficient PTB7:PC70BM-Based Polymer Solar Cell for 8% Efficiency. Polymers 2022, 14, 889. [Google Scholar] [CrossRef]
- Liu, F.; Zhu, J.; Wei, J.; Li, Y.; Lv, M.; Yang, S.; Zhang, B.; Yao, J.; Dai, S. Numerical Simulation: Toward the Design of High-Efficiency Planar Perovskite Solar Cells. Appl. Phys. Lett. 2014, 104, 253508. [Google Scholar] [CrossRef]
- Decock, K.; Zabierowski, P.; Burgelman, M. Modeling Metastabilities in Chalcopyrite-Based Thin Film Solar Cells. J. Appl. Phys. 2012, 111, 043703. [Google Scholar] [CrossRef]
- Burgelman, M.; Decock, K.; Khelifi, S.; Abass, A. Advanced Electrical Simulation of Thin Film Solar Cells. Thin Solid Film. 2013, 535, 296–301. [Google Scholar] [CrossRef]
- Burgelman, M.; Verschraegen, J.; Degrave, S.; Nollet, P. Modeling Thin-Film PV Devices. Prog. Photovolt. Res. Appl. 2004, 12, 143–153. [Google Scholar] [CrossRef]
- Verschraegen, J.; Burgelman, M. Numerical Modeling of Intra-Band Tunneling for Heterojunction Solar Cells in Scaps. Thin Solid Film. 2007, 515, 6276–6279. [Google Scholar] [CrossRef]
- Saidarsan, A.; Guruprasad, S.; Malik, A.; Basumatary, P.; Ghosh, D.S. A Critical Review of Unrealistic Results in SCAPS-1D Simulations: Causes, Practical Solutions and Roadmap Ahead. Sol. Energy Mater. Sol. Cells 2025, 279, 113230. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alzahrani, M.S.; Alahmadi, A.N.M. Electron Transport Layer Optimization for Efficient PTB7:PC70BM Bulk-Heterojunction Solar Cells. Polymers 2022, 14, 3610. [Google Scholar] [CrossRef] [PubMed]
- Momblona, C.; Gil-Escrig, L.; Bandiello, E.; Hutter, E.M.; Sessolo, M.; Lederer, K.; Blochwitz-Nimoth, J.; Bolink, H.J. Efficient Vacuum Deposited P-i-n and n-i-p Perovskite Solar Cells Employing Doped Charge Transport Layers. Energy Env. Sci. 2016, 9, 3456–3463. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, A.; Cai, F.; Tao, L.M.; Zhou, Y.; Zhao, Z.; Chen, Q.; Cheng, Y.B.; Zhou, H. Nickel Oxide Nanoparticles for Efficient Hole Transport in P-i-n and n-i-p Perovskite Solar Cells. J. Mater. Chem. A Mater. 2017, 5, 6597–6605. [Google Scholar] [CrossRef]
- Raoui, Y.; Ez-Zahraouy, H.; Tahiri, N.; El Bounagui, O.; Ahmad, S.; Kazim, S. Performance Analysis of MAPbI3 Based Perovskite Solar Cells Employing Diverse Charge Selective Contacts: Simulation Study. Sol. Energy 2019, 193, 948–955. [Google Scholar] [CrossRef]
- Hossain, M.K.; Toki, G.F.I.; Kuddus, A.; Rubel, M.H.K.; Hossain, M.M.; Bencherif, H.; Rahman, M.F.; Islam, M.R.; Mushtaq, M. An Extensive Study on Multiple ETL and HTL Layers to Design and Simulation of High-Performance Lead-Free CsSnCl3-Based Perovskite Solar Cells. Sci. Rep. 2023, 13, 2521. [Google Scholar] [CrossRef]
- Karimi, E.; Ghorashi, S.M.B. Investigation of the Influence of Different Hole-Transporting Materials on the Performance of Perovskite Solar Cells. Optik 2017, 130, 650–658. [Google Scholar] [CrossRef]
- Bag, A.; Radhakrishnan, R.; Nekovei, R.; Jeyakumar, R. Effect of Absorber Layer, Hole Transport Layer Thicknesses, and Its Doping Density on the Performance of Perovskite Solar Cells by Device Simulation. Sol. Energy 2020, 196, 177–182. [Google Scholar] [CrossRef]
- Anik, M.H.K.; Mahmud, S.; Islam, M.A.; Talukder, H.; Biswas, S.K.; Islam, S. Comparative Performance Analysis and Material Exploration of ECO-Friendly Highly Efficient Perovskite Solar Cells. Semicond. Sci. Technol. 2022, 37, 115004. [Google Scholar] [CrossRef]
- Mahmood, K.; Sarwar, S.; Mehran, M.T. Current Status of Electron Transport Layers in Perovskite Solar Cells: Materials and Properties. RSC Adv. 2017, 7, 17044–17062. [Google Scholar] [CrossRef]
- Bulowski, W.; Szwanda, A.; Gawlińska-Nęcek, K.; Panek, P.; Lipiński, M.; Janusz-Skuza, M.; Szczerba, M.J.; Majchrowicz, Ł.; Mahapatra, A.; Prochowicz, D.; et al. Optimization of the ETL Titanium Dioxide Layer for Inorganic Perovskite Solar Cells. J. Mater. Sci. 2024, 59, 7283–7298. [Google Scholar] [CrossRef]
- Gulomov, J.; Accouche, O.; Aliev, R.; Neji, B.; Ghandour, R.; Gulomova, I.; Azab, M. Geometric Optimization of Perovskite Solar Cells with Metal Oxide Charge Transport Layers. Nanomaterials 2022, 12, 2692. [Google Scholar] [CrossRef]
- Wang, Z.K.; Liao, L.S. Doped Charge-Transporting Layers in Planar Perovskite Solar Cells. Adv. Opt. Mater. 2018, 6, 1800276. [Google Scholar] [CrossRef]
- Hossain, M.K.; Bhattarai, S.; Arnab, A.A.; Mohammed, M.K.A.; Pandey, R.; Ali, M.H.; Rahman, M.F.; Islam, M.R.; Samajdar, D.P.; Madan, J.; et al. Harnessing the Potential of CsPbBr3-Based Perovskite Solar Cells Using Efficient Charge Transport Materials and Global Optimization. RSC Adv. 2023, 13, 21044–21062. [Google Scholar] [CrossRef]
- Mortadi, A.; El Hafidi, E.; Monkade, M.; El Moznine, R. Investigating the Influence of Absorber Layer Thickness on the Performance of Perovskite Solar Cells: A Combined Simulation and Impedance Spectroscopy Study. Mater. Sci. Energy Technol. 2024, 7, 158–165. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, H.; Hu, C.; Zhao, Y.; Ma, X.; Wu, J.; Qi, Y.; Fang, W.; Jia, S.; Yu, J. Performance Analysis of All-Inorganic Cs3Sb2I9 Perovskite Solar Cells with Micro-Offset Energy Level Structure by SCAPS-1D Simulation and First-Principles Calculation. Sol. Energy Mater. Sol. Cells 2023, 260, 112487. [Google Scholar] [CrossRef]
- Koh, T.M.; Krishnamoorthy, T.; Yantara, N.; Shi, C.; Leong, W.L.; Boix, P.P.; Grimsdale, A.C.; Mhaisalkar, S.G.; Mathews, N. Formamidinium Tin-Based Perovskite with Low Eg for Photovoltaic Applications. J. Mater. Chem. A Mater. 2015, 3, 14996–15000. [Google Scholar] [CrossRef]
- Ouslimane, T.; Et-taya, L.; Elmaimouni, L.; Benami, A. Impact of Absorber Layer Thickness, Defect Density, and Operating Temperature on the Performance of MAPbI3 Solar Cells Based on ZnO Electron Transporting Material. Heliyon 2021, 7, e06379. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, J.; Jiao, H.; Li, L.; Zheng, G.; Chen, Y.; Huang, Y.; Zhang, Q.; Shen, C.; Chen, Q.; et al. Chemical Reduction of Intrinsic Defects in Thicker Heterojunction Planar Perovskite Solar Cells. Adv. Mater. 2017, 29, 1606774. [Google Scholar] [CrossRef]
- Samiee, M.; Konduri, S.; Ganapathy, B.; Kottokkaran, R.; Abbas, H.A.; Kitahara, A.; Joshi, P.; Zhang, L.; Noack, M.; Dalal, V. Defect Density and Dielectric Constant in Perovskite Solar Cells. Appl. Phys. Lett. 2014, 105, 153502. [Google Scholar] [CrossRef]
- Kanoun, M.B.; Goumri-Said, S. Exploring Performances of Hybrid Perovskites Tin-Based Photovoltaic Solar Cells: Non-Equilibrium Green’s Functions and Macroscopic Approaches. Phys. B Condens. Matter 2020, 591, 412247. [Google Scholar] [CrossRef]
- Bouich, A.; Marí-Guaita, J.; Soucase, B.M.; Palacios, P. Manufacture of High-Efficiency and Stable Lead-Free Solar Cells through Antisolvent Quenching Engineering. Nanomaterials 2022, 12, 2901. [Google Scholar] [CrossRef]
- Afridi, K.; Noman, M.; Jan, S.T. Evaluating the Influence of Novel Charge Transport Materials on the Photovoltaic Properties of MASnI3solar Cells through SCAPS-1D Modelling. R. Soc. Open Sci. 2024, 11, 231202. [Google Scholar] [CrossRef]
- Shah, M.; Ahmad, I.; Ullah, J.; Hayat, K.; Munawar, M.; Mushtaq, M.; Shah, A.; Shah, S.K. First-Principles Insights and SCAPS-1D Simulations for Optimizing MASnBr3-Based Perovskite Solar Cells. Comput. Mater. Sci. 2025, 250, 113699. [Google Scholar] [CrossRef]

| Photovoltaic Parameters | Symbol | Unit | Hole Transport Layer | Electron Transport Layer | MASnIBr2 |
|---|---|---|---|---|---|
| Thickness | Th | Nm | 200 | 200 | 200 |
| Energy Band Gap | Eg | eV | 2 | 3 | 1.75 |
| Electron Affinity | Χ | eV | 3 | 4 | 3.78 |
| Dielectric Permittivity | 18 | 9 | 8.2 | ||
| Effective Density of States at Conduction Band | Nc | cm−3 | 2 × 1020 | 1 × 1019 | 1 × 1018 |
| Effective Density of States at Valence Band | Nv | cm−3 | 2 × 1020 | 1 × 1019 | 1 × 1018 |
| Hole Thermal Velocity | Ve | cm/s | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron Thermal Velocity | Vh | cm/s | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron Mobility | µe | cm−2/V·s | 4 × 10−4 | 200 | 1.6 |
| Hole Mobility | µh | cm−2/V·s | 4 × 10−4 | 80 | 1.6 |
| Uniform Shallow Donor Doping | Nd | cm−3 | - | 1 × 1016 | 1 × 1015 |
| Uniform Shallow Acceptor Doping | Na | cm−3 | 1 × 1016 | - | 1 × 1015 |
| Defect Density | Nt | cm−3 | 1 × 1014 | 1 × 1014 | 1 × 1015 |
| Interface | Defect Type | Capture Cross-Section Electrons–Holes (cm2) | Energetic Distribution | Total Density (cm−3) (Integrated over All Energies) |
|---|---|---|---|---|
| ETL/MASnIBr2 | Neutral | 1 × 10−17–1 × 10−18 | Single | 1 × 1010 |
| MASnIBr2/HTL | Neutral | 1 × 10−18–1 × 10−19 | Single | 1 × 1010 |
| Year | Absorber Layer | HTL Material | ETL Material | PCE (%) | Ref. |
|---|---|---|---|---|---|
| 2014 | MASnIBr2 | Spiro OMeTAD | TiO2 | 5.73 | [37] |
| 2017 | MASnIBr2 | --- | --- | 3.7 | [36] |
| 2019 | MASn(I0.33Br0.67)3 | Spiro OMeTAD | TiO2 | 3.2 | [38] |
| 2020 | MASnIBr2 | PEDOT:PSS | TiO2 | 16.07 | [67] |
| 2022 | MASnIBr2 | Spiro OMeTAD | TiO2 | 11.74 | [39] |
| 2022 | MASnI3 | Spiro OMeTAD | TiO2 | 9.44 | [68] |
| 2024 | MASnI3 | CuSbS2 | C60 | 20.7 | [69] |
| 2025 | MASnBr3 | Cu2O | WS2 | 22.71 | [70] |
| 2025 | MASnIBr2 | Ideal HTL | Ideal ETL | 20.42 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alahmadi, A.N.M. Numerical Analysis and Design of Hole and Electron Transport Layers in Lead-Free MASnIBr2 Perovskite Solar Cells. Eng 2025, 6, 222. https://doi.org/10.3390/eng6090222
Alahmadi ANM. Numerical Analysis and Design of Hole and Electron Transport Layers in Lead-Free MASnIBr2 Perovskite Solar Cells. Eng. 2025; 6(9):222. https://doi.org/10.3390/eng6090222
Chicago/Turabian StyleAlahmadi, Ahmed N. M. 2025. "Numerical Analysis and Design of Hole and Electron Transport Layers in Lead-Free MASnIBr2 Perovskite Solar Cells" Eng 6, no. 9: 222. https://doi.org/10.3390/eng6090222
APA StyleAlahmadi, A. N. M. (2025). Numerical Analysis and Design of Hole and Electron Transport Layers in Lead-Free MASnIBr2 Perovskite Solar Cells. Eng, 6(9), 222. https://doi.org/10.3390/eng6090222






