A Numerical Investigation of the Trade-Off Between Sound Insulation and Air Ventilation for a Partially Open Door
Abstract
1. Introduction
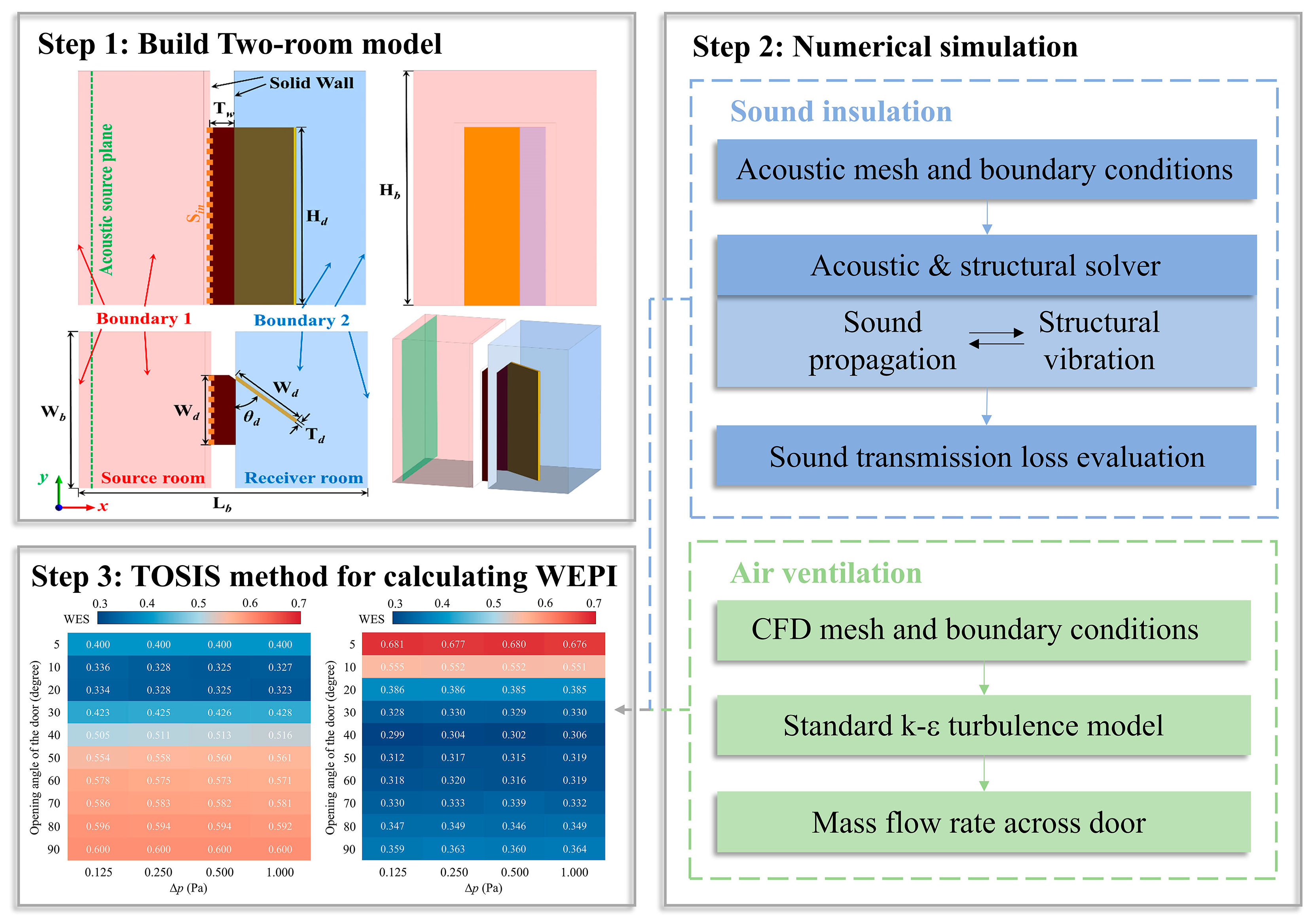
2. Methodologies and Validation
2.1. Geometry of the Investigated Model
2.2. Numerical Methodologies
2.2.1. Acoustic–Structural Solver and Settings
2.2.2. CFD Solver and Settings
2.3. Workplace Environmental Score
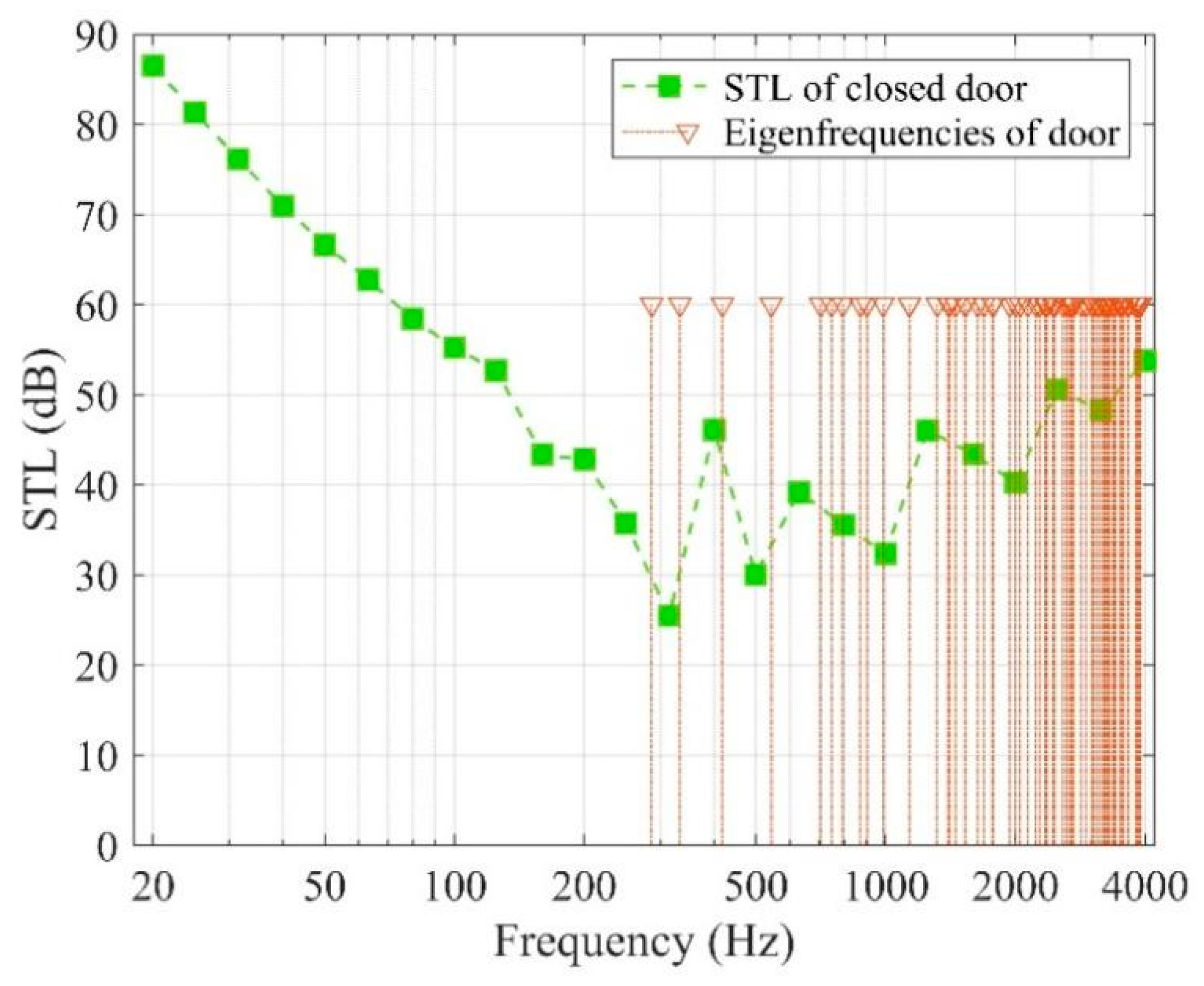
2.4. Validation of the Acoustic–Structural Solver
3. Results
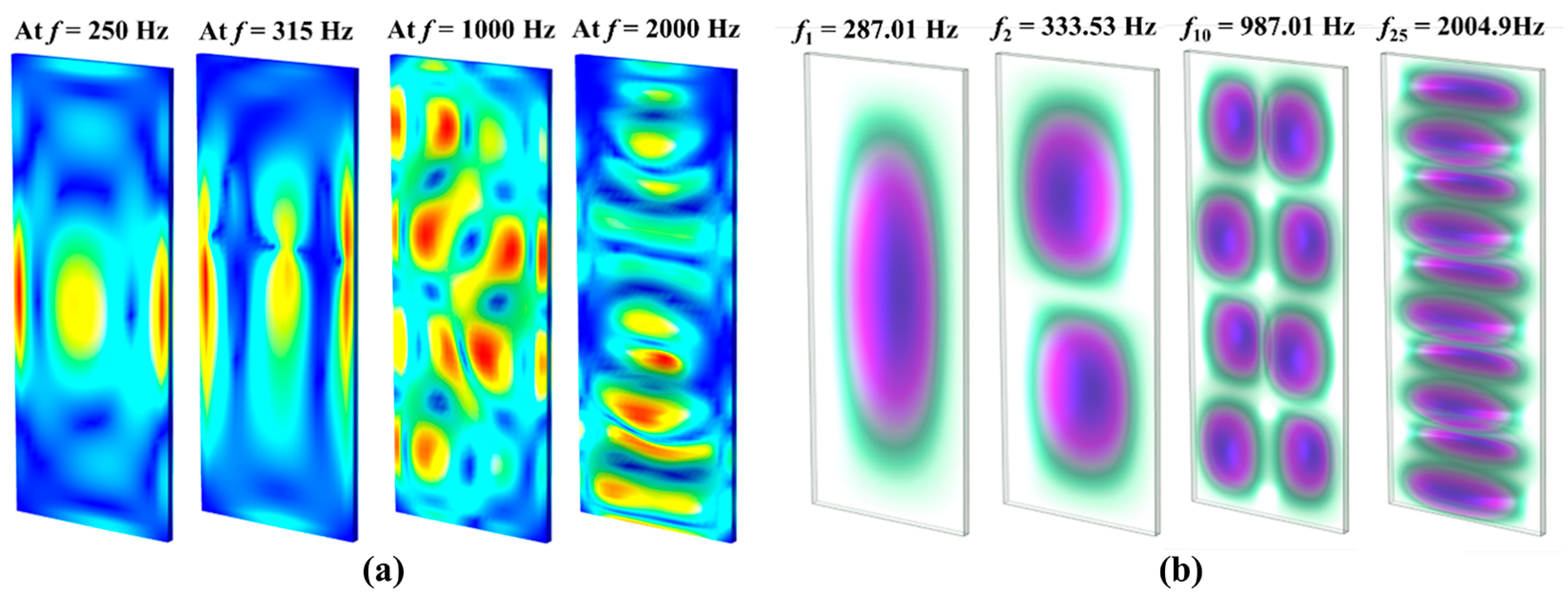
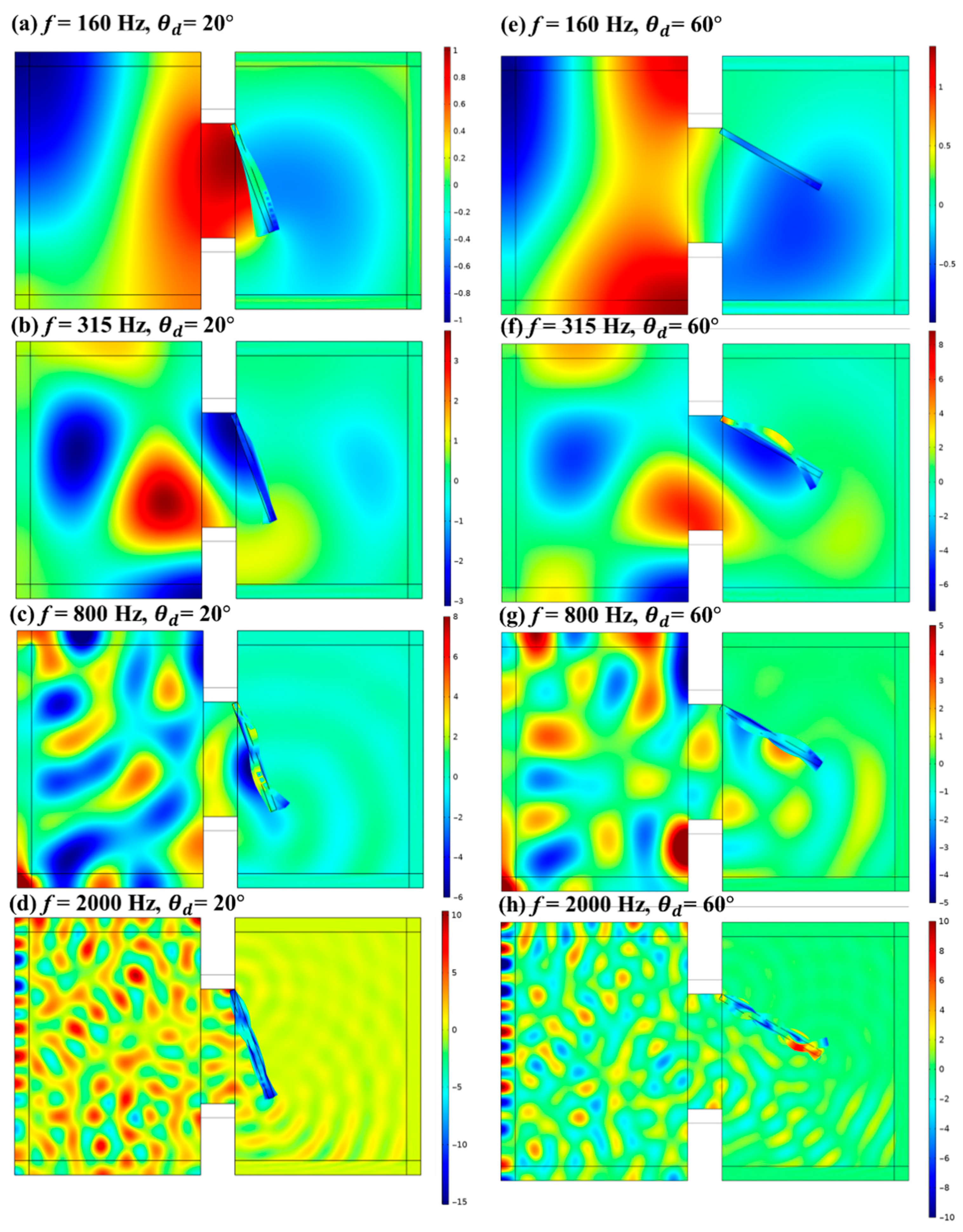
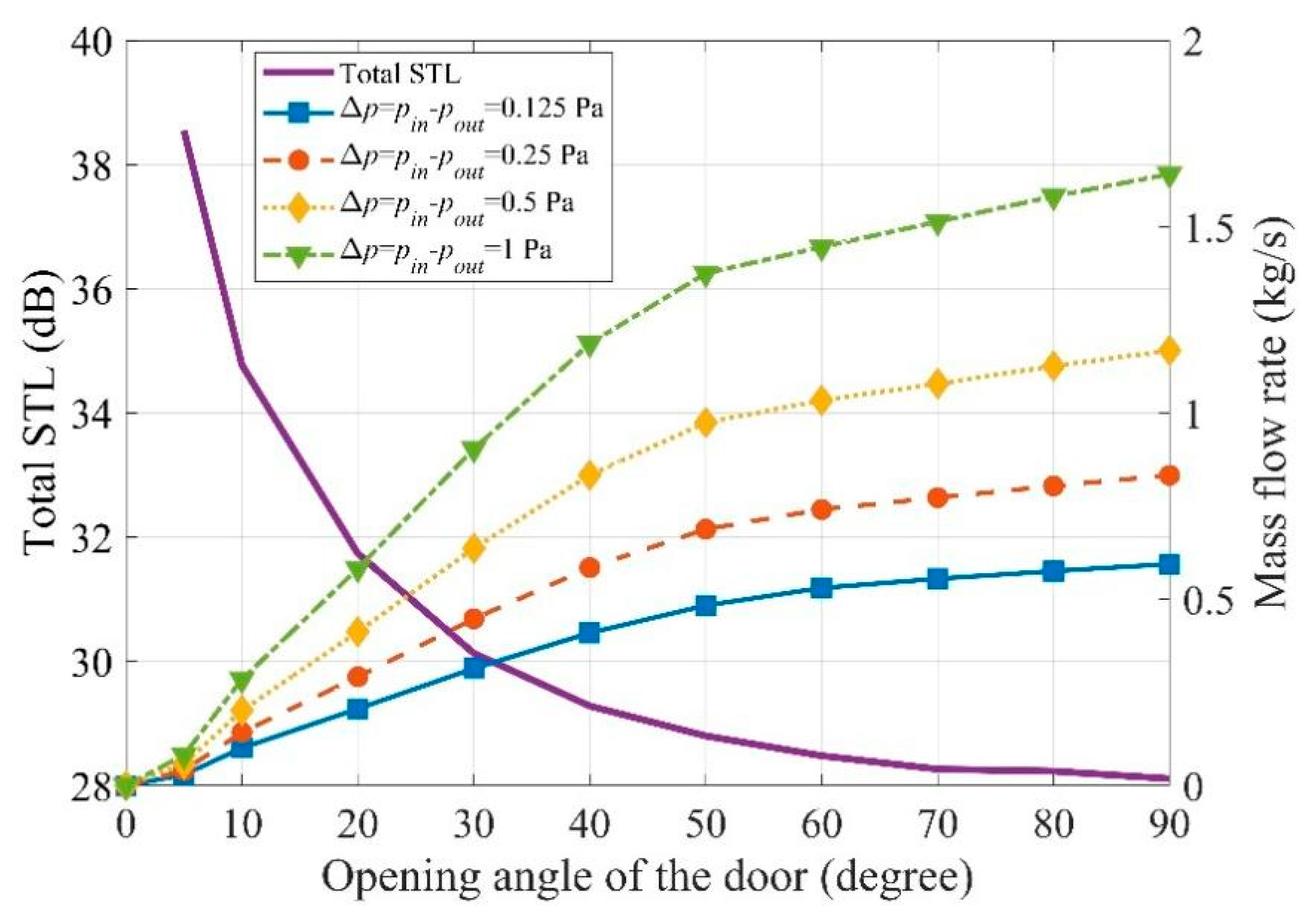
3.1. Sound Transmission Losses with Different Opening Angles
3.2. Sound Insulation and Ventilation Performances with Different Opening Angles
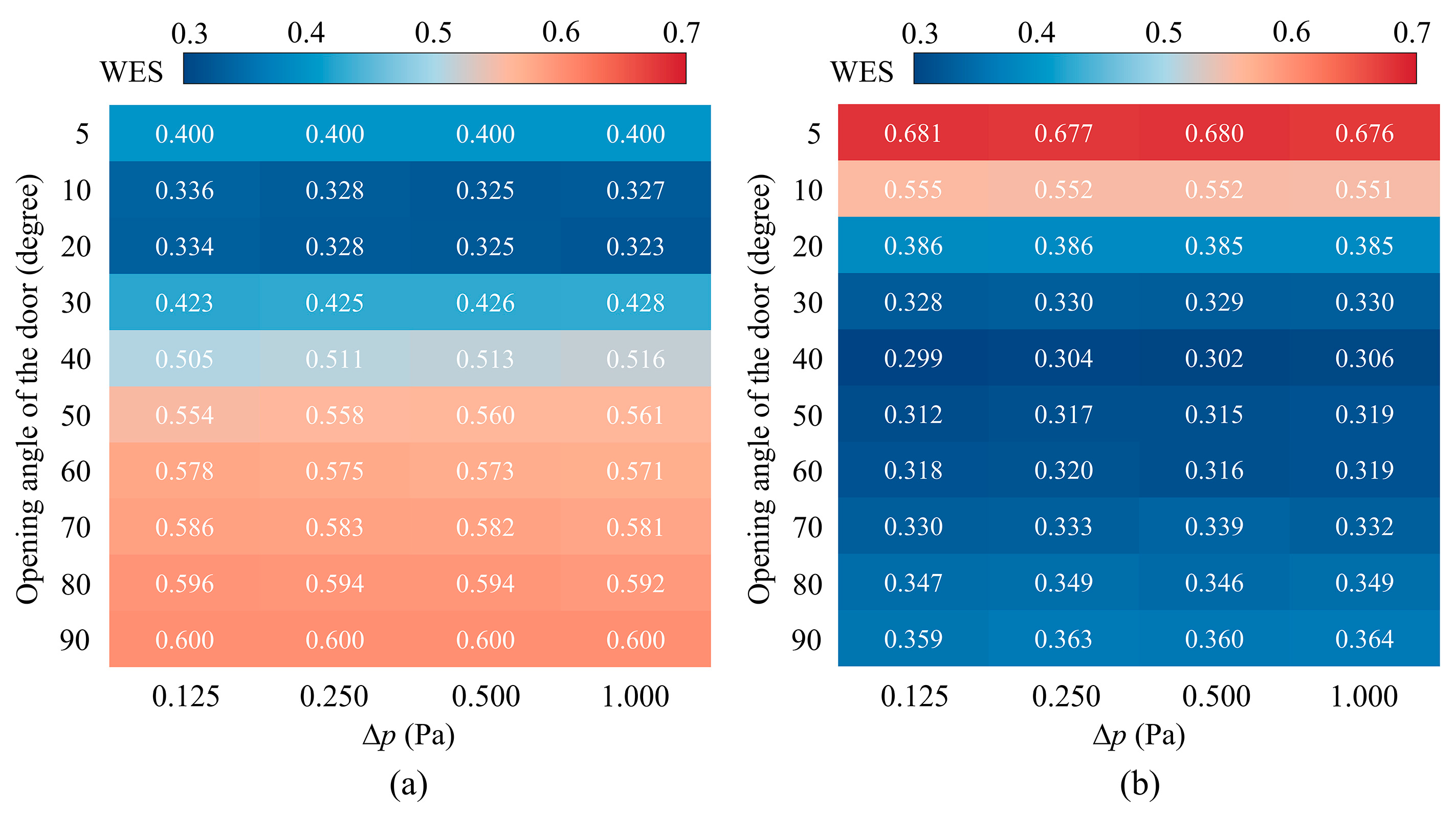
3.3. Evaluation of the Impact on Work Efficiency at Different Opening Angles
4. Conclusions
- (1)
- For high sound insulation requirements, it is recommended that the door opening angle is less than 15°, which can increase the WES by 20% to 25%.
- (2)
- A good compromise between the sound insulation and ventilation performances is in the range of θd = 15°~25°.
- (3)
- The sound insulation effect is negligible once the opening angle is larger than 45°. In this case, it is suggested that the opening angle of the door to be kept with maximum angle to guarantee a better ventilation performance. And as the door opening angle increases, the WES also increases, increasing worker efficiency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| A | amplitude of the planewaves, m |
| cj | mass fraction |
| Ed | young’s modulus of the door, Pa |
| Fv | external force, N |
| Hb | height of the domain, m |
| Hd | height of the door, m |
| k | wavenumber of the sound |
| Lb | length of the domain, m |
| pa | acoustic pressure, Pa |
| pin, pout | total pressure at the inlet and outlet, Pa |
| Ptr | transmitted power, W |
| S | stress tensor of the solid, Pa |
| Td | thickness of the door, m |
| Tw | thickness of the wall, m |
| u | vibration velocity of the structure, m/s |
| Wb | width of the domain, m |
| Wd | width of the door, m |
| Abbreviation | |
| FEM | finite element method |
| PML | perfectly matched layer |
| STL | sound transmission loss, dB |
| WES | workplace environmental score |
| Greek Symbols | |
| θd | opening angle of the door, ° |
| ρd | density of the door, kg/m3 |
| σ | strain tensor of the solid |
| νd | Poisson’s ratio of the door |
| θn, φn, ϕn | random variables |
References
- Chen, S.; He, P.; Yu, B.; Wei, D.; Chen, Y. The challenge of noise pollution in high-density urban areas: Relationship between 2D/3D urban morphology and noise perception. Build. Environ. 2024, 253, 111313. [Google Scholar] [CrossRef]
- Chen, J.; He, L.; Li, X.; Zheng, B.; Wang, T.; Wang, D.; Zou, C. Experimental Investigation on Building Sound Environment: Traffic-Induced Air Noise and Structure-Borne Noise. Buildings 2024, 14, 2380. [Google Scholar] [CrossRef]
- Wang, P.; Xiang, H.; Guo, M.; Shi, Y.; Chong, K.C.; Huang, J.; Ho, H.C. Indoor and roadside exposures to traffic noise and cardiovascular mortality and the role of urban environmental stressors across a high-rise, high-density environment: A case study in Hong Kong. Build. Environ. 2023, 229, 109945. [Google Scholar] [CrossRef]
- Fusaro, G.; Barbaresi, L.; Guidorzi, P.; Garai, M. Investigation of the sound insulation and natural ventilation performance of a metamaterial-based open window. Build. Environ. 2024, 266, 112140. [Google Scholar] [CrossRef]
- Zhang, J.; Pang, L.; Yang, C.; Fan, Y.; Zhao, B.; Cao, X. Experimental Evaluation of Noise Exposure Effects on Subjective Perceptions and Cognitive Performance. Buildings 2024, 14, 1100. [Google Scholar] [CrossRef]
- Santana, E.G.F.; Suzuki, E.H.; Prado, R.T.A.; Kurokawa, F.A. Thermal comfort and indoor air quality in hospitals in the subtropics: Analysis of operating rooms and waiting rooms conditions. Indoor Built Environ. 2024, 33, 916–928. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Yin, H.; Liang, L.; Zu, S.; Gao, L.; Zhang, Y.; Li, A. Experimental study on the CO2 concentration and age of air distribution inside tiny sleeping spaces. Build. Simul. 2024, 17, 591–605. [Google Scholar] [CrossRef]
- Ren, L.; An, F.; Su, M.; Liu, J. Exposure Assessment of Traffic-Related Air Pollution Based on CFD and BP Neural Network and Artificial Intelligence Prediction of Optimal Route in an Urban Area. Buildings 2022, 12, 1227. [Google Scholar] [CrossRef]
- Bader Eddin, M.; Ménard, S.; Laratte, B.; Wu, T.V. A Design Methodology Incorporating a Sound Insulation Prediction Model, Life Cycle Assessment (LCA), and Thermal Insulation: A Comparative Study of Various Cross-Laminated Timber (CLT) and Ribbed CLT-Based Floor Assemblies. Acoustics 2024, 6, 1021–1046. [Google Scholar] [CrossRef]
- Arjunan, A.; Baroutaji, A.; Robinson, J.; Vance, A.; Arafat, A. Acoustic metamaterials for sound absorption and insulation in buildings. Build. Environ. 2024, 251, 111250. [Google Scholar] [CrossRef]
- Sharp, B.H. A Study of Techniques to Increase the Sound Insulation of Building Elements; Wyle Laboratories: Lexington Park, MD, USA, 1973. [Google Scholar]
- Hongisto, V. Sound insulation of doors-part 1: Prediction models for structural and leak transmission. J. Sound Vib. 2000, 230, 133–148. [Google Scholar] [CrossRef]
- Hongisto, V.; KerÄNen, J.; Lindgren, M. SOUND INSULATION OF DOORS—PART 2: COMPARISON BETWEEN MEASUREMENT RESULTS AND PREDICTIONS. J. Sound Vib. 2000, 230, 149–170. [Google Scholar] [CrossRef]
- Soni, K.; Singh, M.; Yadav, Y.K. Sound Transmission Characteristics Through Multi-panel Structures of Wooden Doors and Uncertainty Components in the Measurements. In Recent Developments in Acoustics. Lecture Notes in Mechanical Engineering; Springer: Singapore, 2021. [Google Scholar]
- Gompeters, M.C. The “sound insulation” of circular and slit-shaped apertures. Acta Acust. United Acustica 1964, 14, 1–16. [Google Scholar]
- Gompeters, M.C. The influence of viscosity on sound transmission through small circular apertures in walls of finite thickness. Acta Acust. United Acust. 1964, 15, 191–198. [Google Scholar]
- Wilson, G.P.; Soroka, W.W. Approximation to the Diffraction of Sound by a Circular Aperture in a Rigid Wall of Finite Thickness. J. Acoust. Soc. Am. 1964, 36, 1023. [Google Scholar] [CrossRef]
- Asakura, T.; Sakamoto, S. Improvement of sound insulation of doors or windows by absorption treatment inside the peripheral gaps. Acoust. Sci. Technol. 2013, 34, 241–252. [Google Scholar] [CrossRef]
- Shimizu, T.; Kawai, Y.; Takahashi, D. Numerical analyses and experimental evaluation of reduction technique for sound transmission through gaps. Appl. Acoust. 2015, 99, 97–109. [Google Scholar] [CrossRef]
- Shimizu, T.; Koizumi, S. Study of the compatibility between sound insulation performance and ventilation performance in gaps by installing nonwoven fabrics. Build. Environ. 2015, 94, 335–343. [Google Scholar] [CrossRef]
- Sakamoto, S.; Koseki, S.; Chinda, M.; Abe, S. A silencer incorporated within the thickness of the edge of the door for increasing sound transmission lossa. J. Acoust. Soc. Am. 2018, 144, 3303–3312. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, X.; Zhang, W.; Zhang, W.; Xuan, Y. Optimising multi-vent module-based adaptive ventilation using a novel parameter for improved indoor air quality and health protection. Build. Simul. 2024, 17, 113–130. [Google Scholar] [CrossRef]
- Vilén, L.; Atosuo, J.; Putus, T. The association of voice problems with exposure to indoor air contaminants in health care centres—The effect of remediation on symptom prevalence: A follow-up study. Indoor Built Environ. 2023, 33, 314–324. [Google Scholar] [CrossRef]
- Chen, H.; Ding, X.; Li, R.; Gong, S.; Liu, B.; Li, Q.; Gao, W. An experimental case study of natural ventilation effects on the residential thermal environment and predicted thermal comfort in Kunming. Case Stud. Therm. Eng. 2024, 56, 104198. [Google Scholar] [CrossRef]
- Rocha, L.A.; Gomez, R.S.; Delgado, J.M.P.Q.; Vieira, A.N.O.; Santos, I.B.; Luiz, M.R.; Oliveira, V.A.B.; Oliveira Neto, G.L.; Vasconcelos, D.B.T.; Silva, M.J.V.; et al. Natural Ventilation in Low-Cost Housing: An Evaluation by CFD. Buildings 2023, 13, 1408. [Google Scholar] [CrossRef]
- Furdas, Y.; Yurkevych, Y.; Zhelykh, V.; Ulewicz, M. The Impact of Wind Flow on Multi-storey Buildings: Experimental Studies. In International Scientific Conference EcoComfort and Current Issues of Civil Engineering; Springer International Publishing: Cham, Switzerland, 2023; pp. 83–93. [Google Scholar]
- Myroniuk, K.; Furdas, Y.; Zhelykh, V.; Adamski, M.; Gumen, O.; Savin, V.; Mitoulis, S.-A. Passive Ventilation of Residential Buildings Using the Trombe Wall. Buildings 2024, 14, 3154. [Google Scholar] [CrossRef]
- Rubino, C.; Liuzzi, S.; Fusaro, G.; Martellotta, F.; Scrosati, C.; Garai, M. Balancing ventilation and sound insulation in windows by means of metamaterials: A review of the state of the art. Build. Environ. 2025, 275, 112780. [Google Scholar] [CrossRef]
- Yan, Y.; Kang, M.; Zhang, H.; Lian, Z.; Fan, X.; Sekhar, C.; Wargocki, P.; Lan, L. Does window/door opening behaviour during summer affect the bedroom environment and sleep quality in a high-density sub-tropical city. Build. Environ. 2024, 247, 111024. [Google Scholar] [CrossRef]
- ISO 10140-3:2021; Acoustics—Laboratory measurement of sound insulation of building elements—Part 3: Measurement of impact sound insulation. ISO: Geneva, Switzerland, 2021.
- COMSOL Documentation. User’s Guide on Structural Mechanics Theory. 1998. Available online: https://doc.comsol.com/6.2/docserver/#!/com.comsol.help.sme/sme_ug_theory.06.024.html%233439873 (accessed on 1 October 2024).
- COMSOL Documentation. Sound Transmission Loss Through a Concrete Wall. 2020. Available online: https://cn.comsol.com/model/sound-transmission-loss-through-a-concrete-wall-73371 (accessed on 1 October 2024).
- Zhu, X.; Wang, L.J.; Wang, X.L.; Zheng, Y.D.; Luo, L. Sound insulation performance and modal analysis of asymmetrical insulating laminated glass. J. Low Freq. Noise Vib. Act. Control 2024, 43, 846–862. [Google Scholar] [CrossRef]
- Deng, Z.; Dong, B.; Guo, X.; Wang, X.; Zhang, J. Assessing multi-domain impact of IAQ and noise on productivity with portable air cleaners through physiological signals. Build. Environ. 2024, 254, 111375. [Google Scholar] [CrossRef]
- Du, L.; Lau, S.-K.; Lee, S.E. Experimental study on sound transmission loss of plenum windows. J. Acoust. Soc. Am. 2019, 146, EL489–EL495. [Google Scholar] [CrossRef]
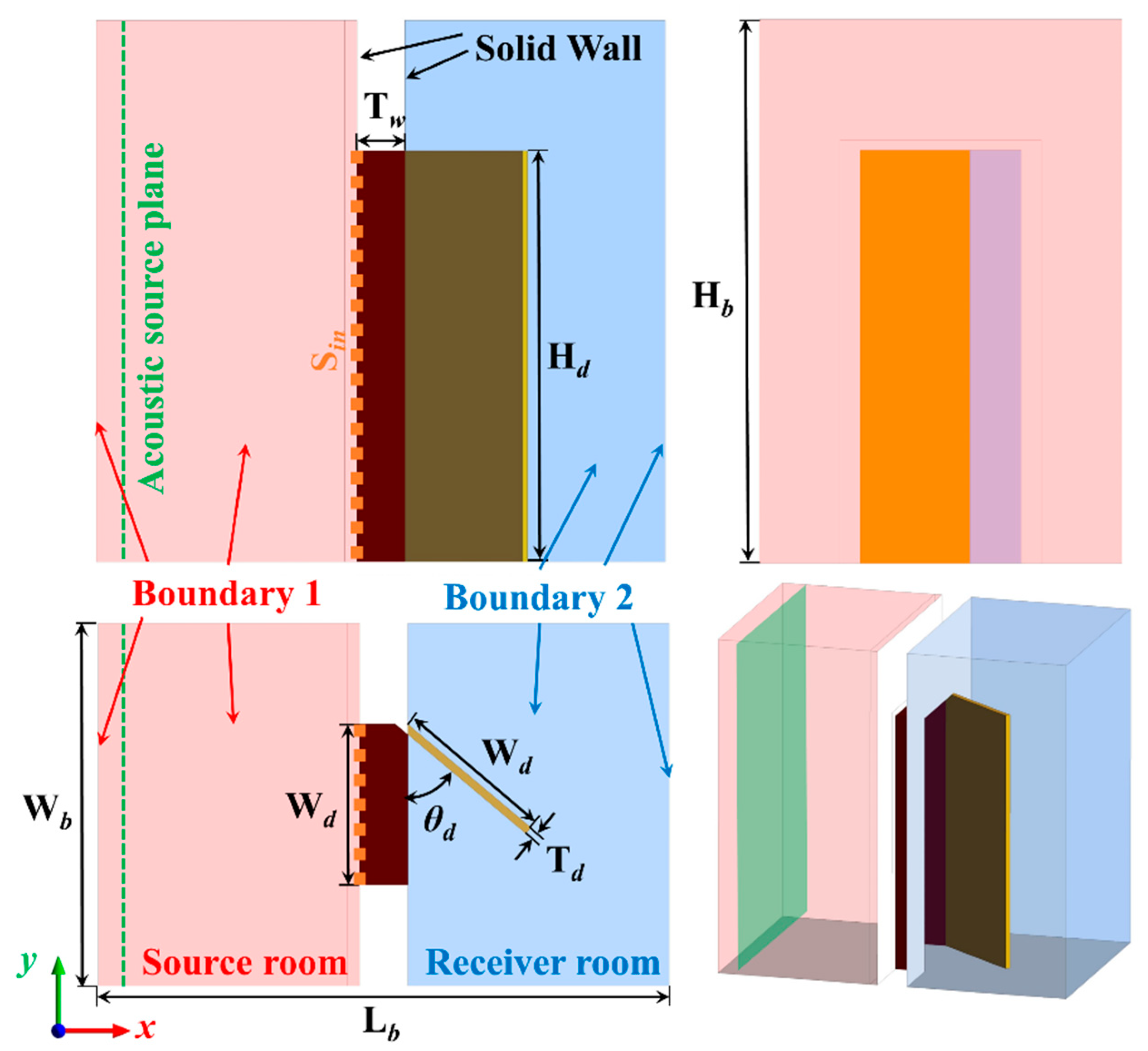

| Parameter | Value |
|---|---|
| Hb (m) | 2.7 |
| Lb (m) | 3.4 |
| Wb (m) | 2.2 |
| Hd (m) | 2.7 |
| Wd (m) | 0.8 |
| Td (m) | 0.04 |
| Tw (m) | 0.24 |
| θd | 0~90° |
| ρd (kg/m3) | 532 |
| Ed (Pa) | 8.2 × 109 |
| νd | 0.4 |
| Opening Angle (θd) | STLTotal *1 (dB) | STLTotal *2 (dB) | Change in Loudness |
|---|---|---|---|
| 5° | 38.55 | 10.44 | Apparent |
| 10° | 34.77 | 6.66 | Noticeable |
| 20° | 31.74 | 3.63 | Perceptible |
| 30° | 30.13 | 2.02 | Barely perceptible |
| 40° | 29.28 | 1.17 | Not perceptible |
| 50° | 28.80 | 0.69 | Not perceptible |
| 60° | 28.48 | 0.37 | Not perceptible |
| 70° | 28.26 | 0.15 | Not perceptible |
| 80° | 28.23 | 0.12 | Not perceptible |
| 90° | 28.11 | 0.00 | Not perceptible |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, X.; Li, M.; Liu, J. A Numerical Investigation of the Trade-Off Between Sound Insulation and Air Ventilation for a Partially Open Door. Eng 2025, 6, 223. https://doi.org/10.3390/eng6090223
Liu J, Li X, Li M, Liu J. A Numerical Investigation of the Trade-Off Between Sound Insulation and Air Ventilation for a Partially Open Door. Eng. 2025; 6(9):223. https://doi.org/10.3390/eng6090223
Chicago/Turabian StyleLiu, Jizhou, Xu Li, Ming Li, and Jiying Liu. 2025. "A Numerical Investigation of the Trade-Off Between Sound Insulation and Air Ventilation for a Partially Open Door" Eng 6, no. 9: 223. https://doi.org/10.3390/eng6090223
APA StyleLiu, J., Li, X., Li, M., & Liu, J. (2025). A Numerical Investigation of the Trade-Off Between Sound Insulation and Air Ventilation for a Partially Open Door. Eng, 6(9), 223. https://doi.org/10.3390/eng6090223








