STID-Mixer: A Lightweight Spatio-Temporal Modeling Framework for AIS-Based Vessel Trajectory Prediction
Abstract
1. Introduction
- Lightweight prediction framework: We propose STID-Mixer, a compact yet expressive model tailored for AIS trajectory prediction. It eliminates the need for convolutional and attention-based mechanisms while preserving high accuracy and scalability.
- Unified spatio-temporal representation: A joint embedding scheme encodes discrete temporal features (e.g., hour, weekday), spatial grid identifiers, and normalized continuous AIS attributes, enabling effective modeling of complex spatio-temporal vessel behaviors.
- Improved predictive performance and efficiency: Extensive experiments show that STID-Mixer consistently outperforms several strong baselines (e.g., LSTM, Transformer, GBDT [14]) in terms of prediction accuracy, F1 score and training time.
- Generalization and practical potential: The model demonstrates robust generalization on large-scale trajectory forecasting tasks, offering a deployable and adaptable solution for real-world maritime behavior modeling.
2. Related Work
3. Materials and Methods
3.1. Training Settings
3.2. AIS Data Cleaning and Preprocessing
- Message Parsing: Raw AIS messages in NMEA 0183 format [29] were parsed to extract essential fields, including Maritime Mobile Service Identity (MMSI), timestamp, longitude, latitude, Speed Over Ground (SOG), and Course Over Ground (COG), which were then stored in structured formats.
- Record-Level Filtering: Redundant or erroneous data were removed through filtering operations, including the elimination of duplicate records, invalid MMSI entries, and records with missing fields or invalid values (e.g., SOG = 0 and COG = 360), which typically indicate non-moving or unreliable observations.
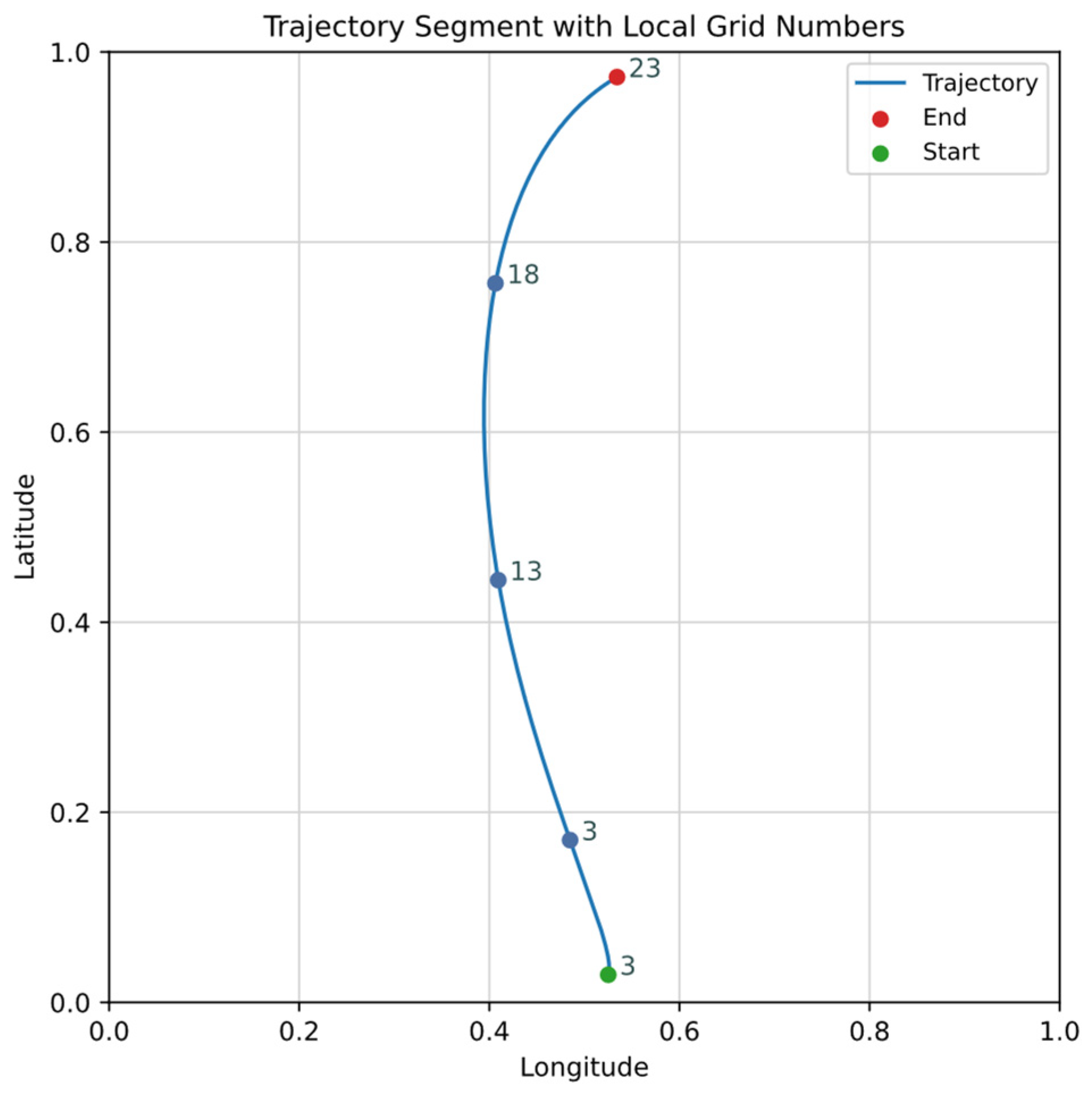
- Trajectory Structuring and Quality Control: At the trajectory level, segmentation was performed based on temporal intervals. Additionally, messages of irrelevant types were excluded, short trajectory segments were discarded, and overly long trajectories were split to ensure manageable sequence lengths for modeling.
- High-Frequency Broadcast Merging: To mitigate the redundancy caused by high-frequency AIS broadcasts—particularly from certain message categories within short time windows—a compression strategy was implemented. Within a sliding window of 25 to 35 s, only the final record in each group of closely spaced messages was retained, effectively sparsifying the trajectory structure and reducing modeling overhead.
3.3. Datasets
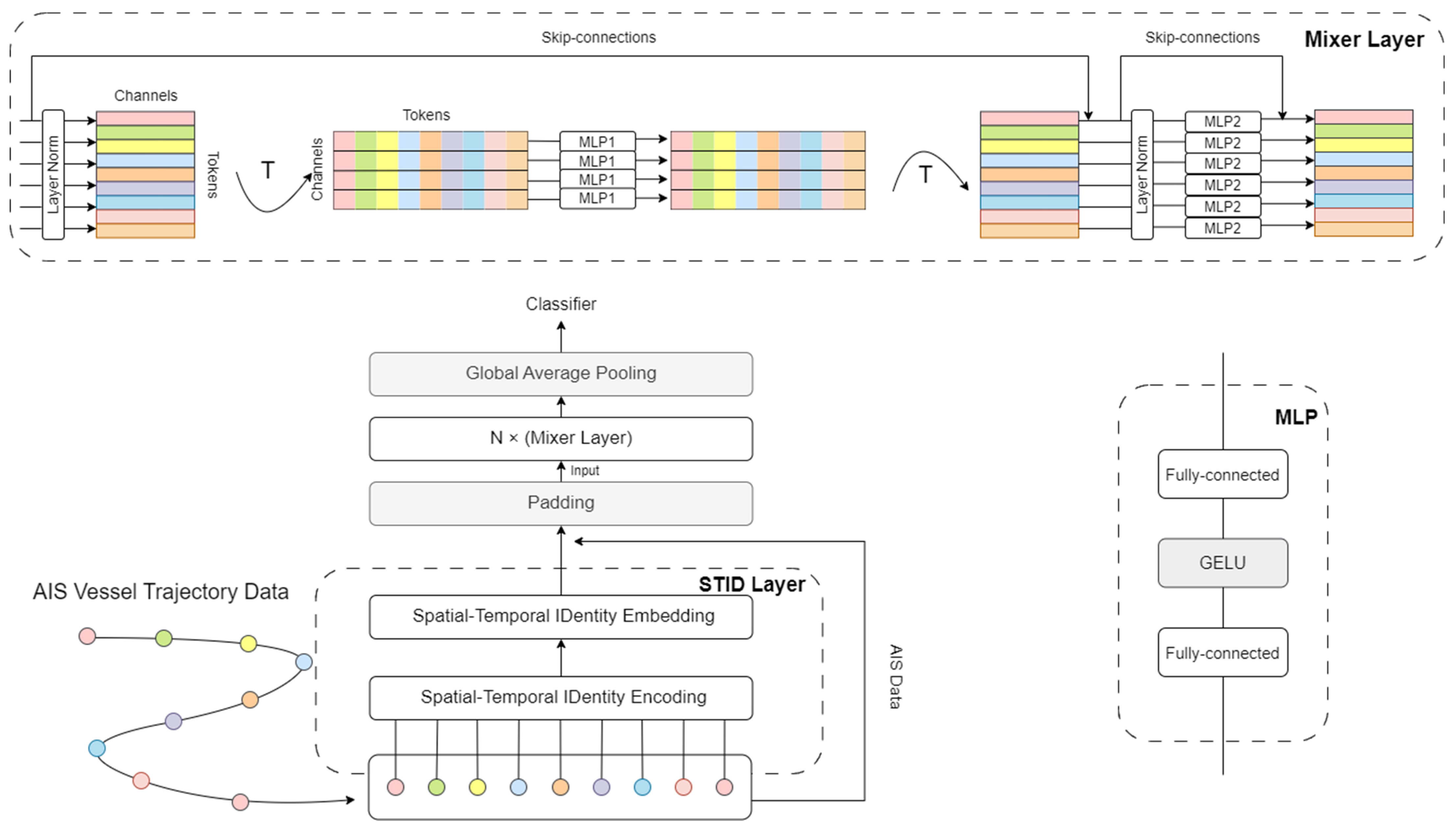
3.4. Model Architecture
- Token Mixing:
- Channel Mixing:
3.5. Evaluation Metrics
- Accuracy: This metric calculates the proportion of predictions that exactly match the ground truth labels, serving as a primary indicator of Top-1 classification performance. Given as the total number of samples and as the number of correctly predicted samples, the accuracy is defined as follows:
- Cross-Entropy Loss: As a standard loss function for multi-class classification tasks, the cross-entropy loss quantifies the divergence between the predicted probability distribution and the true label distribution. During training, the model is optimized by minimizing this loss. Let denote the number of classes, be the binary indicator of the true class, and the predicted probability for class . The loss is defined as follows:
- F1 Score: The F1 score is the harmonic mean of precision and recall, offering a balanced measure of the model’s classification ability across categories. This study reports two variants:
- Micro F1: Calculated by aggregating true positives (TP), false positives (FP), and false negatives (FN) across all classes, it reflects the model’s global performance across the entire dataset:
- Macro F1: Computed by averaging the F1 scores of individual classes, this metric emphasizes the model’s ability to handle imbalanced classes and is especially useful for evaluating performance on underrepresented categories:where is the number of classes, and , and represent the true positives, false positives, and false negatives for class , respectively.
4. Results
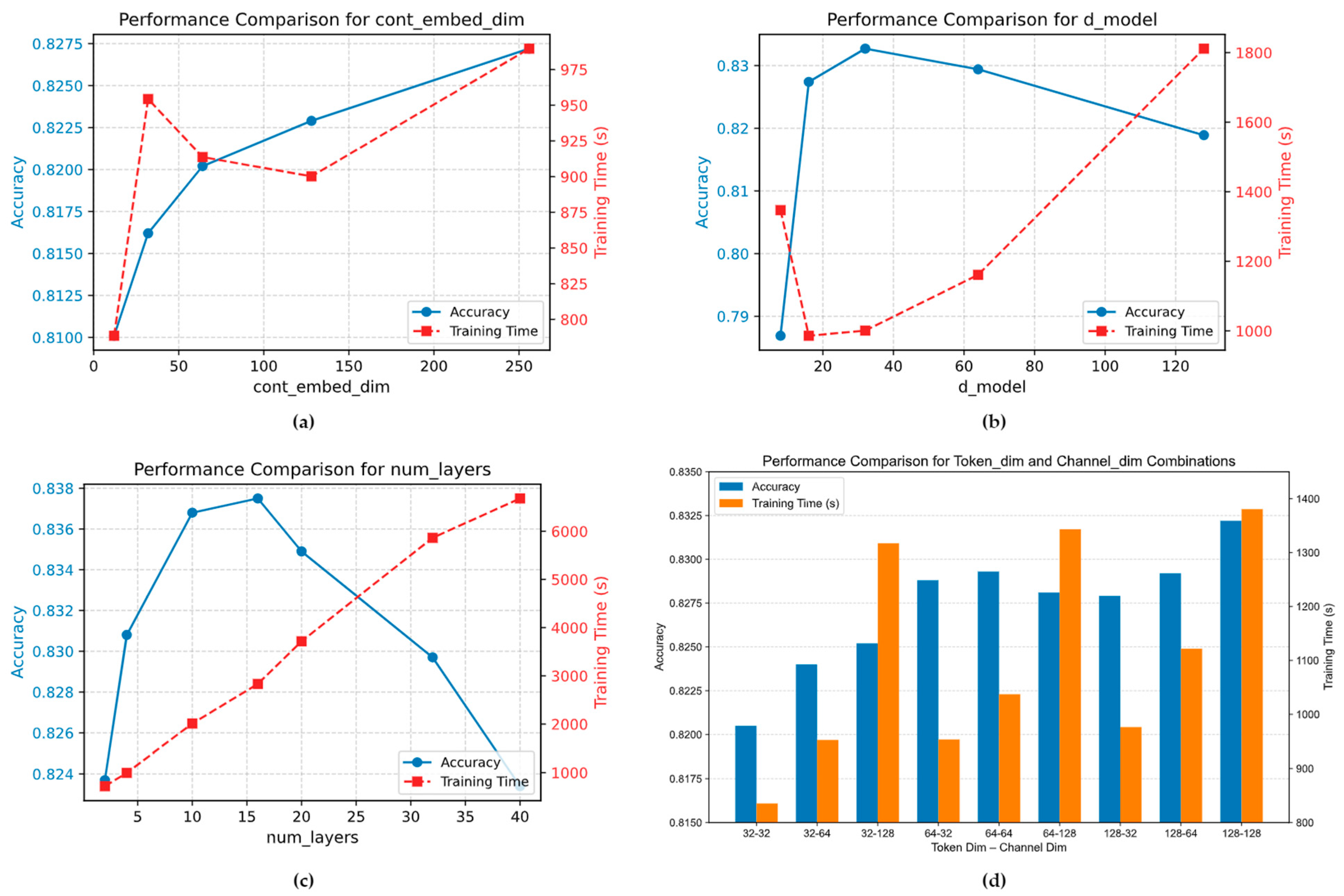
4.1. Hyperparameter Settings
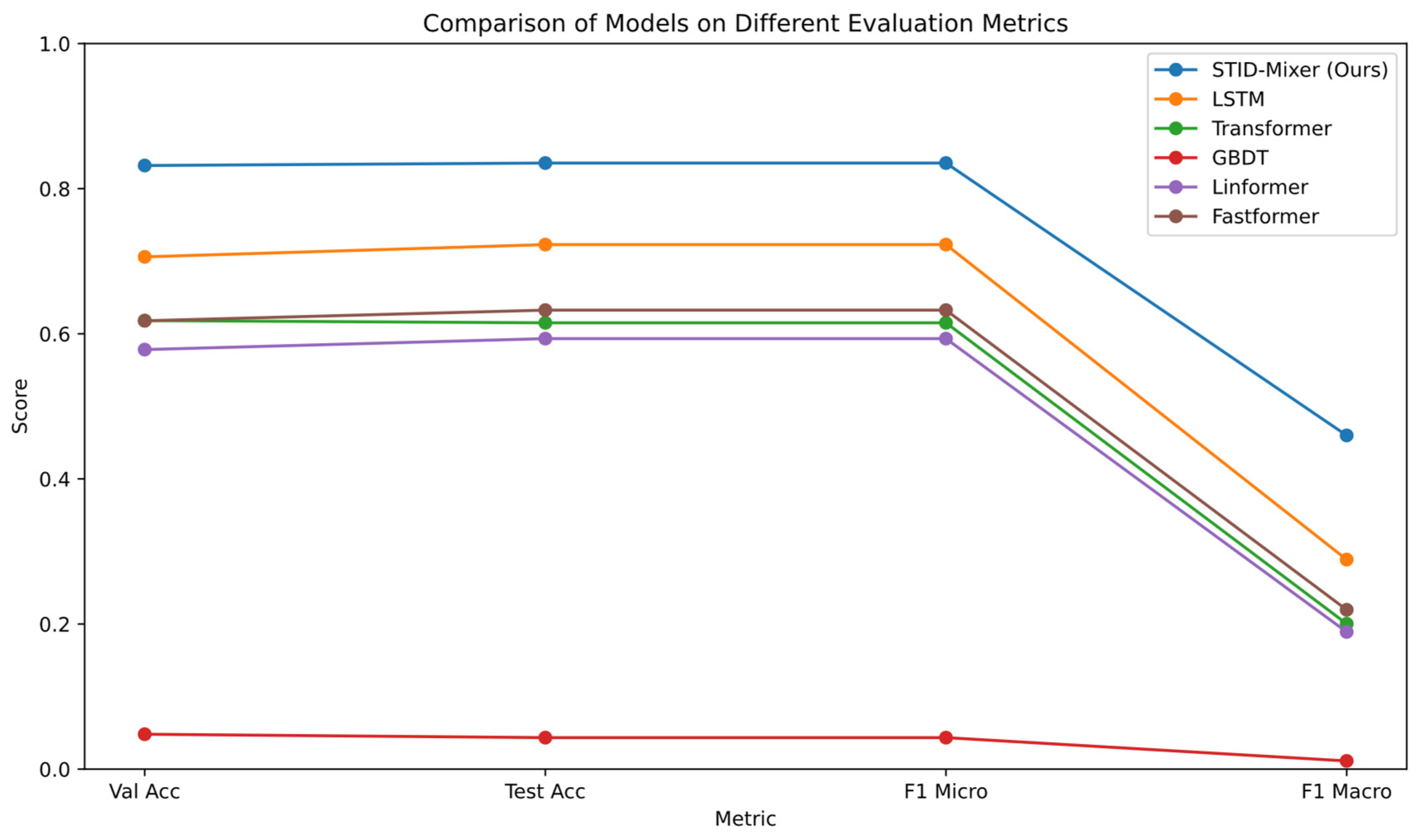
4.2. Comparative Experiments
4.3. Ablation Study
- STID-MLP: Utilizes the full set of discrete spatiotemporal features and continuous features as input but replaces the MLP-Mixer backbone with a standard multilayer perceptron.
- SID-Mixer: Retains only the spatial discrete feature (Grid ID) while removing temporal ID features (Hour and Weekday).
- TID-Mixer: Retains temporal ID features while removing spatial discrete input.
- Cont-Only: A minimal version using only continuous features (SOG, COG, relative time, longitude, and latitude), with no discrete encoding.
| Ablated Model | Test Loss | Test Acc | F1_Macro | Time (s) |
|---|---|---|---|---|
| STID-Mixer | 0.7231 | 0.8353 | 0.4599 | 3452.80 |
| STID-MLP | 1.6037 | 0.6366 | 0.2468 | 1000.02 |
| SID-Mixer | 1.6037 | 0.6344 | 0.2843 | 4358.26 |
| TID-Mixer | 3.1054 | 0.3130 | 0.0713 | 6179.84 |
| Cont-Only | 3.0503 | 0.3199 | 0.0643 | 6218.47 |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIS | Automatic Identification System |
| MMSI | Maritime Mobile Service Identity |
| LON | Longitude |
| LAT | Latitude |
| SOG | Speed Over Ground |
| COG | Course Over Ground |
| VHF | Very High Frequency |
| STID | Spatial-Temporal Identity |
| MLP | Multilayer Perceptron |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| TREAD | Trajectory Reconstruction and Evaluation for Anomaly Detection |
| SGCN | Sparse Graph Convolutional Network |
| MTS | Multivariate Time Series |
| GBDT | Gradient Boosted Decision Tree |
| GELU | Gaussian Error Linear Unit |
References
- Murray, B.; Perera, L.P. An AIS-based deep learning framework for regional ship behavior prediction. Reliab. Eng. Syst. Saf. 2021, 215, 107819. [Google Scholar] [CrossRef]
- Hexeberg, S.; Flåten, A.L.; Brekke, E.F. AIS-based vessel trajectory prediction. In Proceedings of the 2017 20th international conference on information fusion (Fusion), Xi’an, China, 10–13 July 2017; pp. 1–8. [Google Scholar]
- Yang, D.; Wu, L.; Wang, S.; Jia, H.; Li, K.X. How big data enriches maritime research–a critical review of Automatic Identification System (AIS) data applications. Transp. Rev. 2019, 39, 755–773. [Google Scholar] [CrossRef]
- Mazzarella, F.; Arguedas, V.F.; Vespe, M. Knowledge-based vessel position prediction using historical AIS data. In Proceedings of the 2015 Sensor Data Fusion: Trends, Solutions, Applications (SDF), Bonn, Germany, 6–8 October 2015; pp. 1–6. [Google Scholar]
- Rong, H.; Teixeira, A.; Soares, C.G. Ship trajectory uncertainty prediction based on a Gaussian Process model. Ocean Eng. 2019, 182, 499–511. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. In Proceedings of the Advances in Neural Information Processing Systems 34 (NeurIPS 2021), Virtual, 6–14 December 2021; pp. 22419–22430. [Google Scholar]
- Wu, C.; Wu, F.; Qi, T.; Huang, Y.; Xie, X. Fastformer: Additive attention can be all you need. arXiv 2021, arXiv:2108.09084. [Google Scholar]
- Wang, S.; Li, B.Z.; Khabsa, M.; Fang, H.; Ma, H. Linformer: Self-attention with linear complexity. arXiv 2020, arXiv:2006.04768. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI conference on artificial intelligence, Virtual, 2–9 February 2021; pp. 11106–11115. [Google Scholar]
- Pallotta, G.; Vespe, M.; Bryan, K. Vessel pattern knowledge discovery from AIS data: A framework for anomaly detection and route prediction. Entropy 2013, 15, 2218–2245. [Google Scholar] [CrossRef]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Li, H.; Jiao, H.; Yang, Z. AIS data-driven ship trajectory prediction modelling and analysis based on machine learning and deep learning methods. Transp. Res. E Logist. Transp. Rev. 2023, 175, 103152. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Xiao, F.; Ligteringen, H.; Van Gulijk, C.; Ale, B. Comparison study on AIS data of ship traffic behavior. Ocean Eng. 2015, 95, 84–93. [Google Scholar] [CrossRef]
- Tu, E.; Zhang, G.; Rachmawati, L.; Rajabally, E.; Huang, G.-B. Exploiting AIS data for intelligent maritime navigation: A comprehensive survey from data to methodology. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1559–1582. [Google Scholar] [CrossRef]
- Ristic, B.; La Scala, B.; Morelande, M.; Gordon, N. Statistical analysis of motion patterns in AIS data: Anomaly detection and motion prediction. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–7. [Google Scholar]
- Gao, M.; Shi, G.; Li, S. Online prediction of ship behavior with automatic identification system sensor data using bidirectional long short-term memory recurrent neural network. Sensors 2018, 18, 4211. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, R.M. Recurrent neural networks (rnns): A gentle introduction and overview. arXiv 2019, arXiv:1912.05911. [Google Scholar]
- Fang, W.; Chen, Y.; Xue, Q. Survey on research of RNN-based spatio-temporal sequence prediction algorithms. J. Big Data 2021, 3, 97. [Google Scholar] [CrossRef]
- Forti, N.; Millefiori, L.M.; Braca, P.; Willett, P. Prediction oof vessel trajectories from AIS data via sequence-to-sequence recurrent neural networks. In Proceedings of the ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Virtual, 4–8 May 2020; pp. 8936–8940. [Google Scholar]
- Shi, L.; Wang, L.; Long, C.; Zhou, S.; Zhou, M.; Niu, Z.; Hua, G. SGCN: Sparse graph convolution network for pedestrian trajectory prediction. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 20–25 June 2021; pp. 8994–9003. [Google Scholar]
- Cheng, J.C.; Poon, K.H.; Wong, P.K.-Y. Long-Time gap crowd prediction with a Two-Stage optimized spatiotemporal Hybrid-GCGRU. Adv. Eng. Inform. 2022, 54, 101727. [Google Scholar] [CrossRef]
- Lin, Z.; Yue, W.; Huang, J.; Wan, J. Ship trajectory prediction based on the TTCN-attention-GRU model. Electronics 2023, 12, 2556. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, Z.; Wang, F.; Wei, W.; Xu, Y. Spatial-temporal identity: A simple yet effective baseline for multivariate time series forecasting. In Proceedings of the 31st ACM International Conference on Information and Knowledge Management(CIKM 2022), Atlanta, GA, USA, 17–21 October 2022; pp. 4454–4458. [Google Scholar]
- Tolstikhin, I.O.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J. Mlp-mixer: An all-mlp architecture for vision. In Proceedings of the Advances in Neural Information Processing Systems 34 (NeurIPS 2021), Virtual, 6–14 December 2021; pp. 24261–24272. [Google Scholar]
- Ekambaram, V.; Jati, A.; Nguyen, N.; Sinthong, P.; Kalagnanam, J. Tsmixer: Lightweight mlp-mixer model for multivariate time series forecasting. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD ‘23), Long Beach, CA, USA, 6–10 August 2023; pp. 459–469. [Google Scholar]
- Chen, S.-A.; Li, C.-L.; Yoder, N.; Arik, S.O.; Pfister, T. Tsmixer: An all-mlp architecture for time series forecasting. arXiv 2023, arXiv:2303.06053. [Google Scholar]
- National Marine Electronics Association. NMEA 0183 Standard for Interfacing Marine Electronic Devices. Available online: https://www.nmea.org/nmea-0183.html (accessed on 10 June 2024).
- China MSA AIS Service Platform. Available online: https://enav.nhhb.org.cn/nbwebgis/ (accessed on 15 June 2024).
- Li, Q.; Wang, Y.; Shao, Y.; Li, L.; Hao, H. A comparative study on the most effective machine learning model for blast loading prediction: From GBDT to Transformer. Eng. Struct. 2023, 276, 115310. [Google Scholar] [CrossRef]
| MMSI | Time | Hour | Weekday | LON | LAT | Grid_id | SOG | COG | Traj_id |
|---|---|---|---|---|---|---|---|---|---|
| 100899043 | 0.5850 | 11 | 1 | 0.9383 | 0.0032 | 47 | 0.0567 | 0.9250 | 100899043_2 |
| 100899043 | 0.5850 | 11 | 1 | 0.9374 | 0.0050 | 47 | 0.0557 | 0.9269 | 100899043_2 |
| 100899043 | 0.5851 | 11 | 1 | 0.9348 | 0.0121 | 47 | 0.0538 | 0.9272 | 100899043_2 |
| Models | Val Acc | Test Acc | F1_Macro | Total Time (s) | Time/Epoch (s) |
|---|---|---|---|---|---|
| STID-Mixer | 0.8319 | 0.8353 | 0.4599 | 3452.80 | 215.80 |
| LSTM | 0.7060 | 0.7229 | 0.2888 | 19,342.97 | 452.76 |
| Transformer | 0.6182 | 0.6151 | 0.2003 | 17,449.81 | 667.90 |
| GBDT | 0.0481 | 0.0434 | 0.0113 | 23,937.32 | |
| Linformer | 0.5782 | 0.5933 | 0.1891 | 6255.08 | 235.23 |
| Fastformer | 0.6179 | 0.6326 | 0.2196 | 14,318.40 | 505.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhang, J.; Jin, G.; Dong, X. STID-Mixer: A Lightweight Spatio-Temporal Modeling Framework for AIS-Based Vessel Trajectory Prediction. Eng 2025, 6, 184. https://doi.org/10.3390/eng6080184
Wang L, Zhang J, Jin G, Dong X. STID-Mixer: A Lightweight Spatio-Temporal Modeling Framework for AIS-Based Vessel Trajectory Prediction. Eng. 2025; 6(8):184. https://doi.org/10.3390/eng6080184
Chicago/Turabian StyleWang, Leiyu, Jian Zhang, Guangyin Jin, and Xinyu Dong. 2025. "STID-Mixer: A Lightweight Spatio-Temporal Modeling Framework for AIS-Based Vessel Trajectory Prediction" Eng 6, no. 8: 184. https://doi.org/10.3390/eng6080184
APA StyleWang, L., Zhang, J., Jin, G., & Dong, X. (2025). STID-Mixer: A Lightweight Spatio-Temporal Modeling Framework for AIS-Based Vessel Trajectory Prediction. Eng, 6(8), 184. https://doi.org/10.3390/eng6080184







