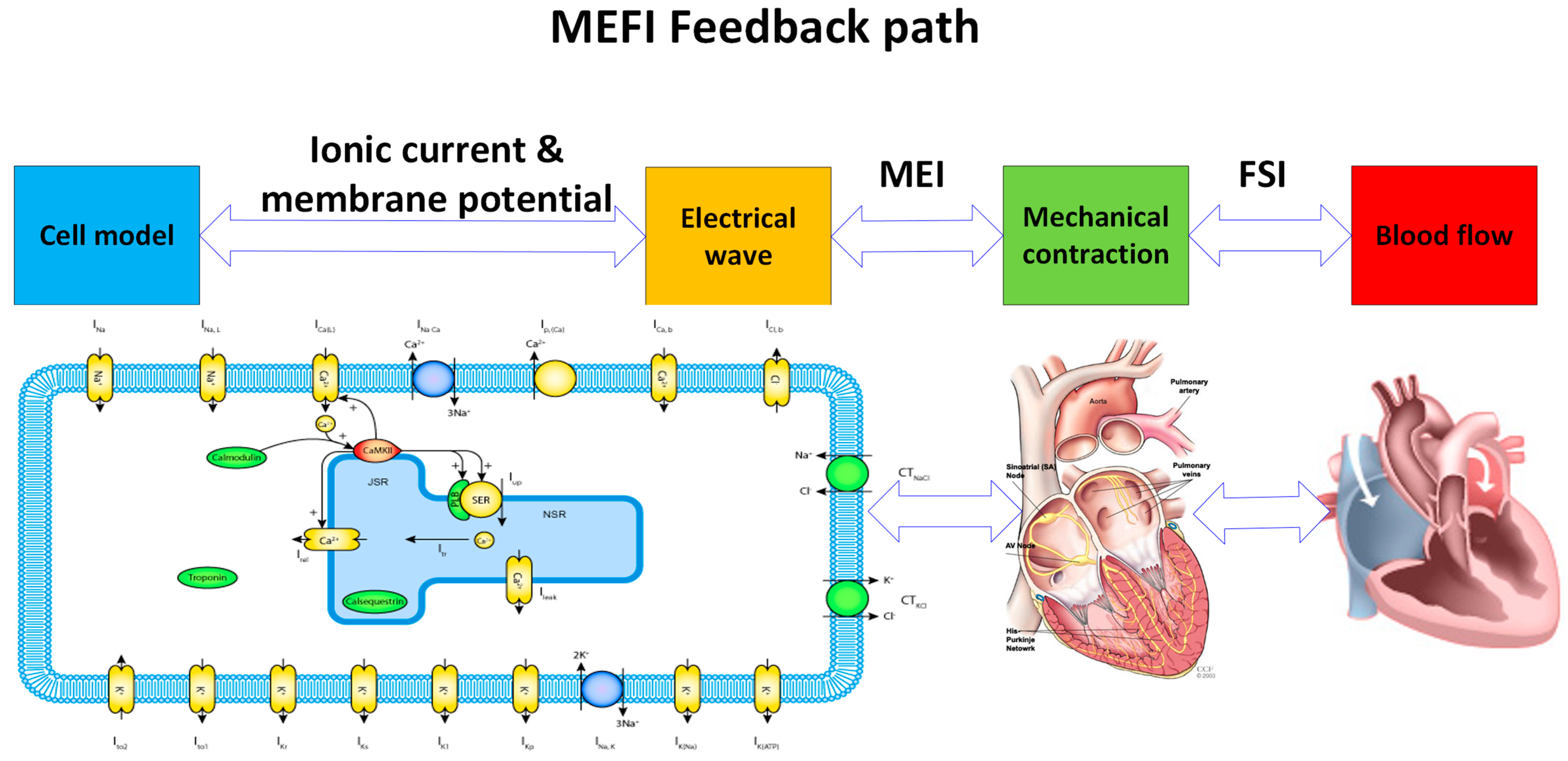
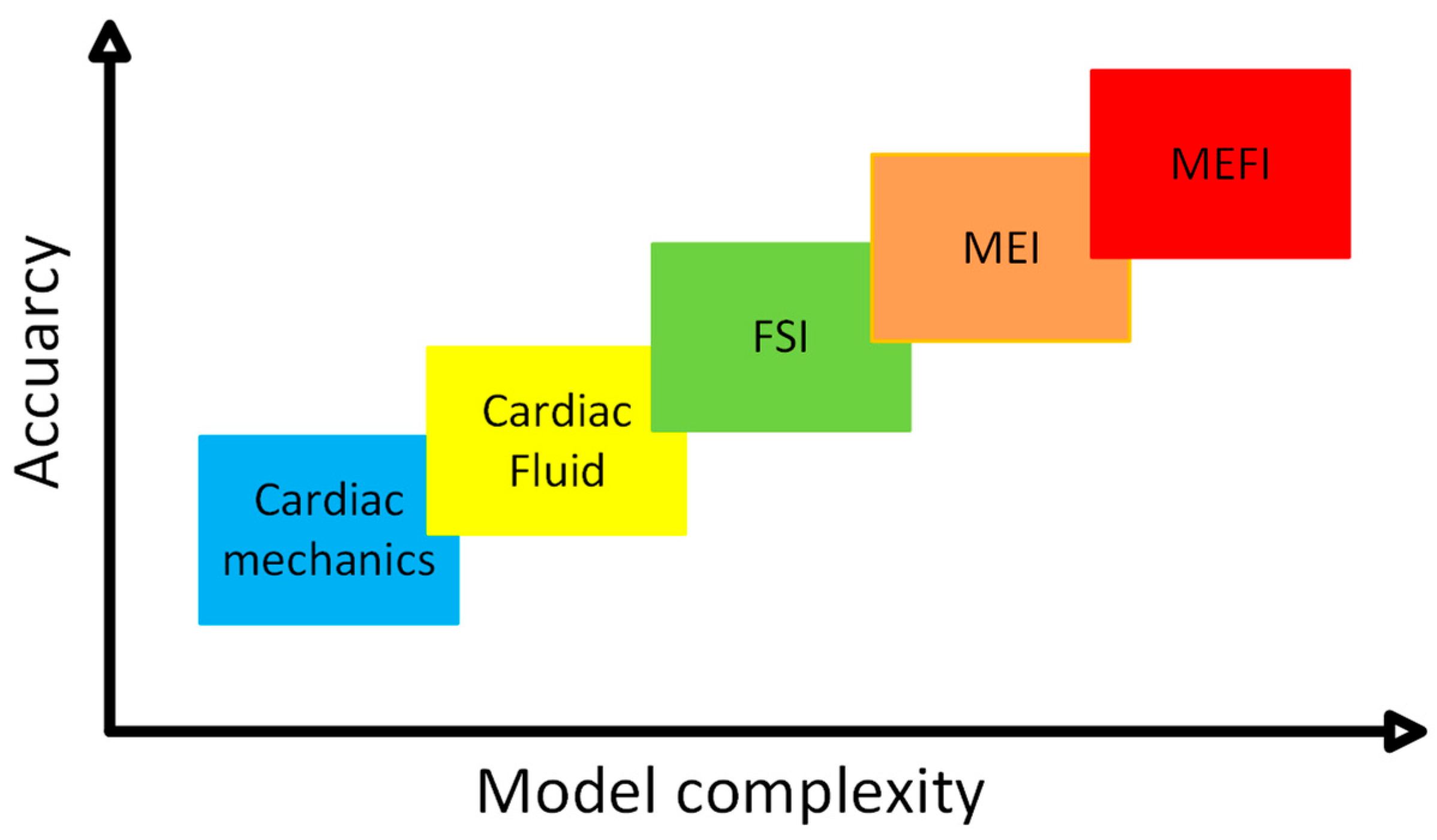
Previous computational models of the MEFI system can be broadly categorized into three groups: fluid–structure interaction (FSI), mechano–electrical interaction (MEI), and fully coupled mechano-electrical-fluid interaction (MEFI) models.
2.1. Cardiac Fluid, Structure (Tissue), or Fluid–Structure Interaction (FSI)
This subsection focuses on models that simulate the interaction between cardiac tissue mechanics and intracardiac blood flow, excluding electrical activity. These fluid–structure interaction (FSI) models are foundational to MEFI modeling, as they capture how mechanical deformation of the heart influences and responds to blood flow dynamics. FSI modeling represents an essential early step in developing integrated cardiovascular simulations. Blood flow dynamics within the heart have been extensively investigated over many years [
9,
10], revealing that blood flow is closely coupled to the heart’s contraction and relaxation cycles through complex kinematic and momentum exchanges between the ventricular chambers and the myocardial walls. Pioneering work by Peskin and McQueen [
11,
12,
13,
14] established foundational cardiac FSI models using the immersed boundary method. Their seminal model primarily addressed fluid–structure interactions, intentionally excluding cardiac electrophysiology due to the considerable complexity such coupling would introduce.
Computational modeling of whole-heart function serves as a powerful tool for investigating cardiac mechanics and hemodynamics. However, many existing fluid–structure interaction (FSI) models of the heart primarily focus on electromechanical aspects, often neglecting physiological valve dynamics and employing simplified fluid models. Feng et al. [
15] addressed these limitations by developing a comprehensive four-chamber heart model that incorporates realistic chamber geometry, detailed valve modeling, hyperelastic myocardial material properties with fiber architecture, and full FSI analysis.
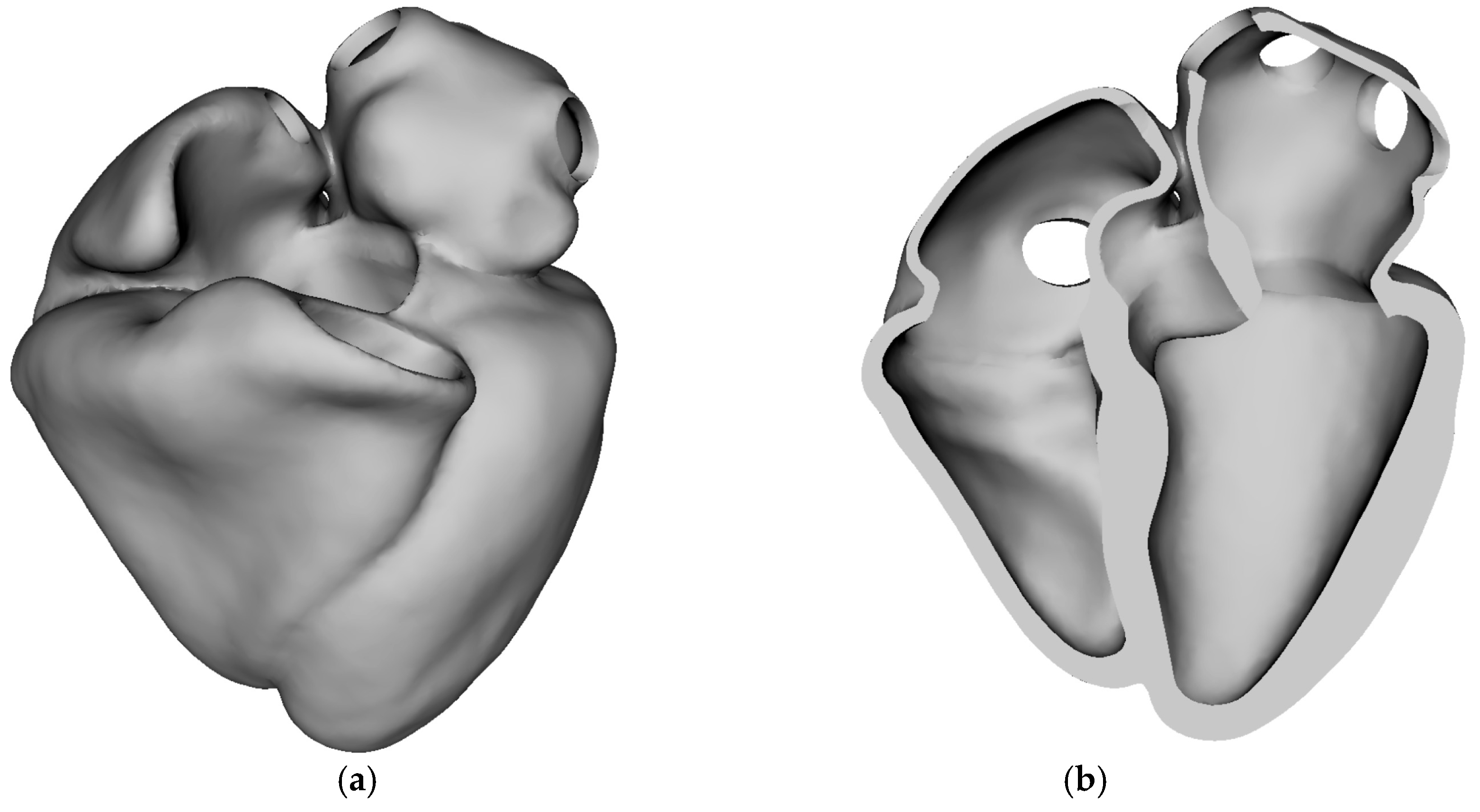
Figure 3 illustrates the three-dimensional stress-free anatomical geometry of the human heart used as the baseline domain for simulation. The geometry consists of all four cardiac chambers—left and right atria, and left and right ventricles—and represents the heart in its unloaded or stress-free state, i.e., before the application of any internal pressure or muscle activation.
Figure 3a shows the external view of the whole heart, providing a full spatial representation of the epicardial surface. Anatomical fidelity includes major chamber contours, apex, and valve orifice locations.
Figure 3b displays a cut-away view, exposing the internal chamber volumes and wall thickness. This view highlights the septal wall separating the left and right ventricles, openings corresponding to valvular inlets/outlets, and smooth chamber transitions necessary for physiological simulation of blood flow and electrical propagation. Stress-free configuration is essential for initializing biomechanical simulations accurately. In real hearts, the geometry seen on imaging (e.g., MRI) already contains pre-stress due to blood pressure and muscular tone. This figure establishes the foundation for all biomechanical and electrophysiological simulations performed in the study. High-fidelity anatomical accuracy and proper reference conditions (stress-free) are critical for meaningful and realistic results in simulations such as cardiac contraction, activation mapping, and pressure–volume loop generation.
Their model was used to study cardiac behavior under various assumptions, including restricted versus free valve annular dynamics and the presence or absence of heart–pericardium interactions. Simulation results successfully captured key physiological phenomena, such as valve leaflet–flow interactions; characteristic left ventricular flow vortices; venous and transvalvular flow waveforms; and realistic heart deformations, including atrioventricular plane movement. The model demonstrated that allowing free annular dynamics improved ventricular filling and atrial emptying during early diastole. Furthermore, the study found that pericardial forces significantly influence atrial wall deformation, particularly during atrial contraction, thereby enhancing atrial filling. Overall, this work establishes a robust framework for comprehensive multiphysics whole-heart modeling that incorporates detailed valve dynamics and fluid–structure interactions.
Jiang et al. [
16] developed a highly scalable, fully implicit finite element algorithm capable of simulating the dynamic deformation of a four-chamber human heart using patient-specific geometry and a heterogeneous hyper-elastic model.
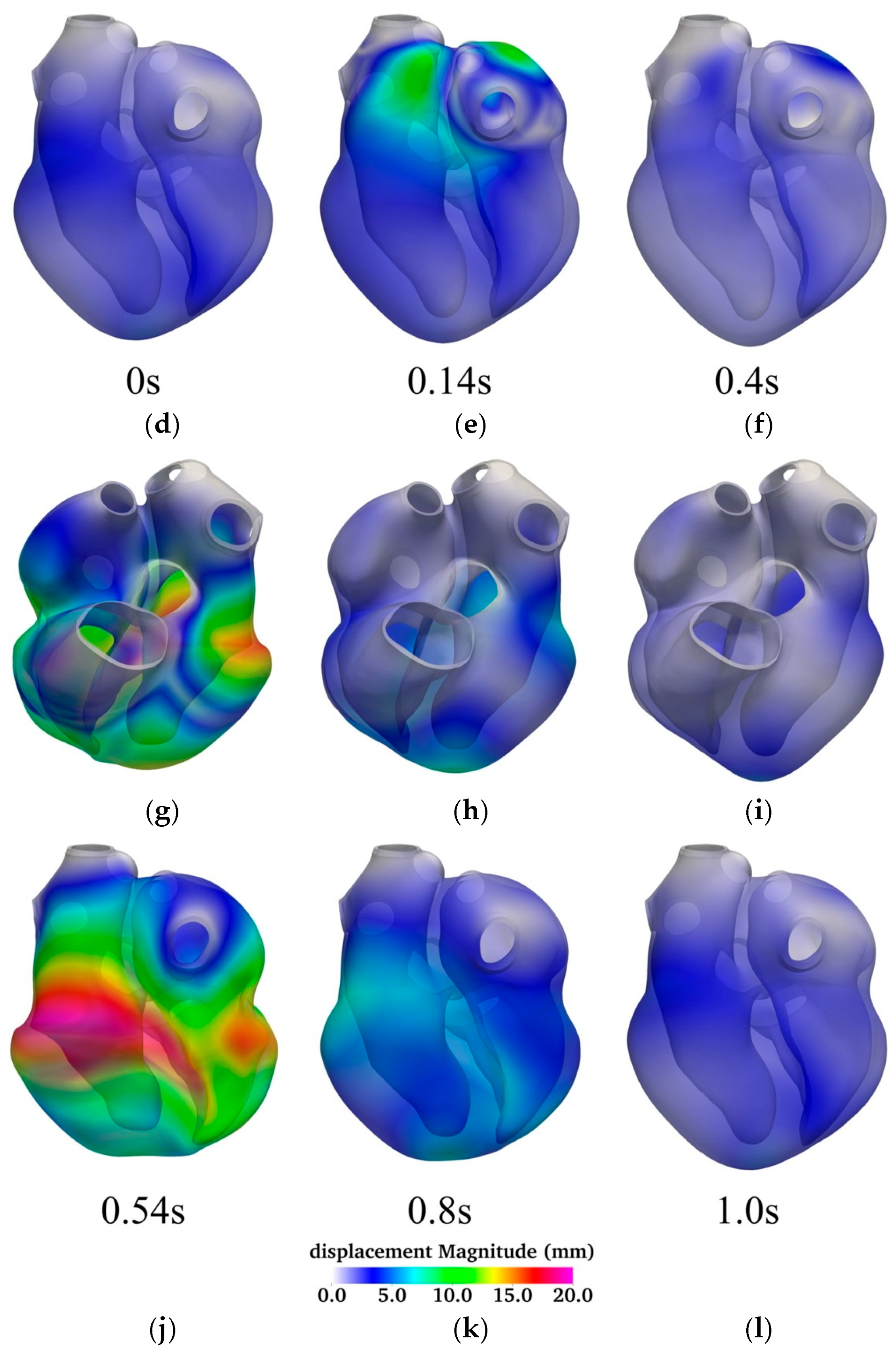
Figure 4 illustrates the temporal evolution of myocardial displacement over a complete cardiac cycle, using a series of six time points—0.0 s, 0.14 s, 0.4 s, 0.54 s, 0.8 s, and 1.0 s—to capture key phases of atrial and ventricular activity. Each time point is represented by a pair of 3D surface plots displaying both anterior (top row) and posterior (bottom row) views of the heart, color-coded by displacement magnitude (in millimeters).
At the start of the cycle (0.0 s; panels
Figure 4a,d), the heart is in its diastolic resting state, exhibiting minimal displacement throughout the myocardium. This corresponds to the phase immediately following passive filling, before atrial systole begins. At 0.14 s (panels
Figure 4b,e), significant displacement is observed in the atria, indicating active atrial contraction. The ventricles at this stage remain largely stationary, reflecting their passive filling phase. This spatially localized deformation is consistent with the timing of atrial systole in the cardiac cycle.
By 0.4 s (panels
Figure 4c,f), atrial contraction subsides, and the ventricles begin to activate. At this point, displacement begins to emerge in the ventricular walls, initiating the ejection phase of the cardiac cycle. The most substantial myocardial deformation occurs at 0.54 s (panels
Figure 4g,j), corresponding to peak ventricular systole. Here, the displacement magnitudes are highest in the ventricular myocardium, especially along the left ventricular free wall and apex, reflecting robust muscle contraction and blood ejection through the outflow tracts.
At 0.8 s (panels
Figure 4h,k), ventricular relaxation is underway. The myocardium begins to return toward its original configuration as the ventricles enter diastole. The overall displacement is reduced but still prominent in regions recovering from active contraction. Finally, by 1.0 s (panels
Figure 4i,l), the heart has nearly completed its cycle and returned to a quiescent state with minimal displacement, poised to initiate the next cycle.
The figure highlights the asynchronous but coordinated nature of atrial and ventricular contractions and underscores the biomechanical dynamics of the heart under physiological conditions. The temporal displacement patterns closely align with the expected timing of mechanical activation, providing a visual and quantitative representation of normal electromechanical coupling.
The model captures the full cardiac anatomy, using a Guccione-based hyper-elastic law for myocardial tissue and a Mooney–Rivlin model for vessel roots, incorporating anisotropic cardiac fiber architecture. A fully implicit method in time and finite element method in space is used, combined with a Newton–Krylov–Schwarz solver for tackling the nonlinear equations efficiently across large-scale processor cores. To deal with computational stiffness during highly nonlinear cardiac phases, the authors implemented a two-level adaptive time-stepping approach to improve convergence and reduce computational time. The method scales efficiently on high-performance computing systems, handling unstructured meshes with over 200 million degrees of freedom and up to 16,384 processor cores.
At any given moment, the displacement
d and velocity
v of a material point are governed by the following partial differential equations [
16]:
where (0,
T) is a time interval of interest,
p is the stress,
ρ is density, and Ω is the reference domain in the stress-free state.
The algorithm is validated through simulations of a complete cardiac cycle on a patient-specific heart. It accurately reproduces physiological behaviors such as displacement and adapts time steps effectively during challenging phases, such as rapid ventricular contraction, as shown in
Figure 4. Their study significantly advances computational cardiac mechanics by enabling large-scale, whole-heart simulations with high fidelity and computational efficiency. It lays the groundwork for future clinical and research applications involving cardiac dynamics and personalized heart modeling.
Personalized cardiac mechanics modeling offers valuable insights into the biomechanical function of the heart in both healthy and diseased states and plays a critical role in supporting treatment planning. However, existing models often rely on medical imaging captured at a single cardiac phase, limiting their effectiveness in analyzing dynamic cardiac behavior across multiple time points. Please note that although cine-MRI (cardiovascular magnetic resonance imaging) captures dynamic motion throughout the cardiac cycle, many computational models still depend on single-phase snapshots. This limitation arises from the difficulties associated with segmenting and aligning images across multiple time points. The challenges stem from the sparse and cross-sectional nature of the image slices, as well as potential misalignments caused by patient movement or inconsistencies in breath-hold positions during image acquisition, making accurate 3D reconstruction from these 2D slices particularly difficult [
17].
A novel inverse finite element analysis (iFEA) framework was designed to estimate the passive mechanical properties of cardiac tissue using time-resolved medical imaging data [
18].
Figure 5 illustrates a comprehensive pipeline for developing patient-specific computational models of cardiac biomechanics, with a focus on the biventricular and left atrial myocardium. The workflow begins with time-resolved, three-dimensional computed tomography (3D CT) scans that capture the cardiac anatomy at various phases of the cardiac cycle. These volumetric images serve as the foundational dataset for the model construction process.
In the image segmentation and morphing phase, the myocardial contours are delineated from CT images at key time points—typically end-diastole (EDV) and end-systole (ESV). This segmentation step can be performed manually using platforms such as SimVascular [
19] and MeshMixer [
20,
21], or through automated pipelines leveraging deep neural networks (DNNs) [
22], which significantly improves reproducibility and scalability across patients. These segmented geometries are then processed to produce a time-varying representation of the myocardial shape and structure.
Next, the segmented surfaces undergo model construction, wherein anatomical fidelity is enhanced by assigning rule-based myocardial fiber orientations and applying boundary conditions that mimic physiological constraints. These conditions include chamber pressures and mechanical supports derived from clinical data or established literature values. Additional geometric refinements and meshing are performed to ensure the model is suitable for finite element analysis.
The final stage involves an optimization process using inverse finite element analysis (iFEA). In this step, the biomechanical properties of the myocardial tissue—such as passive stiffness parameters—and the heart’s unloaded (stress-free) reference configuration are iteratively estimated. The optimization framework uses an inner-outer loop strategy: the inner loop applies an enhanced Sellier algorithm to recover the reference geometry, while the outer loop adjusts the material parameters to minimize the discrepancy between simulated deformations and those observed in the imaging-derived displacement fields over the cardiac cycle.
By incorporating both anatomical and functional data, this modeling framework enables a personalized characterization of myocardial mechanics. Such calibrated models are essential for understanding patient-specific cardiac function, assessing pathological remodeling, and informing therapeutic strategies.
Focusing on passive myocardial behavior, the framework incorporates structurally based anisotropic hyper-elastic material models and physiologically realistic boundary conditions. The governing nonlinear elastodynamics equations were solved using a stabilized variational multiscale method, which has been verified for cardiac mechanics applications.
In the proposed model, the equations of the motion are given as
where
u is the displacement,
v is the velocity,
p is the pressure,
βθ is the isothermal compressibility coefficient,
ρ is the density of the material,
σdev represents the deviatoric part of the Cauchy stress tensor, and
is the gradient operator defined in the spatial coordinates.
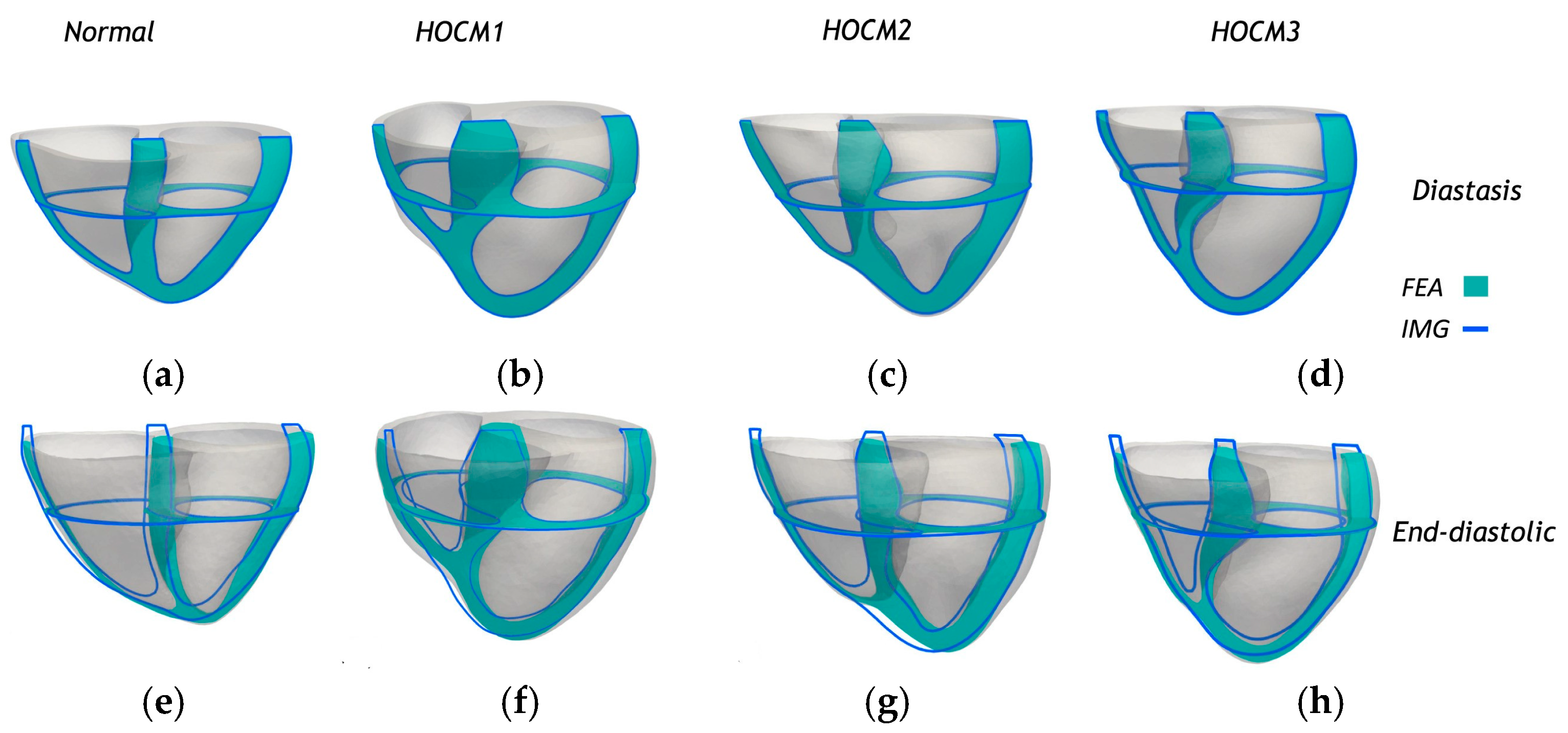
The framework was validated using biventricular and left atrial models reconstructed from cardiac phase-resolved CT images of one healthy subject and three patients with hypertrophic obstructive cardiomyopathy (HOCM).
Figure 6 presents sectional comparisons between the predicted deformations from finite element analysis (FEA) and the corresponding anatomical contours derived from medical imaging (IMG) for the biventricular and left atrial (LA) myocardium. Both longitudinal and transverse cross-sectional views are shown at two distinct cardiac phases: diastasis (
Figure 6a–d) and end-diastole (
Figure 6e–h). The FEA-predicted geometries (shaded in cyan) exhibited a close spatial alignment with the image-based contours (outlined in blue), demonstrating the model’s ability to accurately replicate physiological deformation patterns. This consistency across normal and HOCM cases—labeled HOCM1 (
Figure 6b,f), HOCM2 (
Figure 6c,g), and HOCM3 (
Figure 6d,h)—highlights the robustness of the personalized modeling framework and supports its potential for capturing structural and functional variations in diseased hearts. A comprehensive sensitivity analysis examined the influence of optimization strategies and numerical settings, including fiber orientation, mesh resolution, initial parameter estimates, and variations in material properties. The performance of the proposed iFEA method was also compared to the traditional power-law-based pressure–volume relationship, commonly used in single-phase imaging analysis.
This work demonstrates the potential of dynamic, image-based inverse modeling to enhance the accuracy and clinical relevance of personalized cardiac mechanics.
Schwarz and colleagues [
23,
24] presented a novel computational framework that integrates constrained mixture theory (CMT) into a fluid–structure interaction (FSI) finite element solver, forming a fluid–solid–growth (FSG) model. This model enables long-term, patient-specific predictions of vascular growth and remodeling (G&R) by simulating changes in blood flow (hemodynamics), vessel wall deformation, tissue composition, and material properties over time. The model extended traditional FSI models to include long-term biological growth and remodeling using CMT and integrated fluid dynamics, solid mechanics, and tissue growth in a partitioned iterative algorithm. In addition, the model enabled simulations of disease progression and vascular graft remodeling in both idealized and patient-specific geometries. This study provides a powerful computational tool for studying cardiovascular mechanics and biology over time, which is critical for understanding diseases, designing vascular implants, and personalizing treatment strategies. The integration of CMT with high-fidelity FSI in complex geometries marks a major step forward in computational biomechanics.
Schuster and colleagues [
25] present a computational study that examines how different pulsatile patterns in left ventricular assist devices (LVADs) affect blood washout in the left ventricle. The study introduces a computational framework combining full-order simulations with reduced-order models (ROMs) to efficiently analyze the impact of pulsatile LVAD flow on ventricular washout. Using a simplified 2D model of the left ventricle and a sinusoidal LVAD flow rate, the researchers performed sensitivity analyses to assess washout efficiency. Two pulsatile scenarios were considered—one with a single pulse and another with two consecutive pulses. The results show that short, high-amplitude pulses improve washout most effectively, while the time between pulses had minimal impact. ROMs allowed a significant reduction in computational cost while maintaining high accuracy, enabling large-scale parameter analyses. The findings support incorporating pulsatility in LVADs to reduce stagnation and associated thrombosis risks. Please note that while 2D models offer limited mechanistic insights, developing a personalized computational model for cardiovascular applications requires a detailed, patient-specific 3D anatomical representation of the heart. Such models are essential for electromechanical simulations and for exploring the underlying mechanisms of cardiac diseases, supporting efforts in diagnosis, risk assessment, prognosis, and treatment planning [
17].
2.2. Mechano–Electrical Interaction (MEI)
This section explores models that couple electrical excitation and mechanical contraction in cardiac tissue, typically without incorporating fluid dynamics. Mechano–electrical interaction (MEI) modeling emphasizes the bidirectional feedback between electrophysiology and tissue deformation, providing insights into arrhythmogenesis and electromechanical coupling mechanisms. These models serve as a critical bridge between isolated electrophysiology and more comprehensive MEFI frameworks [
26]. These models were typically one-way coupled, where electrical wave propagation influenced mechanical contraction, but mechanical deformation did not, in turn, affect the electrical activity [
27,
28]. However, important advances were made by Nash and Panfilov [
29], who developed a two-way coupled MEI model demonstrating that tissue deformation can exert feedback effects on electrical excitation and wave propagation. It is important to note that their model was not a whole heart simulation, but rather a continuum-based two-dimensional (2D) tissue model. In their approach, mechanical deformation was incorporated into the electrical conduction equations, although its effects on capacitive and ionic currents were not considered. More recently, Panfilov and colleagues [
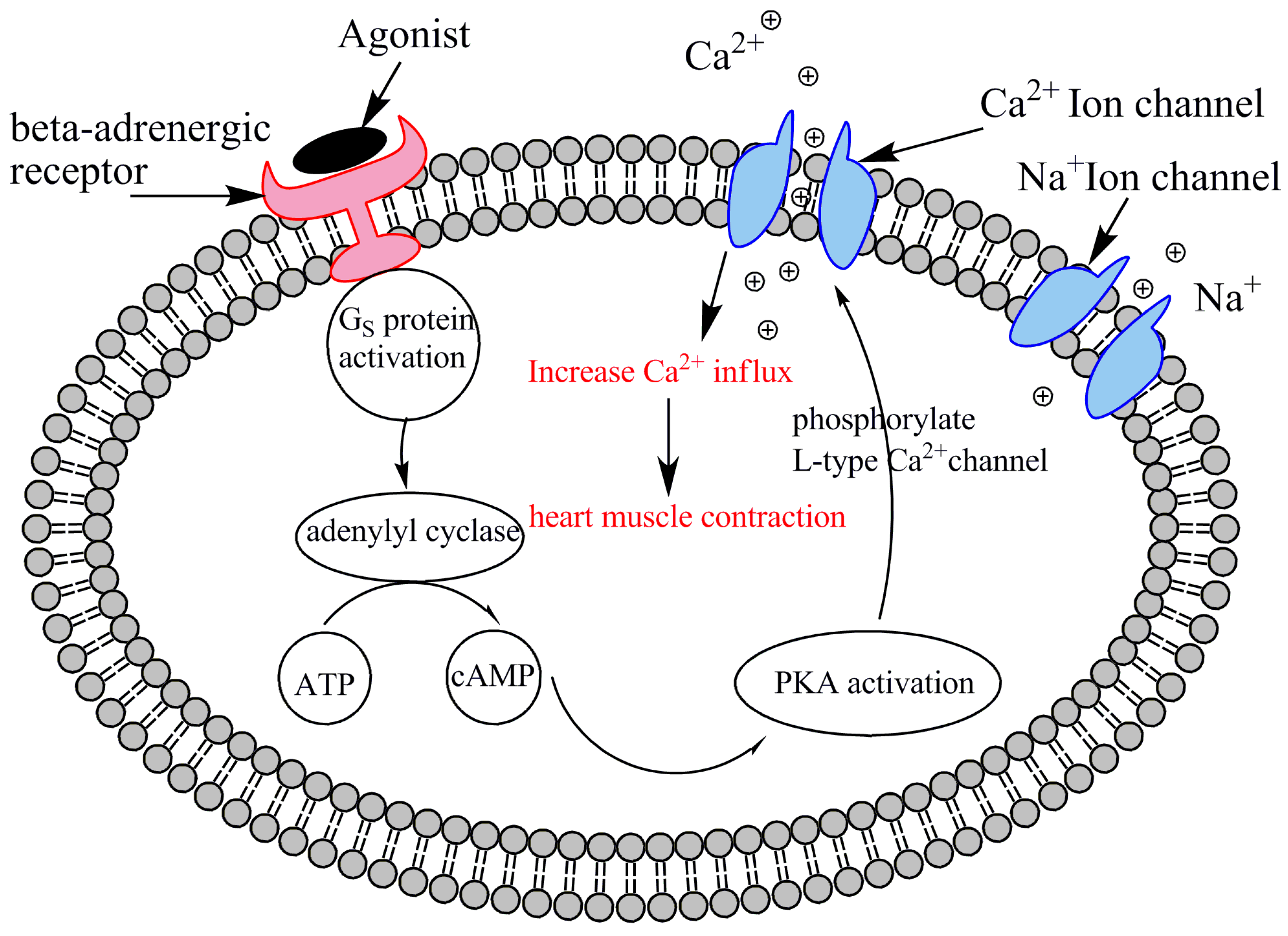
30] extended this model by introducing stretch-activated channels (SACs) into the 2D framework. Upon mechanical stretch, SACs allow an inward current that tends to depolarize cardiac cells. Their results highlighted that mechanical deformation can significantly influence electrical wave rotation and even induce wave breakups, emphasizing the critical role of mechano-electrical feedback in MEFI systems. However, their use of a simplified phenomenological FitzHugh–Nagumo model to represent membrane ionic kinetics limited the biological realism of the simulations. Specifically, the model did not incorporate detailed biophysical mechanisms or account for the behavior of individual ion channels, making it unsuitable for investigating the effects of genetic mutations, pharmacological interventions, or β-adrenergic pathway stimulations that require detailed ionic modeling.
Salvador and colleagues [
31] introduce a latent neural ordinary differential equations (LNODEs) framework as a surrogate model for simulating the pressure–volume and electromechanical simulations of the dynamics of the human heart, especially in heart failure patients.
Figure 7 shows the whole computational pipeline. Top-left: The study utilized a dataset comprising 405 electromechanical simulations derived from a fully personalized four-chamber heart model of a patient with heart failure. These simulations were generated by systematically varying 43 key parameters related to cellular, tissue-level, and cardiovascular properties, as well as boundary conditions. Each simulation included five cardiac cycles under sinus rhythm, with pressure and volume waveforms from the final cycle used for analysis.
Bottom-left: A total of 400 simulations were used to train and validate the latent neural ordinary differential equation (LNODE) model, which captures the time-dependent pressure–volume relationships in the atria and ventricles during the last cardiac cycle. The inputs to the LNODE model include time and model parameters, and hyperparameter tuning is performed using 10-fold cross-validation. Model performance is then assessed on a test set comprising the remaining five simulations.
Bottom-right: The validated LNODE model was employed to conduct a global sensitivity analysis (GSA), identifying how variations in model inputs influence the output quantities of interest.
Top-right: Using the trained LNODE as a surrogate, uncertainty-aware parameter estimation was carried out on the five test simulations, enabling robust calibration of model parameters under uncertainty.
The motivation was to overcome the computational limitations of high-fidelity cardiac models, enabling fast and accurate simulations on standard hardware—paving the way for broader clinical application of digital twin technology in cardiology. The paper presents a fast, accurate, and interpretable surrogate modeling approach for whole-heart simulations using LNODEs. It significantly reduces computational burden while maintaining high fidelity, enabling extensive applications like sensitivity analysis and parameter estimation. This work lays the groundwork for future patient-specific and real-time clinical decision support tools in cardiovascular medicine.
In this framework, the four-chamber heart artificial neural networks (ANN) model was developed as
where
z0 is the initial condition,
z(t) is the state vector,
THB is the heartbeat period,
AVdelay is the atrioventricular delay,
θ is the state model parameter, and
w is the weight of the ANN model.
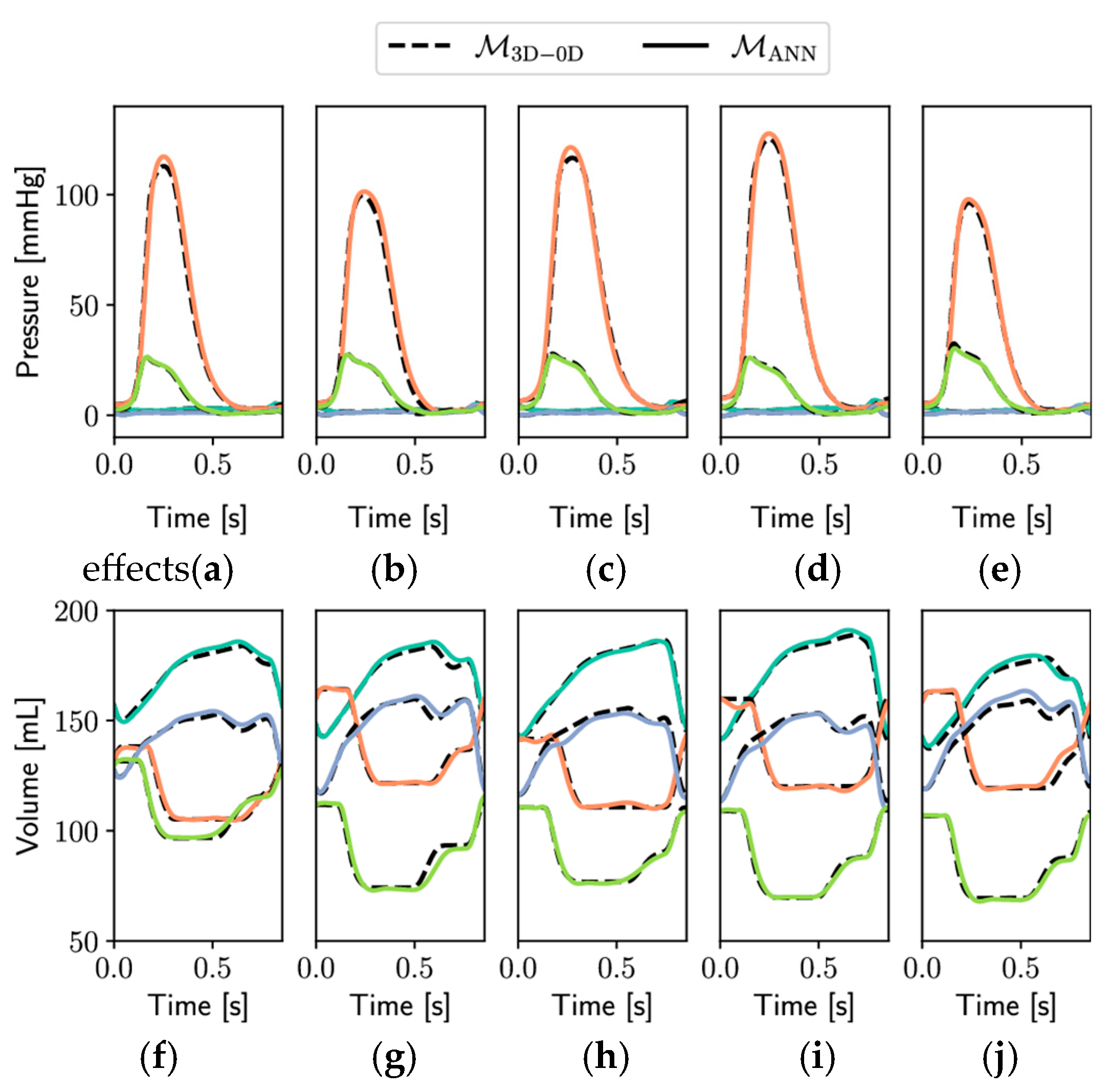
Figure 8 presents a comparative evaluation of pressure (panels
Figure 8a–e) and volume (panels
Figure 8f–j) waveforms generated by two modeling frameworks: the full-order 3D-0D electromechanical model
M3D-0D (dashed lines) and its surrogate counterpart based on an artificial neural network,
MANN (solid lines). Simulations were conducted over a complete cardiac cycle lasting 0.854 s and included five independent test cases (
Ntest = 5), illustrating the generalizability and robustness of the ANN surrogate model.
The top row (
Figure 8a–e) depicts pressure dynamics for the left atrium (LA, light blue), left ventricle (LV, orange), right atrium (RA, blue), and right ventricle (RV, green). Across all test cases, the surrogate model closely replicated the pressure evolution of the full-order model, capturing key physiological features such as atrial filling pressures, rapid ventricular pressure rise during systole, and the sharp decline during diastole. Notably, both the timing and amplitude of peak ventricular pressures aligned well between models, indicating strong temporal fidelity.
The bottom row (
Figure 8f–j) displays volume traces for the same cardiac chambers. The surrogate ANN model demonstrated high accuracy in reproducing the cyclical volume changes associated with ventricular filling and ejection, as well as atrial reservoir and booster phases. Volume trajectories followed the same phase transitions and amplitude modulations seen in the reference model, including end-diastolic and end-systolic plateaus.
Overall, the consistency observed between M3D-0D and MANN across multiple test scenarios underscores the surrogate model’s predictive accuracy and computational efficiency. These results validate the surrogate’s suitability for rapid patient-specific simulations, uncertainty quantification, and clinical decision support in computational cardiology applications.
Fedele and colleagues [
32] introduced a biophysically detailed computational model of the entire human heart, capturing the electromechanical behavior of all four chambers—including both atrial and ventricular contraction—for the first time with this level of accuracy. The model integrates anatomical realism, advanced myocardial fiber architecture, distinct ionic models, and a closed-loop circulatory system, all coupled through strong multiscale and multiphysics interactions, including mechano-electric and fiber–stretch–rate feedback. Implemented efficiently via high-performance computing tools, it reproduces physiological pressure–volume dynamics and cardiac deformation with high fidelity. This work sets a new standard in whole-heart modeling and paves the way for clinically relevant, patient-specific digital heart twins.
2.3. Mechano-Electrical-Fluid Interaction (MEFI)
This subsection reviews fully integrated multiphysics models that simultaneously capture electrical conduction, mechanical contraction, and hemodynamic flow. MEFI models represent the most advanced and physiologically comprehensive class of simulations. They aim to replicate the full cardiac cycle and are foundational for digital twin applications and personalized cardiovascular treatment planning. Several excellent comprehensive reviews have effectively documented the progress made in this area of research [
6,
8,
24,
33,
34,
35,
36,
37,
38,
39,
40,
41].
Recent advances in cardiovascular modeling have increasingly emphasized the integration of fluid dynamics, electromechanical coupling, and digital twin technologies to simulate the complex interactions within the cardiovascular system. Hemodynamic studies highlight the multiscale behavior of blood flow, ranging from high Reynolds number pulsatile flows in the aorta to near-laminar microcirculatory flows, and how these flow patterns influence vascular health, particularly in relation to atherosclerosis and thrombosis [
8]. Computational models of the heart have evolved to include electro–fluid–mechanical interactions (EFMIs), capturing the dynamic coupling between electrical conduction, myocardial deformation, and fluid transport throughout the cardiac cycle [
6]. This integrated approach provides a more physiologically accurate representation of cardiac function and supports the development of patient-specific simulations. The concept of cardiovascular digital twins—virtual replicas of individual patients’ cardiovascular systems—builds on these mechanistic frameworks and introduces machine learning techniques to support personalized diagnostics, prognostics, and treatment planning [
33]. However, widespread implementation remains limited by challenges such as the need for high-quality, multi-modal patient data; difficulties in model calibration and validation; and the lack of large-scale repositories representing diverse populations [
38]. Despite these obstacles, the convergence of data-driven and physics-based modeling holds significant promise for predictive, simulation-based approaches to cardiovascular care.
Watanabe et al. [
42] developed a three-dimensional model that coupled electrical excitation, mechanical contraction, and fluid–structure interaction (FSI). However, in their framework, the coupling between excitation and contraction was one-way, with mechanical deformation not feeding back into the electrical activity. Furthermore, the model utilized phenomenological FitzHugh–Nagumo-type equations to describe cellular excitation and electrical wave propagation, limiting its ability to capture detailed ionic dynamics. More recently, Vigmond et al. [
43] introduced a cable-based modeling approach to study MEFI at the whole-heart level. Unlike continuum models, the cable-based method discretizes the heart’s geometry into small finite volumes, averaging biophysical properties within each volume to better represent the discrete nature of cardiac tissue. This model incorporated realistic heart anatomy and coupled mechanical, electrical, and fluidic interactions. Importantly, it also employed a biophysically detailed ionic model—the Luo–Rudy model—to simulate electrical wave propagation with a greater physiological accuracy. Nevertheless, the mechanical-to-electrical feedback was not included, and the coupling remained one-way. Although good agreement was achieved between model predictions and experimental data, the authors acknowledged that the absence of mechanical feedback limited the model’s ability to fully replicate observed cardiac behaviors. Despite these limitations, the work represented a significant advancement by unifying multiple disciplines and highlighting the value of interdisciplinary approaches in tackling complex cardiovascular simulations.
Gonzalo and colleagues [
44] investigated the hemodynamic consequences of atrial fibrosis using a high-fidelity, patient-specific, multiphysics computational framework that incorporates electrical activity, myocardial mechanics, and blood flow (electro–mechano–fluidic modeling).
Figure 9 illustrates a comprehensive multiphysics, multiscale framework designed to simulate patient-specific cardiac function by integrating electrophysiology, biomechanics, and fluid mechanics. The framework spans multiple spatial scales, from the cellular to the organ level. At the cellular scale, ion channel dynamics regulate membrane potential, which influences intracellular calcium concentration. This calcium signaling triggers myofilament dynamics, leading to the generation of active tension within cardiac muscle fibers. These local stimuli are propagated to the organ/tissue scale, where they drive electrical wavefront propagation throughout the myocardium. The resulting electrical activation initiates mechanical contraction, modeled by the equilibrium of stresses that dictate myocardial deformation. This wall motion is then coupled with fluid mechanics, where the dynamic displacement of the heart walls drives intracardiac blood flow. The figure emphasizes the bidirectional and tightly coupled nature of these processes, allowing for realistic simulation of cardiac function that accounts for patient-specific geometry and physiological behavior across multiple scales.
Patient-specific data was used, and anatomies and fibrosis maps were derived from late gadolinium enhancement MRI (LGE-MRI) for four patients with varying levels of atrial fibrosis. Modeling fibrosis was carried out in fibrotic regions that were assigned altered mechanical properties—specifically increased stiffness and decreased contractility. Four different biomechanical states were simulated for each anatomy: non-fibrotic, stiff-fibrotic, hypocontractile-fibrotic, and fibrotic (combined). The study focused on flow patterns, kinetic energy, and emptying fractions in the left atrium (LA) and left atrial appendage (LAA). The major findings are that fibrosis significantly impairs LA contraction, reducing atrial and appendage emptying fractions. Stiffness and hypocontractility each negatively affect LA function, with amplified impact when combined, and flow changes caused by fibrosis extend throughout the LA, not just near fibrotic regions. In addition, LAA hemodynamics are affected in a more complex, multifactorial manner, influenced by both local fibrosis and global atrial mechanics. Finally, fibrotic effects on LA flow are largely captured by global emptying fraction, but in the LAA, more detailed modeling is needed to understand flow alterations.
The passive myocardium of the left atrium was represented using a transversely isotropic material model characterized by a specific strain energy function:
where
is the volumetric contribution to ensure nearly incompressible material behavior;
k = 650 kPa is the bulk modulus;
J is the determinant of the deformation gradient, constant
a = 2.92 kPa,
b = 5.6;
I1 is the first invariant,
af = 11.84 kPa,
bf = 17.95,
δf = 0.09; and
I4 is an invariant. The blood flow generated by the simulated motion of individualized anatomical structures and fibrosis distributions was captured using a custom-developed computational code.
Figure 10 presents a series of visualizations highlighting the effects of fibrosis on cardiac electrophysiology (Panel A), biomechanics (Panel B), and hemodynamics (Panel C). Panel A demonstrates how activation times differ in a simplified tissue domain between non-fibrotic and fibrotic states, with slower conduction evident in the fibrotic region due to altered conductivity. Panel B illustrates the mechanical consequences of fibrotic remodeling (contraction as measured by physical deformation and strain development), showing variations in myocardial deformation (captured via first principal strain) under four conditions: healthy, hypocontractile-fibrotic, stiff-fibrotic, and combined fibrotic. These simulations reveal the distinct strain patterns associated with each pathological state. Panel C depicts a schematic of a computational fluid dynamics (CFD) model used to simulate atrial blood flow. Boundary conditions are applied at the pulmonary veins (inflow), endocardium (no-slip wall), and mitral valve (dynamic open/closed), with velocity vectors shown in black representing flow during left atrial systole.
Alterations in myocardial stiffness and reduced contractility due to fibrosis led to noticeable changes in the motion of the LA endocardial surface, which in turn influenced intra-atrial flow dynamics. To investigate these effects, flow fields were visualized, and quantitative comparisons of hemodynamic parameters were conducted using the volumetric Lagrangian mesh framework outlined in the analysis methodology. These comparisons provided a deeper understanding of the impact of fibrosis on atrial flow behavior.
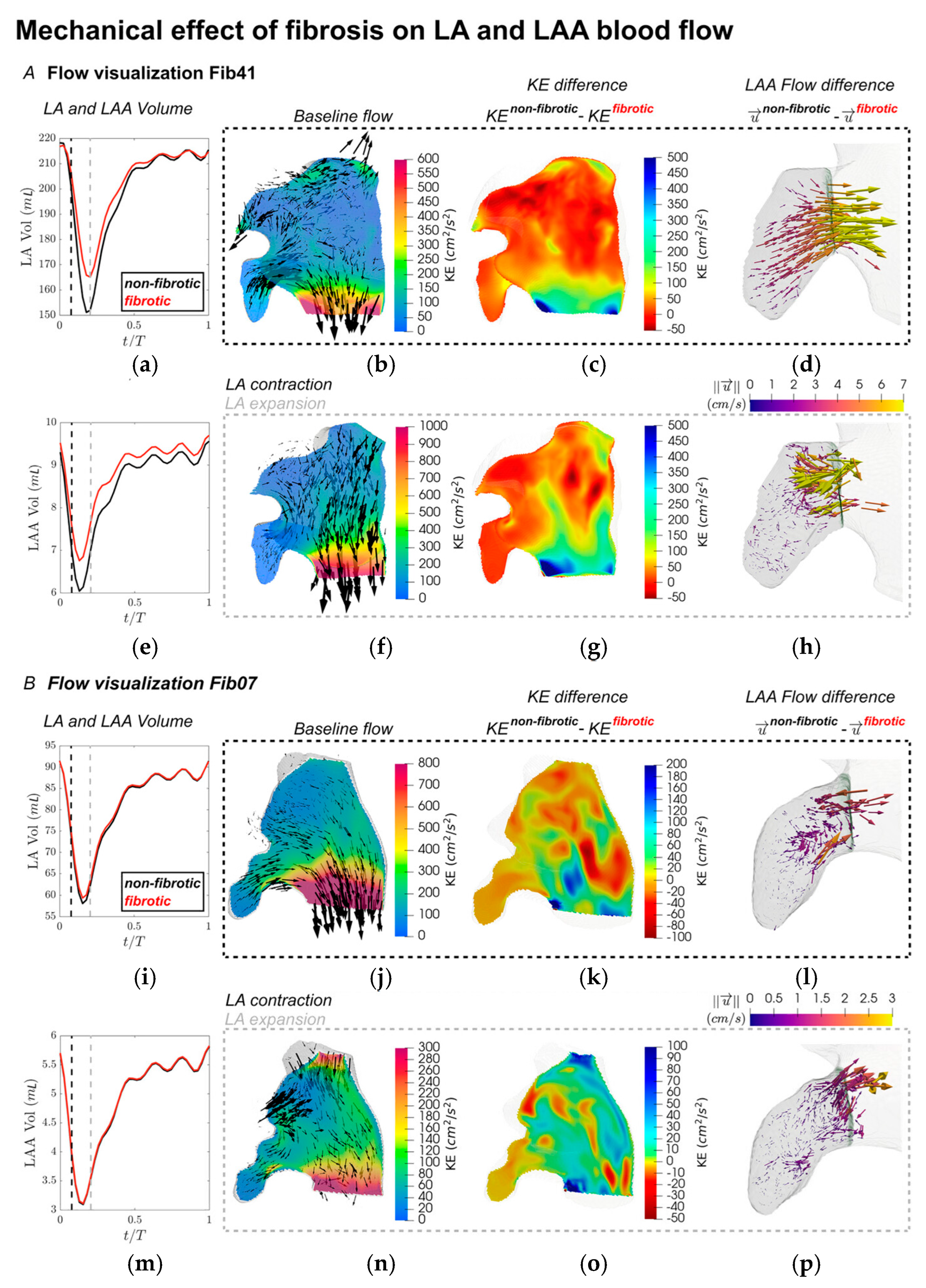
Figure 11 illustrates velocity distributions and flow characteristics captured at two critical phases of the cardiac cycle—specifically, the time points corresponding to the maximum contraction and expansion rates of the LAA, marked by vertical dashed lines (black and grey) in the LA and LAA volume-time plots shown in
Figure 11A,B (a,e,i,m). These time points correspond roughly to the early contraction and expansion of the left atrium. In subject Fib41 (
Figure 11A), the non-fibrotic baseline flow during peak LAA contraction featured a pronounced jet emerging from the LAA, which merged with a strong mitral valve outflow stream. At the same time, the onset of LA contraction led to a reverse flow entering the pulmonary veins (
Figure 11d). When mechanical alterations due to fibrosis were introduced, these organized flow patterns were notably disrupted, especially in regions previously characterized by strong velocities. The kinetic energy (KE) within the atrial chamber was substantially reduced under the fibrotic condition, particularly where the baseline flow was most prominent (
Figure 11c,g). The three-dimensional velocity difference vectors (
Figure 11d,h) illustrate a diminished LAA ejection jet, with reductions of approximately 5 cm/s in the fibrotic state. At the instant of peak LAA expansion (
Figure 11h), the non-fibrotic model showed weaker outflow through the mitral valve while the atrial cavity was refilled by pulmonary venous inflow, accompanied by fluid movement from the LAA opening to its distal region. Similar to earlier observations, the fibrotic model exhibited a drop in KE in these zones, along with slightly decreased flow throughout the atrium. Notably, inflow near the LAA ostium displayed a consistent pattern but was reduced in speed by about 5 cm/s, indicating slower filling dynamics under fibrotic conditions. Fibrosis introduces increased stiffness and reduced compliance in atrial tissue. This mechanical remodeling limits the ability of the left atrium (LA) to expand during ventricular systole (when the atrium acts as a reservoir). As a result, the LA cannot effectively accommodate incoming pulmonary venous return, which in turn reduces the suction force driving blood into the LAA. This diminished reservoir function is reflected in the slower inflow velocities at the LAA ostium.
In contrast, for subject Fib07 (
Figure 11B), the general flow features under the non-fibrotic setting resembled those of Fib41. However, due to a less extensive fibrotic burden, the alterations in KE following fibrosis were less severe. Nonetheless, measurable differences in KE were observed between fibrotic and non-fibrotic simulations across the left atrium, despite most fibrotic tissue being concentrated near the pulmonary vein inlets. Within the LAA specifically, changes in flow were evident but occurred at lower magnitudes (~1 cm/s) and lacked the distinct directionality seen in the higher fibrosis case.
This study provides compelling evidence that atrial fibrosis disrupts cardiac mechanics and flow in ways that may promote blood stasis and thrombus formation, factors critical in stroke risk. By using patient-derived data and advanced simulation techniques, this research offers a path forward for more personalized risk assessment and potential refinement of clinical decision tools.
Bucelli and colleagues [
45,
46] present a computational framework for simulating cardiac function by integrating electrophysiology, fluid dynamics, and solid mechanics in a loosely coupled manner. The authors introduce a fully loosely coupled electro–fluid–structure interaction (EFSI) scheme, designed to simulate the mechanics and hemodynamics of the human heart. The scheme uses a modular approach that separately solves the subproblems of electrophysiology, active force generation, fluid dynamics, and solid mechanics at each timestep, enhancing computational efficiency. The core innovation lies in applying a Robin–Neumann interface condition to manage the fluid–structure interaction explicitly, reducing the high computational costs typically associated with fully coupled models. The scheme is stable under cardiac simulation conditions and significantly reduces computational time compared to monolithic implicit schemes. It can accurately capture physiological indicators such as ventricular volume, pressure evolution, and flow patterns, albeit with some trade-off in mass conservation during isovolumetric phases. Finally, the framework is validated against benchmark models and realistic left ventricular geometries, showing robust performance and scalability. Overall, the study provides a computationally efficient and stable alternative for large-scale heart simulations, enabling future applications in personalized medicine and cardiac device testing.
Viola and colleagues [
47] present a highly detailed, GPU-accelerated, multiphysics digital twin of the human heart. This computational model integrates electrical conduction, muscle contraction, valve dynamics, and blood flow, enabling simulations with over a billion degrees of freedom per heartbeat. It can complete a full cardiac cycle within 12 h on modern GPU clusters. The model accurately replicates physiological heart behavior, including ECG signals, pressure and volume waveforms, and hemodynamic flow structures. Pathological case simulation of a left bundle branch block (LBBB) was simulated by modifying the electrical conduction pathway, leading to reduced cardiac output and altered ECG patterns. Therapeutic simulation of cardiac resynchronization therapy (CRT) was modeled by varying pacemaker lead positions. The model predicted physiological recovery metrics such as ejection fraction and pressure, depending on the lead placement accuracy.
The human heart digital twin is constructed using a multiphysics computational framework designed to simulate cardiovascular flow dynamics with high fidelity. This approach integrates models that account for myocardial electrophysiology, active muscle contraction, passive relaxation, valve mechanics, and blood flow within the cardiac chambers and arterial system. These components are tightly coupled to reflect the complex, interactive behavior of the heart and to capture the resulting mechano-electrical-fluid interaction (MEFI). The blood solver is captured by the incompressible Navier–Stokes and continuity equations:
where blood density
ρ = 1060 Kg/m
3,
u is velocity,
p is the pressure,
τ is the stress tensor,
fIB and
fWK are the force terms.
The motion of the deformable cardiac tissues is modeled using a spring–network structure. The variability in electrophysiological properties across the cardiac network is represented using an advanced, whole-heart electrical modeling approach [
48].
where
v and
vext are the transmembrane and extracellular potential;
and
are the surface-to-volume ratio of cells and the membrane capacitance;
Is is the external triggering stimulus initiating the myocardial depolarization placed in the sino-atrial node; and
and
are the intracellular and extracellular conductivity tensors, respectively.
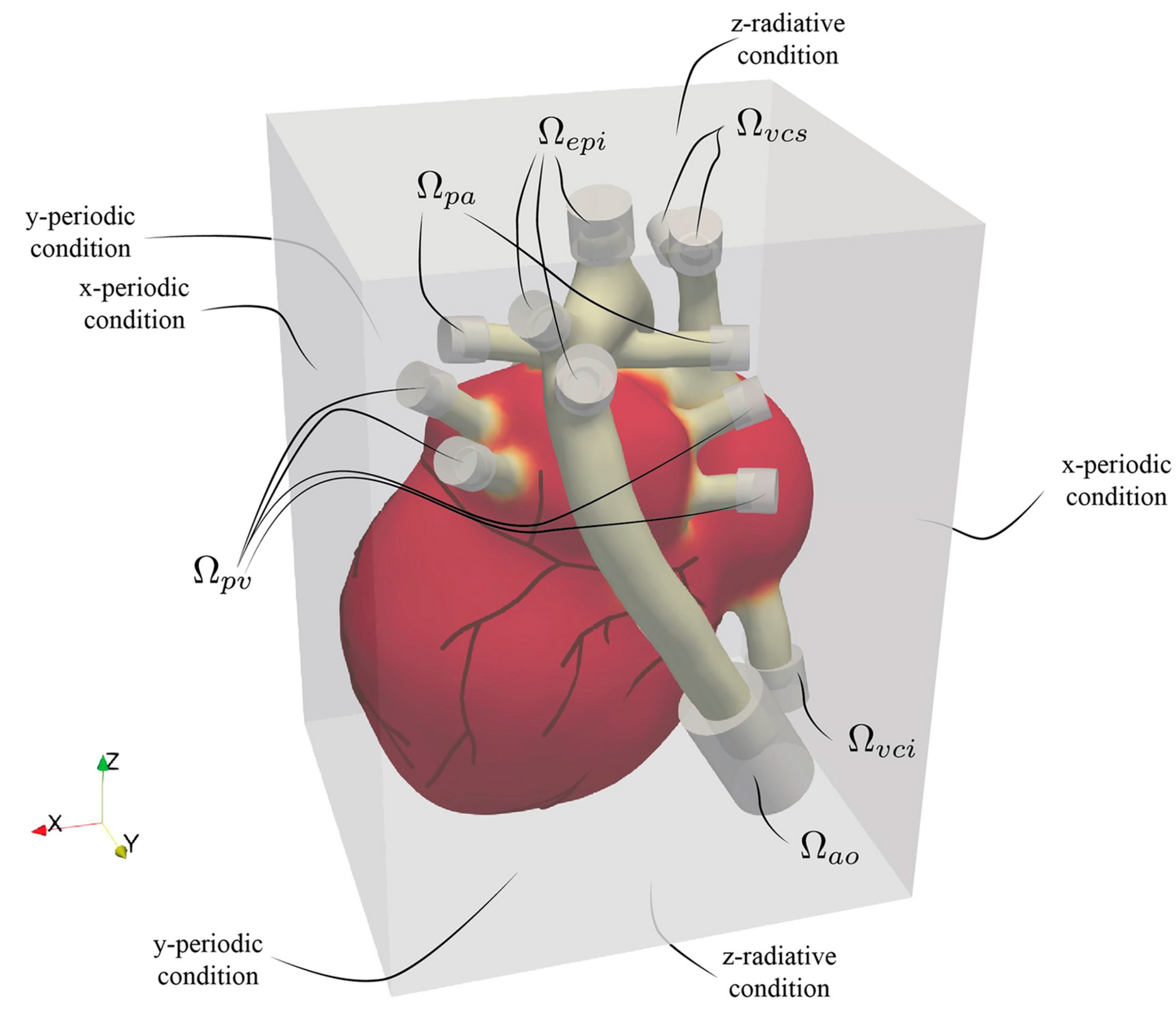
As with immersed boundary methods (IBMs), the heart is embedded within a larger fluid computational domain represented by a Eulerian grid, as illustrated in
Figure 12. The arterial and venous ends—serving as inflow and outflow sites—do not intersect the external boundaries of the fluid domain. Instead, during the cardiac cycle, blood enters through the pulmonary veins and vena cava and exits via the aorta and pulmonary arteries, with flow exchange occurring entirely within the enclosed domain. Because the model focuses solely on the heart and proximal segments of the main vessels, it does not capture the full circulatory system. To account for the excluded vascular network’s resistance, compliance, and inertance, appropriate boundary conditions must be applied at the truncation points. These peripheral hemodynamic properties are often approximated using lumped parameter models (0D models), governed by low-order differential equations similar in structure to electrical circuit analogs. In this setup, where all heart inlets and outlets lie inside the computational domain, the corresponding boundary conditions are enforced via volumetric forcing. While this open-loop scheme prescribes each boundary condition independently, enhanced physiological fidelity could be achieved by transitioning to a closed-loop approach. In such models, outlets are dynamically linked to their corresponding inlets—for instance, connecting the descending aorta’s outflow to the inferior vena cava’s inflow—via a 0D system representing systemic or pulmonary circulation.
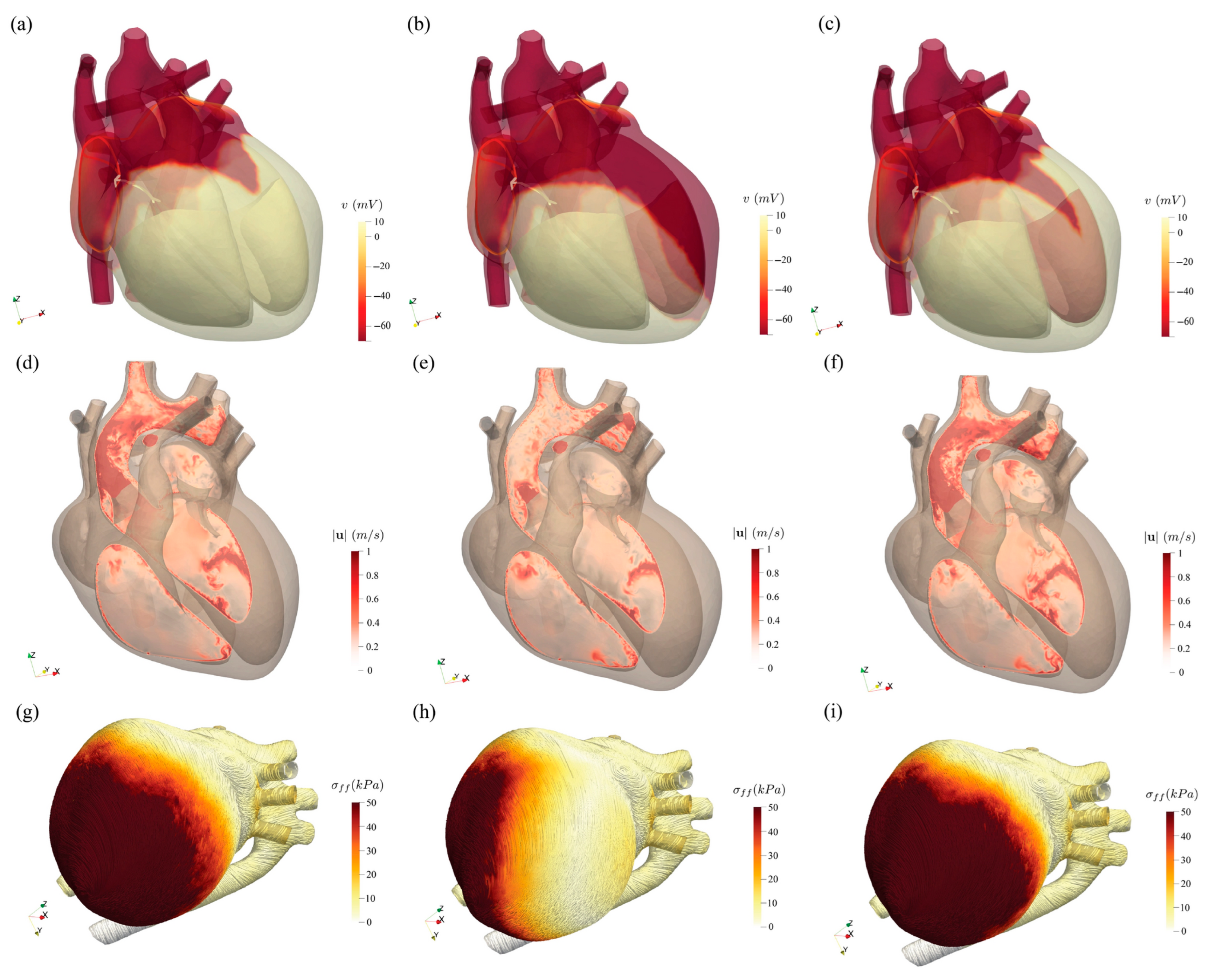
Figure 13 presents a comparative assessment of cardiac electrical activation, blood flow dynamics, and mechanical contraction across three physiological states: healthy, impaired, and resynchronized hearts. The top row shows the spatial distribution of electrical activation potential at 252 ms. In the healthy heart, the activation propagates uniformly across the myocardium, whereas in the impaired heart, the activation is delayed and non-uniform, reflecting dyssynchronous electrical conduction. After resynchronization therapy, the activation pattern becomes more organized and closely resembles the healthy state. The middle row illustrates blood velocity distribution in a cross-sectional plane through the left heart at peak systole (520 ms). The healthy heart exhibits coherent flow patterns indicative of efficient contraction, while the impaired case reveals disorganized and reduced velocities. Following therapy, flow coherence is largely restored. The bottom row depicts myocardial fiber stress at peak systole, where the healthy heart demonstrates high and evenly distributed stress, the impaired heart shows reduced and uneven stress distribution, and the resynchronized heart exhibits improved mechanical function with stress patterns approaching those of the healthy condition. Collectively, this figure highlights the pathological disruptions caused by dyssynchrony and the effectiveness of resynchronization therapy in restoring coordinated electromechanical and hemodynamic function.
Their study demonstrates the feasibility of using synthetic patient cohorts for testing interventions, significantly reducing the ethical and logistical constraints of traditional trials. This work offers a pathway to cost-effective, high-fidelity preclinical testing of cardiovascular treatments and devices, particularly for rare or complex diseases. Overall, the research marks a significant step toward practical in silico clinical trials and supports the future of personalized digital medicine.
Quarteroni and colleagues [
49] present a comprehensive and multiphysics mathematical model of the human heart, developed to simulate cardiac function across multiple scales and support clinically relevant decision making. The model integrates detailed representations of electrophysiology, myocardial mechanics, blood flow, valve motion, coronary circulation, and myocardial perfusion, and it solves the governing equations using high-performance computational techniques. Derived from the first principles of physics and calibrated with patient-specific data from imaging and diagnostics, the model enables simulations of physiological and pathological heart behavior. It has been successfully applied in clinical contexts such as arrhythmia mapping, cardiac resynchronization therapy, aortic valve implantation, and perfusion assessment under stress. The work highlights the growing potential of computational cardiology as a non-invasive, predictive tool to support diagnosis and personalized treatment planning.
Computer simulations of cardiovascular flows hold significant promise for enhancing diagnostic accuracy, optimizing surgical procedures, and enabling virtual testing of novel prosthetic devices. However, their clinical reliability hinges on the fidelity of the underlying models, particularly in the case of the human heart, a highly complex organ governed by tightly coupled multiphysics processes. Viola et al. [
50] present a comprehensive computational model that captures the full electromechanical and hemodynamic behavior of the heart through a fluid–structure–electro interaction (FSEI) framework. By integrating electrophysiology, tissue mechanics, and blood flow within a unified, computationally efficient scheme, the model achieves both accuracy and practical runtimes suitable for clinical use, even on standard computing resources. Demonstrated through simulations of both healthy and infarcted hearts, this tool offers predictive insights that could inform surgical planning and support personalized clinical decision making.