An Efficient Hydrodynamic Force Calculation Method for Pile Caps with Arbitrary Cross-Sections Under Earthquake Based on Finite Element Method
Abstract
1. Introduction
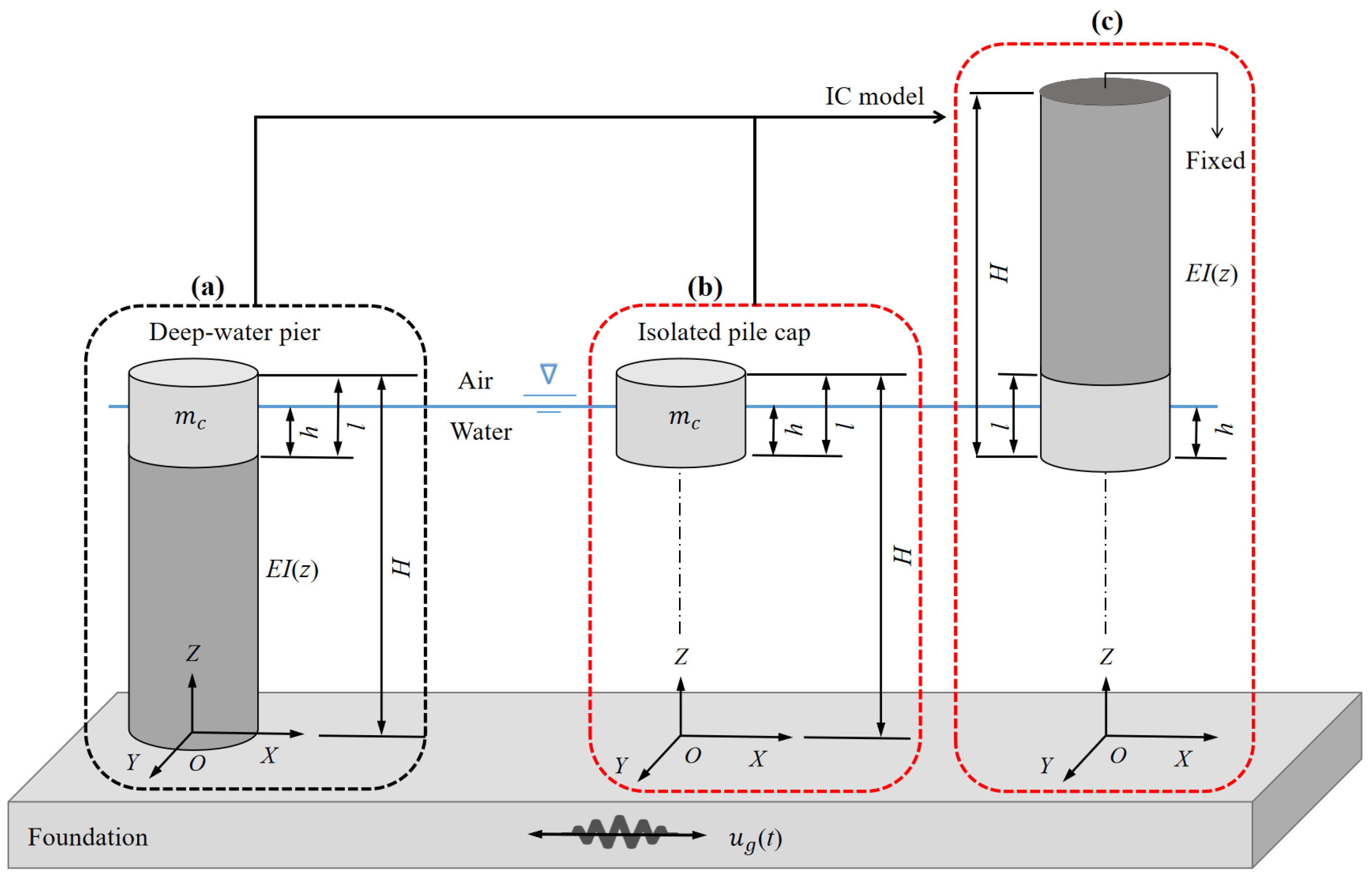
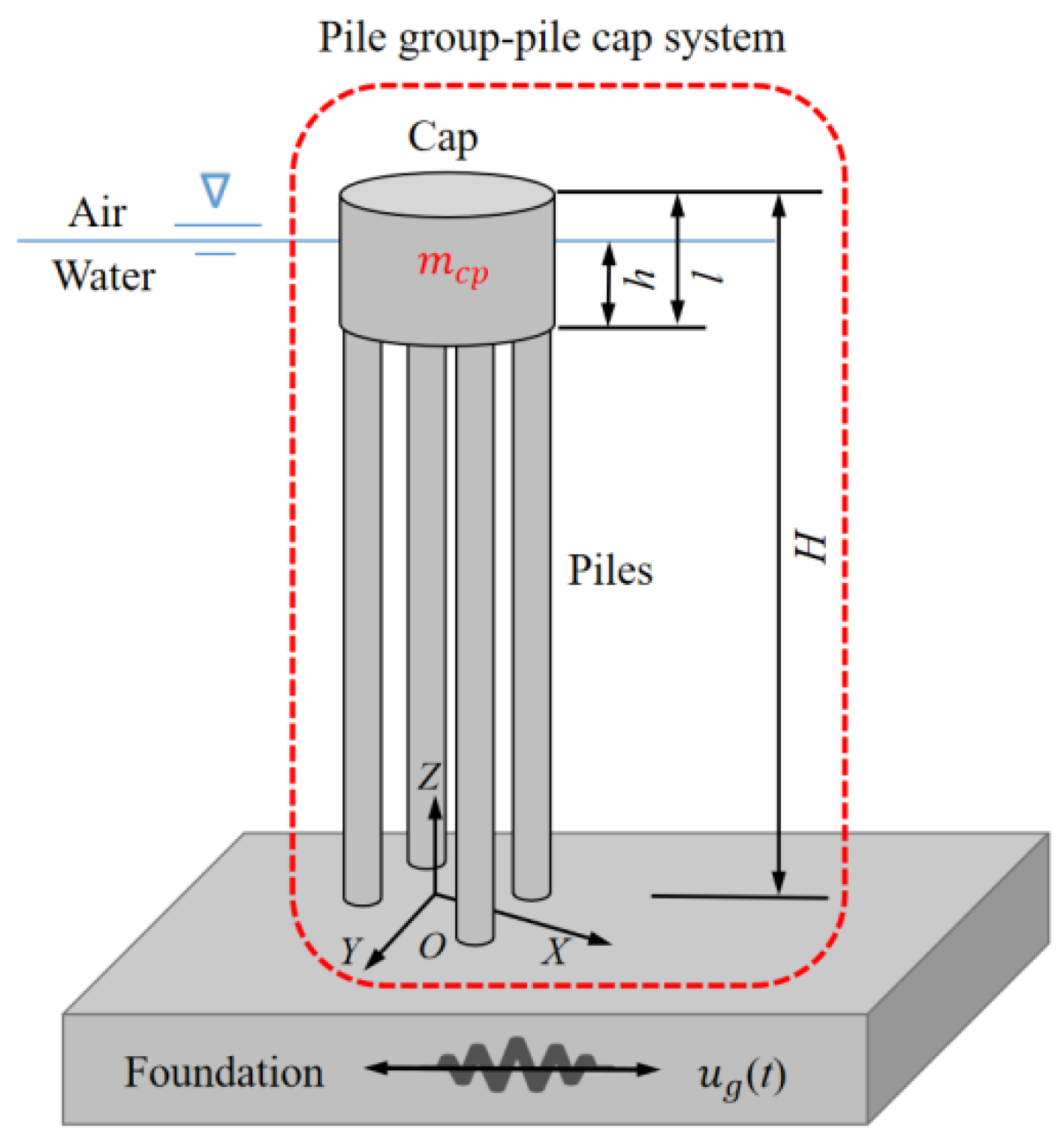
2. Comparison of Hydrodynamic Forces on Pier, Isolated Pile Cap and Pile Cap in Pile Group-Pile Cap System
2.1. Numerical Simulation
2.1.1. Basic Information
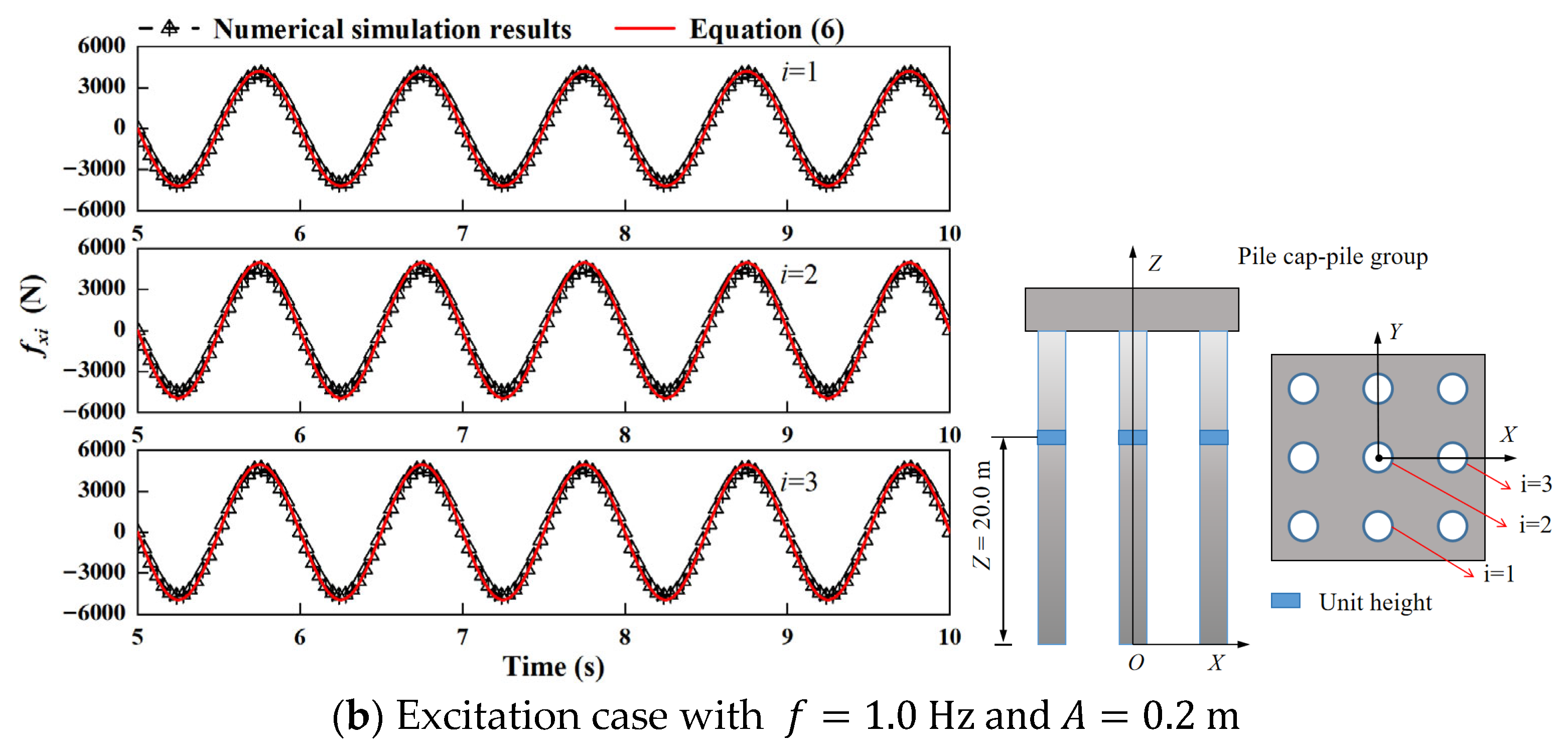
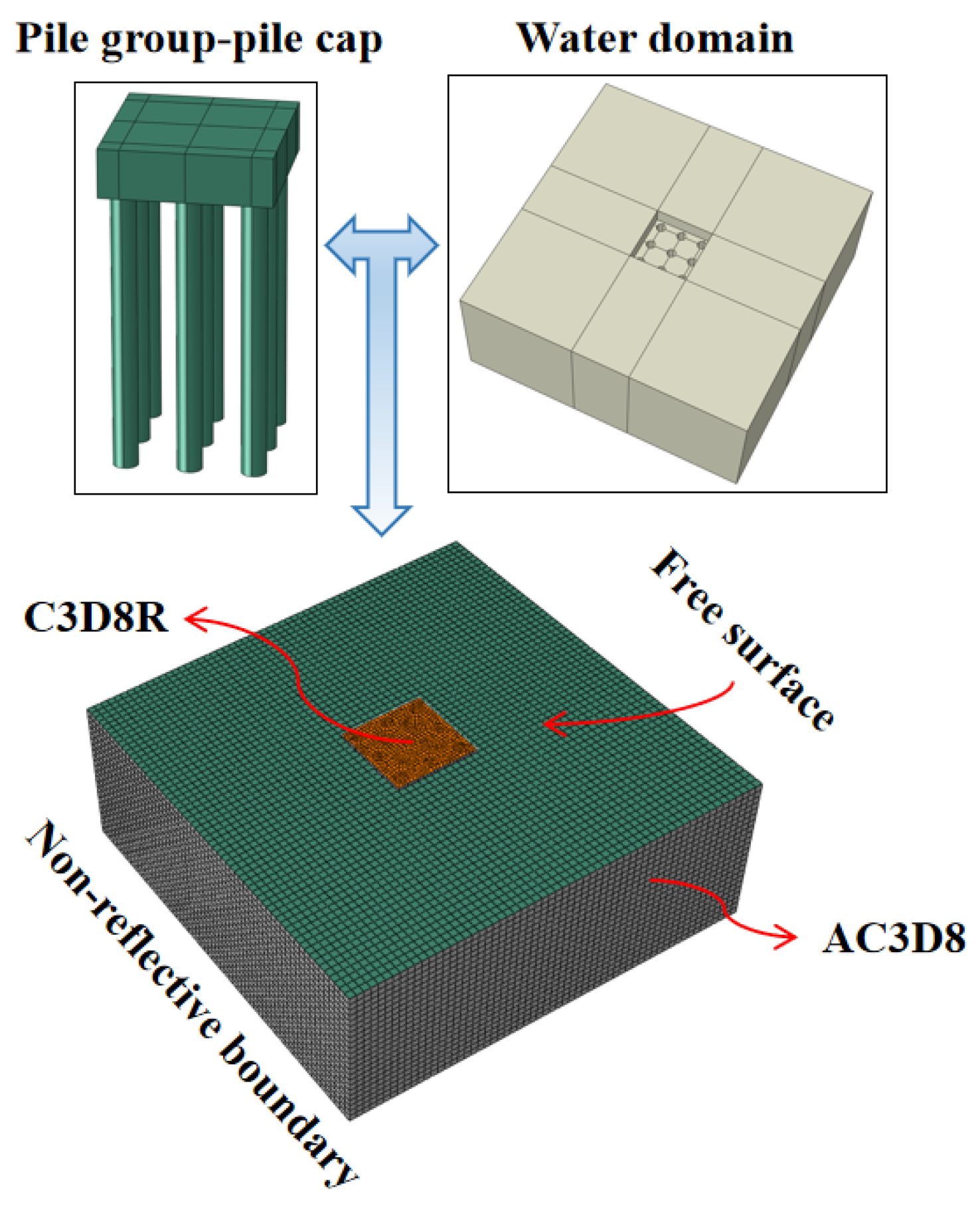
2.1.2. Numerical Model Validation
- Validation of rectangular pier and isolated rectangular pile cap
- 2.
- Validation of pile groups
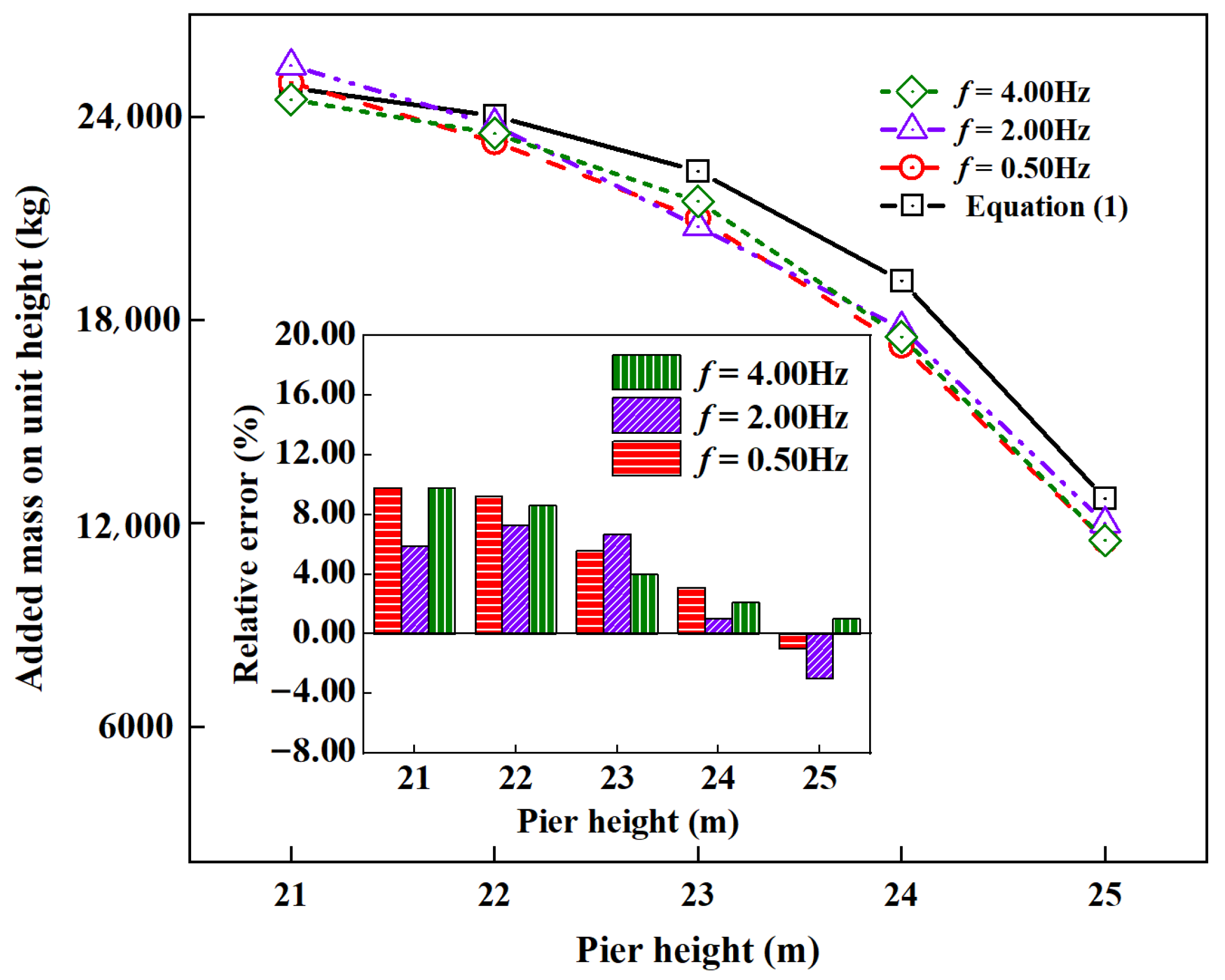
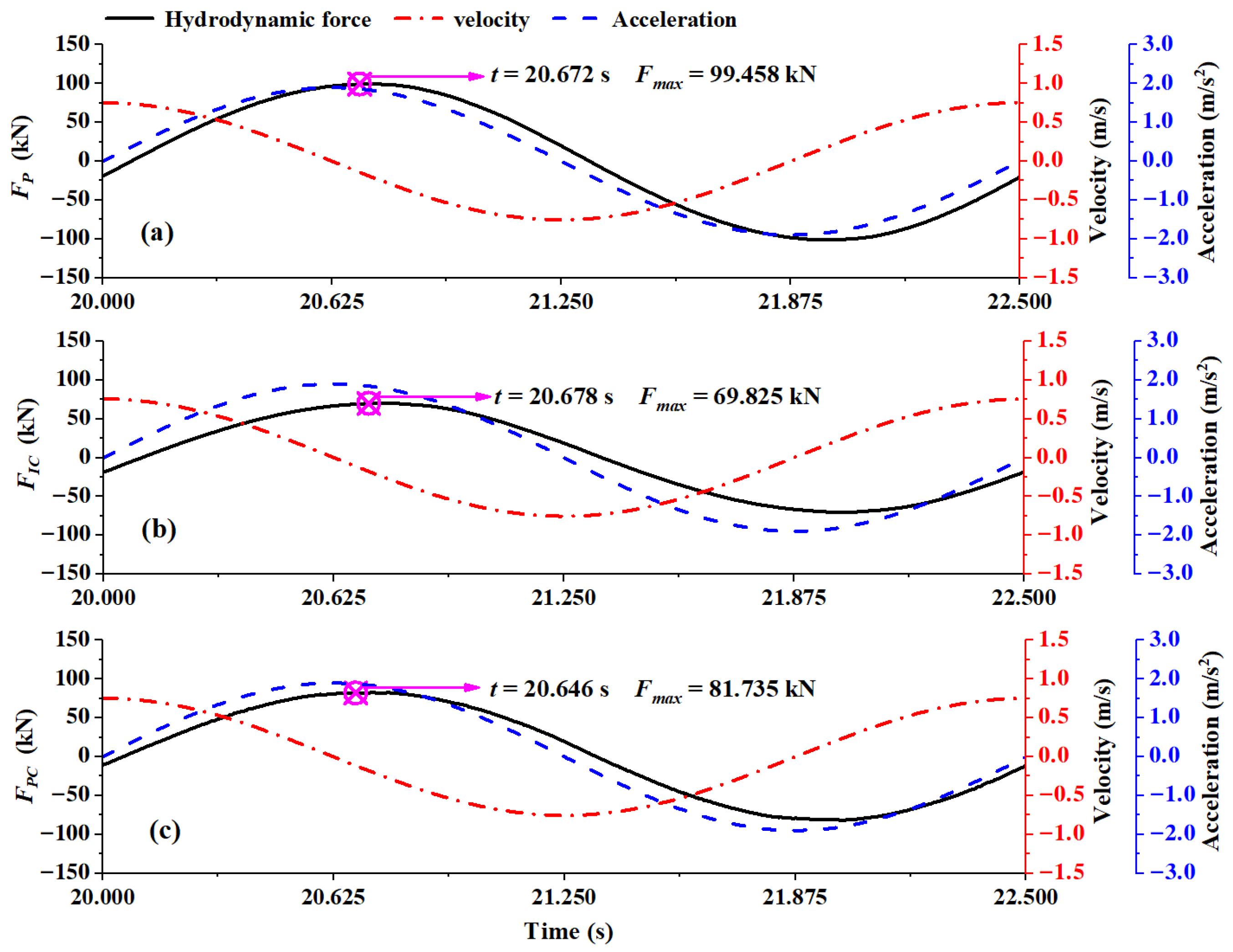
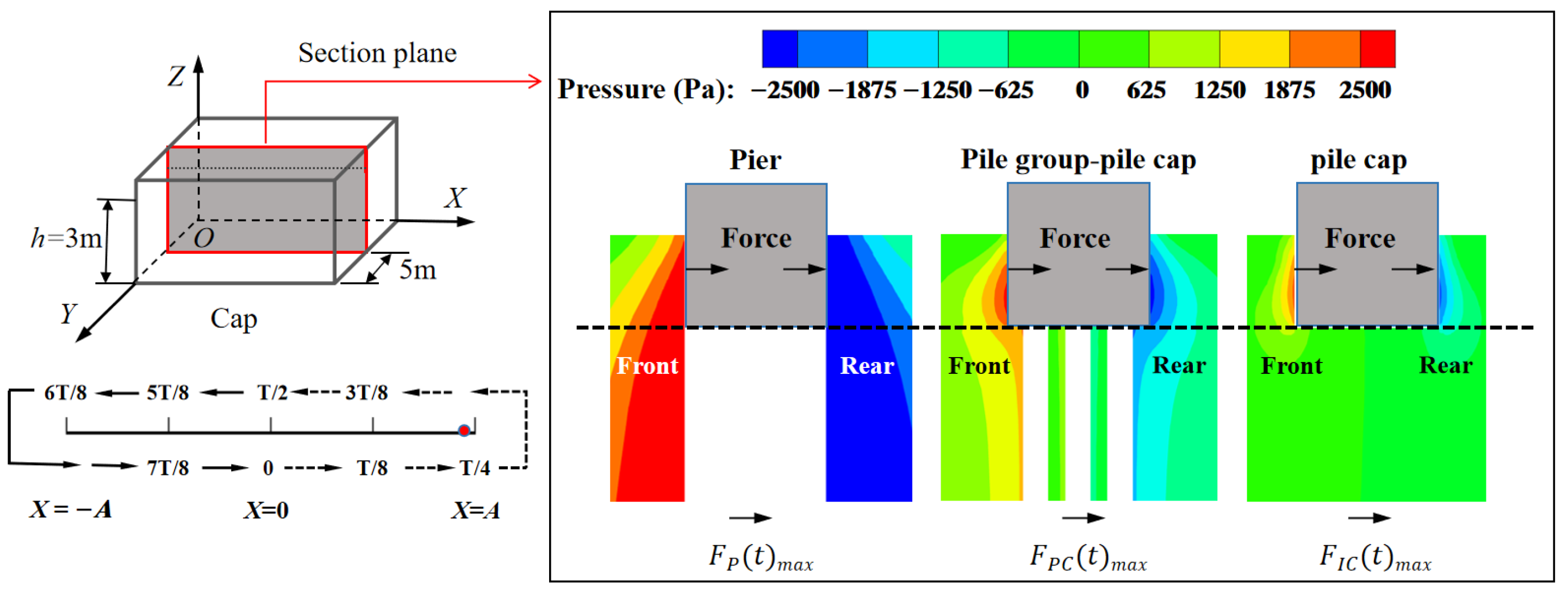
2.2. Comparison of Hydrodynamic Forces Between , and
3. Establishment of Dynamic Equilibrium Equations
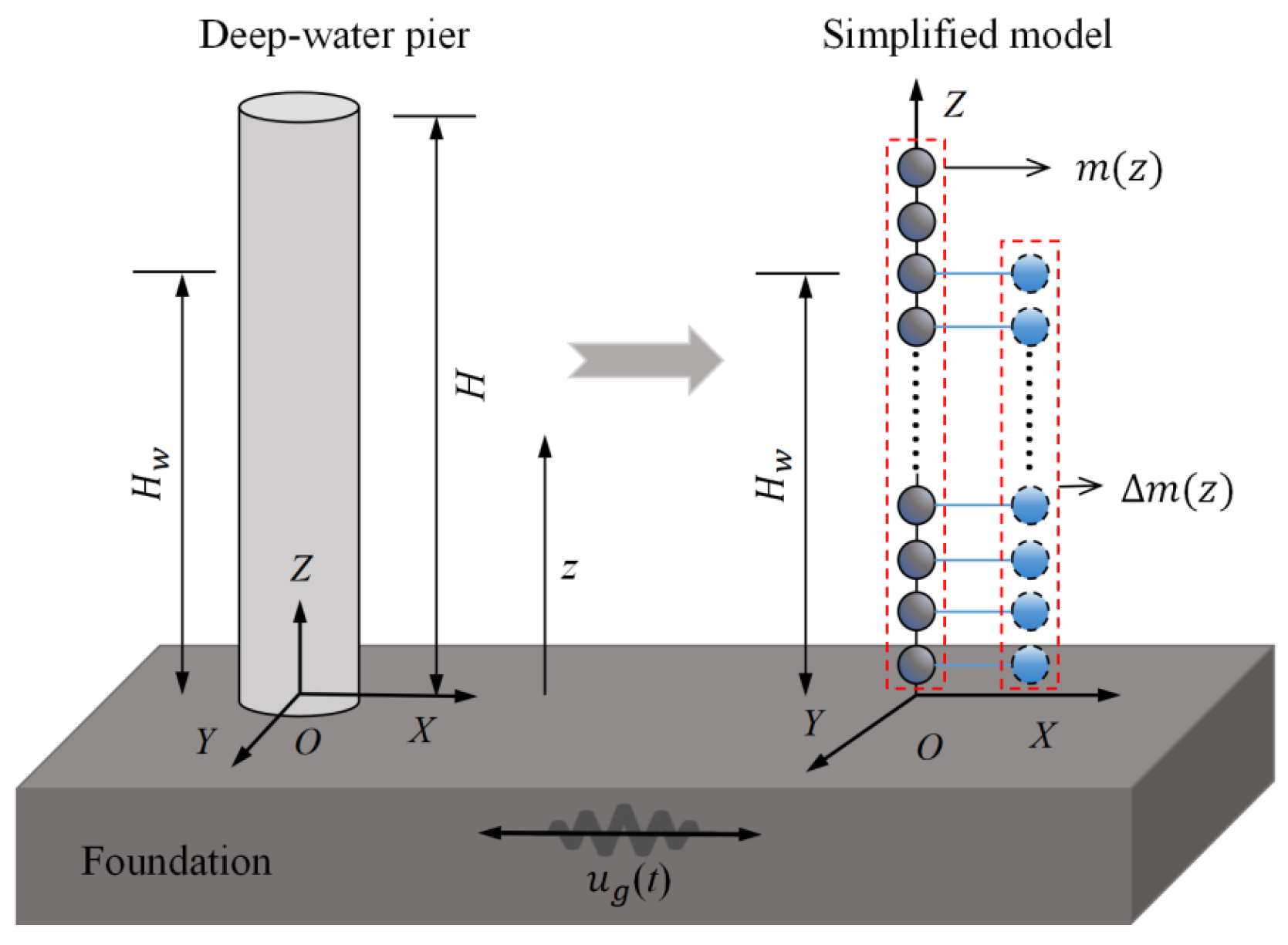
3.1. Motion Equation for Deep-Water Pier Under Earthquake
3.2. Motion Equation for Isolated Pile Cap Without Considering Pile Groups
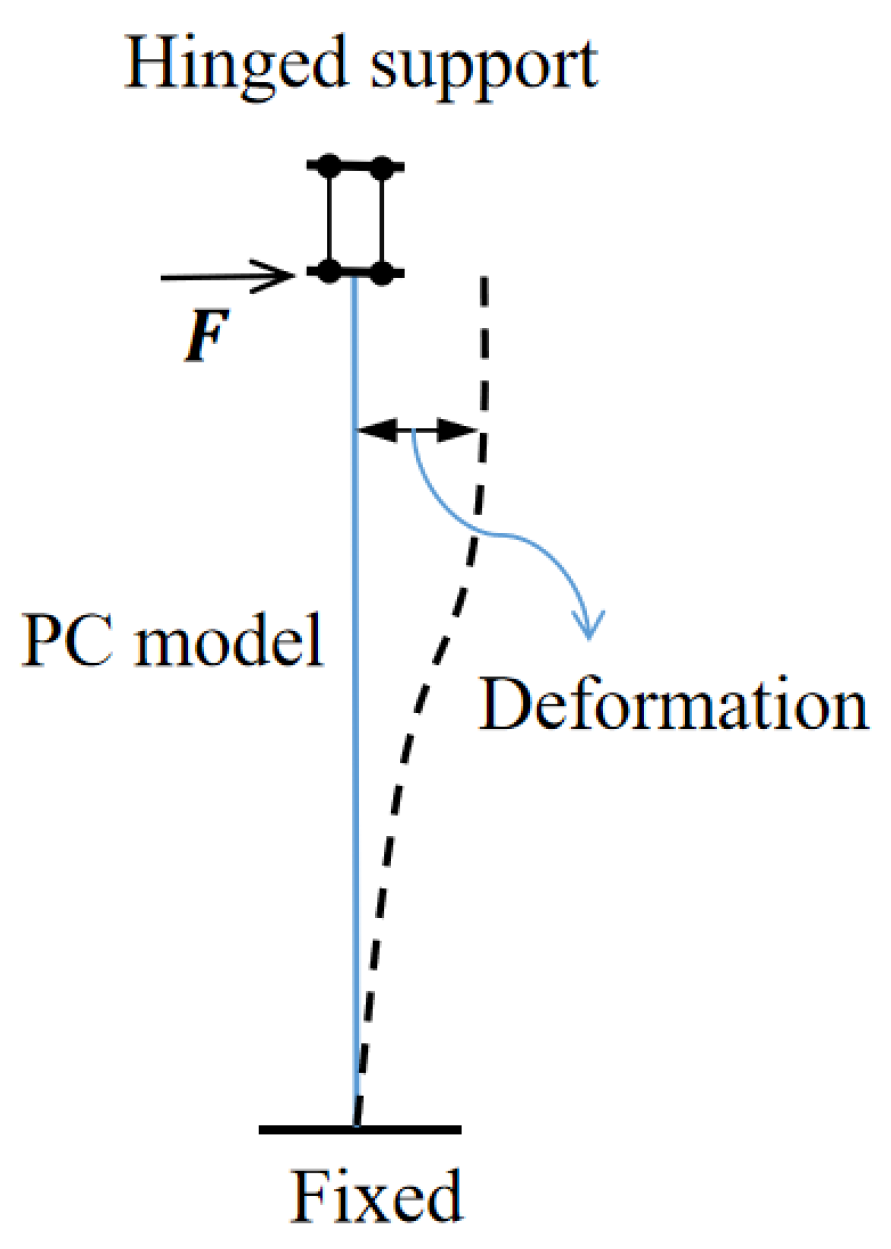
3.3. Motion Equation for Pile Group-Pile Cap System
4. Calculation Method for Added Mass on Pile Caps with Arbitrary Cross-Sections
4.1. Derivation of and
4.2. Acoustic-Solid Coupling Theory
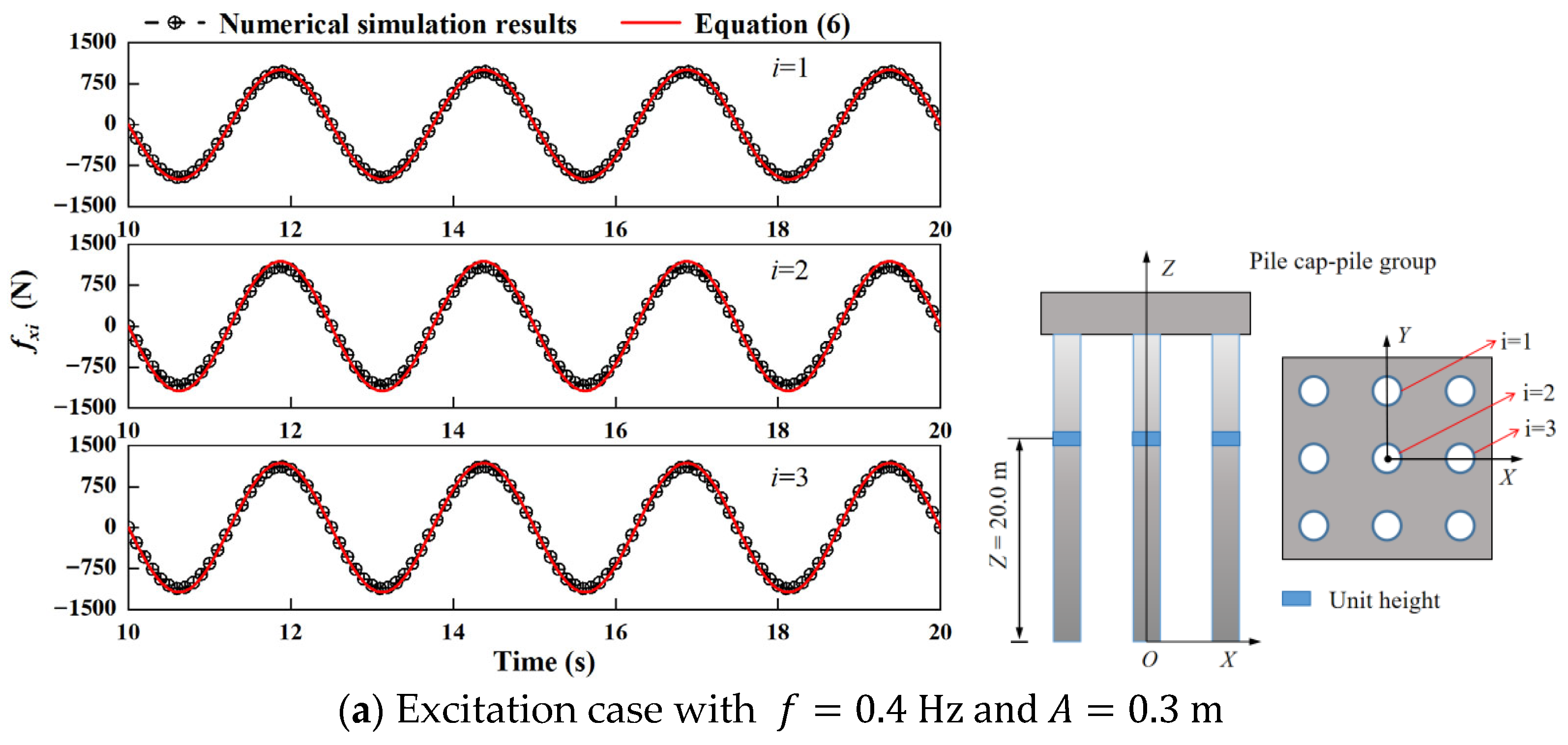
4.3. Verification of and
4.3.1. Engineering Case Application
4.3.2. Comparison of Different Added Mass Calculation Methods for Pile Caps
5. Discussion
6. Conclusions
- (1)
- The existing methods for employing pier calculation methods to estimate hydrodynamic forces on isolated pile caps with the same cross-sections are inaccurate and inapplicable.
- (2)
- The influence of pile groups on the hydrodynamic force on pile caps should be considered in real practice.
- (3)
- The dynamic equilibrium equation of the IC model under seismic action is derived, and the hydrodynamic force calculation method for the isolated pile cap with arbitrary cross-sections is established.
- (4)
- The dynamic equilibrium equation of the PC model under seismic action is derived, and the hydrodynamic force calculation method for the pile cap in the pile group-pile cap system is proposed.
- (5)
- The effectiveness of the hydrodynamic calculation methods proposed in this study is verified, and the proposed method is proven to have a wide application and higher computational efficiency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Ground vibration displacement | |
| Isolated pile cap mass | |
| Isolated pile cap hydrodynamic added mass | |
| Generalized mass for IC model | |
| Generalized stiffness for IC model | |
| Generalized excitation for IC model | |
| Shape function for IC model | |
| Mass per unit height of a single pile | |
| Hydrodynamic added mass per unit height of a single pile | |
| Generalized mass for PC model | |
| Generalized stiffness for PC model | |
| Generalized excitation for PC model | |
| Shape function for PC model | |
| Hydrodynamic added mass on pile cap in pile group-pile cap system | |
| Fundamental frequency of IC model | |
| Fundamental frequency of PC model | |
| Total height of IC and PC model | |
| Water depth | |
| Earthquake excitation | |
| Excitation amplitude | |
| Excitation frequency | |
| Hydrodynamic force on IC model | |
| Hydrodynamic force on PC model | |
| Hydrodynamic force on bridge pier |
References
- Chen, Y.; Yang, L.; Wu, K.; Huang, X. Centrifuge shaking table study on the hydrodynamic effects on a pile foundation bridge pier in soft soil under earthquakes. Mar. Struct. 2022, 85, 10326. [Google Scholar] [CrossRef]
- Yang, W.; Li, Q.; Yeh, H. Calculation method of hydrodynamic force on circular piers during earthquakes. J. Bridge Eng. 2017, 22, 04017093. [Google Scholar] [CrossRef]
- Zhang, W.; Ren, X.; Geng, X.; Zhang, Y.; Yang, W. Study on influence coefficients of hydrodynamic force on dynamic response of deep-water pier under earthquake. Ocean Eng. 2024, 299, 117261. [Google Scholar] [CrossRef]
- Yang, W.; Li, Q. The expanded Morison equation considering inner and outer water hydrodynamic pressure of hollow piers. Ocean Eng. 2013, 69, 79–87. [Google Scholar] [CrossRef]
- Li, Q.; Yang, W. An improved method of hydrodynamic pressure calculation for circular hollow piers in deep water under earthquake. Ocean Eng. 2013, 72, 241–256. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, K.; Qin, S. An efficient numerical model for hydrodynamic added mass of immersed column with arbitrary cross-section. Ocean Eng. 2019, 187, 106192. [Google Scholar] [CrossRef]
- Yang, W.; Li, A.; Deng, L.; Liu, T.; Li, F. Study on characteristics and calculation method of hydrodynamic force on pile group under earthquake. Ocean Eng. 2020, 207, 107375. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, M.; Du, X.; Liu, J.; Chen, J. Simplified evaluation of earthquake-induced hydrodynamic pressure on circular tapered cylinders surrounded by water. Ocean Eng. 2018, 164, 105–113. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, M.; Du, X. A simple added mass model for simulating elliptical cylinder vibrating in water under earthquake action. Ocean Eng. 2019, 179, 351–360. [Google Scholar] [CrossRef]
- Qin, Y.; Tao, X. A Numerical Case Study on Pier Shape Coefficient of Seismic Hydrodynamic Pressure in Design Codes. IOP Conf. Ser. Earth Environ. Sci. 2021, 638, 012052. [Google Scholar] [CrossRef]
- Du, X.; Wang, P.; Zhao, M. Simplified formula of hydrodynamic pressure on circular bridge piers in the time domain. Ocean Eng. 2014, 207, 44–53. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, K.; Qin, S. Bayesian updating model for structural vibration-induced hydrodynamic added mass of circular pile cap submerged in water. J. Eng. Mech. 2020, 146, 04020096. [Google Scholar] [CrossRef]
- Sabunch, T.; Calisal, S. Hydrodynamic coefficients for vertical circular cylinders at finite depth. Ocean Eng. 1981, 8, 25–63. [Google Scholar] [CrossRef]
- Bhatta, D.; Rahman, M. On scattering and radiation problem for a cylinder in water of finite depth. Int. J. Eng. Sci. 2003, 41, 931–947. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, C.; Dong, S. Research status and prospect of seismic response of deep-water bridge pier. J. Traffic Transport. Eng. 2019, 19, 1–13. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, K.; Li, J. Integrated assessment of the hydrodynamic added mass of the deep-water pile-cap foundation considering pile group-pile cap interaction. Ocean Eng. 2022, 244, 110418. [Google Scholar] [CrossRef]
- Yang, H. Research on Current Forces on Cap and Pile-group of Sea-Crossing Bridges. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2023. [Google Scholar]
- Zhang, H.; Yang, W.; Liu, D.; Geng, X.; Dai, W.; Zhang, Y. Influence of blocking ratio on hydrodynamic force on deep-water pier under earthquake. Ocean Eng. 2024, 291, 116385. [Google Scholar] [CrossRef]
- Yang, W.; Lai, W.; Zhu, Q.; Zhang, C.; Li, F. Study on generation mechanism of vertical force peak values on T-girder attacked by tsunami bore. Ocean Eng. 2020, 196, 106782. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, Y.; Zhou, C.; Yang, S. Simplified calculation methods for earthquake-induced hydrodynamic added mass of immersed pile caps with different cross-sections. Ocean Eng. 2023, 284, 115166. [Google Scholar] [CrossRef]
- Yang, W. Study on Hydrodynamic Analysis Methods of Deep-Water Bridges. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2012. [Google Scholar]
- Wang, P. Study on Water-Substructure of Bridge Interaction Under Earthquake Action and Wave Action. Ph.D. Thesis, Beijing University of Technology, Beijing, China, 2017. [Google Scholar]

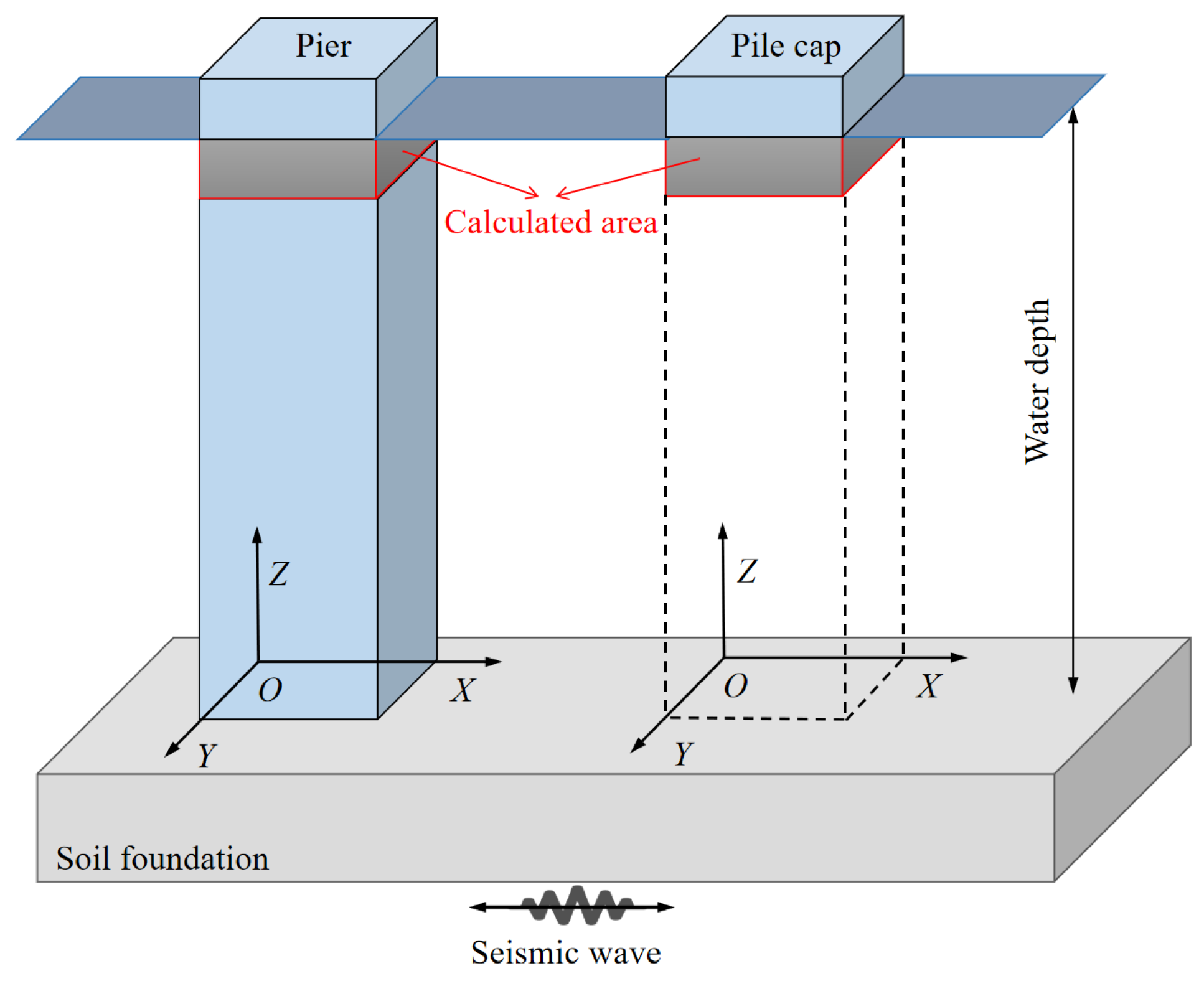


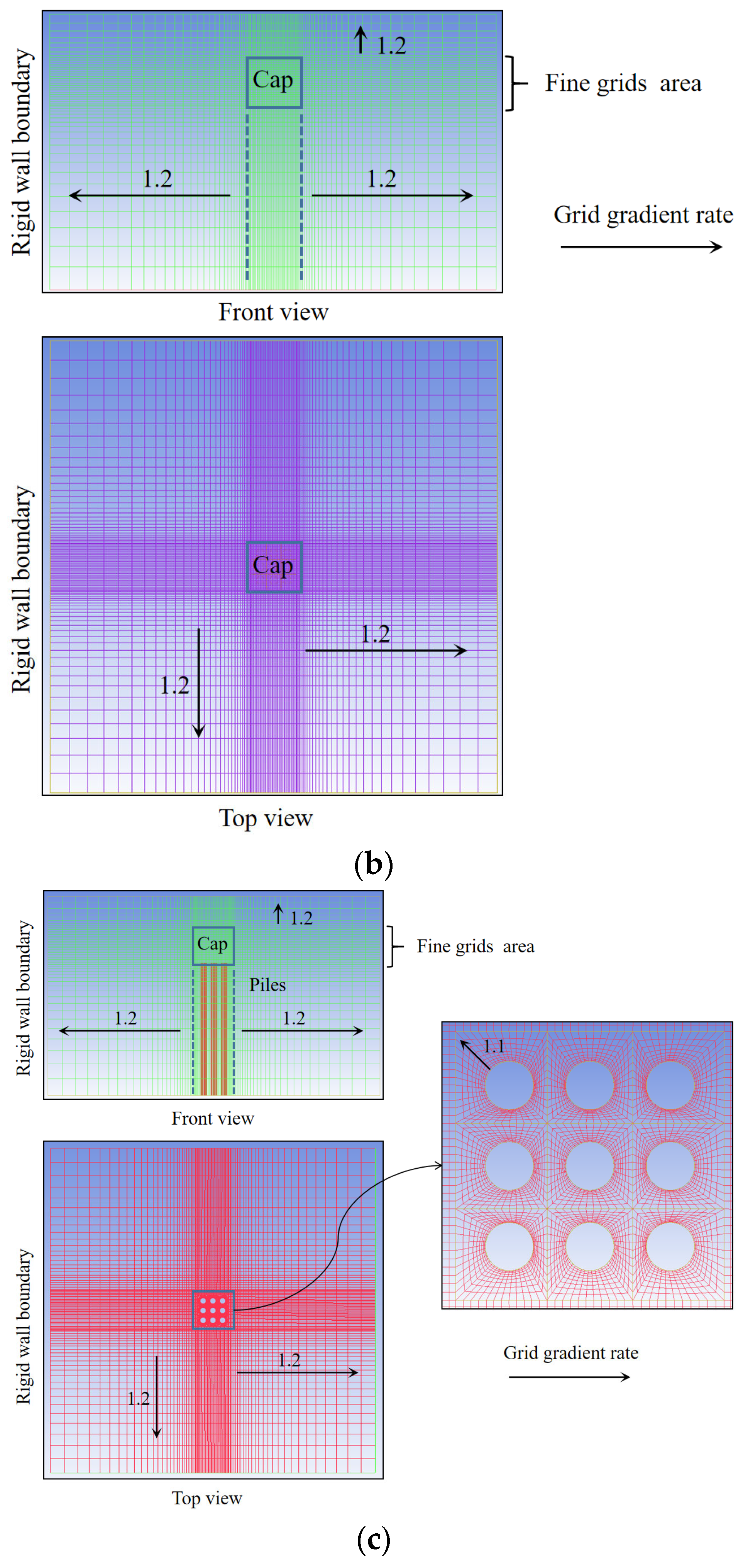





| Structures | Innermost Grid Size (m) | Grid Gradient Rate | Grid Size of the Encrypted Area (m) | Mesh Quantity | Computational Time (h) | ||
|---|---|---|---|---|---|---|---|
| Pier | 0.03 | 1.2 | 0.05 | 216,532 | 14 | ||
| Pile cap | 0.03 | 1.2 | 0.05 | 288,975 | 18 | ||
| Pile cap-pile group | Pile cap | pile group | Pile cap | pile group | 0.05 | 485,724 | 27 |
| 0.03 | 0.02 | 1.2 | 1.1 | ||||
| Structure Type | Calculation Methods and Results (t) | Relative Error (%) | Computational Time (h) | Modeling Process | Advantages and Disadvantages | |
|---|---|---|---|---|---|---|
| Isolated pile cap structure | Equation (38) | 39.21 | 6.42 | ) | Convenient | Efficient and widely applied but requiring modeling |
| Chinese code | 113.25 | 207.33 | - | - | Simple but with very poor precision | |
| Simulation | 36.85 | - | 18 | Complex | High precision but low efficiency and requires complex modeling | |
| Pile group-pile cap structure | Equation (42) | 45.21 | 4.80 | ) | Convenient | Efficient and widely applied but requiring modeling |
| Chinese code | 113.25 | 162.58 | - | - | Simple but with very poor precision | |
| Simulation | 43.13 | - | 27 | Extremely Complex | High precision but low efficiency and requires complex modeling | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Xiao, S.; Geng, X.; Yang, W.; Xu, Y. An Efficient Hydrodynamic Force Calculation Method for Pile Caps with Arbitrary Cross-Sections Under Earthquake Based on Finite Element Method. Eng 2025, 6, 167. https://doi.org/10.3390/eng6070167
Zhang W, Xiao S, Geng X, Yang W, Xu Y. An Efficient Hydrodynamic Force Calculation Method for Pile Caps with Arbitrary Cross-Sections Under Earthquake Based on Finite Element Method. Eng. 2025; 6(7):167. https://doi.org/10.3390/eng6070167
Chicago/Turabian StyleZhang, Wen, Shizhou Xiao, Xiaokun Geng, Wanli Yang, and Yifei Xu. 2025. "An Efficient Hydrodynamic Force Calculation Method for Pile Caps with Arbitrary Cross-Sections Under Earthquake Based on Finite Element Method" Eng 6, no. 7: 167. https://doi.org/10.3390/eng6070167
APA StyleZhang, W., Xiao, S., Geng, X., Yang, W., & Xu, Y. (2025). An Efficient Hydrodynamic Force Calculation Method for Pile Caps with Arbitrary Cross-Sections Under Earthquake Based on Finite Element Method. Eng, 6(7), 167. https://doi.org/10.3390/eng6070167





