Improved Modulation Classification Based on Hough Transforms of Constellation Diagrams Using CNN for the UWA-OFDM Communication System
Abstract
1. Introduction
- Utilization of the HT and edge detection to enhance modulation classification;
- Utilization of an OFDM system based on DCT, Linear Minimum Mean Square Error (LMMSE) equalizer, and CP to mitigate Inter-Symbol Interference (ISI) over the UWA communication channel;
- Performance comparison between the proposed method on a small dataset and existing deep-learning-based methods on large amounts of data;
- Classification of seven modulation schemes, namely 2/8/16-PSK and 4/8/16/32-QAM, which are accurately classified under the effect of estimation errors;
- Obtaining an average classification accuracy of 94% at 10 dB for perfect channel estimation with the UWA OFDM communication system. This represents an improvement of 40% compared to the benchmark model at 10 dB SNR.
2. The Proposed Method
2.1. Underwater Channel Model
2.2. Proposed CNN-Based UWA-OFDM System
2.2.1. Dataset Description
2.2.2. Pre-Processing Phase
2.2.3. Pre-Trained CNN Models
3. Results
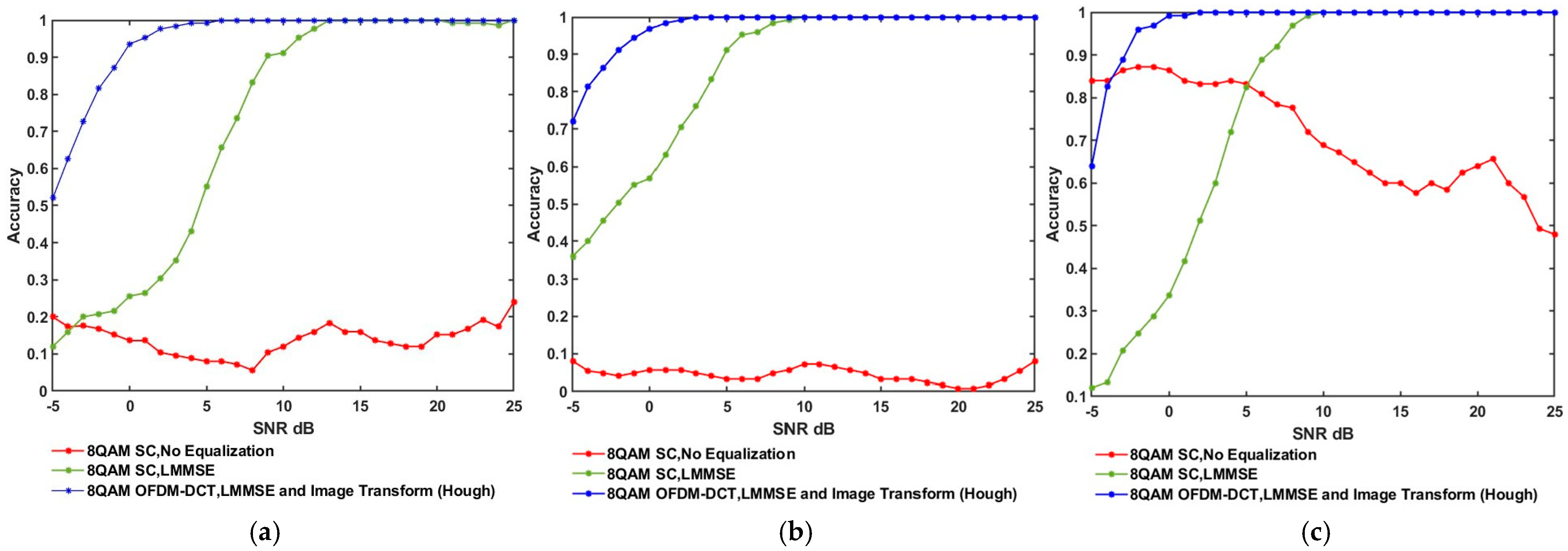
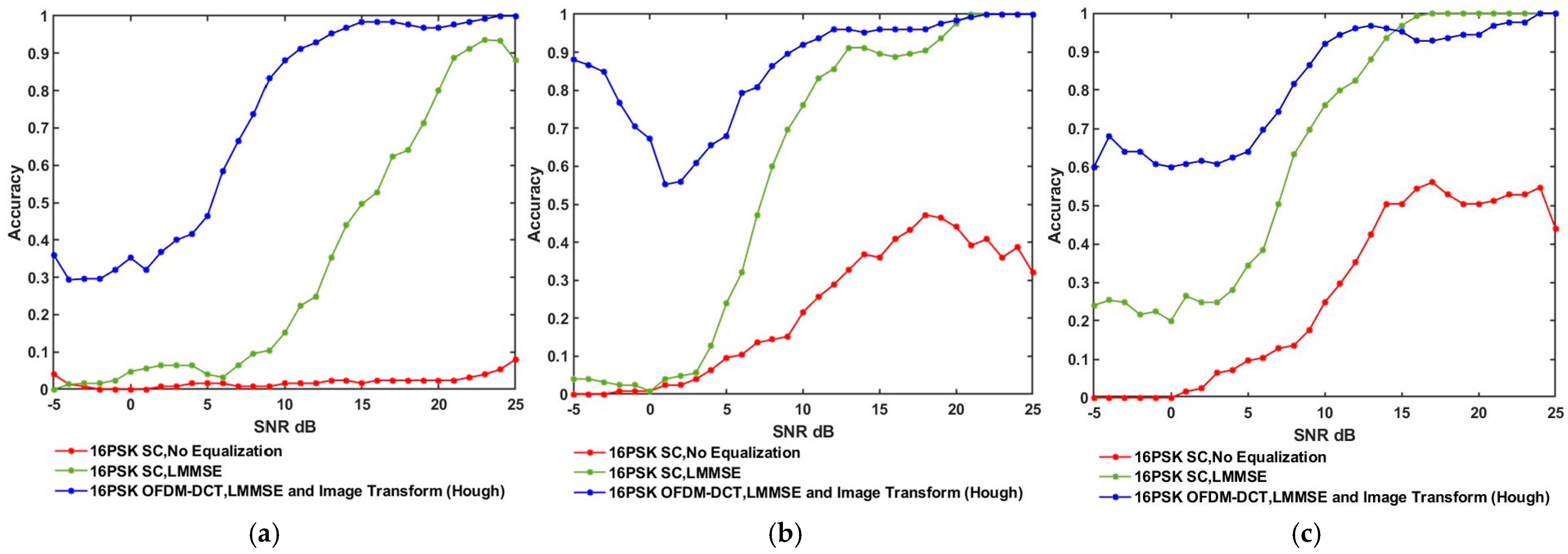
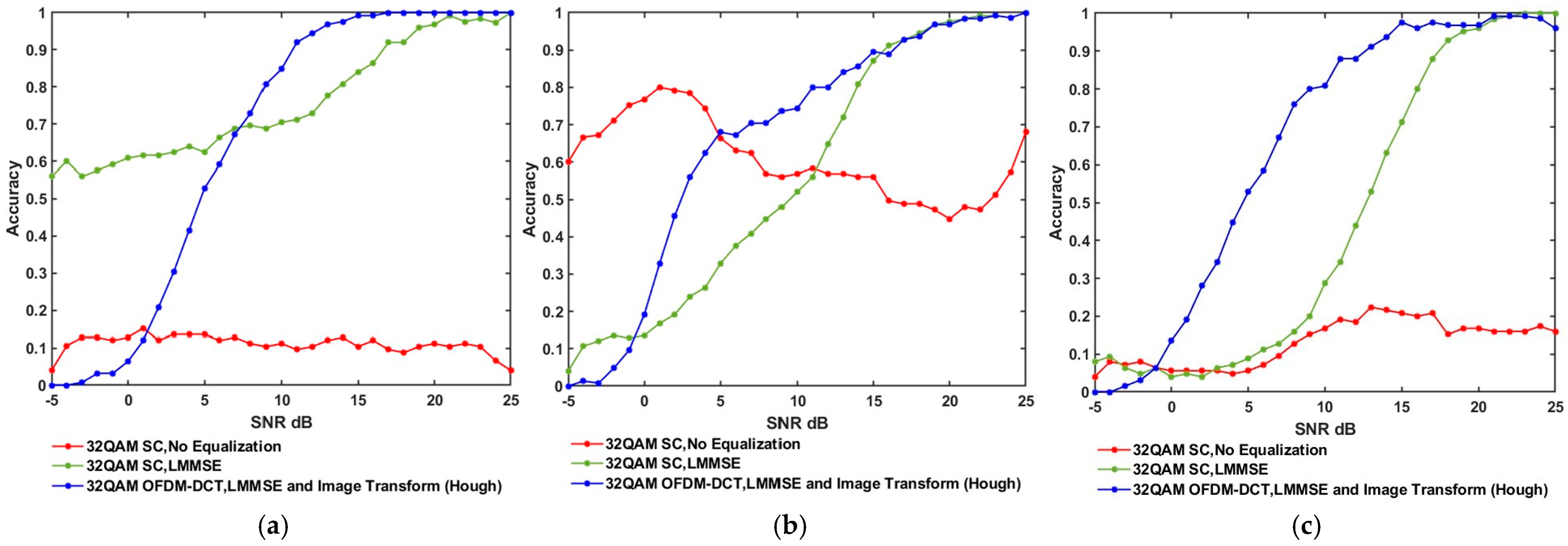
3.1. Result Analysis for Different Modulation Schemes
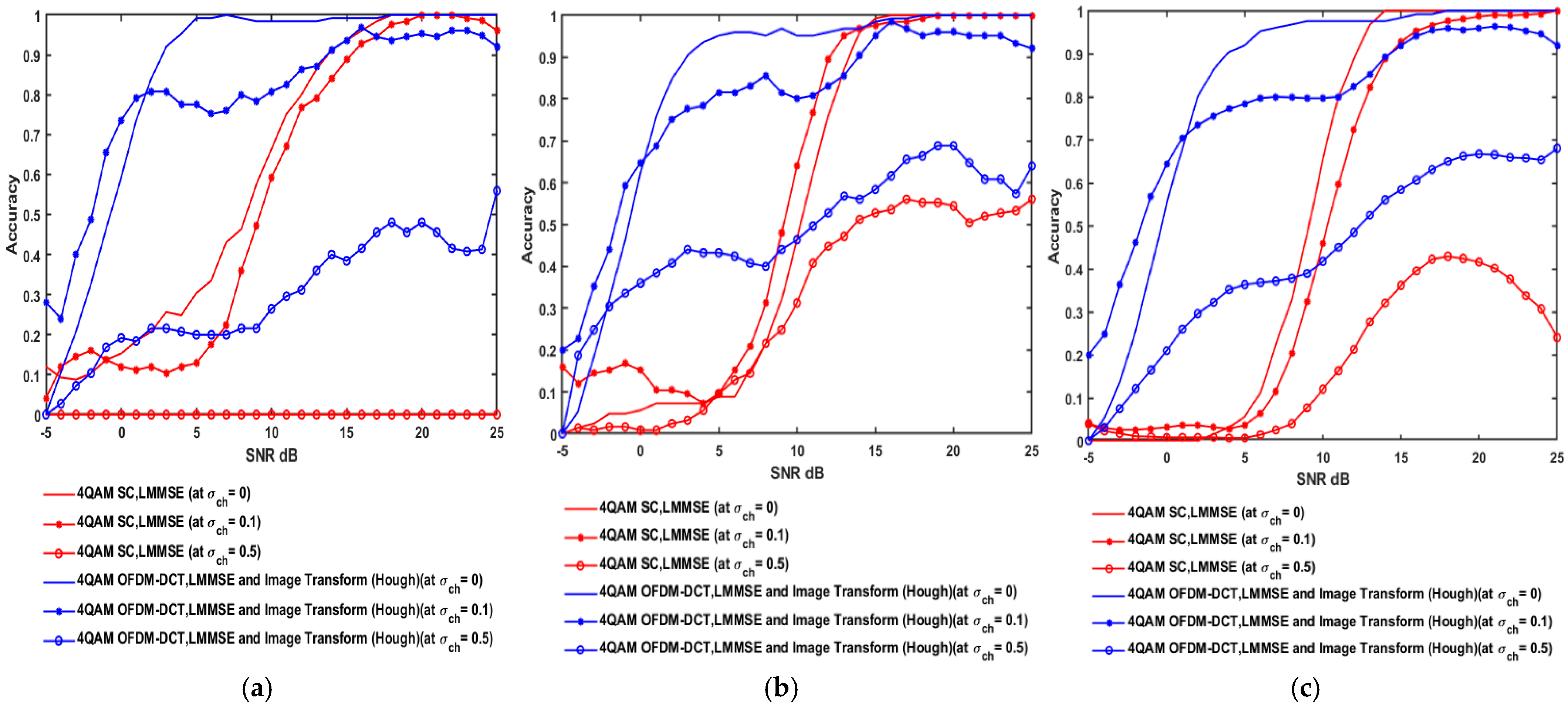
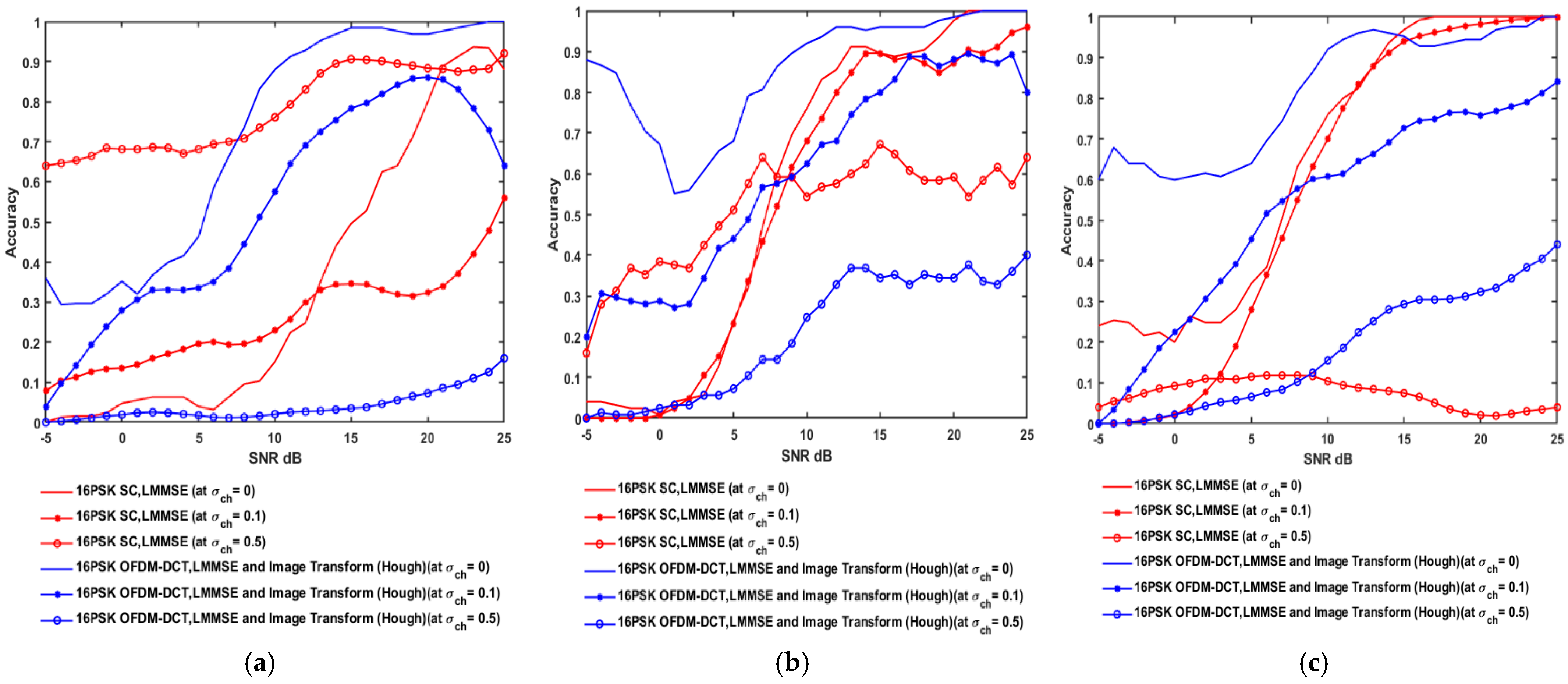
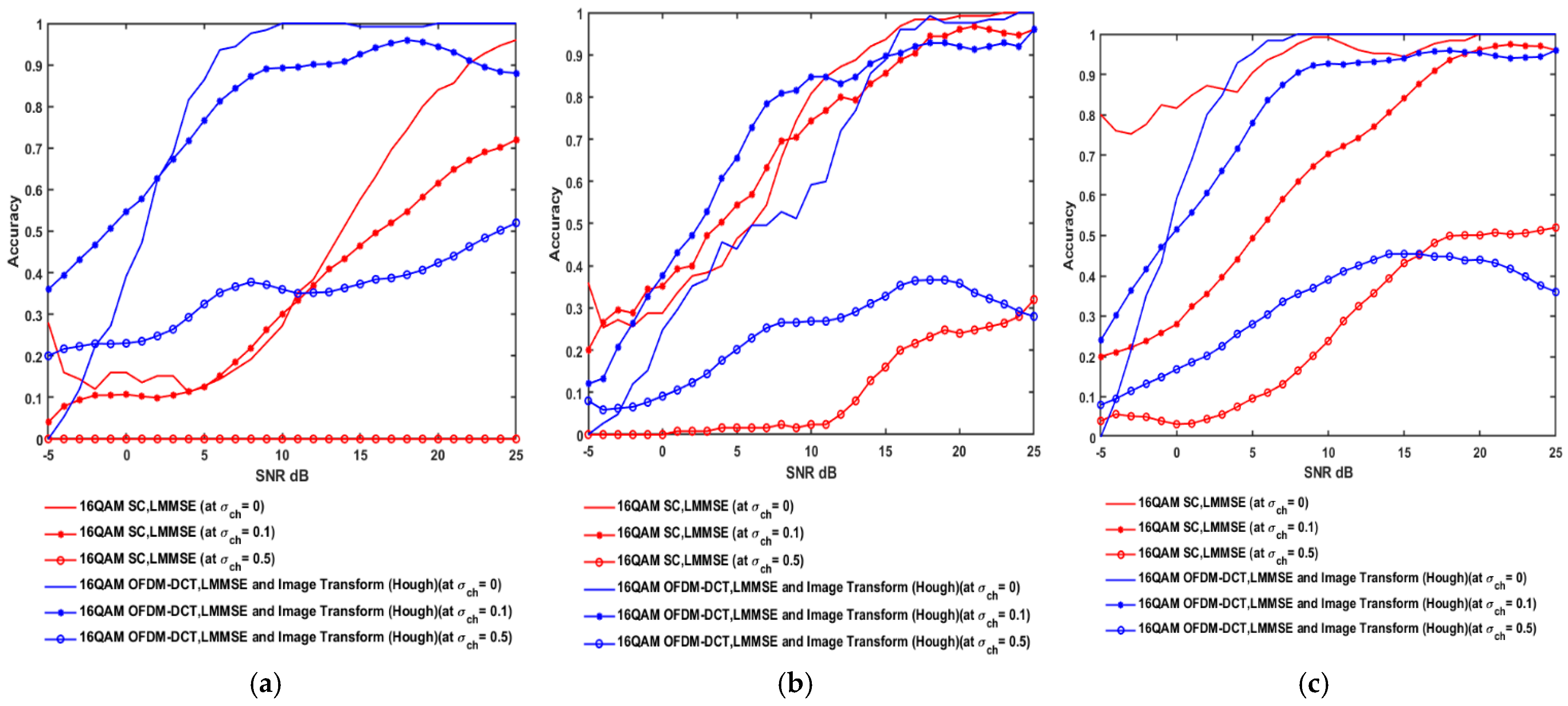
3.2. Result Analysis Under the Effect of Estimation Errors
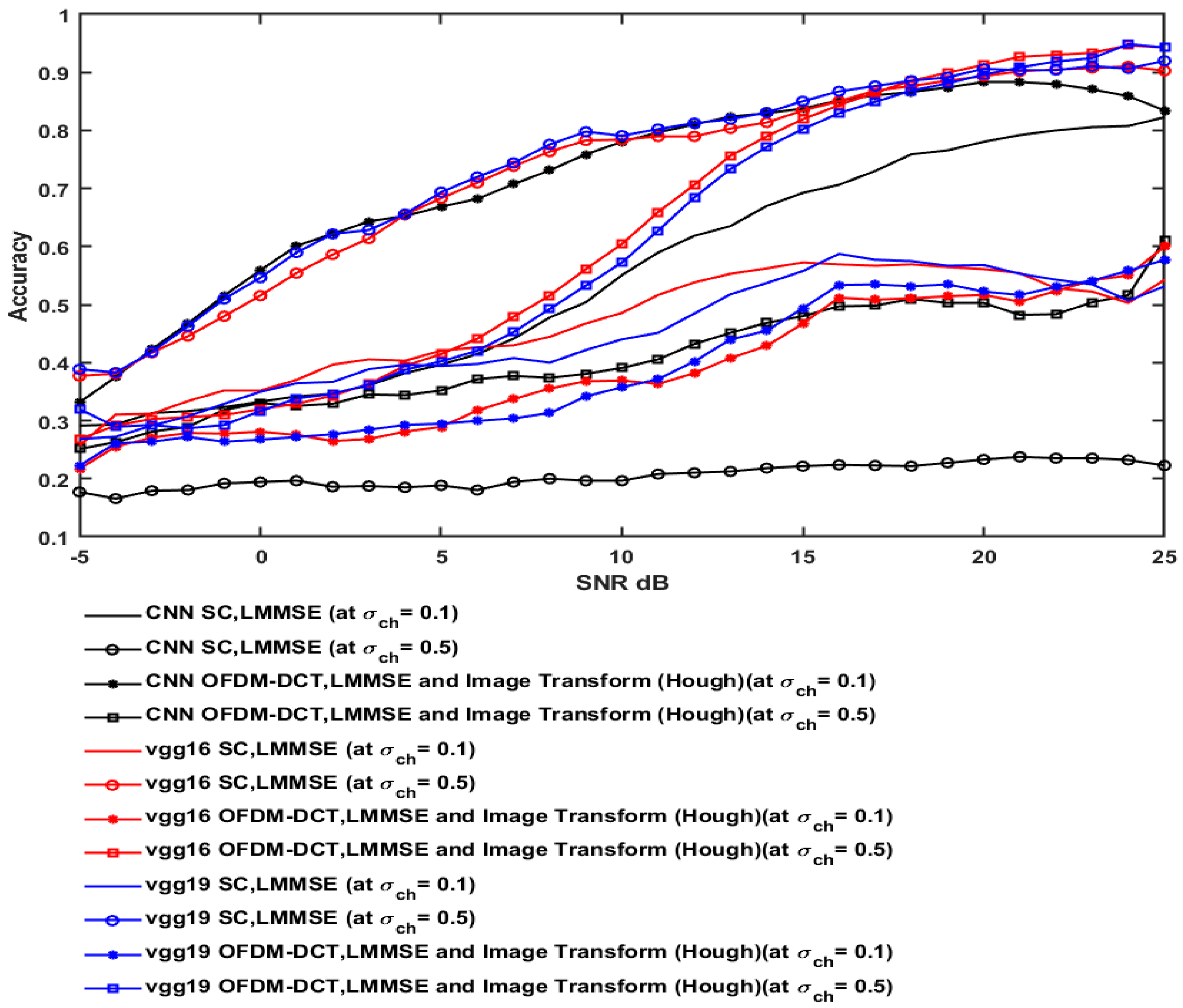
3.3. Comparison Results
3.3.1. Comparison Results Under the Effect of Perfect Channel Estimation
3.3.2. Comparison Results Under the Effect of Estimation Errors
3.4. Model Complexity
3.5. Comparative Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, X.; Yang, H.; Sheng, M. Automatic modulation classification for underwater acoustic communication signals based on deep complex networks. Entropy 2023, 25, 318. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.; Yan, S.; Xu, L.; Hou, C. Sparsity-aware adaptive turbo equalization for underwater acoustic communications in the Mariana trench. IEEE J. Ocean. Eng. 2021, 46, 338–351. [Google Scholar] [CrossRef]
- Alsulami, M.; Elfouly, R.; Ammar, R. Underwater Wireless Sensor Networks: A Review. In Proceedings of the 11th International Conference on Sensor Networks (SENSORNETS 2022), Online, 7–8 February 2022; pp. 202–214. [Google Scholar] [CrossRef]
- Kumar, S.; Chinthaginjala, R.; Anbazhagan, R.; Nyangaresi, V.O.; Pau, G.; Varma, P.S. Submarine acoustic target strength modeling at high-frequency asymptotic scattering. IEEE Access 2024, 12, 4859–4870. [Google Scholar] [CrossRef]
- Marcon, Y.; Kopiske, E.; Leymann, T.; Spiesecke, U.; Vittori, V.; Wahl, T.V.; Wintersteller, P.; Waldmann, C.; Bohrmann, G. Arotary sonar for long-term acoustic monitoring of deep-sea gas emissions. In Proceedings of the OCEANS 2019-Marseille, Marseille, France, 17–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–8. [Google Scholar]
- Jing, L.; He, C.; Huang, J.; Ding, Z. Energy management and power allocation for underwater acoustic sensor network. IEEE Sens. J. 2017, 17, 6451–6462. [Google Scholar] [CrossRef]
- Han, G.; Tang, Z.; He, Y.; Jiang, J.; Ansere, J.A. District partition-based data collection algorithm with event dynamic competition in underwater acoustic sensor networks. IEEE Trans. Ind. Inform. 2019, 15, 5755–5764. [Google Scholar] [CrossRef]
- Khan, M.R.; Das, B.; Pati, B.B. Channel estimation strategies for underwater acoustic (UWA) communication: An overview. J. Frankl. Inst. 2020, 357, 7229–7265. [Google Scholar] [CrossRef]
- Lou, Y.; Ahmed, N.; Lou, Y.; Ahmed, N. Signal Processing in UWAC System. In Underwater Communications and Networks; Textbooks in Telecommunication Engineering; Springer: Cham, Switzerland, 2022; pp. 57–83. [Google Scholar]
- Mishra, J.P.; Singh, K.; Chaudhary, H. Recent advancement of AI technology for underwater acoustic communication. AIP Conf. Proc. 2023, 2752, 050001. [Google Scholar]
- Wan, L.; Zhou, H.; Xu, X.; Huang, Y.; Zhou, S.; Shi, Z.; Cui, J.H. Adaptive modulation and coding for underwater acoustic OFDM. IEEE J. Ocean. Eng. 2014, 40, 327–336. [Google Scholar] [CrossRef]
- Bocus, M.J.; Doufexi, A.; Agrafiotis, D. Performance of OFDM-based massive MIMO OTFS systems for underwater acoustic communication. IET Commun. 2020, 14, 588–593. [Google Scholar] [CrossRef]
- Abdel-Moneim, M.A.; El-Shafai, W.; Abdel-Salam, N.; El-Rabaie, E.S. Abd El-Samie FE. A survey of traditional and advanced automatic modulation classification techniques, challenges, and some novel trends. Int. J. Commun. Syst. 2021, 34, e4762. [Google Scholar] [CrossRef]
- Hui, J.; Sheng, X. Underwater Acoustic Channel; Springer: Singapore, 2022. [Google Scholar]
- Tu, Y.; Lin, Y.; Wang, S.; Dou, Z.; Mao, S. Complex-valued networks for automatic modulation classification. IEEE Trans. Veh. Technol. 2020, 69, 10085–10089. [Google Scholar] [CrossRef]
- Patel, M.; Wang, X.; Mao, S. Data augmentation with Conditional GAN for automatic modulation classification. In Proceedings of the 2nd ACM Workshop on Wireless Security and Machine Learning, Linz, Austria, 13 July 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 31–36. [Google Scholar]
- Endo, T. Analysis of Conventional Feature Learning Algorithms and Advanced Deep Learning Models. J. Robot. Spectr. 2023, 1, 001–012. [Google Scholar] [CrossRef]
- Wang, B.; Wang, H.; Li, Y. Method of Modulation Recognition Technology for Underwater Acoustic Communication Signals in an Impulsive Noise Environment. Signal Process. 2020, 36, 2107–2115. [Google Scholar]
- Marcoux, C.N.; Chandna, B.; Blair, B.J. Blind equalization and automatic modulation classification of underwater acoustic signals. Proc. Meet. Acoust. 2018, 35, 055003. [Google Scholar]
- Xiao, Y.H.; Zhang, Y.F.; Tao, J. CNN-based automatic modulation classification over underwater acoustic channels. In Proceedings of the OCEANS: San Diego–Porto, San Diego, CA, USA, 20–23 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Li, Y.Y.; Liang, S.C. Research on modulation recognition of underwater acoustic communication signal based on deep learning. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2023; Volume 2435, p. 012007. [Google Scholar]
- Zhang, Y.; Li, J.; Zakharov, Y.; Sun, D.; Li, J. Underwater acoustic OFDM communications using deep learning. In Proceedings of the 2nd Franco-Chinese Acoustic Conference (FCAC), Le Mans, France, 29–31 October 2018; p. 6. [Google Scholar]
- Lou, Y.; Ahmed, N. Underwater Communications and Networks; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Kulhandjian, H.; Melodia, T. Modeling underwater acoustic channels in short-range shallow water environments. In Proceedings of the 9th International Conference on Underwater Networks and Systems, Rome, Italy, 12–14 November 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 1–5. [Google Scholar]
- Abraham, D.A. Underwater acoustic signal and noise modeling. In Underwater Acoustic Signal Processing: Modeling, Detection, and Estimation; Springer International Publishing: Cham, Switzerland, 2019; pp. 349–456. [Google Scholar]
- Çavuşlu, M.A.; Altuncu, M.A.; Özcan, H.; Gülağız, F.K.; Şahin, S. Estimation of underwater acoustic channel parameters for Erdek/Turkey region. Appl. Acoust. 2021, 181, 108135. [Google Scholar] [CrossRef]
- Qarabaqi, P.; Stojanovic, M. Statistical characterization and computationally efficient modeling of a class of underwater acoustic communication channels, in Special Issue: Underwater Communications. IEEE J. Ocean. Eng. 2013, 38, 701–717. [Google Scholar] [CrossRef]
- Ramadan, K.; Ahmed; Fiky, S.; Moawad; Dessouky, I.; Fathi; El-Samie, E.A. Equalization and carrier frequency offset compensation for UWA-OFDM communication systems based on the discrete sine transform. Digit. Signal Process. 2019, 90, 142–149. [Google Scholar] [CrossRef]
- Ramadan, K.; Dessouky, M.I.; Elagooz, S.; Elkordy, M.; Abd El-Samie, F.E. Equalization and Carrier Frequency Offset Compensation for Underwater Acoustic OFDM Systems. Ann. Data Sci. 2018, 5, 259–272. [Google Scholar] [CrossRef]
- Ramadan, K.; Dessouky, M.I.; El-Samie, F.E.A.; Fiky, A.S. Equalization and blind CFO estimation for performance enhancement of OFDM communication systems using discrete cosine transforms. Int. J. Commun. Syst. 2020, 33, e3984. [Google Scholar] [CrossRef]
- Varun, R.; Vivekanand-Kini, Y.; Manikantan, K.; Ramachandran, S. Face recognition using Hough transform-based feature extraction. Procedia Comput. Sci. 2015, 46, 1491–1500. [Google Scholar] [CrossRef]
- Bailey, D.; Chang, Y.; Le Moan, S. Analyzing arbitrary curves from the line hough transform. J. Imaging 2020, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- Salehi, S.D.; Gilliland, W.; Kingstedt, O.T. Application of the Hough transform for automated analysis of Kolsky bar data. Exp. Tech. 2022, 46, 153–165. [Google Scholar] [CrossRef]
- MathWorks. Deep Learning Toolbox. Available online: https://www.mathworks.com/help/deeplearning/ug/create-simple-deep-learning-network-for-classification.html (accessed on 13 May 2025).
- MathWorks. Deep Learning Toolbox. Available online: https://www.mathworks.com/help/deeplearning/ref/vgg16.html (accessed on 13 May 2025).
- MathWorks. Deep Learning Toolbox. Available online: https://www.mathworks.com/help/deeplearning/ref/vgg19.html (accessed on 13 May 2025).
- Hong, S.; Zhang, Y.; Wang, Y.; Gu, H.; Gui, G.; Sari, H. Deep learning-based signal modulation identification in OFDM systems, systems. IEEE Access 2019, 7, 114631–114638. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Roy, T.; Clancy, T.C. Over-the-air deep learning-based radio signal classification. IEEE J. Sel. Top. Signal Process. 2018, 12, 168–179. [Google Scholar] [CrossRef]
- Zhang, L.; Lin, C.; Yan, W.; Ling, Q.; Wang, Y. Real-time OFDM signal modulation classification based on deep learning and software-defined radio. IEEE Commun. Lett. 2021, 25, 2988–2992. [Google Scholar] [CrossRef]
- Abdel-Moneim, M.A.; El-Rabaie, S.; El-Samie, F.E.A.; Ramadan, K.; Abdel-Salam, N.; Ramadan, K.F. Efficient CNN-Based Automatic Modulation Classification in UWA Communication Systems Using Constellation Diagrams and Gabor Filtering. In Proceedings of the 3rd International Conference on Electronic Engineering (ICEEM), Menouf, Egypt, 7–8 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]













| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Chanel model | MACE | Central frequency | 16 kHz |
| Transmitter height | 45 m | Number of intra-paths | 20 |
| Receiver height | 60 m | Mean of intra-paths | 25 mv |
| Water depth | 100 m | Variance of intra-paths | 1 µv |
| Channel distance | 1.0 km | Bandwidth of UWA channels | 12 kHz |
| Surface variance | 1.123 m2 | ||
| Bottom variance | 0.5625 m2 |
| Parameter | Basic CNN | VGG-16 | VGG-19 |
|---|---|---|---|
| Training time (Min: s) | 2:66 | 32:58 | 38:38 |
| Epochs | 10 | 6 | 6 |
| Total Iterations | 1970 | 15,150 | 15,150 |
| Iterations/Epoch | 197 | 2525 | 2525 |
| Validation Frequency (Iterations) | 100 | 100 | 100 |
| Learning Rate | 0.0001 | 0.0001 | 0.0001 |
| Hardware Resources | Single GPU | Single GPU | Single GPU |
| BPSK | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basic CNN | VGG-16 | VGG-19 | |||||||
| SNR (dB) | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT |
| −5 | 0.08 | 0.96 | 1 | 0.28 | 1 | 1 | 0.48 | 0.96 | 1 |
| 0 | 0.52 | 1 | 1 | 0.8 | 1 | 1 | 0.84 | 1 | 1 |
| 5 | 0.84 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 10 | 0.84 | 1 | 1 | 0.96 | 1 | 1 | 0.96 | 1 | 1 |
| 15 | 0.88 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 20 | 0.96 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 25 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4QAM | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basic CNN | VGG-16 | VGG-19 | |||||||
| SNR (dB) | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT |
| −5 | 0.08 | 0.12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0.12 | 0.2 | 0.6 | 0 | 0.12 | 0.68 | 0 | 0 | 0.6 |
| 5 | 0 | 0.44 | 1 | 0 | 0.12 | 0.96 | 0 | 0.08 | 0.92 |
| 10 | 0.08 | 0.6 | 0.96 | 0 | 0.44 | 0.92 | 0.04 | 0.6 | 0.96 |
| 15 | 0.32 | 0.92 | 0.96 | 0.36 | 1 | 0.96 | 0.48 | 1 | 0.96 |
| 20 | 0.52 | 1 | 1 | 0.36 | 1 | 1 | 0.68 | 1 | 1 |
| 25 | 0.44 | 1 | 1 | 0.4 | 1 | 1 | 0.6 | 1 | 1 |
| 8PSK | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basic CNN | VGG-16 | VGG-19 | |||||||
| SNR (dB) | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT |
| −5 | 0.12 | 0.12 | 0.6 | 0 | 0.36 | 0 | 0 | 0 | 0.32 |
| 0 | 0.28 | 0.12 | 0.8 | 0 | 0.36 | 0.2 | 0.04 | 0 | 0.36 |
| 5 | 0.36 | 0.2 | 0.88 | 0 | 0.24 | 0.76 | 0.04 | 0 | 0.72 |
| 10 | 0.24 | 0.52 | 0.88 | 0 | 0.12 | 0.8 | 0.04 | 0.04 | 0.52 |
| 15 | 0.4 | 0.68 | 0.92 | 0 | 0.52 | 0.8 | 0.04 | 0.24 | 0.68 |
| 20 | 0.44 | 0.96 | 1 | 0.12 | 0.96 | 0.96 | 0.04 | 0.8 | 0.92 |
| 25 | 0.36 | 1 | 1 | 0.08 | 1 | 1 | 0 | 1 | 1 |
| 8QAM | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basic CNN | VGG-16 | VGG-19 | |||||||
| SNR (dB) | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT |
| −5 | 0.2 | 0.12 | 0.52 | 0.08 | 0.36 | 0.72 | 0.84 | 0.12 | 0.64 |
| 0 | 0.16 | 0.16 | 0.96 | 0.04 | 0.6 | 0.96 | 0.88 | 0.32 | 1 |
| 5 | 0.12 | 0.4 | 1 | 0 | 0.88 | 1 | 0.88 | 0.76 | 1 |
| 10 | 0.04 | 0.88 | 1 | 0.08 | 1 | 1 | 0.84 | 1 | 1 |
| 15 | 0.16 | 1 | 1 | 0.04 | 1 | 1 | 0.72 | 1 | 1 |
| 20 | 0.12 | 1 | 1 | 0 | 1 | 1 | 0.64 | 1 | 1 |
| 25 | 0.24 | 1 | 1 | 0.08 | 1 | 1 | 0.48 | 1 | 1 |
| 16PSK | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basic CNN | VGG-16 | VGG-19 | |||||||
| SNR (dB) | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT |
| −5 | 0.04 | 0 | 0.36 | 0 | 0.04 | 0.88 | 0 | 0.24 | 0.6 |
| 0 | 0 | 0 | 0.36 | 0.04 | 0 | 0.48 | 0 | 0.08 | 0.6 |
| 5 | 0 | 0 | 0.52 | 0.12 | 0.04 | 0.72 | 0.2 | 0.08 | 0.56 |
| 10 | 0 | 0.16 | 0.88 | 0.16 | 0.68 | 1 | 0.24 | 0.72 | 0.92 |
| 15 | 0.04 | 0.68 | 1 | 0.36 | 0.96 | 1 | 0.6 | 1 | 0.96 |
| 20 | 0.04 | 0.76 | 0.96 | 0.56 | 1 | 1 | 0.44 | 1 | 1 |
| 25 | 0.08 | 0.88 | 1 | 0.32 | 1 | 1 | 0.44 | 1 | 1 |
| 16QAM | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basic CNN | VGG-16 | VGG-19 | |||||||
| SNR (dB) | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT |
| −5 | 0.36 | 0.28 | 0 | 0.16 | 0.36 | 0 | 0 | 0.8 | 0 |
| 0 | 0.4 | 0.16 | 0.52 | 0.2 | 0.28 | 0.36 | 0 | 0.92 | 0.68 |
| 5 | 0.24 | 0.16 | 0.84 | 0.12 | 0.32 | 0.44 | 0.04 | 0.88 | 0.92 |
| 10 | 0.32 | 0.28 | 1 | 0.16 | 0.88 | 0.6 | 0 | 1 | 1 |
| 15 | 0.32 | 0.6 | 1 | 0.24 | 0.96 | 0.84 | 0 | 0.96 | 1 |
| 20 | 0.28 | 0.84 | 1 | 0.16 | 0.96 | 1 | 0 | 1 | 1 |
| 25 | 0.24 | 0.96 | 1 | 0.32 | 1 | 1 | 0.12 | 1 | 1 |
| 32QAM | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basic CNN | VGG-16 | VGG-19 | |||||||
| SNR (dB) | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT |
| −5 | 0.04 | 0.56 | 0 | 0.6 | 0.04 | 0 | 0.04 | 0.08 | 0 |
| 0 | 0.04 | 0.64 | 0.12 | 0.8 | 0.12 | 0.2 | 0.08 | 0 | 0.08 |
| 5 | 0.12 | 0.68 | 0.6 | 0.76 | 0.36 | 0.72 | 0.08 | 0.12 | 0.4 |
| 10 | 0.04 | 0.72 | 0.88 | 0.48 | 0.56 | 0.72 | 0.24 | 0.28 | 0.84 |
| 15 | 0.12 | 0.96 | 1 | 0.48 | 0.92 | 0.92 | 0.44 | 0.72 | 1 |
| 20 | 0.08 | 0.96 | 1 | 0.48 | 1 | 0.96 | 0.16 | 0.96 | 0.96 |
| 25 | 0.04 | 1 | 1 | 0.68 | 1 | 1 | 0.16 | 1 | 0.96 |
| Basic CNN Accuracy (BPSK) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.96 | 0.96 | 0.28 | 1 | 0.96 | 0.84 |
| 0 | 1 | 0.99 | 0.37 | 1 | 1 | 0.84 |
| 5 | 1 | 1 | 0.43 | 1 | 1 | 0.83 |
| 10 | 1 | 1 | 0.51 | 1 | 1 | 0.87 |
| 15 | 1 | 1 | 0.56 | 1 | 1 | 0.93 |
| 20 | 1 | 1 | 0.62 | 1 | 1 | 0.94 |
| 25 | 1 | 1 | 0.64 | 1 | 1 | 0.92 |
| VGG-16 Accuracy (BPSK) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 1 | 0.96 | 0.76 | 1 | 0.96 | 0.92 |
| 0 | 1 | 1 | 0.9 | 1 | 1 | 0.88 |
| 5 | 1 | 1 | 0.88 | 1 | 1 | 0.88 |
| 10 | 1 | 1 | 0.96 | 1 | 1 | 0.92 |
| 15 | 1 | 1 | 0.97 | 1 | 1 | 0.95 |
| 20 | 1 | 1 | 0.98 | 1 | 1 | 0.96 |
| 25 | 1 | 1 | 1 | 1 | 1 | 0.92 |
| VGG-19 Accuracy (BPSK) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.96 | 0.96 | 0.88 | 1 | 0.96 | 0.8 |
| 0 | 1 | 0.99 | 0.96 | 1 | 1 | 0.86 |
| 5 | 1 | 1 | 0.96 | 1 | 1 | 0.87 |
| 10 | 1 | 1 | 0.99 | 1 | 1 | 0.9 |
| 15 | 1 | 1 | 1 | 1 | 1 | 0.93 |
| 20 | 1 | 1 | 1 | 1 | 1 | 0.95 |
| 25 | 1 | 1 | 1 | 1 | 1 | 1 |
| Basic CNN Accuracy (4QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.12 | 0.04 | 0 | 0 | 0.28 | 0 |
| 0 | 0.15 | 0.12 | 0 | 0.59 | 0.74 | 0.19 |
| 5 | 0.3 | 0.13 | 0 | 0.99 | 0.78 | 0.2 |
| 10 | 0.66 | 0.59 | 0 | 0.98 | 0.81 | 0.26 |
| 15 | 0.94 | 0.89 | 0 | 0.99 | 0.94 | 0.38 |
| 20 | 1 | 1 | 0 | 1 | 0.95 | 0.48 |
| 25 | 1 | 0.96 | 0 | 1 | 0.92 | 0.56 |
| VGG-16 Accuracy (4QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0 | 0.16 | 0 | 0 | 0.2 | 0 |
| 0 | 0.06 | 0.15 | 0.01 | 0.62 | 0.65 | 0.36 |
| 5 | 0.09 | 0.1 | 0.1 | 0.95 | 0.82 | 0.43 |
| 10 | 0.46 | 0.64 | 0.31 | 0.95 | 0.8 | 0.46 |
| 15 | 0.99 | 0.98 | 0.53 | 0.98 | 0.95 | 0.58 |
| 20 | 1 | 1 | 0.54 | 1 | 0.96 | 0.69 |
| 25 | 1 | 1 | 0.56 | 1 | 0.92 | 0.64 |
| VGG-19 Accuracy (4QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0 | 0.04 | 0.04 | 0 | 0.2 | 0 |
| 0 | 0 | 0.03 | 0.01 | 0.55 | 0.64 | 0.21 |
| 5 | 0.06 | 0.04 | 0.01 | 0.92 | 0.78 | 0.36 |
| 10 | 0.66 | 0.46 | 0.12 | 0.98 | 0.8 | 0.42 |
| 15 | 1 | 0.93 | 0.36 | 0.98 | 0.92 | 0.58 |
| 20 | 1 | 0.99 | 0.42 | 1 | 0.96 | 0.67 |
| 25 | 1 | 1 | 0.24 | 1 | 0.92 | 0.68 |
| Basic CNN Accuracy (8PSK) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.12 | 0.2 | 0 | 0.6 | 0.08 | 0.28 |
| 0 | 0.12 | 0.26 | 0 | 0.69 | 0.22 | 0.24 |
| 5 | 0.21 | 0.29 | 0 | 0.87 | 0.38 | 0.37 |
| 10 | 0.39 | 0.42 | 0 | 0.89 | 0.42 | 0.41 |
| 15 | 0.66 | 0.6 | 0 | 0.92 | 0.42 | 0.52 |
| 20 | 0.94 | 0.79 | 0 | 0.98 | 0.6 | 0.59 |
| 25 | 1 | 0.72 | 0 | 1 | 0.52 | 0.76 |
| VGG-16 Accuracy (8PSK) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.36 | 0.08 | 0 | 0 | 0.08 | 0.04 |
| 0 | 0.36 | 0.07 | 0 | 0.22 | 0.16 | 0.2 |
| 5 | 0.31 | 0.09 | 0.01 | 0.72 | 0.28 | 0.39 |
| 10 | 0.14 | 0.04 | 0.02 | 0.74 | 0.4 | 0.41 |
| 15 | 0.43 | 0.21 | 0.14 | 0.78 | 0.35 | 0.39 |
| 20 | 0.94 | 0.6 | 0.18 | 0.94 | 0.59 | 0.36 |
| 25 | 1 | 0.76 | 0.28 | 1 | 0.68 | 0.44 |
| VGG-19 Accuracy (8PSK) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0 | 0.4 | 0.08 | 0.32 | 0.56 | 0.08 |
| 0 | 0 | 0.24 | 0.21 | 0.33 | 0.32 | 0.22 |
| 5 | 0.01 | 0.2 | 0.31 | 0.67 | 0.33 | 0.35 |
| 10 | 0.1 | 0.04 | 0.49 | 0.62 | 0.48 | 0.4 |
| 15 | 0.26 | 0.09 | 0.68 | 0.66 | 0.51 | 0.46 |
| 20 | 0.74 | 0.37 | 0.76 | 0.93 | 0.72 | 0.46 |
| 25 | 1 | 0.72 | 0.68 | 1 | 0.8 | 0.44 |
| Basic CNN Accuracy (8QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.12 | 0.32 | 0.28 | 0.52 | 0.4 | 0.28 |
| 0 | 0.26 | 0.34 | 0.26 | 0.94 | 0.8 | 0.41 |
| 5 | 0.55 | 0.6 | 0.18 | 0.99 | 0.96 | 0.39 |
| 10 | 0.91 | 0.86 | 0.13 | 1 | 0.98 | 0.51 |
| 15 | 1 | 0.98 | 0.08 | 1 | 1 | 0.63 |
| 20 | 1 | 1 | 0.12 | 1 | 0.98 | 0.62 |
| 25 | 1 | 1 | 0 | 1 | 1 | 0.72 |
| VGG-16 Accuracy (8QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.36 | 0.44 | 0.48 | 0.72 | 0.32 | 0.24 |
| 0 | 0.57 | 0.57 | 0.45 | 0.97 | 0.78 | 0.44 |
| 5 | 0.91 | 0.86 | 0.48 | 1 | 0.97 | 0.41 |
| 10 | 1 | 0.99 | 0.59 | 1 | 0.98 | 0.58 |
| 15 | 1 | 1 | 0.68 | 1 | 0.98 | 0.69 |
| 20 | 1 | 1 | 0.73 | 1 | 0.98 | 0.69 |
| 25 | 1 | 1 | 0.84 | 1 | 1 | 0.56 |
| VGG-19 Accuracy (8QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.12 | 0.64 | 0.24 | 0.64 | 0.32 | 0.12 |
| 0 | 0.34 | 0.73 | 0.26 | 0.99 | 0.85 | 0.28 |
| 5 | 0.82 | 0.92 | 0.34 | 1 | 0.97 | 0.25 |
| 10 | 1 | 1 | 0.53 | 1 | 0.98 | 0.37 |
| 15 | 1 | 1 | 0.65 | 1 | 1 | 0.6 |
| 20 | 1 | 1 | 0.66 | 1 | 0.98 | 0.55 |
| 25 | 1 | 1 | 0.88 | 1 | 1 | 0.28 |
| Basic CNN Accuracy (16PSK) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0 | 0.08 | 0.64 | 0.36 | 0.04 | 0 |
| 0 | 0.05 | 0.14 | 0.68 | 0.35 | 0.28 | 0.02 |
| 5 | 0.04 | 0.2 | 0.68 | 0.46 | 0.34 | 0.02 |
| 10 | 0.15 | 0.23 | 0.76 | 0.88 | 0.57 | 0.02 |
| 15 | 0.5 | 0.35 | 0.91 | 0.98 | 0.78 | 0.04 |
| 20 | 0.8 | 0.32 | 0.88 | 0.97 | 0.86 | 0.07 |
| 25 | 0.88 | 0.56 | 0.92 | 1 | 0.64 | 0.16 |
| VGG-16 Accuracy (16PSK) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.04 | 0 | 0.16 | 0.88 | 0.2 | 0 |
| 0 | 0.01 | 0.01 | 0.38 | 0.67 | 0.29 | 0.02 |
| 5 | 0.24 | 0.23 | 0.51 | 0.68 | 0.44 | 0.07 |
| 10 | 0.76 | 0.68 | 0.54 | 0.92 | 0.62 | 0.25 |
| 15 | 0.9 | 0.9 | 0.67 | 0.96 | 0.8 | 0.34 |
| 20 | 0.98 | 0.87 | 0.59 | 0.98 | 0.88 | 0.34 |
| 25 | 1 | 0.96 | 0.64 | 1 | 0.8 | 0.4 |
| VGG-19 Accuracy (16PSK) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.24 | 0 | 0.04 | 0.6 | 0 | |
| 0 | 0.2 | 0.02 | 0.09 | 0.6 | 0.22 | |
| 5 | 0.34 | 0.28 | 0.12 | 0.64 | 0.45 | |
| 10 | 0.76 | 0.7 | 0.1 | 0.92 | 0.61 | |
| 15 | 0.97 | 0.94 | 0.08 | 0.95 | 0.73 | |
| 20 | 1 | 0.98 | 0.02 | 0.94 | 0.76 | |
| 25 | 1 | 1 | 0.04 | 1 | 0.84 | |
| Basic CNN Accuracy (16QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.28 | 0.04 | 0 | 0 | 0.36 | 0.2 |
| 0 | 0.16 | 0.11 | 0 | 0.39 | 0.55 | 0.23 |
| 5 | 0.13 | 0.12 | 0 | 0.86 | 0.77 | 0.32 |
| 10 | 0.27 | 0.3 | 0 | 1 | 0.89 | 0.36 |
| 15 | 0.58 | 0.47 | 0 | 0.99 | 0.92 | 0.37 |
| 20 | 0.84 | 0.62 | 0 | 1 | 0.94 | 0.42 |
| 25 | 0.96 | 0.72 | 0 | 1 | 0.88 | 0.52 |
| VGG-16 Accuracy (16QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.36 | 0.2 | 0 | 0 | 0.12 | 0.08 |
| 0 | 0.29 | 0.35 | 0 | 0.25 | 0.38 | 0.09 |
| 5 | 0.46 | 0.54 | 0.02 | 0.44 | 0.66 | 0.2 |
| 10 | 0.81 | 0.74 | 0.02 | 0.59 | 0.85 | 0.27 |
| 15 | 0.94 | 0.86 | 0.16 | 0.89 | 0.9 | 0.33 |
| 20 | 0.99 | 0.96 | 0.24 | 0.98 | 0.92 | 0.36 |
| 25 | 1 | 0.96 | 0.32 | 1 | 0.96 | 0.28 |
| VGG-19 Accuracy (16QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.8 | 0.2 | 0.04 | 0 | 0.24 | 0.08 |
| 0 | 0.82 | 0.28 | 0.03 | 0.59 | 0.52 | 0.17 |
| 5 | 0.9 | 0.49 | 0.1 | 0.95 | 0.78 | 0.28 |
| 10 | 0.99 | 0.7 | 0.24 | 1 | 0.93 | 0.39 |
| 15 | 0.94 | 0.84 | 0.43 | 1 | 0.94 | 0.45 |
| 20 | 1 | 0.96 | 0.5 | 1 | 0.95 | 0.44 |
| 25 | 1 | 0.96 | 0.52 | 1 | 0.96 | 0.36 |
| Basic CNN Accuracy (32QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.56 | 0.4 | 0.04 | 0 | 0.2 | 0.16 |
| 0 | 0.61 | 0.36 | 0.01 | 0.06 | 0.35 | 0.32 |
| 5 | 0.62 | 0.43 | 0.02 | 0.53 | 0.48 | 0.37 |
| 10 | 0.7 | 0.45 | 0.01 | 0.85 | 0.74 | 0.35 |
| 15 | 0.84 | 0.54 | 0 | 0.99 | 0.83 | 0.47 |
| 20 | 0.97 | 0.74 | 0 | 1 | 0.81 | 0.37 |
| 25 | 1 | 0.8 | 0 | 1 | 0.88 | 0.64 |
| VGG-16 Accuracy (32QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.04 | 0.04 | 0.12 | 0 | 0.76 | 0.52 |
| 0 | 0.14 | 0.18 | 0.18 | 0.19 | 0.63 | 0.53 |
| 5 | 0.33 | 0.28 | 0.21 | 0.68 | 0.8 | 0.52 |
| 10 | 0.52 | 0.51 | 0.16 | 0.74 | 0.86 | 0.56 |
| 15 | 0.87 | 0.82 | 0.27 | 0.9 | 0.89 | 0.64 |
| 20 | 0.98 | 0.95 | 0.34 | 0.97 | 0.92 | 0.52 |
| 25 | 1 | 0.92 | 0.56 | 1 | 0.96 | 0.56 |
| VGG-19 Accuracy (32QAM) | ||||||
|---|---|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||||
| SNR (dB) | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Perfect Channel Estimation | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.08 | 0 | 0.24 | 0 | 0.44 | 0.8 |
| 0 | 0.04 | 0.03 | 0.35 | 0.14 | 0.48 | 0.74 |
| 5 | 0.09 | 0.08 | 0.27 | 0.53 | 0.71 | 0.62 |
| 10 | 0.29 | 0.46 | 0.2 | 0.81 | 0.83 | 0.59 |
| 15 | 0.71 | 0.83 | 0.32 | 0.98 | 0.87 | 0.63 |
| 20 | 0.96 | 0.96 | 0.34 | 0.97 | 0.91 | 0.54 |
| 25 | 1 | 0.92 | 0.68 | 0.96 | 0.92 | 0.52 |
| Accuracy of the Three Proposed Models over UWA Channel | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basic CNN | VGG-16 | VGG-19 | |||||||
| SNR (dB) | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT | SC, No Equalization | SC, LMMSE | OFDM-DCT, LMMSE, HT |
| −5 | 0.15 | 0.29 | 0.35 | 0.16 | 0.31 | 0.37 | 0.19 | 0.31 | 0.37 |
| 0 | 0.22 | 0.33 | 0.62 | 0.27 | 0.35 | 0.55 | 0.26 | 0.33 | 0.62 |
| 5 | 0.24 | 0.41 | 0.83 | 0.29 | 0.42 | 0.8 | 0.32 | 0.42 | 0.79 |
| 10 | 0.27 | 0.59 | 0.94 | 0.26 | 0.67 | 0.86 | 0.34 | 0.66 | 0.89 |
| 15 | 0.33 | 0.79 | 0.98 | 0.35 | 0.91 | 0.93 | 0.47 | 0.85 | 0.94 |
| 20 | 0.34 | 0.94 | 0.99 | 0.38 | 0.99 | 0.99 | 0.42 | 0.97 | 0.98 |
| 25 | 0.36 | 0.98 | 1 | 0.41 | 1 | 1 | 0.4 | 1 | 0.99 |
| Basic CNN Accuracy | ||||
|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||
| SNR (dB) | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.29 | 0.18 | 0.33 | 0.25 |
| 0 | 0.33 | 0.19 | 0.56 | 0.32 |
| 5 | 0.4 | 0.19 | 0.67 | 0.34 |
| 10 | 0.55 | 0.2 | 0.78 | 0.38 |
| 15 | 0.69 | 0.22 | 0.84 | 0.48 |
| 20 | 0.78 | 0.23 | 0.88 | 0.5 |
| 25 | 0.82 | 0.22 | 0.83 | 0.61 |
| VGG-16 Accuracy | ||||
|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||
| SNR (dB) | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.27 | 0.22 | 0.38 | 0.26 |
| 0 | 0.33 | 0.28 | 0.55 | 0.35 |
| 5 | 0.44 | 0.32 | 0.71 | 0.4 |
| 10 | 0.66 | 0.36 | 0.79 | 0.47 |
| 15 | 0.82 | 0.49 | 0.84 | 0.56 |
| 20 | 0.91 | 0.52 | 0.89 | 0.56 |
| 25 | 0.94 | 0.6 | 0.9 | 0.54 |
| VGG-19 Accuracy | ||||
|---|---|---|---|---|
| SC, LMMSE | OFDM-DCT, LMMSE, HT | |||
| SNR (dB) | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 | Channel Estimation Error at Standard Deviation (σ) = 0.1 | Channel Estimation Error at Standard Deviation (σ) = 0.5 |
| −5 | 0.32 | 0.22 | 0.39 | 0.27 |
| 0 | 0.33 | 0.27 | 0.58 | 0.34 |
| 5 | 0.43 | 0.3 | 0.72 | 0.4 |
| 10 | 0.62 | 0.38 | 0.8 | 0.44 |
| 15 | 0.8 | 0.5 | 0.85 | 0.56 |
| 20 | 0.89 | 0.53 | 0.9 | 0.56 |
| 25 | 0.94 | 0.58 | 0.92 | 0.53 |
| Network | Prediction Time (ms/Example) | Number of Convolution Layers |
|---|---|---|
| Proposed CNN Model | 320 | 3 |
| Proposed VGG-16 Model | 1430 | 13 |
| Proposed VGG-19 Model | 1914 | 16 |
| DL-SMI [37] | 260 | 2 |
| ResNet [38] | 105 | 32 |
| TRNN [39] | 79 | 42 |
| Modulation Type | BPSK | 4QAM | 8PSK | 8QAM | 16PSK | 16QAM | 32QAM | Total |
|---|---|---|---|---|---|---|---|---|
| Basic CNN with Gabor filtering [40] | 1 | 0.24 | 0.09 | 0.09 | 0.05 | 0.25 | 0.32 | 0.29 |
| AlexNet with Gabor filtering [40] | 1 | 0.01 | 0.12 | 0.52 | 0 | 0.46 | 0.29 | 0.34 |
| ResNet 50 with Gabor filtering [40] | 1 | 0.36 | 0 | 0.36 | 0.16 | 0.12 | 0 | 0.29 |
| The proposed Basic CNN with OFDM-DCT, LMMSE equalization, and HT | 1 | 0.6 | 0.8 | 0.96 | 0.36 | 0.52 | 0.12 | 0.62 |
| VGG-16 with OFDM-DCT, LMMSE equalization, and HT | 1 | 0.68 | 0.2 | 0.96 | 0.48 | 0.36 | 0.2 | 0.55 |
| VGG-19 with OFDM-DCT, LMMSE equalization, and HT | 1 | 0.6 | 0.36 | 1 | 0.6 | 0.68 | 0.08 | 0.62 |
| Modulation Type | BPSK | 4QAM | 8PSK | 8QAM | 16PSK | 16QAM | 32QAM | Total |
|---|---|---|---|---|---|---|---|---|
| Basic CNN with Gabor filtering [40] | 1 | 0.66 | 0.4 | 0.4 | 0.32 | 0.53 | 0.49 | 0.54 |
| AlexNet with Gabor filtering [40] | 1 | 0.52 | 0.48 | 0.97 | 0.31 | 0.71 | 0.57 | 0.65 |
| ResNet 50 with Gabor filtering [40] | 1 | 0.8 | 0.28 | 1 | 0.56 | 0.32 | 0.4 | 0.62 |
| The proposed Basic CNN with OFDM-DCT, LMMSE equalization, and HT | 1 | 0.96 | 0.88 | 1 | 0.88 | 1 | 0.88 | 0.94 |
| VGG-16 with OFDM-DCT, LMMSE equalization, and HT | 1 | 0.92 | 0.8 | 1 | 1 | 0.6 | 0.72 | 0.86 |
| VGG-19 with OFDM-DCT, LMMSE equalization, and HT | 1 | 0.96 | 0.52 | 1 | 0.92 | 1 | 0.84 | 0.89 |
| Modulation Type | BPSK | 4QAM | 8PSK | 8QAM | 16PSK | 16QAM | 32QAM | Total |
|---|---|---|---|---|---|---|---|---|
| Basic CNN with Gabor filtering [40] | 1 | 1 | 0.87 | 0.87 | 0.9 | 0.96 | 0.9 | 0.93 |
| AlexNet with Gabor filtering [40] | 1 | 1 | 0.79 | 1 | 0.92 | 1 | 0.99 | 0.96 |
| ResNet 50 with Gabor filtering [40] | 1 | 1 | 0.6 | 1 | 0.88 | 1 | 0.92 | 0.91 |
| The proposed Basic CNN with OFDM-DCT, LMMSE equalization, and HT | 1 | 1 | 1 | 1 | 0.96 | 1 | 1 | 0.99 |
| VGG-16 with OFDM-DCT, LMMSE equalization, and HT | 1 | 1 | 0.96 | 1 | 1 | 1 | 0.96 | 0.99 |
| VGG-19 with OFDM-DCT, LMMSE equalization, and HT | 1 | 1 | 0.92 | 1 | 1 | 1 | 0.96 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Moneim, M.A.; Gerwash, M.K.M.; El-Rabaie, E.-S.M.; Abd El-Samie, F.E.; Ramadan, K.F.; Abdel-Salam, N. Improved Modulation Classification Based on Hough Transforms of Constellation Diagrams Using CNN for the UWA-OFDM Communication System. Eng 2025, 6, 127. https://doi.org/10.3390/eng6060127
Abdel-Moneim MA, Gerwash MKM, El-Rabaie E-SM, Abd El-Samie FE, Ramadan KF, Abdel-Salam N. Improved Modulation Classification Based on Hough Transforms of Constellation Diagrams Using CNN for the UWA-OFDM Communication System. Eng. 2025; 6(6):127. https://doi.org/10.3390/eng6060127
Chicago/Turabian StyleAbdel-Moneim, Mohamed A., Mohamed K. M. Gerwash, El-Sayed M. El-Rabaie, Fathi E. Abd El-Samie, Khalil F. Ramadan, and Nariman Abdel-Salam. 2025. "Improved Modulation Classification Based on Hough Transforms of Constellation Diagrams Using CNN for the UWA-OFDM Communication System" Eng 6, no. 6: 127. https://doi.org/10.3390/eng6060127
APA StyleAbdel-Moneim, M. A., Gerwash, M. K. M., El-Rabaie, E.-S. M., Abd El-Samie, F. E., Ramadan, K. F., & Abdel-Salam, N. (2025). Improved Modulation Classification Based on Hough Transforms of Constellation Diagrams Using CNN for the UWA-OFDM Communication System. Eng, 6(6), 127. https://doi.org/10.3390/eng6060127








