A Transistor Voltage Divider for Low-Power Autonomous Electronic Systems

Abstract

In this study, the operation features of a transformerless voltage divider, with transistor–diode commutation of switchable capacitors, designed to operate as a part of low-power autonomous electronic systems with reduced output voltage are studied both theoretically and experimentally. The analysis is carried out for a divider operation with a constantly or periodically connected voltage source V₀ with unlimited power. It is found that the divider’s efficiency during operation with a constantly connected primary voltage source V₀ with unlimited power is very low. However, the efficiency can reach 60% during the divider’s operation using a periodically connected voltage source V₀ with unlimited power. It has been shown that the efficiency can only reach 40% in the case of using a voltage source with limited power connected to the divider periodically. It has been established that for circuits with transistor–diode commutation of the capacitors, the stabilization effect is much stronger than for circuits with diode commutation of the capacitors. Therefore, an excess of the maximum load voltage relative to the expected value V₀/N is significantly lower for transistor–diode commutation in comparison with diode commutation (N is the number of divider stages). Based on the ideas developed regarding the divider operation, analytical expressions are obtained, enabling us to calculate the parameters of the studied divider circuits in a wide range. The good agreement between the analytical estimations and experimental data suggests that these calculations adequately describe the operation of the dividers, and that the derived analytical expressions can be successfully used during the preliminary design stage. In general, the analysis carried out herein and the developed approach make it possible to significantly narrow the range of search for the necessary system parameters when designing voltage dividers.

1. Introduction

The development of digital technologies has led to rapid growth in information devices for various purposes operating without a connection to stationary power systems. Nowadays, the use of wireless sensor networks (WSNs) is one of the main directions of technology development [1,2,3]. However, the organization of WSNs is associated with a number of problems, where one of the most serious is the autonomous power supply of the network nodes. The most appropriate way to construct these networks is to use independent small-sized devices, which are able to generate electrical energy directly at the location of WSN nodes [4,5,6,7]. One of the most promising types of such microgenerators (or energy harvesters) is the electrostatic microelectromechanical generator (harvester), which converts the energy of mechanical motion or vibrations into electrical energy [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].

The design of electrostatic microelectromechanical generators (EMGs) typically focuses on maximizing their generated electrical power. Since the energy that can be stored by a capacitor and subsequently extracted from it is proportional to the square of the voltage across the capacitor, the operating voltage in EMGs can be increased up to several hundred volts [18,23,24].

However, most modern electronic devices (EMG energy consumers) use power supply voltages of less than 10 V. As a result, connecting them directly to the “high-voltage” EMGs requires an additional matching device that lowers the EMG’s output voltage [9,17,18,19,25].

In the field of power electronics, a large number of AC/DC and DC/DC converters, voltage dividers, and multipliers have been proposed. The characteristic features of their operation are as follows: (1) operation using a primary energy source with infinite power (bus of infinite power), in which the characteristics do not change significantly when the converter is connected, and (2) the use of microprocessor control circuits.

However, the output power produced by typical EMGs is usually only a few tens of microwatts. As a result, when a voltage divider is connected to them, the characteristics of the EMG (as a primary voltage source) change. Therefore, it is not possible to rely on the stability of the primary voltage source characteristics when connecting a divider to an EMG. It should also be noted that the output resistance of energy sources with infinite power, in most cases, has an inductive nature, while the output resistance of EMGs has a capacitive nature.

In addition, in power electronics, during operation at high capacities (from units to hundreds of kilowatts), losses in converter control systems (units of watts) are not very significant. Therefore, in order to achieve good converter performance, complex control circuits are used in power electronics, which are not acceptable during the operation of EMGs. As a result, it is not possible to use circuits designed for power electronics in microsystem engineering without careful analysis and investigation of their operating features. Therefore, the search for new schemes and approaches to solve this problem continues [9,10,17,18,19,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40].

For this purpose, it is proposed to use Zener diodes [9,28,29], the periodic connection of the microgenerator (MG) to the load with an adjustable duty cycle (PWM conversion) [10,19], and circuits based on switchable capacitors [9,30,39,40]. An interesting scheme was proposed and investigated in [31], where both voltage reduction (Dickson charge-pump) and periodic connection to the load were used, enabling users to change the duration of the MG connection to the load and, consequently, the average voltage across the load during the conversion period.

Unfortunately, these studies have focused on estimates of the output power, but the efficiency of these circuits has not been studied. So, it is not possible to compare the efficiency and losses in the proposed converters without additional investigations.

However, the analysis of circuits with Zener diodes [9,28,29] and switchable capacitors [9,30,39,40] for voltage reduction shows that, for these circuits, when the load is connected, part of the energy generated by the EMG is not transferred to the load but is instead lost uselessly. Thus, the voltage reduction is mainly achieved by means of the losses of the energy generated by the EMG, and these losses are primarily caused by converter losses.

As for the EMGs, where special control circuits were used to adjust the connection time of the microgenerator to the load [10,19], the analysis performed in [19] showed that the power consumption of the control circuit in the proposed configuration was about 97.2 µW. This value is too high for such a control circuit to be used in microgenerators. In order to reduce energy consumption, the authors suggested reducing the duration of the load connection phase. They showed that when the duration of the load connection phase was reduced to 0.005% of the total cycle duration (the control circuit remained mostly in sleep mode), the power consumption of the control circuit was reduced to 1.03 µW, which can be acceptable for use in EMGs. However, this significantly reduces the power produced by the system.

Thus, for the proposed schemes, in any case, part of the generated energy is lost together with voltage reduction. In our opinion, circuits based on switchable capacitors seem to be the most promising for converting high AC voltage generated by the EMGs into low DC voltage [32,33].

The conversion principle of the high AC voltage of a primary power source into a low DC voltage in such circuits is based on voltage division using switchable capacitors. In the conversion process, N capacitors connected in series are initially charged from the primary voltage source, and then these capacitors are reconfigured into a parallel connection and discharged to the load [41]. It is assumed in this case that the load voltage will be approximately N times lower than the amplitude value of the primary voltage source.

In [32,33], we have investigated the operation of the diode–capacitor voltage divider with a low-power primary energy source. It was established that, during analysis of the operation of the diode–capacitor voltage divider based on switchable capacitors, it is necessary to consider the reverse capacitances of the discharging diodes, which can significantly affect the divider’s operation. It was found that the division ratio of the diode–capacitor voltage divider did not remain constant, but significantly depended on the load resistance, and the capacitances of the discharging diodes. Therefore, the practical performance of the diode–capacitor voltage divider circuit differs from the “ideal” theoretical analysis and the assumptions commonly made in power electronics. As a result, if the load resistance changes, the parameters of the diode–capacitor voltage divider need to be recalculated. Furthermore, the considered circuit had quite significant energy losses.

In power electronics for reducing losses, instead of a circuit with diode–capacitor commutation of switchable capacitors, a transformerless voltage divider circuit with transistor–diode commutation of switchable capacitors is proposed [41,42,43]. Taking the main features of its operation into account, it still remains unclear how this circuit will operate with a low-power primary energy source.

This paper is dedicated to the study of operation features of the voltage divider circuits with transistor–diode commutation of switchable capacitors designed to work as a part of low-power EMGs, and other low-power autonomous electronic systems, with reduced output voltage.

2. Analysis of the Voltage Divider Operation with Transistor–Diode Commutation of Capacitors

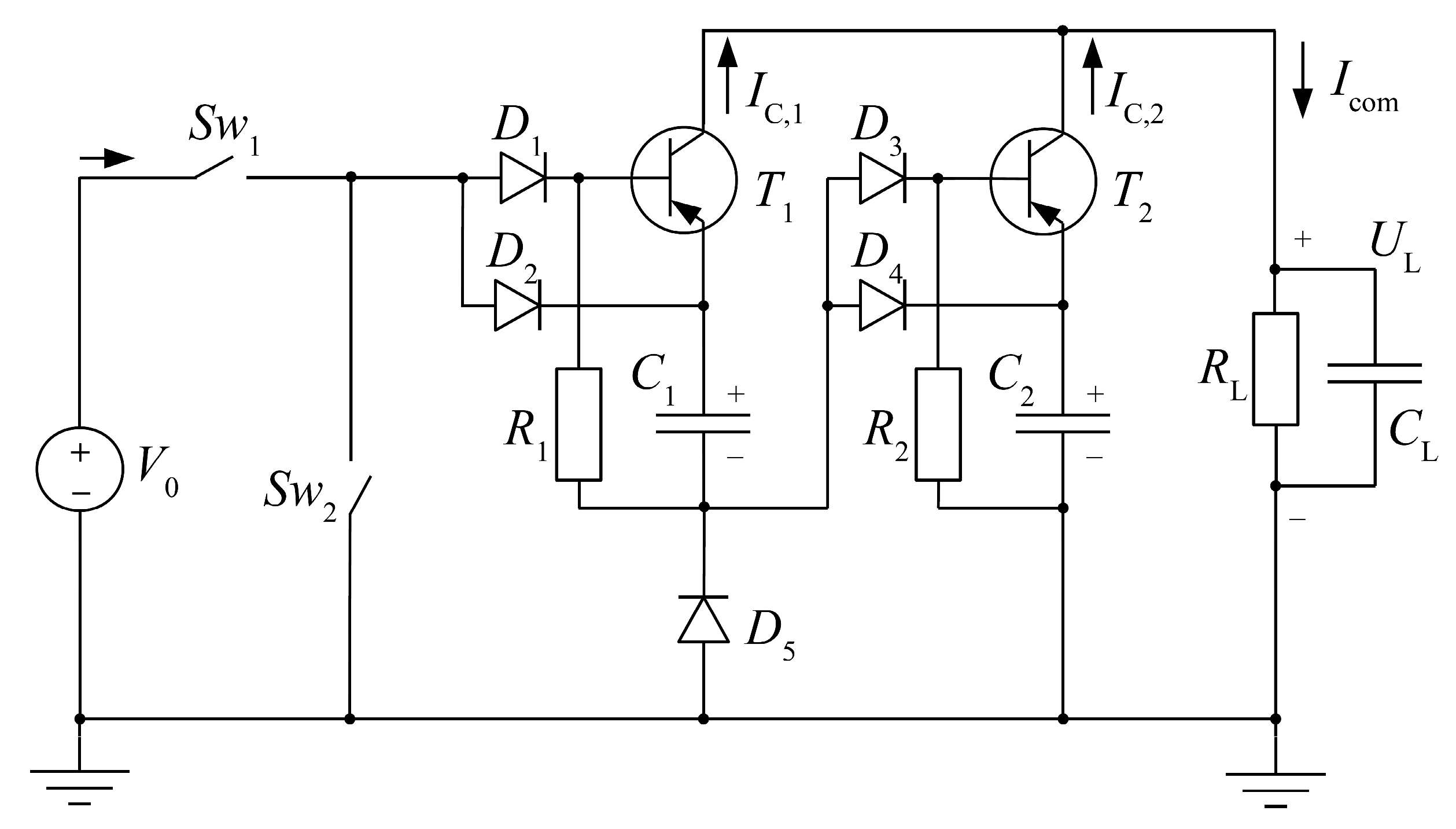
An original structure of the three-stage transformerless voltage divider with transistor–diode commutation of switchable capacitors, and one charging switch, which simplifies the control system, was proposed in [41] (Figure 1a). Simplification is achieved because the control of the charging VT_2,1 and discharging VT_1,i transistor switches is carried out by the same generator of rectangular pulses U_2,1.

In the operation of this voltage divider, the authors [41] distinguish two cycles. In the first cycle (transistor VT_2,1 is switched on), the in-series-connected capacitors C_i are being charged from the primary voltage source V₀ (Figure 1b). At the same time, since the voltage across the resistors R_i exceeds the voltage across the capacitors C_i, the discharging transistors VT_1,i are turned off. In the second cycle (transistor VT_2,1 is switched off), the transistor switches VT_1,i are turned on by the discharging current of capacitors C_i through their base–emitter junctions and limiting resistors R_i. At the same time, the capacitors C_i connected in parallel are discharged through the R_LC_L load (Figure 1c). Then, the two-stroke operation cycle of the divider is repeated.

Such a voltage divider can be used not only in electrostatic microgenerators, but also in other systems where it is necessary to reduce the voltage.

In order to analyze the advantages and disadvantages of this circuit, we consider the operation of this voltage divider, assuming that all the circuit elements of the same type have identical values. Considering that the operation of the diode–capacitor voltage divider is significantly influenced by the reverse capacitances of the discharging diodes [32,33] (in this case, the diodes VD_3,1 and VD_3,2), we will take into account that the charge of their barrier capacitances changes when the discharging diodes are reverse-biased. The base–emitter junction barrier capacitances of the transistors will also be taken into account. To simplify the calculations, we will assume that the barrier capacitances do not depend on the applied voltage.

Next, for clarity, we will analyze the two-stage divider circuit and consider three cases. In the first case, we will assume that the divider is connected to an ideal voltage source V₀ constantly (i.e., the primary voltage source has infinite power, circuit 1). In the second case, we will assume that the divider is also connected to an ideal voltage source V₀, but periodically (circuit 2). In the third case, in comparison with the second one, we will take into account that the primary voltage source has limited power, which is inherent for EMGs (circuit 3).

3. Analysis of Circuit 1 Operation

Figure 2 shows the electrical circuit of the two-stage transformerless voltage divider with transistor–diode commutation and the primary voltage source with unlimited power. In this case, the switch Sw₁ must be permanently switched on, whereas Sw₂ must be switched off.

When the switch Sw₁ is initially turned on, the voltage source V₀ is connected to the divider, initiating the charging process of the capacitances C₁ and C₂, along with the base–emitter junction capacitances of the transistors (C_BE,1 and C_BE,2), and the reverse capacitance of the discharging diode D₅ (C_D5). Since the capacitances C₁ and C₂ have much higher values than the capacitances C_BE,1, C_BE,2, and C_D5, the intrinsic capacitances of the base–emitter junctions of the transistors and the discharging diode are charged first. At the same time, the voltage across C₁ and C₂ remains almost zero and the capacitances C_BE,1, C_BE,2, and C_D5 are charged to the voltages approximately equal to 0.5V₀. Transistors operate in the cut-off mode and their collector currents are small. The load voltage is close to zero and increases very slowly.

During the charging process of C₁ and C₂, their voltages increase; as a result, the voltage between the base and the common wire of the first transistor becomes greater than V₀, and for the second one, greater than 0.5V₀. In this case, diodes D₁ and D₃ are reverse-biased, and the capacitances C_BE,1 and C_BE,2 begin to discharge through resistors R₁ and R₂; the locking voltages across the base–emitter (B-E) junctions of the transistors decrease, but the collector currents increase (sections 1 and 2 in Figure 3). 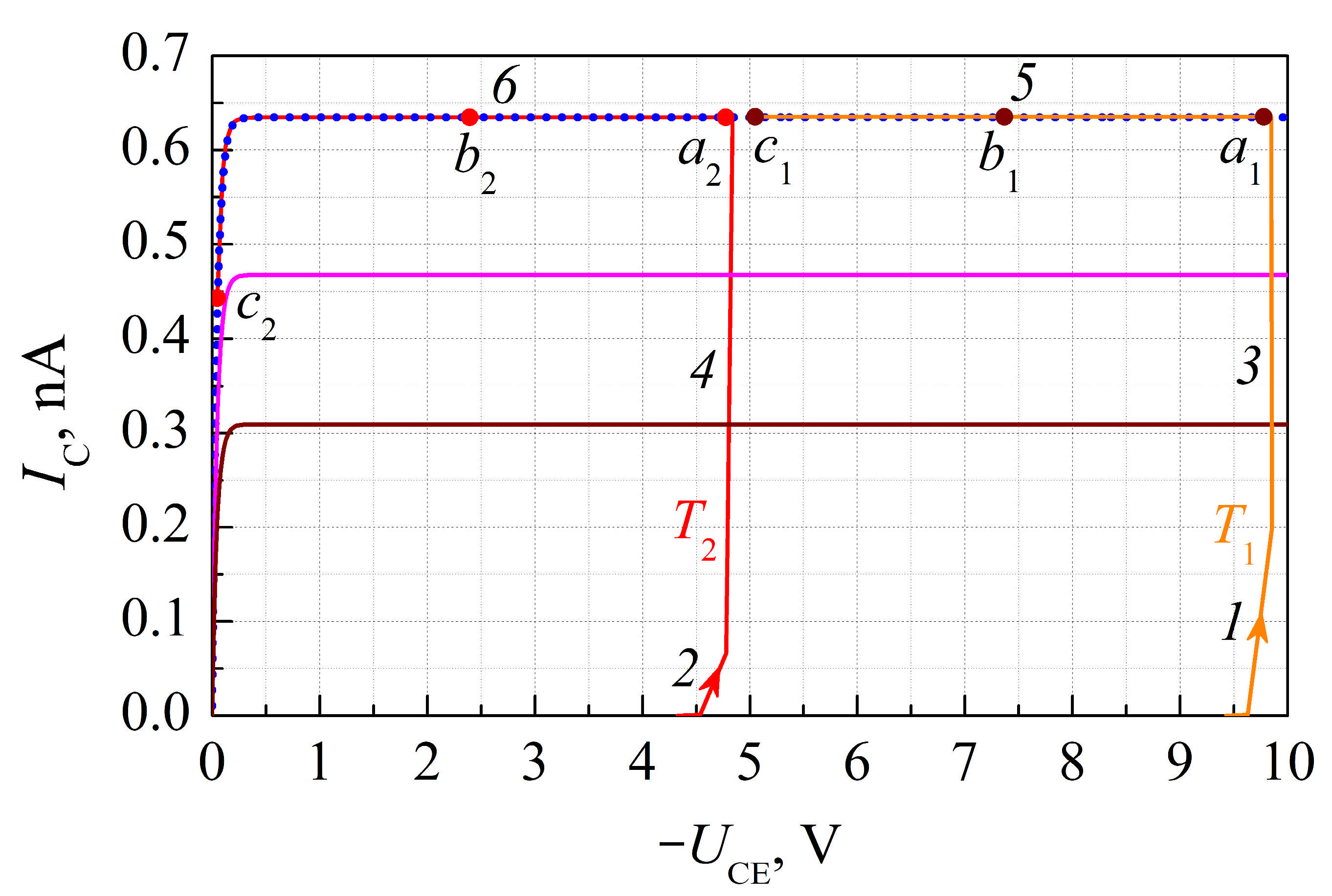Figure 3 shows the dependences of the transistor collector currents versus the collector–emitter (C-E) voltages calculated at C₁ = C₂ = 1 nF; C_L = 10 nF; C_BE,1 = C_BE,2 = 2 pF; C_D5 = 40 pF; R₁ = R₂ = R_L = 10 MΩ; and V₀ = 10 V. At the initial stage (sections 1 and 2 in Figure 3), collector currents grow monotonously. However, on the linear scale, this growth is not immediately visible (sections 1 and 2 have horizontal sections at the beginning). Since the voltage across the load changes slowly at this stage, then, since the main capacitors C₁ and C₂ are charged, the negative C-E voltage of the transistors (U_CE) increases in absolute value.

As the capacitances of the base–emitter junctions C_BE,1 and C_BE,2 discharge, the junctions will begin to open more and more, and the transistors will switch to active mode. In this case, the collector currents of the transistors will increase sharply (sections 3 and 4 in Figure 3), but the collector–emitter voltage will not change significantly, because the voltage across the load capacitor C_L cannot change quickly. As the capacitances C_BE,1 and C_BE,2 are discharged, when the transistor base–emitter voltages change sign, the voltage between the base and the common wire of the first transistor becomes less than V₀, and for the second one is less than 0.5V₀, and the diodes D₁ and D₃ will start to conduct current again. These currents flowing through the resistances R₁ and R₂ will increase the voltage between the base and the common wire, and will prevent the discharge of C_BE,1 and C_BE,2 (transistors will be partially turned off). As a result, equilibrium will be established, and the voltage between the base and the common wire will stop changing. In the steady-state mode, the voltages across the main capacitors C₁ and C₂ and the discharging diode D₅ will remain the same. The base, emitter, and collector currents will also remain the same (sections 5 and 6 in Figure 3). In this case, the total current to the load I_com = I_C,1 + I_C,2 will pass through the circuits V₀ → D₂ → I_E,1 → I_C,1 and V₀ → D₁ → R₁ → D₄ → I_E,2 → I_C,2, and will not change significantly due to the weak dependence of the collector current versus the collector–emitter voltage.

As a result, the load voltage will increase according to the following equation

$$U_{\mathrm{L}}(t)=I_{\mathrm{com}}{R}_{\mathrm{L}}\left(1-\exp \left(-{\displaystyle \frac{t}{C_{\mathrm{L}}{R}_{\mathrm{L}}}}\right)\right)+U_{\mathrm{L}}(0)\exp \left(-{\displaystyle \frac{t}{C_{\mathrm{L}}{R}_{\mathrm{L}}}}\right),$$

whereas the collector–emitter voltages of the transistors will decrease.

As the voltage across the load increases, the current $I_{R_{\mathrm{L}}}$ through R_L will also increase. When $I_{R_{\mathrm{L}}}$ becomes equal to I_com, the load voltage reaches the value of U_L,stab = I_com·R_L and stops changing. It should be noted that if the resistances in the transistor base circuit do not change, the base, emitter, and collector currents also keep their values. As a result, the operating points of the transistors at the dependences I_C,i(U_CE) will remain on the same line when R_L changes, as is shown in Figure 3, but the values of R₁ and R₂ have to be constant in this case. The operating points a_i, b_i, and c_i, shown in Figure 3, are calculated at R_L = 100 MΩ, 2 GΩ, and 4.5 GΩ, correspondingly.

When the load voltage increases, the transistor collector–emitter and collector-base voltages will decrease. As a result, saturation mode can occur instead of the active mode, and the collector currents will begin to decrease sharply. Figure 3 shows that this effect leads to a change in the point c₂ position and to a decrease in the second transistor collector current. In turn, this process also leads to load voltage stabilization. As soon as the load voltage begins to approach the voltage across the capacitor C₂, the collector current of the second transistor will begin to decrease sharply (the collector-base junction of T₂ opens); the total current of the collectors I_com will also begin to decrease, which slows down and eventually stops the increase in the load voltage.

Figure 4 shows the dependence of the load voltage versus the load resistance measured and calculated at several values of resistances R₁ and R₂ in the transistor base circuits, and V₀ = 10 V.

In order to carry out experimental studies, an experimental setup was designed corresponding to the circuit shown in Figure 2. The capacitance of capacitors C₁ and C₂ was 1 nF, and for the load capacitor, C_L = 10 nF. Reed relays EDR201A0500 (Excel Cell Electronic, Taichung, Taiwan) were used as the switches. High-voltage diodes 1N4004 (Vishay Intertechnology, Malvern, PA, USA) with a maximum permissible reverse voltage of 400 V and a reverse capacitance of 40 pF at a reverse voltage of 0 V were used as the diodes. The type of bipolar transistors used was BC557A (Fairchild Semiconductor, Sunnyvale, CA, USA). Figure 5 shows the photograph of the experimental setup (a) and the block diagram of the setup (b); the numbers indicate the components of the measuring system.

During the experimental study, the dependences of the voltage across the capacitor C_L (Figure 2) versus the number of conversion cycles at different load resistances were measured. A voltage repeater based on an AD549KHZ (Analog Devices, Wilmington, MA, USA) operational amplifier with an ultra-low input current (0.1 pA) was used to measure the voltage across the capacitor. The primary power supply voltage was varied from 10 to 12.2 V.

The calculation has been carried out under the assumption that when the load resistance increases, the collector currents remain constant, the same as they were at low load resistances. It can be seen from Figure 4 that the calculation results are in good agreement with the experimental results in the range of low load resistances when the transistors remain in active mode. At the same time, an increase in the resistances R₁ and R₂ in the base circuits shifts the dependences to the range of higher load resistances, because this reduces the currents of the bases, emitters, and collectors.

It follows from the analysis that this circuit (with an unlimited power source) operates as a two-stage voltage divider, where the input voltage division coefficient at high load resistances stops depending on the load resistance and tends to 1/2. At the same time, the load voltage does not change significantly when the load resistance changes and is close to 0.5V₀, while the current through the load resistance is close to 0.5V₀/R_L, i.e., this current decreases when the load resistance increases.

It should be noted, however, that when the divider operates using an ideal constantly connected voltage source V₀ with unlimited power, fairly high currents flow through resistors R₁ and R₂, discharging the source V₀ all the time. Therefore, the base currents of the transistors remain low and the transistors remain at the very beginning of the active mode, and, as a result, their collector currents as well as the current through the load R_L are also small. Consequently, the efficiency of such a circuit turns out to be low.

4. Analysis of Circuit 2 Operation

In this case, the electric circuit of the system will also correspond to the circuit shown in Figure 2, where the switches Sw₁ and Sw₂ have to be switched in opposite phases (by turn).

For odd cycles 1, 3, 5 …, when the source V₀ is connected to the divider (Sw₁ is switched on, Sw₂ is switched off), the current and voltage changes in this circuit occur in the same way as shown in the previous section. During these cycles, the charge of the load circuit RC does not practically occur, and the load capacitor C_L, starting from cycle No. 3 and for further odd cycles, is only discharged through R_L. In this case, the voltage across the load during the k-th odd cycle will change as

$$U_{\mathrm{L},k}(t)=U_{\mathrm{L},k}(t_{\mathrm{st},k})\exp \left(-{\displaystyle \frac{t}{C_{\mathrm{L}}{R}_{\mathrm{L}}}}\right),$$

where $U_{\mathrm{L},k}(t_{\mathrm{st},k})$ is the load voltage at the beginning of the k-th odd cycle.

When the switch Sw₁ is turned off, and the switch Sw₂ is turned on (even cycles 2, 4, 6 …), diodes D₁, D₂, D₃, and D₄ are reverse-biased, and transistors T₁ and T₂ are switched on by the discharging current of capacitors C₁ and C₂ through their base–emitter junctions and limiting resistors R₁ and R₂. At the same time, the currents of the emitters and collectors of the transistors increase sharply.

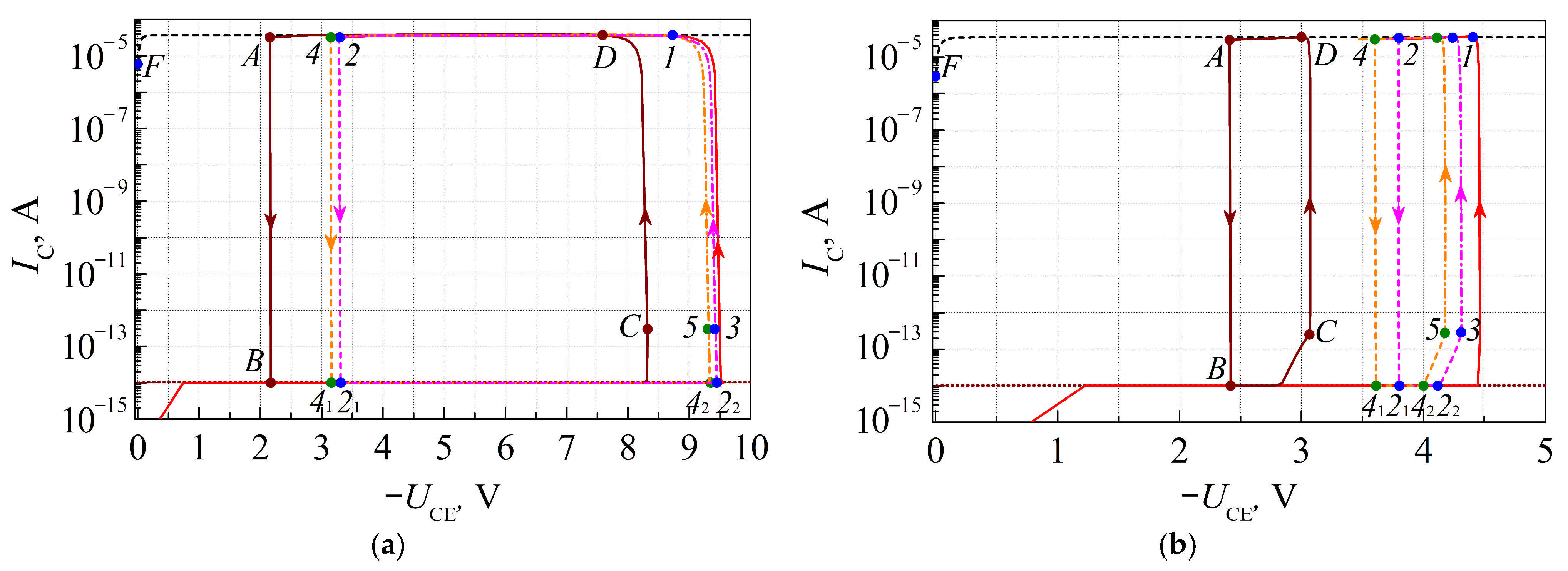
Let us trace the movement of the operating point with coordinates (I_C, U_CE), characterizing the state of the transistors, at the family of output characteristics of I_C(U_CE), shown in Figure 6. It was assumed in calculations that C₁ = C₂ = 1 nF; R₁ = R₂ = 10 MΩ; C_L = 10 nF; R_L = 50 kΩ; C_BE,1 = C_BE,2 = 2 pF; C_D5 = 40 pF; V₀ = 10 V; and τ = 2.5·10⁻⁵ s. Here, τ is the duration of the charge and discharge cycles.

The initial state of the transistors is characterized by the operating point with coordinates (0, 0). When Sw₁ is switched on (and Sw₂ is switched off), transistors T₁ and T₂ are switched to the cut-off mode, and the current flows through them; the magnitude of the current is determined by the base potentials of the turned-off transistors.

Upon applying the turn-on signal at the transistor terminals (Sw₁ is off, Sw₂ is on), the operating points will move to positions 1 at the curves with U_BE = const (Figure 6a,b), since at the first moment, the load capacitor C_L tends to maintain the collector potential constant. Then the capacitor C_L will begin to charge with the time constant τ₁ ≈ C_L·R_L.

As the capacitor C_L is charged, the operating points of the transistors T₁ and T₂ will move along the curves with U_BE = const, and if the duration of the even cycle is short enough relative to the time constant τ₁ (in our case, τ/τ₁ = 0.05), then by the end of the second cycle (the end of the first complete cycle), the operating points will move to positions 2. During this cycle, the expression for estimating the load voltage can be represented as

$$U_{\mathrm{L},k}(t)=I_{\mathrm{com}}{R}_{\mathrm{L}}+\left(U_{\mathrm{L},k}(t_{\mathrm{st},k})-I_{\mathrm{com}}{R}_{\mathrm{L}}\right)\exp \left(-{\displaystyle \frac{t}{C_{\mathrm{L}}{R}_{\mathrm{L}}}}\right),$$

where $U_{\mathrm{L},k}(t_{\mathrm{st},k})$ is the voltage across the load resistance at the beginning of the k-th even cycle and I_com is the sum of the collector currents of the transistors.

By the end of the second cycle (at the beginning of the third one), the transistors will switch to the cut-off mode, and the operating points will move to position 2₁. From this moment, the process of the load capacitor discharging begins. In this case, the operating points move towards points 2₂ and 3. If the duration of the odd cycle (the discharge cycle of the load capacitor) is such that the load capacitor does not have time to fully discharge, then the operating points at the end of this odd cycle will correspond to voltages U_CE lower than those at the end of the previous odd cycle.

When the operating points move between 2₂ and 3, a partial discharge of the base–emitter junction capacitances C_BE,1 and C_BE,2 occurs, the junctions will begin to open, and the transistors will switch to the active mode. Position 3 corresponds to the end of the third cycle and to the beginning of the fourth one. The fourth cycle and the second complete cycle will end at point 4. The fifth cycle in Figure 6a,b will correspond to the movement of the operating points along the trajectory 4 → 4₁ → 4₂ → 5. In this case, the time dependence of the load voltage can be represented as

$$U_{\mathrm{L}}(t)=U_{\mathrm{L},\max }\exp \left(-{\displaystyle \frac{t}{C_{\mathrm{L}}{R}_{\mathrm{L}}}}\right)+F_1(t)+F_2(t),$$

(1)

where F₁(t) and F₂(t) are defined by Equations (A1)–(A4) (see Appendix A).

During the derivation of Equation (1), it was taken into account that at the beginning of an even cycle, the transistors T₁ and T₂, which were reverse-biased before the previous odd cycle, do not turn on immediately. It takes some time to discharge the capacitances C_BE,1 and C_BE,2. Moreover, T₂ begins to open only after T₁ has almost completely opened. These delays are taken into account by the parameters α₁ and α₂, and by using the Heaviside step functions Φ(t − α₁) and Φ(t − α₂) (see Appendix A).

After several cycles of operation, a steady-state mode occurs for which the operating points of the transistors will move along the loop A → B → C → D. In this case, the maximum and minimum output voltages stabilize, and in the steady-state mode, can be evaluated using the following equations:

$$U_{\mathrm{L},\max }={\displaystyle \frac{\beta R_{\mathrm{L}}}{1-\exp \left(-\frac{2\mathsf{\tau }}{C_{\mathrm{L}}{R}_{\mathrm{L}}}\right)}}\left(F_3+F_4\right),\hspace{1em}{U}_{\mathrm{L},\min }=U_{\mathrm{L},\max }\exp \left(-{\displaystyle \frac{\mathsf{\tau }+{\alpha }_1}{C_{\mathrm{L}}{R}_{\mathrm{L}}}}\right)$$

where β is the transistor amplification factor and F₃ and F₄ are determined using Equations (A5) and (A6) (see Appendix A).

The equations obtained show that after reaching the steady-state mode with the periodic connection of the voltage source V₀, the load voltage during the cycle, unlike in the previous circuit (circuit 1), does not remain constant, but pulsates. In this case, the range of the load voltage fluctuations is equal to

$$\Delta U_{\mathrm{L}}=U_{\mathrm{L},\max }\left(1-\exp \left(-{\displaystyle \frac{\mathsf{\tau }+{\alpha }_1}{C_{\mathrm{L}}{R}_{\mathrm{L}}}}\right)\right).$$

(2)

Figure 7 shows the time dependence of the load voltage calculated at the same parameters as the dependences shown in Figure 6. One can see that the voltage ripples at the load resistance R_L = 50 kΩ remain in the steady-state mode too. According to Equation (2), as the load time constant C_LR_L increases, the ripple range decreases.

It should be noted that the considered mode of operation of this circuit is very sensitive to the parameters of the elements used. The variation in the limiting resistances, reverse capacitances of the diodes, and the parameters of the transistors within relatively narrow ranges can significantly change the mode of the divider operation from the near-complete transistor cut-off to the transistor saturation mode. In addition, the studied mode is realized only with a sufficiently short cycle duration. For instance, for the above-presented calculations, the complete cycle duration was 50 μs, i.e., the switching frequency was 20 kHz. At the same time, since for this circuit, the source V₀ is periodically disconnected from the divider, and during these cycles it is not discharged through the limiting resistors R₁ and R₂, the efficiency of this circuit turns out to be significantly higher than that of the previous circuit, and can reach up to 20%.

The high switching frequency significantly narrows the scope of application of such a divider in this mode, especially if it is designed for operation as part of low-power EMGs with low output voltage. The range of mechanical vibrations available in the environment is usually limited to frequencies of a few hundred Hz.

When the switching frequency decreases (the cycle duration increases), the load capacitor can have enough time to charge significantly. In this case, after several switching cycles, the operating point during the even cycles (Figure 6, points F) can significantly shift towards the ordinate axis, and the transistors will switch from active mode to saturation mode. In this case, the collector currents (charging the load) will first begin to decrease, and then they can even change direction, which, in general, will lead to a decrease in the load current and, eventually, to stabilization of the output voltage. The saturation mode is achieved faster by increasing the input voltage, reducing the limiting resistances, and increasing the load resistance. Before the collector currents begin to decrease (at the initial cycles), the operation of the circuit will proceed as described earlier.

It should be noted that even with the periodic connection of the source V₀ for circuit 2 (Figure 2), the switch Sw₂ can be excluded. Let us call such a circuit circuit 2m. In the presence of Sw₂ (circuit 2), during the even cycles (when this switch is on), the diodes D₁ and D₂ are reverse-biased. However, during the even cycles and without Sw₂ (circuit 2m), when the source V₀ is disconnected from the divider, the diodes D₁ and D₂ are connected towards each other, and one of them will always be reverse-biased, so the current through these diodes will be small in this case too. However, using the switch Sw₂ in the previous analysis of circuit 2 simplified the analytical calculations, but for the implementation of circuit 2, it is required to have the control circuit of the switch Sw₂, resulting in additional energy consumption in contrast to circuit 2m. Furthermore, we will analyze circuit 2m (Figure 2), assuming that Sw₂ is turned off all the time.

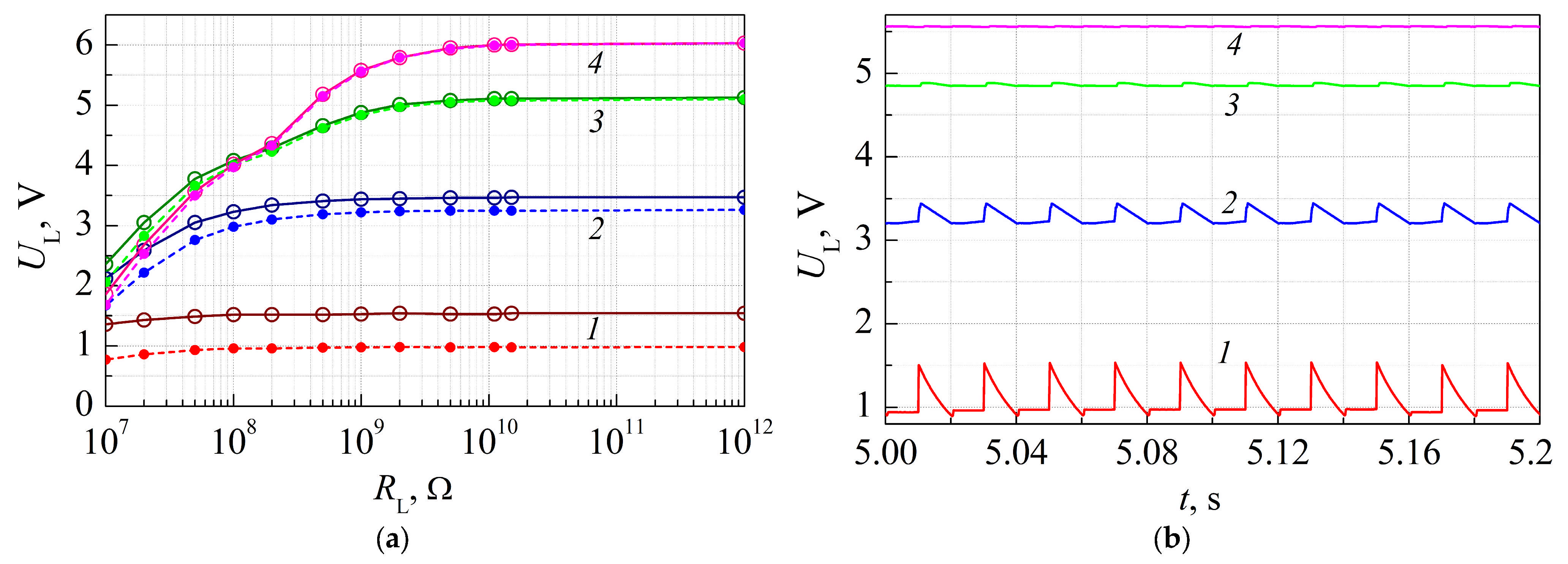
Figure 8a shows the dependences of the maximum (solid lines) and minimum (dashed lines) load voltages for circuit 2m versus the load resistance measured at several limiting resistance values, and V₀ = 10 V, τ = 10 ms.

It can be seen from Figure 8a that as the load resistance increases, the voltage across the load stops increasing, reaching saturation. When the resistance of the limiting resistors increases, the saturation voltage also increases. Thus, the input voltage division coefficient K = U_L/V₀ increases with increasing limiting resistances, and only at R₁ = R₂ = 80 MΩ and R_L > 1 GΩ the division coefficient K ≈ 0.5, which corresponds to the expected value for the two-stage voltage divider, when the divider is periodically connected to an electrical energy source with unlimited power.

Thus, during the design of such a divider for operation as part of EMGs with a low output voltage, it is necessary to carry out appropriate preliminary estimations, and not just assume that the number of the divider stages N guarantees the division coefficient K = 1/N.

Figure 8b shows the time dependences of the load voltage measured at R_L = 1 GΩ for different values of R₁ and R₂. It is obvious from Figure 8 that as the values of the limiting resistors R₁ and R₂, and the load resistance R_L, increase, the output voltage ripple (the difference between the maximum and minimum values of the load voltage) decreases and becomes almost unnoticeable when R_L > 800 MΩ and R₁ = R₂ ≥ 80 MΩ.

Figure 9 shows the dependences of the maximum (a) and minimum (b) voltages across the divider load for circuit 2m versus the load resistance measured and calculated when the divider is periodically connected to the electric power source with unlimited power; the data are presented for several values of the limiting resistances. It is evident that the experiment and the calculations, using the made assumptions, agree well. Thus, it can be assumed that such calculations adequately describe the operation of this divider, and they can be used at the preliminary design stage to find the necessary parameters of the circuit elements.

5. Analysis of Circuit 3 Operation

In order to analyze the operation of the two-stage voltage divider with a primary energy source with limited power (circuit 3), we will use the circuit shown in Figure 10.

For this circuit, the switches Sw₁ and Sw₂ also operate in the opposite phase. During the time intervals when the switch Sw₁ is turned on, the switch Sw₂ is turned off (even cycles). In this case, the capacitor C₀ is charged from the ideal voltage source up to the voltage V₀. Then the switch Sw₁ is turned off, whereas the switch Sw₂ is turned on (odd cycles), and the charged capacitor C₀ is connected to the divider and gives it part of its charge. As a result, during the charging process of the divider, the voltage of its power supply (now it is C₀) will not remain constant. In addition, the voltage which is reached by the divider during the charging phase (odd cycles) will now also depend on the residual charge on the divider (the charge remaining on the divider at the end of its discharging phase to the load during the even cycles). Calculations show that when the divider is connected to the voltage source with limited power (odd cycles), the voltage across the capacitor C₀ will change according to the law

$$U_{C_0}(t)\cong \left(V_0-{\left(1+{\displaystyle \frac{C_0}{C_1}}+{\displaystyle \frac{C_0}{C_2}}\right)}^{-1}\left(V_0-U_{C_1,\mathrm{end}}-U_{C_2,\mathrm{end}}-U_{D_1}-U_{D_3}\right)\right)\exp \left({\displaystyle \frac{-t}{C_0(R_1+R_2)}}\right),$$

(3)

where $U_{C_1,\mathrm{end}}$ and $U_{C_2,\mathrm{end}}$ are the voltages across the capacitors C₁ and C₂ at the end of the even cycle and $U_{D_1}$ and $U_{D_3}$ are the voltages across the diodes D₁ and D₃ at the end of the even cycle before C₀ is connected to the divider. In the derivation of Equation (3), it is taken into account that when the divider is connected (Sw₁ is switched off, Sw₂ is switched on), the capacitor C₀ is at the first moment partly discharged almost instantly to the in-series-connected capacitors C₁ and C₂, and only then does it continue to discharge through the in-series-connected limiting resistors R₁ and R₂.

The main difference between circuit 3 and the above-discussed circuit 2m, where the voltage source V₀ was stable, is in the instability of the power supply voltage (C₀ voltage).

The process of the divider discharging to the load (when Sw₂ is turned off, in even cycles) in this circuit will occur similarly to circuit 2m. It should be noted that, also in this case, at the beginning of the even cycle, the transistors that were turned off during the previous odd cycle do not turn on immediately. It takes some time to discharge the capacitances C_BE,1 and C_BE,2, and this fact was taken into account in deriving Equation (1).

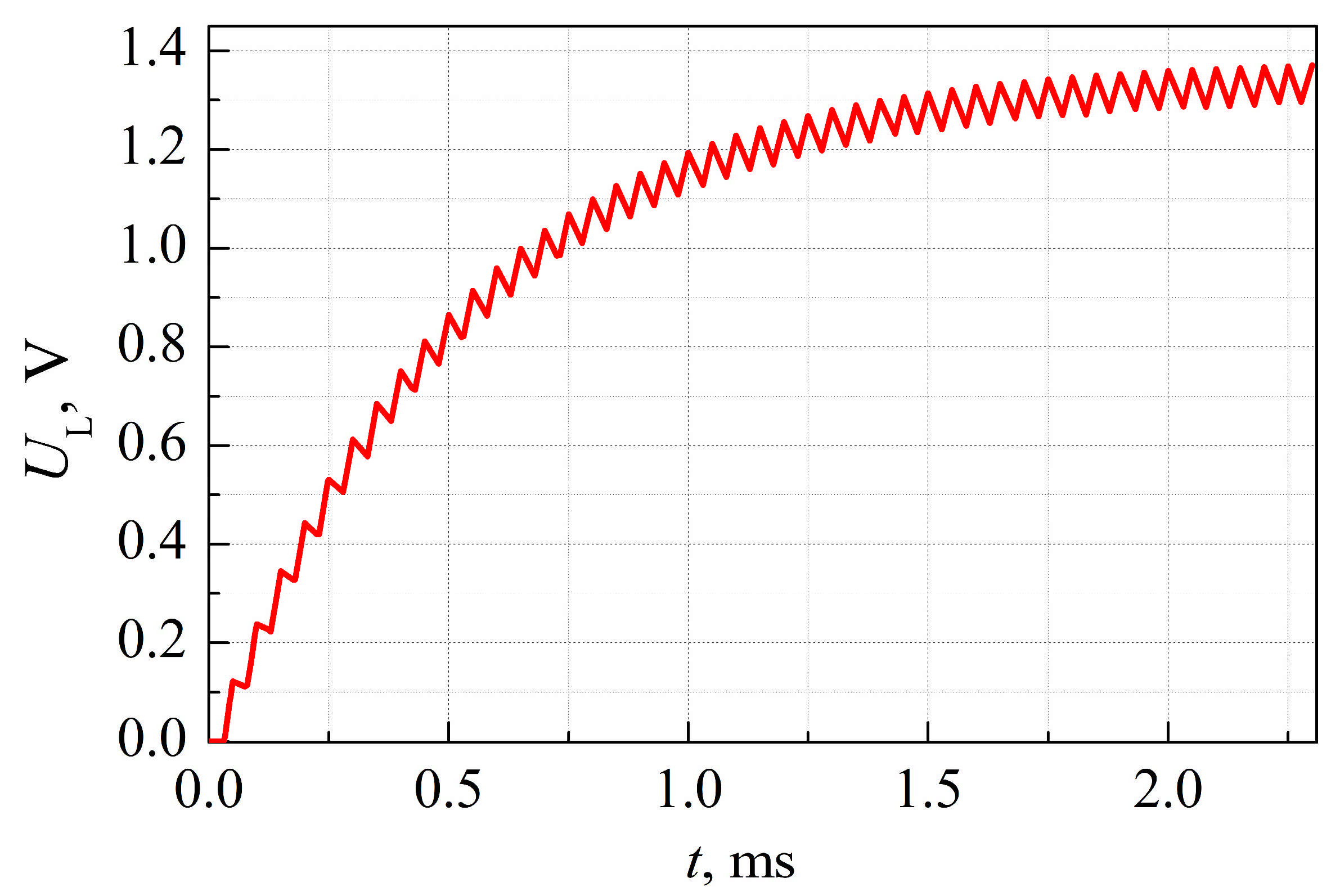
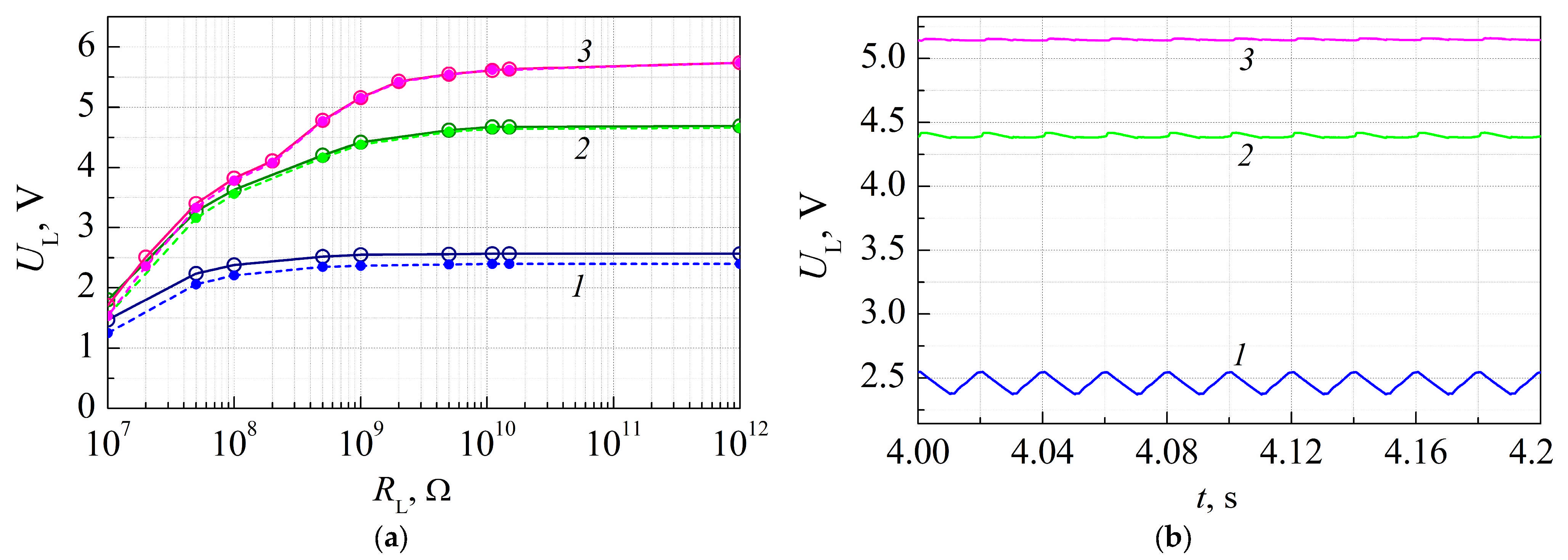
Figure 11 shows the time dependences of the load voltage calculated for circuit 2m and circuit 3, with two values of the load capacitor C_L = 1 nF and 10 nF, resistances R₁ = R₂ = 200 MΩ, and R_L = 10 MΩ. The odd cycle corresponds to the time from 0 to 0.01 s, and the even cycle, from 0.01 to 0.02 s.

During the even cycle, the delay of the voltage growth across the load due to the discharge of the capacitances C_BE,1 and C_BE,2 for the first transistor is about 1.5 ms, and for the second one is about 3.5 ms. As the load capacitance C_L decreases, the voltage oscillations range increases, and the discharge of C_BE,1 and C_BE,2 becomes more pronounced.

It is obvious from Figure 11 that for the same circuit elements, the maximum value of the load voltage for circuit 2m is greater than that for circuit 3. This effect is more evident for values of the limiting resistors R₁ and R₂ in the range from 10 MΩ to 200 MΩ, and the load resistance R_L in the range from 10 MΩ to 100 MΩ. For lower resistances, the currents through the circuits become so high, and the discharge time of the capacitances C_BE,1 and C_BE,2 is so short, that the delay becomes barely noticeable and only one (common) extremum appears. At higher resistances in steady-state mode, the voltage across the load changes weakly, and the charge on the capacitances C_BE,1 and C_BE,2 almost does not change as well. The appearance of two extrema (Figure 11) during the even cycles changes the spectral composition of the output voltage, which must be taken into account during subsequent filtration design.

Figure 12a shows the experimental dependences of the maximum U_L,max and minimum U_L,min load voltages versus the load resistance for circuit 3 measured at C₀ = 1 nF, R₁ = R₂ = 10 MΩ, 80 MΩ, and 200 MΩ. In general, these dependences are similar to the corresponding dependences for circuit 2m, shown in Figure 8a, but they are located a bit lower. As the load resistance increases, the dependences of the maximum and minimum voltages across the load for circuit 3 also reach the saturation level. The value of the saturation voltage depends on the resistances R₁ and R₂ in the transistor base circuit, and when the resistance of the limiting resistors increases, the saturation voltage increases too.

Figure 12b shows the time dependences of the load voltage measured at R_L = 1 GΩ and R₁ = R₂ = 10 MΩ, 80 MΩ, and 200 MΩ for circuit 3. It is obvious from Figure 12 that as the values of the limiting resistors R₁ and R₂ and the load resistance R_L increase, the output voltage ripple decreases.

Figure 13 shows the dependence of the ratio between the maximal load voltages for the circuits with periodic connection of C₀ (circuit 3) and V₀ (circuit 2m) versus the load resistance measured at R₁ = R₂ = 10 MΩ, 80 MΩ, and 200 MΩ. It is obvious from Figure 13 that as the resistances in the transistor’s base circuit decrease, the difference between the maximal voltages for circuits 2m and 3 increases, and can reach 30%. This is because (for circuit 3) the decrease in the limiting resistances leads to an increase in discharge in the capacitor C₀, which directly affects the voltage across it according to Equation (3), while for circuit 2m, the voltage applied to the divider does not change and remains equal to V₀.

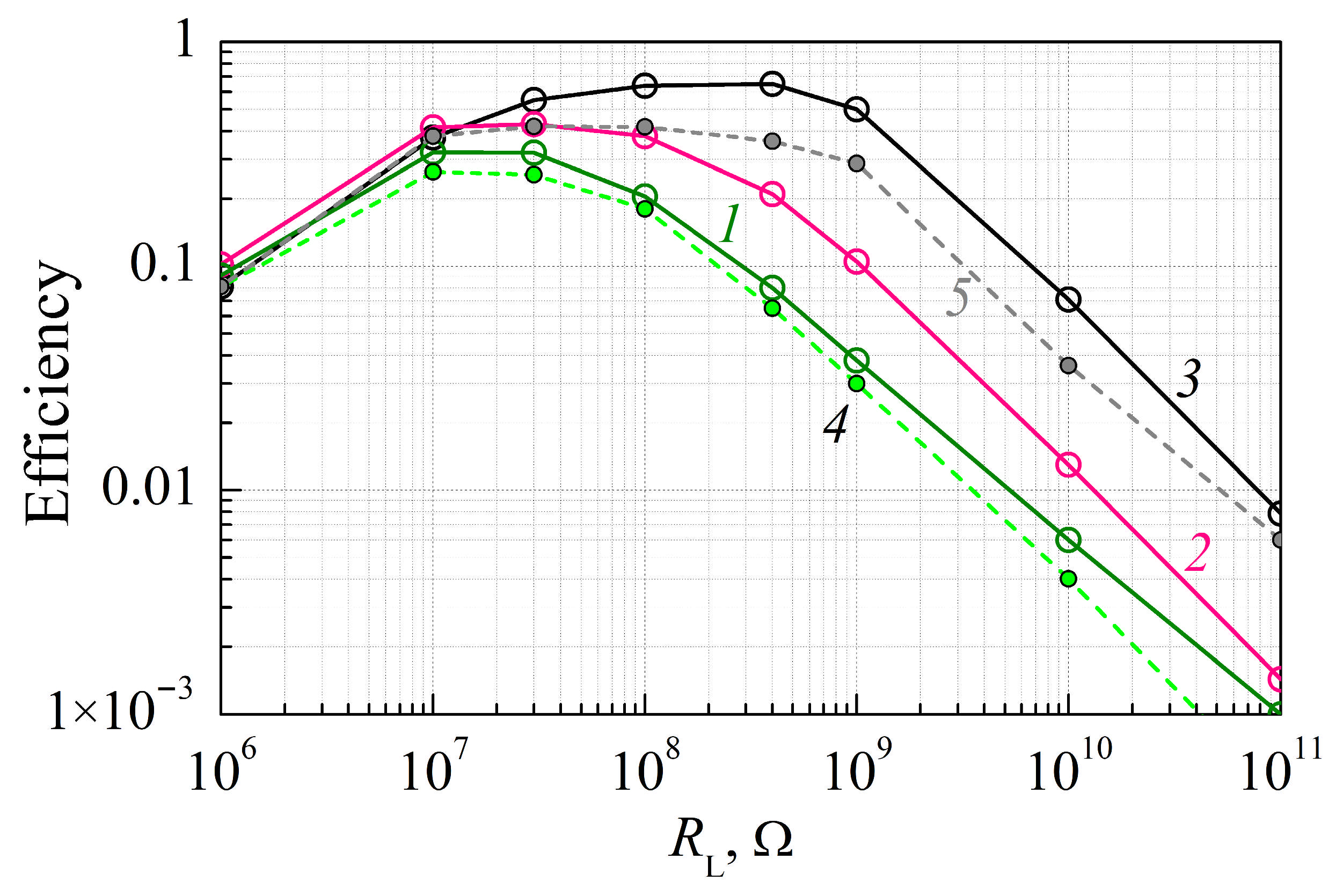
The limited power of the primary voltage source also affects the divider efficiency. Figure 14 shows the dependence of the ratio between the average energy transfer rate to the load (output power) per cycle, and the average energy extraction rate from the primary source V₀ or C₀ per cycle, calculated using experimental data for circuit 2m (solid lines) and circuit 3 (dashed lines), respectively.

It can be seen from Figure 14 that the efficiency can reach 60% for circuit 2m and 40% for circuit 3. Thus, circuit 3 performs the conversion less efficiently than circuit 2m. Also, as the resistance of the limiting resistors increases, the efficiency increases for both circuits. This is due to the decrease in the current through these resistors during the odd cycles.

Moreover, an increase in the limiting resistances R₁ and R₂ leads to an increase in the load resistances R_L, for which the division coefficient of the divider stops changing (Figure 8 and Figure 12).

The analysis shows that it is possible to reduce the effect of the power supply discharge by reducing the odd cycles duration, keeping the complete cycle duration unchanged. Calculations show that for the complete cycle duration of 0.02 s, the reduction in the odd cycles duration from 0.01 s to 0.002 s can increase the efficiency by 5%, and to 0.001 s, by 8%.

Thus, in the process of the voltage divider design, it is necessary to simultaneously take into account the dependence of the load voltage on the load resistance, the dependence of the efficiency on the load and limiting resistances, as well as the dependence of the efficiency on the cycle duration.

In order to verify the adequacy of the developed concepts regarding the operation of the divider circuits with transistor–diode commutation of switchable capacitors, an analysis of the three-stage voltage divider operation was carried out. The electrical circuit of such a divider corresponds to the circuit shown in Figure 1, but with the voltage source (C₀) with limited power, similar to that shown in Figure 10.

Within the framework of the developed theory about the operation of the divider circuits with transistor–diode commutation, the following analytical expressions were obtained for the three-stage voltage divider in order to calculate the dependence of the load voltage versus the resistances of the limiting and the load resistors:

$${\displaystyle V_{\mathrm{L},\max }^{\mathrm{high}}}={\displaystyle \frac{V_0-\left[K_q(1+C_{1,\mathrm{L}}-K_{\mathsf{\tau },\mathrm{ch}})-\left(K_q{K}_{\mathsf{\tau },\mathrm{ch}}-(1+K_{\mathsf{\tau },\mathrm{ch}}{C}_{\mathrm{L},1})R_{1,\mathrm{L}}{U}_{\mathrm{BE}}{K}_{\mathrm{dis},1}\right)(1+2K_{\mathrm{dis}})+F^{*}\right]}{2+\left[2-\left(1+K_{\mathsf{\tau },\mathrm{ch}}{C}_{\mathrm{L},1}\right)K_{\mathrm{dis},2}\right](1+2K_{\mathrm{dis}})+2(2-K_{\mathsf{\tau },\mathrm{ch}}{K}_{\mathrm{dis},2})(1+K_{\mathrm{dis}})C_{D,1}-K_{\mathsf{\tau },\mathrm{ch}}{K}_{\mathrm{dis},2}}},$$

(4)

$$V_{\mathrm{L},\min }={\displaystyle V_{\mathrm{L},\max }^{\mathrm{high}}}{K}_{\mathrm{dis},3}-(1-K_{\mathrm{dis},3})R_{1,\mathrm{L}}{U}_{\mathrm{BE}},$$

(5)

$${\displaystyle V_{\mathrm{L},\max }^{\mathrm{low}}}=U_{D_3}+{\displaystyle \frac{3C_{\mathrm{eq}}}{4C_1}}\left(V_0\left(1-2{\displaystyle \frac{C_D}{C_1}}\right)-3V_D-(U_{D_3}+U_{\mathrm{CE}})\left(1+{\displaystyle \frac{C_1}{C_0}}\right)\right)+{\displaystyle \frac{V_{\mathrm{L},\min }}{4}}\left(1+{\displaystyle \frac{3C_{\mathrm{eq}}}{C_0}}\right),$$

(6)

where ${\displaystyle V_{\mathrm{L},\max }^{\mathrm{high}}}$ and ${\displaystyle V_{\mathrm{L},\max }^{\mathrm{low}}}$ are the maximal load voltages for high and low resistances, respectively, $V_{\mathrm{L},\min }$ is the minimal load voltage, $\Delta q=1.68\cdot {10}^{-10}$ C is the charge accumulated in the transistor base during the saturation mode, V_D is the voltage drop across the opened (forward-biased) diode, and the values of F*, C_1,L, C_L,1, C_D,1, C_sum, C_eq, R_1,L, K_q, K_τ,ch, K_dis,1, K_dis,2, K_dis,3, K_dis are defined by Equations (A7)–(A19) (see Appendix B). The values U_BE = −0.51 V and U_CE = −0.015 V are the voltages of the transistor base–emitter and collector–emitter junctions during the saturation mode and Δτ_ch and Δτ_dis are the durations of the charge (odd cycle) and discharge (even cycle) cycles of the divider.

Similarly to the case of the diode-switching divider [32,33], in this case, it is not possible to obtain one general equation for V_L,max at an arbitrary load resistance. This is because at high load resistances, the discharging diodes VD_3,1 and VD_3,2 (Figure 1) remain reverse-biased throughout the conversion cycle. The voltage across the capacitances of the reverse-biased discharging diodes does not change sign and the entire cycle adds to the voltage across the capacitors C₁ and C₂. However, at low load resistances, when a significant charge is taken from the divider during connection to the load, the capacitances of the discharging diodes have more time to discharge, the voltage across the discharging diodes changes sign, and it is then subtracted from the voltages across the capacitors C₁ and C₂. In the first case, the maximum voltage across the load asymptotically approaches the sum, while in the second case, it approaches the difference between the voltages across the capacitors C₁ and C₂ and the forward-biased discharging diodes VD_3,1 and VD_3,2. The transition from Equation (6) to Equation (4) takes place at ${\displaystyle R_{\mathrm{L}}^{\ast }}$, for which ${\displaystyle V_{\mathrm{L},\max }^{\mathrm{high}}}={\displaystyle V_{\mathrm{L},\max }^{\mathrm{low}}}$.

It should be noted that because in circuits with transistor–diode commutation of switchable capacitors the stabilization effect (transition of transistors to saturation mode) is much stronger than in circuits with diode commutation of switchable capacitors, the excess of V_L,max over the value of V₀/N is significantly less.

Figure 15 shows the dependences of the maximum and minimum load voltages versus the load resistance during the periodical connection of the capacitor C₀ to the three-stage voltage divider measured and calculated using Equations (4)–(6) at V₀ = 10 V, R₁ = R₂ = R₃ = 80 MΩ, C₁ = C₂ = C₃ = C_L = 1 nF, for diodes 1N4149 with the reverse capacitance of 5 pF for different values of C₀, Δτ_ch, and Δτ_dis.

One can see from Figure 15 that the maximum values (curves 1) of the load voltage at C₀ = 4.7 nF are higher than the corresponding voltages at C₀ = 1 nF, especially at low resistances.

The decrease in the maximum voltage across the load resistance, when the capacitance C₀ is decreased, for circuit 3, is due to the fact that when the capacitor C₀ (initially charged up to V₀) is connected to the divider, the voltage across C₀ does not remain constant, but it decreases.

At the same time, the voltage, which the divider reaches during the charging phase (odd cycles), will also depend on the residual charge on the divider. This residual charge remains on the divider (on the discharging capacitors) at the end of the discharging phase of the divider to the load (even cycles). This can be seen from Figure 1b, where instead of the unlimited power source V₀, the limited power source C₀ should be connected.

Since the total charge in the system does not change during the transfer of a part of the charge from C₀ to the divider (odd cycles), assuming C₁ = C₂ = C₃, we have

$$C_0{V}_0+{\displaystyle \frac{1}{N}}{C}_{1}N{V}_{\mathrm{res}}=(C_0+{\displaystyle \frac{1}{N}}{C}_1)V_{\mathrm{ch}},$$

where N is the number of the divider charged capacitors (the number of the divider stages) and V_res is the residual voltage on each of the capacitors C₁, C₂, and C₃ at the end of the previous (even) cycle. It follows that, in an ideal case, during the charging phase, the voltage across N series-connected capacitors C₁, C₂, and C₃ will be equal to

$$V_{\mathrm{ch}}={\displaystyle \frac{C_0{V}_0+\frac{1}{N}{C}_{1}N{V}_{\mathrm{res}}}{C_0+\frac{1}{N}{C}_1}}.$$

At low load resistances, when the load capacitor is rapidly discharged, and the voltages across the load and V_res decrease, the value of V_ch also decreases. If V_res drops to zero, then

$$V_{\mathrm{ch}}={\displaystyle \frac{C_0{V}_0}{C_0+\frac{1}{N}{C}_1}}.$$

Thus, it can be found that with a decrease of C₀, the voltage (and charge) across each of the capacitors C₁, C₂, and C₃ decreases. As a result, during the subsequent even cycle, when the divider is connected to the load (Figure 1c), a smaller charge is transferred to the load and the maximum voltage across the load is also reduced:

$$V_{\mathrm{L},\max }={\displaystyle \frac{N{C}_1}{(C_{\mathrm{L}}+N{C}_1)}}{\displaystyle \frac{C_0{V}_0}{(N{C}_0+C_1)}}\exp \left({\displaystyle \frac{-\Delta {\mathsf{\tau }}_{\mathrm{ch}}}{C_{0}N{R}_1}}\right).$$

It has been taken into account here that during the odd cycle, an additional discharge of C₀ occurs through the limiting resistors.

Our analysis has revealed that within the framework of the developed concepts regarding the operation features of the voltage divider with transistor–diode commutation of switchable capacitors, the calculation results are in good agreement with the experimental data for a wide range of circuit parameters.

6. Conclusions

Experimental and theoretical study of the operation features of the transformerless voltage dividers with transistor–diode commutation of switchable capacitors (TDCSC) designed to work as a part of low-power autonomous electronic systems with reduced output voltage showed the following:

• During the operation from an ideal voltage source V₀ with unlimited power and permanent connection, the two-stage voltage divider circuit operates as the divider, where the division coefficient of the input voltage at high load resistances does not depend on the load resistance and tends to 1/2. In addition, the load voltage does not change significantly and is close to V₀/2 when the load resistance changes, whereas the current through the load resistance is close to V₀/(2R_L), i.e., it decreases when the load resistance increases. Also, during the divider operation from the ideal voltage source V₀ with unlimited power and permanent connection, a fairly high current flows through the limiting resistors all the time. This current discharges the source V₀; as a result, the efficiency of such a circuit turns out to be low.
• When the divider with TDCSC operates from the periodically connected ideal voltage source V₀ with unlimited power, two operation modes can be distinguished:
  If the duration of the even cycle is short compared to the load time constant τ₁ ≈ C_LR_L, then the mode is implemented, where the transistors do not switch to the saturation mode. The condition for the load voltage stabilization in this mode is the equality of the sum of the collector currents to the current through the load resistance. During the simulation of the divider operation in this mode, it is necessary to take into account the time required to discharge the capacitances C_BE,1 and C_BE,2. The efficiency of this circuit turns out to be significantly higher than that of the previous circuit, and can reach 20%.
  When the duration of the even cycle increases, the transistors can switch from active mode to saturation mode. In this case, the collector current’s charging the load will first begin to decrease, and can then even change the direction, which, in general, will lead to a decrease in the load current and, eventually, to the stabilization of the output voltage. The saturation mode is reached faster by increasing the input voltage, reducing the limiting resistances, and increasing the load resistance. During the design of such a divider, it cannot be assumed that the number of stages of the divider N guarantees the division coefficient of 1/N of the output voltage. If the parameters of the divider circuit change, it is necessary to re-evaluate the division coefficient every time. The efficiency of the divider in this mode can reach 60%.
• During the operation of the voltage divider with TDCSC from a voltage source with limited power connected to the divider periodically, the emergence of two extrema for even cycles was revealed, which significantly changes the spectral composition of the output voltage. This effect is more evident at values of limiting resistors in the range from 10 to 200 MΩ and load resistances in the range from 10 to 100 MΩ. The efficiency of the voltage divider with TDCSC in this case can reach 40%.
• The effect of the power supply discharge through the limiting resistances can be reduced by decreasing the duration of the odd cycles, keeping the complete cycle duration unchanged. The reduction in the odd cycle duration can increase the efficiency by 5–8%. Therefore, during the design of the voltage divider with TDCSC, it is necessary to simultaneously take into account the dependence of the load voltage versus the load resistance, the dependence of efficiency versus the load resistance, and the dependence of the efficiency on the cycle duration.

In general, it should be noted that the analytical expressions obtained on the basis of the developed theory regarding the dividers’ operation enable the calculation of the parameters of the studied circuits of the transformerless dividers with TDCSC in a wide range of circuit parameters. The good agreement between theoretical results and experimental data enables the conclusion to be reached that such calculations adequately describe the operation of the dividers with TDCSC, and the derived analytical expressions can be used at the preliminary design stage of the systems, using the dividers with TDCSC, to find the necessary circuit parameters. The results of the analysis and the developed approach make it possible to significantly narrow the range of search for the necessary system parameters during the design stage and consequently reduce the design time.

It should also be noted that with the cascade (sequential) connection of the dividers, their division coefficients are multiplied. Therefore, in order to reduce the primary source voltage by six or more times, instead of one divider with six stages, two series-connected dividers can be used: one, a two-stage voltage divider and the other, a three-stage voltage divider. In this case, only five steps of the divider will be involved, but not six.

In conclusion, it should be noted that the efficiency of the circuits analyzed in this paper, compared with voltage reduction circuits for low-power electrostatic microelectromechanical generators proposed earlier [9,10,28,29,30,31], can be 15–30% higher.