Fatigue Endurance of Continuous Fiber-Reinforced Polymer Matrix Composites Manufactured by 3D Printing
Abstract
1. Introduction
2. Background
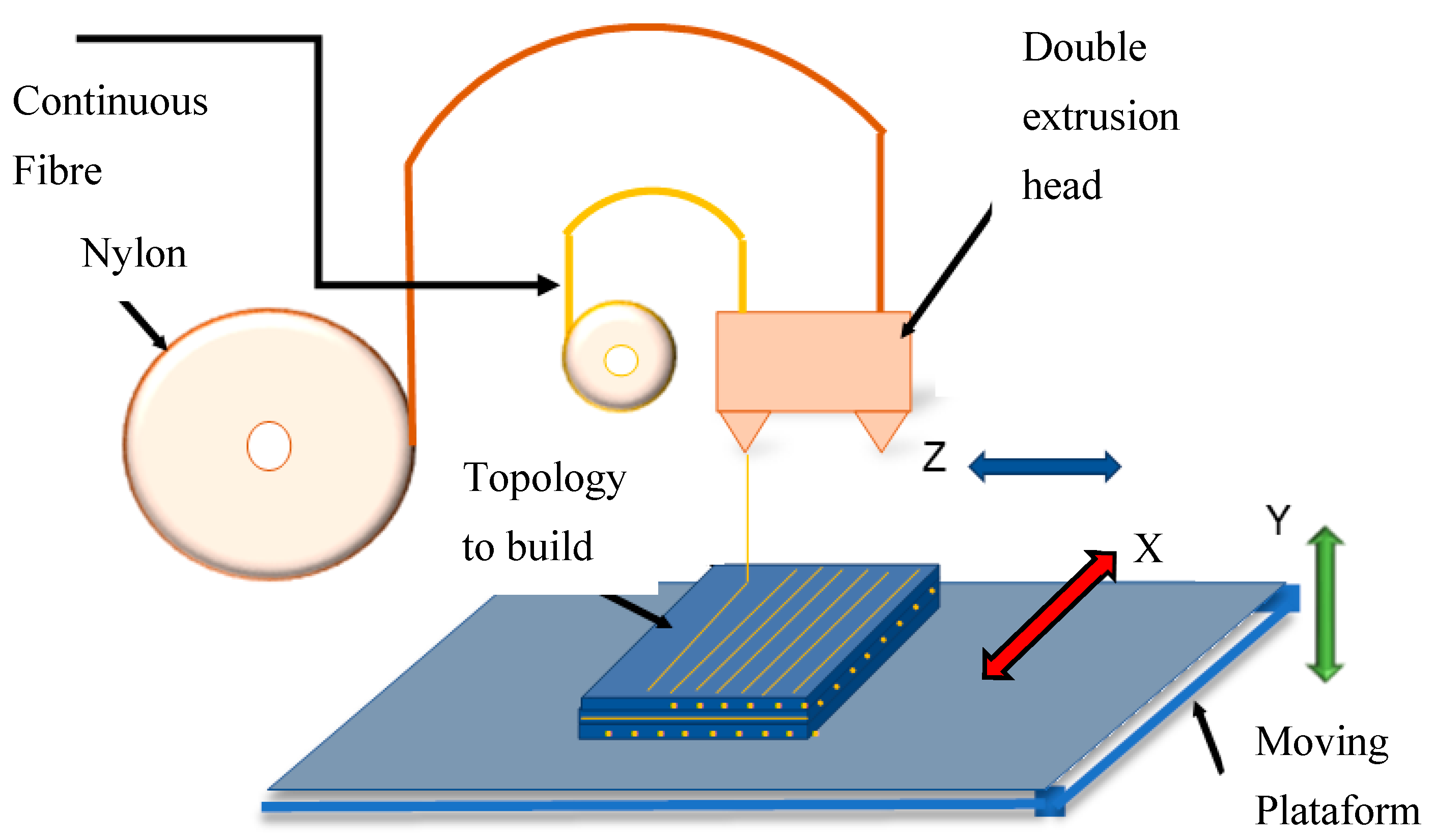
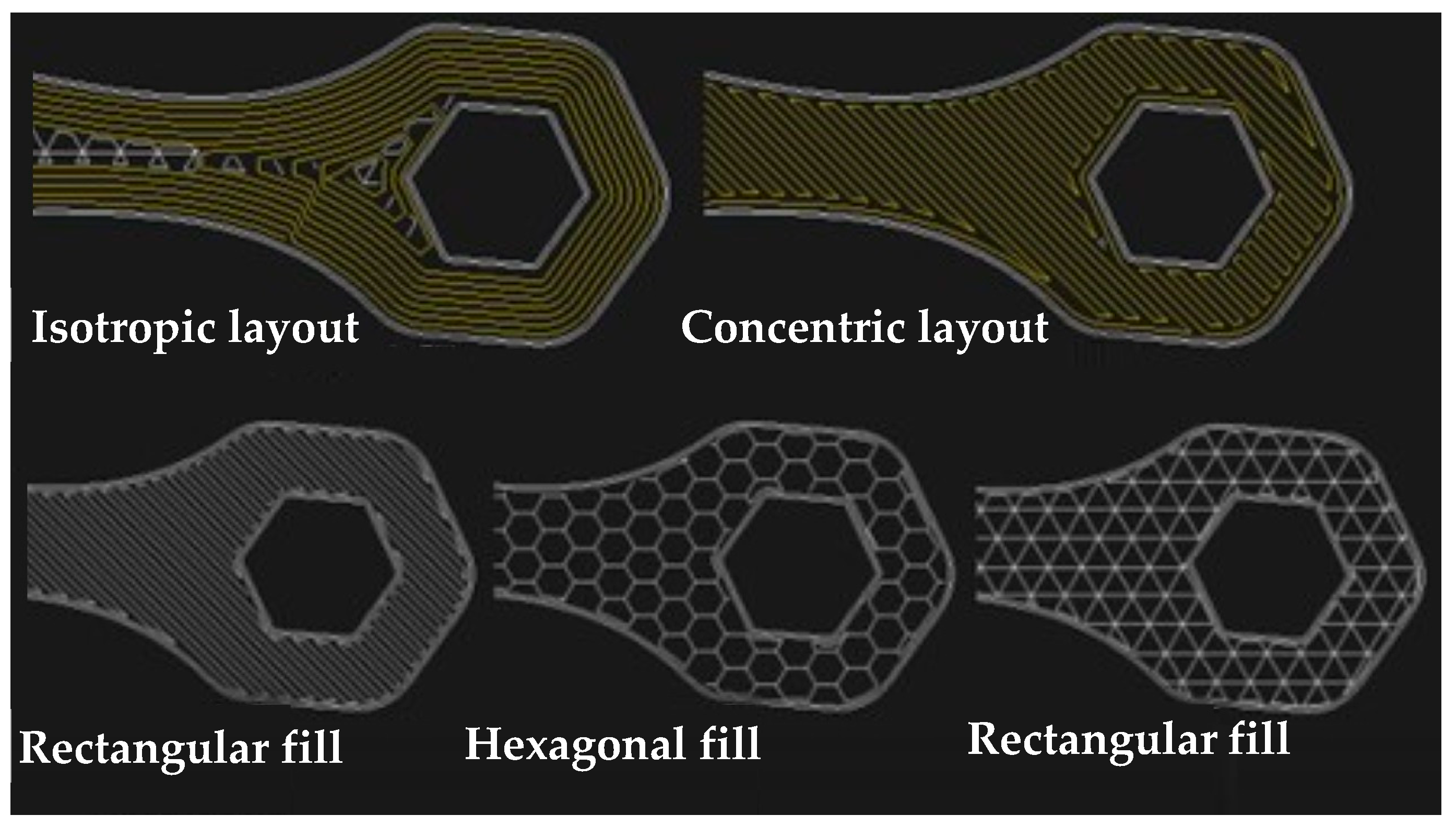
2.1. Additive Manufacturing
2.2. Fatigue
2.3. Data Adjustment
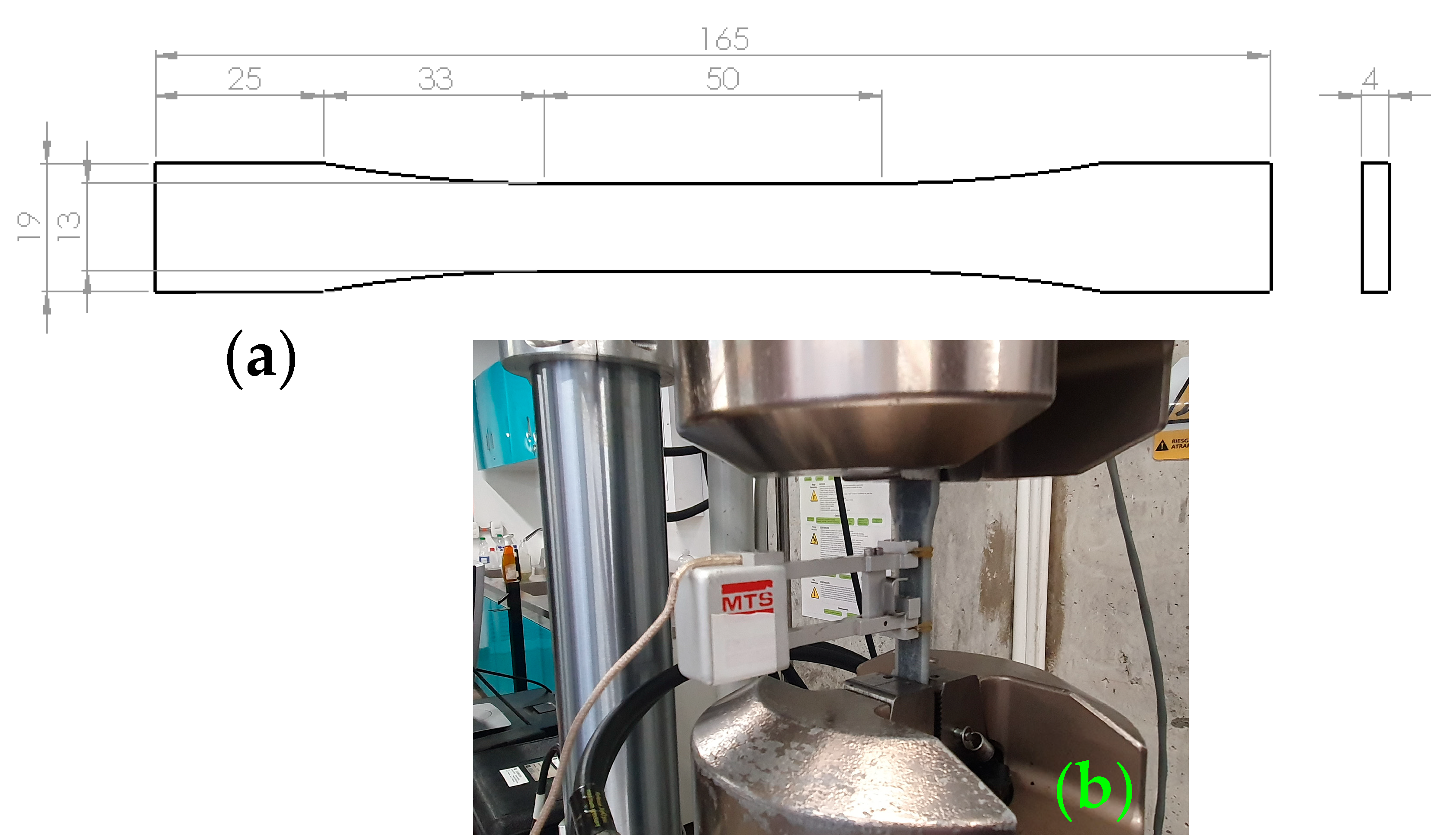
3. Materials and Methods
4. Results
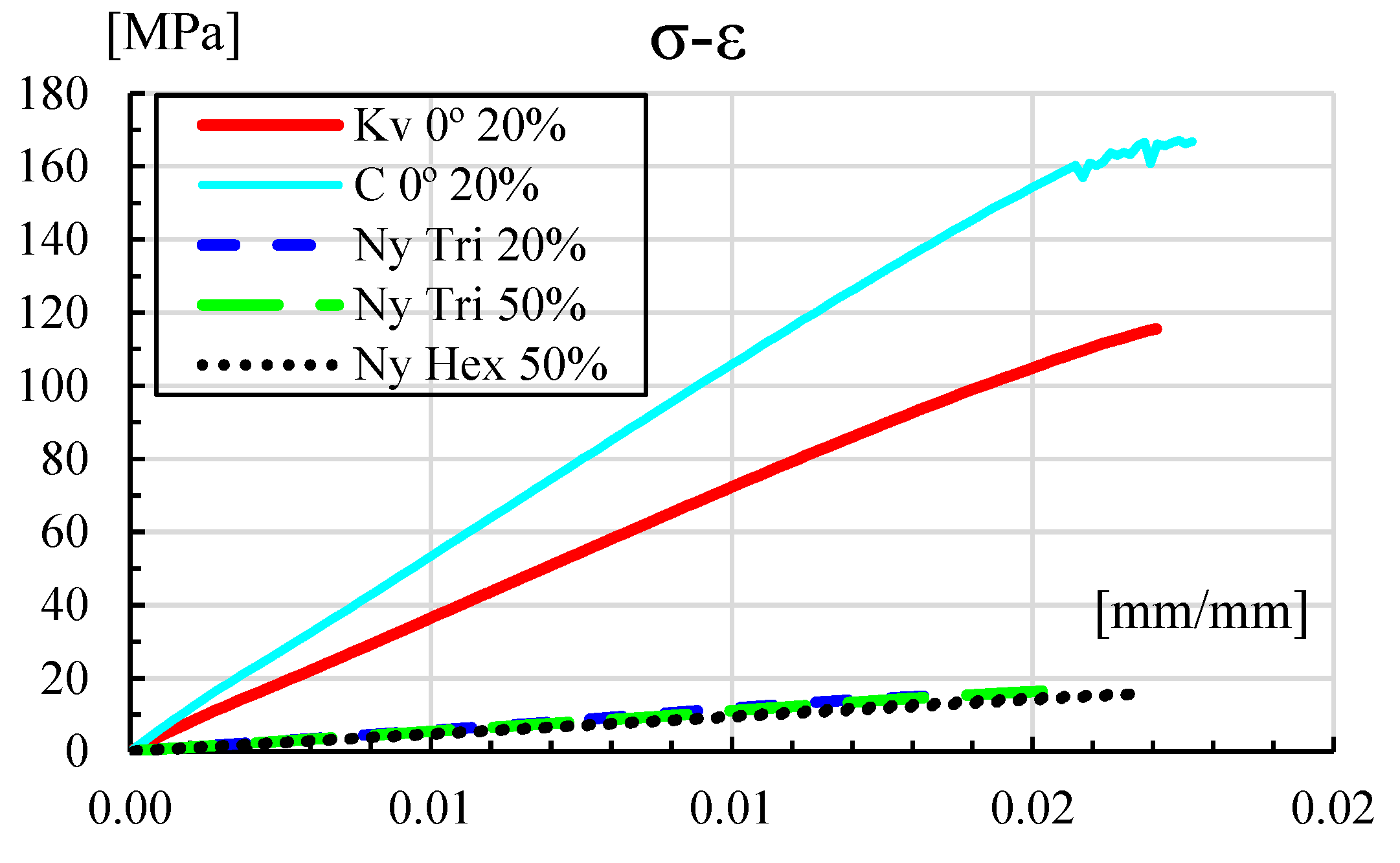
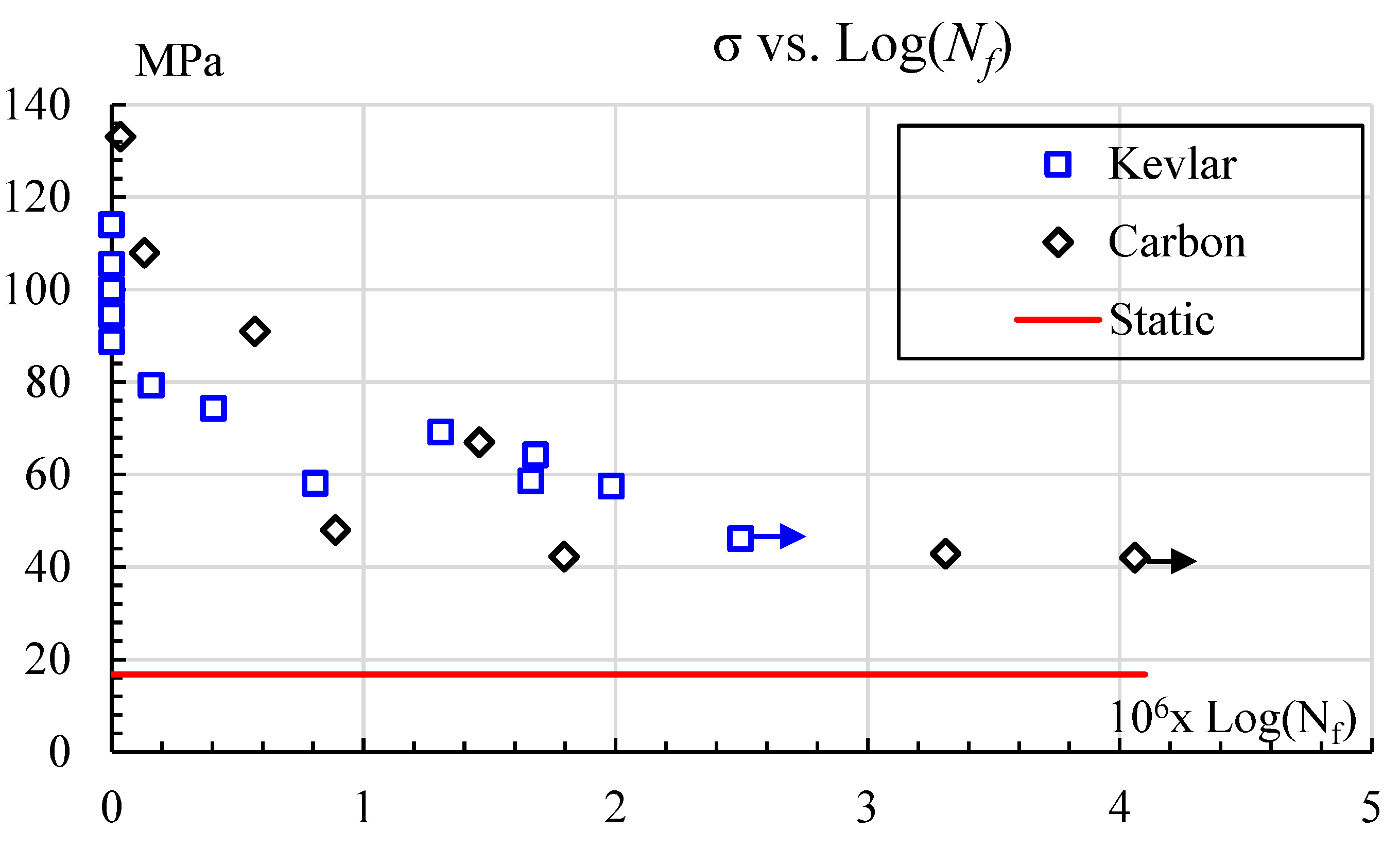
4.1. Mechanical Results
4.2. Failure Modes
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Díaz-Rodríguez, J.G.; Pertúz-Comas, A.D.; González-Estrada, O.A. Mechanical Properties for Long Fibre Reinforced Fused Deposition Manufactured Composites. Compos. B Eng. 2021, 211, 108657. [Google Scholar] [CrossRef]
- Pothnis, J.R.; Hejjaji, A.; Bhatia, G.S.; Comer, A. Failure Analysis under Fatigue Loading of Glass Fibre Reinforced In-Situ Polymerizable Thermoplastic and Bio-Epoxy Based Composites. Compos. Part C Open Access 2025, 17, 100608. [Google Scholar] [CrossRef]
- Shah, D.U. Damage in Biocomposites: Stiffness Evolution of Aligned Plant Fibre Composites during Monotonic and Cyclic Fatigue Loading. Compos. Part A Appl. Sci. Manuf. 2016, 83, 160–168. [Google Scholar] [CrossRef]
- Guo, R.; Li, C.; Niu, Y.; Xian, G. The Fatigue Performances of Carbon Fiber Reinforced Polymer Composites—A Review. J. Mater. Res. Technol. 2022, 21, 4773–4789. [Google Scholar] [CrossRef]
- Paredes, A.C.; Bohórquez, O.; Pertuz, A.; Rueda, Y.; González-Estrada, O.A. Interlaminar Tensile Strength for Composite Materials Made by Additive Manufacturing. J. Phys. Conf. Ser. 2019, 1386, 012002. [Google Scholar] [CrossRef]
- Cheng, P.; Han, Z.; Chen, Y.; Ye, L. Recent Progress in Non-Planar 3D Printing of Continuous Fiber-Reinforced Composites. Compos. Part A Appl. Sci. Manuf. 2025, 194, 108900. [Google Scholar] [CrossRef]
- Pathan, M.; Ponnusami, S.; Pathan, J.; Pitisongsawat, R.; Erice, B.; Petrinic, N.; Tagarielli, V. Predictions of the Mechanical Properties of Unidirectional Fibre Composites by Supervised Machine Learning. Sci. Rep. 2019, 9, 13964. [Google Scholar] [CrossRef]
- Agarwal, K.; Kuchipudi, S.K.; Girard, B.; Houser, M. Mechanical Properties of Fiber Reinforced Polymer Composites: A Comparative Study of Conventional and Additive Manufacturing Methods. J. Compos. Mater. 2018, 52, 3173–3181. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Barocio, E.; Tejada-Ortigoza, V.; Pipes, R.B.; Rodriguez, C.A.; Roman-Flores, A. Characterization of the Mechanical Properties of FFF Structures and Materials: A Review on the Experimental, Computational and Theoretical Approaches. Materials 2019, 12, 895. [Google Scholar] [CrossRef]
- Zhou, L.; Miller, J.; Vezza, J.; Mayster, M.; Raffay, M.; Justice, Q.; Al Tamimi, Z.; Hansotte, G.; Sunkara, L.D.; Bernat, J. Additive Manufacturing: A Comprehensive Review. Sensors 2024, 24, 2668. [Google Scholar] [CrossRef] [PubMed]
- Parrado-Agudelo, J.Z.; Narváez-Tovar, C. Mechanical Characterization of Polylactic Acid, Polycaprolactone and Lay-Fomm 40 Parts Manufactured by Fused Deposition Modeling, as a Function of the Printing Parameters. ITECKNE 2019, 16, 25–31. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies; Springer: New York, NY, USA, 2015; ISBN 978-1-4939-2112-6. [Google Scholar]
- Mwema, F.M.; Akinlabi, E.T. Basics of Fused Deposition Modelling (FDM). In Fused Deposition Modeling. SpringerBriefs in Applied Sciences and Technology; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–15. [Google Scholar]
- Castro, J.T.P.; Meggiolaro, M.A. Fatigue Design Techniques, 3rd ed.; CreateSpace: North Charleston, SC, USA, 2016; ISBN 1530797365. [Google Scholar]
- Alamry, A. Fatigue Damage and Analysis of Laminated Composites: A State-of-the-Art. J. Eng. Res. 2024, 13, 2066–2076. [Google Scholar] [CrossRef]
- Sapkota, A.; Ghimire, S.K.; Adanur, S. A Review on Fused Deposition Modeling (FDM)-Based Additive Manufacturing (AM) Methods, Materials and Applications for Flexible Fabric Structures. J. Ind. Text. 2024, 54, 15280837241282110. [Google Scholar] [CrossRef]
- Muñoz-Vásquez, S.; Mora-Pérez, Z.A.; Ospina-Henao, P.A.; Valencia-Niño, C.H.; Becker, M.; Díaz-Rodríguez, J.G. Finite Element Analysis in the Balancing Phase for an Open Source Transfemoral Prosthesis with Magneto-Rheological Damper. Inventions 2023, 8, 36. [Google Scholar] [CrossRef]
- Rabbi, M.F.; Ertter, J.; Bakis, C.E. Tensile Fatigue Behavior of Short and Continuous Carbon Fiber Reinforced Additively Manufactured Thermoplastic Multiscale Composite. J. Reinf. Plast. Compos. 2024, 44, 1190–1204. [Google Scholar] [CrossRef]
- Pertuz, A.D.; Díaz-Cardona, S.; González-Estrada, O.A. Static and Fatigue Behaviour of Continuous Fibre Reinforced Thermoplastic Composites Manufactured by Fused Deposition Modelling Technique. Int. J. Fatigue 2020, 130, 105275. [Google Scholar] [CrossRef]
- Harber, G.M. Mechanical Properties and Tension-Tension Fatigue Behavior of a Novel Additively Manufactured Polymer Matrix Composite at Room and Elevated Temperature; Air Force Institute of Technology: Wright-Patterson AFB, OH, USA, 2022. [Google Scholar]
- Vidrih, T.; Winiger, P.; Triantafyllidis, Z.; Ott, V.; Terrasi, G.P. Investigations on the Fatigue Behaviour of 3D-Printed Continuous Carbon Fibre-Reinforced Polymer Tension Straps. Polymers 2022, 14, 4258. [Google Scholar] [CrossRef]
- Pertuz-Comas, A.D.; Díaz, J.G.; Meneses-Duran, O.J.; Niño-Álvarez, N.Y.; León-Becerra, J. Flexural Fatigue in a Polymer Matrix Composite Material Reinforced with Continuous Kevlar Fibers Fabricated by Additive Manufacturing. Polymers 2022, 14, 3586. [Google Scholar] [CrossRef]
- ISO/ASTM 52900:2021; Additive Manufacturing—General Principles—Fundamentals and Vocabulary 2021. ISO: Geneva, Switzerland, 2021.
- Thomas, G.; Antoni, M.; Gozdz, S. Three Dimensional Printer with Composite Filament Fabrication 2015; Markforged, Inc.: Watertown, MA, USA, 2015. [Google Scholar]
- Blok, L.G.; Longana, M.L.; Yu, H.; Woods, B.K.S. An Investigation into 3D Printing of Fibre Reinforced Thermoplastic Composites. Addit. Manuf. 2018, 22, 176–186. [Google Scholar] [CrossRef]
- León, B.J.; Díaz-Rodríguez, J.G.; González-Estrada, O.A. Daño En Partes de Manufactura Aditiva Reforzadas Por Fibras Continuas. Rev. UIS Ing. 2020, 19, 161–175. [Google Scholar] [CrossRef]
- Kargar, E.; Ghasemi-Ghalebahman, A. Experimental Investigation on Fatigue Life and Tensile Strength of Carbon Fiber-Reinforced PLA Composites Based on Fused Deposition Modeling. Sci. Rep. 2023, 13, 18194. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Heer, B. Additive Manufacturing of Multi-Material Structures. Mater. Sci. Eng. R Rep. 2018, 129, 1–16. [Google Scholar] [CrossRef]
- Chacón, J.M.; Caminero, M.A.; García-Plaza, E.; Núñez, P.J. Additive Manufacturing of PLA Structures Using Fused Deposition Modelling: Effect of Process Parameters on Mechanical Properties and Their Optimal Selection. Mater. Des. 2017, 124, 143–157. [Google Scholar] [CrossRef]
- Nairn, J.A. Matrix Microcracking in Composites. In Comprehensive Composite Materials; Pergamon Press: Oxford, UK, 2000; Volume 2, pp. 403–432. ISBN 978-0-08-042993-9. [Google Scholar]
- Awaja, F.; Zhang, S.; Tripathi, M.; Nikiforov, A.; Pugno, N. Cracks, Microcracks and Fracture in Polymer Structures: Formation, Detection, Autonomic Repair. Prog. Mater. Sci. 2016, 83, 536–573. [Google Scholar] [CrossRef]
- González-Estrada, O.A.; Pertuz Comas, A.D.; Díaz Rodríguez, J.G. Monotonic Load Datasets for Additively Manufactured Thermoplastic Reinforced Composites. Data Brief 2020, 29, 105295. [Google Scholar] [CrossRef]
- Goh, G.D.; Yap, Y.L.; Agarwala, S.; Yeong, W.Y. Recent Progress in Additive Manufacturing of Fiber Reinforced Polymer Composite. Adv. Mater. Technol. 2019, 4, 1800271. [Google Scholar] [CrossRef]
- Hedayati, R.; Amin Yavari, S.; Zadpoor, A.A. Fatigue Crack Propagation in Additively Manufactured Porous Biomaterials. Mater. Sci. Eng. C 2017, 76, 457–463. [Google Scholar] [CrossRef]
- ASTM D638; Test Method for Tensile Properties of Plastics. American Society for Testing and Materials: West Conshohocken, PA, USA, 2022.
- Markforged Composites Mechanical Properties. REV 5.0. Available online: https://static.markforged.com/downloads/composites-data-sheet.pdf (accessed on 9 October 2025).
- ASTM D3039; Test Method for Tensile Properties of Polymer Matrix Composite Materials. American Society for Testing and Materials: West Conshohocken, PA, USA, 2017.
- Ferdous, W.; Manalo, A.; Peauril, J.; Salih, C.; Raghava Reddy, K.; Yu, P.; Schubel, P.; Heyer, T. Testing and Modelling the Fatigue Behaviour of GFRP Composites—Effect of Stress Level, Stress Concentration and Frequency. Eng. Sci. Technol. Int. J. 2020, 23, 1223–1232. [Google Scholar] [CrossRef]
- Gómez, S.; Ramón, B.; Guzman, R. Comparative Study of the Mechanical and Vibratory Properties of a Composite Reinforced with Fique Fibers versus a Composite with E-Glass Fibers. Rev. UIS Ing. 2018, 13, 43–50. [Google Scholar] [CrossRef]






| Material | E1 [GPa] | σ1 [MPa] | Relative Density |
|---|---|---|---|
| Nylon | 1.7 | 33.5 | 1.1 |
| Standard used | ASTM D638 | ASTM D638 | NA |
| Kevlar fiber | 27 | 610 | 1.2 |
| Carbon | 60 | 800 | 1.2 |
| Standard used | ASTM D3039 [37] | ASTM D3039 | NA |
| Fiber Reinforcement | A | b | R2 | Fatigue Limit, MPa |
|---|---|---|---|---|
| Kevlar | 121.4 | −0.047 | 91.1% | 46.15 |
| Carbon | 2357.4 | −0.263 | 88.31 | 42.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Rodríguez, J.G.; Pertuz-Comas, A.D.; Bohorquez-Becerra, O.R. Fatigue Endurance of Continuous Fiber-Reinforced Polymer Matrix Composites Manufactured by 3D Printing. Eng 2025, 6, 277. https://doi.org/10.3390/eng6100277
Díaz-Rodríguez JG, Pertuz-Comas AD, Bohorquez-Becerra OR. Fatigue Endurance of Continuous Fiber-Reinforced Polymer Matrix Composites Manufactured by 3D Printing. Eng. 2025; 6(10):277. https://doi.org/10.3390/eng6100277
Chicago/Turabian StyleDíaz-Rodríguez, Jorge Guillermo, Alberto David Pertuz-Comas, and Oscar Rodolfo Bohorquez-Becerra. 2025. "Fatigue Endurance of Continuous Fiber-Reinforced Polymer Matrix Composites Manufactured by 3D Printing" Eng 6, no. 10: 277. https://doi.org/10.3390/eng6100277
APA StyleDíaz-Rodríguez, J. G., Pertuz-Comas, A. D., & Bohorquez-Becerra, O. R. (2025). Fatigue Endurance of Continuous Fiber-Reinforced Polymer Matrix Composites Manufactured by 3D Printing. Eng, 6(10), 277. https://doi.org/10.3390/eng6100277









