Abstract
The effects of initial small-scale material nonlinearity on the pre-yield and pre-buckling response of externally pressurized metallic (plane strain) perfect rings (very long cylindrical shells) is investigated. The cylindrically curved 16-node element, based on an assumed quadratic displacement field (in surface-parallel coordinates) and the assumption of linear distribution of displacements through thickness (LDT), is employed to obtain the discretized system equations. The effect of initial small-scale material nonlinearity (assumed hypo-elastic) on the deformation and stress in the pre-yield and pre-buckling regime of a very long relatively thin metallic cylindrical shell (plane strain ring) is numerically investigated. These numerical results demonstrate that the enhanced responses for metallic rings due to initial small-scale nonlinearity are significant enough to not miss attentions from designers and operators of submersibles alike.
1. Introduction
The present study is primarily motivated by the recent compression failure of the Titan submersible in the North Atlantic at about 12,500 ft. depth []. The findings are consistent with what had long-earlier been observed both analytically/computationally as well as experimentally by the first author and his co-authors; see the brief literature review below [,,,,].
Observations made from the fractured portion and detailed theoretical analysis indicate that the failure may have initiated at a stress concentration site such as initial fiber waviness or misalignment, shown, e.g., in Figure 3 of Chaudhuri [], and associated resin-rich areas. Finally, Chaudhuri and Garala [] published a successful analytical/experimental effort at improving the compressive strength/toughness of the CFRP material by using a then-unavailable hybrid carbon/glass commingling concept.
Some of the uncertainties in the failure of thick CFRP cylindrical shells under compressive loading relate to very fundamental questions pertaining to (i) linkage between macro-structural instability, such as buckling/post-buckling failure of a structural component, e.g., a ring or cylindrical shell at the geometric scale of at least several centimeters and larger [,,,,,,,,,,,,], and micro-structural instability, such as kink band type failure at the fiber-matrix level (at the geometric scale of about 10 μm) investigated by Chaudhuri [,,,,,], Chaudhuri and Garala [], Chaudhuri et al. [], Moran and Shih [] and Gutkin et al. [] among others.
Buckling and post-buckling responses of arch/ring/cylindrical shell/panel type structures have been extensively studied in the literature [,,,,,,,,,,,,,,,,,,]. It may be remarked here that since the elastic post-buckling of a ring involves deformation hardening type nonlinearity [,,,,], there is no final loss of stability in the post-buckling stage. This is in sharp contrast to the deformation softening type nonlinearity caused by, e.g., the thickness effect, [,,,,], the presence of distributed fiber misalignments (in fiber reinforced composites) [,], and hypo-elastic or inelastic material properties [,,], in addition to the thickness effect [,,,]. An arch (an open ring with pinned or fixed ends) is, it may be pointed out in this context, probably the simplest special case which exhibits such behaviors as nonlinear load-deflection path, bifurcation and snapping (and combinations thereof) of a general shell, depending on the range of its specific elasto-geometric parameter, defined in terms of its (modified) slenderness ratio [,]. Furthermore, as has been pointed out earlier by Chaudhuri et al. [], the hydrostatic buckling pressure of a complete ring can be obtained as a special case of a hinged uniformly compressed arch with a central angle π.
One major necessary-cum-looked-forward-to item to designers and operators alike is the heretofore unaddressed analysis on the sensitivity of compressive responses of very long cylindrical shells (plane strain rings) to initial small-scale material nonlinearity, which is the primary objective of the present investigation. Applications include but are not limited to submersibles as well as buried and submerged pipelines, and can be of varying thicknesses. The fact that many a metallic material/alloy, such as aluminum, molybdenum, cast iron, stainless steel (304 and 316) among others, is characterized by initial small-scale nonlinearity in the absence of a well-defined yield point, is well-known in the literature. The initial small-scale nonlinearity of longitudinal Young’s modulus of a unidirectional composite under global or macroscopic compression, but local or micro-/nano-scale shear, caused by crystallite disorientations, as detected by the Raman and X-ray measurements, inside a carbon fiber [] is still unavailable in the literature. An approximate derivation of this is currently underway (and will be reported at a future date).
In what follows, a materials-only [] nonlinear three-dimensional cylindrical shell finite element analysis is presented in order to obtain the discretized system of equations. A cylindrically curved 16-node isoparametric element is employed, which is based on an assumed quadratic displacement field (in surface-parallel coordinates) and the assumption of linear distribution of displacements through thickness (LDT) [,]. The effect of initial small-scale material nonlinearity (assumed hypo-elastic) on the pre-buckling as well as the pre-yield response of a metallic (plane strain) ring is thoroughly investigated. Results relating to the extension to the same effect on the deformation and through-thickness stress distribution in the pre-buckling regime of a long asymmetric cross-ply cylindrical shell (plane strain ring) are deferred to a future date. Finally, physically meaningful conclusions are drawn from these numerical results.
2. Three-Dimensional Kinematic Relations for a Shell
Referring to Figure 1 and invoking the theory of parallel surfaces, the coefficients of the first fundamental differential quadratic form of a surface inside a cylindrical shell can be written in terms of their bottom surface (inside wall) counterparts as follows [,,,,]:
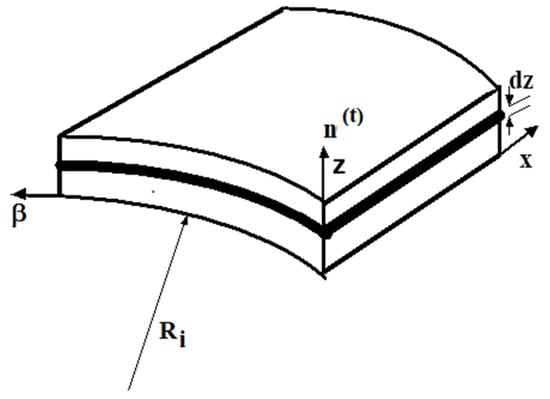
Figure 1.
An infinitesimal element cylindrical shell.
As has been explained earlier by Chaudhuri and Kim [], the inner surface of the cylindrical shell/ring is, from the book-keeping point of view, considered more convenient to serve as the reference surface, since the state of stresses and deformation are primarily three-dimensional in nature. This is in contrast to what is commonly adopted by the classical lamination theory (CLT) or first-order shear deformation theory (FSDT), wherein transverse inextensibility is assumed. The components of the engineering strain in terms of the physical components of the displacement vector at an arbitrary point inside the shell are obtained as follows [,,,,]:
3. Equations of Motion and the Method of Virtual Work
The second Piola-Kirchhoff stress tensor is conjugate to the Green-Lagrange strain tensor in that their properties are also invariant under rigid body motions. When the equilibrium of the body at time t + Δt is first expressed using the principle of virtual displacements with tensor notation, the total Lagrangian formulation requires that
where the and are the Cartesian components of the second Piola-Kirchhoff stress tensor and the total Green-Lagrange strain tensor defined at time t + ∆t, respectively, referred to the initial configurations, while represents the external virtual work. Furthermore,
and
where and represent components of the second Piola-Kirchhoff stress tensor defined at time t, and the incremental components of the same during the subsequent time step Δt, respectively, both referred to the initial configuration. The quantities in Equation (5) denote the linear incremental strain. The incremental constitutive relation, which relates the components of incremental stress and incremental strain both referred to the initial configuration, is given by
in which is the incremental elastic stiffness (material property) tensor, referred to the initial configuration and represented as [Q] in matrix notation (see Section 4 and also refer to Figure 2 below). Substituting Equations (4)–(6) into the left hand side of the Equation (3) finally yields the equations needed for the finite element formulation. The details are available in Chaudhuri and Kim [,].
Because the variation in the strain components is equivalent to the virtual strains, the right hand side of Equation (3) is the virtual work done when the body is subjected to a virtual displacement at time t + ∆t. The corresponding virtual work is given by
where is the surface force vector applied on the surface, S, at time t + ∆t, and is the jth component of the incremental virtual displacement vector evaluated on the loaded surface. When the hydrostatic pressure is applied, the loading path is always deformation-dependent, and the load vector should be evaluated at the current configuration. The external virtual work can, however, be approximated to a sufficient accuracy using the intensity of loading corresponding to time t + ∆t, integrated over the surface area, calculated at the (i − 1)th iteration as follows:
4. Constitutive Relations for an Orthotropic Lamina
Taking into account nonlinear elastic (hypo-elastic) behavior (as opposed to plasticity) and neglecting the thermal and hygrothermal effects, the incremental strain vs. incremental stress relation of an isotropic material in terms of the principal material directions (x, θ, z) is given as follows [,,,]:
In the above equation, the compliance matrix components, , i, j = 1, …, 6, can be approximated analytically by the method of Ramberg and Osgood [], who have suggested that rising stress-strain curves with a smooth knee be represented by the relation [].
where and = σ denote Young’s modulus and normal stress component at time t, respectively, of the material. Details of nomenclature and property definitions of this nonlinear (hypo-elastic) material are shown in Figure 2.
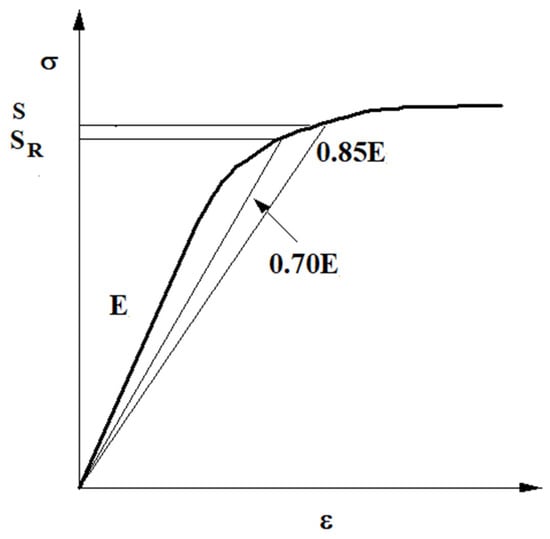
Figure 2.
Definition of parameters in Ramberg-Osgood representation of stress-strain curves [,].
The reference “yield” stress = is defined as the normal stress at which , where is the secant modulus. The exponent, n, known as the hardening parameter, is found from the expression for the secant modulus thus defined:
with
Evaluation of Equation (10a) at gives
where S is the stress at . It may be noted that the linear elastic and the perfectly elastic-plastic (no unloading) cases can be obtained by substituting S = ∞ and n = ∞, respectively, into Equation (9). The incremental stress vs. incremental strain relation can be obtained by inversion of Equation (8) as follows:
5. Isoparametric Finite Element Discretization
In this section, a materially-nonlinear-only displacement-based three-dimensional finite element formulation is presented. An alternative approach to the formulation of thick (laminated) shell nonlinear finite element has recently been developed by Chaudhuri []. The Rayleigh–Ritz finite element method (local shape function), which is useful for modeling structures with somewhat less complex geometrical shapes, such as beams, rings and arches [], has recently been extended to nonlinear analysis of symmetrically laminated shallow circular arches by Kim and Chaudhuri []. A then-unavailable nonlinear resonance (eigenvalue) based semi-analytical approach was introduced by Chaudhuri [] and Chaudhuri et al. [,] for computation of the elastic mode 2 collapse pressure of a moderately-thick to thin isotropic and cross-ply harmonically imperfect rings, which is the harmonically imperfect ring counterpart to the Euler type buckling pressure of a hydrostatically pressurized thin perfect ring [].
The basic steps in the derivation of isoparametric finite element equations are to select the interpolation functions of the displacements and the element coordinates. Because the new element coordinates are obtained by adding the element displacements to the original coordinates in the incremental analysis, the same interpolations can be employed for the displacements and coordinates. In the present study, 16-node quadrilateral elements (Figure 3) are employed because of their computational efficiency, as compared to their lower-order linear counterparts, which are too stiff to model the shear deformation. The details are available in Chaudhuri and Kim [], and are, therefore, omitted here in the interest of brevity of presentation.
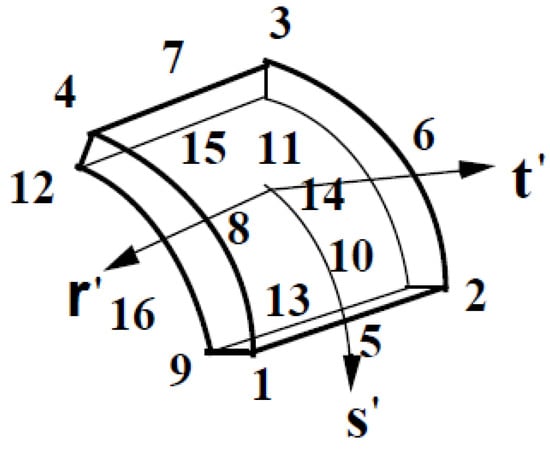
Figure 3.
A 16-node curvilinear side surface-parallel quadratic isoparametric cylindrical shell element [,,,].
On computing the left and right sides of Equations (3) and (7) as sums of integrals over the volume and areas of all finite elements, followed by equating them, and incorporating the boundary conditions, the principle of virtual displacement, in conjunction with the materially-nonlinear-only formulation, is invoked to obtain the incremental equations of motion as follows [,,]:
where
in which the matrices, , and are defined in Equations, (A1), (A2) and (A3), respectively, in Appendix A, while is defined in Equation (12) above, and is given as follows:
Because the nodal point forces at time t + Δt depend nonlinearly on the nodal point displacements, it is necessary to iterate for obtaining a reasonably accurate solution of Equation (13). The most frequently used iteration scheme for solutions of nonlinear finite element equations is the Newton-Raphson iteration, because reformations and triangularizations of stiffness matrices at selective load and iteration steps are more computationally efficient without a significant loss of accuracy. In the Newton-Raphson method, only the stress force vector (i.e., the right hand side of Equation (13)) is modified without changing the stiffness matrix, after each iteration within a certain load step. The details of the algorithm employed for solving Equation (13) are available in Section 5 of Chaudhuri and Kim [], and Appendix-C of Kim and Chaudhuri [], and will not be repeated here in the interest of brevity of presentation.
In actual computer programming, the active columns and the addresses of the diagonal elements of the total stiffness matrix are stored effectively in an one-dimensional array, and an effective subroutine COLSOL (active column solver) is used to finally obtain the incremental displacement for the unbalanced force, ∆R(i−1) = {fL} − {fN} in the (i − 1)th iteration. The iteration is continued until the out-of-balance load vector and the displacement increments are sufficiently small, i.e., the iteration scheme is terminated at the current load step and moves to the next load step, when the force convergence criterion,
with || · || denoting the Euclidean norm of the column vector, and the energy convergence criterion,
are simultaneously satisfied. Here , = 5 × 10−3 represent the preset force and energy tolerances. In the nonlinear regime, which starts right at the start in the present initial small-scale material nonlinearity scenario, the Newton-Raphson method with a relatively smaller magnitude of the load increment would require, as expected, similarly smaller number of iterations, and vice versa. Otherwise, it may introduce serious errors and, indeed, diverge from the exact solution. Solution of the resulting nonlinear equations by the Newton-Raphson (with Aitken acceleration) has earlier been verified by the BFGS (Broyden Fletcher Goldfarb Shanno) iterative scheme, thus validating computational accuracy of both the schemes [,]. Furthermore, the importance of selection of proper step size of the loading in the nonlinear range is amply demonstrated by Chaudhuri and Abu-Arja []. One improperly chosen large step size in the middle of this process can induce an artificially created chaotic situation, even if the previous and subsequent load step sizes are properly selected.
Bathe and Cimento [] have provided general guidelines for the number of iterations needed to achieve convergence within the prescribed tolerance in the context of Aitken acceleration, while cautioning about the empirical nature of the topic of rate of convergence. Rapid convergence rate is defined as one, when convergence with prescribed tolerance (such as what is described above) is achieved for a given load step within 4 iterations or less. The physical situation reflected by the relatively steeply rising stress-strain plot and/or pressure-deflection curves, presented in Section 6 below, that arises from the initial small-scale nonlinearity and that does not deviate too far from linear elastic equilibrium path fits this description. When a similar convergence with prescribed tolerance is achieved within 4 to 12 iterations, it is classified as the moderately fast convergence. This physico-computational scenario arises when the computed equilibrium path passes through the knee region with rapidly decreasing stiffness, as depicted in, e.g., Figure 4 of Kim and Chaudhuri [], Figure 7 of Hsia and Chaudhuri [], Figure 5 of Kim and Chaudhuri [], Figure 8 of Chaudhuri and Hsia [], Figure 6 of Kim and Chaudhuri [], Figures 8 and 11 of Chaudhuri and Kim [], Figure 11 of Chaudhuri and Kim [], Figure 6 of Chaudhuri [], Figure 11 of Kim and Chaudhuri [], Figure 7 of Chaudhuri and Kim [], Figures 8, 9 and 11 of Chaudhuri and Kim [], Figures 8–11 of Chaudhuri and Kim [], Figures 4 and 5 of Chaudhuri [], Figure 8 of Chaudhuri [], Figure 5 of Chaudhuri [], and Figure 3 of Chaudhuri []. Finally, when a similar convergence with prescribed tolerance takes more than 12 iterations, it is classified as slow. This is exemplified by the physico-computational scenario that entails almost flat or flattening region close to the limit point on the computed equilibrium path with approaching zero-stiffness or nearly so signaling the onset of localization, as displayed in Figure 6 of Kim and Chaudhuri [], Figures 8 and 11 of Chaudhuri and Kim [], Figure 11 of Chaudhuri and Kim [], Figure 6 of Chaudhuri [], Figure 11 of Kim and Chaudhuri [], Figure 7 of Chaudhuri and Kim [], Figures 8, 9 and 11 of Chaudhuri and Kim [], Figures 8–11 of Chaudhuri and Kim [], Figures 4 and 5 of Chaudhuri [], Figure 8 of Chaudhuri [], and Figure 5 of Chaudhuri [].
The procedure for computation of the hydrostatic buckling pressure of a ring is outlined by Kim and Chaudhuri [].
The finite element model of a quarter of the plane strain (perfect) ring along with the prescribed boundary conditions is presented in Figure 4. Double-symmetry conditions permit every model under consideration to be limited to only a quarter of the ring such that the corresponding surface-parallel displacements vanish along the center lines and the buckled shapes are assumed to be symmetric. Because the loading and geometric symmetries are assumed, boundary conditions on the surfaces in Figure 4 can be prescribed as follows []:
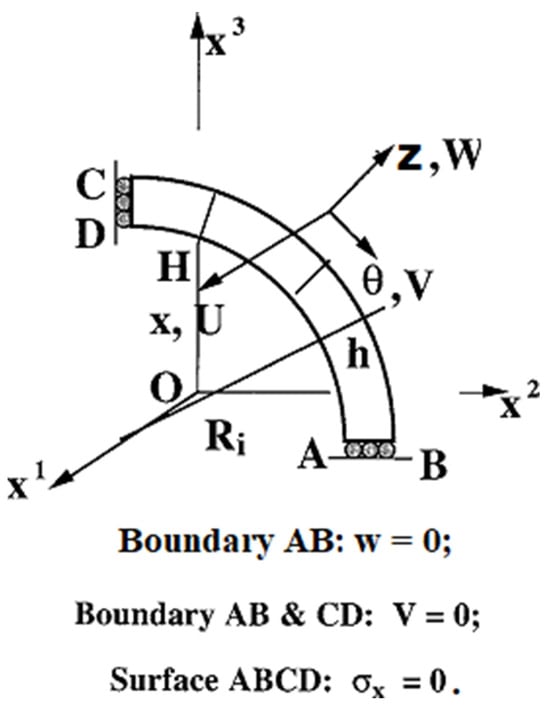
Figure 4.
Finite element model of a perfect ring [].
- (a)
- Geometric Symmetry:
- (b)
- Loading Symmetry:
The plane strain condition in the three-dimensional model is obtained by applying the displacement constraints as shown below:
where the superscript, i, denotes element number.
6. Results and Discussion
Hsia and Chaudhuri [] have established the accuracy as well as relatively rapid convergence characteristics of the present 16 node isoparametric element, employed for fully nonlinear analysis of perfect shallow homogeneous isotropic cylindrical panels. Kim and Chaudhuri [] have shown the convergence of the critical buckling pressure, computed by the finite element analysis, of a perfect thin finite cylindrical shell; see their Table 1. They also have compared thus-converged buckling pressure, , with its classical counterpart, , obtained using the Donnell shell theory []. The 4.5% (approximately) higher magnitude of the “converged” finite element buckling pressure (in comparison to its classical Donnell theory counterpart) is attributable to the simplified nature of the Donnell shell theory in which certain curvature effect is neglected, in a manner similar to the von Karman type nonlinearity. Chaudhuri and Hsia [] have shown, in their Figure 2, a comparison of results, computed using their serendipity-type cubic (24-node) and the present quadratic (16-node) quadrilateral shell elements, of a homogeneous isotropic shallow thin panel. Kim and Chaudhuri [] and Hsia and Chaudhuri [] have examined the accuracy of the von Karman type nonlinearity on the computed response of a moderately thick isotropic ring and a thin-shallow clamped cylindrical panel, respectively.
Example 1. Pre-Buckling and Pre-Yield Response of Relatively Thin Perfect Isotropic Rings with Small-Scale Material Nonlinearity Subjected to External Pressures
Pre-buckling and pre-yield response of a relatively thin (Ri/h = 25.64) perfect isotropic stainless steel 316 ring with small-scale material nonlinearity, subjected to external pressure, is numerically investigated. The inner radius, Ri, and thickness, h, of the ring under investigation are 10.16 cm (4 in.) and 3.9624 mm (0.156 in.), respectively. The initial elastic properties are given as follows: E = 206.85 GPa (30 Msi) and ν = 0.3.
The yield stress is 206.843 MPa (30 ksi). A typical stress–strain curve for stainless steel with definitions of key material parameters is depicted in Figure 1 of Arrayago et al. []. The initial (pre-yield/pre-buckling) portion of the stress-strain plot for stainless steel 316, showing small scale material nonlinearity is displayed in Figure 5.
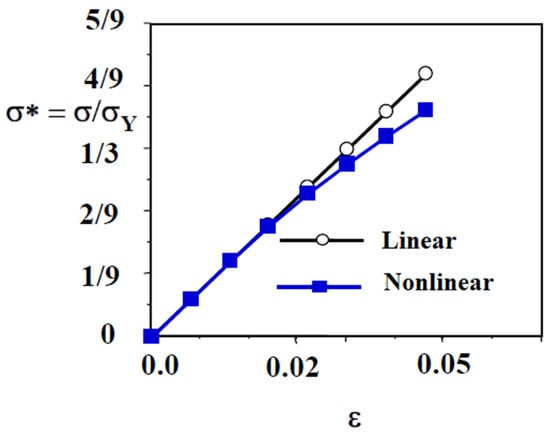
Figure 5.
Initial pre-yield stress–strain curve for stainless steel 316 with initial small-scale nonlinearity.
Before presenting numerical results for relatively thin isotropic perfect rings with initial small-scale material nonlinearity, those pertaining to thin and moderately thick linear elastic perfect rings are reproduced first and compared with their classical counterparts [,], , under two different loading conditions (see Table 1 of Chaudhuri []). As has been discussed above in Section 4, double-symmetry conditions permit the model under consideration to be limited to only a quarter of the geometry such that the corresponding surface-parallel displacements vanish along the centerlines and the buckled shapes are assumed to be symmetric. The ring geometry is described in detail in Figure 2 of Kim and Chaudhuri [].
A convergence check of the present analysis is available in Table 1 of Kim and Chaudhuri [], which shows that the displacement and buckling pressure of the perfect ring converge reasonably fast with the 10 × 1 mesh, used in conjunction with the reduced integration scheme to prevent shear locking [,]. The present computed values for hydrostatic buckling pressure are somewhat higher than their classical counterparts, = E/[4(h/R)3], because of the effects of the transverse shear/normal (primarily shear) deformation and circumferential compressibility, which have softening effects, being not accounted for in the classical buckling analysis. The exact buckling pressure and displacement are, however, obtained for the constant directional pressure as shown in Table 1 of Kim and Chaudhuri [], which are higher than the computed hydrostatic buckling pressure because of the membrane action.
Table 2 of Chaudhuri [] has presented comparison of the buckling pressure, , computed by using the present FEA (see also Ref. []) with its nonlinear resonance counterpart, for the afore-mentioned two loading conditions. The relative difference, defined as, , for the hydrostatic pressure and radial pressure loading cases are 1.006% and 1.215%, respectively, which testifies to the accuracy of both sets of results. The slight difference is possibly due to the assumption of transverse inextensibility in the nonlinear resonance analysis [], while the present FEA permits transverse normal deformation. = 2.895 MPa (419.849262 psi).
Figure 6 presents the comparison for plots, depicting the normalized pressure, vs. normalized deflection, w* = w/h, of the crown of the relatively thin (Ri/h = 25.64) perfect quarter-ring (see point D, Figure 4), for linear elastic and initial small-scale nonlinear material properties. This plot shows that the pressure-deflection curve for the perfect ring with initial small-scale material nonlinearity deviates from the corresponding linear elastic response by as much as 15% (approx.) as the buckling pressure is approached (88% of ).
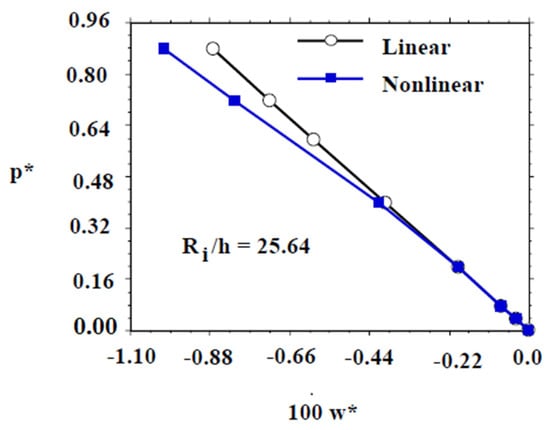
Figure 6.
Normalized hydrostatic pressure vs. normalized deflection curve for a perfect relatively thin (Ri/h = 25.64) stainless steel 316 ring.
Figure 7 and Figure 8 exhibit similar comparisons for plots, depicting the normalized pressure, vs. normalized radial or transverse () and hoop or circumferential () strains, respectively, of the crown of the relatively thin (Ri/h = 25.64) perfect quarter-ring (see point D, Figure 4), for linear elastic and initial small-scale nonlinear material properties. These plots similarly show that the pressure-strain curves for the perfect ring with initial small-scale material nonlinearity deviate from their linear elastic response counterparts by as much as 16.67% and 13.64%, respectively, as the buckling pressure is approached (88% of ). As expected, the transverse normal strain values are about two orders of magnitude smaller than their circumferential strain counterparts, because of the relative thinness of the ring. It is interesting to observe the trends of the two deviations exhibiting opposite directions. The reason is the Poisson effect. However, the radial strains are so small, that this effect does not have any practical impact.
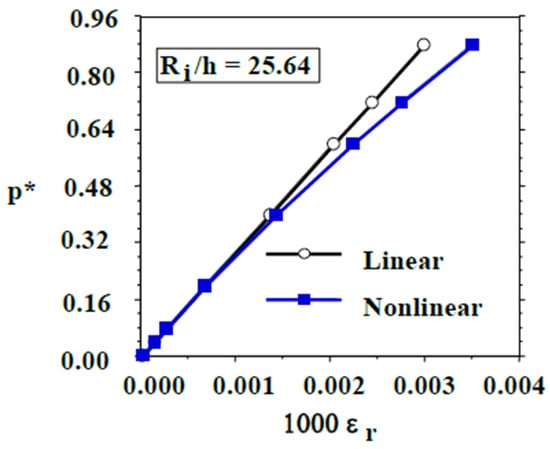
Figure 7.
Normalized hydrostatic pressure vs. transverse normal strain curve for a perfect relatively thin (Ri/h = 25.64) stainless steel 316 ring.
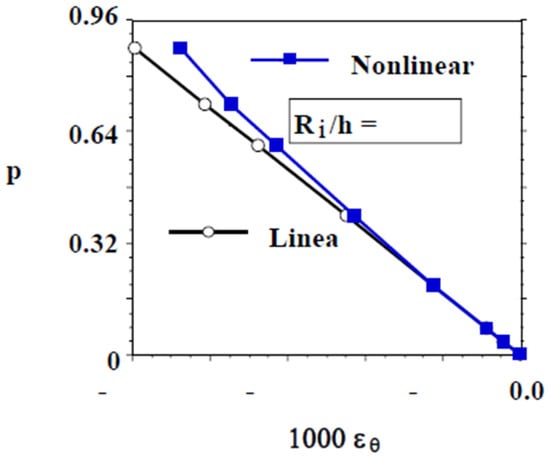
Figure 8.
Normalized hydrostatic pressure vs. circumferential strain curve for a perfect relatively thin (Ri/h = 25.64) stainless steel 316 ring.
Plots, depicting the normalized pressure, vs. normalized circumferential or hoop ( = ) stress, of the crown of the relatively thin (Ri/h = 25.64) perfect quarter-ring, for linear elastic and initial small-scale nonlinear material properties, are displayed in Figure 9. Again, the pressure vs. hoop stress curve for the perfect ring with initial small-scale material nonlinearity deviates from its linear elastic response counterpart by as much as 10.89% (approx.) as the buckling pressure is approached (88% of ). These enhanced responses due to initial small-scale nonlinearity are significant enough to not miss attentions from designers and operators of submersibles alike.
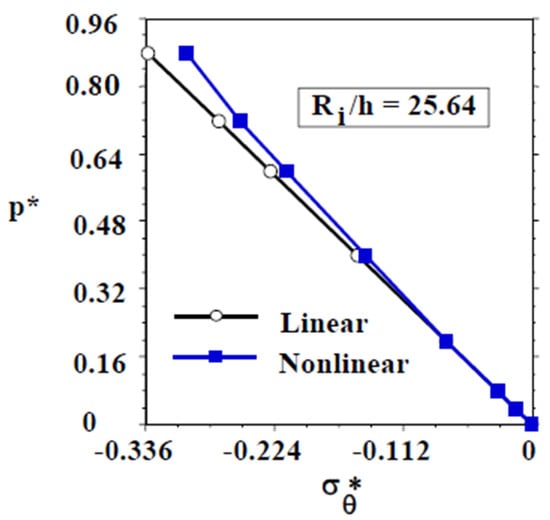
Figure 9.
Normalized hydrostatic pressure vs. circumferential stress curve for a perfect relatively thin (Ri/h = 25.64) stainless steel 316 ring.
7. Summary and Conclusions
The effects of initial small-scale material nonlinearity on the pre-yield and pre-buckling response of externally pressurized metallic (plane strain) perfect rings (very long cylindrical shells) is investigated. The cylindrically curved 16-node isoparametric element, based on an assumed quadratic displacement field (in surface-parallel coordinates) and the assumption of linear distribution of displacements through thickness (LDT), is utilized to obtain the discretized system of equations. The effect of initial small-scale material nonlinearity (assumed hypo-elastic) on the deformation and stress field in the pre-yield stress and pre-buckling regime of a perfect relatively thin (Ri/h = 25.64) metallic very long cylindrical shell (plane strain ring) is numerically investigated, with the objective of understanding its early-stage compressive behavior. What follows is a list of useful and physically meaningful conclusions drawn from the numerical results:
- (i)
- Initial small-scale material nonlinearity has a pronounced effect on the pre-yield stress and pre buckling compressive response a perfect metallic relatively thin (Ri/h = 25.64) very long cylindrical shell (plane strain ring) under investigation.
- (ii)
- Numerical results suggest that the pressure-deflection curve for a perfect relatively thin (Ri/h = 25.64) stainless steel 316 ring with initial small-scale material nonlinearity deviates from the corresponding linear elastic response by as much as 15% (approx.) as the buckling pressure is approached (88% of ).
- (iii)
- The pressure vs. transverse and circumferential strain curves for the perfect relatively thin (Ri/h = 25.64) stainless steel 316 ring with initial small-scale material nonlinearity deviate from their linear elastic response counterparts by as much as 16.67% and 13.64%, respectively, as the buckling pressure is approached (88% of ).
- (iv)
- The transverse normal strain values are about two orders of magnitude smaller than their circumferential strain counterparts, because of the relative thinness of the ring.
- (v)
- The pressure vs. hoop stress curve for the perfect relatively thin (Ri/h = 25.64) stainless steel 316 ring with initial small-scale material nonlinearity deviates from its linear elastic response counterpart by as much as 10.89% (approx.) as the buckling pressure is approached (88% of ).
- (vi)
- These enhanced responses for metallic rings due to initial small-scale nonlinearity are significant enough to not miss attentions from designers and operators of submersibles alike.
Author Contributions
Conceptualization, R.A.C.; Methodology, R.A.C.; Software, D.K.; Validation, R.A.C. and D.K.; Formal analysis, R.A.C. and D.K.; Investigation, R.A.C. and D.K.; Resources, R.A.C.; Data curation, R.A.C. and D.K.; Writing—original draft, R.A.C.; Writing—review & editing, R.A.C.; Supervision, R.A.C.; Project administration, R.A.C.; Funding acquisition, R.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
Author Deokjoo Kim was employed by the company TAEJIN Technology. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Linear differential operator matrix relating the linear incremental strain components to incremental displacement components | |
| b, t | Subscript or superscript indicating the bottom and the top surface, respectively |
| Incremental elastic stiffness (material property) tensor | |
| Differential loading surface area evaluated at the first iteration of each load step when hydrostatic pressure is applied | |
| Infinitesimal control volume | |
| Linear incremental component of the 6 × 1 strain vector | |
| {fL} | Applied load vector |
| {fL} | Applied load vector at the time t + ∆t |
| {fN} | Nonlinear internal force vector |
| {fN}(i) | Nonlinear internal force vector at the ith iteration of the time step between t and t + ∆t |
| Coefficient of the first fundamental differential quadratic form of a parallel surface in the jth direction, j = 1 (x), 2 (θ), 3 (z) | |
| Coefficient of the first fundamental differential quadratic form of the bottom surface in the θ direction | |
| h | Thickness of the shell/ring |
| [KL] | Linear global stiffness matrix |
| m, n | Ratio of reference yield stress to the corresponding modulus, and strain hardening parameter, respectively, in the Ramberg-Osgood representation |
| N | Total number of elements |
| n(t) | Unit normal vector for the top surface with respect to the fixed coordinate system |
| pr, p | Applied general and uniform, respectively, hydrostatic pressure |
| pcr | Classical buckling pressure of a long cylindrical shell (plane strain ring) |
| , | Incremental elastic stiffness (material property) matrix, and its components, respectively |
| Ri | Inner radius of a long perfect cylindrical shell (plane strain ring) |
| External virtual work done on a body | |
| r | Radial coordinate of a point in an undeformed perfect ring |
| Loading surface area evaluated at the first iteration of each load step when hydrostatic pressure is applied | |
| Incremental stress component | |
| Second Piola-Kirchhoff stress tensor at time t + Δt | |
| 9 × 9 stress matrix evaluated at time t | |
| 6 × 1 stress vector evaluated at time t | |
| t | Time as an index |
| ,, | Incremental nodal displacement components at the jth node on the bottom surface in x1 (or x), x2 (or θ), and z directions, respectively |
| ,, | Incremental nodal displacement components at the jth node on the top surface in x1 (or x), x2 (or θ), and z directions, respectively |
| x, θ, z | Coordinates of a point |
| Total Green-Lagrangian strain tensor evaluated at time t + ∆t | |
| , | Force and energy convergence criteria, respectively |
| [Φ] | Quadratic global interpolation function matrix |
| Quadratic element interpolation function in terms of r’ and s’ |
Appendix A. Definition of Certain Matrix Operators
The matrix referred to in Equations (14) and (15a,b) is given by [,,]
The layer-wise linear distribution of displacement matrix, [TBT], referred to in Equations (14) and (15a,b), can be written as follows:
The quadratic global interpolation function matrix, [Φ], referred to in Equations (14) and (15a,b), is given by [,,,]
wherein
and {0} is 1 × 8 null matrix. , j = 1, …, 8, are the shape functions as used for displacements and coordinates. Finally, stress vector, , referred to in Equation (15b), is given as follows:
References
- Casey, S. The Abyss: The Titan Submersible Disaster Was Years in the Making, New Details Reveal. Vanit, 17 August 2023. Available online: https://www.vanityfair.com/news/2023/08/titan-submersible-implosion-warnings (accessed on 29 January 2024).
- Couch, W.P.; Ward, G.D.; Blumenberg, W.F. Investigation of Filament-Reinforced Plastic Deep Submergence Pressure Hulls July 1966 to March 1969; Department of the Navy, Naval Ship Research & Development Center: Washington, DC, USA, 1969. [Google Scholar]
- Garala, H.J. Structural Evaluation of 8-Inch Diameter Graphite-Epoxy Composite Cylinders Subjected to External Hydrostatic Compressive Loading; DTRC Report 89/016; David Taylor Research Center: Bethesda, MD, USA, 1989. [Google Scholar]
- Garala, H.J.; Chaudhuri, R.A. Structural evaluation of advanced composite thick-section cylinders under bi-axial compressive loading. In Mechanics of Thick Composites; Rajapakse, Y., Ed.; ASME AMD: New York, NY, USA, 1993; Volume 162, pp. 227–236. [Google Scholar]
- Hahn, H.T.; Sohi, M.M. Buckling of a fiber bundle embedded in epoxy. Compos. Sci. Technol. 1986, 27, 25–41. [Google Scholar] [CrossRef]
- Abdallah, M.G.; Gascoigne, H.E.; Cairnes, D.S.; Patton, K.B. Measurement of deformation in thick composite rings subjected to external pressure. In Proceedings of the SEM’s Spring Conference on Experimental Mechanics and Manufacturer’s Exhibit, Albuquerque, NM, USA, 4–6 June 1990. [Google Scholar]
- Chaudhuri, R.A. Prediction of the compressive strength of thick-section advanced composite laminates. J. Compos. Mater. 1991, 25, 1244–1276. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Garala, H.J. Analytical/experimental evaluation of hybrid commingled carbon/glass/epoxy thick-section composites under compression. J. Compos. Mater. 1995, 29, 1695–1718. [Google Scholar] [CrossRef]
- Hunt, G.W.; Lucena Neto, E. Localized buckling in long axially-loaded cylindrical shells. J. Mech. Phys. Solids 1991, 39, 881–894. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. A nonlinear zigzag theory for finite element analysis of highly shear-deformable laminated anisotropic shells. Compos. Struct. 2008, 85, 350–359. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kim, D. On propagation of shear crippling (kinkband) instability in a long imperfect laminated composite cylindrical shell under external pressure. Int. J. Solids Struct. 1997, 34, 3455–3486. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kim, D. Localization and shear-crippling (kinkband) instability in a thick imperfect laminated composite ring under hydrostatic pressure. Int. J. Solids Struct. 2003, 40, 7063–7092. [Google Scholar] [CrossRef]
- Kim, D.; Chaudhuri, R.A. Effect of lamination sequence on the localization and shear crippling instability in thick imperfect cross-ply rings under external pressure. Compos. Struct. 2007, 80, 504–513. [Google Scholar] [CrossRef]
- Kim, D.; Chaudhuri, R.A. Influence of localized imperfection on the instability of isotropic/cross-ply cylindrical shells/rings under external pressure. Compos. Struct. 2005, 67, 57–70. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Effects of thickness and fibre misalignment on compression fracture in cross-ply (very) long cylindrical shells under external pressure. Proc. R. Soc. A Lond. 2015, 471, 20150147. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Effects of fiber misalignment and transverse shear modulus on localization and shear crippling instability in thick imperfect cross-ply rings under external pressure. Compos. Struct. 2008, 82, 587–599. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kim, D. Influence of localized imperfection and surface-parallel shear modulus nonlinearity on the instability of a thin cross-ply cylindrical shell under external pressure. Compos. Struct. 2008, 82, 235–244. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kim, D. Sensitivity of the post-localization response of a thick cross-ply imperfect ring to transverse Young’s modulus nonlinearity. Compos. Struct. 2008, 84, 44–55. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kim, D. Effects of thickness and transverse shear modulus nonlinearity on the post-“yield” and post-localization response of an externally pressurized imperfect cross-ply ring. Compos. Struct. 2009, 88, 83–96. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Stress intensity factor and energy release rate of externally pressurized thick cross-ply (very) long cylindrical shells with low-hardening transverse shear modulus nonlinearity. Eng. Fract. Mech. 2016, 151, 138–160. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Localization, delocalization and compression fracture in externally pressurized thick cross-ply (very) long cylindrical shells with material non-linearity: A multi-scale and multi-physics analysis. Int. J. Non-Linear Mech. 2016, 84, 68–81. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Comparison of stress singularities of kinked carbon and glass fibres weakening compressed unidirectional composites: A three-dimensional trimaterial junction stress singularity analysis. Philos. Mag. 2014, 94L, 625–667. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. A micro-kink theory for determination of shear modulus of a unidirectional composite lamina. Compos. Struct. 2010, 92, 395–400. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Xie, M.S.; Garala, H.J. Stress singularity due to kink band weakening a unidirectional composite under compression. J. Compos. Mater. 1996, 30, 672–691. [Google Scholar] [CrossRef]
- Moran, P.M.; Shih, C.F. Kink band propagation and broadening in ductile matrix fiber composites, experiments and analysis. Int. J. Solids Struct. 1998, 35, 1709–1722. [Google Scholar] [CrossRef]
- Gutkin, R.; Pinho, S.T.; Robinson, P.; Curtis, P.T. On the transition from shear-driven fibre compressive failure to fibre kinking in notched CFRP laminates under longitudinal compression. Compos. Sci. Tech. 2010, 70, 1223–1231. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability, 2nd ed.; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Simitses, G.J. Buckling and post-buckling of imperfect cylindrical shells: A review. Appl. Mech. Rev. 1986, 39, 1517–1524. [Google Scholar] [CrossRef]
- Jones, R.M.; Morgan, H.S. Buckling and vibration of cross-ply laminated circular cylindrical shells. AIAA J. 1975, 13, 664–671. [Google Scholar] [CrossRef]
- Bradford, M.A.; Uy, B.; Pi, Y.L. In-plane elastic stability of arches under a central load. ASCE J. Eng. Mech. 2002, 128, 710–719. [Google Scholar] [CrossRef]
- Fu, L.; Waas, A.M. Initial postbuckling behavior of thick rings under uniform external hydrostatic pressure. ASME J. Appl. Mech. 1995, 62, 338–345. [Google Scholar] [CrossRef]
- Wu, B.; Yu, Y.; Li, Z. Analytical approximations to large post-buckling deformation of elastic rings under uniform hydrostatic pressure. Int. J. Mech. Sci. 2007, 49, 661–668. [Google Scholar] [CrossRef]
- Djondjorov, P.A.; Vassilev, V.M.; Mladenov, I.M. Analytic description and explicit parametrization of the equilibrium shapes of elastic rings and tubes under uniform hydrostatic pressure. Int. J. Mech. Sci. 2011, 53, 355–364. [Google Scholar] [CrossRef]
- Kim, D.; Chaudhuri, R.A. Effect of thickness on buckling of perfect cross-ply rings under external pressure. Compos. Struct. 2007, 81, 525–532. [Google Scholar] [CrossRef]
- Kim, D.; Chaudhuri, R.A. Postbuckling of moderately thick imperfect rings under external pressure. ASCE J. Eng. Mech. 2006, 132, 1273–1276. [Google Scholar] [CrossRef]
- Kerdegarbakhsh, M.; Kiani, Y.; Esfahani, S.E.; Eslami, M.R. Postbuckling of FGM rings. Int. J. Solids Struct. 2014, 85, 187–195. [Google Scholar] [CrossRef]
- Asemi, K.; Kiani, Y. Postbuckling up to collapse of polar orthotropic linearly elastic rings subjected to external pressure. Int. J. Struct. Stab. Dyn. 2016, 16, 1450091. [Google Scholar] [CrossRef]
- Kim, D.; Chaudhuri, R.A. Postbuckling behavior of symmetrically laminated thin shallow circular arches. Compos. Struct. 2009, 87, 101–108. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. A nonlinear resonance (eigenvalue) approach for computation of elastic collapse pressures of harmonically imperfect relatively thin rings. Thin-Walled Struct. 2018, 127, 344–353. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kim, D.; Pavliga, J.R. A nonlinear resonance (eigenvalue) approach for computing elastic collapse pressure of a moderately thick cross-ply imperfect ring. Compos. Struct. 2008, 82, 117–126. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Kim, D.; Pavliga, J.R. Effects of thickness and modal imperfection amplitude on elastic collapse pressure of a cross-ply imperfect ring. Compos. Struct. 2008, 86, 370–384. [Google Scholar] [CrossRef]
- Hsia, R.L.; Chaudhuri, R.A. Geometrically nonlinear analysis of cylindrical shells using surface-parallel quadratic elements. Comput. Struct. 1996, 61, 1143–1154. [Google Scholar] [CrossRef]
- Kim, D.; Chaudhuri, R.A. Full and von Karman geometrically nonlinear analyses of laminated cylindrical panels. AIAA J. 1995, 33, 2173–2181. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Hsia, R.L. Effect of thickness on large-deflection behavior of shells. AIAA J. 1999, 37, 403–405. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Hsia, R.L. Effect of thickness on the large elastic deformation behavior of laminated shells. Compos. Struct. 1999, 44, 117–128. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. Localization, delocalization, and compression fracture in moderately thick transversely isotropic bilinear rings under external pressure. ASME J. Eng. Mater. Technol. 2006, 128, 603–610. [Google Scholar] [CrossRef]
- Kim, D.; Chaudhuri, R.A. Localized buckling of a bilinear elastic ring under external pressure. ASCE J. Eng. Mech. 2005, 131, 221–224. [Google Scholar] [CrossRef]
- Chaudhuri, S.N.; Chaudhuri, R.A.; Benner, R.E.; Penugonda, M. Raman spectroscopy for characterization of interfacial debonds between carbon fibers and polymer matrices. Compos. Struct. 2006, 76, 375–387. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures in Engineering Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1982. [Google Scholar]
- Chaudhuri, R.A. A degenerate triangular shell element with constant cross-sectional warping. Comput. Struct. 1988, 28, 315–325. [Google Scholar] [CrossRef]
- Seide, P.; Chaudhuri, R.A. Triangular finite element for analysis of thick laminated shells. Int. J. Numer. Methods Eng. 1987, 24, 1563–1579. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. A new three-dimensional shell theory in general (non-lines-of-curvature) coordinates for analysis of curved panels weakened by through/part-through holes. Compos. Struct. 2009, 89, 321–332. [Google Scholar] [CrossRef]
- Chaudhuri, R.A.; Seide, P. An approximate method for prediction of transverse shear stresses in a laminated shell. Int. J. Solids Struct. 1987, 23, 1145–1161. [Google Scholar] [CrossRef]
- Chaudhuri, R.A. On the prediction of interlaminar shear stresses in a thick laminated general shell. Int. J. Solids Struct. 1990, 26, 499–510. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress Strain Curves by Three Parameters; NACA-TN 902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1934. [Google Scholar]
- Chaudhuri, R.A.; Abu-Arja, K.R. Plastic deformation of a boron/aluminum tube under multi-axial loadings. Comput. Struct. 1986, 24, 915–921. [Google Scholar] [CrossRef]
- Bathe, K.J.; Cimento, A.P. Some practical procedures for the solution of nonlinear finite element equations. J. Comput. Meth. Appl. Mech. Eng. 1980, 22, 59–85. [Google Scholar] [CrossRef]
- Amazigo, J.C.; Frazer, W.B. Buckling under external pressure of cylindrical shells with dimple shaped initial imperfections. Int. J. Solids Struct. 1971, 7, 883–900. [Google Scholar] [CrossRef]
- Arrayago, I.; Real, E.; Gardner, L. Description of stress–strain curves for stainless steel alloys. Mater. Design 2015, 87, 540–552. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).