Fundamental Components and Principles of Supervised Machine Learning Workflows with Numerical and Categorical Data
Abstract
1. Introduction
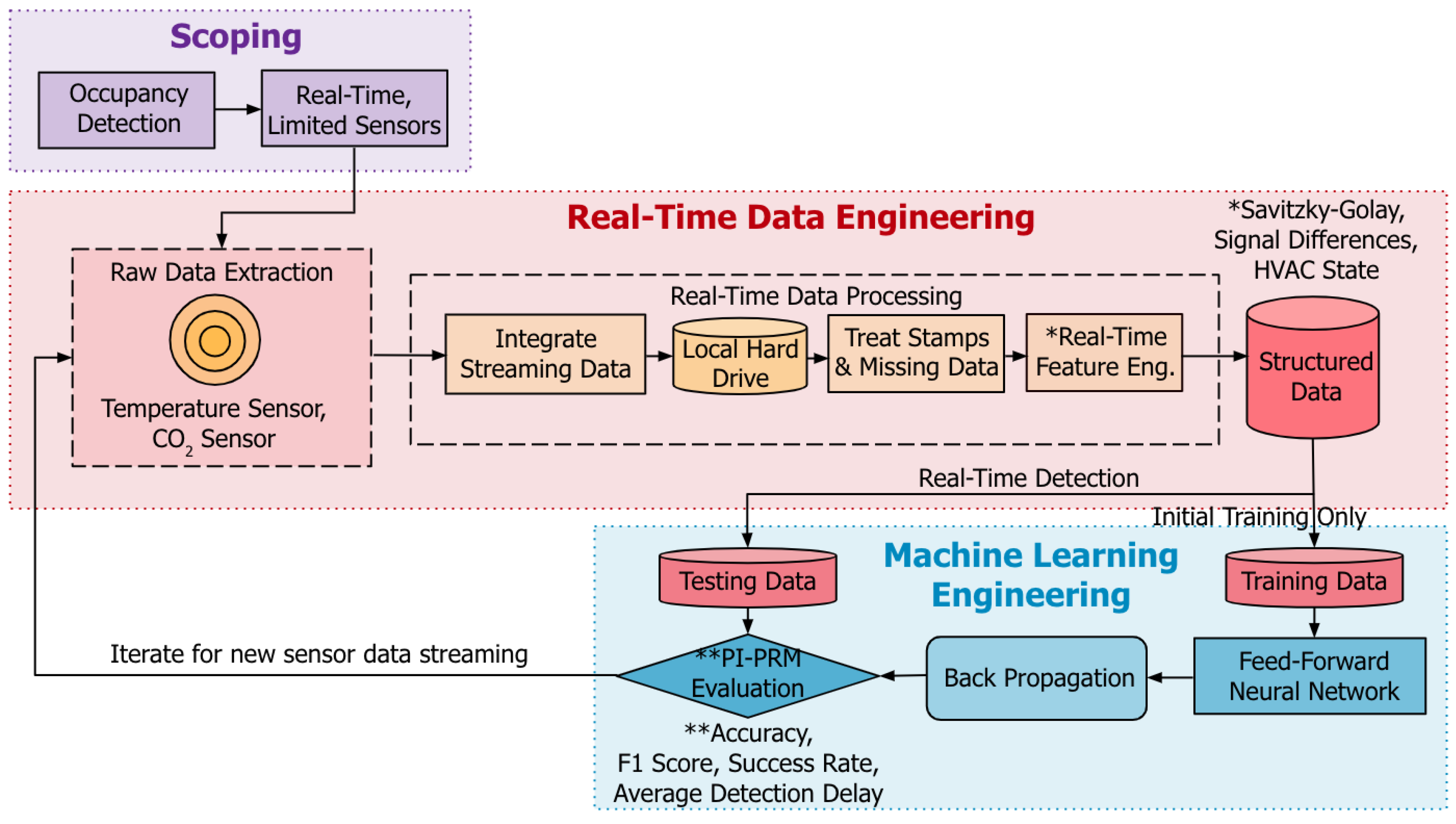
2. End-to-End Architecture of Machine Learning Workflows
3. Data Engineering
3.1. Data Pipeline: Extraction, Loading and Transformation
3.2. Feature Engineering
3.2.1. Feature Generation
3.2.2. Feature Transformation
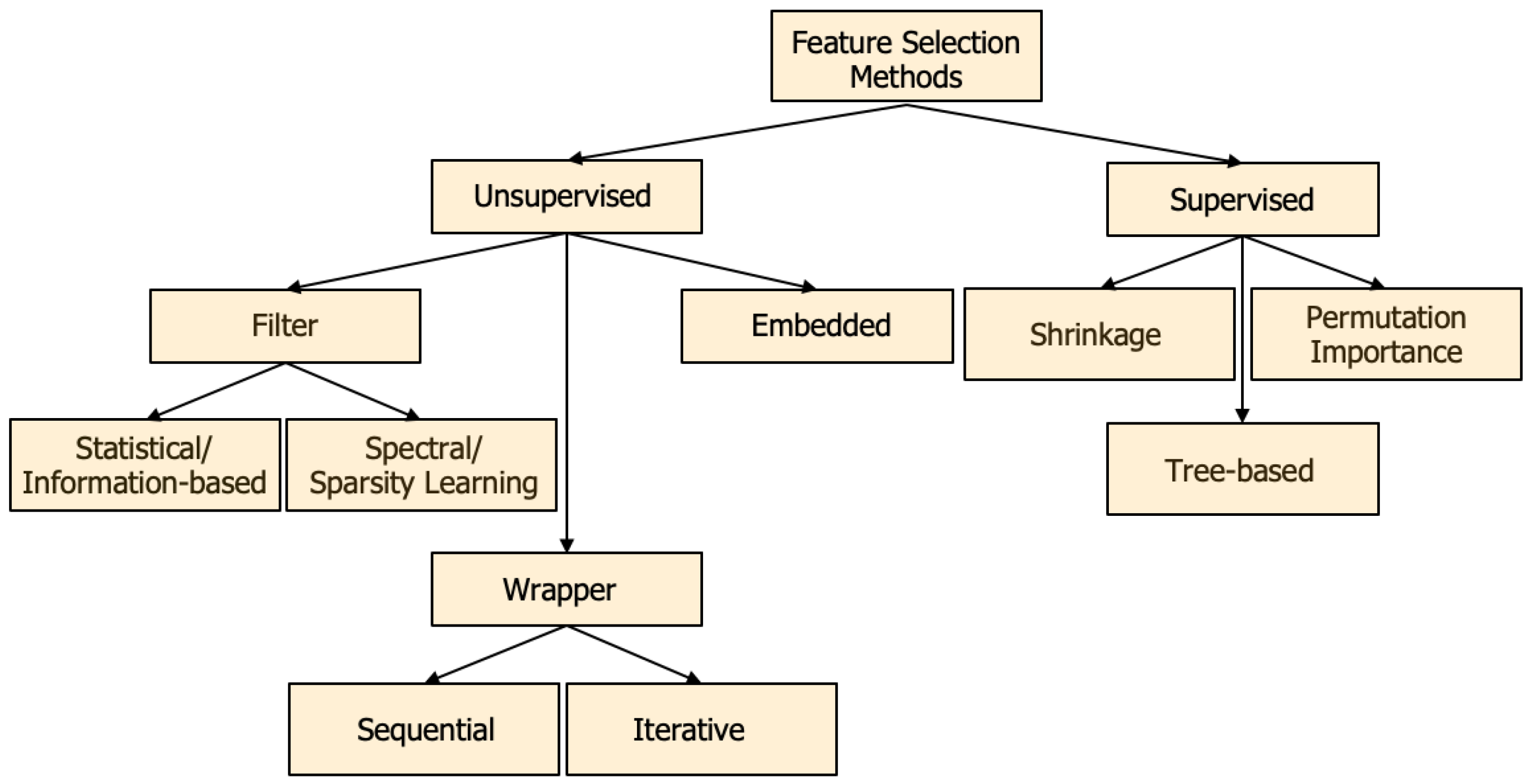
3.2.3. Feature Selection
- Filter methods [88,89,90]: In this category of methods, feature selection is a pre-processing step to the machine learning model training, and these methods are time-efficient:
- (a)
- Statistical/information-based: These methods maximize feature relevance by maximizing a dependence measure, such as variance, covariance, entropy [90], linear correlation [91], Laplacian score [92], and mutual information. Representative methods include Feature Selection with Feature Similarity (FSFS) [91] based on Maximal Information Compression Index (MICI) and Relevance Redundancy Feature Selection (RRFS) [93]. Fisher’s criterion [94] is only used in supervised learning.
- (b)
- Spectral/sparsity learning: These methods perform spectral analysis or combine spectral analysis with spectral learning. They find a trade-off between Goodness-of-Fit and a feature similarity measure. Representative methods include Multi-Cluster Feature Selection (MCFS) [95], Unsupervised Discriminative Feature Selection (UDFS) [96], and Non-negative Discriminative Feature Selection (NDFS) [89].
- Wrapper methods [88,89,90]: In this category, feature selection is intertwined with the machine learning model training and hence evaluated by the model performance. These methods are more accurate than filter methods but less time-efficient:
- (a)
- Sequential methods: These methods perform clustering on each feature subset and evaluate the clustering results based on some criterion. They can be based on Expectation Maximization or the Trace Criterion [97], or on the min/max of intra/inter-cluster variance [98] and a decision can be made based on a score that provides feature ranking. Another alternative is the Simplified Silhouette Sequential Forward Selection (SS-SFS) proposed in [99].
- (b)
- Iterative methods: Ref. [100] performs clustering and feature selection simultaneously by evaluating feature weights called feature saliences. Other iterative methods include Local Learning-based Clustering with Feature Selection (LLC-fs) [101], Embedded Unsupervised Feature Selection (EUFS) [102], and Dependence Guided Unsupervised Feature Selection (DGUFS) [103].
- Embedded methods: In this category, feature selection is part of the machine learning model training process [104].
- Shrinkage-based methods [106]: Single-output or multi-output regression models with - or -regularization can be trained via k-fold cross-validation (CV) to optimize a shrinkage parameter which trades-off model bias for variance. Penalization of the model weights with an norm is appropriate for feature selection because it can introduce feature sparsity (Lasso estimator [107]) when penalization with an norm (Ridge Regression [69]) does not force feature weights to zero. The combination of the two is called Elastic Net, which is useful when there is a group of features with high pairwise correlations [108]. Multi-output regression models perform better when outputs are correlated, i.e., when multi-task learning is desired, instead of independent task learning [109,110]. Multi-output models utilize an norm penalization term, which either includes or excludes a feature from the model for all outputs [111]. In the multi-output case, the average weight of a feature across all outputs is obtained, and then these average weights are normalized in the range (relative importance) with the min-max scaling method so that a rank of feature relative importance is derived [23].
- Tree-based methods: CART can be trained in a supervised sense and provide feature ranking as a byproduct of the training process [71] in single-output or multi-output Decision Trees (DTs) [112]. DTs are over-sensitive to the training set, irrelevant information, and noise; therefore, prior unsupervised feature selection is strongly encouraged via one of the methods proposed above. Moreover, DTs are known to overfit, and hence, ensembles of DTs [112], such as Bagging (bootstrap aggregation) [113], Boosted Trees [114] and Rotation Forests, are constructed to cope with overfitting. The RF, a characteristic example of Bagging, can generate diverse trees by bootstrap sampling and/or randomly selecting a subset of the features during learning [115,116]. Although an RF is faster and easier to train than a boosted tree [117,118,119], it is less accurate and sacrifices the intrinsic interpretability (explanation of output value and feature ranking) present in DTs [69]. In particular, feature selection happens inherently in single-output and multi-output DTs as the tree is being constructed since the splitting criteria used at each node select the feature which performs the most successful separation of the remaining examples [71]. Therefore, in RFs, feature ranking is either impurity-based, such as the Mean Decrease in Impurity (MDI), or permutation-based, such as Permutation Importance [115]. MDI is also known as Mean Decrease Gini or Gini Importance.
- Permutation Importance [115] is not only useful in RFs which have lost the inherent feature-ranking mechanism of the tree but in other supervised machine learning models as well. Permutation Importance is better than MDI because it is not computed on the training set but on the Out-of-Bag (OoB) sample and is, therefore, more useful to inform the feature importance for predictions [115]. Moreover, MDI significantly favors numerical features over categorical ones as well as high-cardinality categorical features (many categories) over low-cardinality ones [115], something that does not happen with Permutation Importance. The Permutation Importance of a feature is calculated as the difference between the original error and the average permuted error of this feature, over a number of specified repetitions [115]. The permuted error of each feature (the OoB error) occurs when that feature is permuted (shuffled). Permutation is a mechanism that breaks the relationship between that feature and the target variables, revealing the importance of a feature to the model training accuracy [120]. In trees and other supervised methods which use a feature-ranking approach to feature selection, the least-performing features in terms of relative importance can be excluded from the feature set.
3.2.4. Automated Feature Extraction
| Automated FE Tool | Operation | Tool Tested On | Developer | Paper |
|---|---|---|---|---|
| ExploreKit | Feature generation and ranking | DT, SVM, RF | UC Berkeley | [125] |
| One Button Machine | Feature discovery in relational DBs | RF, XGBOOST | IBM | [126] |
| AutoLearn | Feature generation and selection | kNN, LR, SVM, RF, Adaboost, NN, DT | IIIT | [127] |
| GeP Feature Construction | Feature generation from GeP on DTs | kNN, DT, Naive Bayes | Wellington University | [128] |
| Cognito | Feature generation and selection | N/A | IBM | [129] |
| RLFE | Feature generation and selection | RF | IBM | [130] |
| LFE | Feature transformation | LR, RF | IBM | [131] |
4. Machine Learning Engineering
4.1. Models and Algorithms for Supervised Learning with Numerical and Categorical Data
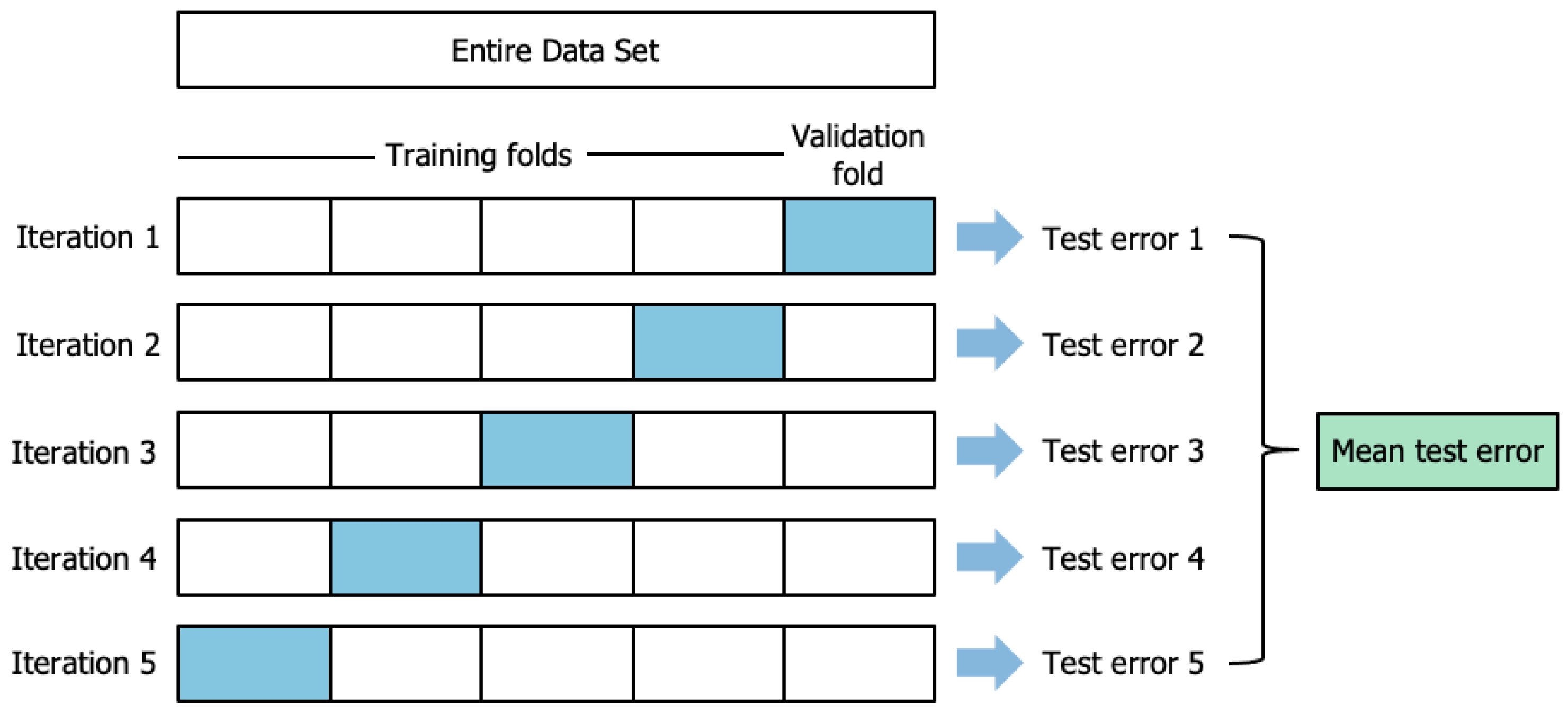
4.2. Model Training and Validation
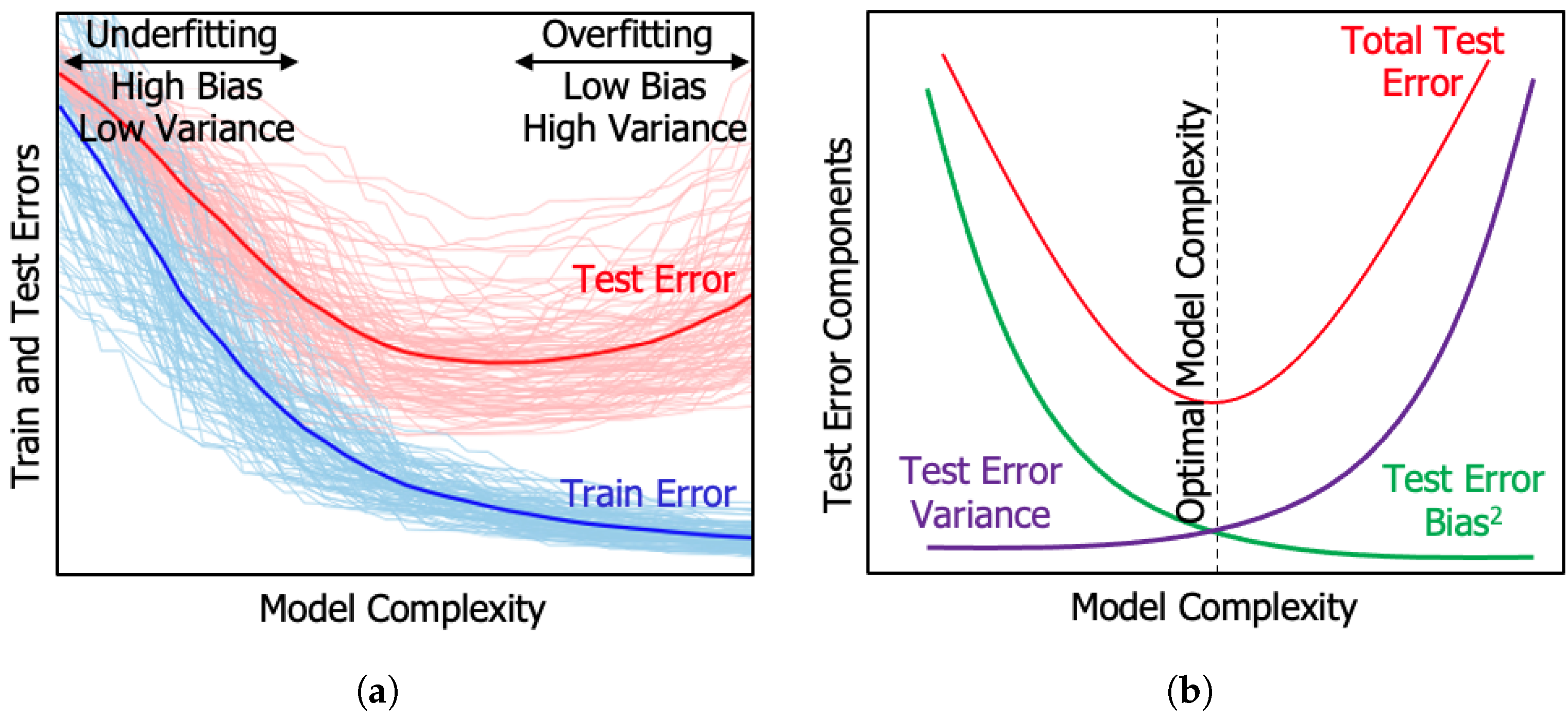
4.3. Model Evaluation
- Linear relationship between each feature and each target variable: this assumption can be verified in the testing set by constructing scatter plots of each output vs each feature.
- Homoscedasticity, i.e., constant residual variance for all the values of a feature: this assumption can be verified by plotting the residuals vs. each feature in the testing set.
- Independence of residual observations, which is the same as the independence of target variable observations (commonly violated in time series data): this can be verified by checking that the autocorrelation of the residual observations is non-zero with the Durbin–Watson test since that would indicate sample dependence.
- Normality of the target variable observations: this can be verified by constructing QQ plots of the residuals against the theoretical normal distribution and observing the straightness of the produced line.
5. Model Deployment
5.1. Testing
5.1.1. Unit Testing
5.1.2. Performance Testing
5.1.3. Integration Testing
5.1.4. System Testing
5.1.5. Acceptance Testing
5.1.6. A/B Testing
5.2. Model Deployment
5.3. Monitoring and Maintenance
5.4. Security Considerations
6. Automation in Machine Learning Workflows
6.1. AutoML Methods
- Black-box hyperparameter optimization:
- (a)
- Model-free black-box optimization methods include grid search in a finite range, which, however, suffers from the CoD and random search, where random search samples configurations at random until a certain budget for the search is exhausted [206]. This works better than grid search when some hyperparameters are much more important than others, which is very often the case [206]. Covariance Matrix Adaption Evolutionary Strategy (CMA-ES) [207], is one of the most competitive black-box optimization algorithms.
- (b)
- Bayesian optimization has gained interest due to DNN tuning for image classification [203,208], speech recognition [209] and neural language modeling [202]. For an in-depth introduction to Bayesian optimization, the interested reader is referred to [210,211]. Many recent advances in Bayesian optimization do not treat hyperparameter tuning as a black-box anymore, i.e., multi-fidelity hyperparameter turning, Bayesian optimization with meta-learning, and Bayesian optimization taking the pipeline structure into account [212,213].
- Multi-fidelity optimization: These methods are less costly than black-box optimization methods, which approximately assess the quality of hyperparameter settings. Multi-fidelity methods introduce heuristics inside an algorithm, using low-fidelity approximations of the actual loss function to reduce runtime. Such heuristics include hyperparameter tuning on a small data subset or feature subset and training for a few iterations by using CV or down-sampled images. Learning curve-based prediction for early stopping is used, as well as Bandit-based (successive halving [214] and Hyperband [215]) algorithms for algorithm selection based on low-fidelity algorithm approximations. Moreover, Bayesian Optimization Hyperband (BOHB) [216] combines Bayesian optimization and HyperBand to achieve a combination of strong anytime performance (quick improvements in the beginning by using low fidelities in HyperBand) and strong final performance (good performance in the long run by replacing HyperBand’s random search by Bayesian optimization). For adaptive fidelity options, see [36].
6.2. AutoML Systems
7. A Supervised Classification Workflow Example
8. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHO | Automated Hyperparameter Optimization |
| AIC | Akaike Information Criterion |
| ALA | Adaptive Linear Approximation |
| API | Application Programming Interface |
| AUC | Area Under Curve |
| Auto-WEKA | Automatic Model Selection and Hyperparameter Optimization |
| BDW | Best Daubechies Wavelet Coefficients |
| BFC | Best Fourier Coefficients |
| BIC | Bayesian Information Criterion |
| BOHB | Bayesian Optimization Hyperband |
| CART | Classification and Regression Tree |
| CASH | Combined Algorithm Selection and Hyperparameter optimization |
| CI/CD | Continuous Integration Continuous Delivery or Deployment |
| CMA-ES | Covariance Matrix Adaption Evolutionary Strategy |
| CoD | Curse of Dimensionality |
| CV | Cross-Validation |
| DB | Database |
| DDoS | Distributed Denial-of-Service |
| DevOps | Development Operations |
| DFS | Deep Feature Synthesis |
| DGUFS | Dependence Guided Unsupervised Feature Selection |
| DNN | Deep Neural Network |
| DT | Decision Tree |
| ELT | Extract, Load, Transform |
| ETL | Extract, Transform, Load |
| EUFS | Embedded Unsupervised Feature Selection |
| FIR | Finite Impulse Response |
| FN | False Negative |
| FP | False Positive |
| FSFS | Feature Selection with Feature Similarity |
| GeP | Genetic Programming |
| GP | Gaussian Process |
| HVAC | Heating Ventilation and Air Conditioning |
| IARPA | Intelligence Advanced Research Projects Activity |
| KDD | Knowledge Discovery from Data |
| kNN | k-Nearest Neighbors |
| LARS | Lasso Regression |
| LBFGS | Broyden–Fletcher–Goldfarb–Shanno |
| LDS | Linear Discriminant Analysis |
| LLC-fs | Local Learning-based Clustering with feature selection |
| LR | Logistic Regression |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MCFS | Multi-Cluster Feature Selection |
| MDI | Mean Decrease in Impurity |
| MDL | Minimum Description Length |
| MICI | Maximal Information Compression Index |
| ML | Machine Learning |
| MLOps | Machine Learning Operations |
| MRDTL | Multi-Relational Decision Tree Learning |
| MSE | Mean Squared Error |
| NAS | Neural Automated Search |
| NDFS | Non-negative Discriminative Feature Selection |
| NN | Neural Network |
| NNI | Neural Network Intelligence |
| OLS | Ordinary Least Squares |
| OoB | Out-of-Bag |
| OOP | Object Oriented Programming |
| PoLP | Principle of Least Privilege |
| PCA | Principal Component Analysis |
| REFSVM | Recursive Feature Elimination Support Vector Machines |
| RF | Random Forest |
| RICA | Reconstruction Independent Component Analysis |
| RMSE | Root Mean Squared Error |
| ROC | Receiver Operating Characteristic |
| RRFS | Relevance Redundancy Feature Selection |
| SLA | Service Level Agreement |
| SQL | Structured Query Language |
| SRM | Structural Risk Minimization |
| SS-SFS | Simplified Silhouette Sequential Forward Selection |
| SVD | Singular Value Decomposition |
| SVM | Support Vector Machines |
| TDD | Test-Driven Development |
| TN | True Negative |
| TOC | Total Operating Characteristic |
| TP | True Positive |
| TPOT | Tree-based Pipeline Optimization Tool |
| UDFS | Unsupervised Discriminative Feature Selection |
| VPC | Virtual Private Cloud |
References
- Gibert, D.; Mateu, C.; Planes, J. The rise of machine learning for detection and classification of malware: Research developments, trends and challenges. J. Netw. Comput. Appl. 2020, 153, 102526. [Google Scholar] [CrossRef]
- Bravo-Rocca, G.; Liu, P.; Guitart, J.; Dholakia, A.; Ellison, D.; Falkanger, J.; Hodak, M. Scanflow: A multi-graph framework for Machine Learning workflow management, supervision, and debugging. Expert Syst. Appl. 2022, 202, 117232. [Google Scholar] [CrossRef]
- Bala, A.; Chana, I. Intelligent failure prediction models for scientific workflows. Expert Syst. Appl. 2015, 42, 980–989. [Google Scholar] [CrossRef]
- Quemy, A. Two-stage optimization for machine learning workflow. Inf. Syst. 2020, 92, 101483. [Google Scholar] [CrossRef]
- Grabska, E.; Frantz, D.; Ostapowicz, K. Evaluation of machine learning algorithms for forest stand species mapping using Sentinel-2 imagery and environmental data in the Polish Carpathians. Remote Sens. Environ. 2020, 251, 112103. [Google Scholar] [CrossRef]
- Liu, R.; Misra, S. A generalized machine learning workflow to visualize mechanical discontinuity. J. Pet. Sci. Eng. 2022, 210, 109963. [Google Scholar] [CrossRef]
- He, S.; Wang, Y.; Zhang, Z.; Xiao, F.; Zuo, S.; Zhou, Y.; Cai, X.; Jin, X. Interpretable machine learning workflow for evaluation of the transformation temperatures of TiZrHfNiCoCu high entropy shape memory alloys. Mater. Des. 2023, 225, 111513. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, G.; Dong, J.; Xing, X.h.; Dai, J.; Zhang, C. MiYA, an efficient machine-learning workflow in conjunction with the YeastFab assembly strategy for combinatorial optimization of heterologous metabolic pathways in Saccharomyces cerevisiae. Metab. Eng. 2018, 47, 294–302. [Google Scholar] [CrossRef] [PubMed]
- Wong, W.K.; Joglekar, M.V.; Saini, V.; Jiang, G.; Dong, C.X.; Chaitarvornkit, A.; Maciag, G.J.; Gerace, D.; Farr, R.J.; Satoor, S.N.; et al. Machine learning workflows identify a microRNA signature of insulin transcription in human tissues. Iscience 2021, 24, 102379. [Google Scholar] [CrossRef] [PubMed]
- Paudel, D.; Boogaard, H.; de Wit, A.; Janssen, S.; Osinga, S.; Pylianidis, C.; Athanasiadis, I.N. Machine learning for large-scale crop yield forecasting. Agric. Syst. 2021, 187, 103016. [Google Scholar] [CrossRef]
- Haghighatlari, M.; Hachmann, J. Advances of machine learning in molecular modeling and simulation. Curr. Opin. Chem. Eng. 2019, 23, 51–57. [Google Scholar] [CrossRef]
- Reker, D. Practical considerations for active machine learning in drug discovery. Drug Discov. Today Technol. 2019, 32, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Narayanan, H.; Dingfelder, F.; Butté, A.; Lorenzen, N.; Sokolov, M.; Arosio, P. Machine learning for biologics: Opportunities for protein engineering, developability, and formulation. Trends Pharmacol. Sci. 2021, 42, 151–165. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.; Kwak, J.; Lee, S. Machine learning workflow for the oil uptake prediction of rice flour in a batter-coated fried system. Innov. Food Sci. Emerg. Technol. 2021, 74, 102796. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Lv, A.; Cheng, L.; Aghighi, M.A.; Masoumi, H.; Roshan, H. A novel workflow based on physics-informed machine learning to determine the permeability profile of fractured coal seams using downhole geophysical logs. Mar. Pet. Geol. 2021, 131, 105171. [Google Scholar] [CrossRef]
- Gharib, A.; Davies, E.G. A workflow to address pitfalls and challenges in applying machine learning models to hydrology. Adv. Water Resour. 2021, 152, 103920. [Google Scholar] [CrossRef]
- Kampezidou, S.I.; Ray, A.T.; Duncan, S.; Balchanos, M.G.; Mavris, D.N. Real-time occupancy detection with physics-informed pattern-recognition machines based on limited CO2 and temperature sensors. Energy Build. 2021, 242, 110863. [Google Scholar] [CrossRef]
- Fu, H.; Kampezidou, S.; Sung, W.; Duncan, S.; Mavris, D.N. A Data-driven Situational Awareness Approach to Monitoring Campus-wide Power Consumption. In Proceedings of the 2018 International Energy Conversion Engineering Conference, Cincinnati, OH, USA, 9–11 July 2018; p. 4414. [Google Scholar]
- Kampezidou, S.; Wiegman, H. Energy and power savings assessment in buildings via conservation voltage reduction. In Proceedings of the 2017 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 23–26 April 2017; pp. 1–5. [Google Scholar]
- Kampezidou, S.I.; Romberg, J.; Vamvoudakis, K.G.; Mavris, D.N. Scalable Online Learning of Approximate Stackelberg Solutions in Energy Trading Games with Demand Response Aggregators. arXiv 2023, arXiv:2304.02086. [Google Scholar]
- Kampezidou, S.I.; Romberg, J.; Vamvoudakis, K.G.; Mavris, D.N. Online Adaptive Learning in Energy Trading Stackelberg Games with Time-Coupling Constraints. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 718–723. [Google Scholar]
- Gao, Z.; Kampezidou, S.I.; Behere, A.; Puranik, T.G.; Rajaram, D.; Mavris, D.N. Multi-level aircraft feature representation and selection for aviation environmental impact analysis. Transp. Res. Part C Emerg. Technol. 2022, 143, 103824. [Google Scholar] [CrossRef]
- Tikayat Ray, A.; Cole, B.F.; Pinon Fischer, O.J.; White, R.T.; Mavris, D.N. aeroBERT-Classifier: Classification of Aerospace Requirements Using BERT. Aerospace 2023, 10, 279. [Google Scholar] [CrossRef]
- Tikayat Ray, A.; Pinon Fischer, O.J.; Mavris, D.N.; White, R.T.; Cole, B.F. aeroBERT-NER: Named-Entity Recognition for Aerospace Requirements Engineering using BERT. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar] [CrossRef]
- Tikayat Ray, A. Standardization of Engineering Requirements Using Large Language Models. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2023. [Google Scholar] [CrossRef]
- Tikayat Ray, A.; Cole, B.F.; Pinon Fischer, O.J.; Bhat, A.P.; White, R.T.; Mavris, D.N. Agile Methodology for the Standardization of Engineering Requirements Using Large Language Models. Systems 2023, 11, 352. [Google Scholar] [CrossRef]
- Shrivastava, R.; Sisodia, D.S.; Nagwani, N.K. Deep neural network-based multi-stakeholder recommendation system exploiting multi-criteria ratings for preference learning. Expert Syst. Appl. 2023, 213, 119071. [Google Scholar] [CrossRef]
- van Dinter, R.; Catal, C.; Tekinerdogan, B. A decision support system for automating document retrieval and citation screening. Expert Syst. Appl. 2021, 182, 115261. [Google Scholar] [CrossRef]
- Li, X.; Zheng, J.; Li, M.; Ma, W.; Hu, Y. One-shot neural architecture search for fault diagnosis using vibration signals. Expert Syst. Appl. 2022, 190, 116027. [Google Scholar] [CrossRef]
- Kim, J.; Comuzzi, M. A diagnostic framework for imbalanced classification in business process predictive monitoring. Expert Syst. Appl. 2021, 184, 115536. [Google Scholar] [CrossRef]
- Jin, Y.; Carman, M.; Zhu, Y.; Xiang, Y. A technical survey on statistical modelling and design methods for crowdsourcing quality control. Artif. Intell. 2020, 287, 103351. [Google Scholar] [CrossRef]
- Boeschoten, S.; Catal, C.; Tekinerdogan, B.; Lommen, A.; Blokland, M. The automation of the development of classification models and improvement of model quality using feature engineering techniques. Expert Syst. Appl. 2023, 213, 118912. [Google Scholar] [CrossRef]
- Zhang, Y.; Kwong, S.; Wang, S. Machine learning based video coding optimizations: A survey. Inf. Sci. 2020, 506, 395–423. [Google Scholar] [CrossRef]
- Moniz, N.; Cerqueira, V. Automated imbalanced classification via meta-learning. Expert Syst. Appl. 2021, 178, 115011. [Google Scholar] [CrossRef]
- Waring, J.; Lindvall, C.; Umeton, R. Automated machine learning: Review of the state-of-the-art and opportunities for healthcare. Artif. Intell. Med. 2020, 104, 101822. [Google Scholar] [CrossRef]
- Kefalas, M.; Baratchi, M.; Apostolidis, A.; van den Herik, D.; Bäck, T. Automated machine learning for remaining useful life estimation of aircraft engines. In Proceedings of the 2021 IEEE International Conference on Prognostics and Health Management (ICPHM), Detroit, MI, USA, 7–9 June 2021; pp. 1–9. [Google Scholar]
- Tikayat Ray, A.; Bhat, A.P.; White, R.T.; Nguyen, V.M.; Pinon Fischer, O.J.; Mavris, D.N. Examining the Potential of Generative Language Models for Aviation Safety Analysis: Case Study and Insights Using the Aviation Safety Reporting System (ASRS). Aerospace 2023, 10, 770. [Google Scholar] [CrossRef]
- Hayashi, M.; Tamai, K.; Owashi, Y.; Miura, K. Automated machine learning for identification of pest aphid species (Hemiptera: Aphididae). Appl. Entomol. Zool. 2019, 54, 487–490. [Google Scholar] [CrossRef]
- Espejo-Garcia, B.; Malounas, I.; Vali, E.; Fountas, S. Testing the Suitability of Automated Machine Learning for Weeds Identification. AI 2021, 2, 34–47. [Google Scholar] [CrossRef]
- Koh, J.C.; Spangenberg, G.; Kant, S. Automated machine learning for high-throughput image-based plant phenotyping. Remote Sens. 2021, 13, 858. [Google Scholar] [CrossRef]
- Warnett, S.J.; Zdun, U. Architectural design decisions for the machine learning workflow. Computer 2022, 55, 40–51. [Google Scholar] [CrossRef]
- Khalilnejad, A.; Karimi, A.M.; Kamath, S.; Haddadian, R.; French, R.H.; Abramson, A.R. Automated pipeline framework for processing of large-scale building energy time series data. PLoS ONE 2020, 15, e0240461. [Google Scholar] [CrossRef]
- Michael, N.; Cucuringu, M.; Howison, S. OFTER: An Online Pipeline for Time Series Forecasting. arXiv 2023, arXiv:2304.03877. [Google Scholar] [CrossRef]
- Hapke, H.; Nelson, C. Building Machine Learning Pipelines; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Kolodiazhnyi, K. Hands-On Machine Learning with C++: Build, Train, and Deploy End-To-End Machine Learning and Deep Learning Pipelines; Packt Publishing Ltd.: Burmingham, UK, 2020. [Google Scholar]
- El-Amir, H.; Hamdy, M. Deep Learning Pipeline: Building a Deep Learning Model with TensorFlow; Apress: New York, NY, USA, 2019. [Google Scholar]
- Zheng, A.; Casari, A. Feature Engineering for Machine Learning: Principles and Techniques for Data Scientists; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018. [Google Scholar]
- Meisenbacher, S.; Turowski, M.; Phipps, K.; Rätz, M.; Müller, D.; Hagenmeyer, V.; Mikut, R. Review of automated time series forecasting pipelines. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2022, 12, e1475. [Google Scholar] [CrossRef]
- Wang, M.; Cui, Y.; Wang, X.; Xiao, S.; Jiang, J. Machine learning for networking: Workflow, advances and opportunities. IEEE Netw. 2017, 32, 92–99. [Google Scholar] [CrossRef]
- Kreuzberger, D.; Kühl, N.; Hirschl, S. Machine learning operations (mlops): Overview, definition, and architecture. IEEE Access 2023, 11, 31866–31879. [Google Scholar] [CrossRef]
- di Laurea, I.S. MLOps-Standardizing the Machine Learning Workflow. Ph.D. Thesis, University of Bologna, Bologna, Italy, 2021. [Google Scholar]
- Allison, P.D. Missing Data; Sage Publications: Los Angeles, CA, USA, 2001. [Google Scholar]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2019; Volume 793. [Google Scholar]
- Candes, E.; Recht, B. Exact matrix completion via convex optimization. Commun. ACM 2012, 55, 111–119. [Google Scholar] [CrossRef]
- Candès, E.J.; Tao, T. The power of convex relaxation: Near-optimal matrix completion. IEEE Trans. Inf. Theory 2010, 56, 2053–2080. [Google Scholar] [CrossRef]
- Candes, E.J.; Plan, Y. Matrix completion with noise. Proc. IEEE 2010, 98, 925–936. [Google Scholar] [CrossRef]
- Johnson, C.R. Matrix completion problems: A survey. In Proceedings of the Matrix Theory and Applications; American Mathematical Society: Providence, RI, USA, 1990; Volume 40, pp. 171–198. [Google Scholar]
- Recht, B. A simpler approach to matrix completion. J. Mach. Learn. Res. 2011, 12, 3413–3430. [Google Scholar]
- Kennedy, A.; Nash, G.; Rattenbury, N.; Kempa-Liehr, A.W. Modelling the projected separation of microlensing events using systematic time-series feature engineering. Astron. Comput. 2021, 35, 100460. [Google Scholar] [CrossRef]
- Elmagarmid, A.K.; Ipeirotis, P.G.; Verykios, V.S. Duplicate record detection: A survey. IEEE Trans. Knowl. Data Eng. 2006, 19, 1–16. [Google Scholar] [CrossRef]
- Hlupić, T.; Oreščanin, D.; Ružak, D.; Baranović, M. An overview of current data lake architecture models. In Proceedings of the 2022 45th Jubilee International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 23–27 May 2022; pp. 1082–1087. [Google Scholar]
- Vassiliadis, P. A survey of extract–transform–load technology. Int. J. Data Warehous. Min. 2009, 5, 1–27. [Google Scholar] [CrossRef]
- Vassiliadis, P.; Simitsis, A. Extraction, Transformation, and Loading. In Encyclopedia of Database Systems; Springer: Boston, MA, USA, 2009; Volume 10. [Google Scholar]
- Dash, T.; Chitlangia, S.; Ahuja, A.; Srinivasan, A. A review of some techniques for inclusion of domain-knowledge into deep neural networks. Sci. Rep. 2022, 12, 1040. [Google Scholar] [CrossRef] [PubMed]
- Dara, S.; Tumma, P. Feature extraction by using deep learning: A survey. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018; pp. 1795–1801. [Google Scholar]
- Lee, J.; Bahri, Y.; Novak, R.; Schoenholz, S.S.; Pennington, J.; Sohl-Dickstein, J. Deep neural networks as gaussian processes. arXiv 2017, arXiv:1711.00165. [Google Scholar]
- Benoit, K. Linear regression models with logarithmic transformations. Lond. Sch. Econ. 2011, 22, 23–36. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; Volume 2. [Google Scholar]
- Piryonesi, S.M.; El-Diraby, T.E. Role of data analytics in infrastructure asset management: Overcoming data size and quality problems. J. Transp. Eng. Part B Pavements 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Grus, J. Data Science from Scratch: First Principles with Python; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Sharma, V. A Study on Data Scaling Methods for Machine Learning. Int. J. Glob. Acad. Sci. Res. 2022, 1, 23–33. [Google Scholar] [CrossRef]
- Leznik, M.; Tofallis, C. Estimating Invariant Principal Components Using Diagonal Regression; University of Hertfordshire: Hatfield, UK, 2005. [Google Scholar]
- Ahsan, M.M.; Mahmud, M.P.; Saha, P.K.; Gupta, K.D.; Siddique, Z. Effect of data scaling methods on machine learning algorithms and model performance. Technologies 2021, 9, 52. [Google Scholar] [CrossRef]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models; Marshall University: Untington, WV, USA, 1996. [Google Scholar]
- Yeo, I.K.; Johnson, R.A. A new family of power transformations to improve normality or symmetry. Biometrika 2000, 87, 954–959. [Google Scholar] [CrossRef]
- Fisher, R.A. Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika 1915, 10, 507–521. [Google Scholar] [CrossRef]
- Anscombe, F.J. The transformation of Poisson, binomial and negative-binomial data. Biometrika 1948, 35, 246–254. [Google Scholar] [CrossRef]
- Box, G.E.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Holland, S. Transformations of Proportions and Percentages. 2015. Available online: http://stratigrafia.org/8370/rtips/proportions.html (accessed on 10 December 2023).
- Cormode, G.; Muthukrishnan, S. An improved data stream summary: The count-min sketch and its applications. J. Algorithms 2005, 55, 58–75. [Google Scholar] [CrossRef]
- Kessy, A.; Lewin, A.; Strimmer, K. Optimal whitening and decorrelation. Am. Stat. 2018, 72, 309–314. [Google Scholar] [CrossRef]
- Higham, N.J. Analysis of the Cholesky Decomposition of a Semi-Definite Matrix; University of Manchester: Manchester, UK, 1990. [Google Scholar]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Lakhina, A.; Crovella, M.; Diot, C. Diagnosing network-wide traffic anomalies. ACM SIGCOMM Comput. Commun. Rev. 2004, 34, 219–230. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Zhang, C.; Li, C.; Xu, C. Autoencoder inspired unsupervised feature selection. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2941–2945. [Google Scholar]
- Solorio-Fernández, S.; Carrasco-Ochoa, J.A.; Martínez-Trinidad, J.F. A review of unsupervised feature selection methods. Artif. Intell. Rev. 2020, 53, 907–948. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Y.; Liu, J.; Zhou, X.; Lu, H. Unsupervised feature selection using nonnegative spectral analysis. In Proceedings of the AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012; Volume 26, pp. 1026–1032. [Google Scholar]
- Yu, L.; Liu, H. Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 856–863. [Google Scholar]
- Mitra, P.; Murthy, C.; Pal, S.K. Unsupervised feature selection using feature similarity. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 301–312. [Google Scholar] [CrossRef]
- He, X.; Cai, D.; Niyogi, P. Laplacian score for feature selection. In Proceedings of the 18th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; Volume 18. [Google Scholar]
- Ferreira, A.J.; Figueiredo, M.A. An unsupervised approach to feature discretization and selection. Pattern Recognit. 2012, 45, 3048–3060. [Google Scholar] [CrossRef]
- Park, C.H. A feature selection method using hierarchical clustering. In Proceedings of the Mining Intelligence and Knowledge Exploration, Tamil Nadu, India, 18–20 December 2013; pp. 1–6. [Google Scholar]
- Cai, D.; Zhang, C.; He, X. Unsupervised feature selection for multi-cluster data. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 333–342. [Google Scholar]
- Yang, Y.; Shen, H.T.; Ma, Z.; Huang, Z.; Zhou, X. ℓ 2, 1-norm regularized discriminative feature selection for unsupervised learning. In Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011. [Google Scholar]
- Dy, J.G.; Brodley, C.E. Feature selection for unsupervised learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Breaban, M.; Luchian, H. A unifying criterion for unsupervised clustering and feature selection. Pattern Recognit. 2011, 44, 854–865. [Google Scholar] [CrossRef]
- Hruschka, E.R.; Covoes, T.F. Feature selection for cluster analysis: An approach based on the simplified Silhouette criterion. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; Volume 1, pp. 32–38. [Google Scholar]
- Law, M.H.; Figueiredo, M.A.; Jain, A.K. Simultaneous feature selection and clustering using mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1154–1166. [Google Scholar] [CrossRef] [PubMed]
- Zeng, H.; Cheung, Y.m. Feature selection and kernel learning for local learning-based clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1532–1547. [Google Scholar] [CrossRef]
- Wang, S.; Pedrycz, W.; Zhu, Q.; Zhu, W. Unsupervised feature selection via maximum projection and minimum redundancy. Knowl. Based Syst. 2015, 75, 19–29. [Google Scholar] [CrossRef]
- Guo, J.; Zhu, W. Dependence guided unsupervised feature selection. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Liu, H.; Motoda, H. Feature Extraction, Construction and Selection: A Data Mining Perspective; Springer: New York, NY, USA, 1998; Volume 453. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; Volume 26. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical learning with sparsity. Monogr. Stat. Appl. Probab. 2015, 143, 143. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Obozinski, G.; Taskar, B.; Jordan, M. Multi-Task Feature Selection; Technical Report; Department of Statistics, University of California: Berkeley, CA, USA, 2006; Volume 2. [Google Scholar]
- Argyriou, A.; Evgeniou, T.; Pontil, M. Multi-task feature learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; Volume 19. [Google Scholar]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Kocev, D.; Vens, C.; Struyf, J.; Džeroski, S. Ensembles of multi-objective decision trees. In Proceedings of the European Conference on Machine Learning, Warsaw, Poland, 17–21 September 2007; pp. 624–631. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kocev, D.; Džeroski, S.; White, M.D.; Newell, G.R.; Griffioen, P. Using single-and multi-target regression trees and ensembles to model a compound index of vegetation condition. Ecol. Model. 2009, 220, 1159–1168. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Boosting and additive trees. In The Elements of Statistical Learning; Springer: New York, NY, USA, 2009; pp. 337–387. [Google Scholar]
- Madeh Piryonesi, S.; El-Diraby, T.E. Using machine learning to examine impact of type of performance indicator on flexible pavement deterioration modeling. J. Infrastruct. Syst. 2021, 27, 04021005. [Google Scholar] [CrossRef]
- Piryonesi, S.M.; El-Diraby, T.E. Data analytics in asset management: Cost-effective prediction of the pavement condition index. J. Infrastruct. Syst. 2020, 26, 04019036. [Google Scholar] [CrossRef]
- Segal, M.; Xiao, Y. Multivariate random forests. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 80–87. [Google Scholar] [CrossRef]
- Bellman, R. Adaptive Control Processes: A Guided Tour. J. R. Stat. Soc. Ser. A 1962, 125, 161–162. [Google Scholar] [CrossRef][Green Version]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Gao, Z. Representative Data and Models for Complex Aerospace Systems Analysis. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2022. [Google Scholar]
- Thudumu, S.; Branch, P.; Jin, J.; Singh, J.J. A comprehensive survey of anomaly detection techniques for high dimensional big data. J. Big Data 2020, 7, 42. [Google Scholar] [CrossRef]
- Katz, G.; Shin, E.C.R.; Song, D. Explorekit: Automatic feature generation and selection. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 979–984. [Google Scholar]
- Lam, H.T.; Thiebaut, J.M.; Sinn, M.; Chen, B.; Mai, T.; Alkan, O. One button machine for automating feature engineering in relational databases. arXiv 2017, arXiv:1706.00327. [Google Scholar]
- Kaul, A.; Maheshwary, S.; Pudi, V. Autolearn: Automated feature generation and selection. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 217–226. [Google Scholar]
- Tran, B.; Xue, B.; Zhang, M. Genetic programming for feature construction and selection in classification on high-dimensional data. Memetic Comput. 2016, 8, 3–15. [Google Scholar] [CrossRef]
- Khurana, U.; Turaga, D.; Samulowitz, H.; Parthasrathy, S. Cognito: Automated feature engineering for supervised learning. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 1304–1307. [Google Scholar]
- Khurana, U.; Samulowitz, H.; Turaga, D. Feature engineering for predictive modeling using reinforcement learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Nargesian, F.; Samulowitz, H.; Khurana, U.; Khalil, E.B.; Turaga, D.S. Learning Feature Engineering for Classification. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; Volume 17, pp. 2529–2535. [Google Scholar]
- Li, H.; Chutatape, O. Automated feature extraction in color retinal images by a model based approach. IEEE Trans. Biomed. Eng. 2004, 51, 246–254. [Google Scholar] [CrossRef] [PubMed]
- Dang, D.M.; Jackson, K.R.; Mohammadi, M. Dimension and variance reduction for Monte Carlo methods for high-dimensional models in finance. Appl. Math. Financ. 2015, 22, 522–552. [Google Scholar] [CrossRef]
- Donoho, D.L. High-dimensional data analysis: The curses and blessings of dimensionality. AMS Math Challenges Lect. 2000, 1, 32. [Google Scholar]
- Atramentov, A.; Leiva, H.; Honavar, V. A multi-relational decision tree learning algorithm–implementation and experiments. In Proceedings of the International Conference on Inductive Logic Programming, Szeged, Hungary, 29 September–1 October 2003; pp. 38–56. [Google Scholar]
- Kanter, J.M.; Veeramachaneni, K. Deep feature synthesis: Towards automating data science endeavors. In Proceedings of the 2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Paris, France, 19–21 October 2015; pp. 1–10. [Google Scholar]
- Weimer, D.; Scholz-Reiter, B.; Shpitalni, M. Design of deep convolutional neural network architectures for automated feature extraction in industrial inspection. CIRP Ann. 2016, 65, 417–420. [Google Scholar] [CrossRef]
- Schneider, T.; Helwig, N.; Schütze, A. Industrial condition monitoring with smart sensors using automated feature extraction and selection. Meas. Sci. Technol. 2018, 29, 094002. [Google Scholar] [CrossRef]
- Laird, P.; Saul, R. Automated feature extraction for supervised learning. In Proceedings of the First IEEE Conference on Evolutionary Computation. IEEEWorld Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994; pp. 674–679. [Google Scholar]
- Le, Q.; Karpenko, A.; Ngiam, J.; Ng, A. ICA with reconstruction cost for efficient overcomplete feature learning. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Volume 24. [Google Scholar]
- Ngiam, J.; Chen, Z.; Bhaskar, S.; Koh, P.; Ng, A. Sparse filtering. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Volume 24. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
- Mallat, S. Group invariant scattering. Commun. Pure Appl. Math. 2012, 65, 1331–1398. [Google Scholar] [CrossRef]
- Bruna, J.; Mallat, S. Invariant scattering convolution networks. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1872–1886. [Google Scholar] [CrossRef]
- Andén, J.; Mallat, S. Deep scattering spectrum. IEEE Trans. Signal Process. 2014, 62, 4114–4128. [Google Scholar] [CrossRef]
- Mallat, S. Understanding deep convolutional networks. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150203. [Google Scholar] [CrossRef]
- Rizk, Y.; Hajj, N.; Mitri, N.; Awad, M. Deep belief networks and cortical algorithms: A comparative study for supervised classification. Appl. Comput. Inform. 2019, 15, 81–93. [Google Scholar] [CrossRef]
- Rifkin, R.M.; Lippert, R.A. Notes on Regularized Least Squares; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Yin, R.; Liu, Y.; Wang, W.; Meng, D. Sketch kernel ridge regression using circulant matrix: Algorithm and theory. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3512–3524. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Bulso, N.; Marsili, M.; Roudi, Y. On the complexity of logistic regression models. Neural Comput. 2019, 31, 1592–1623. [Google Scholar] [CrossRef]
- Belyaev, M.; Burnaev, E.; Kapushev, Y. Exact inference for Gaussian process regression in case of big data with the Cartesian product structure. arXiv 2014, arXiv:1403.6573. [Google Scholar]
- Serpen, G.; Gao, Z. Complexity analysis of multilayer perceptron neural network embedded into a wireless sensor network. Procedia Comput. Sci. 2014, 36, 192–197. [Google Scholar] [CrossRef]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Fleizach, C.; Fukushima, S. A Naive Bayes Classifier on 1998 KDD Cup; Technical Report; Department of Computer Science and Engineering, University of California: Los Angeles, CA, USA, 1998. [Google Scholar]
- Jensen, F.V.; Nielsen, T.D. Bayesian Networks and Decision Graphs; Springer: New York, NY, USA, 2007; Volume 2. [Google Scholar]
- Claesen, M.; De Smet, F.; Suykens, J.A.; De Moor, B. Fast prediction with SVM models containing RBF kernels. arXiv 2014, arXiv:1403.0736. [Google Scholar]
- Cardot, H.; Degras, D. Online principal component analysis in high dimension: Which algorithm to choose? Int. Stat. Rev. 2018, 86, 29–50. [Google Scholar] [CrossRef]
- Veksler, O. Nonparametric Density Estimation Nearest Neighbors, KNN; Haifa University: Haifa, Israel, 2013. [Google Scholar]
- Raschka, S. STAT 479: Machine Learning Lecture Notes. Available online: https://pages.stat.wisc.edu/~sraschka/teaching/stat479-fs2019/ (accessed on 10 December 2023).
- Sani, H.M.; Lei, C.; Neagu, D. Computational complexity analysis of decision tree algorithms. In Proceedings of the Artificial Intelligence XXXV: 38th SGAI International Conference on Artificial Intelligence, AI 2018, Cambridge, UK, 11–13 December 2018; pp. 191–197. [Google Scholar]
- Buczak, A.L.; Guven, E. A survey of data mining and machine learning methods for cyber security intrusion detection. IEEE Commun. Surv. Tutorials 2015, 18, 1153–1176. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Cai, D.; He, X.; Han, J. Training linear discriminant analysis in linear time. In Proceedings of the 2008 IEEE 24th International Conference on Data Engineering, Cancun, Mexico, 7–12 April 2008; pp. 209–217. [Google Scholar]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-validation. In Encyclopedia of Database Systems; Springer: New York, NY, USA, 2009; Volume 5, pp. 532–538. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Efron, B. Bootstrap methods: Another look at the jackknife. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 569–593. [Google Scholar]
- Breiman, L. Bias, Variance, and Arcing Classifiers; Technical Report; Department of Statistics, University of California: Berkeley, CA, USA, 1996. [Google Scholar]
- Syakur, M.; Khotimah, B.; Rochman, E.; Satoto, B.D. Integration k-means clustering method and elbow method for identification of the best customer profile cluster. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Surabaya, Indonesia, 9 November 2017; Volume 336, p. 012017. [Google Scholar]
- Palacio-Niño, J.O.; Berzal, F. Evaluation metrics for unsupervised learning algorithms. arXiv 2019, arXiv:1905.05667. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On clustering validation techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Perry, P.O. Cross-Validation for Unsupervised Learning; Stanford University: Stanford, CA, USA, 2009. [Google Scholar]
- Airola, A.; Pahikkala, T.; Waegeman, W.; De Baets, B.; Salakoski, T. An experimental comparison of cross-validation techniques for estimating the area under the ROC curve. Comput. Stat. Data Anal. 2011, 55, 1828–1844. [Google Scholar] [CrossRef]
- Breiman, L.; Spector, P. Submodel selection and evaluation in regression. The X-random case. Int. Stat. Rev. 1992, 60, 291–319. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Volume 14, pp. 1137–1145. [Google Scholar]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- McCulloch, C.E.; Searle, S.R. Generalized, Linear, and Mixed Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Kühl, N.; Hirt, R.; Baier, L.; Schmitz, B.; Satzger, G. How to conduct rigorous supervised machine learning in information systems research: The supervised machine learning report card. Commun. Assoc. Inf. Syst. 2021, 48, 46. [Google Scholar] [CrossRef]
- Caruana, R.; Niculescu-Mizil, A. Data mining in metric space: An empirical analysis of supervised learning performance criteria. In Proceedings of the tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 69–78. [Google Scholar]
- Beck, K. Test-Driven Development: By Example; Addison-Wesley Professional: Boston, MA, USA, 2003. [Google Scholar]
- Washizaki, H.; Uchida, H.; Khomh, F.; Guéhéneuc, Y.G. Studying Software Engineering Patterns for Designing Machine Learning Systems. In Proceedings of the 2019 10th International Workshop on Empirical Software Engineering in Practice (IWESEP), Tokyo, Japan, 13–14 December 2019; pp. 49–495. [Google Scholar] [CrossRef]
- Gamma, E.; Helm, R.; Johnson, R.; Johnson, R.E.; Vlissides, J.; Booch, G. Design Patterns: Elements of Reusable Object-Oriented Software; Addison-Wesley Professional: Boston, MA, USA, 1995. [Google Scholar]
- Kohavi, R.; Longbotham, R. Online Controlled Experiments and A/B Testing. Encycl. Mach. Learn. Data Min. 2017, 7, 922–929. [Google Scholar]
- Rajasoundaran, S.; Prabu, A.; Routray, S.; Kumar, S.S.; Malla, P.P.; Maloji, S.; Mukherjee, A.; Ghosh, U. Machine learning based deep job exploration and secure transactions in virtual private cloud systems. Comput. Secur. 2021, 109, 102379. [Google Scholar] [CrossRef]
- Abran, A.; Moore, J.W.; Bourque, P.; Dupuis, R.; Tripp, L. Software Engineering Body of Knowledge; IEEE: Piscataway, NJ, USA, 2004; p. 25. [Google Scholar]
- Pytest: Helps You Write Better Programs. Available online: https://docs.pytest.org/en/7.4.x/ (accessed on 10 December 2023).
- Unittest: Unit Testing Framework. Available online: https://docs.python.org/3/library/unittest.html (accessed on 10 December 2023).
- JUnit. Available online: https://junit.org/junit5 (accessed on 10 December 2023).
- Mockito. Available online: https://site.mockito.org/ (accessed on 10 December 2023).
- Ardagna, C.A.; Bena, N.; Hebert, C.; Krotsiani, M.; Kloukinas, C.; Spanoudakis, G. Big Data Assurance: An Approach Based on Service-Level Agreements. Big Data 2023, 11, 239–254. [Google Scholar] [CrossRef]
- Mili, A.; Tchier, F. Software Testing: Concepts and Operations; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Li, P.L.; Chai, X.; Campbell, F.; Liao, J.; Abburu, N.; Kang, M.; Niculescu, I.; Brake, G.; Patil, S.; Dooley, J.; et al. Evolving software to be ML-driven utilizing real-world A/B testing: Experiences, insights, challenges. In Proceedings of the 2021 IEEE/ACM 43rd International Conference on Software Engineering: Software Engineering in Practice (ICSE-SEIP), Madrid, Spain, 25–28 May 2021; pp. 170–179. [Google Scholar]
- Manias, D.M.; Chouman, A.; Shami, A. Model Drift in Dynamic Networks. IEEE Commun. Mag. 2023, 61, 78–84. [Google Scholar] [CrossRef]
- Wani, D.; Ackerman, S.; Farchi, E.; Liu, X.; Chang, H.w.; Lalithsena, S. Data Drift Monitoring for Log Anomaly Detection Pipelines. arXiv 2023, arXiv:2310.14893. [Google Scholar]
- Schneider, F. Least privilege and more [computer security]. IEEE Secur. Priv. 2003, 1, 55–59. [Google Scholar] [CrossRef]
- Mahjabin, T.; Xiao, Y.; Sun, G.; Jiang, W. A survey of distributed denial-of-service attack, prevention, and mitigation techniques. Int. J. Distrib. Sens. Netw. 2017, 13, 1550147717741463. [Google Scholar] [CrossRef]
- Certified Tester Foundation Level (CTFL) Syllabus. Technical Report, International Software Testing Qualifications Board, Version 2018 v3.1.1. Available online: https://astqb.org/assets/documents/CTFL-2018-Syllabus.pdf (accessed on 10 December 2023).
- Lewis, W.E. Software Testing and Continuous Quality Improvement; Auerbach Publications: Boca Raton, FL, USA, 2004. [Google Scholar]
- Martin, R.C. Clean Code: A Handbook of Agile Software Craftsmanship; Pearson Education: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Thomas, D.; Hunt, A. The Pragmatic Programmer: Your Journey to Mastery; Addison-Wesley Professional: Boston, MA, USA, 2019. [Google Scholar]
- Hutter, F.; Kotthoff, L.; Vanschoren, J. Automated Machine Learning: Methods, Systems, Challenges; Springer: New York, NY, USA, 2019. [Google Scholar]
- Melis, G.; Dyer, C.; Blunsom, P. On the state of the art of evaluation in neural language models. arXiv 2017, arXiv:1707.05589. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 25. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the International Conference on Machine Learning. PMLR, Atlanta, GA, USA, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Sculley, D.; Snoek, J.; Wiltschko, A.; Rahimi, A. Winner’s curse? On pace, progress, and empirical rigor. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Hansen, N. The CMA evolution strategy: A comparing review. In Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms; Springer: Berlin/Heidelberg, Germany, 2006; pp. 75–102. [Google Scholar]
- Snoek, J.; Rippel, O.; Swersky, K.; Kiros, R.; Satish, N.; Sundaram, N.; Patwary, M.; Prabhat, M.; Adams, R. Scalable bayesian optimization using deep neural networks. In Proceedings of the International Conference on Machine Learning. PMLR, Lille, France, 6–11 July 2015; pp. 2171–2180. [Google Scholar]
- Dahl, G.E.; Sainath, T.N.; Hinton, G.E. Improving deep neural networks for LVCSR using rectified linear units and dropout. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8609–8613. [Google Scholar]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; De Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2015, 104, 148–175. [Google Scholar] [CrossRef]
- Brochu, E.; Cora, V.M.; De Freitas, N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning. arXiv 2010, arXiv:1012.2599. [Google Scholar]
- Zeng, X.; Luo, G. Progressive sampling-based Bayesian optimization for efficient and automatic machine learning model selection. Health Inf. Sci. Syst. 2017, 5, 2. [Google Scholar] [CrossRef]
- Zhang, Y.; Bahadori, M.T.; Su, H.; Sun, J. FLASH: Fast Bayesian optimization for data analytic pipelines. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francsisco, CA, USA, 13–17 August 2016; pp. 2065–2074. [Google Scholar]
- Jamieson, K.; Talwalkar, A. Non-stochastic best arm identification and hyperparameter optimization. In Proceedings of the Artificial Intelligence and Statistics. PMLR, Cadiz, Spain, 9–11 May 2016; pp. 240–248. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- Falkner, S.; Klein, A.; Hutter, F. BOHB: Robust and efficient hyperparameter optimization at scale. In Proceedings of the International Conference on Machine Learning. PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 1437–1446. [Google Scholar]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Ravi, S.; Larochelle, H. Optimization as a model for few-shot learning. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural architecture search: A survey. J. Mach. Learn. Res. 2019, 20, 1997–2017. [Google Scholar]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning transferable architectures for scalable image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8697–8710. [Google Scholar]
- Zela, A.; Klein, A.; Falkner, S.; Hutter, F. Towards automated deep learning: Efficient joint neural architecture and hyperparameter search. arXiv 2018, arXiv:1807.06906. [Google Scholar]
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Aging evolution for image classifier architecture search. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 2, p. 2. [Google Scholar]
- Runge, F.; Stoll, D.; Falkner, S.; Hutter, F. Learning to design RNA. arXiv 2018, arXiv:1812.11951. [Google Scholar]
- Swersky, K.; Snoek, J.; Adams, R.P. Freeze-thaw Bayesian optimization. arXiv 2014, arXiv:1406.3896. [Google Scholar]
- Domhan, T.; Springenberg, J.T.; Hutter, F. Speeding up automatic hyperparameter optimization of deep neural networks by extrapolation of learning curves. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Klein, A.; Falkner, S.; Springenberg, J.T.; Hutter, F. Learning curve prediction with Bayesian neural networks. In Proceedings of the International Conference on Learning Representations, Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Baker, B.; Gupta, O.; Raskar, R.; Naik, N. Accelerating neural architecture search using performance prediction. arXiv 2017, arXiv:1705.10823. [Google Scholar]
- Real, E.; Moore, S.; Selle, A.; Saxena, S.; Suematsu, Y.L.; Tan, J.; Le, Q.V.; Kurakin, A. Large-scale evolution of image classifiers. In Proceedings of the International Conference on Machine Learning. PMLR, Sydney, Australia, 6–11 August 2017; pp. 2902–2911. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Simple and efficient architecture search for convolutional neural networks. arXiv 2017, arXiv:1711.04528. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Efficient multi-objective neural architecture search via lamarckian evolution. arXiv 2018, arXiv:1804.09081. [Google Scholar]
- Cai, H.; Chen, T.; Zhang, W.; Yu, Y.; Wang, J. Efficient architecture search by network transformation. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Cai, H.; Yang, J.; Zhang, W.; Han, S.; Yu, Y. Path-level network transformation for efficient architecture search. In Proceedings of the International Conference on Machine Learning. PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 678–687. [Google Scholar]
- Saxena, S.; Verbeek, J. Convolutional neural fabrics. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Pham, H.; Guan, M.; Zoph, B.; Le, Q.; Dean, J. Efficient neural architecture search via parameters sharing. In Proceedings of the International Conference on Machine Learning. PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 4095–4104. [Google Scholar]
- Bender, G.; Kindermans, P.J.; Zoph, B.; Vasudevan, V.; Le, Q. Understanding and simplifying one-shot architecture search. In Proceedings of the International Conference on Machine Learning. PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 550–559. [Google Scholar]
- Liu, H.; Simonyan, K.; Yang, Y. Darts: Differentiable architecture search. arXiv 2018, arXiv:1806.09055. [Google Scholar]
- Cai, H.; Zhu, L.; Han, S. Proxylessnas: Direct neural architecture search on target task and hardware. arXiv 2018, arXiv:1812.00332. [Google Scholar]
- Xie, S.; Zheng, H.; Liu, C.; Lin, L. SNAS: Stochastic neural architecture search. arXiv 2018, arXiv:1812.09926. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Volume 24. [Google Scholar]
- Desautels, T.; Krause, A.; Burdick, J.W. Parallelizing exploration-exploitation tradeoffs in gaussian process bandit optimization. J. Mach. Learn. Res. 2014, 15, 3873–3923. [Google Scholar]
- Ginsbourger, D.; Le Riche, R.; Carraro, L. Kriging is well-suited to parallelize optimization. In Computational Intelligence in Expensive Optimization Problems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 131–162. [Google Scholar]
- Hernández-Lobato, J.M.; Requeima, J.; Pyzer-Knapp, E.O.; Aspuru-Guzik, A. Parallel and distributed Thompson sampling for large-scale accelerated exploration of chemical space. In Proceedings of the International Conference on Machine Learning. PMLR, Sydney, Australia, 6–11 August 2017; pp. 1470–1479. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Parallel algorithm configuration. In Proceedings of the Learning and Intelligent Optimization: 6th International Conference, LION 6, Paris, France, 16–20 January 2012; pp. 55–70. [Google Scholar]
- Zhang, C.; Xie, Y.; Bai, H.; Yu, B.; Li, W.; Gao, Y. A survey on federated learning. Knowl. Based Syst. 2021, 216, 106775. [Google Scholar] [CrossRef]
- Nagarajah, T.; Poravi, G. A review on automated machine learning (AutoML) systems. In Proceedings of the 2019 IEEE 5th International Conference for Convergence in Technology (I2CT), Bombay, India, 29–31 March 2019; pp. 1–6. [Google Scholar]
- Thakur, A.; Krohn-Grimberghe, A. Autocompete: A framework for machine learning competition. arXiv 2015, arXiv:1507.02188. [Google Scholar]
- Ferreira, L.; Pilastri, A.; Martins, C.M.; Pires, P.M.; Cortez, P. A comparison of AutoML tools for machine learning, deep learning and XGBoost. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 847–855. [Google Scholar]
- Kotthoff, L.; Thornton, C.; Hoos, H.H.; Hutter, F.; Leyton-Brown, K. Auto-WEKA: Automatic model selection and hyperparameter optimization in WEKA. In Automated Machine Learning: Methods, Systems, Challenges; Springer: Cham, Switzerland, 2019; pp. 81–95. [Google Scholar]
- Komer, B.; Bergstra, J.; Eliasmith, C. Hyperopt-sklearn: Automatic hyperparameter configuration for scikit-learn. In Proceedings of the ICML Workshop on AutoML, Austin, TX, USA, 6–12 July 2014; Volume 9, p. 50. [Google Scholar]
- Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.; Blum, M.; Hutter, F. Efficient and robust automated machine learning. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Feurer, M.; Eggensperger, K.; Falkner, S.; Lindauer, M.; Hutter, F. Auto-Sklearn 2.0: Hands-free automl via meta-learning. J. Mach. Learn. Res. 2020, 23, 1–61. [Google Scholar]
- Olson, R.S.; Moore, J.H. TPOT: A tree-based pipeline optimization tool for automating machine learning. In Proceedings of the Workshop on Automatic Machine Learning. PMLR, Cadiz, Spain, 9–11 May 2016; pp. 66–74. [Google Scholar]
- Zimmer, L.; Lindauer, M.; Hutter, F. Auto-pytorch: Multi-fidelity metalearning for efficient and robust autodl. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3079–3090. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Song, Q.; Hu, X. Auto-keras: An efficient neural architecture search system. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1946–1956. [Google Scholar]
- Peng, H.; Du, H.; Yu, H.; Li, Q.; Liao, J.; Fu, J. Cream of the Crop: Distilling Prioritized Paths For One-Shot Neural Architecture Search. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Microsoft Research. NNI Related Publications. Available online: https://nni.readthedocs.io/en/latest/notes/research_publications.html (accessed on 10 December 2023).
- Erickson, N.; Mueller, J.; Shirkov, A.; Zhang, H.; Larroy, P.; Li, M.; Smola, A. Autogluon-tabular: Robust and accurate automl for structured data. arXiv 2020, arXiv:2003.06505. [Google Scholar]
- Pandey, P. A Deep Dive into H2O’s AutoML. Available online: https://h2o.ai/blog/2019/a-deep-dive-into-h2os-automl/ (accessed on 10 December 2023).
- Wang, C.; Wu, Q.; Weimer, M.; Zhu, E. Flaml: A fast and lightweight automl library. Proc. Mach. Learn. Syst. 2021, 3, 434–447. [Google Scholar]
- Shchur, O.; Turkmen, C.; Erickson, N.; Shen, H.; Shirkov, A.; Hu, T.; Wang, Y. AutoGluon-TimeSeries: AutoML for Probabilistic Time Series Forecasting. arXiv 2023, arXiv:2308.05566. [Google Scholar]
- Khider, D.; Zhu, F.; Gil, Y. autoTS: Automated machine learning for time series analysis. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 9–13 December 2019; Volume 2019, p. PP43D–1637. [Google Scholar]
- Schafer, R.W. What is a Savitzky-Golay filter? [lecture notes]. IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]

| Scaling Method | Scaled Feature | Scaling Effect | ML Algorithm/Model |
|---|---|---|---|
| Min-Max | k-Means, kNN, SVM | ||
| Standardization (z-score) | , | Linear/Logistic Regression, NN | |
| l2-Normalization | Vector Space Model |
| Encoding Method | Original Feature | Transformed Features | Result |
|---|---|---|---|
| Ordinal Encoding | string1, string2, … | 1, 2, … | Nonordinal categorical data becomes ordinal |
| One-Hot Encoding | string1, string2, … | 001, 010, … | k features for k categories, only one bit is “on” |
| Dummy Encoding | string1, string2, … | 001, 010, …, (000) | features for k categories, reference category is 0 |
| Effect Encoding | string1, string2, … | 001, 010, …, (-1-1-1) | k features for k categories, reference category is −1 |
| ML Model/Algorithm | Parametric | Linear | Train, Test, Space Complexity | Paper |
|---|---|---|---|---|
| Ordinary Least Squares (OLS) | ✓ | ✓ | , , | [148] |
| Kernel Ridge Regression | ✓ | ✓ | , -, | [149] |
| Lasso Regression (LARS) | ✓ | ✓ | , -, - | [150] |
| Elastic Net | ✓ | ✓ | , -, - | [108] |
| Logistic Regression | ✓ | ✓ | , , | [151] |
| GP Regression | ✗ | ✗ | , -, | [152] |
| Multi-Layer Perceptron | ✓ | ✗ | ★ | [153,154] |
| RNN/LSTM | ✓ | ✗ | ★ | - |
| CNN | ✓ | ✗ | ★ | - |
| Transformers | ✓ | ✗ | ★ | - |
| Radial Basis Function NN | ✗ | ✗ | ★ | - |
| DNN | ✓ | ✗ | ★ | - |
| Naive Bayes Classifier | ✓ | ✓ | , , | [155] |
| Bayesian Network | ✗ | ✗ | ★ | [156] |
| Bayesian Belief Network | ✓ | ✗ | ★ | - |
| SVM | ✗ | ✓ | , , | [157] |
| PCA | ✗ | ✓ | , -, | [158] |
| kNN | ✗ | ✗ | , , | [159,160] |
| CART | ✗ | ✗ | , , | [161] |
| RF | ✗ | ✗ | , , | [162] |
| Gradient Boost Decision Tree | ✗ | ✗ | , , | [163] |
| LDA | ✓ | ✓ | , -, , | [164] |
| CV Category | Specific CV Method | Result |
|---|---|---|
| Exhaustive CV | Leave-p-out CV | models trained |
| Leave-one-out CV | models trained | |
| Non-Exhaustive CV | k-fold CV | k models trained |
| Holdout | 1 model trained | |
| Repeated Random Sub-Sampling | k models trained | |
| Validation (also known as Monte Carlo CV) | ||
| Nested CV | k*l-fold CV | models trained |
| k-fold CV with validation and test set | k models trained with test set |
| Performance Index | Formula | Purpose |
|---|---|---|
| Mean Squared Error (MSE) | Regression | |
| Root Mean Squared Error (RMSE) | Regression | |
| Mean Absolute Error (MAE) | Regression | |
| Mean Absolute Percentage Error (MAPE) | Regression | |
| Coefficient of Determination () | Regression | |
| Adjusted Coefficient of Determination (A-) | Regression | |
| Confusion Matrix | TP, TN, FP, FN | Classification |
| Accuracy | Classification | |
| Balanced Accuracy | Classification | |
| Misclassification | Classification | |
| F1-Score | Classification | |
| F-Score | Classification | |
| Receiver Operating Characteristic (ROC) | Graphical | Classification |
| Area Under Curve (AUC) | Graphical | Classification |
| Total Operating Characteristic (TOC) | Graphical | Classification |
| Method | Approach to Speed-Up | Paper |
|---|---|---|
| Lower fidelity estimates | Less epochs, data subsets, downscaled models/data, etc. | [215,216,220,221,222,223] |
| Learning curve extrapolation | Performance extrapolated after few epochs | [224,225,226,227] |
| Weight inheritance/network morphisms | Models warm-started with inherited weights | [228,229,230,231,232] |
| One-Shot models/weight sharing | One-shot model’s weights shared across architectures | [233,234,235,236,237,238] |
| Software | Problem Automated | AutoML Method | Paper |
|---|---|---|---|
| Auto-WEKA | CASH | Bayesian optimization | [248] |
| Auto-WEKA 2.0 | CASH with parallel runs | Bayesian optimization | [249] |
| Hyperopt-Sklearn | Space search of random hyperparameters | Bayesian otimization | [250] |
| Auto-Sklearn | Improved CASH with algorithm ensembles | Bayesian optimization | [251,252] |
| TPOT | Classification with FE | GeP | [253] |
| Auto-Net | Automates DNN tuning | Bayesian optimization | [36] |
| Auto-Net 2.0 | Automates DNN tuning | BOHB | [36] |
| Automatic Statistician | Automates data science | Various | [36] |
| AutoPytorch | Algo. selection, ensemble constr., hyperpar. tuning | Bayesian opt., meta-learn. | [254] |
| AutoKeras | NAS, hyperpar. tuning in DNN | Bayesian opt. guides network morphism | [255] |
| NNI | NAS, hyperpar. tuning, model compression, FE | One-shot modes, etc. | [256,257] |
| TPOT | Hyperpar. tuning, model selection | GeP | [253] |
| AutoGluon | Hyperpar. tuning | - | [258] |
| H2O | DE, FE, hyperpar. tuning, ensemble model selection | Random grid search, Bayesian opt. | [259] |
| FEDOT | Hyperparameter tuning | Evolutionary algorithms | - |
| Auto-Sklearn 2 | Model selection | Meta-learning, bandit strategy | [252] |
| FLAML | Algorithm selection, hyperpar. tuning | Search strategies | [260] |
| AutoGluon-TS | Ensemble constr. for time-series forecasting | Probabilistic time-series | [261] |
| AutoTS | Time-series data analysis | Various | [262] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kampezidou, S.I.; Tikayat Ray, A.; Bhat, A.P.; Pinon Fischer, O.J.; Mavris, D.N. Fundamental Components and Principles of Supervised Machine Learning Workflows with Numerical and Categorical Data. Eng 2024, 5, 384-416. https://doi.org/10.3390/eng5010021
Kampezidou SI, Tikayat Ray A, Bhat AP, Pinon Fischer OJ, Mavris DN. Fundamental Components and Principles of Supervised Machine Learning Workflows with Numerical and Categorical Data. Eng. 2024; 5(1):384-416. https://doi.org/10.3390/eng5010021
Chicago/Turabian StyleKampezidou, Styliani I., Archana Tikayat Ray, Anirudh Prabhakara Bhat, Olivia J. Pinon Fischer, and Dimitri N. Mavris. 2024. "Fundamental Components and Principles of Supervised Machine Learning Workflows with Numerical and Categorical Data" Eng 5, no. 1: 384-416. https://doi.org/10.3390/eng5010021
APA StyleKampezidou, S. I., Tikayat Ray, A., Bhat, A. P., Pinon Fischer, O. J., & Mavris, D. N. (2024). Fundamental Components and Principles of Supervised Machine Learning Workflows with Numerical and Categorical Data. Eng, 5(1), 384-416. https://doi.org/10.3390/eng5010021









