Enhancing Seismic Resilience: Evaluating Buildings with Passive Energy Dissipation Strategies
Abstract
1. Introduction
2. Description of the Buildings
2.1. Damper Characteristics
2.2. Damper Variations
2.3. Limitations of the Study
3. Results and Discussion
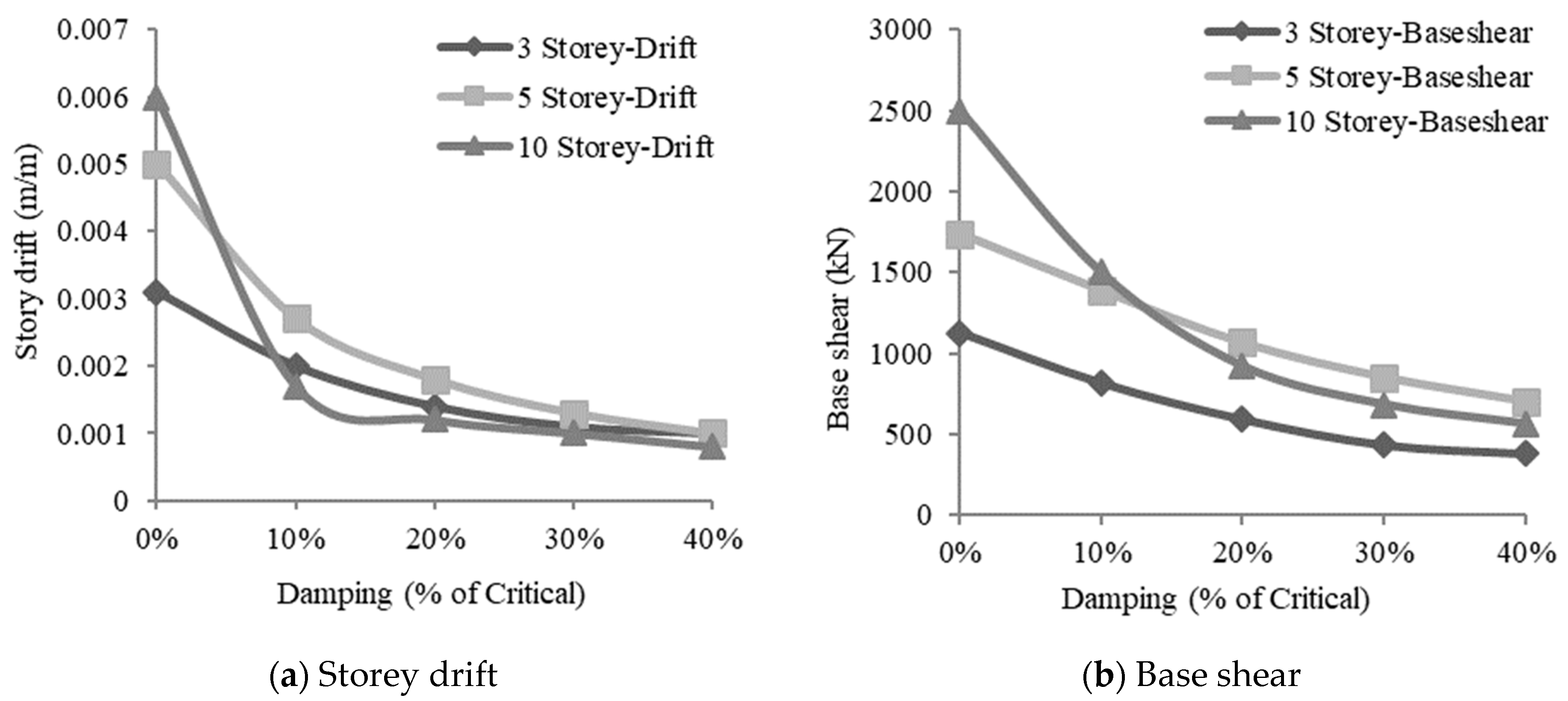
3.1. Building Behaviour without Installing Dampers
3.2. Response of Buildings with Dampers
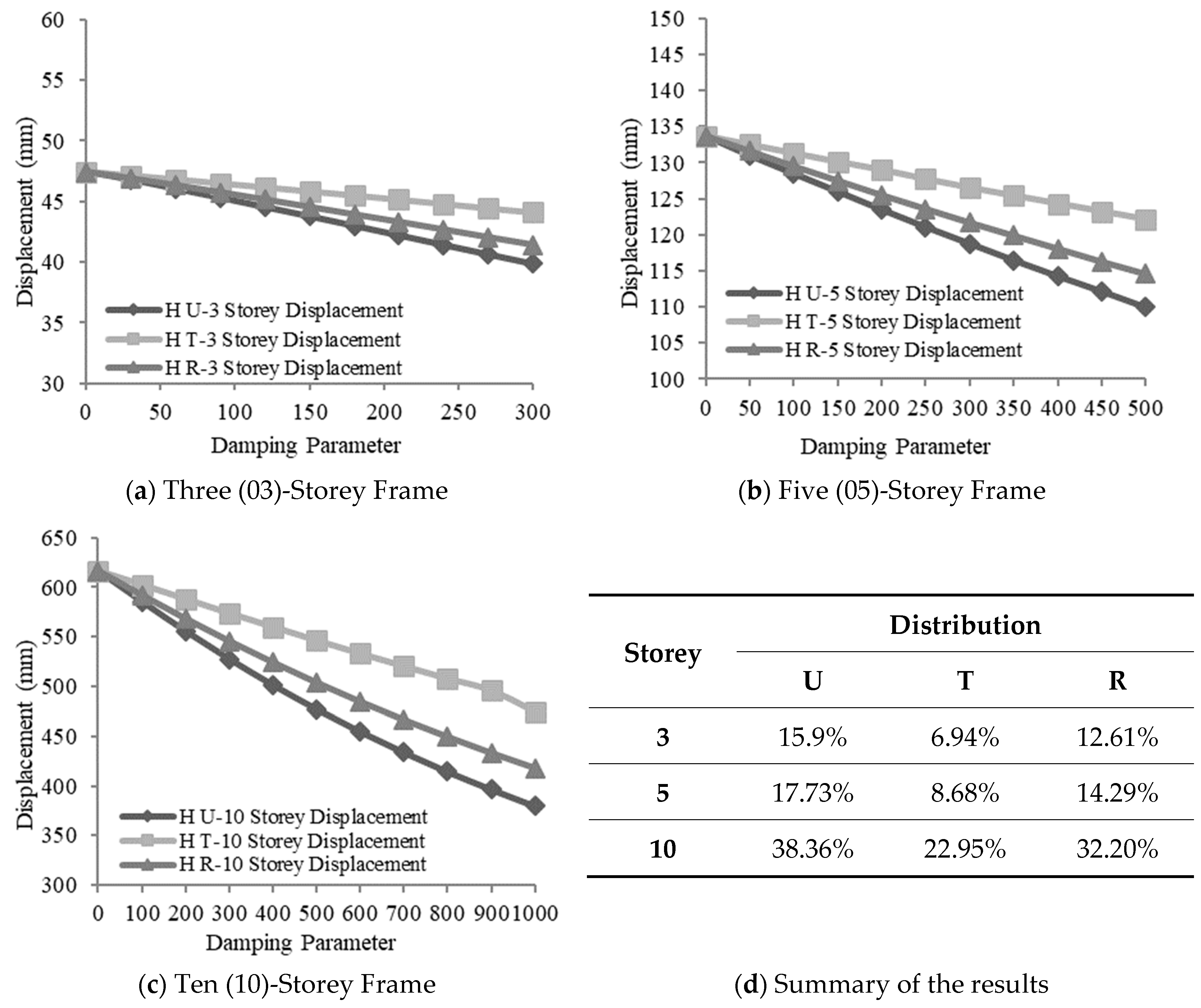
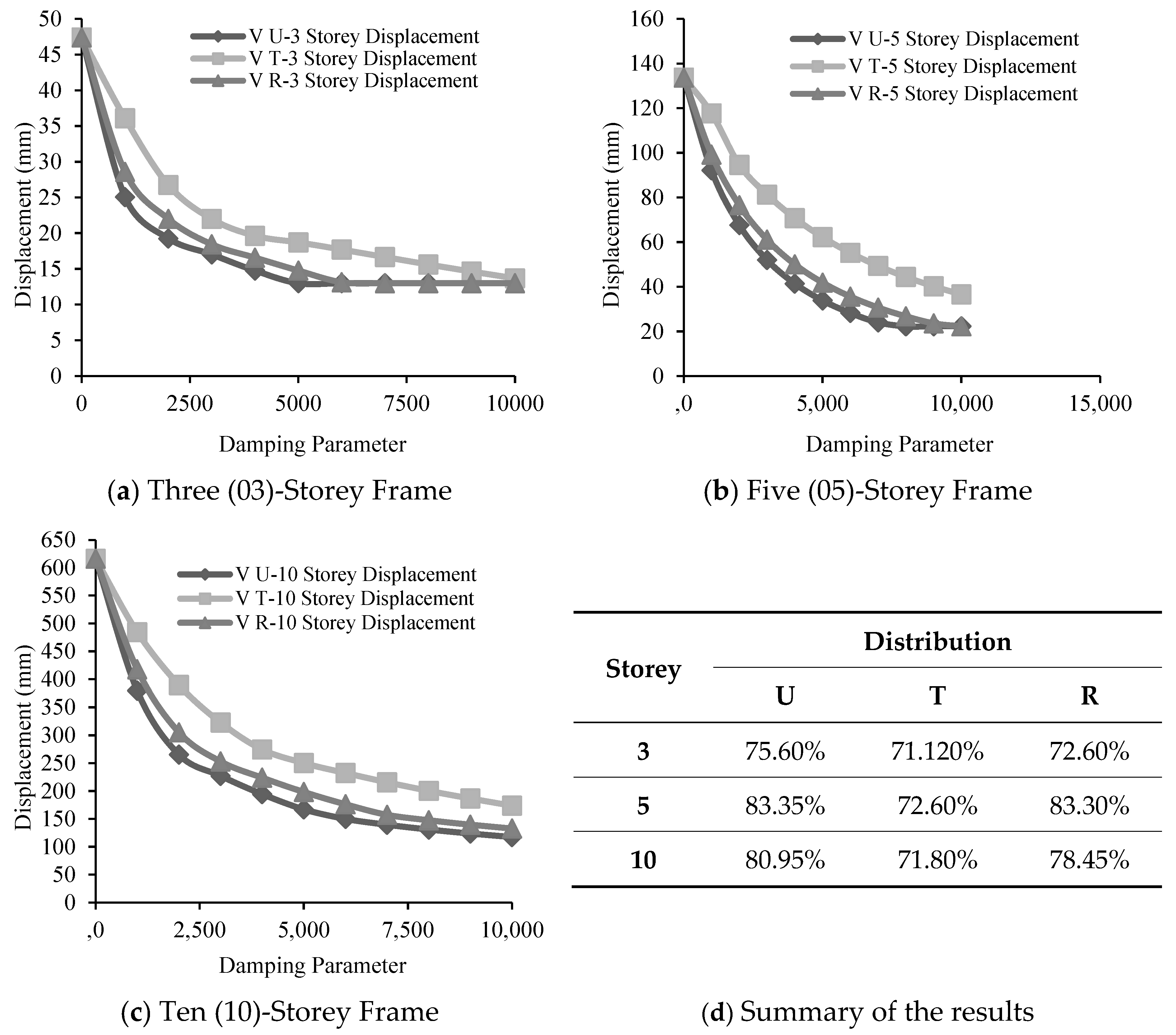
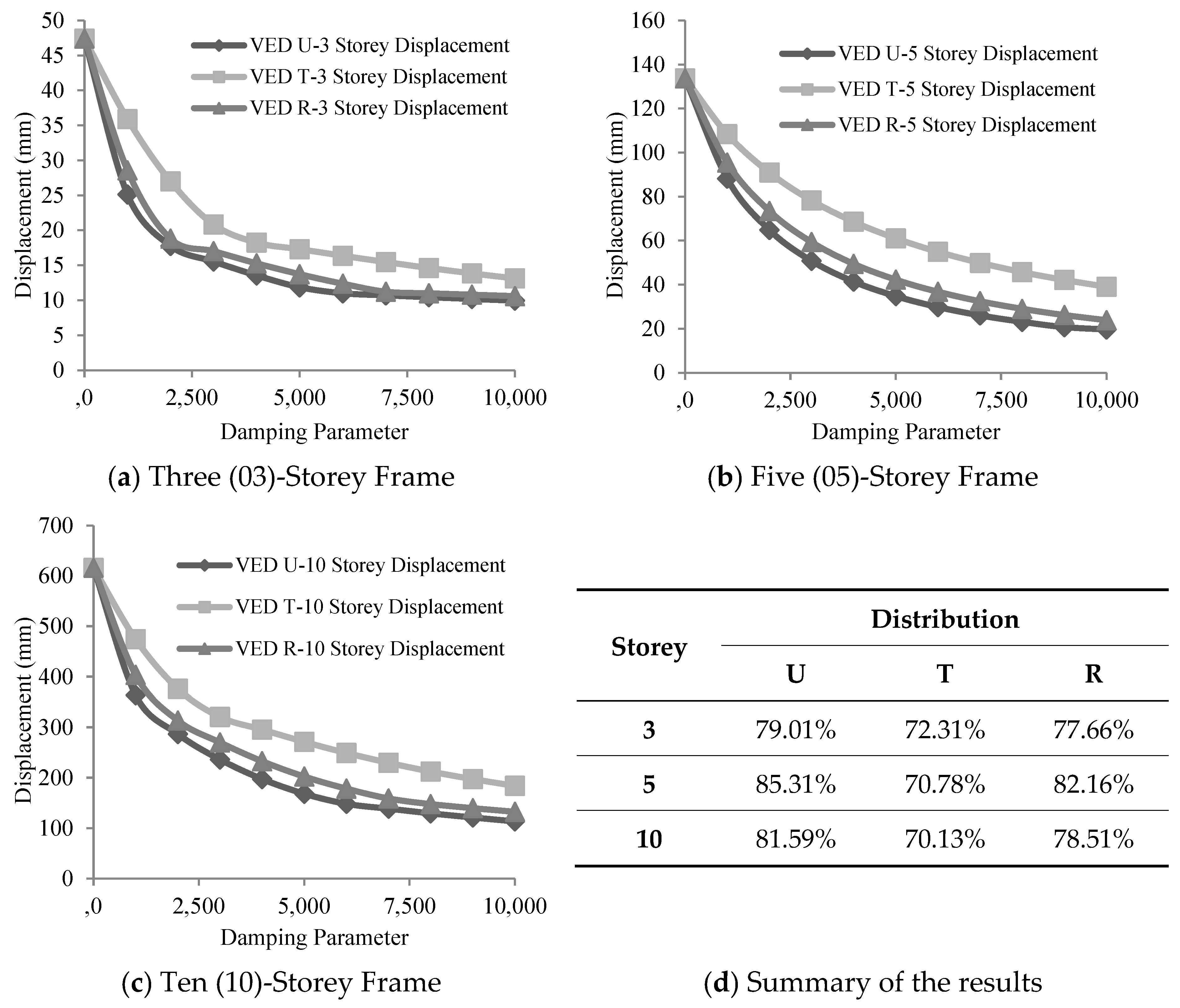
3.2.1. Effect of Variation in Damping Parameters on Displacement
Hysteretic Damper
Friction Damper
Viscous Damper
Viscoelastic Damper
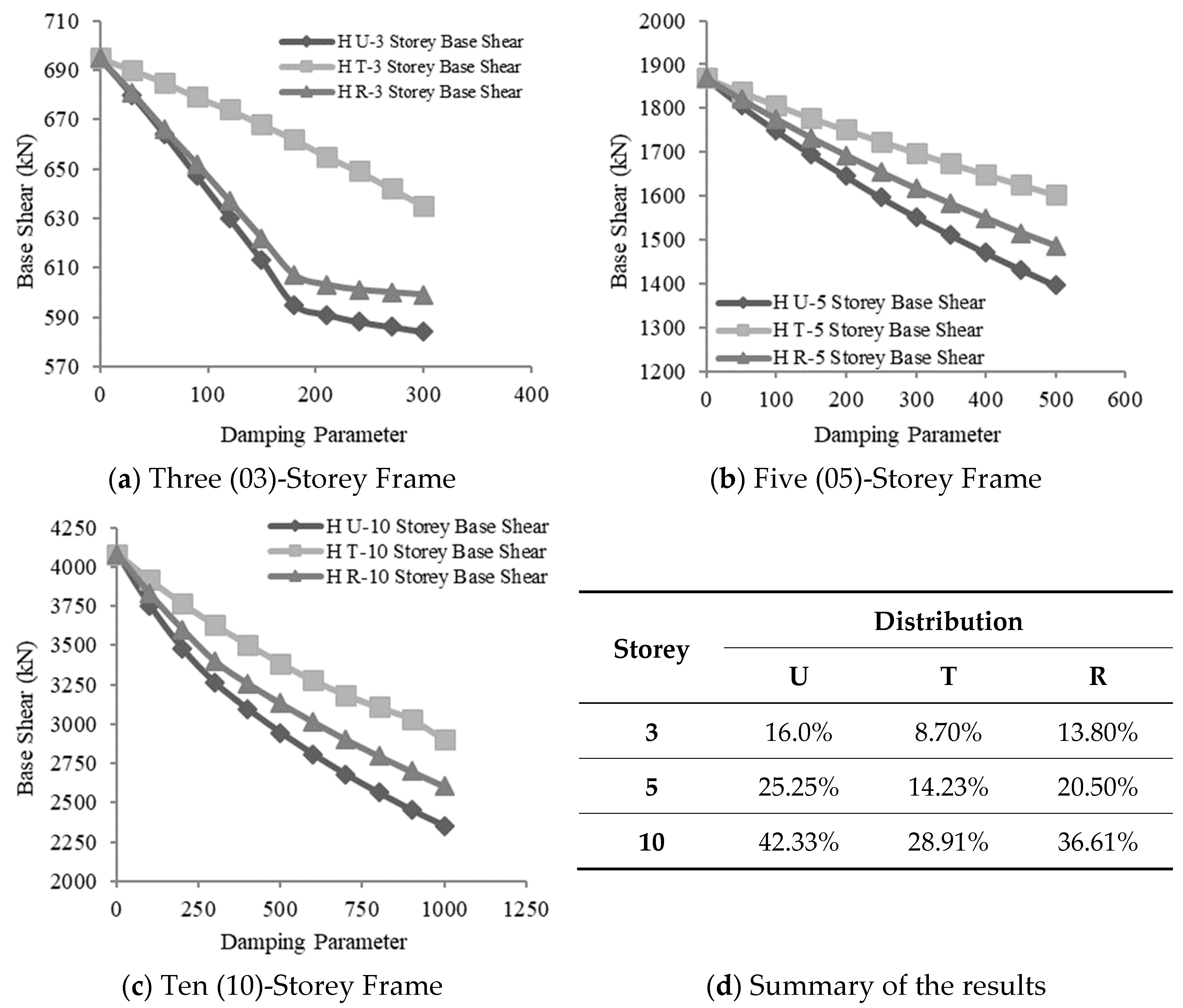
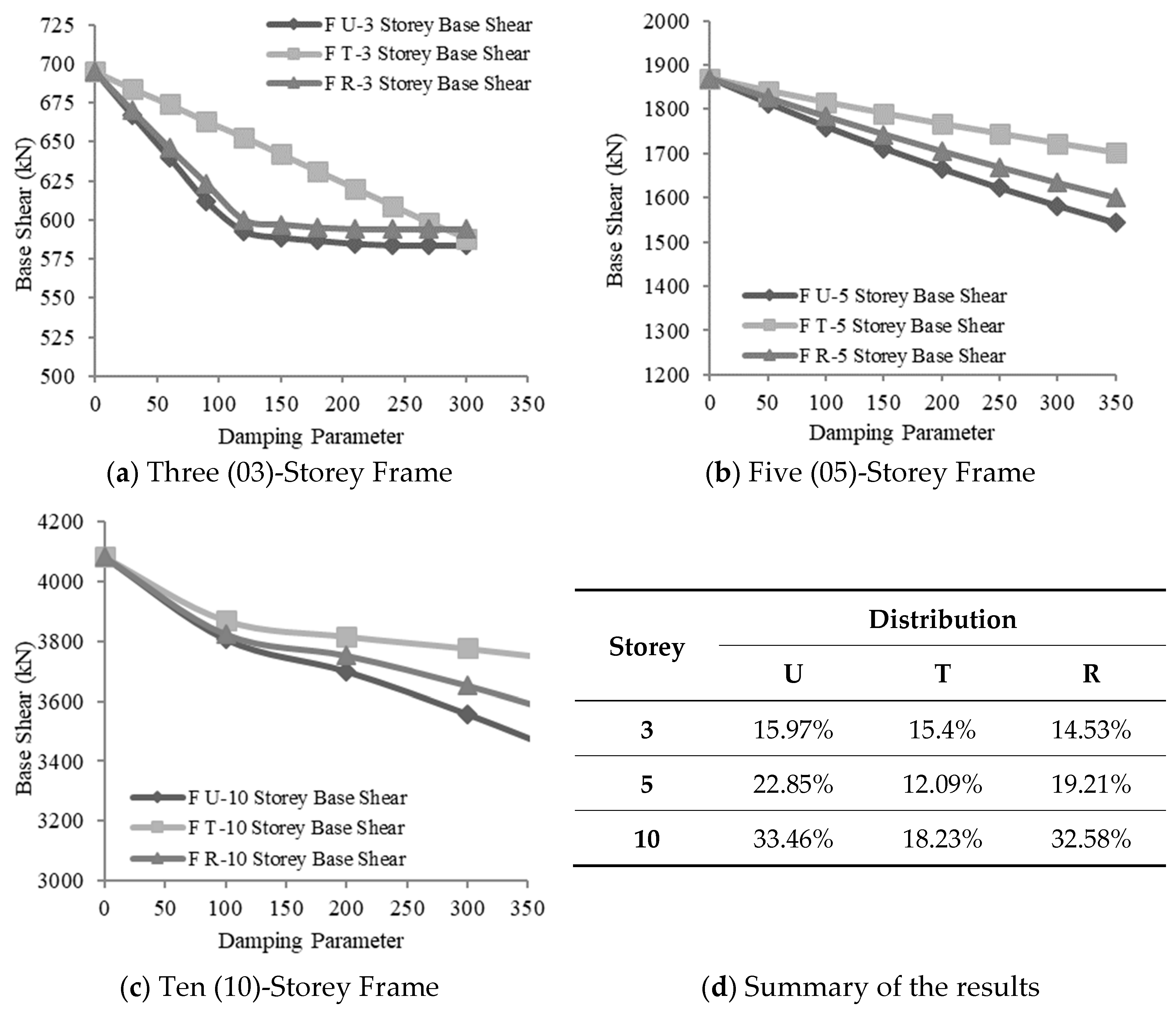
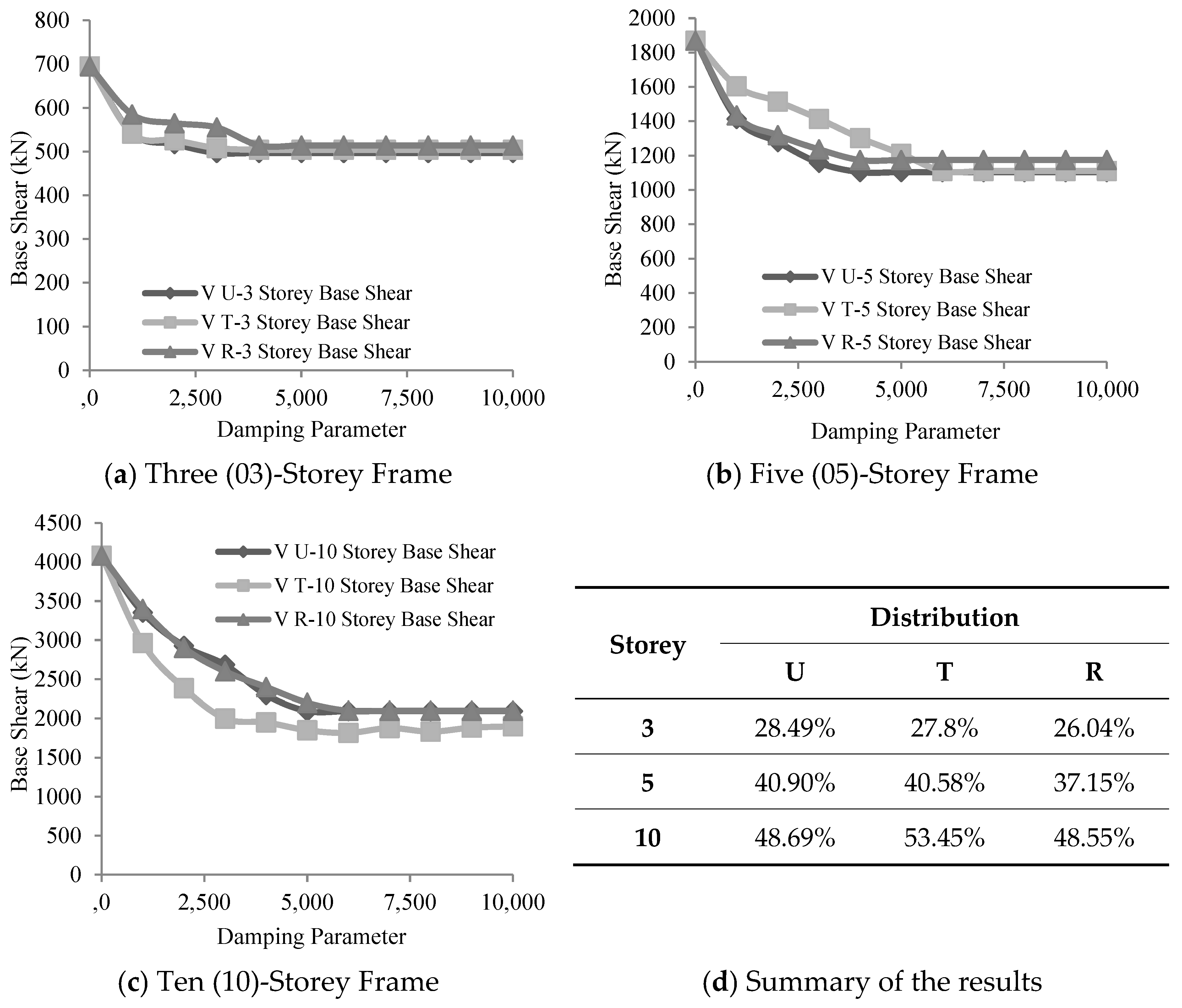
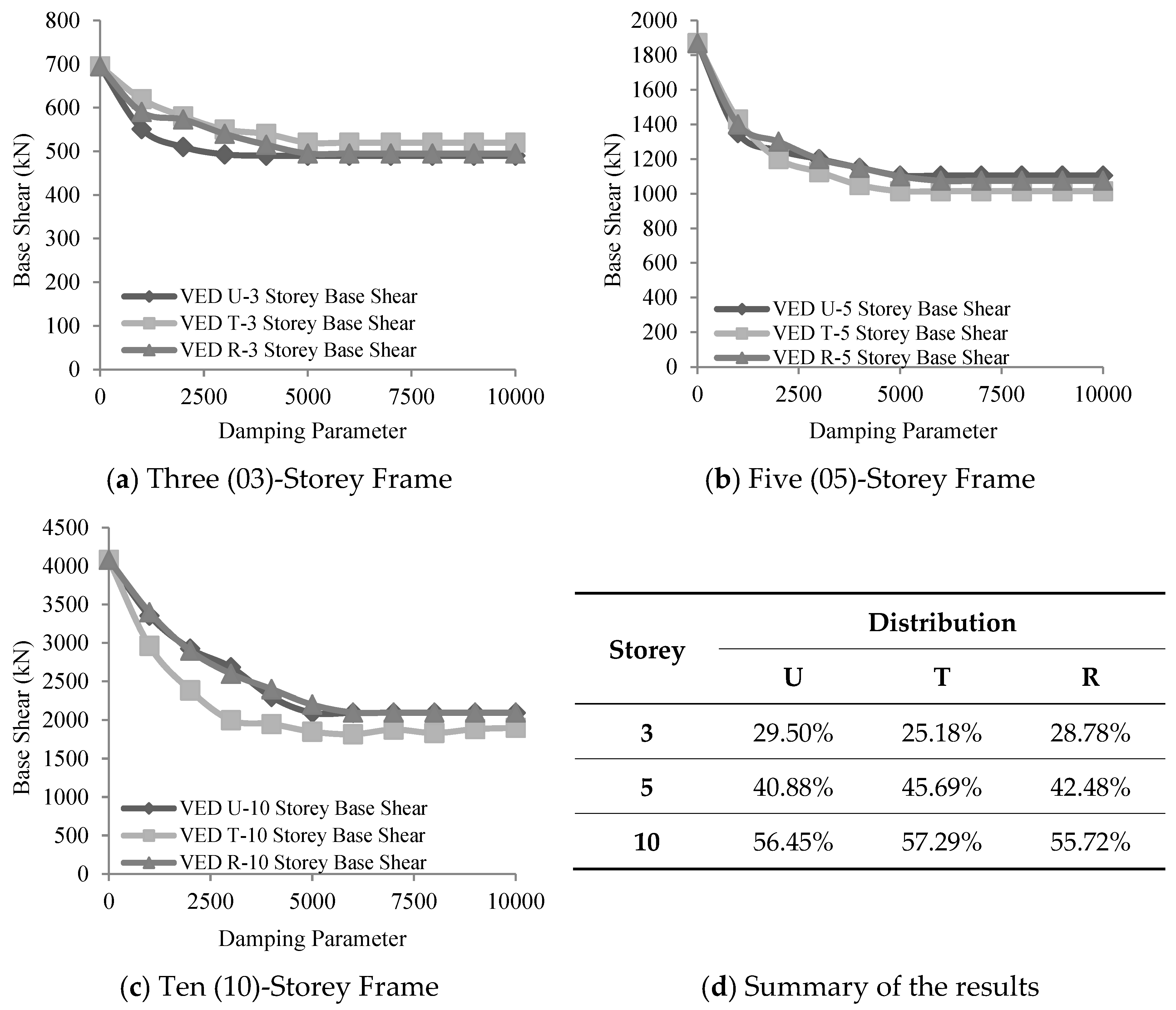
3.2.2. Effect of Variation in Damping Parameters on Base Shear
Hysteretic Damper
Friction Damper
Viscous Damper
Viscoelastic Damper
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DP | Damping parameter |
| ETABS | Extended tall analysis of buildings and structures |
| F | Friction |
| g | Gravitational acceleration |
| H | Hysteretic |
| PEDD | Passive energy dissipation devices |
| PGA | Peak ground acceleration |
| R | Reverse-triangular distribution |
| T | Triangular distribution |
| U | Uniform distribution |
| V | Viscous |
| VE | Viscoelastic |
References
- Desramaut, N.; Modaressi, H.; Le Cozannet, G. Earthquake Damage BT—Encyclopedia of Natural Hazards; Bobrowsky, P.T., Ed.; Springer: Dordrecht, The Netherlands, 2013; pp. 223–225. ISBN 978-1-4020-4399-4. [Google Scholar]
- Shaban, N.; Caner, A. Prototype Testing of a New Passive Energy Dissipation Device for Seismic Retrofit of Bridges. Front. Built Environ. 2016, 2, 23. [Google Scholar] [CrossRef][Green Version]
- Safi, W.A.; Hibino, Y.; Kusunoki, K.; Mukai, T.; Sanada, Y. The Structural Performance of Reinforced Concrete Members with Monolithic Non-Structural Walls. Buildings 2020, 10, 87. [Google Scholar] [CrossRef]
- Ibrahim, Y.E.; Hameed, A.; Qazi, A.U.; Rasool, A.M.; Latif, M.F.; Qureshi, M.U. Experimental response of cold-formed steel stud shear wall with hardboard sheathing under seismic loading. Case Stud. Constr. Mater. 2021, 15, e00574. [Google Scholar] [CrossRef]
- FEMA-273; NEHRP Guidelines for the Seismic Rehabilitation of Buildings. Federal Emergency Management Agency: Washington, DC, USA, 1997.
- FEMA-P440a; Effects of Strength and Stiffness Degradation on Seismic Response. Federal Emergency Management Agency: Washington, DC, USA, 2009.
- FEMA-440; Improvement of Nonlinear Static Seismic Analysis Procedures. Federal Emergency Management Agency: Washington, DC, USA, 2005.
- FEMA-356; Prestandard and Commentary for the Seismic Rehabilitation of Buildings. Federal Emergency Management Agency: Washington, DC, USA, 2000.
- Constantinou, M.; Soong, T.; Dargush, G. Passive Energy Dissipation Systems for Structural Design and Retrofit; Monograph No. 1; MCEER: Buffalo, NY, USA, 1998. [Google Scholar]
- Amr, S.E.; Di Sarno, L. Response of Structures. In Fundamentals of Earthquake Engineering; Wiley Online Books; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; pp. 47–118. ISBN 9780470024867. [Google Scholar]
- Rai, D.C. Future trends in earthquake-resistant design of structures. Curr. Sci. 2000, 79, 1291–1300. [Google Scholar]
- Wang, C.; Ayyub, B.M. Time-dependent seismic resilience of aging repairable structures considering multiple damage states. Earthq. Eng. Resil. 2022, 1, 73–87. [Google Scholar] [CrossRef]
- Afzal, M.F.; Matsumoto, Y.; Nohmi, H.; Sakai, S.; Su, D.; Nagayama, T. Comparison of Radar Based Displacement Measurement Systems with Conventional Systems in Vibration Measurements at a Cable Stayed Bridge. In Proceedings of the 11th German-Japan Bridge Symposium, Osaka, Japan, 30–31 August 2016. [Google Scholar]
- Hameed, A.; Afzal, M.F.U.D.; Javed, A.; Rasool, A.M.; Qureshi, M.U.; Mehrabi, A.B.; Ashraf, I. Behavior and Performance of Reinforced Concrete Columns Subjected to Accelerated Corrosion. Metals 2023, 13, 930. [Google Scholar] [CrossRef]
- Nakamura, Y.; Okada, K. Review on seismic isolation and response control methods of buildings in Japan. Geoenviron. Disasters 2019, 6, 7. [Google Scholar] [CrossRef]
- Soong, T.; Dargush, G. Passive Energy Dissipation Systems in Structural Engineering; John Wiley & Sons Ltd.: Chichester, UK, 1997. [Google Scholar]
- Symans, M.D.; Constantinou, M.C. Semi-active control systems for seismic protection of structures: A state-of-the-art review. Eng. Struct. 1999, 21, 469–487. [Google Scholar] [CrossRef]
- Soong, T.T.; Spencer, B.F. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Symans, M.; Charney, F.; Whittaker, A.; Constantinou, M.; Kircher, C.; Johnson, M.; McNamara, R. Energy Dissipation Systems for Seismic Applications: Current Practice and Recent Developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Hameed, A.; Qazi, A.; Rasool, A.M. Seismic Performance of Low to Medium Rise Reinforced Concrete Buildings using Passive Energy Dissipation Devices. Pakistan J. Eng. Appl. Sci. 2014, 14, 1–16. [Google Scholar]
- Sorace, S.; Terenzi, G. Analysis, Design, and Construction of a Base-Isolated Multiple Building Structure. Adv. Civ. Eng. 2014, 2014, 585429. [Google Scholar] [CrossRef]
- Cobo del Arco, D.; Raventós, I.; Mohr, S. Seismic Isolated Continuous Railway Composite Bridges in the North of Algeria. Struct. Eng. Int. 2019, 31, 72–75. [Google Scholar] [CrossRef]
- Zheng, W.; Tan, P.; Li, J.; Wang, H.; Liu, Y.; Xian, Z. Superelastic pendulum isolator with multi-stage variable curvature for seismic resilience enhancement of cold-regional bridges. Eng. Struct. 2023, 284, 115960. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Zhang, R. Editorial for “recent advances in the design of structures with passive energy dissipation systems”. Appl. Sci. 2020, 10, 2819. [Google Scholar] [CrossRef]
- Augusti, G. Dynamics of structures: Theory and applications to earthquake engineering. Meccanica 1996, 31, 719–720. [Google Scholar] [CrossRef]
- Madsen, L.P.B.; Thambiratnam, D.P.; Perera, N.J. Seismic response of building structures with dampers in shear walls. Comput. Struct. 2003, 81, 239–253. [Google Scholar] [CrossRef]
- Shao, D.; Pall, A.; Soli, B. Friction dampers for seismic upgrade of a 14-story patient tower with a 36-foot tall soft-story. In Proceedings of the 8th US National Conference on Earthquake Engineering 2006, San Francisco, CA, USA, 18–22 April 2006. [Google Scholar]
- Marko, J.; Thambiratnam, D.; Perera, N. Influence of damping systems on building structures subject to seismic effects. Eng. Struct. 2004, 26, 1939–1956. [Google Scholar] [CrossRef]
- Ribakov, Y. Using viscous and variable friction dampers for improving structural seismic response. Struct. Des. Tall Spec. Build. 2011, 20, 579–593. [Google Scholar] [CrossRef]

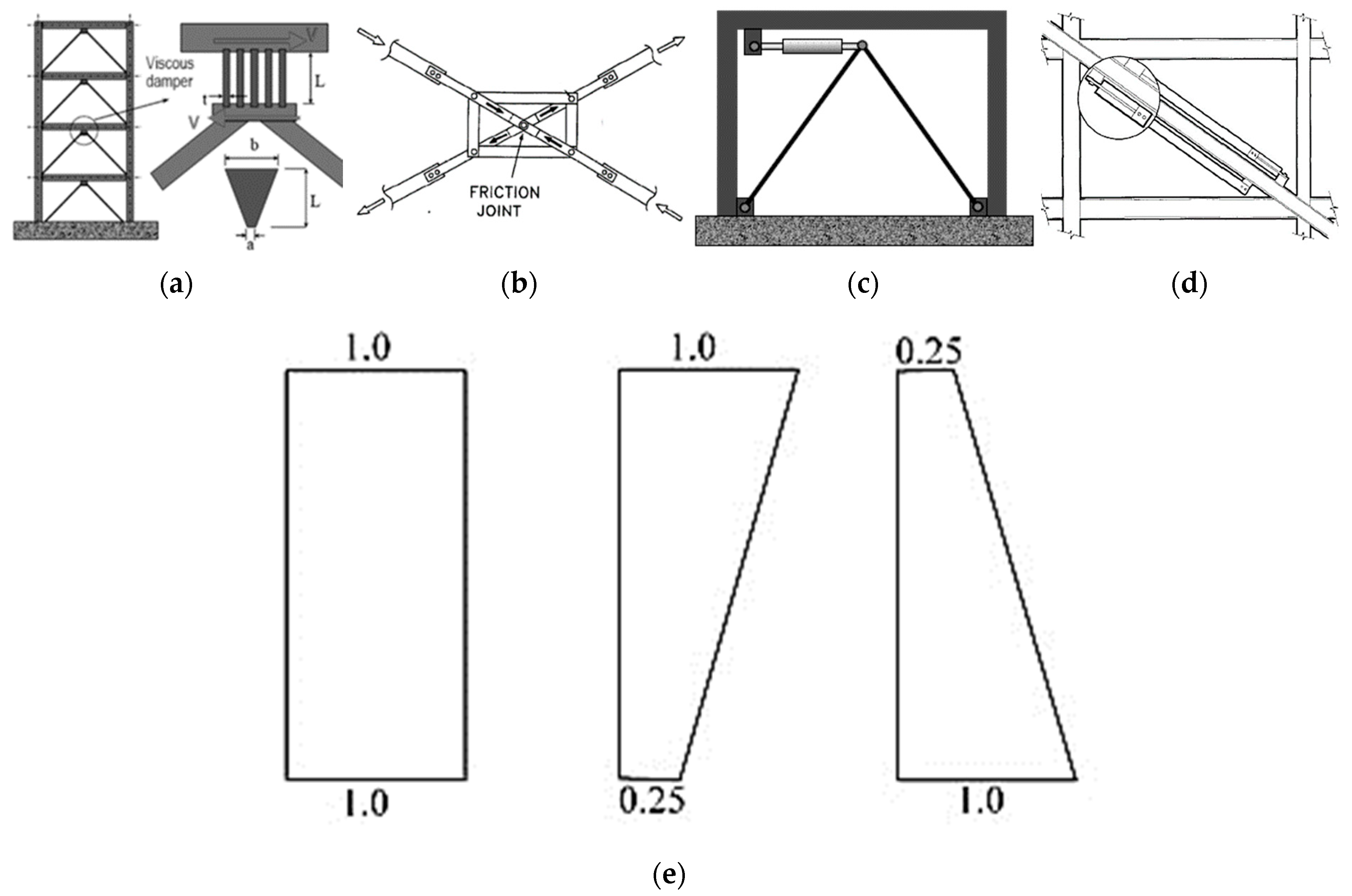
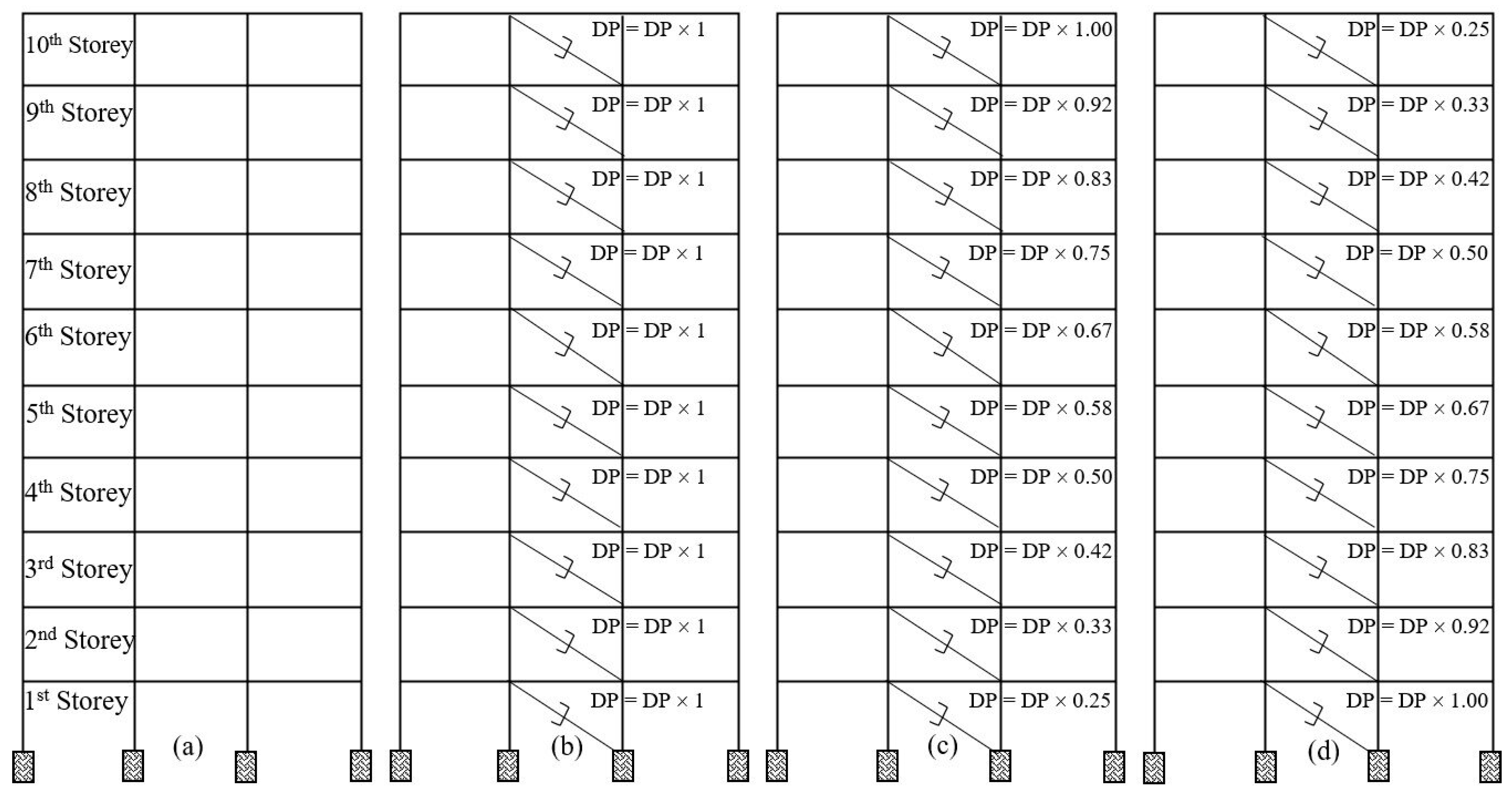

| Parameters | Three (03)-Storey | Five (05)-Storey | Ten (10)-Storey |
|---|---|---|---|
| X-direction grids/bays | 3 | 3 | 3 |
| Y-direction grids/bays | 1 | 1 | 1 |
| X-direction grid/bay width (m) | 7.5 | 7.5 | 7.5 |
| Number of storeys | 3 | 5 | 10 |
| Column size (mm) | 500 × 500 | 600 × 600 | 700 × 700 |
| Beam size (mm) | 400 × 600 | 400 × 600 | 500 × 600 |
| Fundamental Time Period (s) | 0.468 | 0.670 | 1.10 |
| Case No. | Damper Types | ||||
|---|---|---|---|---|---|
| Hysteretic or Friction Dampers | Viscous Dampers | Viscoelastic Dampers | |||
| 10-Storey | 5-Storey | 3-Storey | All Buildings | All Buildings | |
| Py (kN) for Hysteretic Dampers or Fy (kN) for Friction Dampers | Damping Coefficient C (kN-s/m) | Effective Stiffness KEFF (kN/m) | |||
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 100 | 50 | 30 | 1000 | 2000 |
| 3 | 200 | 100 | 60 | 2000 | 4000 |
| 4 | 300 | 150 | 90 | 3000 | 6000 |
| 5 | 400 | 200 | 120 | 4000 | 8000 |
| 6 | 500 | 250 | 150 | 5000 | 10,000 |
| 7 | 600 | 300 | 180 | 6000 | 12,000 |
| 8 | 700 | 350 | 210 | 7000 | 14,000 |
| 9 | 800 | 400 | 240 | 8000 | 16,000 |
| 10 | 900 | 450 | 270 | 9000 | 18,000 |
| 11 | 1000 | 500 | 300 | 10,000 | 20,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasool, A.M.; Afzal, M.F.U.D.; Rashid, M.U. Enhancing Seismic Resilience: Evaluating Buildings with Passive Energy Dissipation Strategies. Eng 2024, 5, 367-383. https://doi.org/10.3390/eng5010020
Rasool AM, Afzal MFUD, Rashid MU. Enhancing Seismic Resilience: Evaluating Buildings with Passive Energy Dissipation Strategies. Eng. 2024; 5(1):367-383. https://doi.org/10.3390/eng5010020
Chicago/Turabian StyleRasool, Ali Murtaza, Muhammad Faheem Ud Din Afzal, and Muhammad Usman Rashid. 2024. "Enhancing Seismic Resilience: Evaluating Buildings with Passive Energy Dissipation Strategies" Eng 5, no. 1: 367-383. https://doi.org/10.3390/eng5010020
APA StyleRasool, A. M., Afzal, M. F. U. D., & Rashid, M. U. (2024). Enhancing Seismic Resilience: Evaluating Buildings with Passive Energy Dissipation Strategies. Eng, 5(1), 367-383. https://doi.org/10.3390/eng5010020







