Abstract
With the rapid development of modern technologies, autonomous or robotic construction sites are becoming a new reality in civil engineering. Despite various potential benefits of the automation of construction sites, there is still a lack of understanding of their complex nature combining physical and cyber components in one system. A typical approach to describing complex system structures is to use tools of abstract mathematics, which provide a high level of abstraction, allowing a formal description of the entire system while omitting non-essential details. Therefore, in this paper, autonomous construction is formalised using categorical ontology logs enhanced by abstract definitions of individual components of an autonomous construction system. In this context, followed by a brief introduction to category theory and ologs, exemplary algebraic definitions are given as a basis for the olog-based conceptual modelling of autonomous construction systems. As a result, any automated construction system can be described without providing exhausting detailed definitions of the system components. Existing ologs can be extended, contracted or revised to fit the given system or situation. To illustrate the descriptive capacity of ologs, a lattice of representations is presented. The main advantage of using the conceptual modelling approach presented in this paper is that any given real-world or engineering problem could be modelled with a mathematically sound background.
1. Introduction
Civil engineering is widely considered very traditional, especially in comparison to other engineering disciplines, such as mechanical engineering, mainly because of the unique character of each structure. Even for standard residential buildings, the particular conditions on each construction site may require changes in the design and modelling of the building, which may affect the entire construction process. This one-of-a-kind-production has been a major obstacle on the way to integrating modern technologies and automation in the field of civil engineering for a long time. Furthermore, the availability of cheap manual labour and the small and medium-sized enterprise structure of the construction sector have hindered advances in research and development. Recently, the development of integrating affordable yet highly flexible industrial robots into the digital design flow of architecture and construction has prompted a surge in robotic systems in construction [1].
The spectrum of automation in construction ranges from industrial and on-site prefabrication to autonomous on-site robots. However, for mobile in-situ construction robots, only prototypes have been presented so far; see, for example, works [2,3,4]. This is mainly because industrial robots are designed for repetitive tasks in controlled environments and are now used in manufacturing systems for different types of materials, for example, timber [5], masonry [6], and concrete [7]. In this regard, the transition to autonomous mobile on-site robots requires modifications to the robotic system, possibly adding wheels for movement, tracking or scanning devices for orientation and perception of obstacles, other robots or human co-workers. Furthermore, each construction site is unique, implying that a robot must adapt to sudden changes in environmental conditions.
As the success of robotic construction evidently depends on the interaction of robotic systems with the environment, it has been stated in [8] that design and construction systems have to be aligned to the capabilities of the robot arm and tolerances of the material, i.e., weight, friction, rigidity, as well as the robotic placement and potential connection systems. In addition to the one-of-a-kind character, structures are an aggregation of possibly hundreds of work steps for each individual part of the structure. From structural work to interior fitting, robotic systems have to be able to handle each step of the way and, therefore, need to interact or collaborate with the environment and other robots on the same construction site. Therefore, advanced feedback and localisation systems, e.g., external or integrated sensors, cameras or laser scanners, are required to cope with tolerances, uncertainties and possibly human interaction. To overcome these obstacles, a workflow and prototypes for autonomous construction sites have been presented in [4,9].
However, summarising current results related to robotic construction sites, it is noticeable that researchers solely present particular solutions, aiming to address specific tasks. This approach results in creating somehow similar yet different workflows, each highlighting specific aspects of robotic construction sites relevant to a particular task. Furthermore, each prototype uses different tools as well as system components and is based on different types of robotic manipulators from various manufacturers programmed by different types of code to control the robots, emphasising the lack of a general approach to modelling robotic construction sites that would be applicable to different tasks. Therefore, this paper aims to provide a fundamental basis for the conceptual modelling of robotic construction sites based on mathematical abstractions and, in particular, category theory.
In recent years, several results related to the formal modelling of engineering systems have been presented. In particular, abstract approaches based on graph theory [10], abstract Hilbert spaces [11,12], relational algebra [13,14], predicate logic [15,16], type theory [17,18], and category theory [19,20,21,22] have been proposed. However, direct use of these results in the context of autonomous construction sites is difficult because of the coupled system robot-construction site, which requires conceptual modelling not only of a robot itself but also its surrounding and, in particular, kinematic constraints on robot movements. Therefore, to overcome this difficulty, the use of categorical ontology logs, or simply ologs, combined with an abstract algebraic approach is proposed in this paper.
Ologs were introduced by Spivak and Kent in [23] and are based on category theory, implying that ologs have a strong mathematical basis while providing the flexibility of general-purpose ontologies. In particular, ologs provide two distinct features making them very attractive for practical use:
- (i)
- Ologs follow the ideas of “lattice of theories” presented in [24], implying, simply speaking, that the same system can be represented by ologs with different levels of details, thus constituting a lattice of representations. This point of view can be adapted to the conceptual modelling of autonomous construction sites or engineering systems in general. A system could be modelled on a very general level at first and, after that, by using specific movements along the lattice, such as contraction, expansion, revision, and analogy, specific parts of the system can be “zoomed in”.
- (ii)
- The categorical foundation of ologs provides a clear formal procedure for relating two different ologs. This procedure is based on the concept of common ground, which is represented by a third olog related to the two other ologs. Practically, it implies that different ologs can be created for individual parts of an engineering system and then coupled together in one system of ologs.
Although ologs have the obvious advantages discussed above, they also share an obstacle typical for all general-purpose ontologies: a subjective worldview of the ontology creator. Therefore, to overcome this obstacle, in this paper, we propose a slight modification of the concept of common ground presented in [23]. This modification is based on a two-step procedure: at first, formal definitions of individual components of an autonomous construction site, based on an abstract algebraic approach presented in [13], are introduced; after that, the abstract definitions are used as a common ground for all ologs describing an autonomous construction site. In this case, the subjectivity of the ologs’ creator worldview can be overcome, and thus, a formally sound lattice of ologs, representing an autonomous construction site, will be obtained.
This paper aims to provide a basis to overcome the previously mentioned issues of conceptual modelling of automated construction sites by coupling ologs with abstract algebraic definitions. In this context, algebraic definitions are used as a common basis for olog-based conceptual modelling of autonomous construction systems. As a result, any automated construction system can be described, without providing exhausting detailed definitions of the system components. Existing ologs can easily be extended, contracted or revised to fit the given system or situation. With these operations, e.g., revision, precise translation terminologies are provided. To illustrate the capacity of ologs, a lattice of representations for automated construction sites is presented. The main advantage of using the conceptual modelling approach presented in this paper is that any given real-world scenario or engineering problem could be modelled with a mathematically sound background.
The paper is organised as follows: Section 2 provides a few basic facts about category theory and ologs; Section 3 introduces an abstract description of autonomous construction sites, used as the common ground for olog-based representation of advanced structures presented in Section 4; finally, a discussion on the results of the paper and remarks on further applications are provided in Section 5.
2. Fundamentals of Category Theory and Ologs
In this section, the concept of ologs for the purpose of conceptual modelling of real-life scenarios is described, following a basic introduction to category theory as mathematical basis of ologs.
2.1. Basics of Category Theory
Ologs are based on category theory, and therefore, to support the reader in the upcoming discussion, a few basic definitions of category theory are provided in this section. Generally speaking, category theory can be seen as an abstract theory of functions studying different mathematical structures (objects) and relations between them [25]. A category is introduced via the following definition:
Definition 1
([25]).A category consists of the following data:
- (i)
- Objects:
- (ii)
- Arrows:
- (iii)
- For each arrow f, there are given objects,called the domain and codomain of f. We writeto indicate thatand.
- (iv)
- Given arrowsand, i.e., with, there is given an arrowcalled the composite of f and g.
- (v)
- For each object A, there is given an arrowcalled the identity arrow of A.
- These data are required to satisfy the following laws:and.
A category is everything satisfying this definition, and therefore, very general objects can be put together to form a category by specifying relations between objects via the arrows, which are sometimes called morphisms. This generality is the starting point for introducing ologs, as it will be shown later. Mappings between different categories are introduced by the notion of a functor:
Definition 2
([25]).A functorbetween categoriesandis a mapping of objects to objects and arrows to arrows in such a way that:
- (i)
- ;
- (ii)
- ;
- (iii)
- .
- That is, F respects domains and codomains, identity arrows, and composition. In other words, functors are structure-preserving mappings between categories.
2.2. Introduction to Ologs
Ologs, in general, as first introduced in [23], are intended to provide a framework for knowledge representation, in order to organise data and results, to make them comprehensible and comparable to other scientists. As stated by the name, ontology logs are closely related to ontologies, which focus on defining what entities exist, thus consequently categorising entities and defining relationships between these categories. In engineering applications, ontologies are used to develop models of reality. Subsequently, ologs are intended to structure and represent the results of defining entities and modelling relationships between categories by recording them in a structure based on category theory.
However, as for every model, the structure is highly dependent on the subjective worldview of the creator(s). When creating ontologies, subjectivity should be eliminated as far as possible, as it may lead to information not being perceived by readers as intended by the creators. Hence, ologs are aware that the views of the creators and readers may not correspond. Therefore, ologs do not attempt to accurately reflect reality but to be structurally sound and accurate in correspondence with the views of the creator. However, discrepancies in the views of different creators do not prevent ologs from being aligned and connected. Because of the strong mathematical basis provided by category theory, ologs can be linked and precisely connected by functors, as the main advantage for conceptual modelling.
Functors allow ologs to be referenceable by other authors and, in addition, extendable since any model, respectively olog, needs to be extended in order to correctly represent new developments, features or different views. Moreover, the mapping of ologs by functors allows the generation of precise translation terminologies between models. Thus, as well as being represented as graphs, ologs can serve as database schemas that provide a human-readable interface, with the components of ologs representing tables and attributes to translate one system of tables into another. Therefore, the basic components and the respective graphic representation of ologs are presented in the following.
To keep the presentation short, the detailed discussion on the construction of ologs and their structure from [23,26] is compressed in the form of one definition. More advanced concepts from ologs theory will be discussed at the places of their direct use for the olog-based description of engineering systems. Additionally, to support the reader, the definition of ologs is placed in the engineering context. The following definition introduces ologs:
Definition 3.
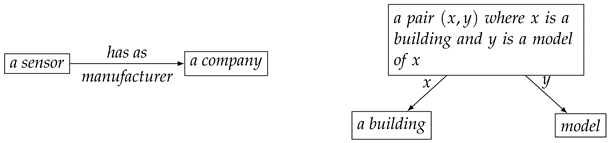
An olog is a category, which has types as objects, aspects as arrows, and facts as commutative diagrams. The types, aspects, and facts are defined as follows:
- A type is an abstract concept represented as a box containing a singular indefinite noun phrase. Types are allowed to have compound structure, i.e., being composed of smaller units. The following boxes are types:
- Aspects are functional relationships between the types represented by labelled arrows in ologs. Consider a functional relationship called f between types X and Y, which can be denoted, then X is called the domain of definition for the aspect f, and Y is called the set of result values of f. Here are two examples of using aspects:
- Facts are commutative diagrams, i.e., graphs with some declared path equivalences, in ologs. Facts are constructed by composing several aspects and types.
Facts, represented by commutative diagrams, have a crucial role in practical applications of ologs, because facts can be straightforwardly converted into databases of knowledge; see [23,26] again for a detailed discussion. Thus, ologs provide a general framework for knowledge representation supporting an easy integration into the engineering modelling process via the link to databases.
With the definition of types, aspects, and facts, the main components of ologs have been introduced. However, as shown in Definition 3, the construction of ologs as graphs follows several rules, in order to keep the system readable, such as the declaration of types should begin with “a” or “an” and aspects with a verb. Detailed information on the construction of ologs can be found in [23].
3. Abstract Description of Autonomous Construction Sites
For enhancing ologs with more objective constructions, it is necessary to provide a formal common ground for the development of ologs of an autonomous construction site. Therefore, this section provides an abstract algebraic description of essential parts definitions, such as robot and robotic environment, constituting an autonomous construction site. As a result of this section, an abstract framework for describing autonomous construction is created.
It is important to remark that existing definitions of a robot attempt to find a balance between being too vague and too specific, with a valid general definition regarding robots seemingly missing or still subject to debate given the sheer amount of robot variations. An overview of several varying robot definitions is given in [27]. Although this section takes steps in this direction, it is not the aim to claim that the definitions provided below should be used as an industry standard. Additionally, it is worth remarking that it is certainly possible to connect existing definitions of a construction robot to the abstract constructions presented in this paper. However, this connection goes beyond the scope of the current paper and is therefore kept for future work.
Because of the predominant role in research and development as stated above, robots in the following context are considered industrial robots, with their components, structure, and operation described in [28]. The aim of this work is to illustrate how the coupling of the abstract algebraic approach and ologs can improve the conceptual modelling of autonomous construction sites.
In terms of abstract constructions, it is possible to follow either the top-to-bottom approach by first defining an autonomous construction site and then scaling it down to its components, or the bottom-to-top approach, by defining the components and then scaling them up to the autonomous construction site. For the purpose of this article, the first approach will be used. Therefore, we start with the following definition:
Definition 4
(Autonomous construction site).An autonomous construction site or a robotic environment is the object, where
- is a task to be solved by robots on a construction site;
- is an n-tuple of robots;
- is the object describing human–robot interaction on a construction site;
- is a set of pairs representing environmental conditions on a construction site;
- is a 4-tuple of GPS information for important parts of a construction site;
- is a base station controlling the autonomous construction site.
Let us discuss the role of each component from Definition 4 in more detail:
- The is represented by a tuple , where is a natural language sentence formulating the task, and is a formalisation of in terms of a sequence of control signals controlling cyber components of the autonomous construction site.
- The n-tuple of robots evidently contains information about all robots used on the construction site. A precise definition of a robot in the framework of the abstract approach presented in this paper is provided in Definition 5.
- Considering that autonomous construction sites naturally combine human workers and robots, it is necessary to address the question of human–robot interaction [29]. However, an abstract definition of such an interaction goes beyond the scope of the current paper. Therefore, we address the point of human–robot interaction simply by placing a specific object for it, which can still be defined later without the need to change any other definition presented in this paper.
- The role of set is to provide information about environmental conditions on a construction site. In this way, this information is formalised in terms of a denotation and the corresponding value .
- For integration of a robotic system in the construction progress, it is necessary to provide information on the positioning of the robotic system, as well as all essential parts of the construction site. For that purpose, the 4-tuple is introduced, where O denotes the object, and are object coordinates.
- Finally, cyber parts of the autonomous construction site must be controlled, and therefore, the base station needs to be included in the definition.
In summary, Definition 4 provides an abstract point of view on autonomous construction sites. This abstract point of view helps to “sieve out”all details that are not critical for the first stage of planning and designing an autonomous construction site.
Next, an abstract description of a robot needs to be introduced. It is also necessary to take into account that a robotic system can generally be subdivided into two parts: a physical part (physical components of the systems) and a logical part (control and communication signals). Hence, an abstract definition must also reflect this coupled nature of a robot. Therefore, the following definition is proposed:
Definition 5
(Robot).A robot is the object = , where
- is a robotic controller generating control signals;
- is a finite set of kinematic properties of a robot;
- is a k-tuple of physical properties of a robot;
- is an n-tuple of sensors installed on a robot;
- is an m-tuple of actuators installed on a robot.
For providing a clear practical interpretation of this definition, let us now discuss the robot components individually:
- The robotic controller is needed for a communication with a base station introduced in Definition 4, and in general, it sends a sequence of control signals for operating the robot.
- A set of kinematic properties represents physical constraints limiting the possible movements of a robot. In practice, is determined by the kinematic chain that is formed by the series of manipulators, connected by joints, and may differ in specifications and movement, providing the (internal) axes of the robot. Furthermore, a robot system may consist of external axes, e.g., track systems. The degrees of freedom of the robotic system is the combination of internal and external axes determined by the kinematic chain. Based on the kinematic properties representing specific constraints, the robotic controller is able to generate control signals for the robot to reach target coordinates in the determined work area. Additionally, it is important to notice that for making consistent from the point of view of set theory, it is assumed that all kinematic constraints are formalised in terms of equations and inequalities, i.e., mathematical expressions.
- The tuple contains robot specification information (e.g., type, manufacturer, or information about a motor driving the system), which includes information. Physical properties have to be also known for generating control signals by the robotic controller .
- Evidently, various sensors might be installed on a robot for measuring environmental conditions, as well as important physical quantities of a robot itself, e.g., the temperature of individual parts. These sensors are combined in an n-tuple .
- Similar to sensors, various actuators need to be installed on a robot and are activated via control signals. These actuators are combined an m-tuple .
For completing basic abstract definitions related to autonomous construction sites, it is necessary to introduce abstract descriptions of sensors and actuators. Abstract definitions for sensors and sensor networks have already been introduced in [13], and a sensor is then defined as follows:
Definition 6
(Sensor, [13]). A sensor is the object , where
- is an n-tuple of finite index sets;
- is an n-tuple of measurements with,;
- is a k-tuple of specifications (type information).
By this definition, sensors are allowed to measure several physical quantities, and not just one. Moreover, for simplicity, we assume that . Nonetheless, it is important to remark that the case is also of practical interest for further use of measurements, i.e., data and signal analysis, since it underlines that not all measured data can be used, but only a subset, which corresponds to the idea of frame analysis and sparse representations [30].
Further, the following definition of a sensor cluster has been presented in [13]:
Definition 7
(Sensor cluster, [13]). A sensor cluster is the object , where
- is a sensor node or a base station controlling the sensor cluster;
- is an n-tuple of sensors, introduced in Definition 6;
- is an m-tuple of relations.
In this definition, the m-tuple of relation specifies the rules of communication between sensors, which are specified during the sensor network design; see [14,31] for specific examples of relations and practical meanings of the relations in wireless sensor network modelling.
Taking into account Definition 7, it is also possible to change Definition 5 of a robot by replacing the n-tuple of sensors with the sensor cluster . However, this approach might be a bit inconsistent because typically robots have built-in sensors, which are directly controlled by the robotic controller and not by a separated sensor node , as required by Definition 7. Therefore, the current form of Definition 5 is preferred. Moreover, if extra sensors need to be installed on a robot, then it is always possible to combine both definitions via the composition
where the composition ∘ represents communication rules between the sensor node and the robotic controller. Hence, the separation of two definitions provides more flexibility in terms of the descriptive capabilities of the whole abstract framework.
Finally, following Definition 6, let us now introduce a definition for an actuator:
Definition 8
(Actuator).An actuator is the object, where
- is a sensor node or a base station controlling the actuator;
- is an actuation signal;
- is an k-tuple of specifications (typing information).
This definition is based on the fact that each actuator has a sensor node attached to it, controlling the actuation process. The control of the actuation process is realised via the corresponding control model embedded into the sensor node, which is abstracted here in terms of the actuation signal . The k-tuple of specification information represents standard information about the actuator (e.g., type, manufacturer).
Further, if necessary, a definition of an actuator cluster, similar to a sensor cluster introduced in Definition 7, can be provided. In this case, actuators have to be combined in a tuple, and another tuple of relation, specifying communications between various actuators and base stations, must be introduced. For the purpose of this paper, a definition of an actuator cluster is omitted. Instead, Definition 8 shall conclude by defining a common ground for an autonomous construction site, which shall subsequently be used for creating ologs.
4. Olog Representations of Robotic Construction Sites
In this section, the abstract definitions of autonomous construction sites introduced in Section 3 will be used as a common ground for creating olog representations of autonomous construction sites. In particular, the concept of the lattice of representations will be discussed and illustrated by examples.
Ologs reflect the idea of lattice of theories by a lattice of representations, see again [23], as mentioned in Section 1. Formally, the lattice of representations is represented by an entailment pre-order as part of the global category of specifications. Practically, it means that it is possible to move between different ologs by using four operations/mapping, see Figure 1: contraction , expansion , revision , and analogy .
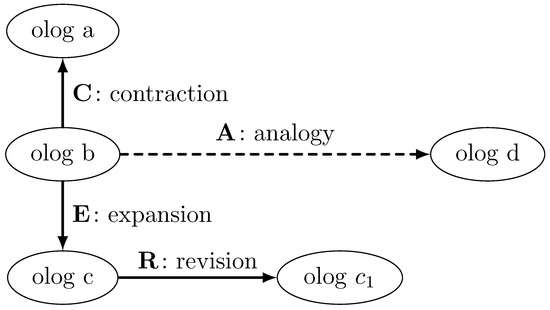
Figure 1.
A general idea of the lattice of representation concept.
More general or detailed ologs are created, by moving upwardes or downwards, respectively, between ologs, i.e., by contraction or expansion , as it is indicated in Figure 1. In addition, ologs may be revised to update or remove details, which is realised via revision , or translated into another olog, using a morphism.
As mentioned in Section 3, a top-to-bottom approach was chosen for olog development. Therefore, we start our lattice of representations by developing olog for describing an autonomous construction site based on Definition 4. The olog starts at type A, the autonomous construction site itself. Based on Definition 4, an autonomous construction site consists of a tuple of tasks , an n-tuple of robots , a human–robot interaction , a set of pairs of environmental conditions , a 4-tuple of GPS information , and a base station . Every object of the autonomous construction site is represented by a type in the corresponding olog illustrated in Figure 2.
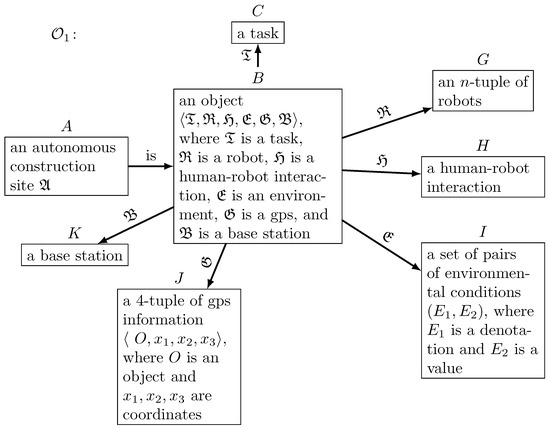
Figure 2.
Olog representation of an autonomous construction site.
In conformity with Section 2.2, every type begins with a or an. An aspect is connecting a type, representing all possible objects of that type, called domain, with another type, called codomain, representing a subset of possible results. The olog presented in Figure 2 provides a very general description of an autonomous construction site. To provide a better overview, several arrows connecting types have been omitted. These connecting arrows constitute facts about an autonomous construction site. For example, by connecting type A and type K via an arrow labelled as has, we would obtain the following fact: an autonomous construction site has a base station. Similarly, other facts can be deduced from olog .
Next, let us illustrate how expansion works on the example of olog . We formally apply an expansion mapping to , which results in adding more types and connecting arrows to the original olog of an autonomous construction site. Figure 3 presents the results of this expansion, a new olog .
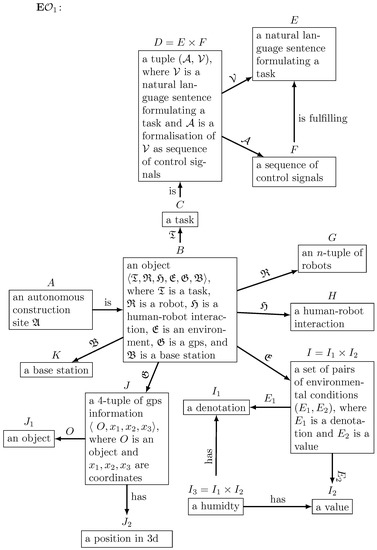
Figure 3.
Olog representation of an autonomous construction site after the application of an expansion mapping .
Evidently, olog has been expanded with more types and more facts provided by commutative paths, for example, the triangle . Additionally, for illustrative purposes, we have added type as humidity, which is a particular instance of an environmental condition. This shows how concrete data can be added to an abstract olog, implying that an olog can be directly translated into a database of knowledge about an autonomous construction site.
Further, let us illustrate how contraction works by the example of olog . It is important to underline that is not required, meaning that by contracting an expanded olog, we do not need to obtain the original olog. Figure 4 illustrates a possible (one of many) output(s) of applying a contraction mapping to olog , where some details of Definition 4 have been omitted.
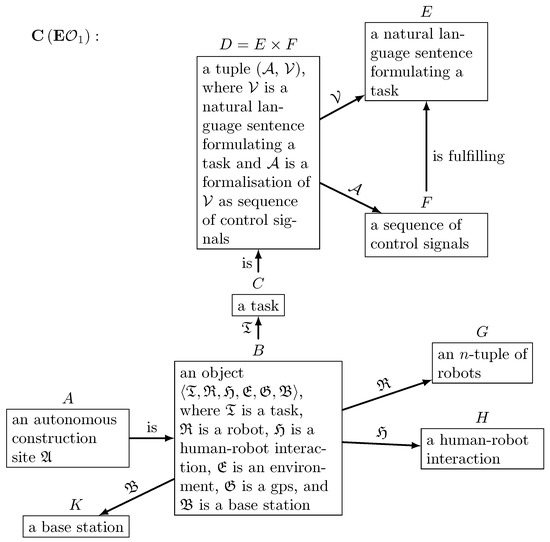
Figure 4.
Olog representation of an autonomous construction site after the application of a contraction mapping to the expanded olog .
Thus, we have the following diagram on the level of ologs:

- where the dashed arrow indicates that we cannot arrive at olog from the olog in one step, and a combination of contractions and expansions is required. Hence, we obtain a lattice of representations containing several ologs that are convertible between each other and represent different levels of details about an autonomous construction site.
Similar to the construction of olog , ologs for Definitions 5–8 can be established. For illustrative purposes, only the olog for a robot is presented, while the other ologs will only be denoted. For keeping consistency with the order of definition presented in Section 3, let us denote by an olog for a robot, by an olog for a sensor, by an olog for a sensor cluster, and by an olog for an actuator. Figure 5 presents olog , which is based on Definition 5. Similar to olog , olog might be expanded or contracted in different ways, as well as some arrows making olog commute, and facts could be easily added.
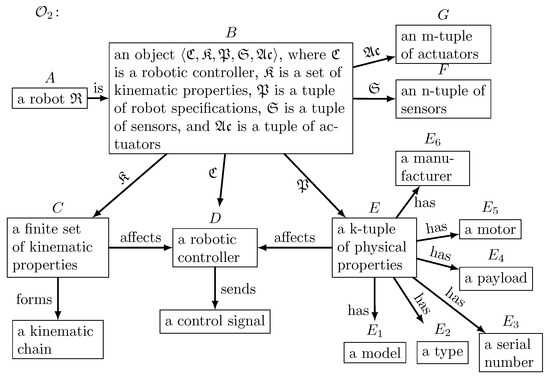
Figure 5.
Olog representation of a robot based on Definition 5.
In addition, a potential connection between ologs and is worth discussing. In general, there are two possibilities to formally connect these ologs:
- (i)
- Olog can be expanded to include olog as a sub-part.
- (ii)
- Olog can be expanded to include olog , and then the resulting olog should be contracted to olog .
From the point of view of constructing a lattice of theories (or representations), the first approach is preferable, while an olog containing more information and, thus, in this sense, a more general olog can be generated from . Following this, let us further introduce formal denotations:
- denotes the olog obtained by expanding the autonomous construction site olog by adding the robot olog to it;
- denotes the olog obtained by expanding the olog by adding the sensor olog to it;
- denotes the olog obtained by expanding the olog by adding the actuator olog to it.
Thus, we obtain the following lattice of representations:
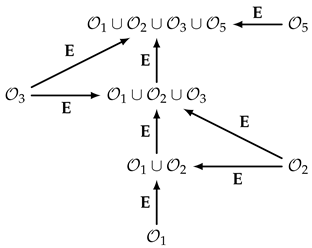
Evidently, all arrows can be reverted and, hence, turned into a contraction of ologs. The diagram above provides a clear structure of how different parts of a system “autonomous construction site” are connected. This structure underlines advantages of working with abstract definitions introduced in Section 3 in combination with ologs:
- (i)
- The resulting ontological description can be easily extended by adding new definitions and ologs without a need for changing previous results;
- (ii)
- The lattice of representation can even be created at first, serving as a guideline for creating ologs and definitions;
- (iii)
- Each olog can be directly converted into a database, see again [23], and, thus, used as a basis for practical implementations of ontologies and formal representations.
It is also worth underlining that the composition of expansion followed by contraction can be viewed as a “zoom-in” operation on an olog. This operation can be seen as a special kind of revision , when a type of the original olog is expanded and then everything except this expansion is removed. This procedure corresponds to the second alternative on connecting ologs and , as discussed above.
Next, let us briefly illustrate a revision of an olog. According to [23], a revision is a composite, which uses a contraction to discard irrelevant details, followed by an expansion to add new facts. Referring back to the discussion around Definition 7, it is possible to replace an n-tuple of sensors in the definition of a robot with a sensor cluster . For olog , it means that revision is applied. Figure 6 shows the resulting olog . It is worth noting that this revision of ologs, as well as of the definition, can be easily performed within the abstract approach proposed in this paper.
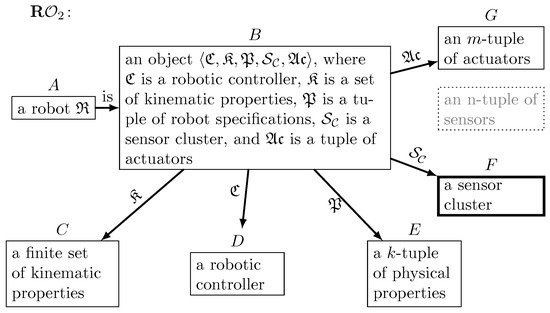
Figure 6.
Illustration of olog revision on the example the robot-olog .
Finally, let us briefly discuss how analogy mapping works. An analogy is obtained by systematically renaming all types and aspects of an olog to describe/model a different real-world situation. For example, a mobile unmanned aerial vehicle can be seen as a system, which is similar to a robot. In this case, an analogy between olog and olog , describing a mobile unmanned aerial vehicle, can be created. This analogy is formally represented by the diagram
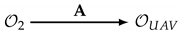
Exemplarily, an analogy could mean that the types for kinematic properties need to be renamed or reorganised, or the type for a robotic controller needs to be replaced by a remote controller device. Evidently, Definition 5 needs to be adapted then as well, which can be easily accomplished within the abstract approach proposed in this paper.
5. Discussion and Conclusions
In this paper, a conceptual modelling approach for autonomous construction based on categorical ontology logs coupled with abstract algebraic definitions was presented. The motivation for this coupling is twofold: first, introducing abstract definitions of individual components of an autonomous construction system allows removing subjectivity, which is typical for ontology-based representations; and second, these abstract definitions serve as a common ground for ologs making the whole framework easily extendable and interpretable. Therefore, after introducing abstract definitions of individual components of an autonomous construction system, several ologs for these definitions have been developed. Moreover, basic operations, i.e., contraction, expansion, revision, and analogy, have been discussed.
Let us now summarise and discuss the main points of the paper:
- Abstract description of autonomous construction sitesSeveral abstract definitions formalising autonomous construction sites have been introduced in Section 3. The idea of these definitions is to provide a common ground for an olog-based description of autonomous construction. A top-to-bottom approach for conceptual modelling of autonomous construction sites has been chosen. Hence, starting with an autonomous construction site, definitions of its more detailed components have been added step-by-step. The main advantage of this approach is that the resulting conceptual modelling framework is scaleable and extendable with more details, if necessary. Any of the Definitions 4–8 can be revised or updated without the need for a general restructuring of the complete framework presented in this paper.It is also important to underline that the field of robotic construction still misses generally accepted “standard” definitions. Therefore, the results presented in Section 3 should not be understood in the way of the definitions to become an industrial standard but rather as an approach on how to address practical engineering problems on a more abstract level sieving out all concrete details.
- Olog-based representations of autonomous constructionAn olog-based representation of autonomous construction sites has been presented in Section 4. As described in Section 2.2, ologs are designed to handle the subjectivism of the creator of the abstract model. This point has been further strengthened by coupling ologs with abstract definitions introduced in Section 3. This coupling makes the relation and comparison, as well as the translation of ologs, even more mathematically sound and formal. Hence, the ologs presented in this paper can be straightforwardly implemented in the form of databases, as well as the extension/contraction rules. Further, if more details are desired in a concrete application, these details can be easily added via revision of existing ologs, as has been demonstrated in the paper.
- Lattice of representationsFinally, Section 4 presents a lattice of representations, which is developed by extending and revising existing ologs. Arguably, the concept of the lattice of representations is the most powerful tool of olog-based description of engineering systems. First, the lattice can be easily extended without the need for changing previous results. In this case, a new olog is simply added to the lattice, and the corresponding extension is then formally defined. Second, the lattice of representation can even be created first and, hence, provide a guideline for creating ologs and missing definitions.
It is also beneficial to provide a few comments on practical applications of the conceptual modelling framework presented in this paper:
- The first step should be the formal creation of a lattice of representations, where, of course, instead of ologs, only names of important parts to be described are written. In this step, it is important to decide what should be the least detailed olog and how many different parts need to be modelled.
- Collect/create definitions of all parts to be described by ologs. In this step, it is important to keep the balance between the number of details and the level of abstractions. This balance is generally to be defined by the modeller and the objective of the work. Evidently, existing definitions, for example, industry standards, can be used, or new definitions can be developed, as has been done in this paper.
- Create ologs for each part and fit them into the lattice of representations defined in Step 1. Further, if necessary, ologs can be converted into databases and connected to other conceptual models, if available.
In summary, the results presented in this paper indicate that a coupling of ologs and abstract algebraic definitions provides a high degree of flexibility to the resulting framework. Moreover, as it has been shown in some examples, the abstract framework can be easily extended with new definitions and, hence, with new ologs. Therefore, ologs are proposed to overcome the issues of incomparable prototypes and isolated solutions of systems for autonomous construction. As a result, any automated construction system can be described without providing exhausting detailed definitions of the system components, as existing ologs can be extended, contracted or revised to fit the given system or situation. To illustrate the capacity of ologs, an exemplary lattice of representations for autonomous construction sites has been presented. Additionally, the results obtained for autonomous construction can be transferred to other fields of engineering by using analogy operations on two levels: adapting ologs and translating the respective definitions. Thus, the results presented in this paper can be seen not only as an attempt to formalise an autonomous construction but as a general approach to formalising engineering problems.
For future work, since the definitions for a robot and an autonomous construction site are only exemplary, the detailed description of a complete system of autonomous construction would be of relevance to determine the exact ramifications and parameters of describing such a complex system by means of ologs. Subsequently, the process of how an existing olog representation of an autonomous construction system can be translated or revised into another system needs to be examined. Furthermore, the investigation of different systems would allow the identification of matching parameters in order to identify possible system-inherent properties in order to approach a general system definition, if required.
Further direction of future work could be related to using the abstract definitions presented in Section 3 in concrete engineering applications. In particular, using these definitions in the context of path optimisation on graphs with the help of Clifford operator calculus, as it has been presented in [31], to further underline the advantages of coupling abstract mathematics and engineering.
Author Contributions
Conceptualisation, D.L. (Daniel Luckey) and D.L. (Dmitrii Legatiuk); methodology, D.L. (Daniel Luckey) and D.L. (Dmitrii Legatiuk); writing—original draft preparation, D.L. (Daniel Luckey); writing—review and editing, D.L. (Daniel Luckey) and D.L. (Dmitrii Legatiuk); funding acquisition, D.L. (Dmitrii Legatiuk). All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the German Research Foundation (DFG) through grant LE 3955/4-1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the writing of the manuscript.
Abbreviations
The following abbreviations are used in this manuscript:
| Olog | Ontology log |
| UAV | Unmanned aerial vehicle |
References
- Bock, T. The future of construction automation: Technological disruption and the upcoming ubiquity of robotics. Autom. Constr. 2015, 59, 113–121. [Google Scholar] [CrossRef]
- Keating, S.; Lel, J.; Cai, L.; Oxman, N. Toward site-specific and self-sufficient robotic fabrication on architectural scales. Sci. Robot. 2017, 2, eaam8986. [Google Scholar] [CrossRef] [PubMed]
- Hack, N.; Dörfler, K.; Walzer, A.N.; Wangler, T.; Mata-Falcón, J.; Kumar, N.; Buchli, J.; Kaufmann, W.; Flatt, R.J.; Gramazio, F.; et al. Structural stay-in-place formwork for robotic in situ fabrication of non-standard concrete structures: A real scale architectural demonstrator. Autom. Constr. 2020, 115, 103197. [Google Scholar] [CrossRef]
- Wagner, H.J.; Alvarez, M.; Kyjanek, O.; Bhiri, Z.; Buck, M.; Menges, A. Flexible and transportable robotic timber construction platform—TIM. Autom. Constr. 2020, 120, 103400. [Google Scholar] [CrossRef]
- Willmann, J.; Knauss, M.; Bonwetsch, T.; Apolinarska, A.A.; Gramazio, F.; Kohler, M. Robotic timber construction—Expanding additive fabrication to new dimensions. Autom. Constr. 2016, 61, 16–23. [Google Scholar] [CrossRef]
- Dörfler, K.; Sandy, T.; Giftthaler, M.; Gramazio, F.; Kohler, M.; Buchli, J. Mobile Robotic Brickwork. In Robotic Fabrication in Architecture, Art and Design 2016; Reinhardt, D., Saunders, R., Burry, J., Eds.; Springer: Cham, Switzerland, 2016; pp. 204–217. [Google Scholar]
- Lindemann, H.; Gerbers, R.; Ibrahim, S.; Dietrich, F.; Herrmann, E.; Dröder, K.; Raatz, A.; Kloft, H. Development of a Shotcrete 3D-Printing (SC3DP) Technology for Additive Manufacturing of Reinforced Freeform Concrete Structures. In First RILEM International Conference on Concrete and Digital Fabrication—Digital Concrete 2018. DC 2018. RILEM Bookseries; Wangler, T., Flatt, R., Eds.; Springer: Cham, Switzerland, 2018; Volume 19, pp. 204–217. [Google Scholar]
- Helm, V.; Willmann, J.; Gramazio, F.; Kohler, M. In-Situ Robotic Fabrication: Advanced Digital Manufacturing Beyond the Laboratory. In Gearing up and Accelerating Cross-fertilization between Academic and Industrial Robotics Research in Europe: Technology Transfer Experiments from the ECHORD Project. Springer Tracts in Advanced Robotics; Röhrbein, F., Veiga, G., Natale, C., Eds.; Springer: Cham, Switzerland, 2014; Volume 94, pp. 63–83. [Google Scholar]
- Chai, H.; Wagner, H.J.; Guo, Y.; Qi, Y.; Menges, A.; Yuan, P.F. Computational design and on-site mobile robotic construction of an adaptive reinforcement beam network for cross-laminated timber slab panels. Autom. Constr. 2022, 142, 104536. [Google Scholar] [CrossRef]
- Keitel, H.; Karaki, G.; Lahmer, T.; Nikulla, S.; Zabel, V. Evaluation of coupled partial models in structural engineering using graph theory and sensitivity analysis. Eng. Struct. 2011, 33, 3726–3736. [Google Scholar] [CrossRef]
- Dutailly, J.C. Hilbert Spaces in Modelling of Systems; 2014; 47p. Available online: https://hal.archives-ouvertes.fr/hal-00974251 (accessed on 14 August 2021).
- Dutailly, J.C. Common Structures in Scientific Theories; 2014; 34p. Available online: https://hal.archives-ouvertes.fr/hal-01003869 (accessed on 14 August 2021).
- Legatiuk, D.; Smarsly, K. An abstract approach towards modeling intelligent structural systems. In Proceedings of the 9th European Workshop on Structural Health Monitoring, Manchester, UK, 10–13 July 2018. [Google Scholar]
- Nefzi, B.; Schott, R.; Song, Y.Q.; Staples, G.S.; Tsiontsiou, E. An operator calculus approach for multi-constrained routing in wireless sensor networks. In Proceedings of the 16th ACM International Symposium on Mobile Ad Hoc Networking and Computing, New York, NY, USA, 22–25 June 2015. [Google Scholar]
- Vassilyev, S.N. Method of reduction and qualitative analysis of dynamic systems: I. J. Comput. Syst. Int. 2006, 17–25. [Google Scholar] [CrossRef]
- Vassilyev, S.N.; Davydov, A.V.; Zherlov, A.K. Intelligent control via new efficient logics. In Proceedings of the 17th World Congress The International Federation of Automatic Control, Seoul, Republic of Korea, 6–11 July 2008. [Google Scholar]
- Gürlebeck, K.; Nilsson, H.; Legatiuk, D.; Smarsly, K. Conceptual modelling: Towards detecting modelling errors in engineering applications. Math. Methods Appl. Sci. 2020, 43, 1243–1252. [Google Scholar] [CrossRef]
- Legatiuk, D.; Nilsson, H. Abstract modelling: Towards a typed declarative language for the conceptual modelling phase. In Proceedings of the 8th International Workshop on Equation-Based Object-Oriented Modeling Languages and Tools, Weßling, Germany, 1 December 2017. [Google Scholar]
- Foley, J.D.; Breiner, S.; Subrahmanian, E.; Dusel, J.M. Operands for complex system design specification, analysis and synthesis. Proc. R. Soc. 2021, 477. [Google Scholar]
- Gürlebeck, K.; Hofmann, D.; Legatiuk, D. Categorical approach to modelling and to coupling of models. Math. Methods Appl. Sci. 2017, 40, 523–534. [Google Scholar] [CrossRef]
- Kavrakov, I.; Legatiuk, D.; Gürlebeck, K.; Morgenthal, G. A categorical perspective towards aerodynamic models for aeroelastic analyses of bridges. R. Soc. Open Sci. 2019, 6, 181848. [Google Scholar] [CrossRef] [PubMed]
- Legatiuk, D. Mathematical modelling by help of category theory: Models and relations between them. Mathematics 2022, 9, 1946. [Google Scholar] [CrossRef]
- Spivak, D.; Kent, R. Ologs: A categorical framework for knowledge representation. PLoS ONE 2012, 7, e24274. [Google Scholar] [CrossRef] [PubMed]
- Sowa, J. Knowledge Representation: Logical, Philosophical, and Computational Foundations; Brooks/Cole: Pacific Grove, CA, USA, 2000. [Google Scholar]
- Awodey, S. Category Theory; Oxford University Press Inc.: New York, NY, USA, 2010. [Google Scholar]
- Spivak, D. Category Theory for Scientists; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Haidegger, T. Taxonomy and Standards in Robotics. In Encyclopedia of Robotics; Ang, M.H., Khatib, O., Siciliano, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Lynch, K.M.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Brosque, C.; Galbally, E.; Khatib, O.; Fischer, M. Human-Robot Collaboration in Construction: Opportunities and Challenges. In Proceedings of the 2020 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 26–27 June 2020; pp. 1–8. [Google Scholar]
- Christensen, O. An Introduction to Frames and Riesz Bases; Springer International Publishing: Heidelberg, Germany, 2016. [Google Scholar]
- Syarif, A.; Abouaissa, A.; Idoumghar, L.; Lorenz, P.; Schott, R.; Staples, S.G. New path centrality based on operator calculus approach for wireless sensor network deployment. IEEE Trans. Emerg. Top. Comput. 2019, 7, 162–173. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).