Sliding Mode Control for Single-Phase Grid-Connected Voltage Source Inverter with L and LCL Filters
Abstract
:1. Introduction
2. System Description
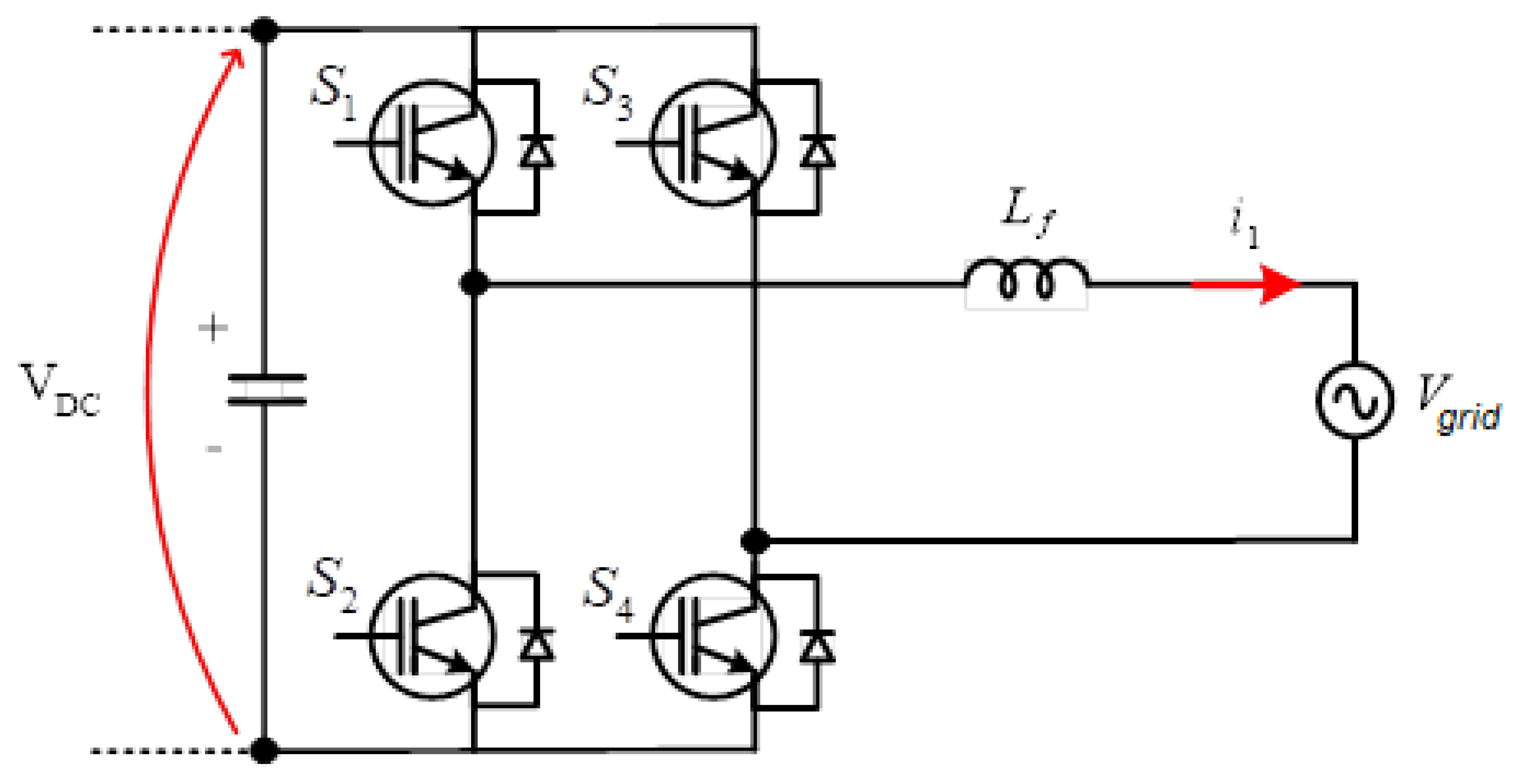
2.1. VSI Plus L Filter
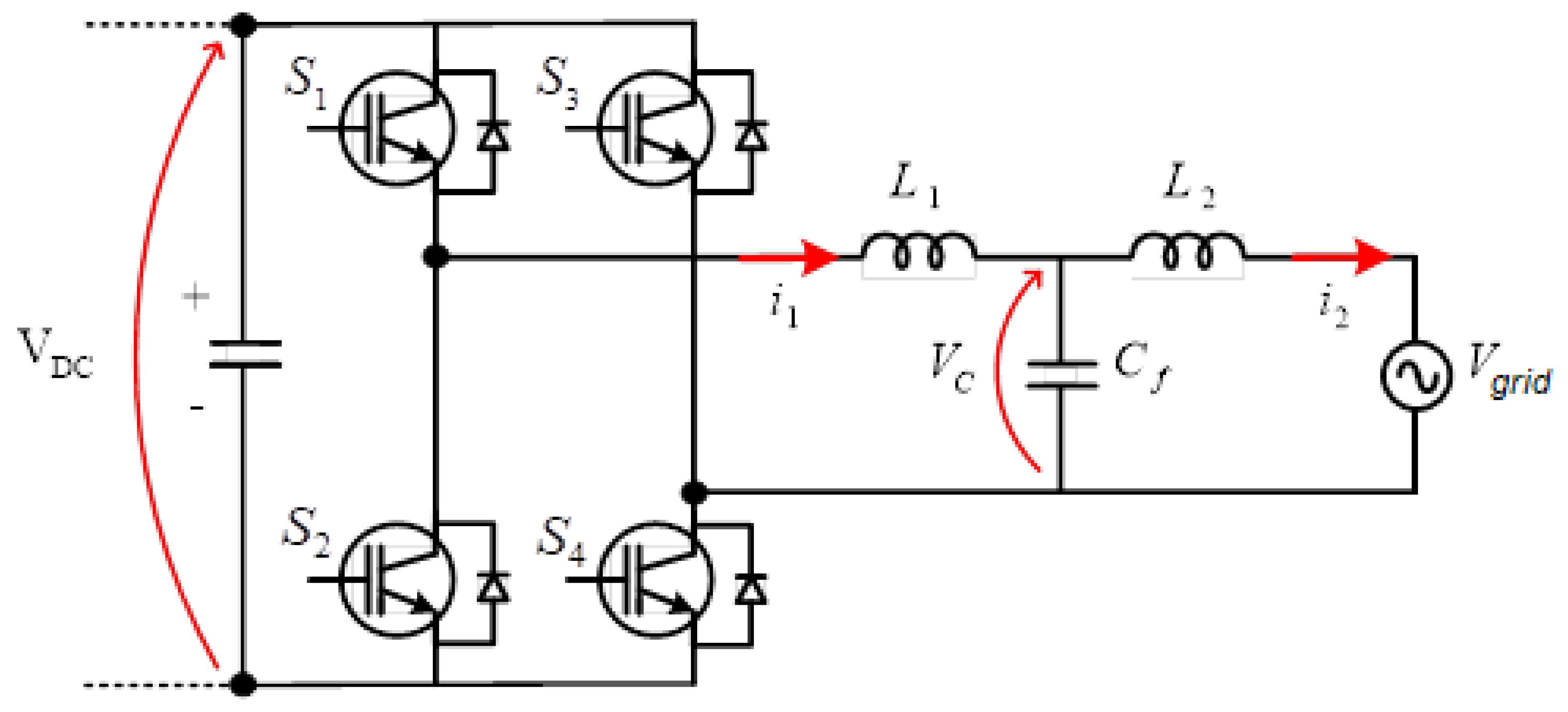
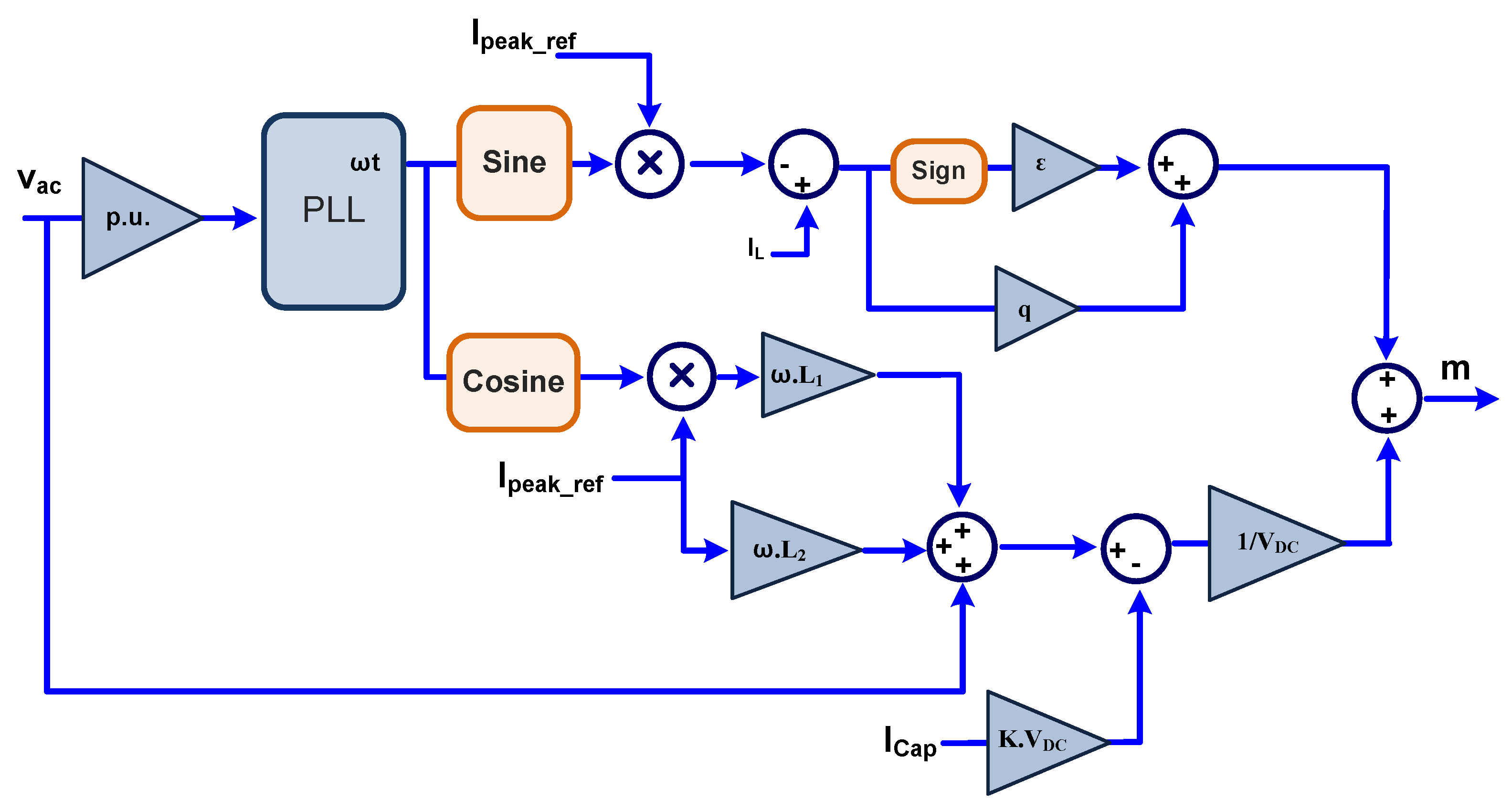
2.2. VSI Plus LCL Filter
- The value of the capacitance is limited by the decrease in the power factor that occurs at rated power (usually lower than 5% [17]);
- The total value of the inductance must be less than 0.1 p.u. to limit the voltage drop during operation. Otherwise, a higher value of DC voltage is required to guarantee the current controllability, resulting in more losses in the system;
- To avoid resonance problems among the lower and higher portions of the harmonic spectrum, the resonance frequency must be in the following range (14), concerning the grid frequency and the switching frequency [7]:
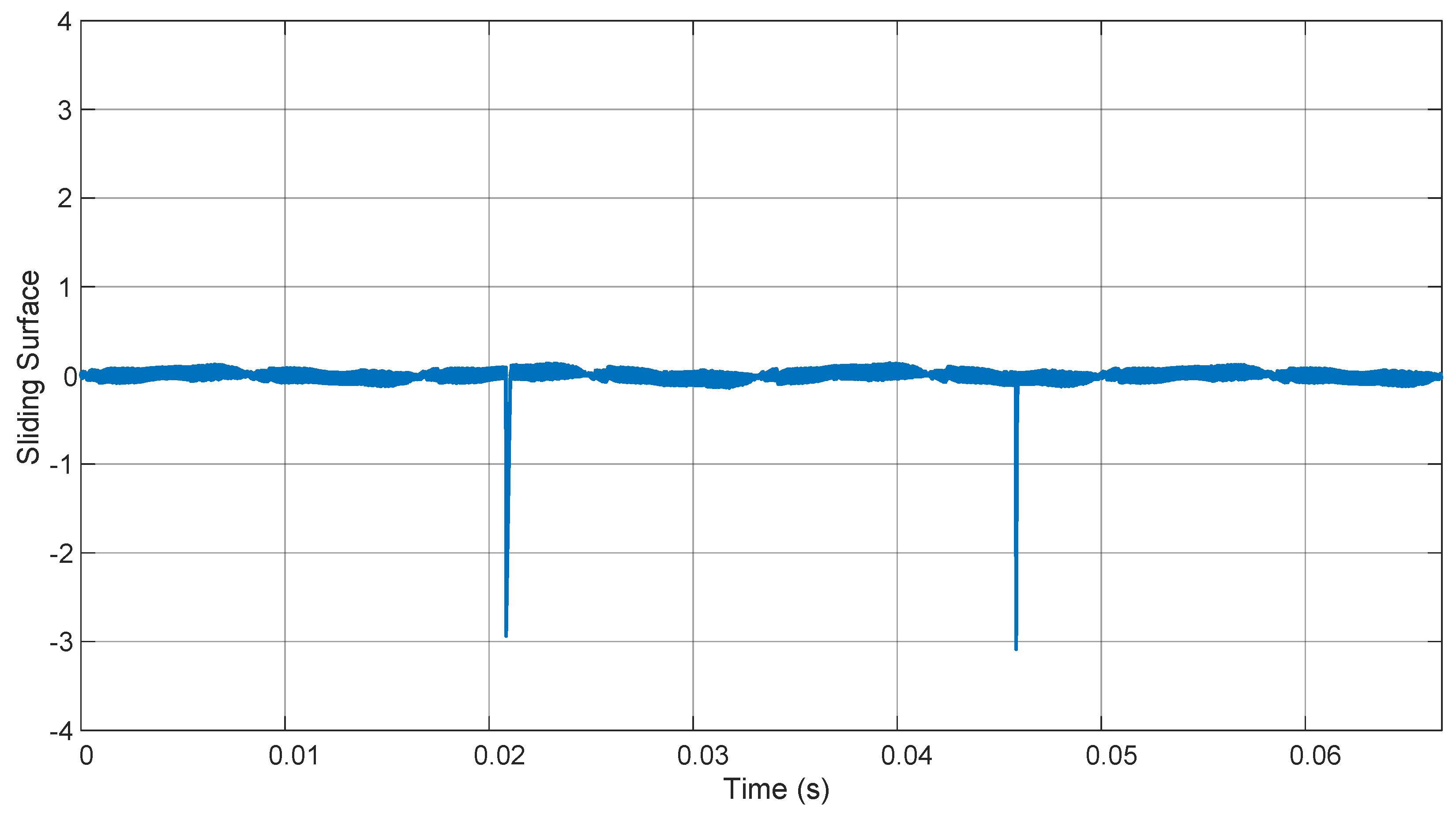
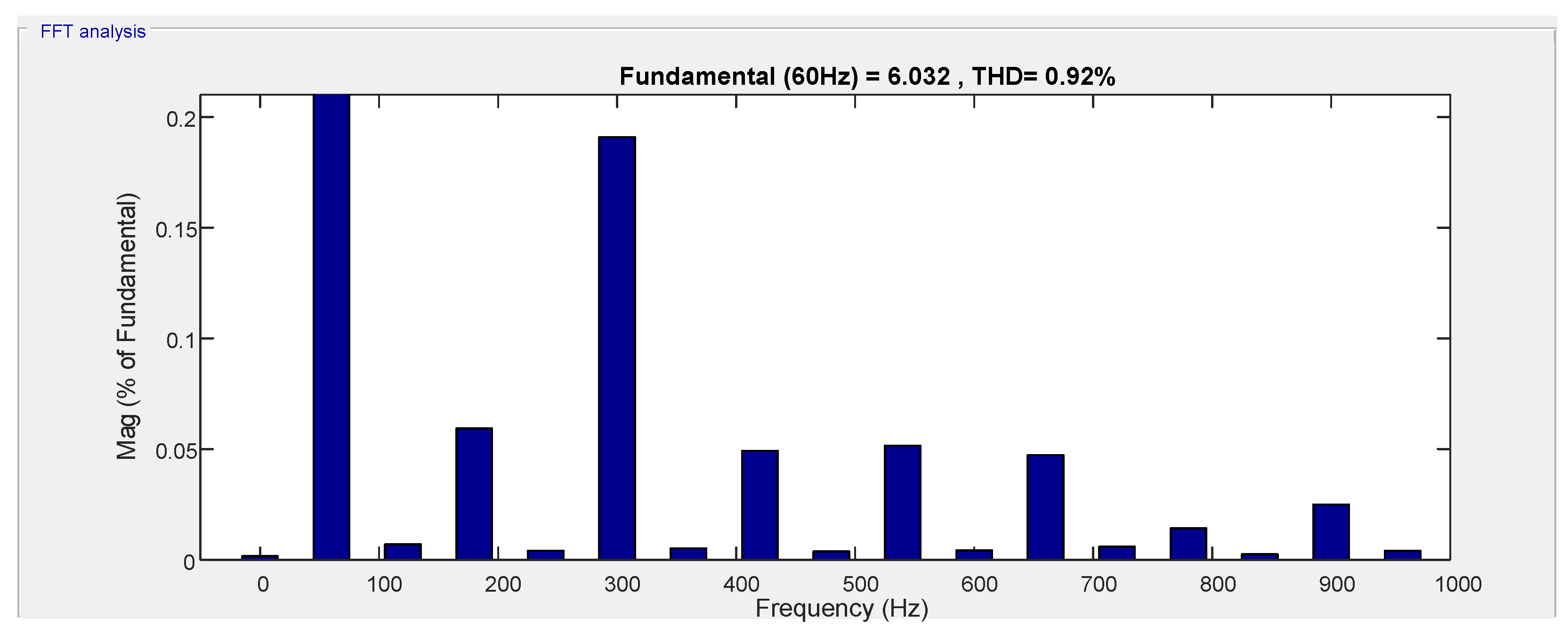
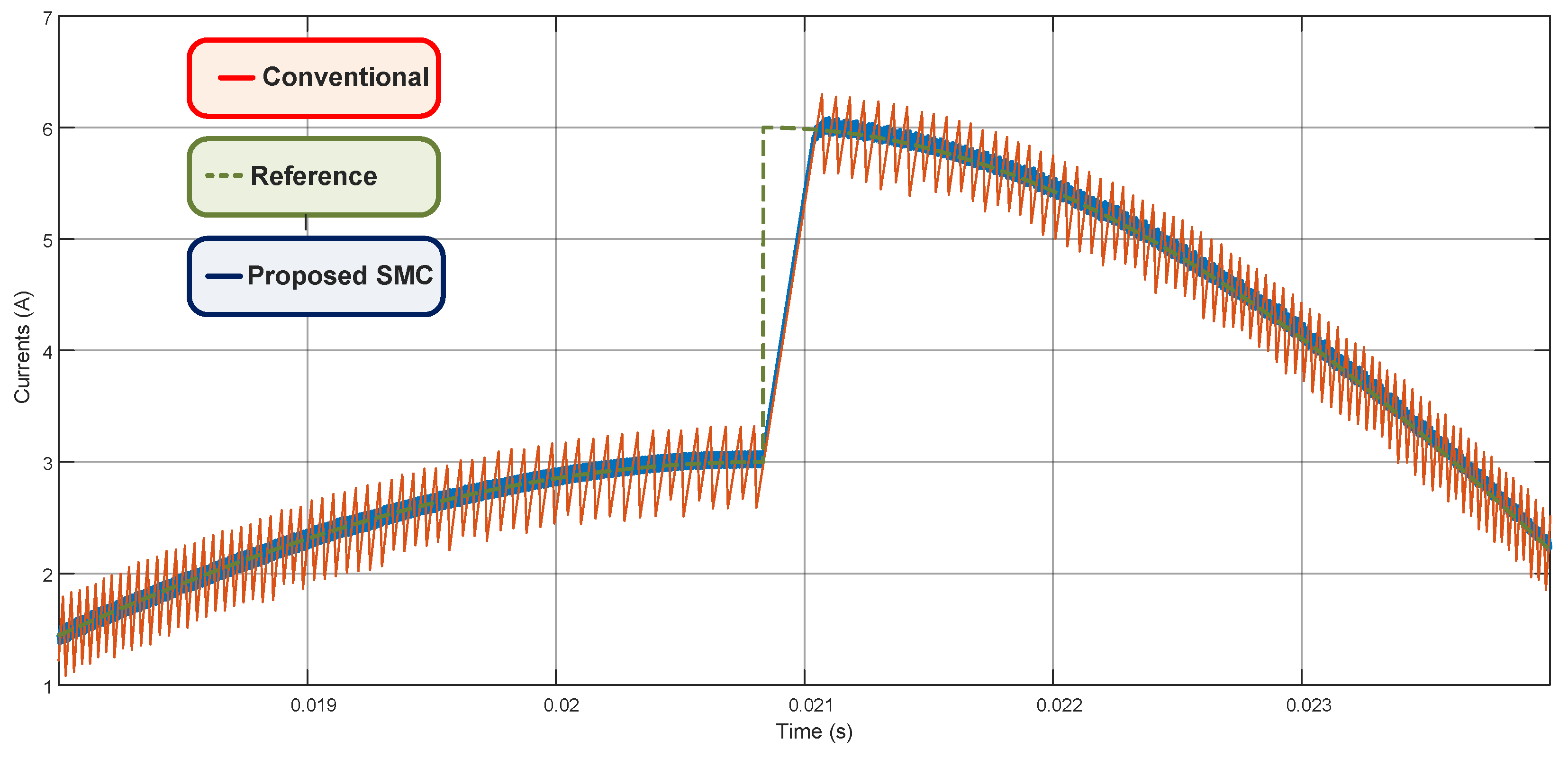
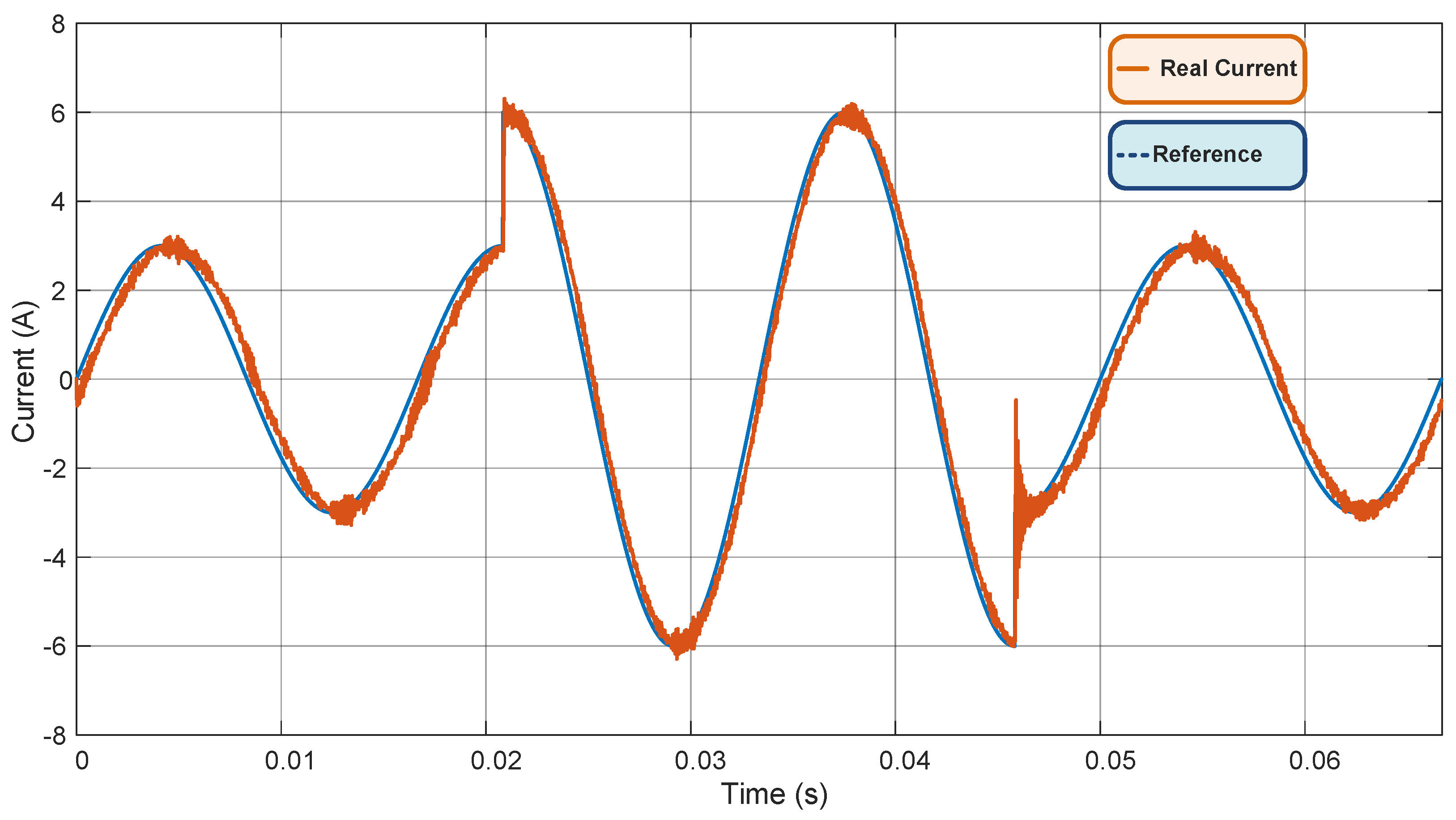
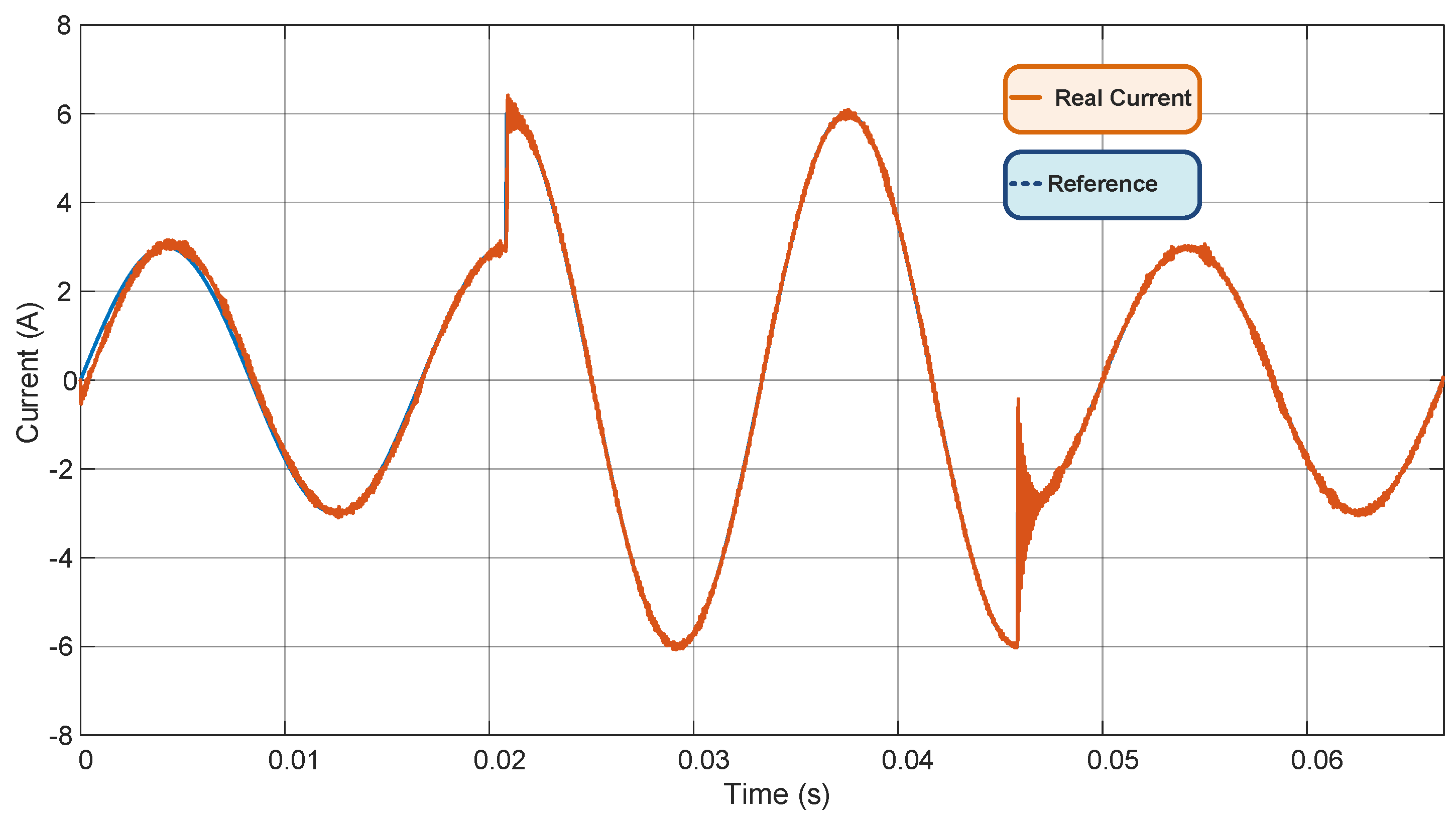
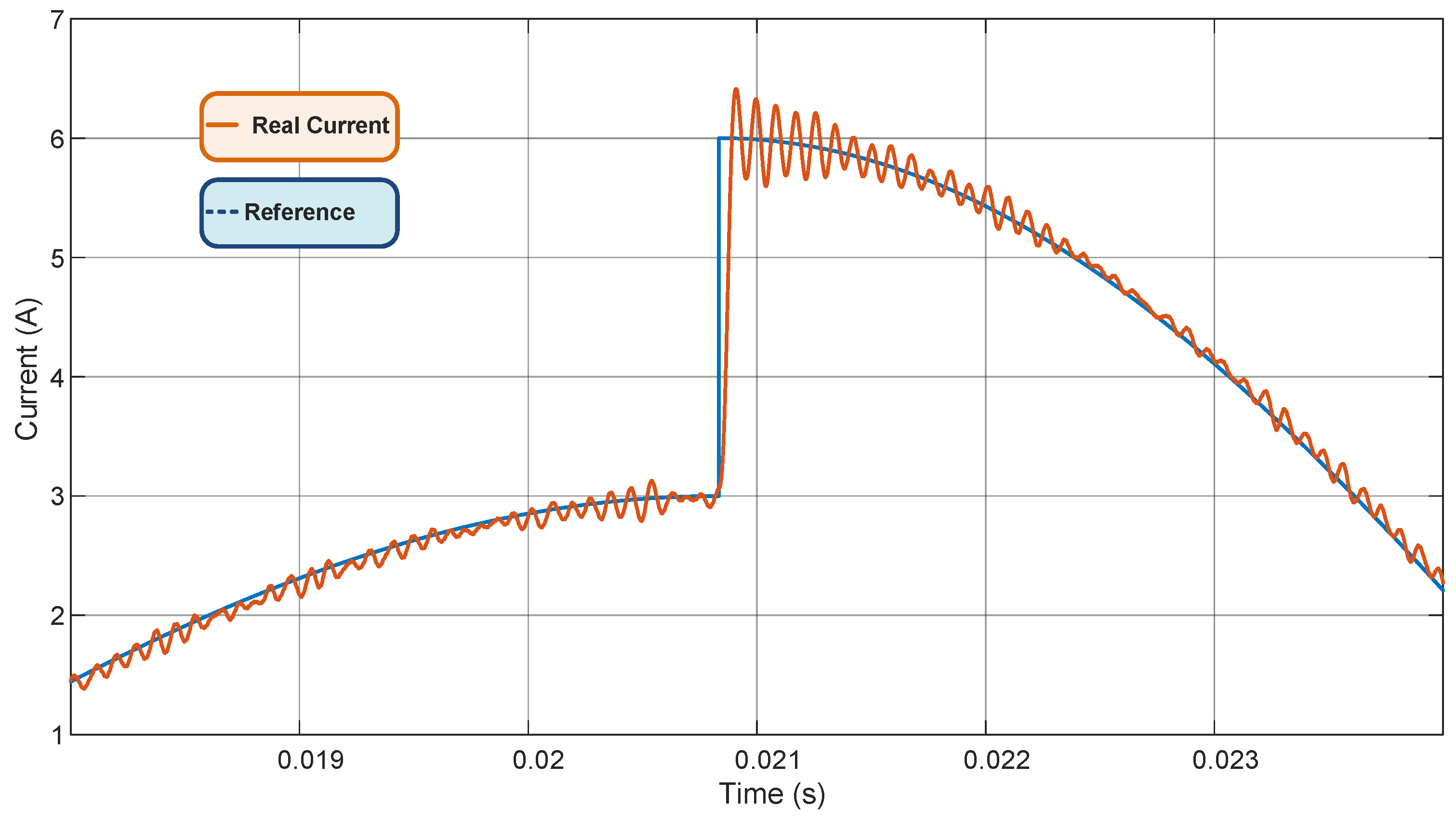
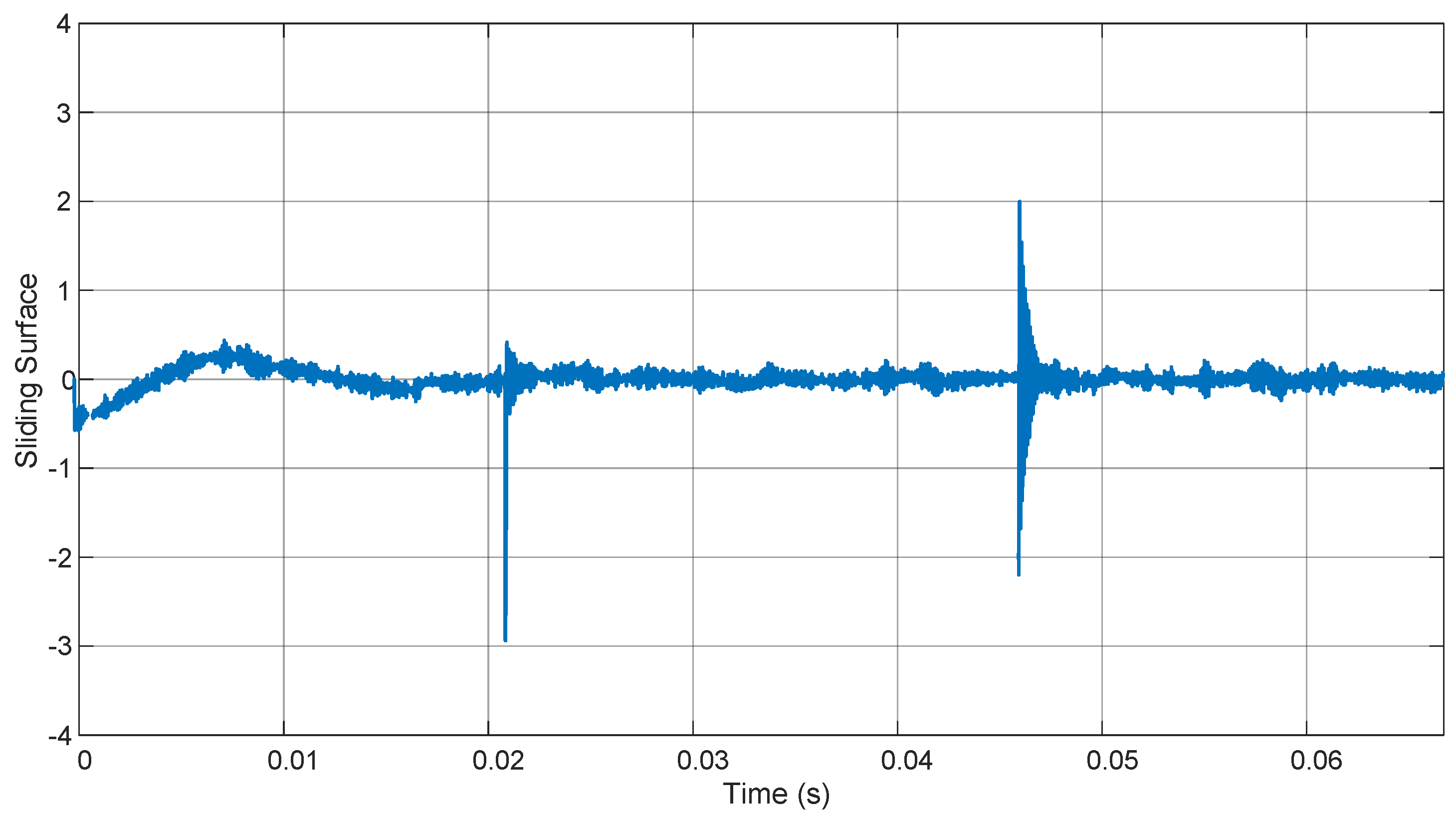
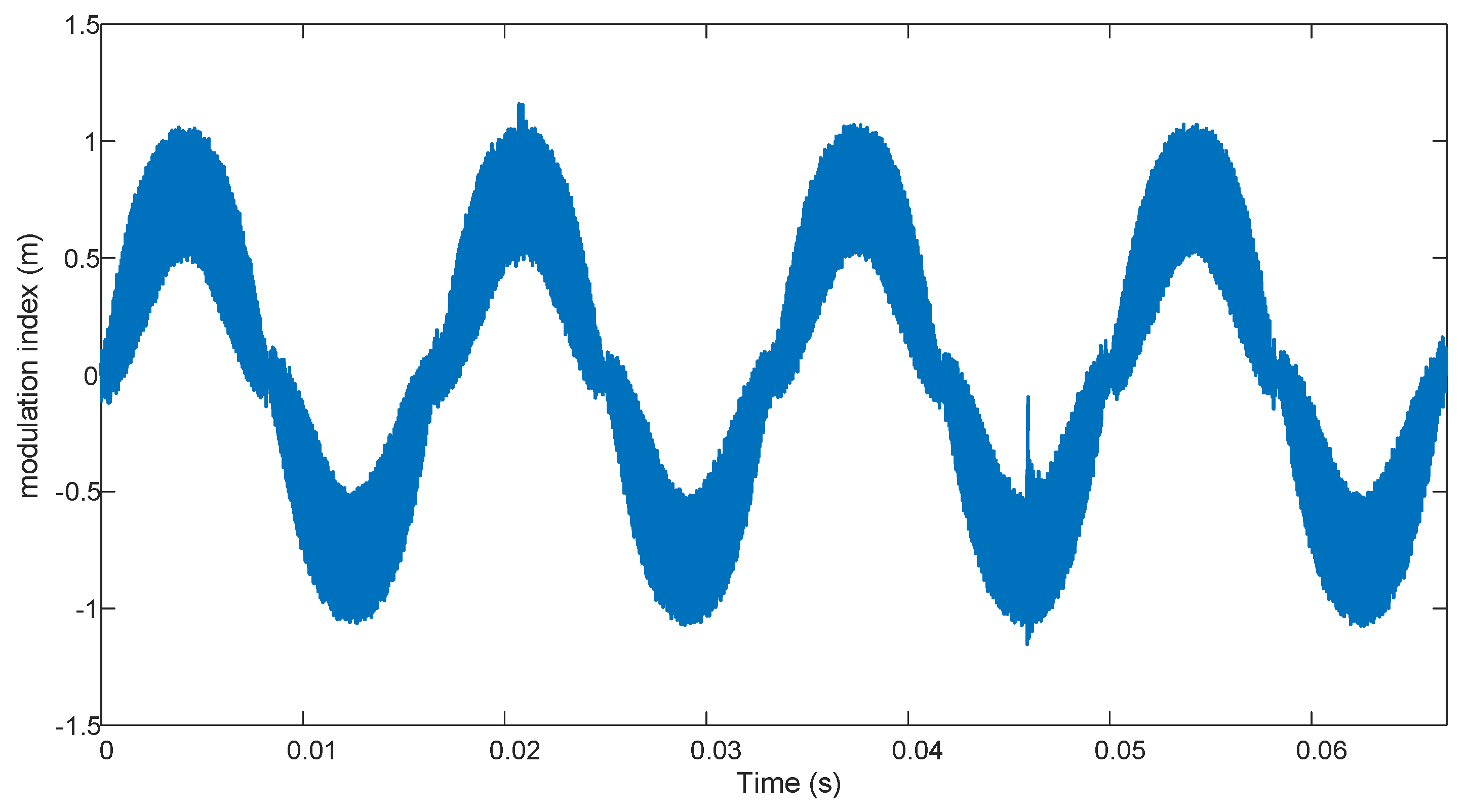
3. Results and Discussion
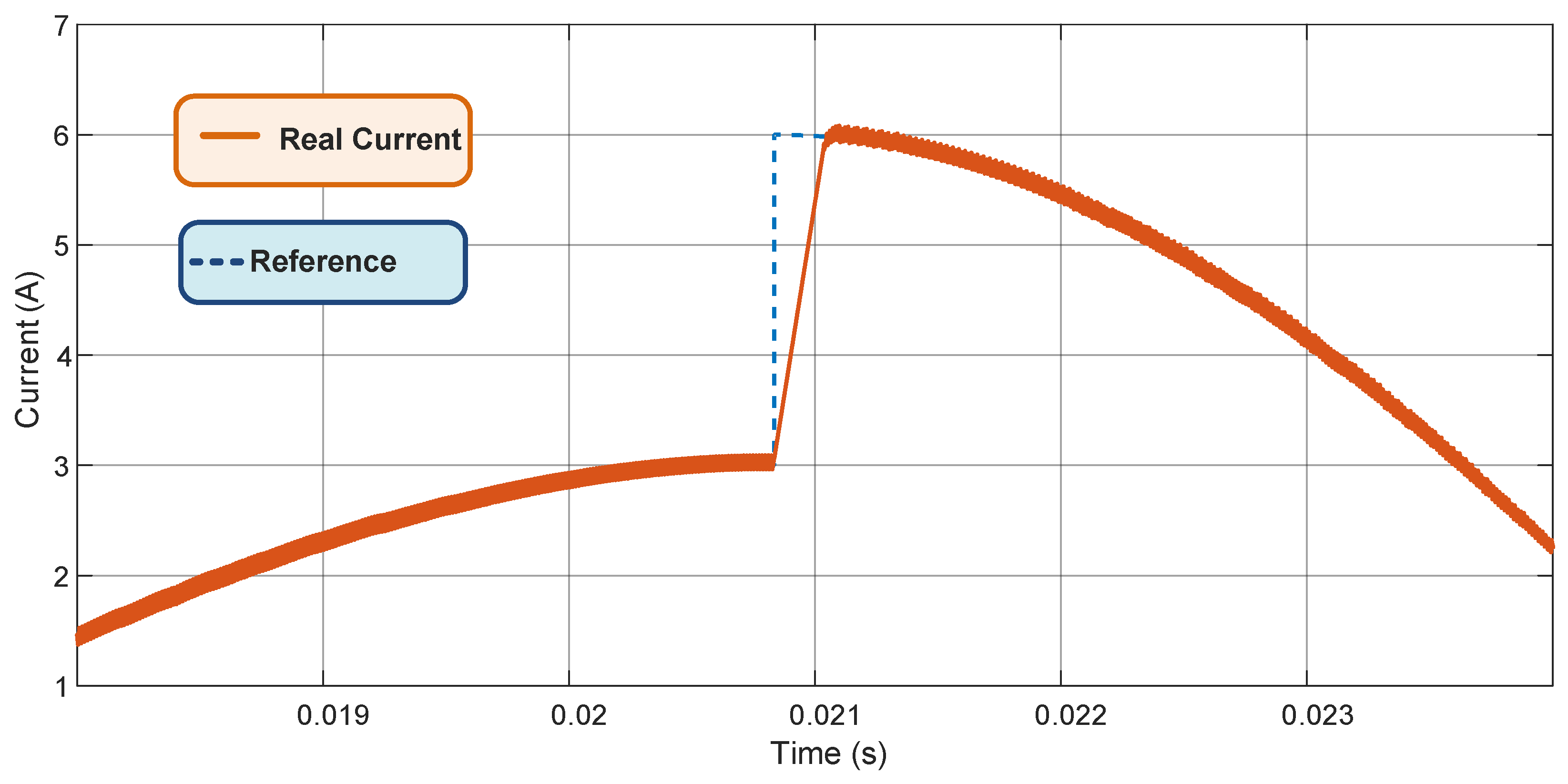
3.1. VSI Plus L Filter
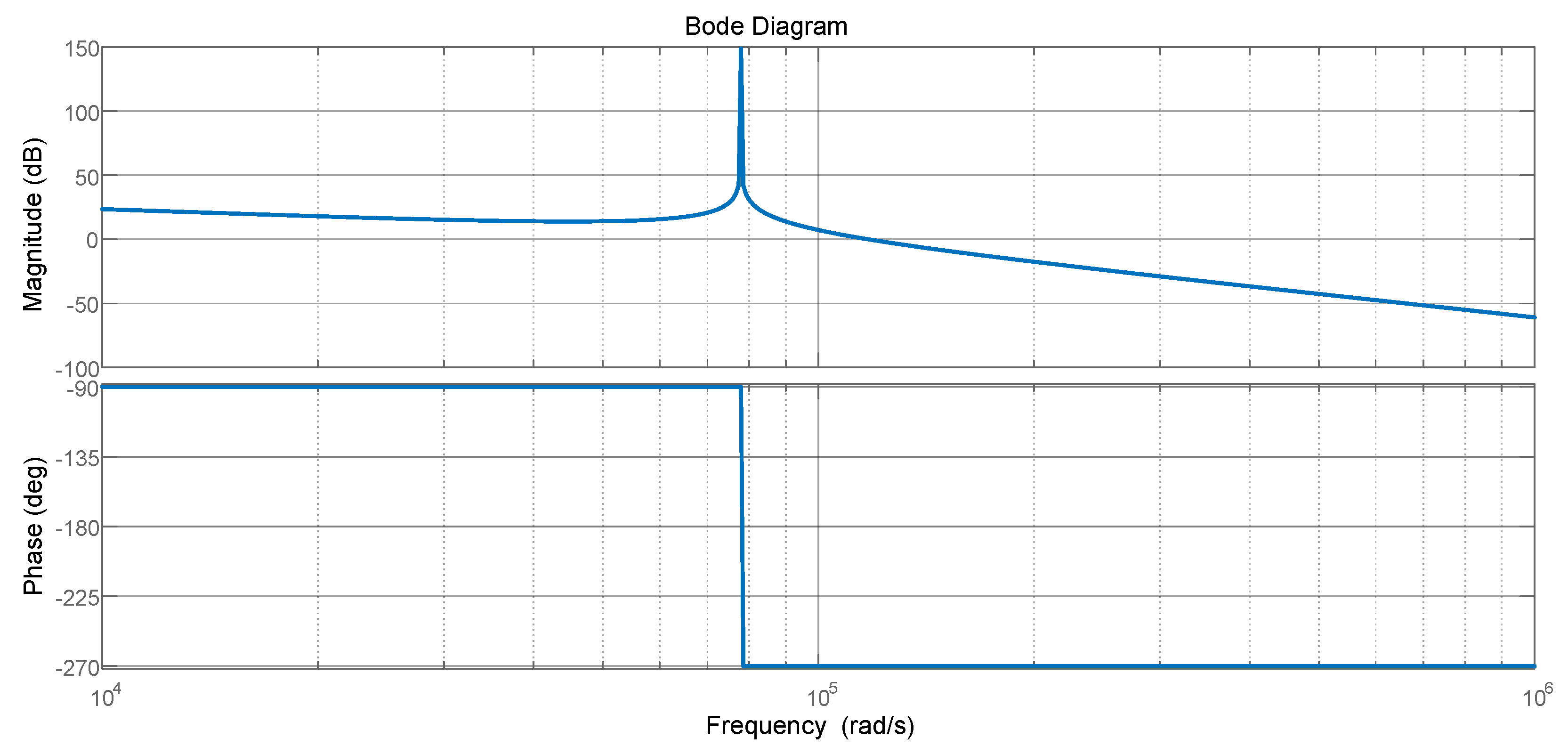
3.2. VSI Plus LCL Filter
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Liserre, E.M.; Sauter, T.; Hung, J.Y. Future Energy Systems: Integrating Renewable Energy Sources into the Smart Power Grid Through Industrial Electronics. IEEE Trans. Ind. Electron. 2010, 4, 18–37. [Google Scholar] [CrossRef]
- REN21. Renewables 2019 Global Status Report. 2019. Available online: https://www.ren21.net/wp-content/uploads/2019/05/gsr_2019_full_report_en.pdf (accessed on 5 October 2021).
- IEA. Renewable Energy Market Update—May 2022. 2022. Available online: https://www.iea.org/reports/renewable-energy-market-update-may-2022 (accessed on 1 June 2022).
- Brito, M.A.G.; Sampaio, L.P.; Galotto, L., Jr.; Canesin, C.A. Evaluation of the Main MPPT Techniques for Photovoltaic Applications. IEEE Trans. Ind. Electron. 2013, 60, 1156–1167. [Google Scholar] [CrossRef]
- Hao, X.; Yang, X.; Liu, T.; Huang, L.; Chen, W. A Sliding-Mode Controller with Multi-Resonant Sliding Surface for Single-Phase Grid-Connected VSI with an LCL-Filter. IEEE Trans. Power Electron. 2013, 5, 2259–2268. [Google Scholar] [CrossRef]
- Hill, W.A.; Kapoor, S.C. Effect of Two-Level PWM Sources on Plant Power System Harmonics. In Proceedings of the Conference Record of 1998 IEEE Industry Applications Conference, St. Louis, MO, USA, 15 October 1998. [Google Scholar]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and Control of an LCL-Filter-Based Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Ruan, X.; Wang, X.; Pan, D.; Yang, D.; Li, W.; Bao, C. Control Techniques for LCL-Type Grid-Connected Inverters; Springer: Singapore, 2017. [Google Scholar]
- Santos, L.M.; Lucas, L.A.; Brito, M.A.G.; Garcia, R.C. Analysis of Digital Current Controllers for Single-Phase Grid-Connected Photovoltaic Inverters. In Proceedings of the Intercon, IEEE XXVI International Conference on Electronics, Electrical Engineering and Computing, Lima, Peru, 12–14 August 2019. [Google Scholar]
- Twining, E.; Holmes, D.G. Grid Current Regulation of a Three-Phase Voltage Source Inverter with an LCL Input Filter. IEEE Trans. Power Electron. 2003, 5, 888–895. [Google Scholar] [CrossRef] [Green Version]
- Vieira, R.P. Contribuições ao Acionamento e Controle Sensorless Aplicado ao Motor de Indução Bifásico Assimétrico. Ph.D. Thesis, Federal University of Santa Maria, Santa Maria, Brazil, 2012. [Google Scholar]
- De Oliveira, T.R. Controle por Modos Deslizantes de Sistemas Incertos com Direção de Controle Desconhecida. Ph.D. Thesis, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil, 2006. [Google Scholar]
- Utkin, V.I. Variable Structure Systems with Sliding Modes. IEEE Trans. Autom. Control. 1977, 4, 212–222. [Google Scholar] [CrossRef]
- Gao, W.; Hung, J.C. Variable Structure Control of Nonlinear Systems: A New Approach. IEEE Trans. Ind. Electron. 1993, 2, 45–55. [Google Scholar]
- Svensson, J. Synchronization Methods for Grid-Connected Voltage Source Converters. IEE Proc. Gen. Transm. Distrib. 2001, 148, 229–235. [Google Scholar] [CrossRef] [Green Version]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Kluwer Academic Publisher: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Chang, L.; Song, P.; Diduch, C. Development of Standards for Interconnecting Distributed Generators with Electric Power Systems. In Proceedings of the IEEE Annual Power Electronics Specialists Conference, Recife, Brazil, 12–16 June 2005. [Google Scholar]
- Jia, Y.; Zhao, J.; Fu, X. Direct Grid Current Control of LCL-Filtered Grid-Connected Inverter Mitigating Grid Voltage Disturbance. IEEE Trans. Power Electron. 2013, 29, 1532–1541. [Google Scholar]
- Ogata, K. Modern Control Engineering; Prentice Hall: Hoboken, NJ, USA, 2020. [Google Scholar]
- De Vegte, J. Feedback Control Systems, 3rd revised ed.; Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Lucas, L.A.; Brito, M.A.G.; Garcia, R.C. A photovoltaic multi-functional converter with multi-resonant controller coefficients improved by a genetic algorithm. In Proceedings of the Intercon, IEEE XXVI International Conference on Electronics, Electrical Engineering and Computing, Lima, Peru, 12–14 August 2019. [Google Scholar]
- Song, F.; Smith, S.M. Design of Sliding Mode Fuzzy Controllers for an Autonomous Underwater Vehicle without System Model. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000; Volume 9, pp. 835–840. [Google Scholar]
- Glower, J.S.; Munighan, J. Designing Fuzzy Controllers from a Variable Structures Standpoint. IEEE Trans. Fuzzy Syst. 1997, 2, 138–144. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Output power | 500 W |
| Input voltage | 250 V |
| Grid RMS voltage | 127 V |
| Grid fundamental Frequency | 60 Hz |
| Switching frequency | 40 kHz |
| Grid current ripple | 4.5% |
| Component | Value |
|---|---|
| 1.65 mH | |
| 25.7 µH | |
| 6.5 µF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Brito, M.A.G.; Dourado, E.H.B.; Sampaio, L.P.; da Silva, S.A.O.; Garcia, R.C. Sliding Mode Control for Single-Phase Grid-Connected Voltage Source Inverter with L and LCL Filters. Eng 2023, 4, 301-316. https://doi.org/10.3390/eng4010018
de Brito MAG, Dourado EHB, Sampaio LP, da Silva SAO, Garcia RC. Sliding Mode Control for Single-Phase Grid-Connected Voltage Source Inverter with L and LCL Filters. Eng. 2023; 4(1):301-316. https://doi.org/10.3390/eng4010018
Chicago/Turabian Stylede Brito, Moacyr A. G., Egon H. B. Dourado, Leonardo P. Sampaio, Sergio A. O. da Silva, and Raymundo C. Garcia. 2023. "Sliding Mode Control for Single-Phase Grid-Connected Voltage Source Inverter with L and LCL Filters" Eng 4, no. 1: 301-316. https://doi.org/10.3390/eng4010018
APA Stylede Brito, M. A. G., Dourado, E. H. B., Sampaio, L. P., da Silva, S. A. O., & Garcia, R. C. (2023). Sliding Mode Control for Single-Phase Grid-Connected Voltage Source Inverter with L and LCL Filters. Eng, 4(1), 301-316. https://doi.org/10.3390/eng4010018






