New Possibilities for Constructing Heuristic Solutions to Problems of Electromagnetic Diffraction
Abstract
:1. Introduction
1.1. Relevance of Heuristic Solutions
- -
- Investigation of relatively large objects that do not have solutions obtained by more rigorous methods. Such objects include, for example, targets with low radar signature, non-axisymmetric satellite communication antennas, etc. The propagation of radio waves in urban environments may also be studied using heuristic methodologies.
- -
- Improving performance in calculating urgent problems, including those problems that have solutions obtained using other approaches.
- -
- Physical interpretation of numerical solutions, which is especially important in cases where they differ from the experimental results.
1.2. Known Heuristic Approaches
1.3. Reference Problems for Constructing Heuristic Solutions
- Linear integral (3D): This is a solution in the PO approximation to the diffraction problem on a plane perfectly conducting scatterer. In this case, the far zone condition (FZC) is fulfilled both for the source and for the observation point. The integral over the area of the scatterer is reduced to an integral over its contour [13,14,15]. If the FZC is not fulfilled, the technique described in [16] can be applied.
- Reflection and transmission coefficients (1D) R and T for an unbounded plane.
1.4. Motivation to Develop New Heuristic Approaches
- Insufficient accuracy of known heuristic approaches.
- Insufficient performance of the solver.
- Lack of the required number of rigorous analytical solutions, on the basis of which, a solver can be built for a specific practical problem.
- The need for a physical interpretation of the numerical solution and the identification of physical phenomena that were not taken into account by the old heuristic approaches.
2. New MFC Approach and Its Differences from Traditional Approaches
- first, determine the unaccounted phenomenon and find an expression for it, then add it to the primary heuristic formula and carry out verification (as in the MEW);
- or, first, find the difference between the strict solution and the primary heuristic formula, and then find a physical phenomenon that determines this difference (as in the MFC).
3. Formulas Used in the MFC
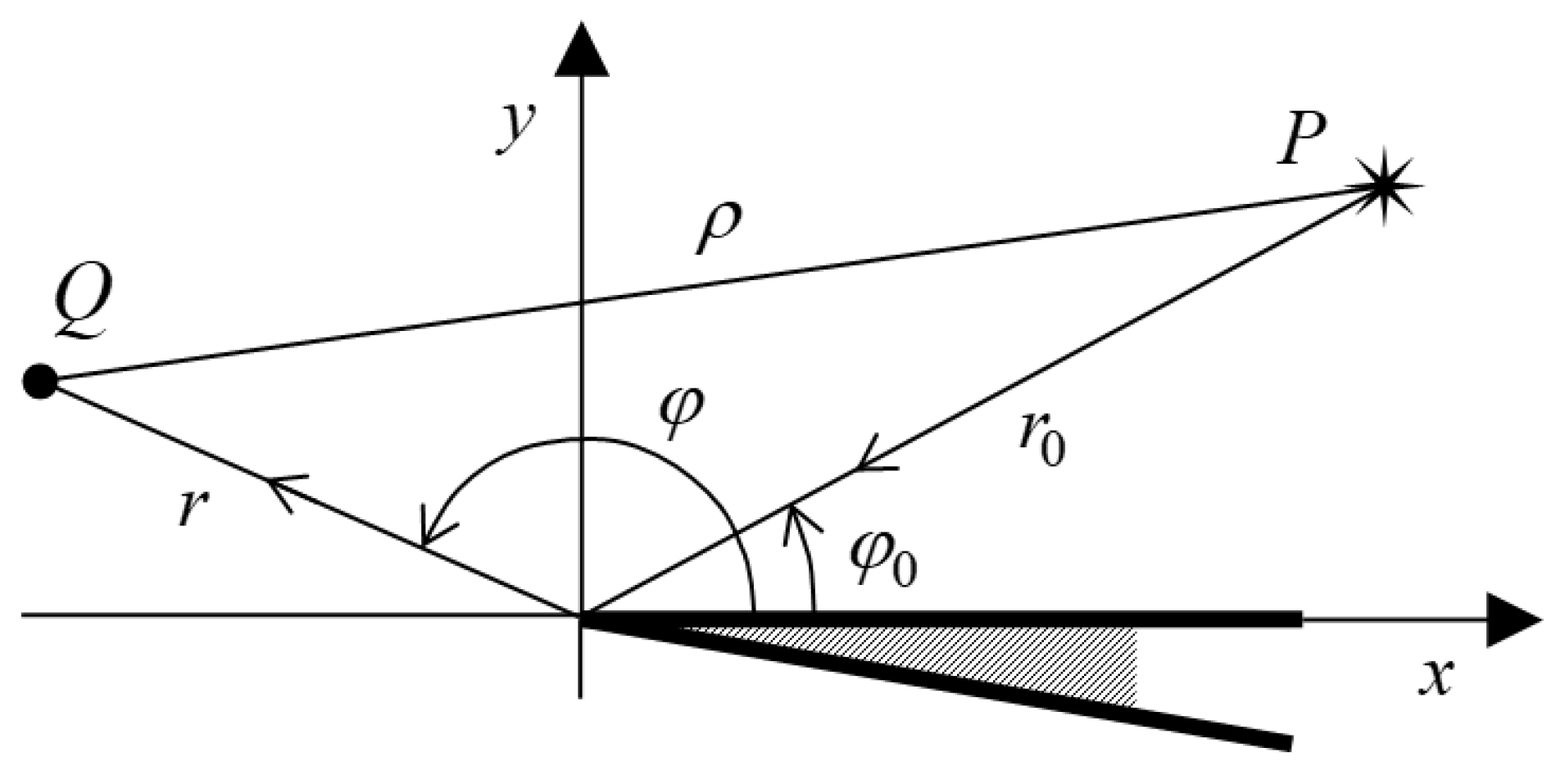
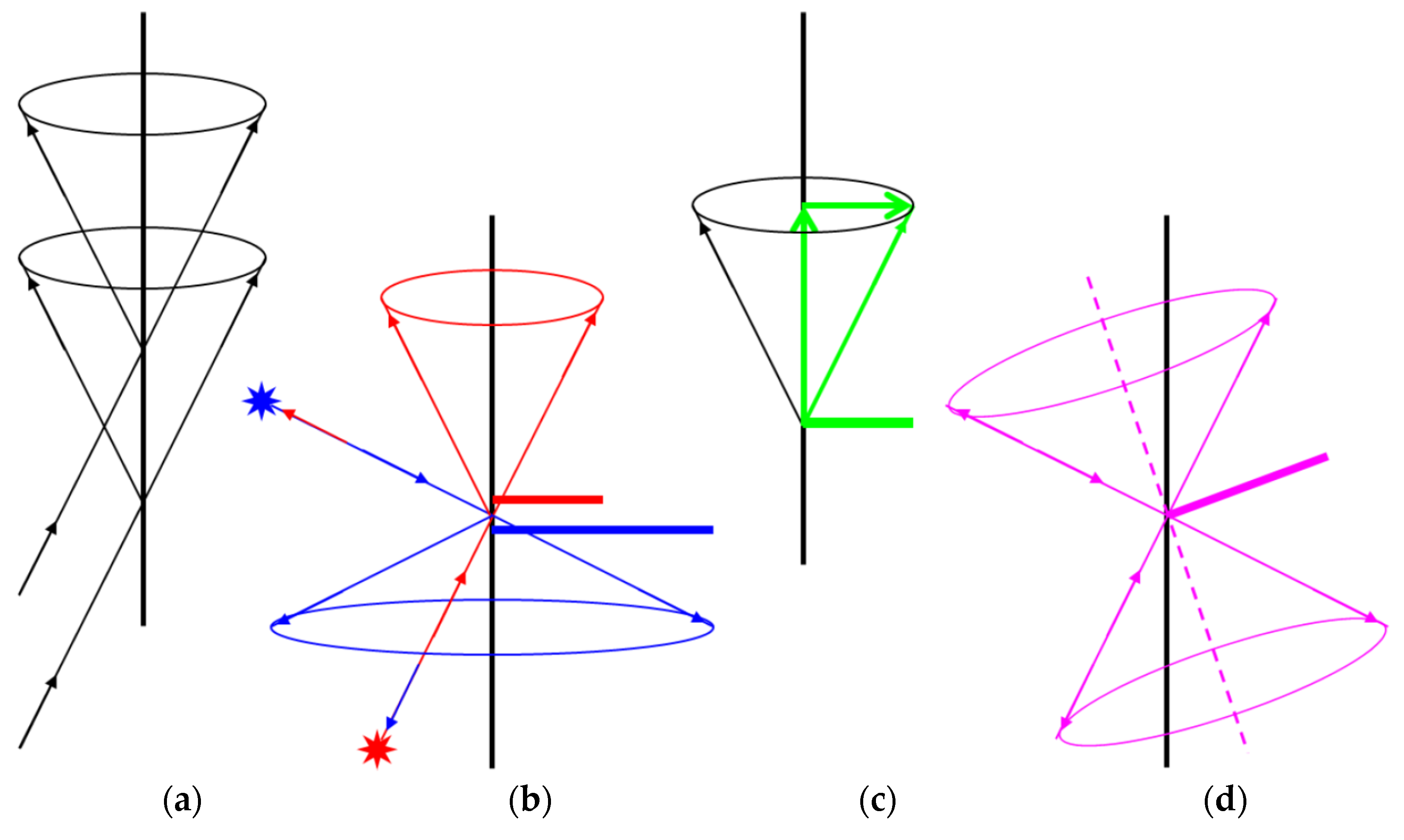
3.1. Partitioning the Formula for a 2D Edge
3.2. Linear Integral in the PO Approximation
3.3. Diffraction Coefficients for a Perfectly Conducting Half-Plane F and G with a Geometry Pattern
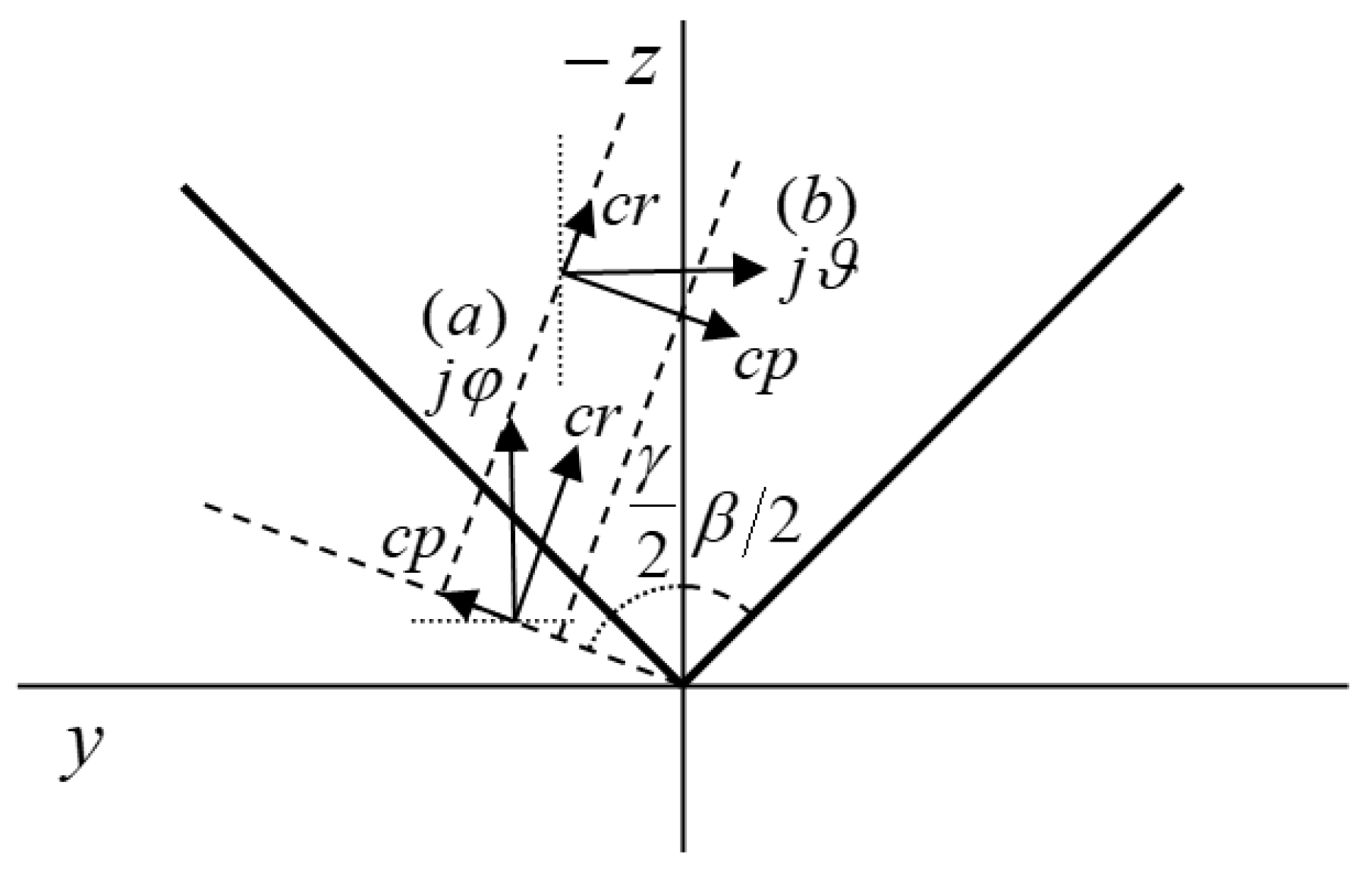
3.4. Modifying Functions for a Perfectly Conducting Plane Angular Sector
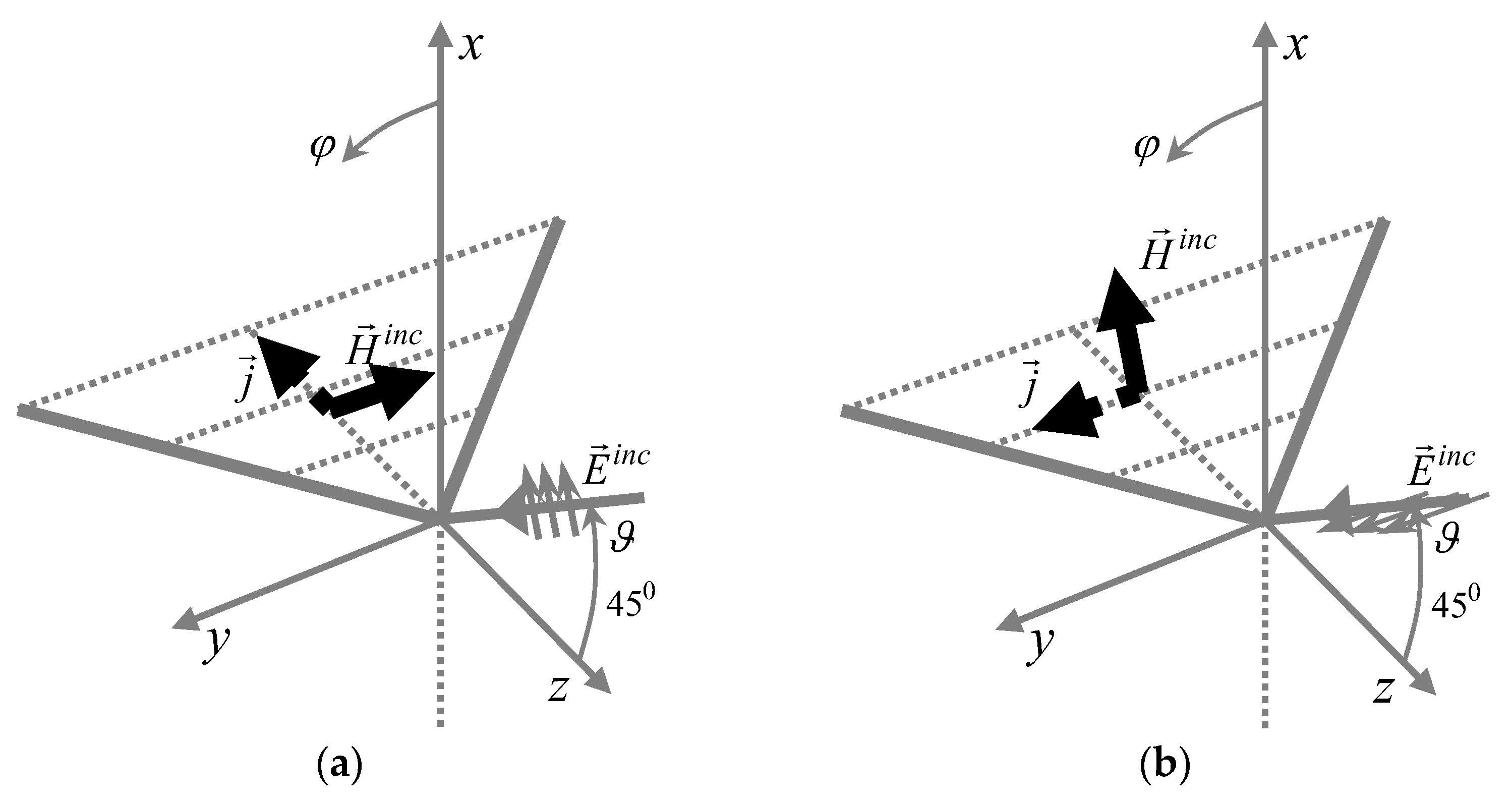
3.5. Diffraction Coefficients GDC (Generalized Diffraction Coefficients) and PODC (Physical Optics Diffraction Coefficients) for a Semitransparent Half-Plane
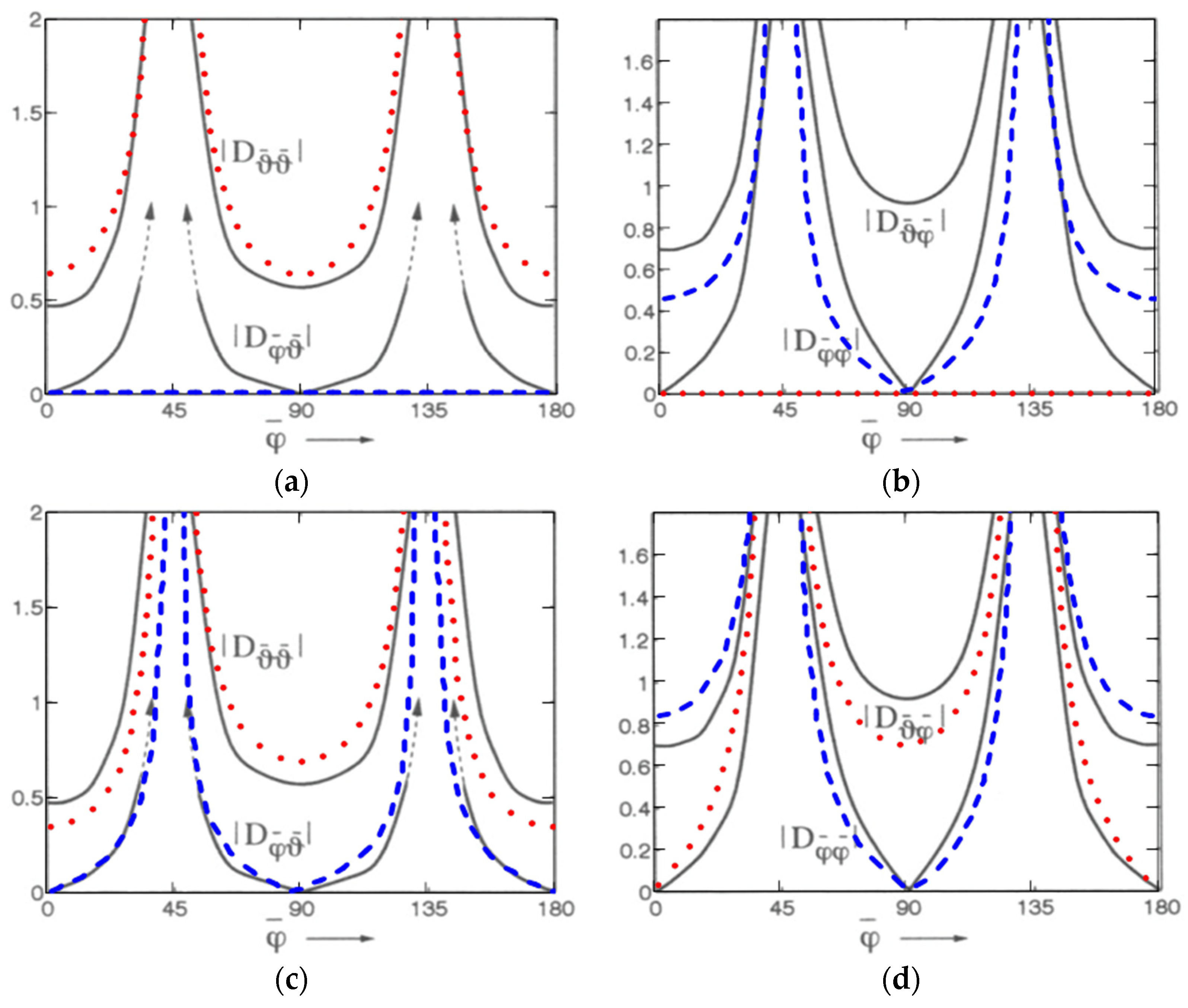
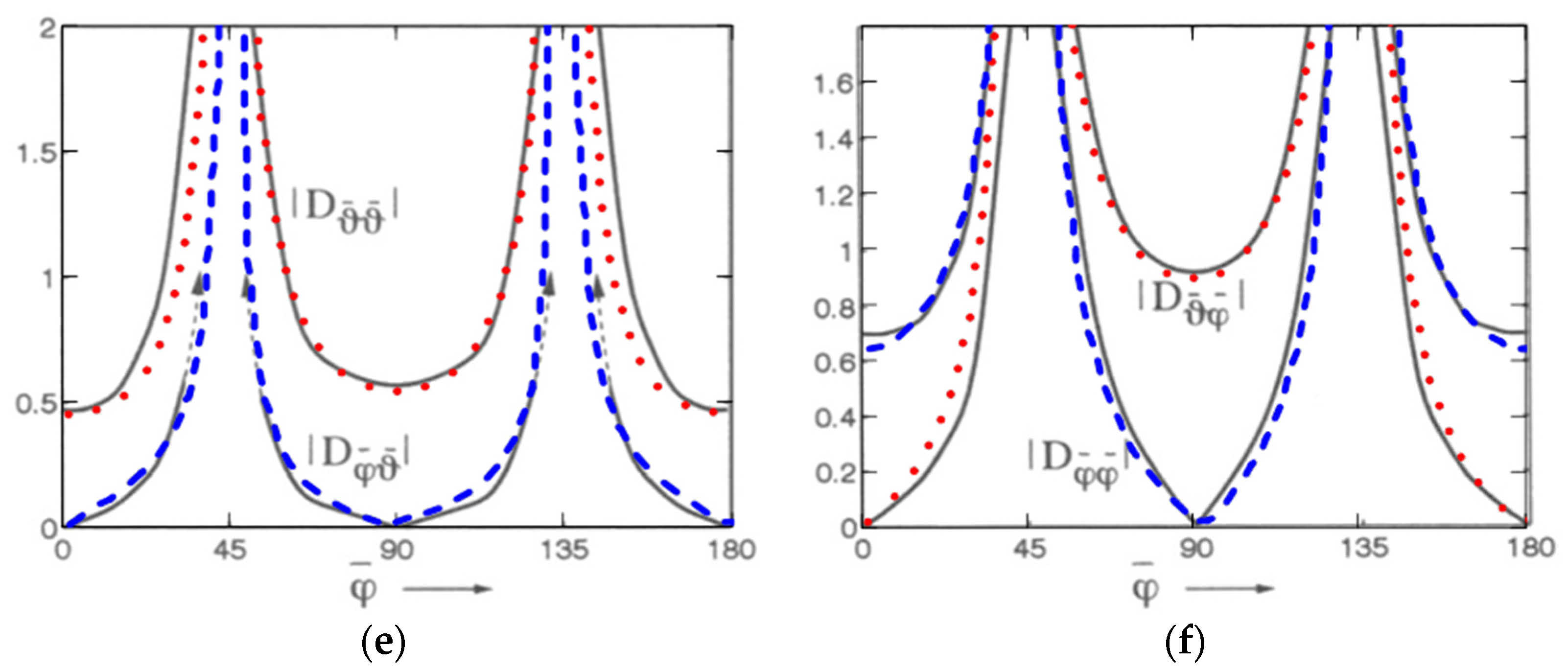
4. Results Obtained Using the MFC
5. List of Fundamental Components
- Components of the 2D formulas (4)–(7) for the scattered field, v(ψ), (2), (3).
- Linear integral with emphasis on the contributions of individual edges (13).
- R and T coefficients for an unbounded flat surface.
- Diffraction coefficients with R and T GDC (24), (25) and PODC (26), (27). Specific values of R and T are determined by a given type of boundary conditions.
- The polarization component of the diffraction coefficient [4].
- The geometric component of the diffraction coefficient [4].
- Modifying functions cpγ and crγ (23) for a plane angular sector.
6. Prospects for the Application of New Heuristic Approaches
- Numerical solutions require large computer resources, software and programmers. Modern computers cannot cope with some tasks, so one has to use heuristic approaches.
- Rigorous analytical solutions are lacking for most of the vast variety of edges that do not have analytical solutions.
- The need to improve the performance of solvers for the study of specific types of tasks, such as, for instance, inverse problems.
7. Discussion
- conducting of ray tracing;
- recognition and classification of the type of obstacle in the path of the beam;
- account according to the selected formula [47].
8. Conclusions
Funding
Conflicts of Interest
References
- Hönl, H.; Maue, A.W.; Westpfahl, K. Handbuch der Physik; Flügge, S., Ed.; Springer: Berlin/Heidelberg, Germany, 1961; Mir: Moscow, Russia, 1964; Volume 25/1, p. 218. [Google Scholar]
- Kravtsov, Y.A.; Zhu, N.Y. Theory of Diffraction: Heuristic Approaches; Alpha Science Int.: Oxford, UK, 2010. [Google Scholar]
- Vesnik, M.V. The Method of the Generalized Eikonal. New Approaches in the Diffraction Theory; Walter de Gruyter GmbN: Berlin, Germany; Boston, MA, USA, 2015; ISBN 978-3-11-031112-9. [Google Scholar]
- Vesnik, M.V. Physical Interpretation of Strict Solutions of Diffraction Problems by Heuristic Relations. J. Math. Sci. 2019, 239, 751–770. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Pergamon Press: Oxford/London, UK, 1968. [Google Scholar]
- Keller, J.B. Geometrical Theory of Diffraction. J. Opt. Soc. Am. 1962, 52, 116–130. [Google Scholar] [CrossRef]
- James, G.L. Geometrical Theory of Diffraction for Electromagnetic Waves; Peter Peregrinus Ltd.: London, UK, 1976. [Google Scholar]
- Borovikov, V.A.; Kinber, B.E. Geometrical Theory of Diffraction; IEEE: London, UK, 1994. [Google Scholar]
- Ufimtsev, P.Y. Method of Edge Waves in the Physical Theory of Diffraction; Sovetskoe Radio, US Air Force Foreign Technology Division: Moscow, Russia, 1962; pp. 1–1154. [Google Scholar]
- Ufimtsev, P.Y. Theory of Edge Diffraction in Electromagnetics; Tech Science Press: Encino, CA, USA, 2003; ISBN 0-9657001-7-8. [Google Scholar]
- Ufimtsev, P.Y. Fundamentals of the Physical Theory of Diffraction; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ozturk, A.K.; Paknys, R.; Trueman, C.W. Vertex Diffracted Edge Waves on a Perfectly Conducting Plane Angular Sector. IEEE Trans. Antennas Propag. 2011, 59, 888–897. [Google Scholar] [CrossRef]
- Gordon, W.B. Far field approximations to the Kirchhoff-Helmholtz representations of scattered fields. IEEE Trans. Antennas Propag. 1975, 23, 590–592. [Google Scholar] [CrossRef]
- Vesnik, M.V.; Ufimtsev, P.Y. An Asymptotic Feature of Corner Waves Scattered by Polygonal Plates. Electromagnetics 1992, 12, 265–272. [Google Scholar] [CrossRef]
- Vesnik, M.V. Elimination of Infinites in Diffraction Coefficients of Physical Optics Current’s Components for a Shadow Contour of a Scatterer. In Proceedings of the 1995 International Symposium on Electromagnetic Theory, St. Petersburg, Russia, 23–26 May 1995; pp. 407–409. [Google Scholar]
- Johansen, P.M.; Breinbjerg, O. An Exact Line Representation of the Physical Optics Scattered Field: The Case of a Pefrectly Conducting Polyhedral Structure Illuminated by Electric Hertzian Dipoles. IEEE Trans. Antennas Propag. 1995, 43, 689–696. [Google Scholar] [CrossRef] [Green Version]
- Klinkenbusch, L. Electromagnetic Scattering by a Quarter Plane. In Proceedings of the 2005 IEEE Antennas and Propagation Society International Symposium, Washington, DC, USA, 3–8 July 2005; Volume 3B, pp. 163–166. [Google Scholar]
- Albani, M.; Capolino, F.; Maci, S. Vertex diffraction coefficient for a quarter plane. URSI Int. Symp. EM Theory Pisa Italy 2004, 1146–1148. [Google Scholar]
- Albani, M.; Capolino, F.; Maci, S. Diffraction at the vertex of a quarter plane. Ant. Prop. Soc. Int. Symp. IEEE 2004, 1991–1994. [Google Scholar]
- Vesnik, M.V. On a Possibility of Constructing a Refined Heuristic Solution for the Problem of Diffraction by a Plane Angular Sector. J. Commun. Technol. Electron. 2011, 56, 531–543. [Google Scholar] [CrossRef]
- Vesnik, M.V. Efficiency of Different Heuristic Approaches to Calculation of Electromagnetic Diffraction by Polyhedrons and other Scatterers. Radio Sci. 2014, 49, 945–953. [Google Scholar] [CrossRef]
- Capolino, F.; Albani, M.; Maci, S.; Tiberio, R. Double Diffraction at a Pair of Coplanar Skew Edges. IEEE Trans. Antennas Propag. 1997, 45, 1219–1226. [Google Scholar] [CrossRef]
- Albani, M.; Capolino, F.; Maci, S.; Tiberio, R. Diffraction at a Thick Screen Including Corrugations on the Top Face. IEEE Trans. Antennas Propag. 1997, 45, 277–283. [Google Scholar] [CrossRef] [Green Version]
- Vesnik, M.V.; Kravtsov, Y.A. Subection 5.1.7 Diffraction by Bodies with Wedges: Method of Generalised Eikonal (MGE). In Theory of Diffraction: Heuristic Approaches; Kravtsov, Y.A., Zhu, N.Y., Eds.; Alpha Science International Ltd.: Oxford, UK, 2010. [Google Scholar]
- Vesnik, M.V. The Analytical Solution for the Electromagnetic Diffraction on 2-D Perfectly Conducting Scatterers of Arbitrary Shape. IEEE Trans. Antennas Propag. 2001, 49, 1638–1644. [Google Scholar] [CrossRef]
- Vesnik, M.V. Analytical solution for the 2D diffraction of electromagnetic wave by a truncated wedge. J. Commun. Technol. Electron. 2012, 57, 1061–1072. [Google Scholar] [CrossRef]
- Vesnik, M.V. Use of the generalized eikonal in the analytic solution of the problem of electromagnetic-wave diffraction by a 2D perfectly conducting half-plate. J. Commun. Technol. Electron. 2008, 53, 131–142. [Google Scholar] [CrossRef]
- Vesnik, M.V. Using of 2-Dimensional Solution in 3-Dimensional Problems. Radiotekhnika Elektron. 1993, 38, 1416–1423. [Google Scholar]
- Raman, C.V.; Krishnan, K.S. The Diffraction of Light by Metallic Screens. Proc. R. Soc. Lond. A 1927, 116, 254–267. [Google Scholar] [CrossRef]
- Shmoys, J. Diffraction by a Half-Plane with a Special Impedance Variation. IRE Trans. Antennas Propag. 1959, 7, 88–90. [Google Scholar] [CrossRef]
- Luebbers, R.J. Finite conductivity uniform GTD versus knife edge diffraction in prediction of propagation path loss. IEEE Trans. Antennas Propag. 1984, 32, 70–76. [Google Scholar] [CrossRef]
- Holm, P.D. A New Heuristic UTD Diffraction Coefficient for Nonperfectly Conducting Wedges. IEEE Trans. Antennas Propag. 2000, 48, 1211–1219. [Google Scholar] [CrossRef]
- El-Sallabi, H.M.; Ioannis, T.; Rekanos, I.T.; Vainikainen, P. A New Heuristic Diffraction Coefficient for Lossy Dielectric Wedges at Normal Incidence. IEEE Antennas Wirel. Propag. Lett. 2002, 1, 165–168. [Google Scholar] [CrossRef]
- Soni, S.; Bhattacharya, A. New heuristic diffraction coefficient for modeling of wireless channel. Prog. Electromagn. Res. C 2010, 12, 125–137. [Google Scholar] [CrossRef] [Green Version]
- Vesnik, M.V. Physical interpretation of the numerical solution for the diffraction problem of an electromagnetic wave on a plane perfectly conducting scatterer. J. Radioelectron. 2017. (In Russian). Available online: http://jre.cplire.ru/jre/apr17/7/text.pdf (accessed on 8 November 2021).
- Vesnik, M.V. Properties of Diffraction Coefficients in the Problem of Diffraction by 3D Plane Polygon. I. Principles of the Method of Fundamental Components. J. Commun. Technol. Electron. 2020, 65, 1236. [Google Scholar] [CrossRef]
- Vesnik, M.V. Properties of Diffraction Coefficients in the Problem of Diffraction by 3D Plane Polygon. II. Application of the Method of Fundamental Components in Practical Problems. J. Commun. Technol. Electron. 2020, 65, 1353. [Google Scholar] [CrossRef]
- Senior, T.B.A. Half plane edge diffraction. Radio Sci. 1975, 10, 645. [Google Scholar] [CrossRef]
- Senior, T.B.A. Diffraction tensors for imperfectly conducting edges. Radio Sci. 1975, 10, 911. [Google Scholar] [CrossRef]
- Voitovich, N.N.; Katsenelenbaum, B.Z.; Korshunova, E.N.; Pangonis, L.I.; Pereyaslavets, M.L.; Sivov, A.N.; Shatrov, A.D. Electromagnetics of Antennas with Semitransparent Surfaces. A Method of Constructive Synthesis; Nauka: Moscow, Russia, 1989. [Google Scholar]
- Bankov, S.E. Integrated Microwave Optics; Fizmatlit: Moscow, Russia, 2018. [Google Scholar]
- Klionovski, K.; Bankov, S.E. Electromagnetic wave scattering by a half-plane with generalized semitransparent boundary conditions. Waves Random Complex Media 2020, 1–12. [Google Scholar] [CrossRef]
- Bankov, S.E.; Vesnik, M.V.; Kravchenko, V.F. Heuristic Solution to the Diffraction Problem on a Superconducting Half-Plane. J. Commun. Technol. Electron. 2020, 65, 398–405. [Google Scholar] [CrossRef]
- Vesnik, M.V. Using the Method of Base Components for a Heuristic Solution to the Diffraction Problem on a Half-Plane with Nonideal Boundary Conditions. J. Commun. Technol. Electron. 2019, 64, 1211–1217. [Google Scholar] [CrossRef]
- Vesnik, M.V.; Bankov, S.E. Heuristic solution to the problem of diffraction of a TE-polarized electromagnetic wave on a semitransparent half-plane. Waves Random Complex Media 2021, 1–12. [Google Scholar] [CrossRef]
- Vesnik, M.V. Analytical heuristic solution for the problem of elastic wave diffraction by a polygonal flat 3D scatterer. In Proceedings of the International Conference Days on Diffraction, St. Petersburg, Russia, 27–31 May 2013; p. 27. [Google Scholar]
- Vesnik, M.V. Calculation of Diffraction Attenuation on Radio Waves Propagation Paths in Urban Environment. Phys. Bases Instrum. 2018, 7, 73–79. (In Russian) [Google Scholar] [CrossRef]
- Vesnik, M.V.; Kalinichev, V.I. Features of electromagnetic diffraction on a perfectly conducting flat rectangle. In Proceedings of the Vth All-Russian Microwave Conference, Moscow, Russia, 28 November 2017; pp. 114–118. (In Russian). [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vesnik, M.V. New Possibilities for Constructing Heuristic Solutions to Problems of Electromagnetic Diffraction. Eng 2022, 3, 27-41. https://doi.org/10.3390/eng3010004
Vesnik MV. New Possibilities for Constructing Heuristic Solutions to Problems of Electromagnetic Diffraction. Eng. 2022; 3(1):27-41. https://doi.org/10.3390/eng3010004
Chicago/Turabian StyleVesnik, Michael V. 2022. "New Possibilities for Constructing Heuristic Solutions to Problems of Electromagnetic Diffraction" Eng 3, no. 1: 27-41. https://doi.org/10.3390/eng3010004
APA StyleVesnik, M. V. (2022). New Possibilities for Constructing Heuristic Solutions to Problems of Electromagnetic Diffraction. Eng, 3(1), 27-41. https://doi.org/10.3390/eng3010004





