A Critical Review of the Equivalent Stoichiometric Cloud Model Q9 in Gas Explosion Modelling
Abstract
:1. Introduction
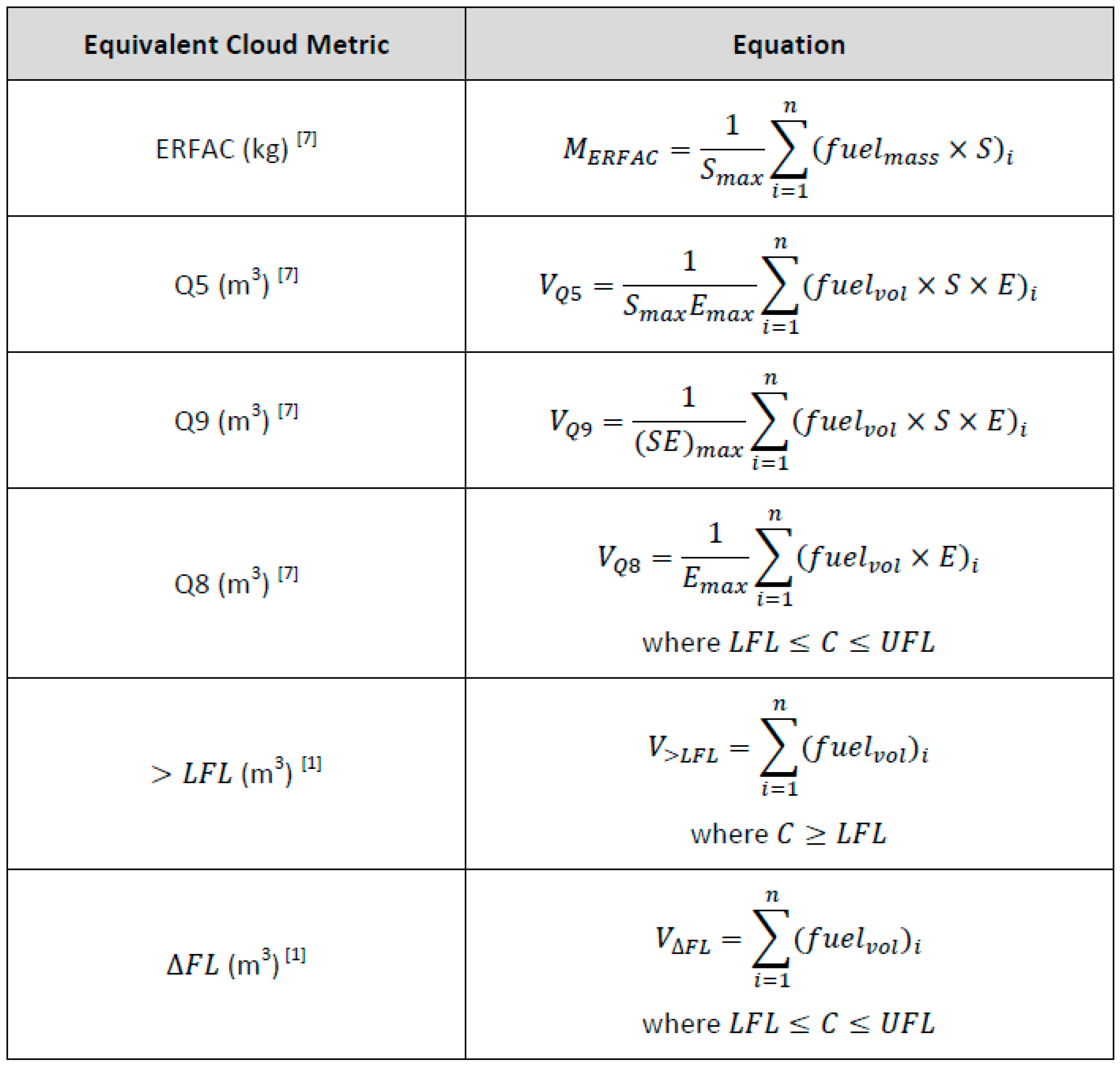
1.1. One specific ESC Model—Q9
1.2. Importance of ESC
1.3. Objective
- (a)
- Provide a detailed evaluation of Q9 with experimental data from the large-scale experimental data set (BFTSS Phase 3B) (More details are given in Section 5.1) which specifically addressed scenarios that Q9 is designed for.
- (b)
- To clear up confusion generated by two publications: one (by authors of this paper) which concludes that Q9 under-predicts systematically [2] and the other which concludes that Q9 is overconservative (i.e., over-predicts) [3]. The latter paper did not cite the former, hence creating the current unchallenged impression that Q9 is over-conservative for readers who are not aware of the first.
1.4. Structure of This Paper
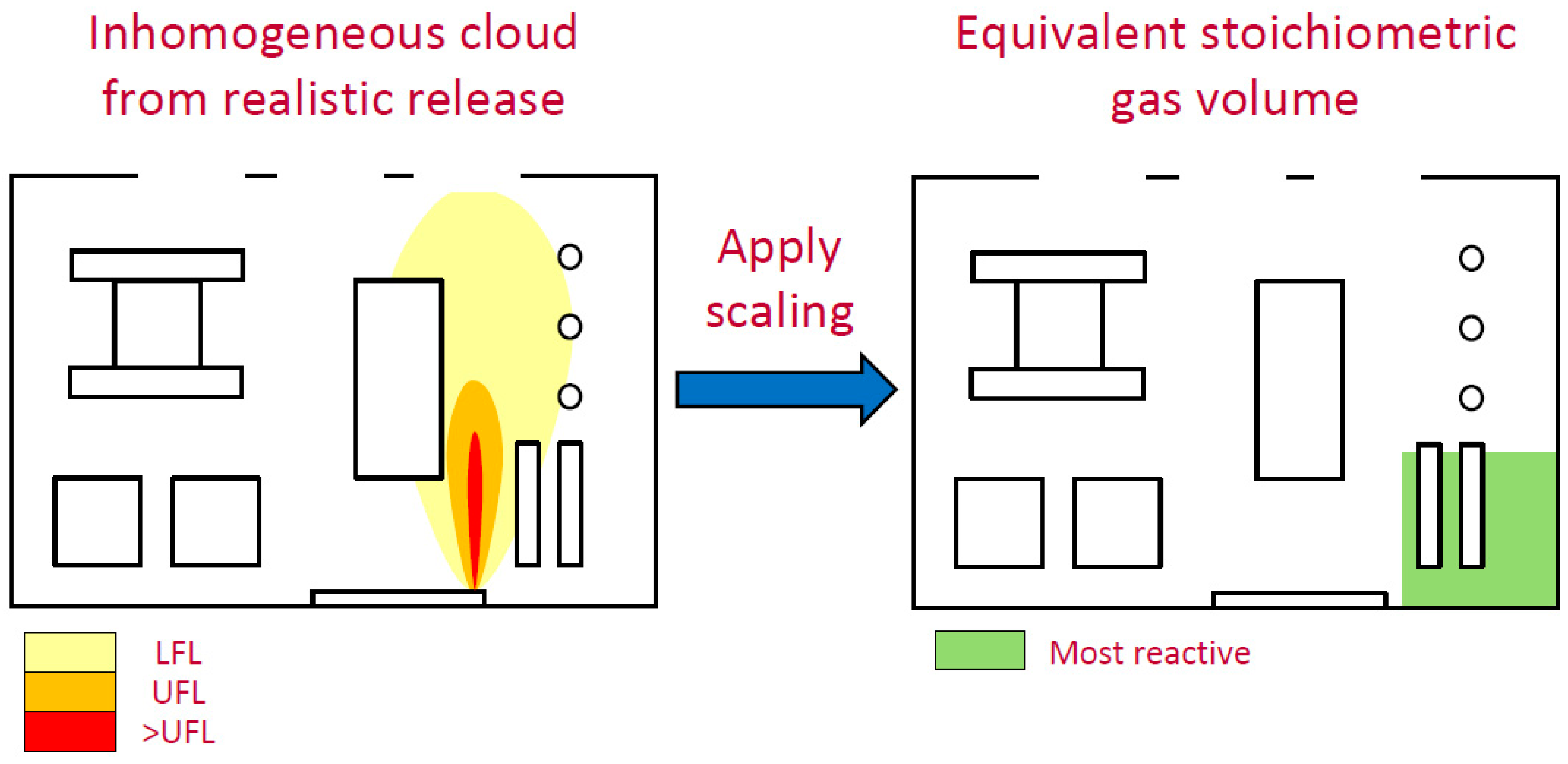
2. Evolution of Equivalent Stoichiometric Cloud
2.1. An Historic Perspective
2.2. Evolution and Type of ESC Volume Methodology
- (i)
- (ii)
- Procedures of assessment: while the high overpressure observed caused concern, there was a common acknowledgement that the theoretical worst-case scenarios used in Phase 2 to test the explosion model is not representative of real-life situations in accidents.
3. Underlying Assumption of ESC Methodology
4. Case for Re-Assessment of Q9
5. Methodology
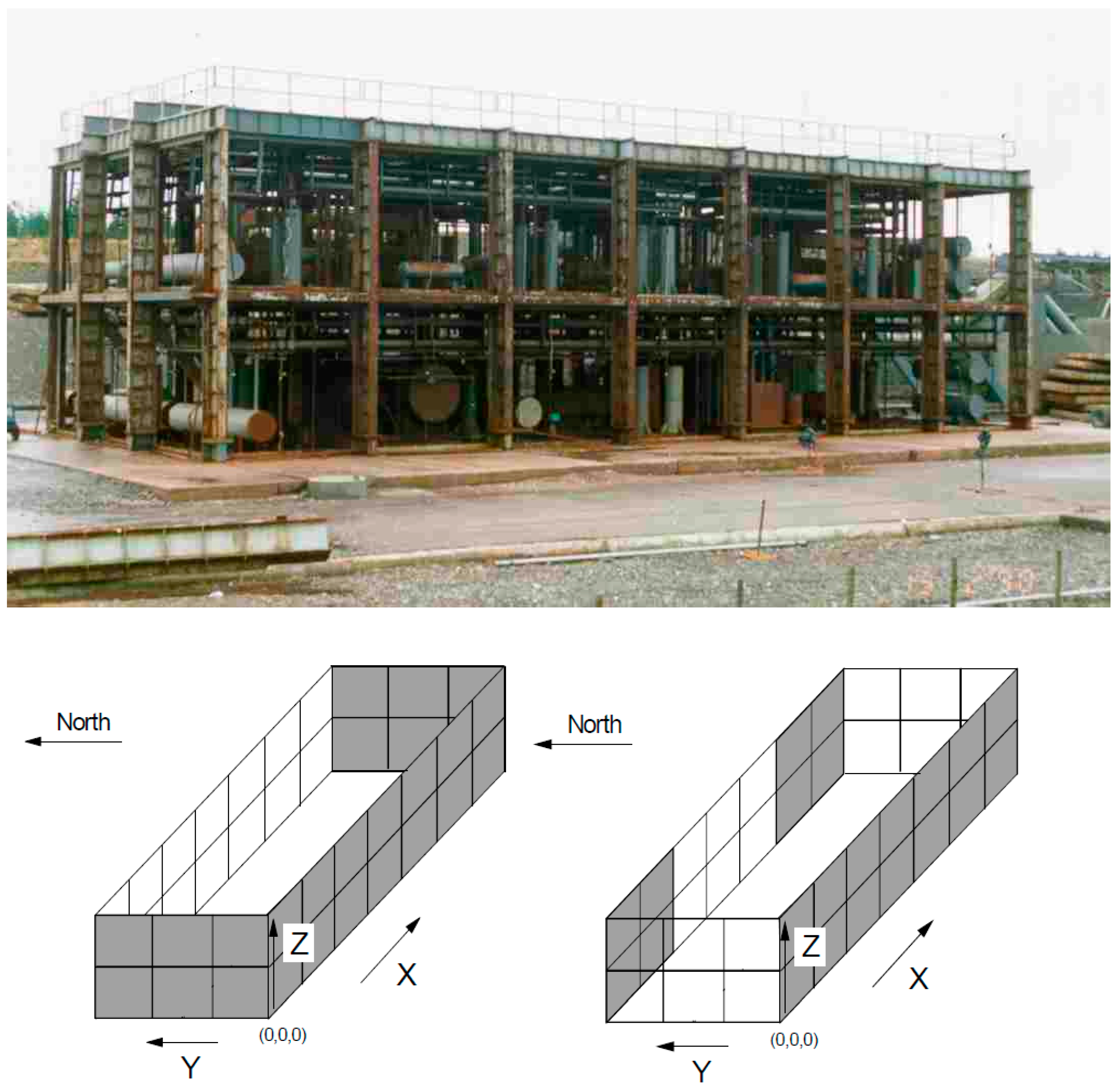
5.1. Dataset from Phase 3B
5.2. Previous Work on Flammable Volumes
5.3. Versions of FLACS Used
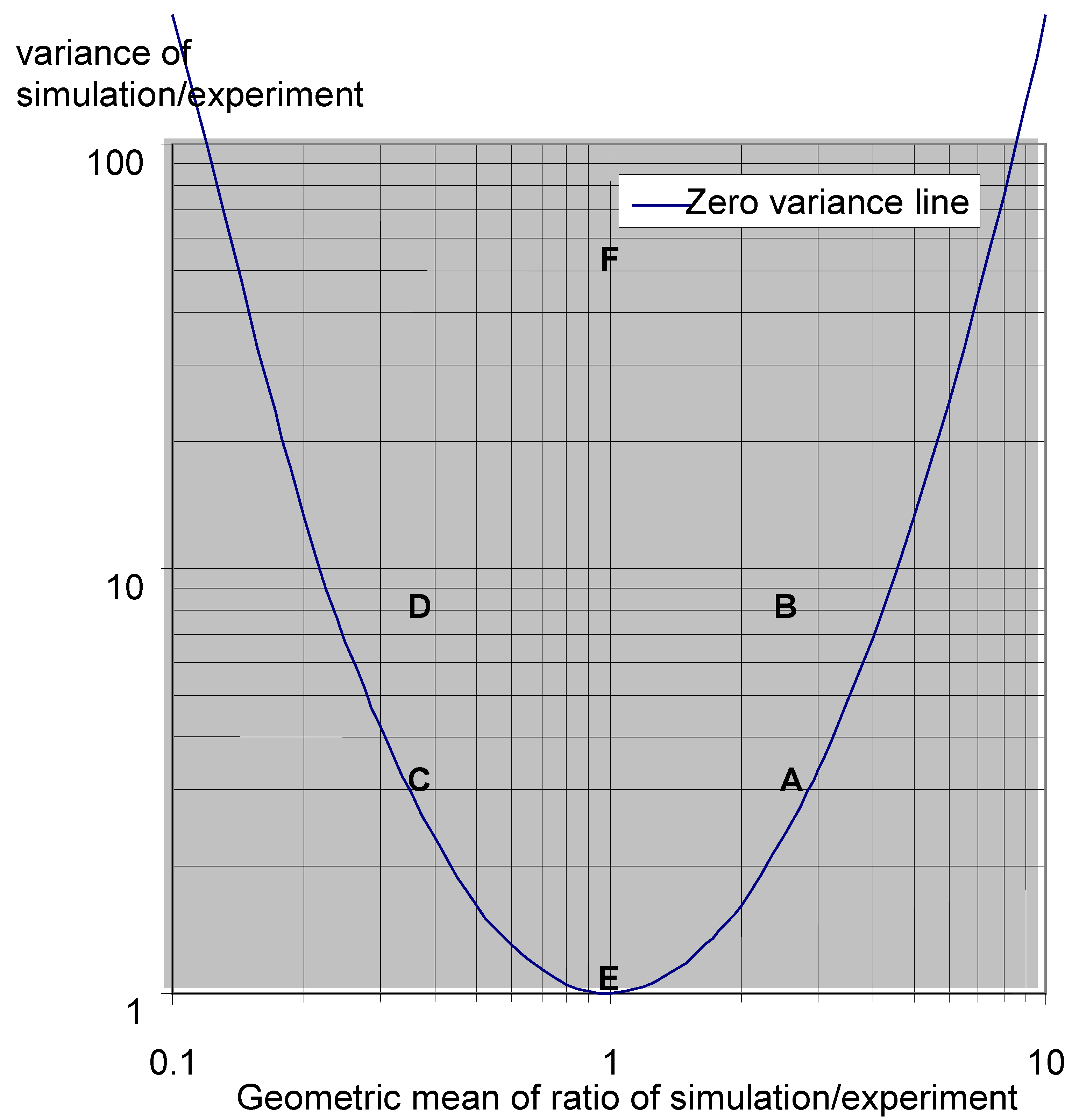
5.4. Format of Comparison—The MV Diagram
- P = predicted overpressure
- O = observed or measured overpressure
- <X> denotes expectation value of X
- (a)
- Scale
- (b)
- Ease of comparison of the two key characteristics of model predictions
6. Results and Evaluation
6.1. Estimation of Overpressures by Direct FLACS Dispersion-Explosion Simulations
Effect of Control Volume Sizes—Grid Dependency for Dispersion-Explosion Linked Simulations
6.2. The ESC Model—Q9
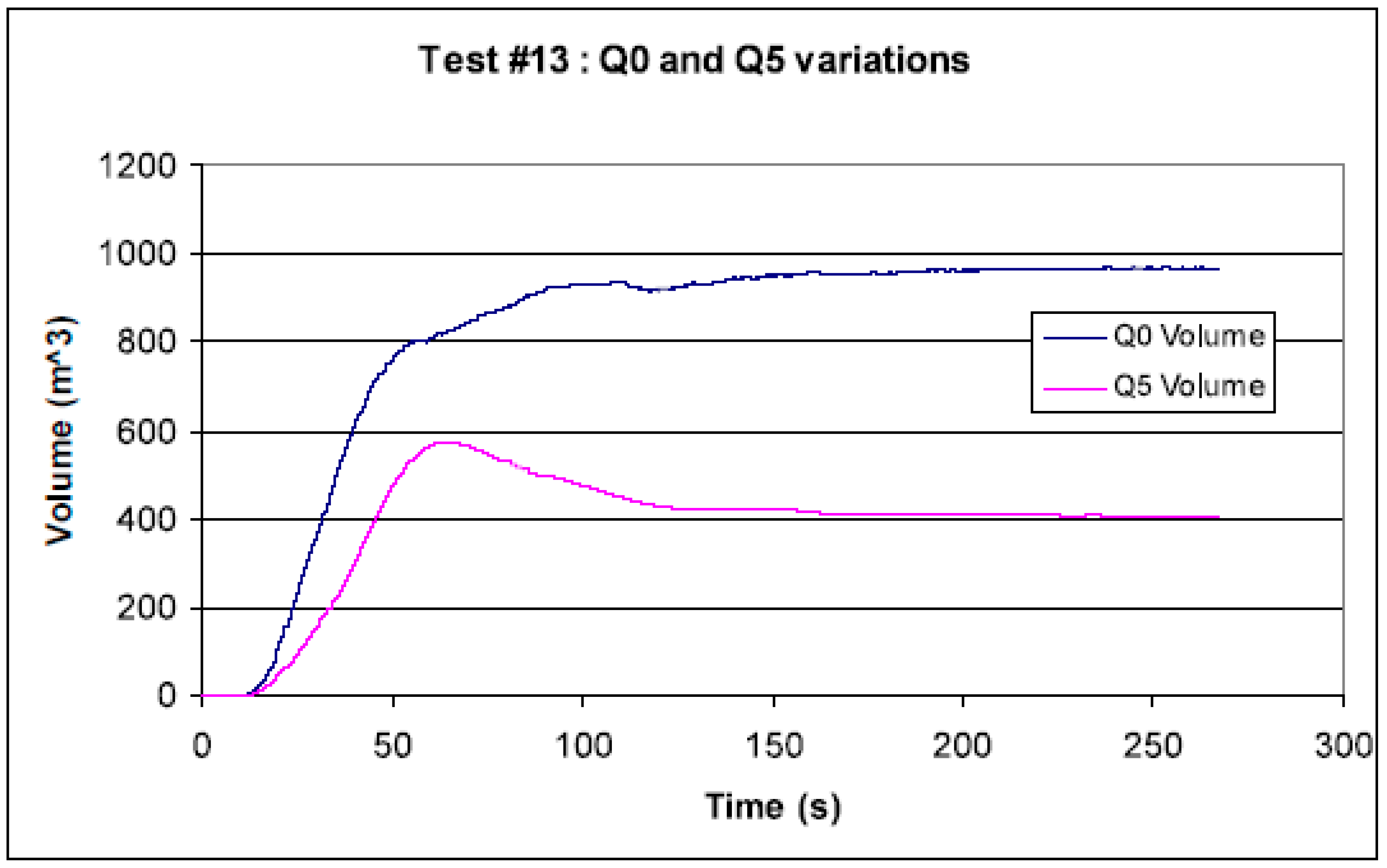
6.2.1. Cloud Volumes Derived from Experimental Data
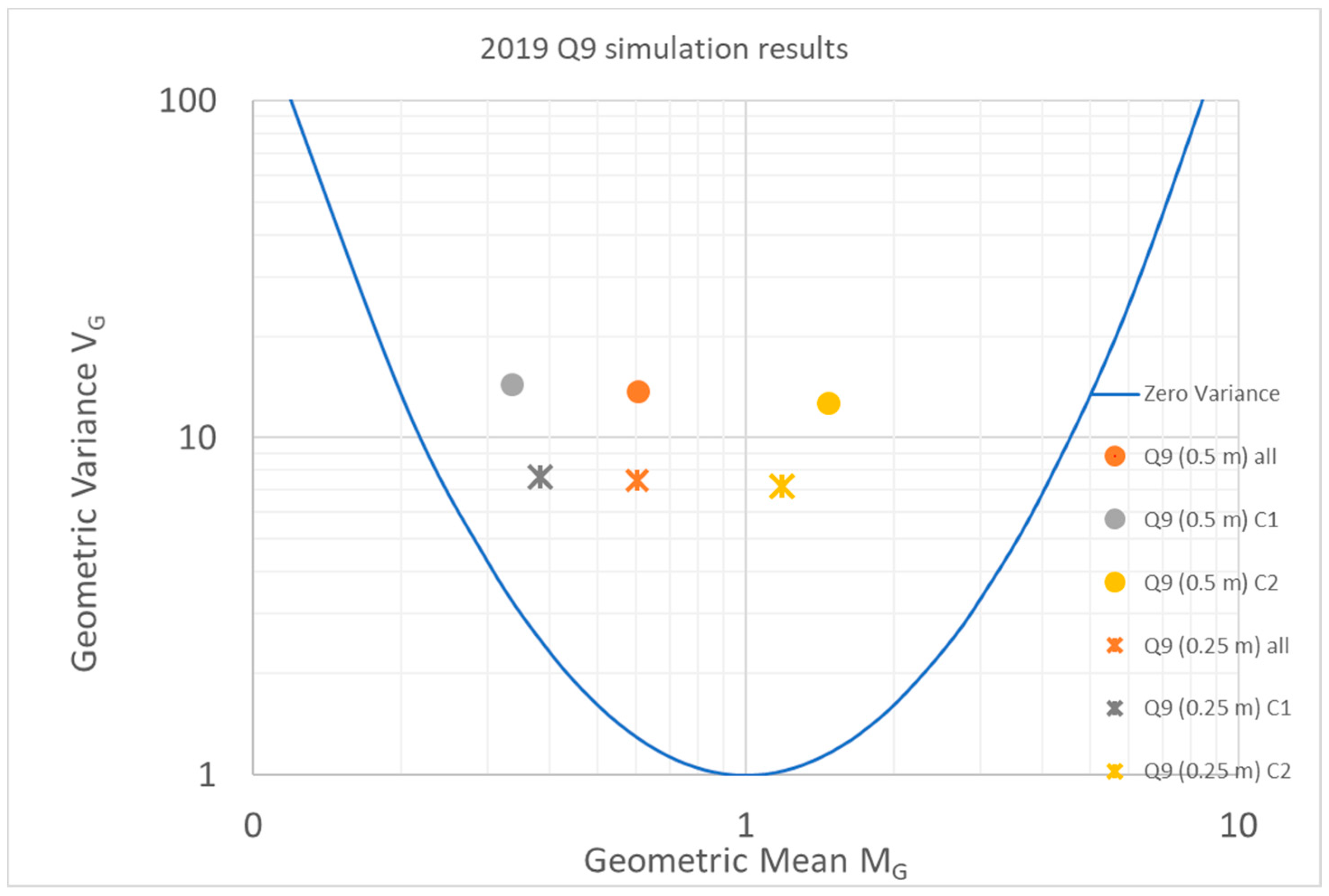
6.2.2. Cloud Volumes Derived from FLACS Dispersion Simulations
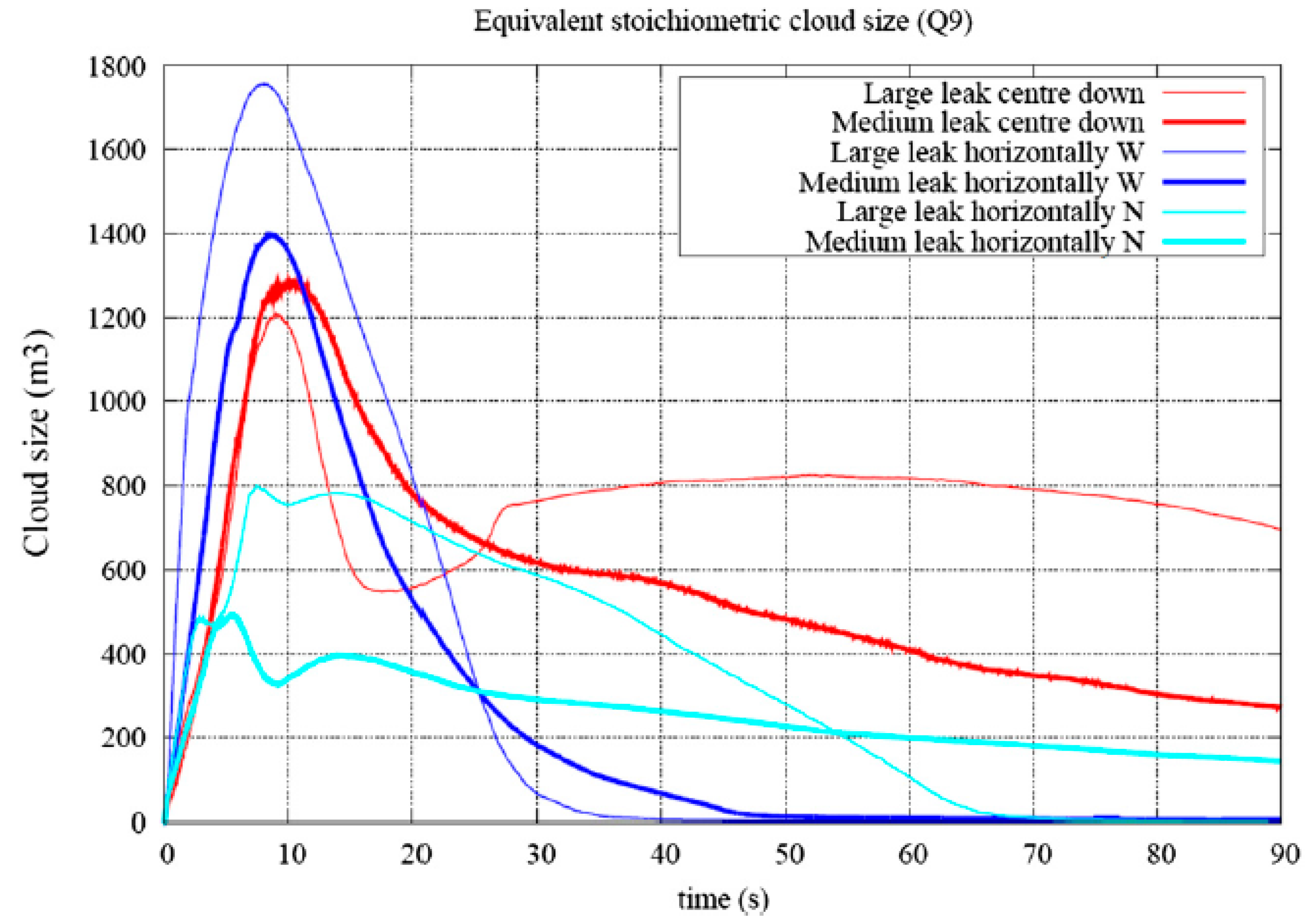
6.3. Sensitivity to Cloud Locations
7. Discussions
7.1. Consistency of Results
7.2. Sensitivity of FLACS to Boundary Properties
7.3. Reliability of Direct Dispersion–Explosion Simulations
7.4. Q9 Is Not Conservative
7.5. Complexity and Accuracy
7.6. Key Learning
7.6.1. Recommended Usage of Q9 Is Inadequate
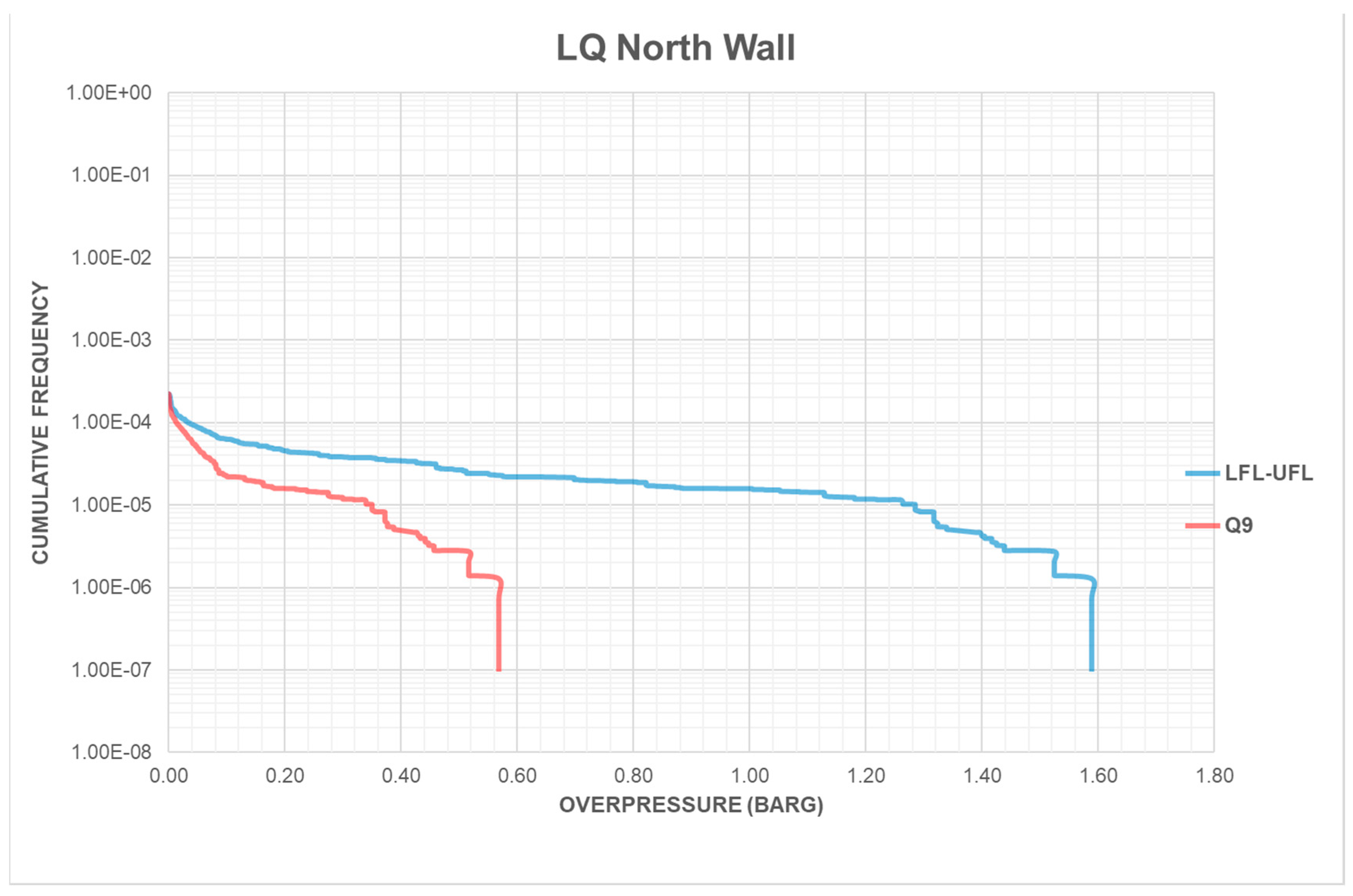
7.6.2. Applications of ESC in Probabilistic Explosion Analysis to Exceedance Curve
- (i)
- The DAL derived from the Q9 model is more than three times smaller than that from the ∆FL model, e.g., 0.4 bar and 1.3 bar, respectively at a cumulative frequency of 10−5/yr. The magnitude of DAL varies according to the level of exceedance set. At 10−4/yr. The magnitude of overpressure is much lower, though the ratio remains similar.
- (ii)
- The maximum overpressure calculated also varies about three-fold: 1.6 bar compared with 0.6 bar for the ∆FL and Q9 models, respectively. This higher maximum overpressure is probably not used for structural design of the blast wall in a risk-based approach. However, there are impacts on hazard management, e.g., on (a) emergency planning and management and (b) siting and layout particularly for onshore facilities at an early stage of design, e.g., the concept selection stage.
7.6.3. Recognised Evaluation and Presentation Format
7.6.4. An Explosion Risk Assessment in Practice
- (a)
- Adherence to guidance: this would require carrying out simulations using different grid sizes depending on results of dispersion calculations. As a typical ERA involves large numbers (of order a 1000) of simulations, there is a temptation to bypass or approximate this step given time and cost pressure.
- (b)
- The effect of mixing or using different grid sizes is difficult to quantify—as can be seen above, FLACS is grid sensitive. The net effect of mixing results obtained using various grid sizes has not yet been quantified.
7.6.5. Quality Control Issues
7.7. More Recent Data on Hydrogen
7.8. Application of Q9 in Reality
7.9. Expectation and Reality—Application Outstripping Capability
7.9.1. Refinement of Transient Nature of Releasees
7.9.2. Advanced CFD/FE Analysis
8. Conclusions
9. Observations
- There is an assumption that the Q9 model is more accurate because it contains more physics than one containing less. This is not true. The devil is in the missing physics. The true arbiter is validation with full scale data.
- Recognition is lacking in the industry of the limitation of the code, and the lack of appropriate data and validation. As a result, ever more complex analyses are being carried out where there is no validation or detailed scientific evaluation to support them (e.g., time varying risk calculation, time and spatially coupled-load–response analysis on structures, etc.).
- Recognised model evaluation protocols should be used in all publications on model validation or model evaluation. This provides clarity and avoid confusion.
- The hydrogen economy is fast developing. The application of the Q9 model to hydrogen requires a separate evaluation/validation exercise based on hydrogen data derived from experiments at appropriate scale.
10. Recommendations
- (a)
- Develop an appropriate ESC model through vigorous scientific methods and validated by appropriate scale data.
- (b)
- Q9 should be used with caution; a full account of systematic underprediction and large variance should be made.
- (c)
- Generate appropriate large-scale data with a wider range of conditions than those of Phase 3B, e.g., involving a range of geometries and boundary wall arrangements, and non-steady scenarios, such as simulation of blow downs and delayed ignition. The industry should form a JIP to address this.
- (d)
- The issue of variability due to users in the execution of ERA, particularly involving the Q9 model should be addressed. A JIP that goes someway to address this issue was suggested by the Health and Safety Laboratory on a joint ERA inter-comparison exercise involving key consultants [15].
- (e)
- The validity and applicability of coupled explosion loading/structural response analysis should be clarified. This could involve a guidance to define correct application, evaluation against data to establish confidence limits, etc.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ∆FL | Concentration between upper and lower flammability limits. |
| > LFL | Concentration above the lower flammability limit. |
| MG | Geometric mean. |
| VG | Geometric variance. |
| BFTSS | Blast and Fire for Topside Structure joint industry—the name of a series of JIPs spanning over more than a decade. There are four phases: 1, 2, 3a and 3b. |
| CFD | Computation fluid dynamics. |
| CMI | Christian Michelsen Institute. |
| DAL | Design accidental load. |
| ERA | Explosion risk assessment. |
| ESC | Equivalent stoichiometric cloud. This refers to dispersion-based ESC where not specifically stated in the text. |
| FE | Finite Element |
| JIP | Joint industry project. |
| LFL | Lower flammability limit. |
| MEGGE | Model evaluation group for gas explosion. |
| MV diagram | Mean–variance diagram |
| Phase 3B | One of the phases of the BFTSS project which addressed realistic release scenarios |
| Q9 | One of the widely used models of ESC. Its definition is in 2. |
| UFL | Upper flammability limit. |
References
- Norwegian Oil Industry Association. Risk and Emergency Preparedness Assessment—Norsok Standard Z-013; Norwegian Technology Centre: Oslo, Norway, 2001. [Google Scholar]
- Tam, V.H.Y.; Wang, M.; Savvides, C.N.; Tunc, E.; Ferraris, S.; Wen, J.X. Simplified flammable gas volume methods for gas explosion modelling from pressurized gas releases: A comparison with large scale experimental data. In Institution of Chemical Engineers Symposium Series; IChemE: London, UK, 2008. [Google Scholar]
- Hansen, O.R.; Gavelli, F.; Davis, S.G.; Middha, P. Equivalent cloud methods used for explosion risk and consequence studies. J. Loss Prev. Process. Ind. 2013, 26, 511–527. [Google Scholar] [CrossRef]
- HMSO. The Flixborough Disaster: Report of the Court of Inquiry; HMSO Stationery Office: London, UK, 1975. [Google Scholar]
- Prörtner, H. Gas cloud explosions and resulting blast effects. Nucl. Eng. Des. 1977, 41, 59–67. [Google Scholar] [CrossRef]
- Gugan, K. Unconfined Vapour Cloud Explosions; Institution of Chemical Engineers: London, UK, 1979. [Google Scholar]
- Berg, A.V.D. The multi-energy method: A framework for vapour cloud explosion blast prediction. J. Hazard. Mater. 1985, 12, 1–10. [Google Scholar] [CrossRef]
- Mercx, W.P.M.; van den Berg, A.C.; van Leeuwen, D. Application of Correlations to Quantify the Source Strength of Vapour Cloud Explosions in Realistic Situations. Final Report for the Project: ’GAMES’; TNO Report PML 1998-C53; Netherlands Organization forApplied Scientific Research (TNO): The Hague, The Netherland, 1998; p. 156. [Google Scholar]
- Cullen, W.D. The Public Inquiry into the Piper Alpha Diasater; HMSO: London, UK, 1990; Volume 1–2. [Google Scholar]
- Tam, V.H.Y.; Langford, D. Design of the BP Andrew platform. In International Conference on Health, Safety and Environment in Oil and Gas Exploration and Production; ERA Technology: London, UK, 1994; pp. 3.6.1–3.6.10. [Google Scholar]
- Selby, C.; Burgan, B. Blast and Fire Engineering for Topside Structures Phase 2; Final Summary Report; The Steel Construction institute: London, UK, 1998. [Google Scholar]
- Al-Hassan, T.; Johnson, D.M. Gas explosions in Large Scale Offshore Module Geometries: Overpressures, Mitigation and Repeatability. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE 98, Lisbon, Portugal, 5–6 July 1998. [Google Scholar]
- Shearer, M.J.; Tam, V.H.; Corr, B. Analysis of results from large scale hydrocarbon gas explosions. J. Loss Prev. Process. Ind. 2000, 13, 167–173. [Google Scholar] [CrossRef]
- Cleaver, R.P.; Britter, R.E. A workbook approach to estimating the flammable volume produced by a gas release. FABIG Newsl. 2001, 30, 5–7. [Google Scholar]
- Stewart, J.R.; Gant, S. A Review of the Q9 equivalent cloud method for explosion modelling. FABIG Newsl. March 2009, 75, 16–25. [Google Scholar]
- Coldrick, S. How do we demonstrate that a consequence model is fit-for-purpose? Inst. Chem. Eng. Symp. Series 2017, 162, 1–9. [Google Scholar]
- Johnson, D.M.; Cleaver, R.P. Gas Explosions in Offshore Modules Following Realistic Releases (Phase 3B): Final Summary Report; Advantica: British Gas, Loughborough, 2002. [Google Scholar]
- Oil and Gas UK. Fire and Explosion Guidelines—Issue 2; Oil and Gas UK: London, UK, 2018. [Google Scholar]
- Selby, C.; Burgan, B. Explosion Model Evaluation Project; Report RT 738; The Steel Construction Institute: London, UK, 1998. [Google Scholar]
- Hanna, S.R.; Strimaitis, D.G.; Chang, J.C. Evaluation of fourteen hazardous gas models with ammonia and hydrogen fluoride field data. J. Hazard. Mater. 1991, 26, 127–158. [Google Scholar] [CrossRef]
- Ivings, M.; Lea, C.; Webber, D.; Jagger, S.; Coldrick, S. A protocol for the evaluation of LNG vapour dispersion models. J. Loss Prev. Process. Ind. 2013, 26, 153–163. [Google Scholar] [CrossRef]
- Tam, V.H.Y. Explosion model evaluation. FABIG Newsl. 1998, 22, 34–36. [Google Scholar]
- Bowerman, H.; Owens, G.W.; Rumley, J.H.; Tolloczko, J.J.A. Interim Guidance Notes for Design and Protection of Top-Side Structures against Explosion and Fire; SCI-P-112; The Steel Construction Institute: London, UK, 1992. [Google Scholar]
- Cleaver, R.P.; Burgess, S.; Buss, G.Y.; Savvides, C.; Tam, V.H.Y.; Connolly, S.; Britter, R.E. Analysis of Gas Build-Up from High Pressure Natural Gas Releases in Naturally Ventilated Offshore Modules. In 8th Annual Conference on Offshore Installations: Fire and Explosion Engineering; ERA Technology: London, UK, 1999; pp. 1–12. [Google Scholar]
- Savvides, C.; Tam, V.H.Y.; Kinnear, D. Dispersion of Fuel in Offshore Modules: Comparison of Predictions Using Fluent and Full Scale Experiments. In Major Hazards Offshore Conference; ERA Technology: London, UK, 2001; pp. 1–14. [Google Scholar]
- Savvides, C.; Tam, V.H.Y.; Os, J.E.; Hansen, O.; Wingerden, K.; Van Renoult, J. Dispersiion of Fuel in Offshore Modules: Comparison of Predictions Using FLACS and Full Scale Experiments. In Major Hazards Offshore Conference; ERA Technology Report: London, UK, 2001; pp. 1–8. [Google Scholar]
- Chang, J.C.; Hanna, S.R. Air quality model performance evaluatione. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar]
- Tam, V.H.; Corr, B. Development of a limit state approach for design against gas explosions. J. Loss Prev. Process. Ind. 2000, 13, 443–447. [Google Scholar] [CrossRef]
- Corr, R.B.; Frieze, P.A.; Tam, V.H.Y.; Snell, R.O. Development of the Limit State Approach for Design of Offshore Platforms. In Proceedings of the Conference on Fire and Explosion Engineering, ERA Technology, Leatherhead, UK, December 1999. [Google Scholar]
- Holen, J. Comparison of five corresponding explosion risk studies performed by five different consultants. In Major Hazards Offshore Conference Proceedings; ERA Technology: London, UK, 2001. [Google Scholar]
- Wen, J.; Rao, V.M.; Tam, V. Numerical study of hydrogen explosions in a refuelling environment and in a model storage room. Int. J. Hydrog. Energy 2010, 35, 385–394. [Google Scholar] [CrossRef]
- Tanaka, T.; Azuma, T.; Evans, J.; Cronin, P.; Johnson, D.; Cleaver, R. Experimental study on hydrogen explosions in a full-scale hydrogen filling station model. Int. J. Hydrog. Energy 2007, 32, 2162–2170. [Google Scholar] [CrossRef]
- Caretta, G. Coupled Modelling and Experiments in Structural Response to Blast Loading. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2004. [Google Scholar]
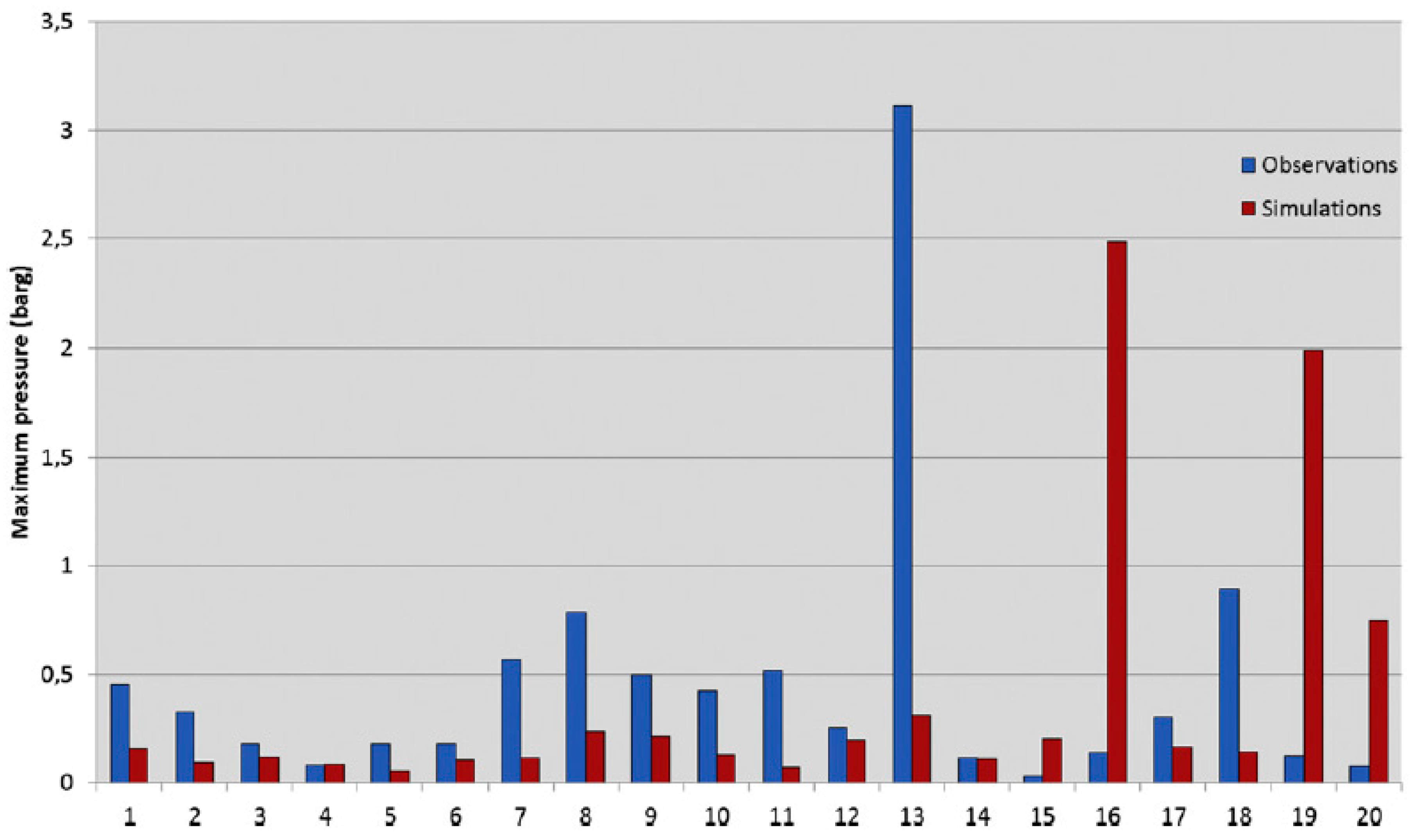
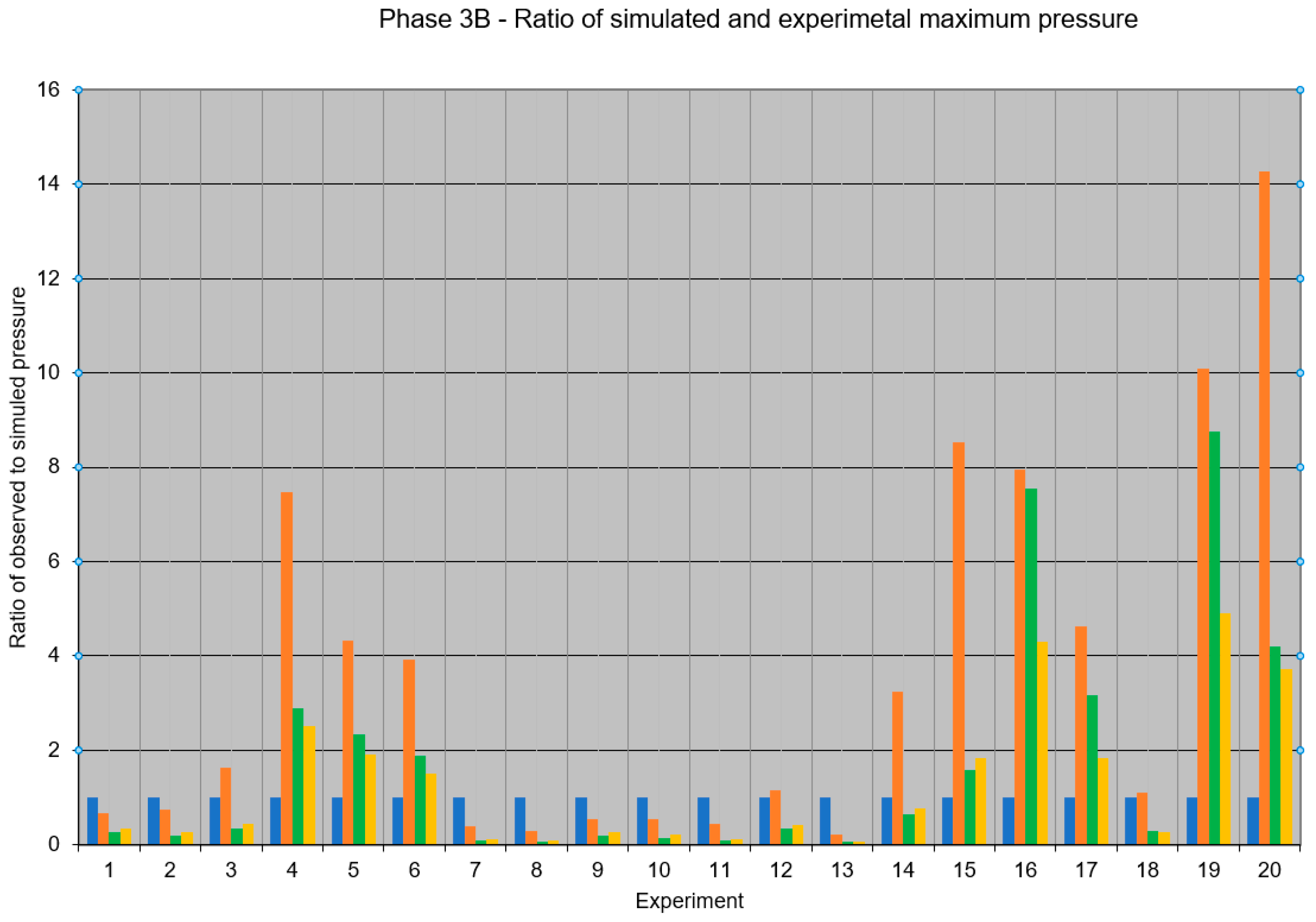
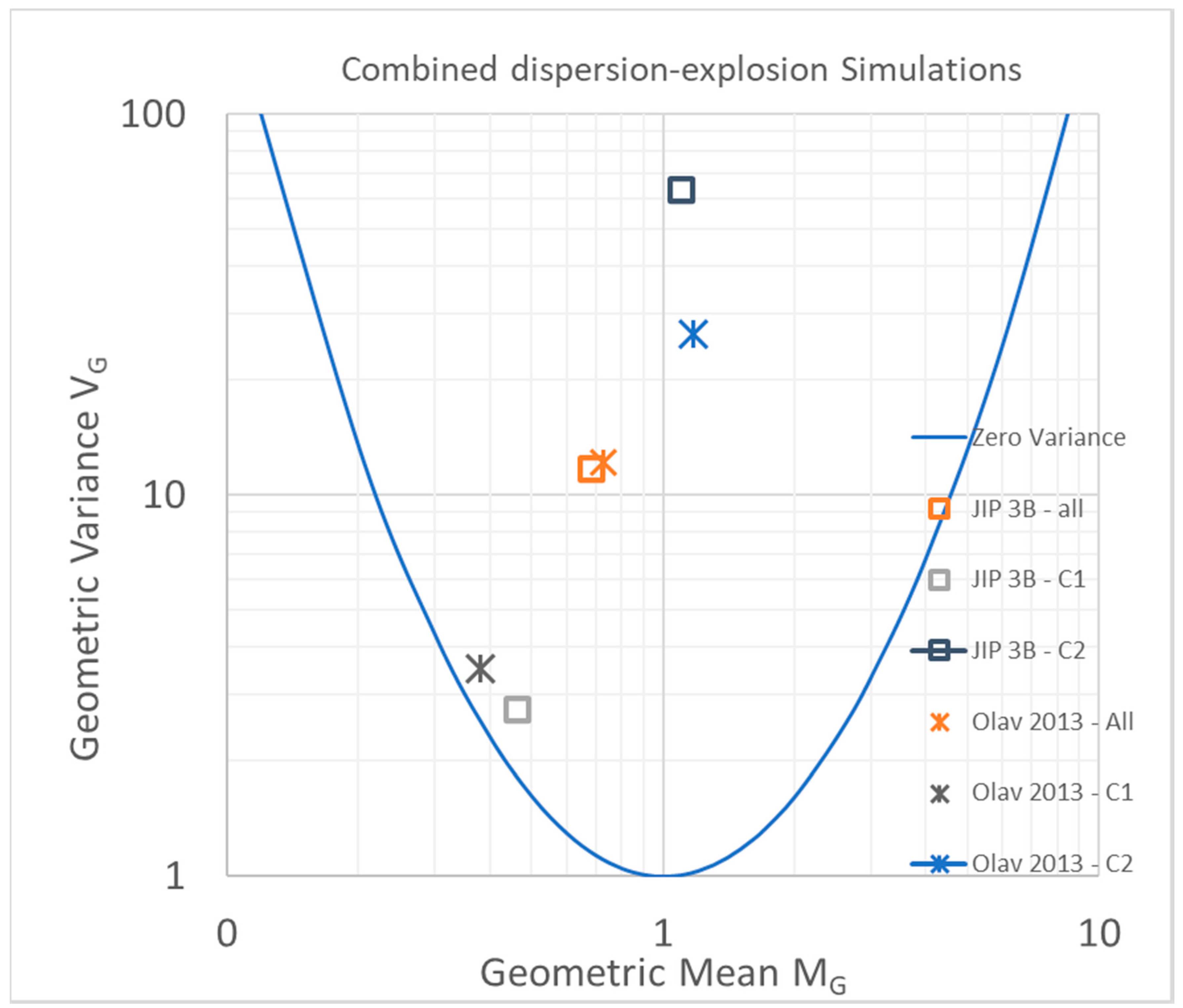
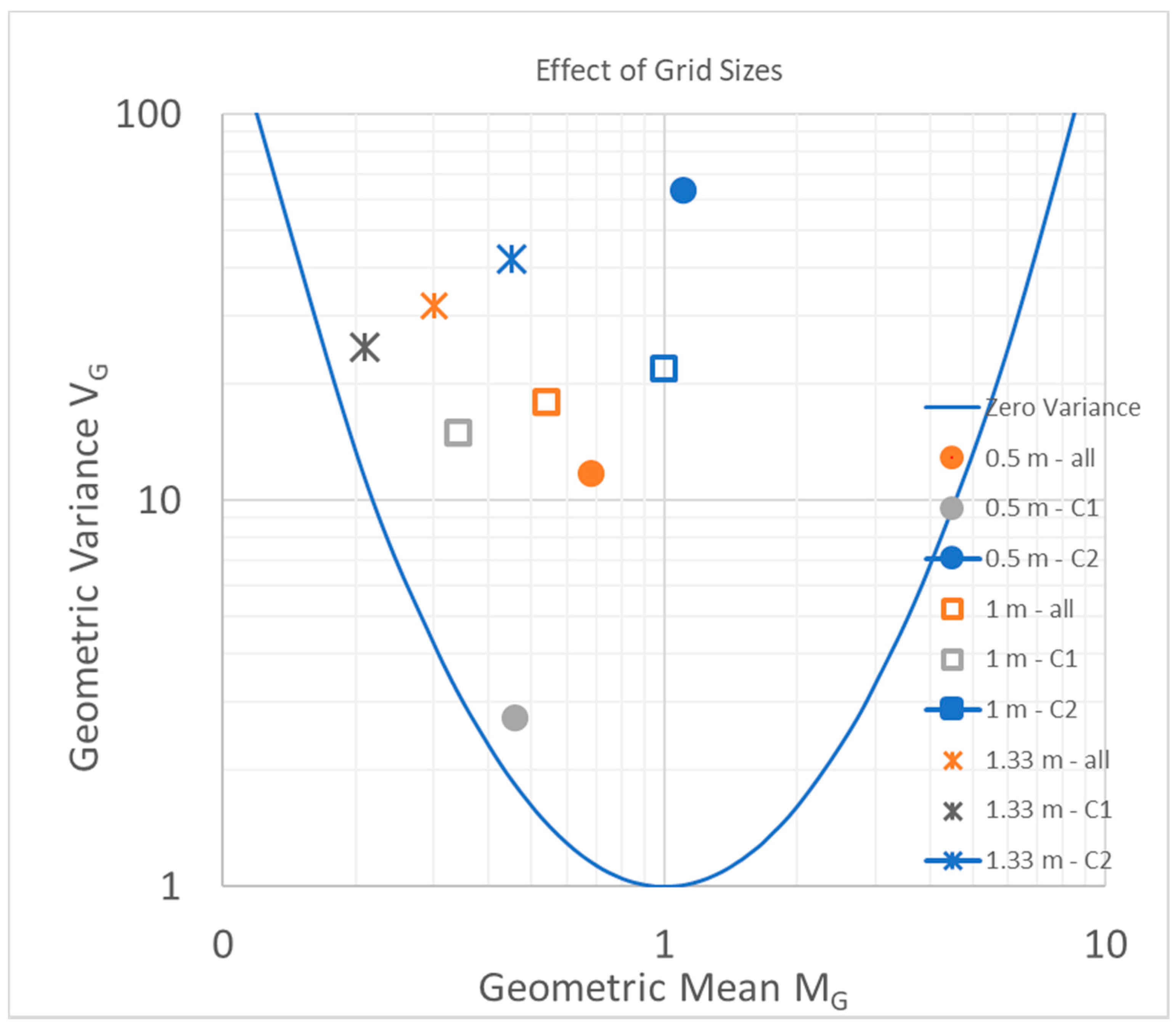
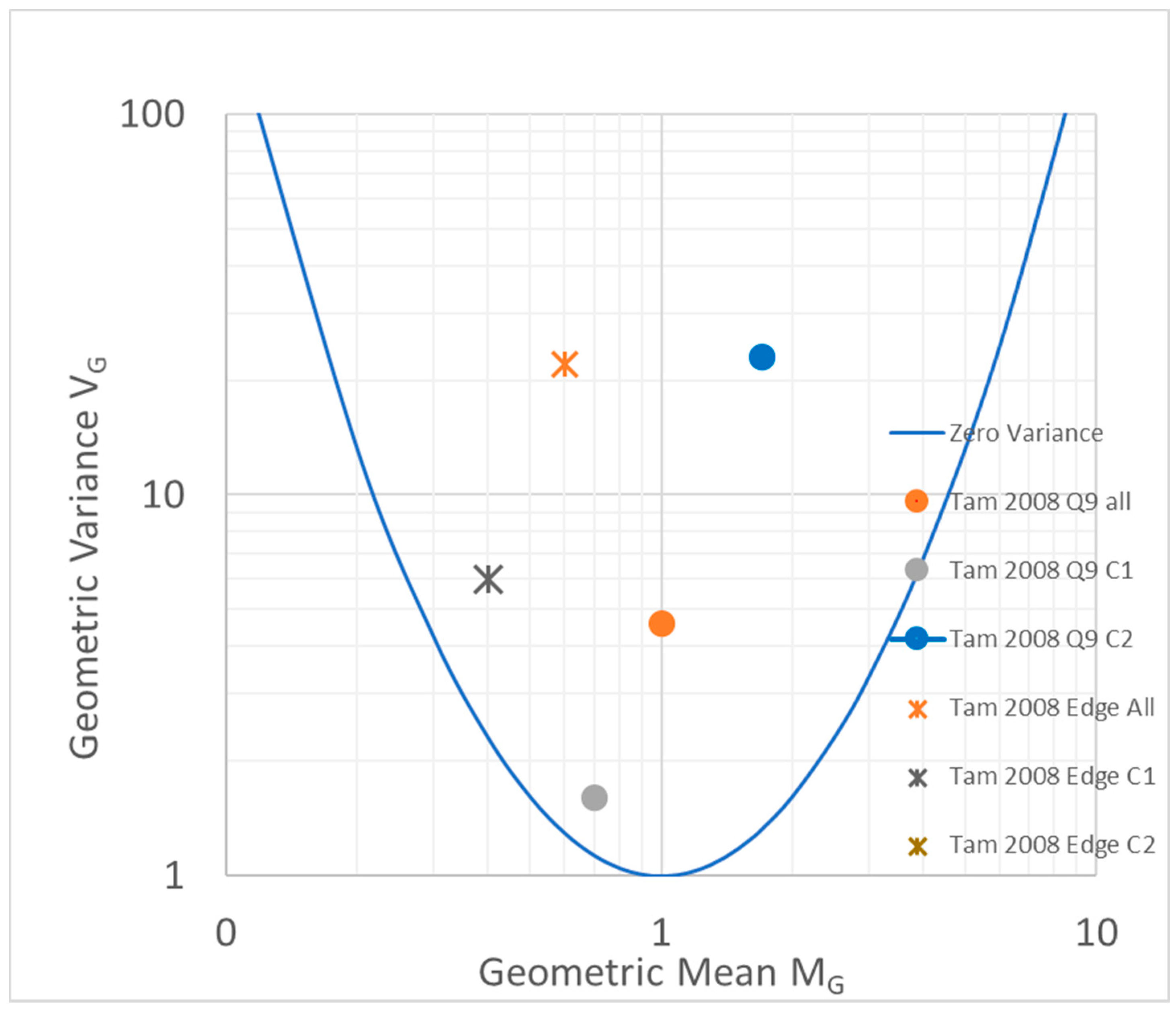
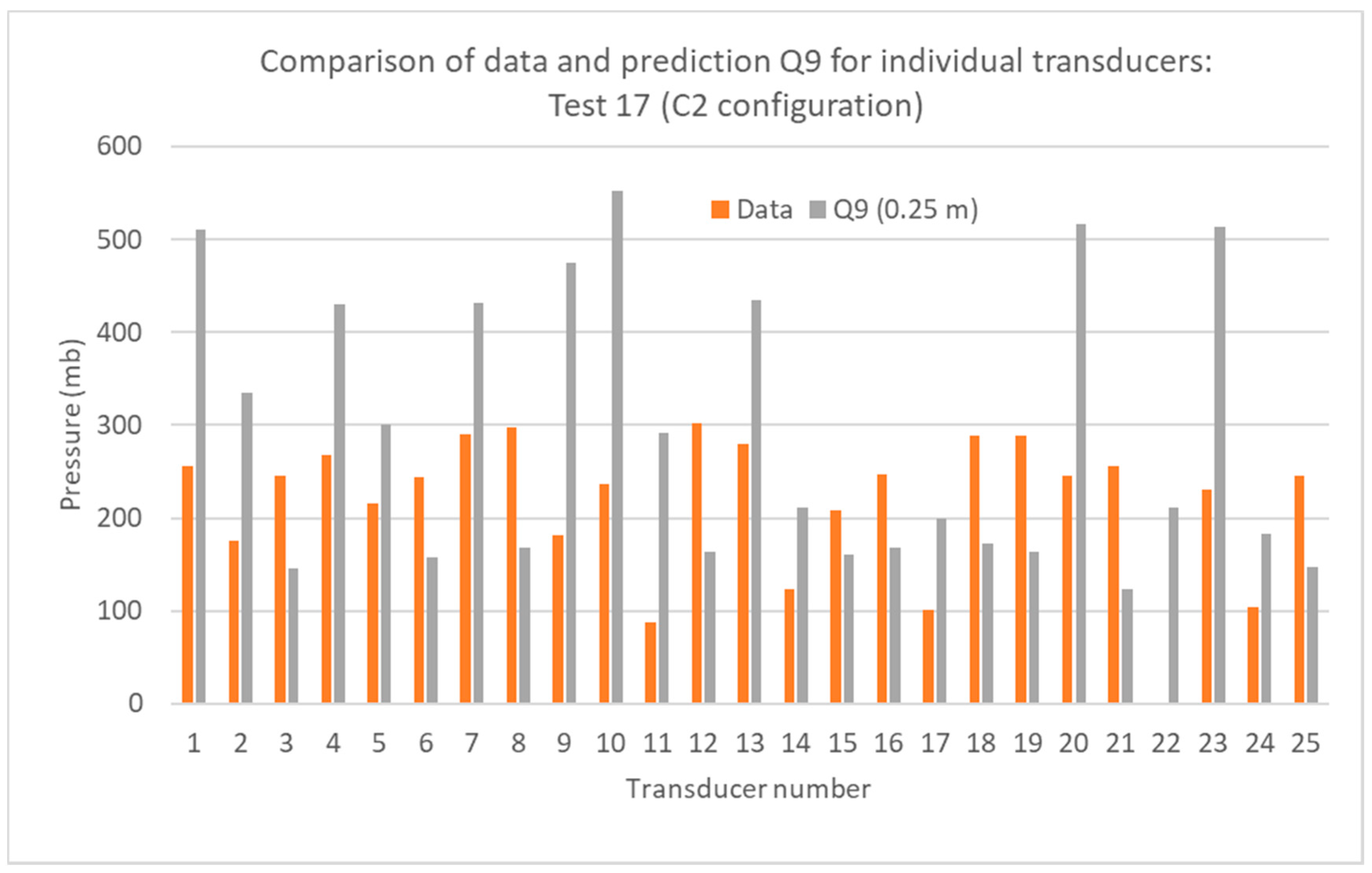
| Source | Hansen et al., 2013 [3] | Phase 3B Report [17] | ||
|---|---|---|---|---|
| MG | VG | MG | VG | |
| All | 0.73 | 12.2 | 0.68 | 11.7 |
| C1 only | 0.38 | 3.50 | 0.46 | 2.73 |
| C2 only | 1.17 | 26.5 | 1.10 | 63.6 |
| Grid Sizes | 0.5 m | 1 m | 1.33 m | |||
|---|---|---|---|---|---|---|
| MG | VG | MG | VG | MG | VG | |
| All | 0.68 | 11.7 | 0.54 | 18 | 0.30 | 32 |
| C1 only | 0.46 | 2.73 | 0.34 | 15 | 0.21 | 25 |
| C2 only | 1.10 | 63.6 | 1.0 | 22 | 0.45 | 42 |
| Maximum P | Average P | |||
|---|---|---|---|---|
| MG | VG | MG | VG | |
| All | 1.0 | 4.6 | 0.9 | 3.7 |
| C1 only | 0.7 | 1.6 | 0.7 | 1.7 |
| C2 only | 1.7 | 23 | 1.6 | 12 |
| Grid Size—0.5 m | Grid Size—0.25 m | |||
|---|---|---|---|---|
| MG | VG | MG | VG | |
| All | 0.6 | 13.7 | 0.6 | 7.5 |
| C1 only | 0.3 | 14.3 | 0.4 | 7.7 |
| C2 only | 1.5 | 12.7 | 1.2 | 7.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tam, V.H.Y.; Tan, F.; Savvides, C. A Critical Review of the Equivalent Stoichiometric Cloud Model Q9 in Gas Explosion Modelling. Eng 2021, 2, 156-180. https://doi.org/10.3390/eng2020011
Tam VHY, Tan F, Savvides C. A Critical Review of the Equivalent Stoichiometric Cloud Model Q9 in Gas Explosion Modelling. Eng. 2021; 2(2):156-180. https://doi.org/10.3390/eng2020011
Chicago/Turabian StyleTam, Vincent H. Y., Felicia Tan, and Chris Savvides. 2021. "A Critical Review of the Equivalent Stoichiometric Cloud Model Q9 in Gas Explosion Modelling" Eng 2, no. 2: 156-180. https://doi.org/10.3390/eng2020011
APA StyleTam, V. H. Y., Tan, F., & Savvides, C. (2021). A Critical Review of the Equivalent Stoichiometric Cloud Model Q9 in Gas Explosion Modelling. Eng, 2(2), 156-180. https://doi.org/10.3390/eng2020011






