Conundrum of Hydrologic Research: Insights from the Evolution of Flood Frequency Analysis

Abstract

Given the apparent gap between scientific research and engineering practice, this paper tracks the dominating perspectives that have shaped the growth of hydrological research. Based on five eras, dominated with specific paradigms and/or ideologies, this paper highlights the punctuated growth of flood frequency analysis comparative to the enormous progress made in hydrological modeling can be claimed by the 20th century. The historical narrative underpinning this inquiry indicates that progress in hydrological understanding can be characterized by two contrasting claims: modeling breakthroughs and inconclusive results. Contradicting statistical assumptions, complex modeling structures, the standardization of specific techniques, and the absence of any unified physical meaning of the research results brought an apparent conflict between the scope of hydrologic research and the scope of end users, i.e., civil engineers. Some hydrologists argue that the debates associated with hydrologic progress, i.e., the evolution of statistical methods, dating back to the 1960s remain unaddressed, with each era introducing additional uncertainty, questions, and concerns. Progress, for it to happen, needs synthesis among scientists, engineers, and stakeholders. This paper concludes that, in a similar way to how physicists acknowledge the conflicts between quantum and Newtonian physics, hydrology too can benefit from acknowledging divergent principles emerging from engineering practice. While many advanced analytical tools—though varied in form—are grounded in the assumption that past data can predict future conditions, the contrasting view that past data cannot always do so represents a key philosophical foundation for resilience-based civil engineering design. Acknowledging contrasting philosophies describing the nature of reality can help illuminate the conundrum in the scope of hydrological research and can enable synthesis activities aimed at ‘putting the puzzle together’.

1. Introduction

Throughout the 20th century, notable progress has been made in understanding hydrology. However, unlike groundbreaking discoveries such as Darcy’s law, rational method [1], and the law of evaporation [2], there have been relatively few truly revolutionary breakthroughs in the field of hydrology [3] in last thirty or forty years. Furthermore, it appears that scientists and engineers are increasingly pursuing separate paths as hydrology has become a part of geoscience [4] rather than an appendage of engineering. This shift is evident in recent hydrological reviews that underscore the importance of surface–groundwater interactions, one of the key themes in geoscience research [5,6]. Indeed, the practice side of the hydraulic engineering community may be seen as conservative and resistant to innovation, whereas on the other side, the proliferation and fragmentation of the scope of hydrologic research become apparent.

Concerning engineering applications, some do argue that focusing on fulfilling engineering and societal requirements hinders progress in hydrology [7]. Criticism is directed towards an excessive emphasis on refining the design parameter, such as the return period of a probable maximum flow, rather than the concept, with concerns raised that adhering to an incorrect concept may still yield seemingly satisfactory results [7]. The evolving science of hydrology, therefore, strives to offer a deeper comprehension of the underlying physics [3] rather than solely concentrating on a singular design parameter for hydraulics. In contrast, it is argued that addressing social needs acts as a positive driving force for progress [3]. For instance, the practical necessity for regional flood estimation has spurred progress in comprehending the influence of climate change on regional flood dynamics [3]. With humans assuming a pivotal interactive role, criticism is directed towards the fact that the social and/or application dimension is not explicitly integrated within the geoscience framework [8].

Given the contrasting paradigms of hydrology, this paper tracks and discusses the achievements and disenchantments of hydrologic research throughout the 19th and 20th centuries. There are studies [9,10,11,12] that provide an account of hydrologic advances, with very few studies that delve deeply into the debatable progress of hydrology [3,7,13]. This review paper provides a historical narrative of hydrologic progress underpinning the scope of flood frequency analysis, a critical tool for engineering design. The paper highlights and/or speculates five eras, each dominated by specific paradigms and/or ideologies shaping the scope of hydrologic research. The overarching goal of this review is to trace how hydrologic science has evolved through shifting paradigms, gradually moving away from its original focus on flood frequency analysis, the paradigm that once defined the discipline. The specific objectives of this review paper are to (i) provide a concise narrative of different eras in hydrologic research, highlighting both achievements and disenchantments; (ii) examine the evolving scope of flood frequency analysis; and (iii) identify the key conundrums that continue to define the scope of hydrologic research.

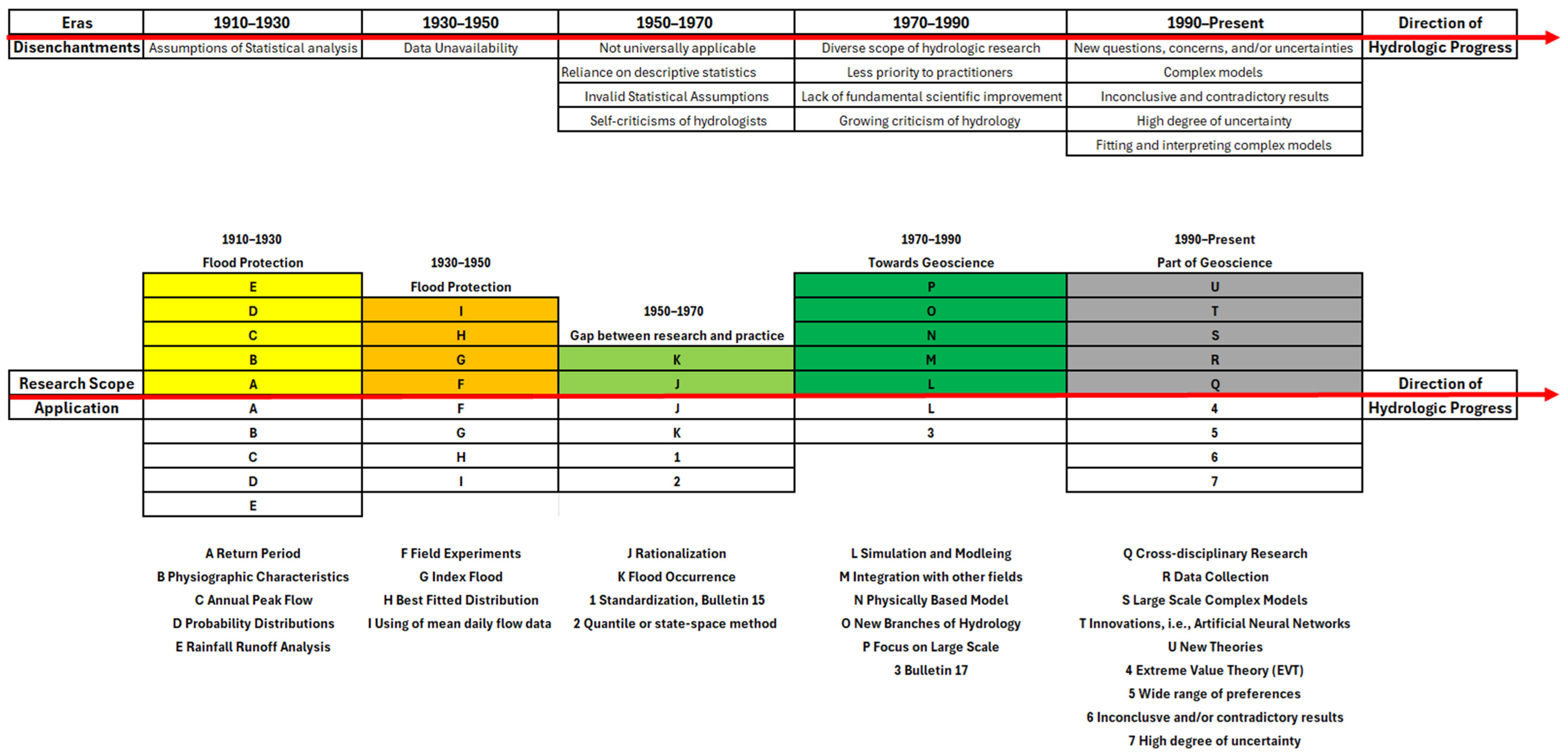
2. Eras of Achievements and Disenchantments

The progress made in hydrology over the past century can be interpreted in various ways. In relation to the growth of flood frequency analysis, progress appears to be divided into five distinct eras—representing specific achievements and disenchantments—defined by dominant paradigms that shaped the field (Figure 1). The eras suggested by earlier studies [3,14] were adapted and extended to the present day to represent two distinct claims of hydro-logic progress: modeling breakthroughs and inconclusive results.

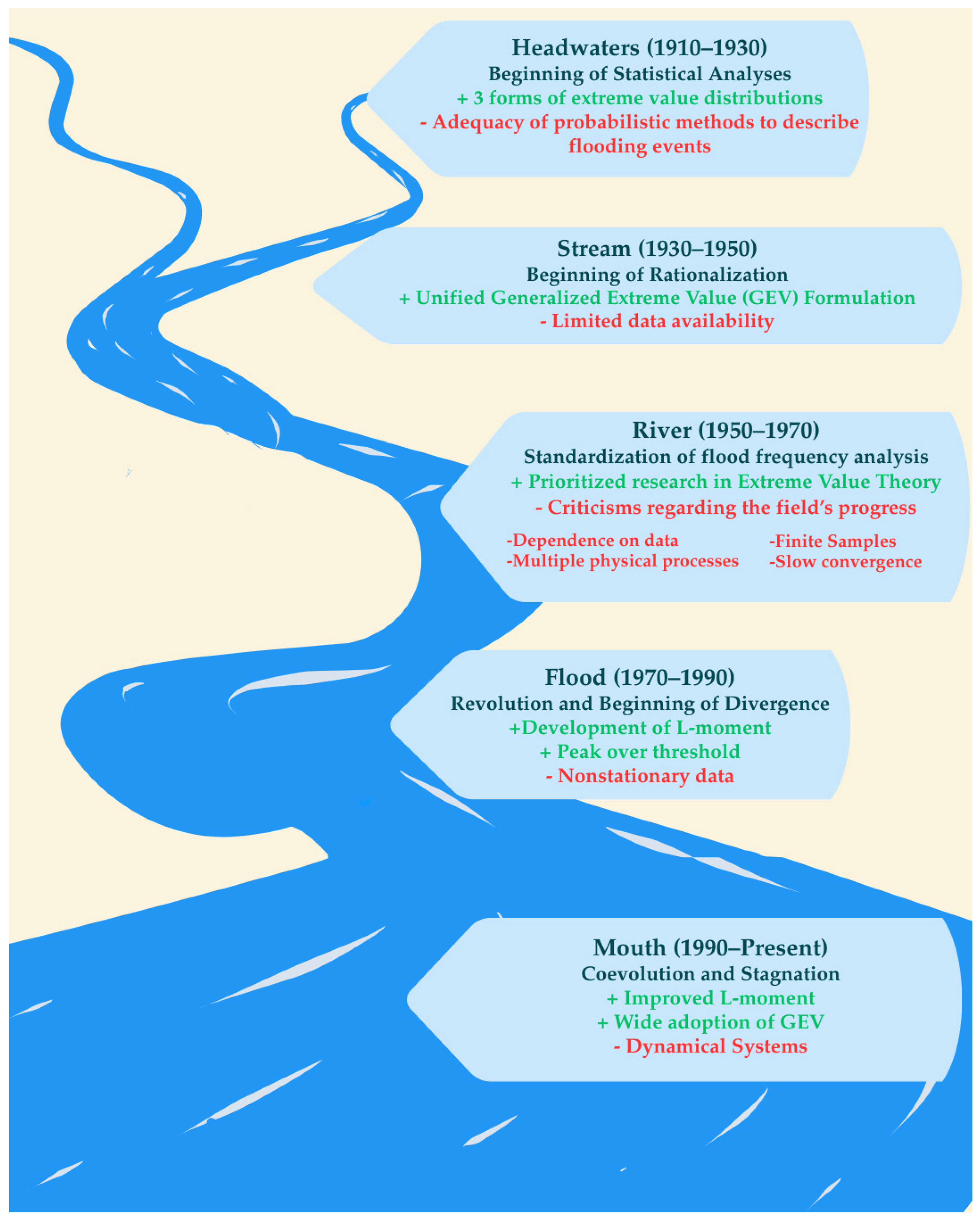
2.1. Beginning of Statistical Analyses (1910–1930)

At the beginning of the 1900s, with the availability of stream gauges and rain gauges, national-scale hydrological networks were established [15]. With data from stream gauges, statistical flood frequency analysis arguably started with a pioneering paper in 1914 [16]; the work attempted to relate the discharge of a specified return period to the drainage area [16]. In addition, two other formulas were presented in the work, one relating annual maximum daily flows to drainage area and one relating annual peak flows to maximum daily flows [16]. The work also initiated the approach of developing a relationship between the peak flow coefficient, defined as the ratio of the instantaneous peak and the corresponding mean daily flow, and the physiographic characteristics of the basin [16]. The concept of probability paper was also introduced in 1914 [17]; in the corresponding work, the use of the lognormal (LN) distribution was proposed as a model for peak flows. Later, this suggestion was revised; in the revised work, it was suggested to use a three-parameter distribution including skew while using the logarithmic probability paper [18]. The use of the log-Pearson type III (LP3) distribution was later deemed more appropriate because the LN distribution, which is a special case of the LP3 distribution with a log-space skew of zero, was commonly believed to be a reasonable model for annual maximum flood flows [19]. Also, the concept of the geologic dating of rare floods emerged in this era, introducing the use of tree-ring evidence to extend flood histories for extreme-event analysis [20].

Following the pioneering works on probabilistic analyses, specific debates began focusing on (1) how to appropriately relate the discharge to the physiographic and/or watershed characteristics [21] and (2) how to select an underlying probability distribution that fits data across different regions of the United States [21]. There were also dissenting voices raised against the adequacy of probabilistic methods to describe the flood events [22]. Nonetheless, the acceptance of probabilistic methods had been established by the end of this era, particularly because of the clear benefits to society, with more reliable flood protection measures and reduced damages [3].

Although statistical flood frequency analysis was the key focus of hydrologists in this era [3], the work on rainfall–runoff analysis also gained momentum. In fact, one of the most widely used models, the Green-Ampt model, was introduced in 1911 [23]. The Green-Ampt model was a physically based model, which represents the infiltration process assuming a homogeneous soil profile and a uniform distribution of initial soil water content. After the original model was presented [23], the Green-Ampt model was modified by scientists [24]. This technique is still used in the conceptual model, the National Weather Service River Forecasting System (NWSRFS) [25].

2.2. Towards Further Understanding and Beginning of Rationalization (1930–1950)

The debates about the underlying probability distribution continued in this era. In a classic work on flood frequency analysis, data were plotted on probability paper, logarithmic probability paper, log-log, semi-log, and Cartesian coordinate paper [26]. Nonetheless, no conclusion was made as to the proper procedure [26]. It became apparent that the compilation of more data is essential before making some sort of correlation of results [26]. Later, in the 1940s, the United States Geological Survey (USGS) adopted the Weibull plotting position and plotted annual peak flows on Gumbel probability paper [27].

A few key developments were made in using the sequence of mean daily flow data to estimate the peak flow [26]. In these works, the ratio of peak flow to maximum mean daily flow was represented as a function of ratios of maximum daily flow to preceding day flow and maximum daily flow to succeeding day flow [26]. Further progress was made with the development of the index flood method, in which a non-dimensional flood frequency curve was obtained for a homogeneous region by scaling the floods of a given frequency by the index flood, for instance, the mean annual flood [28]. The index flood is then related to the drainage basin characteristics, particularly drainage basin area [28].

Following the index flood method, the USGS began producing flood frequency reports state by state based on the index flood method [21]. However, larger drainage areas were found not to fit the regional relations, and separate relations were developed for use along the major rivers in a state [21]. Several alternative relationships for discharge were proposed in the literature during this era, and the various factors affecting the floods in different regions of the United States were discussed extensively [26].

Given the inadequacy of statistical analyses and the presence of sites with little or no history of stream gauging, the rationalization of hydrological processes began to address the pressing need for erosion control and forest management [3]. Field experiments were carried out to understand and derive cause–effect relationships. The experiments resulted in the development of Horton’s infiltration equation [29]. The Horton equation [29] is one of the most widely used semi-empirical models. The classical exhaustion process in nature was used in the Horton equation to derive the infiltration capacity variation with time during rain. Although the Horton equation is semi-empirical, it reveals a similar pattern of infiltration rate decline from the initial infiltration rate to the stable infiltration rate as other physically based models such as the Green-Ampt model [30].

2.3. Towards Standardization of Flood Frequency Analyses (1950–1970)

The statistical debates and concerns from the 1950s and 60s influenced various federal agencies to initiate programs and/or projects. For instance, a research project on flood frequency analysis, led by the USGS, was established in 1956 [31], where the issue of selecting an appropriate plotting position was reinstated. Following this work, the USGS embraced the annual flood series instead of the partial-duration series for flood frequency analysis [31]. The USGS also adopted the Weibull distribution [31]. Nonetheless, it was noted that larger drainage areas did not conform to general relationships, and a single non-dimensional flood–frequency relation was not universally applicable. Consequently, it was asserted that flood frequency curves for recorded stream flows should not be extended much beyond their period of record [31]. The need to investigate the relationships between flood frequency and magnitude under different conditions, such as drainage basin features and climate [31], was also acknowledged. Later works from the USGS introduced the quantile or state-space method [32,33]. In the quantile method, the flood–frequency relations for each measured site are estimated, and values are picked off at chosen probabilities of occurrence, or quantiles; the quantile flows are then correlated with basin characteristics [32,33].

Another development, perhaps the most significant, was the establishment of the Water Resources Council (WRC), which was tasked with reviewing frequency analysis methods and recommending best practices for federal agencies. The WRC’s findings were published in Bulletin 15 in 1968 [34], where they tested six probability distributions: Gum-bel, log-Gumbel, two-parameter LN, three-parameter LN, two-parameter gamma, and LP3 [34]. The report recommended the log-Pearson Type III distribution for logarithms of annual peak flow data. It also referenced Bulletin 13 [35] for parameter estimation procedures. In Bulletin 13 [35], it was noted that the method of moments was the most common for parameter estimation with the Gumbel distribution, and the LP3 distribution was typically fitted using a log-space method of moments estimator that included regional skew information.

With Bulletin 15 [34], the need to analyze floods based on their frequency was widely recognized and standardized. Such standardization was widely accepted primarily due to economic considerations related to the planning and design of structures [36]. The standardization of the magnitude–frequency relationship of floods was crucial for making hydro-economic decisions for rapidly developing urbanization. Additionally, the growing public demand for flood insurance highlighted the importance of economic design, which relied heavily on understanding the magnitude–frequency relationship of floods. With the wide acceptance of the statistical approach, specific hydrologic principles explaining flood occurrences, such as the flood hydrograph, were also widely accepted and deemed well understood. Hydraulic engineers still apply these principles to forecast and reconstruct flood events based on prior and current physical and meteorological conditions and determine the peak discharge or flood volume of a specific frequency using statistical approaches.

With the widespread use and acceptance of statistical methods, certain criticisms arose regarding the field’s actual progress [37]. The criticism [37] particularly focused on the persistent reliance on maximum precipitation and maximum probable precipitation, the lack of research on the actual structure of extreme events, the use of long-range statistical forecasts based solely on meteorological data, and the reliance on descriptive statistics. The primary criticism was that hydrology was seen more as an appendage of engineering rather than a science, which hindered its development and progress [37].

Despite the self-criticisms of hydrologists, progress was made in the rationalization of hydrological processes. One of the key developments was the SCS Curve Number methods [3]. The Soil Conservation Service Curve Number (SCS-CN), an empirical method, was developed in 1954 and was publicized by the Soil Conservation Service (now called the Natural Resources Conservation Service), U.S. Department of Agriculture. The concept of the SCS curve number has since been revised in 1964, 1965, 1971, 1972, 1985, and 1993. The primary reason for its wide applicability and acceptability lies in the fact that it accounts for most runoff-producing watershed characteristics: soil type, land use/treatment, surface condition, and antecedent moisture condition.

2.4. Revolution and Beginning of Divergence (1970–1990)

The 1960s marked the beginning of the computer revolution, significantly advancing hydrologic modeling in the subsequent years. The advent of faster computers enabled numerical solutions of the partial differential equations fundamental to hydrology and te development of sophisticated data collection methods. Major breakthroughs in this era included the simulation of the entire hydrologic cycle [38]; the development of two- and three-dimensional models [39]; the simultaneous simulation of water flow, sediment, and pollutant transport [40]; the integration of hydrology with geomorphology for detailed river basin representation [41]; and the development of physically based distributed models [42], among others. Theories from fluid mechanics, statistics, information theory, and mathematics were employed and became part of hydrology, such as catastrophe theory [43]. As a result, new branches of hydrology were born, such as digital or numerical hydrology and statistical or stochastic hydrology [44,45]. In the context of climate change, a global view of hydrology, with a much larger scale, was also introduced [46], which was supported by new remote sensing products becoming available.

In the following years, several important hydrologic models were developed in the U.S., each evolving into fundamental tools used in the field today. The key models include HEC-1 [47], which in its current form is HEC-HMS (Hydrologic Modeling Simulation), SWMM (Storm Water Management Model) [48]; NWS-RFS (National Weather Service River Forecast System) [49]; SSARR (Streamflow Synthesis and Reservoir Regulation) System [50]; and the USGS Rainfall–Runoff Model [51], which later became the PRMS (Precipitation Runoff Modeling System) [52].

With the advent of the digital computing era, stochastic models of discharge were developed as an alternative means of estimating flood frequencies, particularly in situations where long discharge records were unavailable to support the reliable fitting of traditional flood frequency distributions. These hydrologic models enabled the generation of synthetic time series representing potential future inputs, often by modifying historical records to make them consistent with anticipated future conditions. They also made it possible to simulate discharge hydrographs, rather than being limited to monthly or annual summaries of flow data. The origins of stochastic input generation for flood frequency estimation can be traced to the seminal work in 1972 [53], which emphasized the importance of relating peak streamflow statistics to the underlying statistics of climatic and watershed parameters. This pioneering research established the theoretical foundation for connecting stochastic representations of rainfall and catchment behavior with probabilistic estimates of flood magnitude and frequency. However, as subsequent works demonstrated, the challenge lies in the assumptions required to construct such hydrologic models [54]. Issues such as unrealistic or unstable outputs, limited availability of observational data, the complex scaling behavior of rainfall and discharge processes, and constraints in model validation introduce significant uncertainties [54]. These limitations continue to complicate the practical application and general acceptance of hydrologic models and/or stochastic approaches in flood frequency analysis.

With the initiation of the diverse scope of hydrologic research, the need to have a unified flood frequency analysis heightened, particularly in relation to the different probability analyses used by the U.S. Army Corps of Engineers (USACE) and the statistical probability standards adopted by the Federal Emergency Management Agency (FEMA) [55]. The initiatives taken led to the adoption of specific administrative procedures for flood frequency analysis, as reported in Bulletin 17 [56]. Bulletin 17 [56] provided recommendations for the treatment of outliers, the estimation of the regional skew, the use of historical flood information, and the use of log-Pearson Type III distribution for annual peak flows. With this assertion, the USGS employed LP3 distribution to determine quantiles for its regression equations [56], and FEMA mandated LP3 distribution for flood insurance studies. Another consequence of the choice of using LP3 distribution was a plethora of research works on the properties of LP3 distribution and its parameters, particularly the estimation of a value of skew to use for either an at-site analysis or a regional analysis [57,58,59,60]. Bulletin 17 was later succeeded by Bulletin 17A, which was subsequently replaced by Bulletin 17B in 1982 and Bulletin 17C in 2018. Nonetheless, each updated Bulletin recommends the use of log-Pearson Type III distribution, and the estimation of the distribution parameters based on sample moments.

Although the field of flood frequency analysis expanded over time, at the end of the revolution era, it became a topic of less priority for many hydrologists. By the late 1980s, a gap between research and practice in flood studies had become apparent. It was argued that researchers were not giving enough attention to issues that mattered to practitioners [61]. Criticisms emerged about the assumptions used in statistical analyses, which were often invalid [7,37]. It was clear that fundamental scientific improvements were necessary before methods like the “best fit” distribution could be effectively applied in flood frequency analysis for engineering purposes. Additionally, growing criticism of hydrology as simply an offshoot of engineering spurred further changes [7]. Over time, hydrology evolved into a distinct branch of geoscience, moving away from its earlier association with engineering. This shift in perspective is also evident in the citation analysis study performed in 2015 [62].

2.5. Coevolution and Stagnation (1990–Present)

At the beginning of this era, hydrology positioned itself as a branch of Geoscience [4]. The integration of various cross-disciplinary areas within the field of hydrology was promoted. The key areas of integration include climatology [63], geomorphology [64], hydraulics [65], soil physics [66], geology [67], ecosystems [46], and social science [68], among others. The development of sophisticated remote sensing tools made it possible to acquire spatial data for larger areas. With large-scale spatial data, modeling at large spatial scales, such as a large river basin like the Mississippi, and at small temporal scales, such as seconds or minutes, was undertaken [63]. Likewise, geographical information systems (GIS) were developed for processing huge quantities of raster and vector data. With high quantities of data, the appeal of more complex models intensified to provide detailed information about specific points within the catchment and different components of the hydrologic cycle [67]. The most recent innovations include artificial neural networks, fuzzy logic, genetic programming, wavelet models [69], and the integration of entropy theory [67], copula theory [70], chaos theory [71], and network theory [71]. Each new technological advancement has contributed to substantial progress, leading to a sense of euphoria. However, each new approach and/or theory implemented created new questions, concerns, and/or uncertainties that could not be resolved [3]. Nonetheless, the trend of developing more integrated and sophisticated models can be expected to continue.

On the other hand, the literature on flood frequency analysis reveals a wide range of preferences for specific distribution and parameter estimation methods [72,73,74,75,76,77,78,79], resulting in inconclusive and occasionally contradictory recommendations. For instance, while some research highlights the stability and reduced bias of the L-moments method [76,77], others note the need for statistical indicator corrections for L-moments due to variations in series length and the non-linear nature of parameter estimation [80]. The impact of including reliable historical records in flood frequency analysis yields mixed outcomes, with some studies reporting an increase in upper quantiles [81] and others a decrease [82]. Recently, a flood frequency analysis was undertaken [83], updating the methods and data used in the 1980s; it was concluded that a high degree of uncertainty associated with flood estimation remains unresolved [83]. These findings were echoed in another study [84]. The uncertainties stemming from the reconstruction of historical and paleo floods also remain unresolved.

It should be noted that the statistical modeling of extreme events has evolved into a specialized branch of statistics known as Extreme Value Analysis (EVA), with significant applications in hydrology [85]. Over time, both the theory and models in this field have advanced substantially, particularly in methodologies for multivariate extreme events [86] and related areas such as spatial [87], temporal [88], and spatiotemporal [89] extreme value modeling. However, the lack of a unified best practice for modeling univariate extremes, along with the challenges of fitting and interpreting complex models with intricate structures, complicates the practical application of these advanced techniques for end users. Here, it is worth noting that efforts to establish a unified practice have continued, as reflected in the recent work in 2024, which addresses the challenges of unifying practices through a comprehensive review and new mathematical developments, most notably the introduction of K-moments, designed to advance risk analysis of hydrological extremes [90].

In addition to the most recent breakthroughs in statistical flood frequency analysis, the field of stochastics also represents major accomplishments. Hydrologists have successfully bridged advanced mathematical theories, such as fractals and chaos, with practical hydrologic applications to address the inherent uncertainty in rainfall–runoff processes. A recent study, for instance, analyzed streamflow behavior across eight orders of magnitude and highlighted that, despite variations in climatic regimes and hydrological conditions, certain stochastic similarities persist [91]. These underlying patterns can enable hydrologists to discern the hidden structure of the target process.

3. Scope of Flood Frequency Analysis

Research and practice in flood frequency analysis primarily focus on determining the best-fitting probability distribution for annual peak flow data. Nonetheless, three key perspectives can be identified in statistical research that govern the goal and scope of the flood frequency analysis: (1) investigating the emergence of extreme flood events, (2) unification of extreme value distributions, and (3) identifying the most suitable statistical distribution. The research in Extreme Value Theory (EVT) embodies the interest in exploring counterintuitive behaviors and the emergence of extreme phenomena, going beyond estimation [92]. According to the EVT, the unified Generalized Extreme Value (GEV) distribution is the unique limiting distribution for the normalized maxima of a sequence of independent and identically distributed random variables, and it is widely employed for optimal model fitting [93]. Conversely, a wide range of probability distributions has been proposed and evaluated over time to determine and highlight the suitability of distributions for specific locations. Below, EVT, GEV, and various probability distributions are discussed as three key scopes of current research in flood frequency analysis.

3.1. Research Scope of Extreme Value Theory (EVT)

EVT refers to the statistical theory concerning extreme values, values occurring at the tails of a heavy-tailed distribution. One of the earliest discoveries of heavy-tail phenomena came in the early 1900s when Vilfredo Pareto observed that the distribution of wealth tends to follow a power law distribution. Initially, extreme values were conceptualized as very large values from the tails of normal distributions, not as values from a distribution in and of itself [94]. A separate distribution for extreme values in heavy tails was first proposed in 1927 [95]. In the following year, three asymptotic forms of extreme value distributions were introduced [96], later formally proved in 1943 [97]. As suggested by the Fisher and Tippett theory, for a single process, the behavior of the maxima can be described by the three extreme value distributions—Gumbel, Frechet, and negative Weibull [96]. These distributions were first popularized in the book “Statistics of Extremes” [94]. This book was the first comprehensive review of extreme value theory, detailing the three types of generalized GEV distribution, also known as types I, II, and III.

The Dutch government was probably the first to prioritize research in EVT [98] for understanding and mitigating extreme events, following a devastating storm surge in the North Sea in 1953 that claimed around 1700 lives. Later, EVT gained broader acceptance among hydrologists, largely due to the work of J.R.M. Hosking and his colleagues in the 1980s and 1990s. Hosking, along with J.R. Wallis and E.F. Wood, demonstrated the practical utility of EVT in hydrological frequency analysis, particularly for modeling extreme rainfall and flood events [73].

EVT consists of several key theoretical pillars, each addressing different aspects and justifications of modeling extremes, such as the Fisher–Tippett–Gnedenko theorem (Block Maxima) [96,97], Pickands–Balkema–de Haan theorem (Peaks Over Threshold) [99], Limit Laws and Domains of Attraction [96,97], Second-Order Extreme Value Theory [100], non-stationary EVT [101], multivariate EVT [102], and Bayesian EVT [101], among others. While the Block Maxima approach reduces the data considerably by taking maxima of long blocks of data, e.g., annual maxima, the Peaks Over Threshold approach analyzes excesses over a high threshold. Both approaches have theoretical justifications and can be characterized in terms of a Poisson process, which allows for simultaneous with parameters concerning both the frequency and intensity of extreme events. Theories in relation to the Limit Laws and Domains of Attraction aim to differentiate between light- and heavy-tailed probability distributions and determine the specific type of heavy-tailed distribution. The most popular tests to distinguish heavy-tailed probability distributions include Tail Index Estimation, i.e., the Hill Estimator Test [103]; Graphical and Diagnostic tools, i.e., Q-Q Plot [104]; and tests for Domain of Attraction membership, i.e., Likelihood Ratio Tests [105] and the Anderson–Darling test [106]. Most recent developments in EVT have been extended through second-order methods to improve convergence and bias correction, non-stationary models to account for changing environments, multivariate approaches to capture dependence in joint extremes, and Bayesian frameworks to provide full uncertainty quantification and hierarchical modeling.

While the core objective of EVT revolves around estimating the best-fitting distribution for extremes, its broader research significance lies in uncovering the underlying mechanisms and paradoxical behaviors that govern extreme phenomena. Research in EVT discloses that specific distributions, including heavy- and light-tailed distributions, correspond to specific characteristics and/or governing principles (

Table 1. Understanding heavy- and light-tailed distributions in EVT.

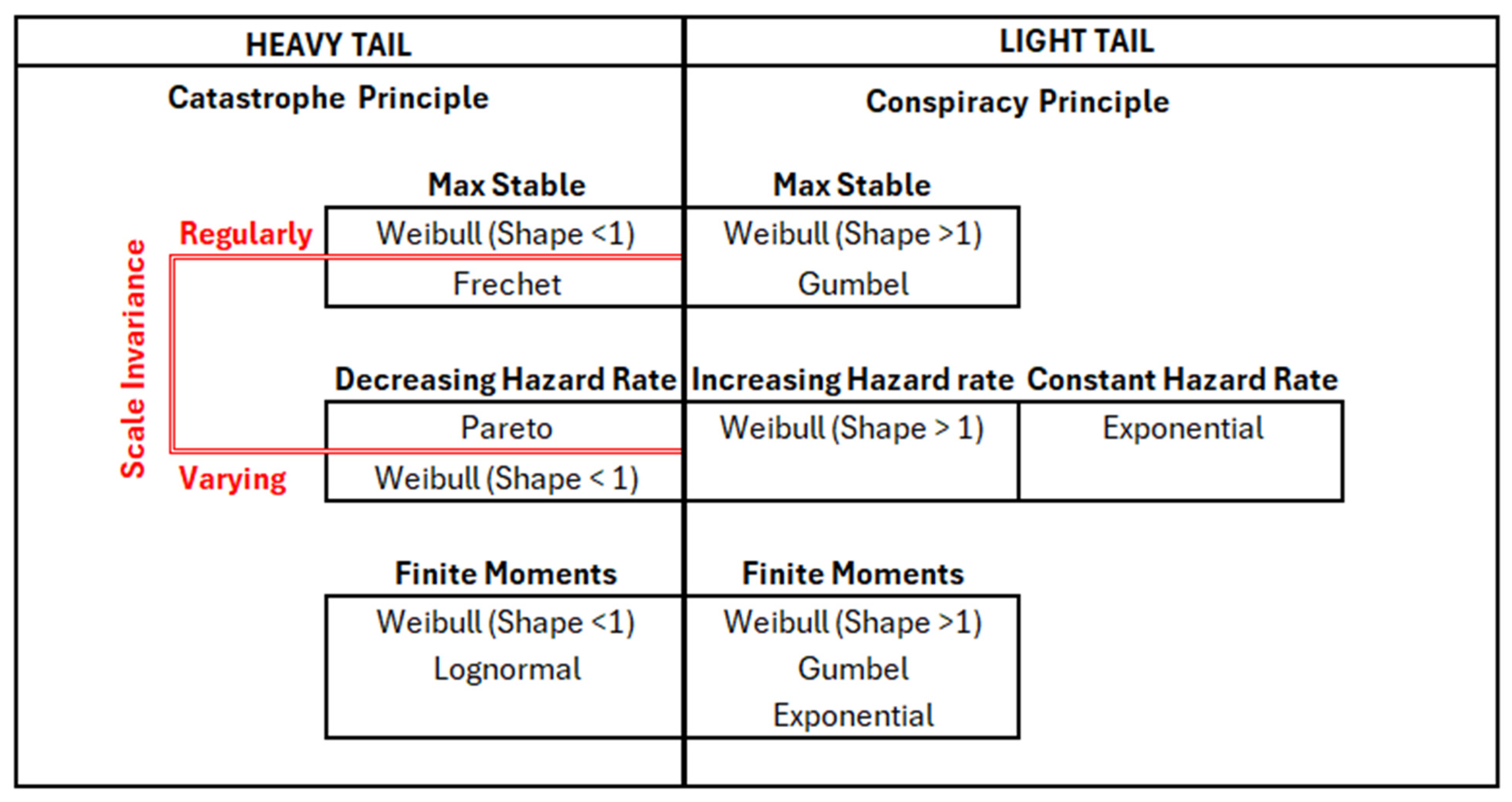
Heavy-Tailed Distributions [92,108,109,110]
Distributions	Specific Characteristics	Disenchantment
Pareto Distribution	Pareto principle Catastrophe principle Decreasing hazard rate with time Scale-invariance (i.e., scale-free) Regularly Varying Distributions Can have infinite variance and/or mean Large values are much more likely to occur than exponential distribution Also known as power law or fat-tailed distribution Decreasing hazard rate with time	No definite definition Flawed identification and measurement Technical complexity Should not be solely relied on for estimation, i.e., Pareto distribution Only useful for exploration analysis of data, i.e., Pareto distribution May be misleading when using the log–log plot as a statistical tool Very difficult to identify precise scale invariance or power law distribution in real observations Difficult to study probabilistic and stochastic models using real data without applying transformations Difficult to verify Catastrophe principle for Weibull and Lognormal distributions Difficult to calculate mean residual life for specific distributions, i.e., Weibull distribution Contrasting assumptions and explanations of heavy-tailed behavior, i.e., Mandelbrot’s optimization-based model versus Simon’s preferential attachment model, preferential attachment model versus optimization-based approaches Classical parametric approaches can be misleading Any estimate should be validated through multiple alternate hypotheses
Weibull Distribution	Catastrophe principle Heavier tail than the Exponential and lighter tail than the Pareto Heavy tail when shape parameter is less than one All moments are finite Decreasing hazard rate with time Max stable distribution
Frechet Distribution	Catastrophe principle Regularly Varying Distributions Max stable distribution Asymptotic scale invariance in relation to the tail of the distribution
Lognormal Distribution	Catastrophe principle Multiplicative process All moments are finite
Light Tail Distributions [108,109,110,111]
Weibull Distribution	Conspiracy principle Decreasing residual life Increasing hazard rate Max stable distribution	No definite definition Flawed identification and measurement
Gumbel Distribution	Conspiracy principle Max stable distribution
Exponential Distribution	Conspiracy principle On the boundary between heavy and light tail distributions One parameter, growth rate Memoryless property Constant hazard rate
Key Terms and Concepts
Heavy-tailed distribution: Tail of the distribution decreases more slowly than the exponential distribution.
Pareto principle: The wealthiest 20% of the population holds 80% of the wealth.
Catastrophe principle: A single, exceptionally large value dominates the sum or event.
Conspiracy principle: Many small or moderate deviations collectively produce an extreme outcome.
Hazard rate: Likelihood of an impending failure with the age of the component.
Regularly varying distribution: Scale invariant and follow power law.
Scale invariance: If the scale (or units) with which the samples from the distribution are measured is changed, then the shape of the distribution is unchanged.
Memoryless property: Regardless of how long someone has already waited, the expected remaining waiting time is the same as if they had just arrived.
Multiplicative process: Situations where growth happens proportionally to the current size.
Max stable distributions: Limiting distributions of extremal processes, and the class of max-stable distributions is made up of three families of distributions—the Fréchet, the Weibull, and the Gumbel.

, Figure 2). For instance, multiplicative processes are fundamentally tied to the emergence of heavy-tailed distributions. Heavy-tailed distributions can also emerge from additive processes, but only when one starts with infinite variance heavy-tailed distributions. Under extremal processes, heavy-tailed distributions can emerge when starting from distributions with finite variance. However, extremal processes and additive processes are not closely connected with heavy-tailed distributions as multiplicative processes. Certain distributions, including the Pareto and Fréchet distributions, display properties consistent with regularly varying distributions (Table 1, Figure 2). Additionally, distributions such as Pareto and Weibull exhibit a distinct characteristic; their hazard rates decrease over time, a feature that can have important implications for risk management strategies (Table 1, Figure 2). Such characterization of distributions, along with the best-fitted approach, can allow for a more reasonable explanation for the most appropriate best-fitted distribution. Since there are many wrong reasons why models may work well [107], it is essential to explain the reason of why a distribution is best fitted with a particular dataset.

Despite a century of mathematical and statistical developments in Extreme Value Theory (EVT), significant controversy and debate persist regarding the identification, measurement, and modeling of heavy-tailed phenomena (Table 1). For example, many early findings in EVT have been proved erroneous as more advanced statistical methods revealed limitations in their assumptions and methodologies [111,112]. In addition, classical approaches of parameter estimation, based on regression and maximum likelihood estimation, have enormous potential for misuse due to the assumption that the data comes from an exact, parametric power law distribution, an assumption that is nearly always false [92]. Therefore, it is crucial to think carefully about whether parametric or semi-parametric analysis is appropriate for the data in question. While many tools are available to help answer the question of whether the parametric or semi-parametric approach is more appropriate, often it is the case that one is left with some uncertainty about which approach to apply. If parametric estimation is appropriate, Maximum Likelihood Estimation (MLE) might be a reliable and effective estimator. However, the fit produced by the MLE should be assessed in two key ways: (1) evaluating its statistical significance through goodness-of-fit tests and (2) testing the power-law hypothesis by comparing it against alternative parametric assumptions using methods such as likelihood ratio tests, cross-validation, or Bayesian approaches. When parametric analysis is unsuitable, the situation becomes more complex, leaving two main approaches: (1) applying parametric tools to censored data or (2) employing extremal estimators. In practice, the most reliable strategy is to strengthen confidence in estimates by seeking consistency across different estimation methods.

3.2. Application of Generalized Extreme Value Distribution (GEV)

A foundational advancement in EVT was the unification of the three extreme value distributions under a GEV framework [113]. This pivotal work shifted the field’s focus from the probabilistic classification of limits to statistical modeling and application. In the ensuing decades, research concentrated heavily on parameter estimation and inference for the GEV distribution, leading to the development of various methods including Maximum Likelihood Estimation (MLE) [94], the Method of Moments (MOM) [94], Probability Weighted Moments (PWM) [114], and later, Bootstrap techniques [115] and Bayesian methods [116]. More recently, there has been a growing trend toward using hybrid or mixed approaches [117] and machine learning methods [118], with the Informer model emerging as one of the latest machine learning applications for modeling rainfall–runoff processes [119]. Despite this diversification, a consensus on a superior estimator has never been established. Each new method was typically developed to address the limitations of its predecessors, yet none has wholly supplanted the others [3]. MLE, one of the earliest approaches, remains the most theoretically optimal under standard conditions [116,120]. Also, Probability Weighted Moments (PWM)/L-Moments remains the most widely used method among engineers due to its robustness with small samples and computational simplicity.

With the successful application of parameter estimation methods, i.e., MLE, PWM and L moments, research on extension and/or modification of the GEV distribution accelerated in 1990s. Most of the research was largely motivated by the persistent challenges observed in real-world applications. Some of these challenges had been recognized as early as 1950s, such as limitations arising from finite sample sizes [94], slow convergence [94], and statistical dependence [94]. Subsequently, additional challenges were recognized, including the influence of multiple physical processes [27] and non-stationarity [121], with the complexities of dynamic systems emerging as the most recent concern [122]. Most of the significant research efforts aimed at addressing these issues have taken place during the convolution era (1990 to present) (

Table 2. Eras of euphoria and disenchantment in the growth of EVT and/or GEV.

Era	Euphoria	Disenchantment	Addressing Disenchantment
Beginning of statistical analysis (1910–1930)	Separate distribution for extreme events [100] Three asymptotic forms of extreme value distributions [101]	Adequacy of probabilistic methods to describe the flood events [22]
Beginning of rationalization (1930–1950)	Formally proved Fisher and Tippett theory: Unified GEV formulation [102] Limit Laws and Domains of Attraction [102] First popularized in the book “Statistics of Extremes” [94]	Limitation of available data 1 [26,94]
Standardization of flood frequency analysis (1950–1970)	Prioritized research in EVT [98]	Finite Samples 1 [26,94] Slow Convergence 2 [94] Dependence on Data 3 [94] Multiple Physical processes 4 [32,124] Criticisms regarding the field’s actual progress [37]	Seasonal and Stratified 4 [124]
Revolution and beginning of divergence (1970–1990)	Development of L moment, robustness in small samples [124] Peak over Threshold [99,125]	Non-stationary 5 [121]	Mixed Distributions 4 [126] De-clustering or Extremal Index 3,6 [127]
Coevolution and stagnation (1990–present)	Expanded and formalized L moment [73] Widespread adoption of GEV [123]	Dynamical Systems 6 [122]	Regional Frequency Analysis 1 [73] Application of L Moment 1 [73,123] Time-Varying GEV/GPD Parameters 5 [85] Non-Stationary Models 4,5 [85] Hybrid EVT Models 4 [102] Probability-Weighted Moments (PWM) 1 [114] Practical Development of POT 1,2,3 [115] Bootstrap or Resampling 1,2 [128] Copula and Tail Dependence Model 3 [129] Max Stable Processes 3 [130] Conditional Extreme Models 3,4 [131] Bayesian or Hierarchical 1,3,4,5,6 [132] EVT with Physical Indicators 6 [133] Machine Learning and EVT Hybrids 3,4,5,6 [134]
Key Terms and Concepts
Fisher and Tippett theory: For a single process, the behavior of the maxima can be described by the three extreme value distributions–Gumbel, Frechet, and negative Weibull.
Limit Laws and Domains of Attraction: Aims to differentiate between light- and heavy-tailed probability distributions and determine the specific type of heavy-tailed distribution.
Peak over threshold: Uses all exceedances above a chosen threshold, providing more data and often better estimates of tail behavior and extreme quantiles.
Slow convergence: Maxima or exceedances approach GEV or GPD distributions only slowly with increasing sample size.
Multiple Physical processes: The presence of multiple physical processes (e.g., rainfall–runoff mechanisms, snowmelt, tropical storms, or seasonal climate drivers) can violate EVT assumptions.
Nonstationary: A non-stationary process exhibits trends, shifts, or cycles, meaning its behavior evolves rather than staying stable.
Dynamical systems: A dynamical system describes how the state of a physical system evolves over time according to deterministic laws.

^{1, 2, 3, 4, 5, 6} denotes specific disenchantments and various attempts to address those specific disenchantments.

). Key directions include the development of multivariate GEV models, non-stationary GEV formulations, Bayesian approaches, and hybrid GEV frameworks, among others (Table 2). The key emphasis of this research on improving practical applications likely contributed to the widespread adoption of the GEV during the 1990s [73,123]. The evolution of GEV and/or EVT across different eras, each defined by its own phases of euphoria and disenchantment, is presented in Figure 3.

The rapid progress in GEV research in the convolution era has brought trade-offs (Table 2); although more tools are now available than ever, practitioners must devote considerable effort to selecting the most appropriate one for their task. While the end user’s choice can be informed by criteria such as simplicity, robustness, standardization, interpretability, and theoretical justification, alongside statistical challenges like finite sample sizes, the final decision often remains context-dependent and subject to the practitioner’s judgment. In addition, many recent advancements have yet to fully resolve long-standing challenges, such as slow convergence and finite samples, while new concerns, such as dynamic system behavior, continue to emerge. Recent evidence also suggests that extreme maxima are not always independent, as commonly assumed in the GEV framework [135]. A recent study introduced a probabilistic index based on the likelihood of peak-over-threshold events occurring across multiple temporal scales, which revealed significant clustering of extremes [135]. This behavior was linked to the persistence inherent in the parent process, indicating that traditional independence assumptions may overlook important temporal dependencies [135]. Consequently, alternative mathematical approaches are needed to properly account for such hidden persistence in extremes. Future research should therefore focus on uncovering the stochastic properties of extremes in natural processes [135], where dependent mechanisms manifest across various time scales and continue to challenge conventional GEV assumptions and practices. Ultimately, balancing resource requirements with correctness and complexity remains a central concern in applying GEV methods.

In summary, the history of GEV research reflects a cycle in which each wave of innovation is accompanied by moments of disenchantment. Yet, the steady stream of advances has continued to expand GEV applications, often aimed at addressing persistent challenges. While in some countries, i.e., Europe and Australia, GEV has become the primary tool for flood frequency analysis, other agencies—particularly in the United States—have favored alternative methods, most notably the log-Pearson Type III distribution.

3.3. Performance of Probability Distributions

At present, a wide variety of probability distributions are available to model the statistics of flood events [136]. The most common theoretical probability distributions have either two or three parameters, since goodness-of-fit (GOF) measures, such as the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC), penalize models for overfitting [137]. Compared with hypothesis tests, information-based criteria perform better at extreme upper-tail events, which is the focus of flood frequency analysis [138]. However, higher orders are sometimes used, as evidenced by the four-parameter generalized gamma distribution or the Burr distribution, which have the advantage of more fully defining the behavior at the tails of the distributions [136,139]. In fact, a recent global-scale analysis of key hydrological cycle processes found the truncated mixed Pareto–Burr–Feller distribution to be both theoretically sound and practically applicable across thousands of rainfall and runoff records worldwide [140]. The study applied specific methods to account for variations in record length and seasonality among stations [140]. Because parameter estimation can be a computationally intensive process, two-parameter distributions have the advantage of requiring estimation of only two parameters and are thus more computationally economical [139]. A disadvantage of these distributions is that when estimating their parameters, it is not possible to calibrate their higher-order moments (e.g., coefficient of variation, skewness, kurtosis). Some two-parameter distributions, in fact, have constant values of these metrics (e.g., Weibull, Gumbel, Normal, Exponential Shifted, Fréchet), while others have distinct values of higher-order moments (e.g., Gamma or Pearson III, log-normal, chi, and inverse chi), which gives them an advantage in predicting extreme events which are at the tails of the distributions [139]. Since the method of moments (MOM) requires subjective judgment to find best-fit parameters, the L- and LH-moments methods are sometimes recommended to fit the parameters for two-parameter distributions [139]. Recently, in comparing the use of thirteen two-parameter distributions for stationary flood frequency analysis, it was found that their predictions were bounded by the Fréchet and Rayleigh distributions, which tend to overestimate and underestimate the extreme values, respectively [139]. In the same case study, the log-normal distribution was identified as the best-fitting model for the annual maximum flow data based on thirty-eight years of records from the Siret River in Romania [139].

Three-parameter distributions have a parameter that characterizes the shift in the distribution in addition to parameters for scale and shape, which adds to the flexibility of these distributions in applications across different datasets, such as by regime. In a recent study, the performance of three-parameter probability distributions was evaluated in FFA using annual maximum flow data from ten rivers across Czechia and Poland, covering three basins with records spanning 49 to 133 years [141]. Many datasets exhibited non-stationarity, so Maximum Likelihood Estimation (MLE) was employed for parameter estimation [141]. Despite variations in hydrologic regime (pluvial or nival), catchment area, and sample size, these factors did not significantly affect the results [141]. Among the four tested distributions, most provided satisfactory fits to both PDFs and CDFs, except for the Pearson Type III distribution, which performed poorly for non-stationary data [141].

The optimal model, whether a two- or three-parameter distribution, can be determined according to the specific locations or watersheds where the suitability of specific distributions is being assessed. For example, watersheds of multiple scales in the Blue Nile River Basin of Ethiopia were studied, and it was concluded that the GEV model, a three-parameter distribution, provided the most robust predictions [136]. GEV was also found to perform well in Iraq’s Euphrates River [142], in Canada [143], and in South Africa [144]. On the other hand, it was found that FFA for the Tana River Basin in Kenya performed best with Gamma (Pearson III) or log-normal distributions [137]. Pearson Type III has also been found to be best for maximum flow estimation across China [145]. In fact, the USGS in Bulletin 17C recommends the use of log-Pearson Type III based on numerous studies across the United States [146]. The log-Pearson Type III has also been shown to provide the best predictions in the Danube River Basin of Germany [147].

In summary, three probability distributions—GEV, log-Pearson Type III, and log-normal—are most commonly applied in flood frequency analysis worldwide [144]. However, identifying the best-fitting distribution remains a challenge, particularly when data availability is limited for a given location. To address data scarcity, several approaches have been proposed, including model averaging [148], subsampling and trimming techniques [149], and data simulation based on limited observed records [150], among others. Although Bayesian inference was once considered computationally demanding, it now offers a valuable means of correcting for risk underestimation that may result from fitting statistical distributions to short or incomplete datasets [80]. In situations where hydrologic data is sparse or entirely absent, empirical hydrologic correlations can often provide more practical insights than statistical models [151]. Ultimately, since each probability distribution exhibits distinct strengths and limitations, selecting a single universally optimal model is neither desirable nor feasible in many real-world applications.

4. Conundrum in the Scope of Hydrologic Research

Several decades ago, persistent misconceptions in hydrology were explored [7,37], which remain highly relevant to contemporary hydrologic research. The persistent issues include prioritizing numerical accuracy over conceptual soundness in models, the potential for flawed concepts to yield seemingly reasonable results, the arbitrary nature of statistical models, and the reliance on self-referential systems, among others [7,37]. The use of data-driven Artificial Intelligence models, such as machine learning (ML) models, trained on synthetic data—primarily designed to capture input-output relationships—appears to echo persistent misconceptions from decades past. While ML models can achieve strong performance, they may not always be interpretable, comprehensible, and/or acceptable to all relevant stakeholders. In fact, the applicability of any model becomes complicated if it lacks the ability to go beyond identifying patterns and establish a causal relation. If ML or any data-driven approaches fail to provide a comprehensive explanation of model behavior to the users, focusing solely on how specific inputs influence outcomes for a specific site, they risk perpetuating the same concerns of interpretability that plagued certain statistical models.

A well-designed machine learning (ML) or statistical model should not only produce decisions that are easily understood by all relevant stakeholders but also contribute to the advancement of fundamental system knowledge. This deeper understanding can serve as a foundation for the development of more robust conceptual and physically based models, which is one of the scientific targets for global hydrologic research mentioned within the Panta Rhei Science Plan (PRSP), the International Association of Hydrological Sciences (IAHS) strategic science plan for 2013–2023 [152]. It is often argued that data-driven statistical hydrologic models have played a crucial role in advancing system knowledge, ultimately facilitating the development of more robust conceptual and physically based models; a similar trajectory is expected for modern data-driven approaches [153]. However, pursuits of more comprehensive and physically based models face three significant challenges. Firstly, the acquisition of large volumes of high-quality data—coupled with advanced technologies such as radiocarbon dating, dendrochronology, and mining—can make research costs prohibitively high. Secondly, little work has been undertaken on how large an improvement in the accuracy of hydrologic analysis might be expected so that the scope, goal, and cost of hydrologic research can be optimized. Thirdly, even with optimized resource allocation and the successful development of a more comprehensive physically based model, its practical application remains constrained by the complexity of real-world heterogeneity, the absence of a unified theory for sub-grid scale integration, limitations in solution methodologies, and the challenges associated with dimensionality in parameter calibration [154]. Also, regarding model development, two contrasting goals prevail in hydrology; one advocates for increasingly comprehensive global-scale models [3], while other hydrologists favor simpler simulations grounded in well-understood physical principles [7]. Regardless of individual approaches or goals, hydrologic research must remain attuned to evolving societal needs by aligning agendas with external developments and embracing a philosophy of “connecting the dots” through integrative, cross-disciplinary thinking [3].

Concerns have been raised about elements of reality that have been ignored in the pursuits of hydrology for the past few decades [155], given the absence of unified principles, goals, or standards bridging scientific exploration and applications. In fact, the absence of any groundbreaking advancements or unified theory in hydrology over the past few decades is acknowledged by hydrologists [3]. While scientists continue to develop increasingly complex and advanced models in the pursuit of enhancing system knowledge and predictive capabilities, hydraulic engineers still rely on flood frequency analysis methods dating back to the 1910s. Concerns that arose as early as the 19th century—such as regulated flows, ungauged areas, and common statistical limitations (homogeneity, reliability, and randomness)—remain either inadequately addressed or only vaguely mentioned in current guidelines. In fact, the well-known challenges of statistical flood frequency analysis, which are both statistical and hydrological in nature, are still rarely addressed together [82]. Whereas the proliferation of models and the fragmentation of knowledge have led to an upsurge of inconclusive philosophical debates [156], the problem with the societal application of hydrologic research becomes more aggravated, with inconclusive or contradictory research findings [3].

With apparent trends of fragmentation within hydrologic science and engineering, there is also a significant gap in how the public perceives and understands science and technology. With increasing uncertainties surrounding climate change, hazard events, socio-economic impacts, and limited resources, engineers have already started to shift from risk-based design to resilience-based design [157], with a philosophy that “past data no longer predicts the future”. In resilience-based design, the primary focus is on response and recovery after a failure occurs, rather than solely on assessing the probability of failure, though this remains important. Instead of large-scale, centralized projects, the emerging trend is moving towards smaller, decentralized projects. Such new initiatives within engineering may directly contradict the philosophy that past data can predict the future, thereby undermining the data-driven large-scale approach taken in recent hydrologic endeavors.

5. Conclusions

This review article presents a reflective perspective on the evolution of hydrologic science, tracing its breakthroughs and disenchantments through successive eras of technological progress and shifting societal priorities. From the discussion, the following conclusions can be drawn. (i) The progress of hydrological research can be criticized for the lack of any genuine discoveries in the last few decades, whereas the dominant ideologies and/or paradigms are apparently shaped by technological revolution in the last few decades. (ii) An apparent conflict exists between hydrology as a geoscience and hydrology as an appendage of engineering, particularly in the context of flood frequency analysis, which continues to grapple with limitations first recognized in the early nineteenth century. (iii) To address the proliferation and fragmentation of hydrologic research, accepted paradigms and/or philosophies should be reevaluated and fragmented research findings should be synthesized. Although hydrologic models vary widely, and there is seemingly a proliferation of knowledge, most approaches share the same underlying theoretical principles. For example, data-driven methods operate on the premise that “past data can predict future outcomes”, while statistical analyses treat events as inherently random. Amid seemingly diverse yet philosophically similar, inconclusive, and sometimes contradictory findings, hydrology has continued to drift away from engineering practice. In response, engineers have filled this gap by standardizing specific flood frequency procedures and adopting resilience-based approaches that look beyond historical data, prioritizing societal recovery and response options. To foster truly diverse perspectives, research should embrace alternative philosophies and/or contexts just as physicists recognize the coexistence of contrasting frameworks—Newtonian physics and quantum mechanics—to explain nature. Just as ancient Greek myths—such as the Ogygian and Deucalion floods—once served to explain catastrophic deluges before a major intellectual leap led to the use of Newtonian physics to describe the physical world, hydrology too must make a similar transformative leap [158]. It is essential to reconsider widely accepted theoretical principles and paradigms in hydrology, such as using statistical analysis to explain extreme flood events. Given the growing prioritization of climate change and ecohydrology over other topics, with certain watersheds receiving more attention than others, the shift in interests and/or needs calls for a critical discussion on how to address the gaps left behind in the evolving role of hydrology in engineering applications. Establishing a unified standard, acknowledging the trends in engineering and scientific fields, requires effective collaboration between statisticians, scientists, and engineers from related fields. Tangible pathways for collaboration may include establishing task forces jointly led by research centers, engineering societies, and government agencies; co-designing studies in which stakeholders help define research questions, data needs, and modeling approaches; creating formal mechanisms for comparing, integrating, and synthesizing insights from physically based, data-driven, and statistical models; and adopting frameworks that align scientific modeling with engineering design and community preparedness. Ultimately, regardless of the direction taken by engineers, scientists, or policymakers, it is essential that these decisions are clearly communicated to the public.