A Neural Network Inverse Optimization Procedure for Constitutive Parameter Identification and Failure Mode Estimation of Laterally Loaded Unreinforced Masonry Walls
Abstract
:1. Introduction
2. Materials and Methods
2.1. General
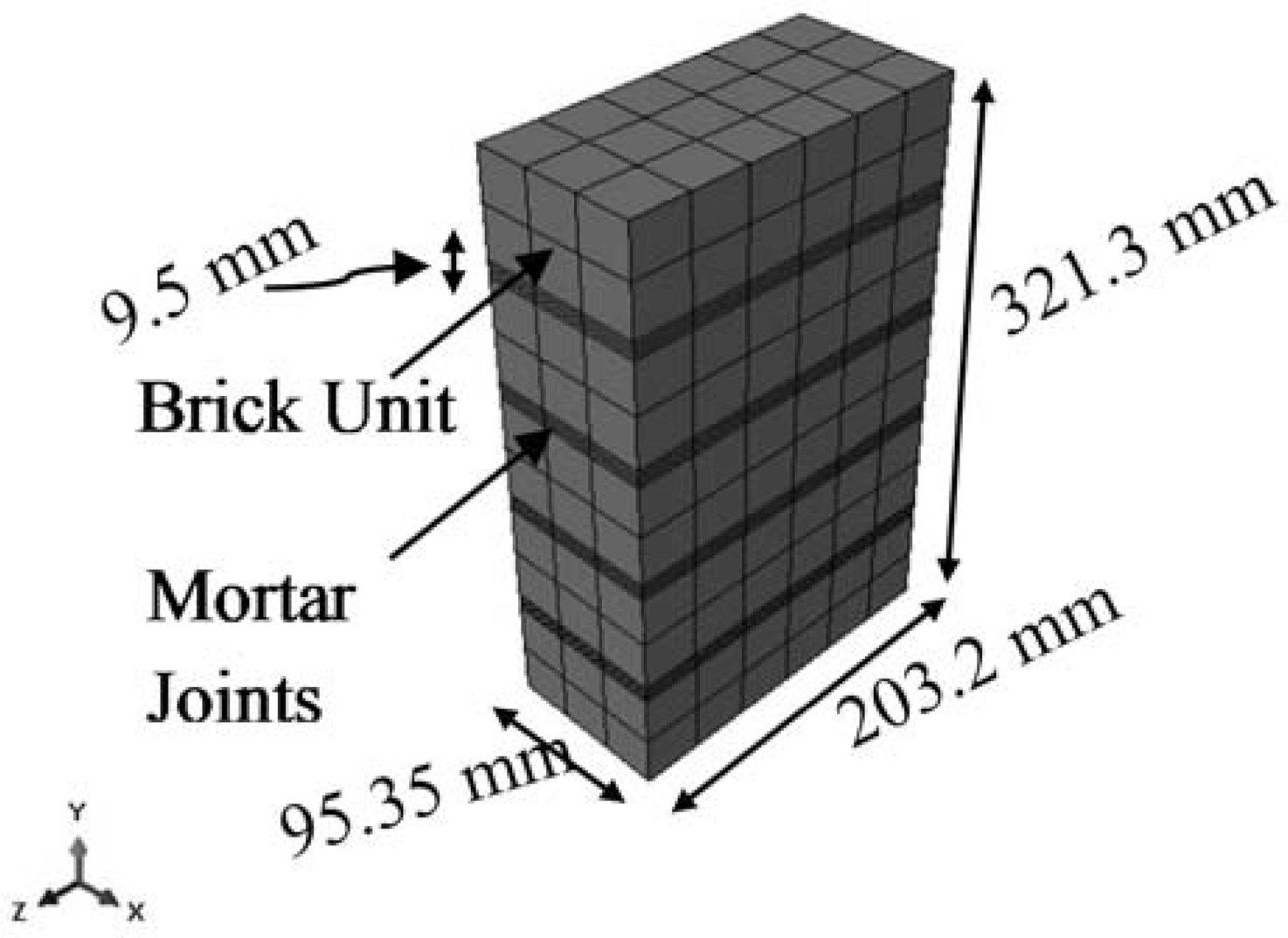
2.2. Description of the Prism Model
- The moduli of elasticity (EC, EM) of the brick and the mortar respectively;
- The dilation angle in the p–q plane of the brick and the mortar ψ;
- The flow potential eccentricity of the brick and the mortar ε;
- The ratio of initial equibiaxial compressive yield stress to initial uniaxial compressive yield stress σb0/σc0;
- The ratio of the second stress invariant on the tensile meridian to that on the compressive meridian at initial yield of the brick and the mortar Kc;
- The Poisson ratio of the mortar, νM, since it has a major influence on the behaviour of masonry;
- The initial yield stress value of brick material in compression, σc0,C for crushing strain equal to 0.0.
- The initial yield stress value of mortar material in compression, σc0,M for crushing strain equal to 0.0.
- The cracking strain in tension, εtf, for failure stress value equal to 0.1σt0, where σt0 is the failure stress value for cracking strain equal to 0.0. σt0 is assumed to be equal to 0.1σc0,C for brick material and 0.1σc0,M for mortar material.
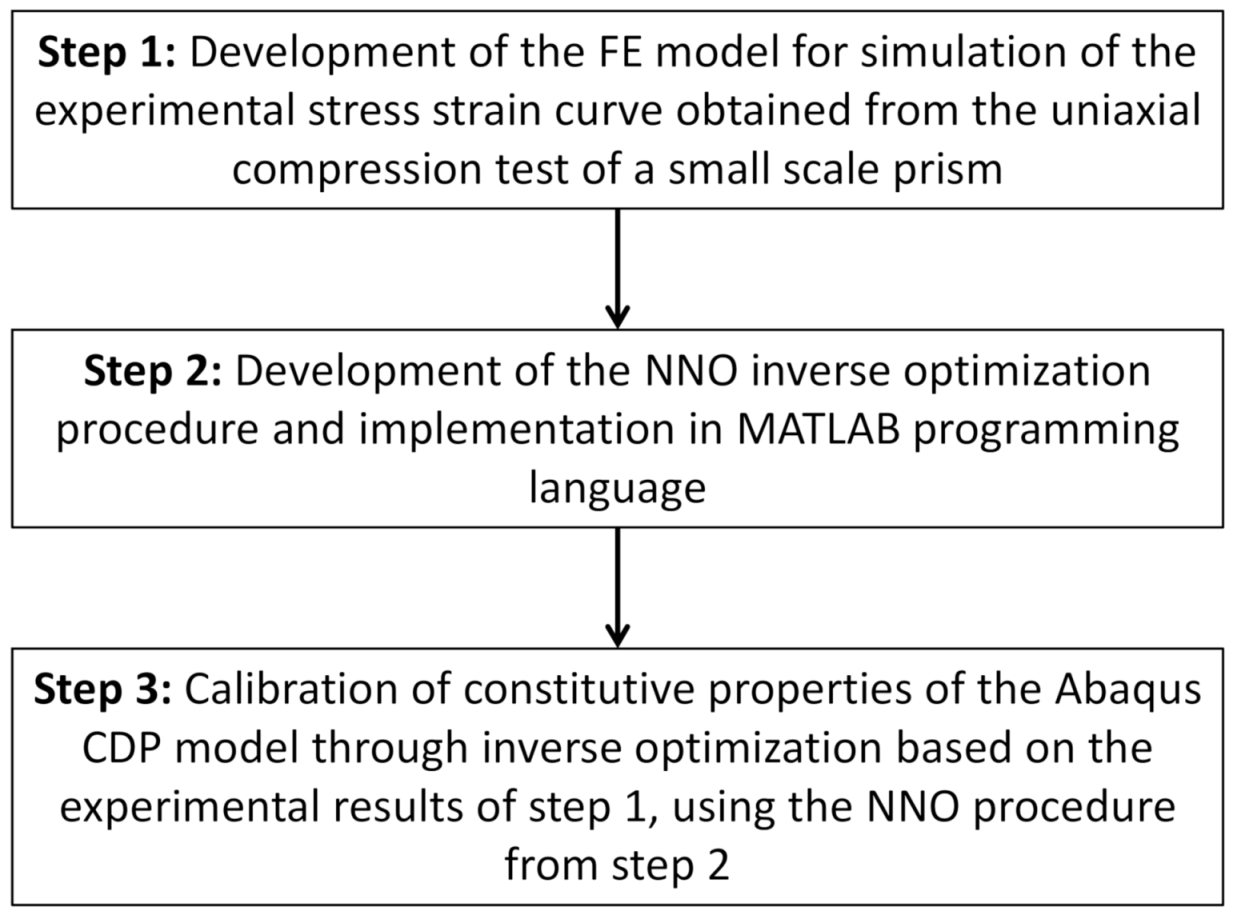
2.3. Proposed Methodology for Material Parameter Identification
| Algorithm 1. Neural Optimization. |
| 1: Read the experimental stress-strain curve SSexp |
| 2: Define M combinations of the 10 design variables |
| 3: for k from 1 to M |
| 4: Perform simulation in ABAQUS corresponding to parameters xk |
| 5: Read kth stress-strain curve and append it in array SSraw |
| 6: end for |
| 7: Initialize err = +∞ and j = 1 |
| 8: while j ≤ maxIter & err > tol |
| 9: Train an Artificial Neural Network (ANN), net, as follows: |
| ● Training function: Bayesian regularization |
| ● Input training data: xk, k = 1…M |
| ● Output training data: norm(SSexp − SSraw,k ), k = 1…M |
| 10: Find optimum values xj by Interior Point optimization as follows: |
| ● Objective function: the ANN net, fANN (see previous step) |
| ● Initial guess: xj−1 |
| ● Constraints: xi,lb ≤ xi,j ≤ xi,ub |
| 11: Perform simulation in ABAQUS corresponding to parameters xj |
| 12: Read stress-strain curve and append it in array SSraw |
| 13: Update err = norm(SSexp − SSraw,j ) < tol |
| 14: Update j = j + 1 |
| 15: end while |
2.3.1. Initial Sets of Values Assigned to the Design Variables
2.3.2. Calculation of Initial Stress Strain Curves
2.3.3. Discretization of Stress Strain Curves
2.3.4. Training of the ANN
- J is the Jacobian nt by nw matrix, where nt is the number of entries in the training set and nw is the number of the design variables (weights and biases), containing all the first order partial derivatives of F with respect to w (J = ∂F/∂w).
- λ is the damping factor which is adjusted at each iteration according to the convergence rate of the optimization process. If the reduction in the error is rapid, then λ can be reduced, which gradually makes the algorithm behave in a way similar to that of the Gauss Newton algorithm. In the opposite case of insufficient reduction in the residual, then λ can be increased, which makes the algorithm resemble the gradient descent algorithm.
- E is the error vector containing the residual for each input vector that is used for training the network.
- δ is the update of the weights
- Bayesian regularization minimizes a linear combination of squared errors and weights (cost function), mainly to overcome the problem in interpolating noisy data [38,39]. Two Bayesian hyperparameters α and β are used in the cost function, which determines the direction that the learning process must seek, in order not only to minimize the errors but the weights as well. These parameters are updated after each training cycle. The cost function is given by the following equation:where Ee is the sum of squared errors and Ew is the sum of squared weights. The Bayesian parameters are updated using MacKay’s [40] formulae as follows:C = βEe + αEwγ = nw − [α∙ tr(H−1)]β = (nt − γ)/(2Ee)α = γ/(2Ew)
| Algorithm 2. Backpropagation with Bayesian regularization. |
| 1: Compute the jacobian J = ∂F/∂w |
| 2: Compute the error gradient g = JTE |
| 3: Compute the Hessian approximation H = JTJ |
| 4: Compute the cost function C = βEe + αEw |
| 5: Solve (JTJ + λI)δ = JTE to find δ |
| 6: Update the network weights: w’ = w + δ |
| 7: Calculate C using w’ |
| 8: if C has not decreased, then discard w’, increase λ and go to step 5; |
| else if C has decreased, then decrease λ |
| 9: Update the Bayesian parameters |
2.3.5. Optimization Procedure
- N Step. A direct (Newton) step in (X,s). This step attempts to solve the Karush Kuhn Tucker (KKT) equations [42,43] for the approximate problem using a linearized Lagrangian as follows:where H is the Hessian of the Lagrangian of the approximate equality constrained minimization problem, calculated according to the BFGS formula [44,45,46], Jg is the Jacobian of the inequality constraint function g(X), S is a diagonal matrix with entries si, λ denotes the Lagrange multiplier vector associated with constraints g(X), Λ is a diagonal matrix with entries λi, and e is a vector of ones the same size as g(X). Equation (12) defines the direct step (ΔX, Δs).
- CG Step. A CG (Conjugate Gradient) step, using a trust region. The conjugate gradient approach to solve the approximate problem, Equation (10) adjusts both X and s, keeping the slacks s positive. The algorithm obtains Lagrange multipliers by approximately solving the KKT equations by:subject to λ > 0. The following quadratic approximation to Equation (10) is minimized in a trust region of radius R:∇XL = ∇XfANN + ∑iλi∇gi(X) = 0subject to the linearized constraints:minΔX,Δs{∇fANNTΔX + ½ΔXT∇XX2LΔX + μeTS−1Δs + ½ΔsTS−1ΛΔs}g(X) + JgΔX + Δs = 0
2.3.6. Evaluation of the Stress-Strain Curve of the Optimal Point
2.4. Material Parameter Identification Results
3. Results & Discussion
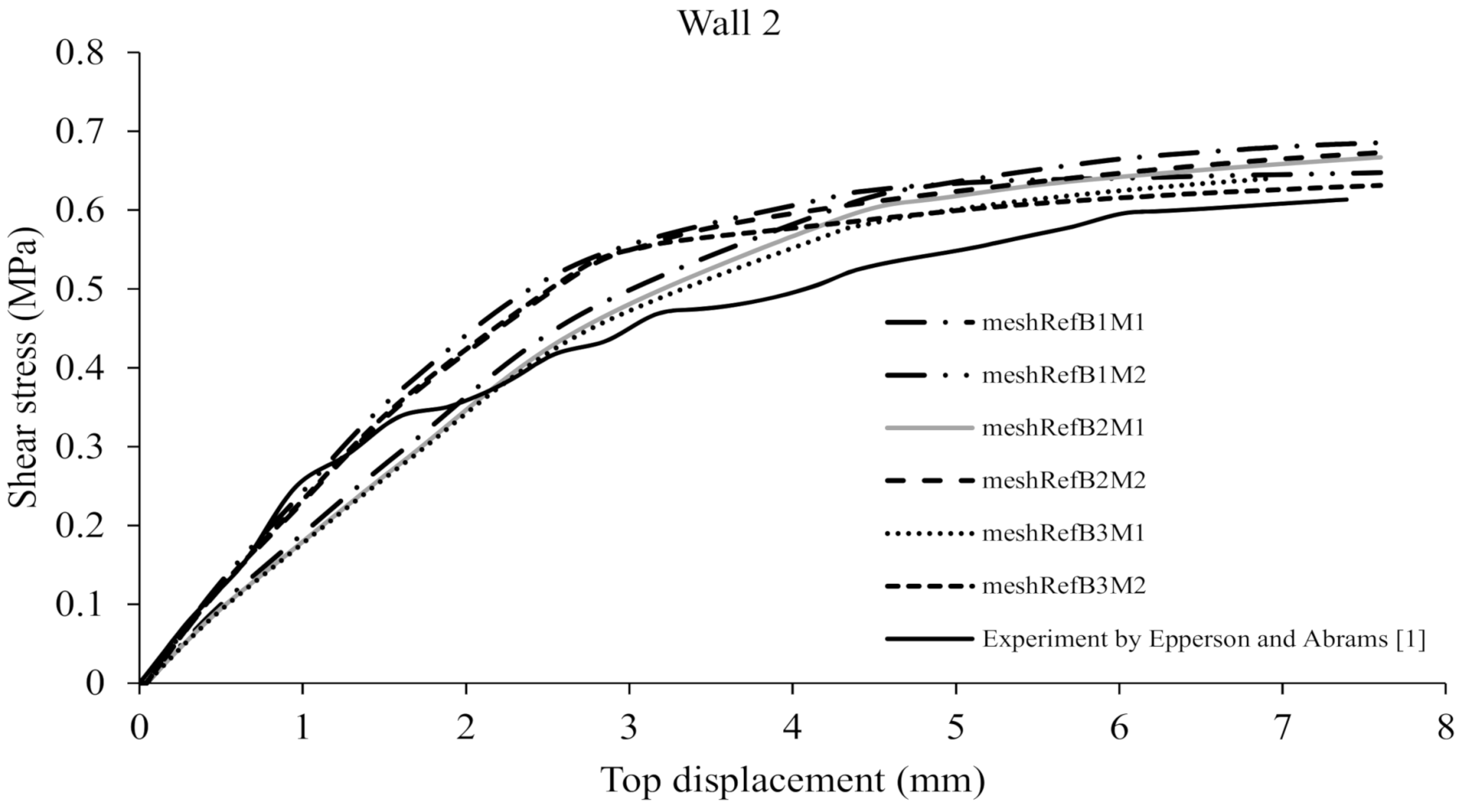
3.1. Mesh Convergence Study
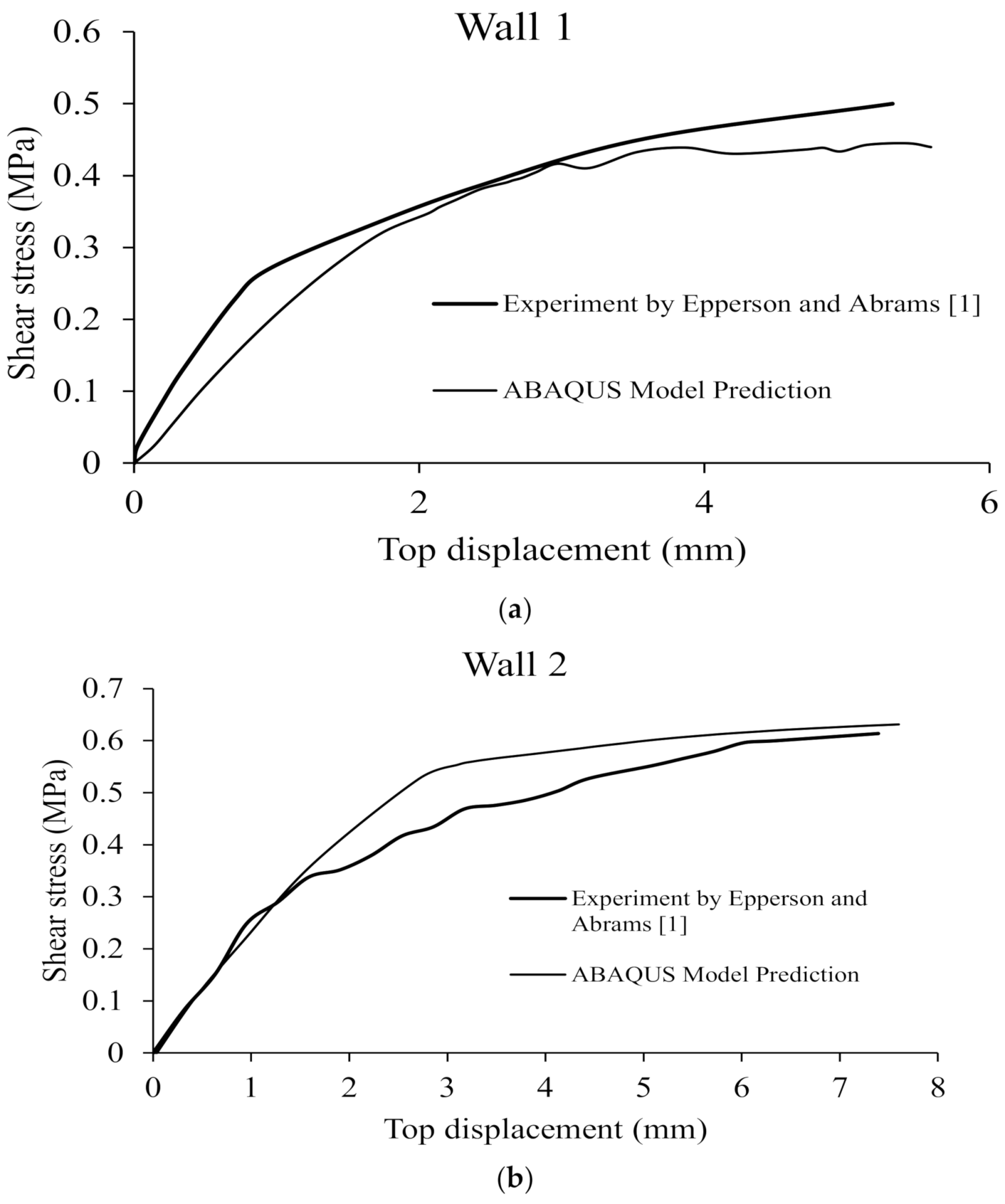
3.2. Model Validation
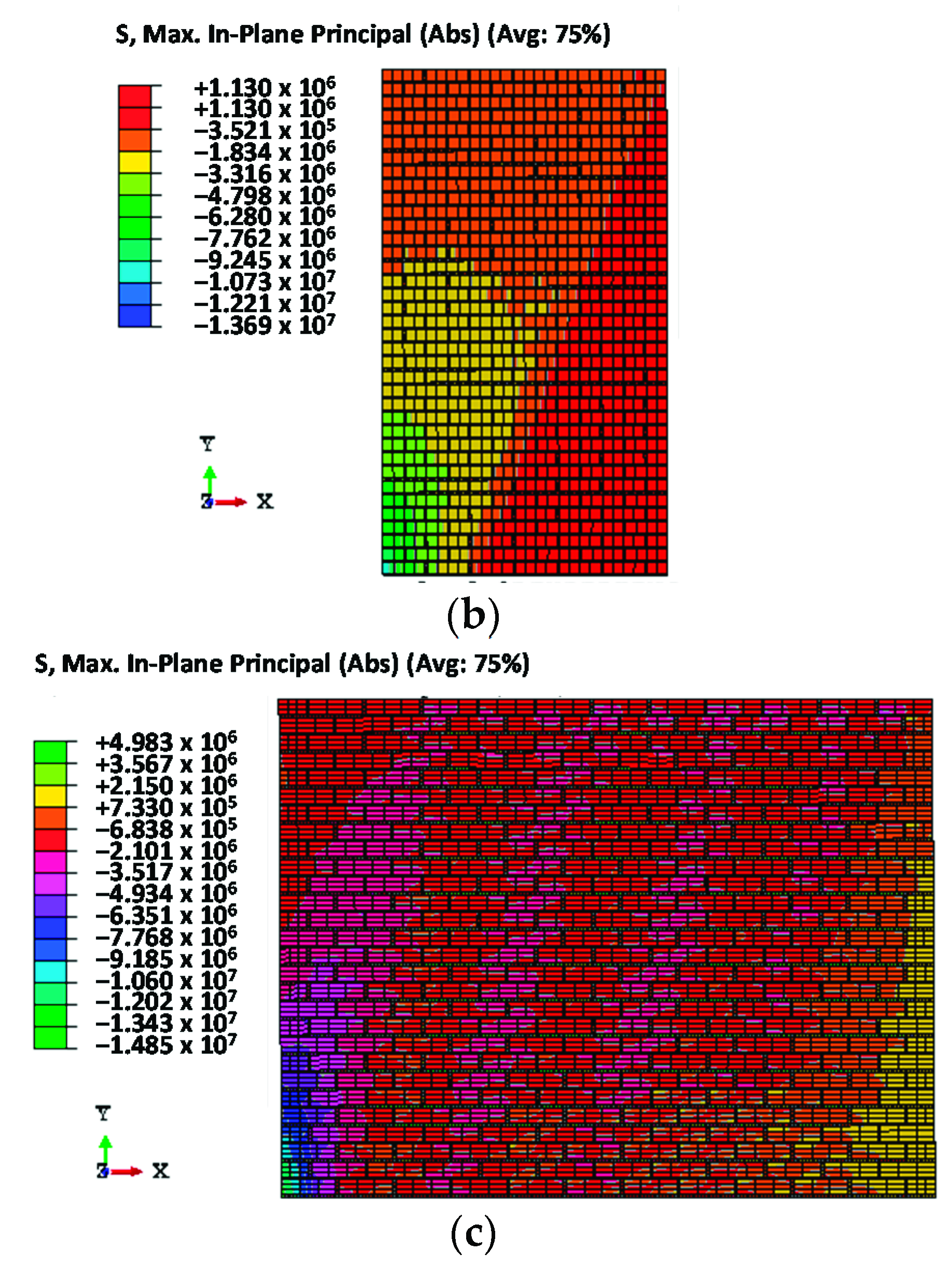
3.3. Failure Modes and Failure Criteria
3.3.1. Flexural Cracks
3.3.2. Shear Sliding
3.3.3. Diagonal Compressive Splitting
3.3.4. Diagonal Tension Cracking
3.4. Influence of Vertical Compressive Stress
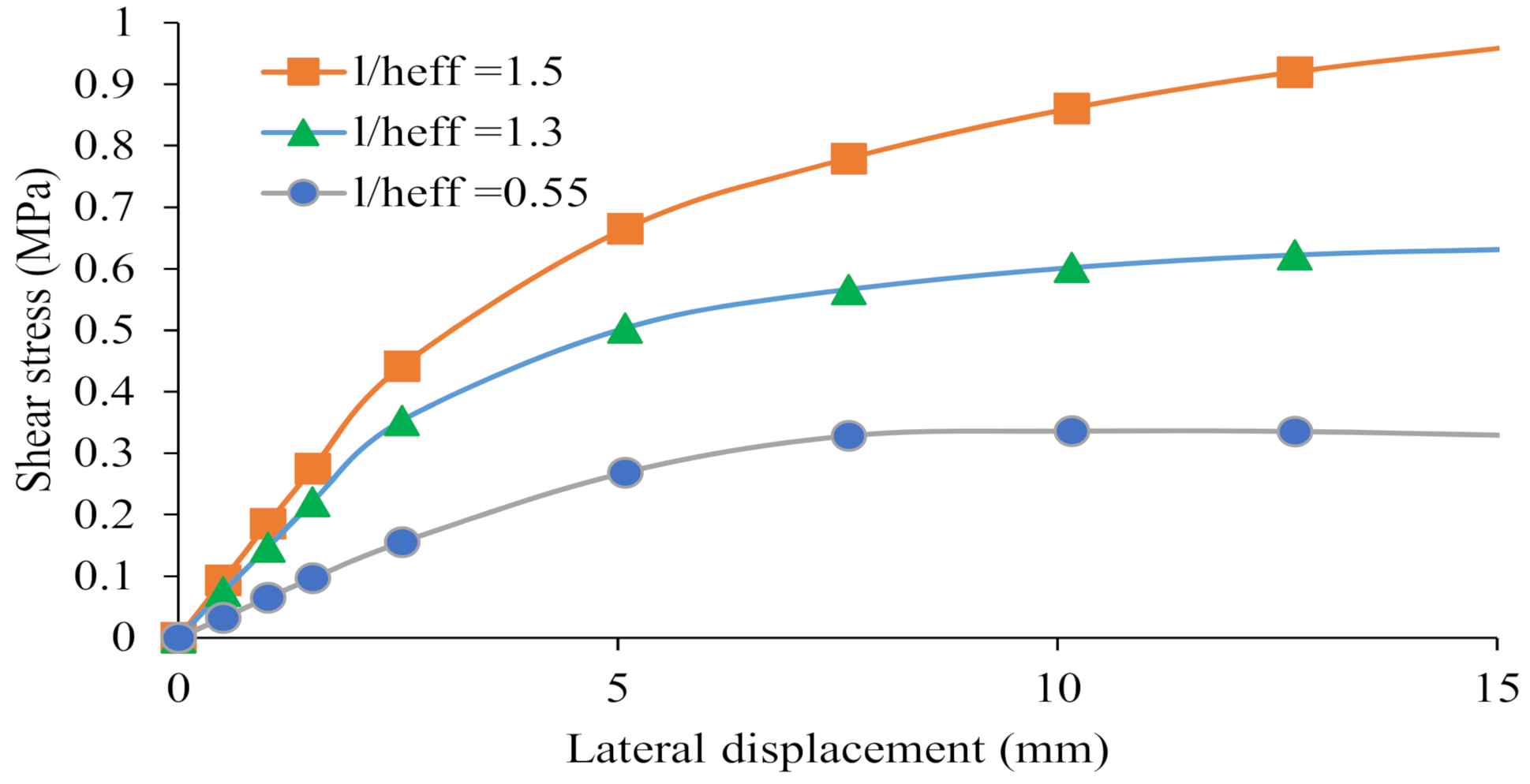
3.5. Influence of Aspect Ratio
3.6. Influence of Material Sensitivity
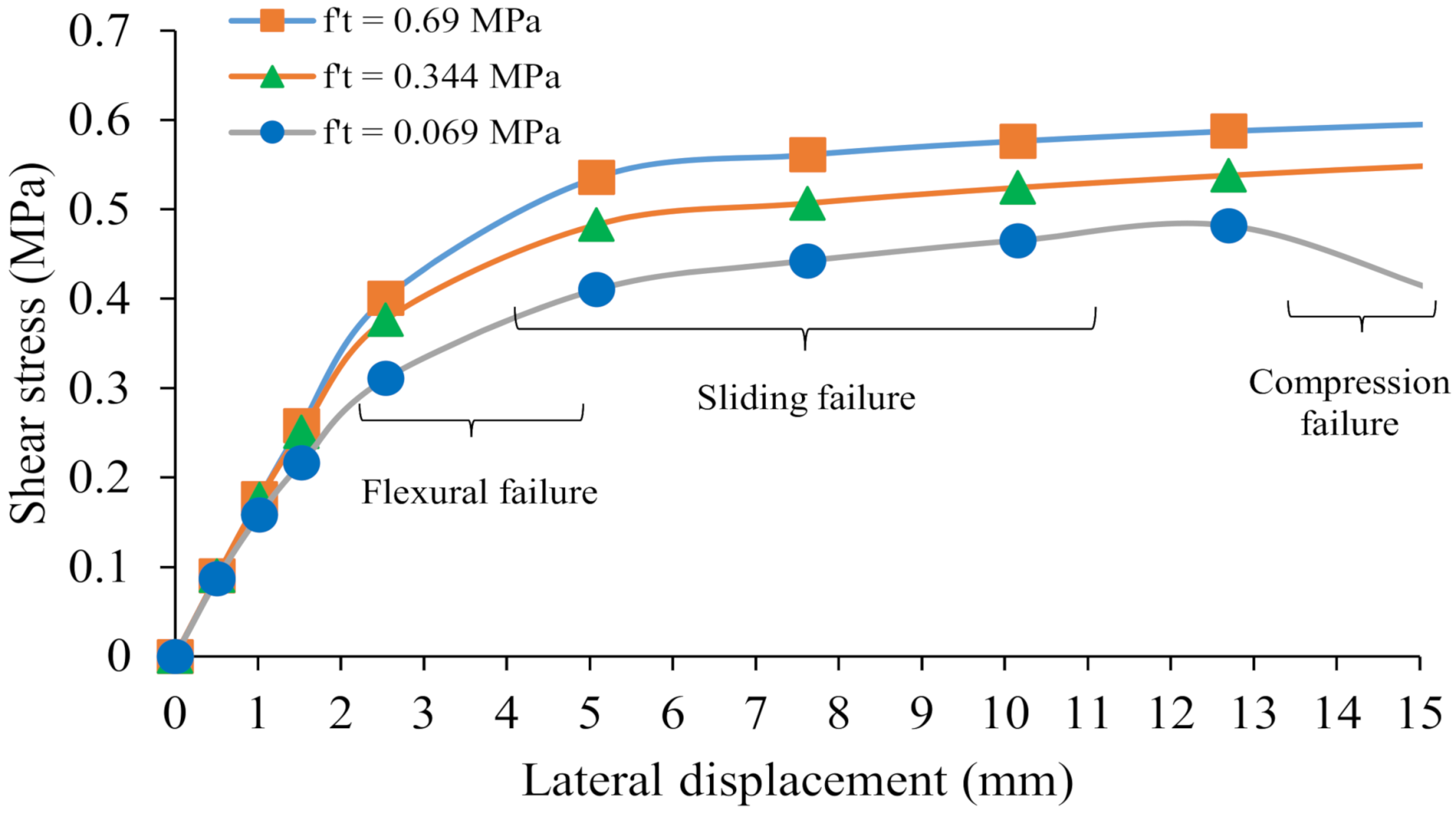
3.6.1. Flexural Tensile Strength
3.6.2. Compressive Strength
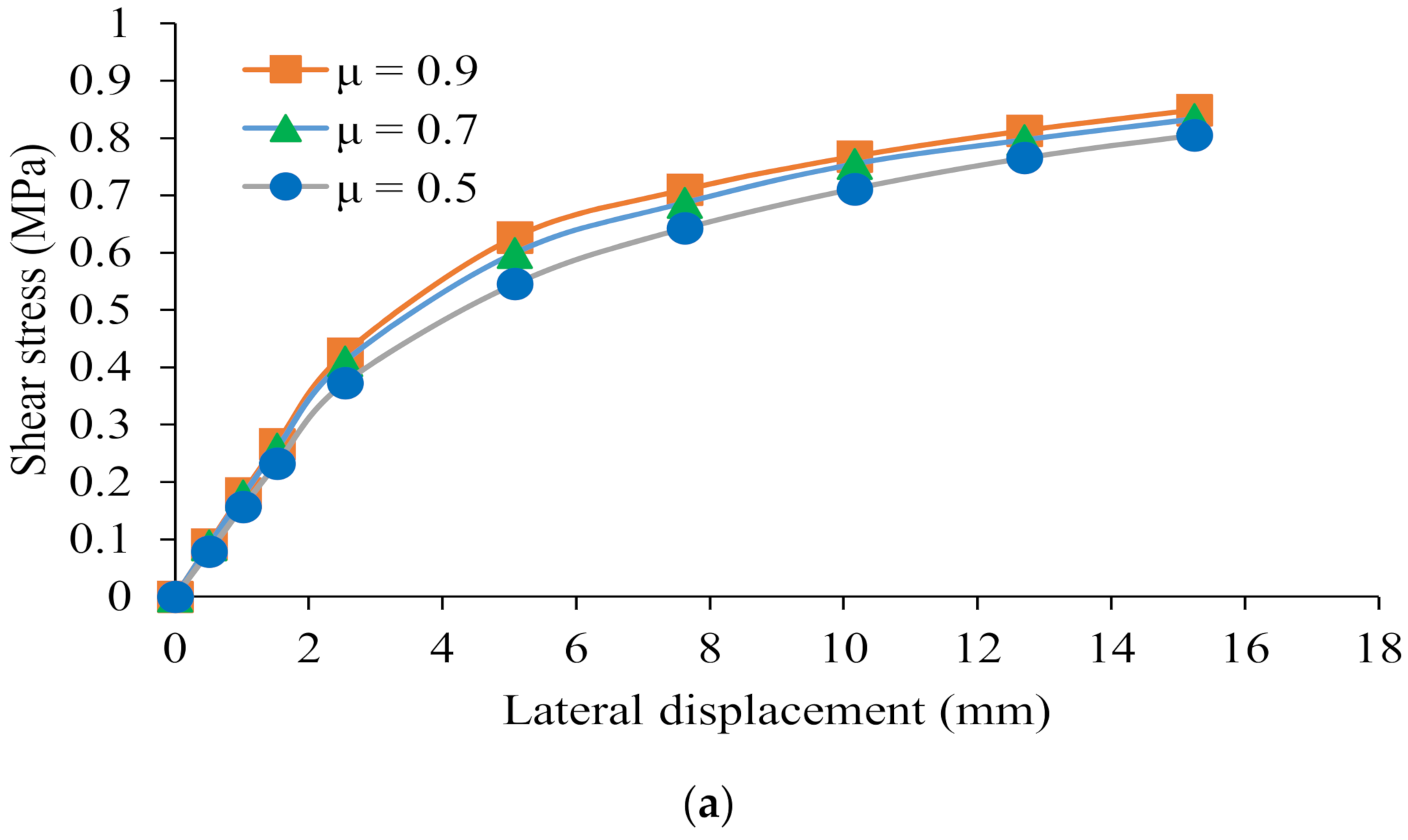
3.6.3. Coefficient of Friction and Cohesion Stress
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Literature Review Summary
| References | Keywords | Finding |
| [1,2,3,4] | Masonry Walls, Shear strength evaluation, Nondestructive evaluation | (a) Determine of vertical compressive stress for masonry walls subjected to in-plane lateral loads. (b) Conducted paramteric study to evalute shear strength. |
| [5,6,7,8,9,10,11] | Concrete damage plasticity CDP, Constitutive model | (a) Developed concrete damage plasticity constititve mode and validated with numerical/experiment data. (b) Calibrate material parameters and validated with experimental observations. |
| [12,13,14,15,16,17,18,19,20,21,22,23] | Parameters Identification, FE, Calibration, Optimization | Study masonry mesoscale/macroscale model subjected to load combination and compared its results with those of a finite element (FE) model to identify the material parameters. |
| [24,25,26,27] | Masonry walls, strength evaluation, Aspect ratio | Investigate the effects of various factors, i.e., unit type, vertical pre compression level, aspect ratio, size, and boundary conditions, on the displacement capacity of URM walls. |
| [28,29,30,31] | Optimization, Calibration, Material parameters identification | Calibrate masonry model, characterize the material parameters based on experimental observations |
| [32,33] | Optimization, Least squares, Material parameters | Optimization algorithm to minimize the errors of the differences between experiment-based measurements and the calculated response of the model. |
References
- Epperson, G.S.; Abrams, D.P. Nondestructive Evaluation of Masonry Buildings; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1990; Volume 89. [Google Scholar]
- Abrams, D.P.; Shah, N. Cyclic Load Testing of Unreinforced Masonry Walls; Illinois Univ at Urbana Advanced Construction Technology Center: Champaign, IL, USA, 1992. [Google Scholar]
- Xu, W.; Abrams, D.P. Evaluation of Lateral Strength and Deflection for Cracked Unreinforced Masonry Walls; Illinois Univ at Urbana Advanced Construction Technology Center: Champaign, IL, USA, 1992. [Google Scholar]
- Chaimoon, K.; Attard, M.M. Modeling of unreinforced masonry walls under shear and compression. Eng. Struct. 2007, 29, 2056–2068. [Google Scholar] [CrossRef]
- Lotfi, H.; Shing, P. An appraisal of smeared crack models for masonry shear wall analysis. Comput. Struct. 1991, 41, 413–425. [Google Scholar] [CrossRef]
- Grassl, P.; Jirásek, M. Damage-plastic model for concrete failure. Int. J. Solids Struct. 2006, 43, 7166–7196. [Google Scholar] [CrossRef] [Green Version]
- Lubliner, J. A simple model of generalized plasticity. Int. J. Solids Struct. 1991, 28, 769–778. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Gambarotta, L.; Lagomarsino, S. Damage models for the seismic response of brick masonry shear walls. Part I: The mortar joint model and its applications. Earthq. Eng. Struct. Dyn. 1997, 26, 423–439. [Google Scholar] [CrossRef]
- Kmiecik, P.; Kamiński, M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011, 11, 623–636. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Chisari, C.; Macorini, L.; Amadio, C.; Izzuddin, B.A. Identification of mesoscale model parameters for brick-masonry. Int. J. Solids Struct. 2018, 146, 224–240. [Google Scholar] [CrossRef]
- Chisari, C. Inverse Techniques for Model Identification of Masonry Structures; Università degli studi di Trieste: Trieste, Italy, 2015. [Google Scholar] [CrossRef] [Green Version]
- Chisari, C.; Macorini, L.; Amadio, C.; Izzuddin, B. An inverse analysis procedure for material parameter identification of mortar joints in unreinforced masonry. Comput. Struct. 2015, 155, 97–105. [Google Scholar] [CrossRef] [Green Version]
- Chisari, C. Tolerance-based Pareto optimality for structural identification accounting for uncertainty. Eng. Comput. 2019, 35, 381–395. [Google Scholar] [CrossRef] [Green Version]
- Caliò, I.; Marletta, M.; Pantò, B. A new discrete element model for the evaluation of the seismic behaviour of unreinforced masonry buildings. Eng. Struct. 2012, 40, 327–338. [Google Scholar] [CrossRef]
- Carmeliet, J. Optimal estimation of gradient damage parameters from localization phenomena in quasi-brittle materials. Mech. Cohesive-Frict. Mater. Int. J. Exp. Model. Comput. Mater. Struct. 1999, 4, 1–16. [Google Scholar] [CrossRef]
- Muñoz-Rojas, P.; Cardoso, E.; Vaz, M. Parameter identification of damage models using genetic algorithms. Exp. Mech. 2010, 50, 627–634. [Google Scholar] [CrossRef]
- Nazari, A.; Sanjayan, J.G. Modelling of compressive strength of geopolymer paste, mortar and concrete by optimized support vector machine. Ceram. Int. 2015, 41, 12164–12177. [Google Scholar] [CrossRef]
- Toropov, V.V.; van der Giessen, E. Parameter identification for nonlinear constitutive models: Finite Element simulation—Optimization—Nontrivial experiments. In Optimal Design with Advanced Materials; Elsevier: Amsterdam, The Netherlands, 1993; pp. 113–130. [Google Scholar]
- Sarhosis, V.; Sheng, Y. Identification of material parameters for low bond strength masonry. Eng. Struct. 2014, 60, 100–110. [Google Scholar] [CrossRef] [Green Version]
- Jankowiak, T.; Lodygowski, T. Identification of parameters of concrete damage plasticity constitutive model. Found. Civ. Environ. Eng. 2005, 6, 53–69. [Google Scholar]
- Toropov, V.; Garrity, S. Material parameter identification for masonry constitutive models. In Proceedings of the Eighth Canadian Masonry Symposium, Jasper, AB, Canada, 31 May–3 June 1998; pp. 551–562. [Google Scholar]
- Magenes, G.; Calvi, G.M. In-plane seismic response of brick masonry walls. Earthq. Eng. Struct. Dyn. 1997, 26, 1091–1112. [Google Scholar] [CrossRef]
- Agnihotri, P.; Singhal, V.; Rai, D.C. Effect of in-plane damage on out-of-plane strength of unreinforced masonry walls. Eng. Struct. 2013, 57, 1–11. [Google Scholar] [CrossRef]
- Salmanpour, A.H.; Mojsilović, N.; Schwartz, J. Displacement capacity of contemporary unreinforced masonry walls: An experimental study. Eng. Struct. 2015, 89, 1–16. [Google Scholar] [CrossRef]
- Howlader, M.K.; Masia, M.; Griffith, M. Numerical analysis and parametric study of unreinforced masonry walls with arch openings under lateral in-plane loading. Eng. Struct. 2020, 208, 110337. [Google Scholar] [CrossRef]
- Labibzadeh, M.; Zakeri, M.; Shoaib, A.A. A new method for CDP input parameter identification of the ABAQUS software guaranteeing uniqueness and precision. Int. J. Struct. Integr. 2017, 8, 264–284. [Google Scholar] [CrossRef]
- Birtel, V.; Mark, P. Parameterised finite element modelling of RC beam shear failure. In Proceedings of the 2006 ABAQUS Users’ Conference, Boston, MA, USA, 23–25 May 2006; Volume 14. [Google Scholar]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Albu Jasim, Q.J.M. Probabilistic Calibration of Unreinforced Masonry Wall Properties: From Constitutive Material Models to Structural Performance. Ph.D. Thesis, Texas A & M University, College Station, TX, USA, 2020. [Google Scholar]
- Simulia, D. Abaqus Version 2021HF5 (6.21-6) Documentation USA; Dassault Systemes Simulia Corporation: Johnston, RI, USA, 2021. [Google Scholar]
- MATLAB. R2021a; MathWorks Inc.: Natick, MA, USA, 2021. [Google Scholar]
- Papazafeiropoulos, G.; Muñiz-Calvente, M.; Martínez-Pañeda, E. Abaqus2Matlab: A suitable tool for finite element post-processing. Adv. Eng. Softw. 2017, 105, 9–16. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Foresee, F.D.; Hagan, M.T. Gauss-Newton approximation to Bayesian learning. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 12 June 1997; pp. 1930–1935. [Google Scholar] [CrossRef]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Program. 2000, 89, 149–185. [Google Scholar] [CrossRef] [Green Version]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- MacKay, D.J. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Waltz, R.A.; Morales, J.L.; Nocedal, J.; Orban, D. An interior algorithm for nonlinear optimization that combines line search and trust region steps. Math. Program. 2006, 107, 391–408. [Google Scholar] [CrossRef]
- Karush, W. Minima of Functions of Several Variables with Inequalities as Side Constraints. Master’s thesis, The University of Chicago, Chicago, IL, USA, 1939. [Google Scholar]
- Kuhn, H.; Tucker, A. Nonlinear Programming. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 31 July–12 August 1950. [Google Scholar]
- Broyden, C.G. The convergence of a class of double-rank minimization algorithms 1. general considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef] [Green Version]
- Goldfarb, D. A family of variable-metric methods derived by variational means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of quasi-Newton methods for function minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to Nonlinear Finite Element Analysis: With Applications to Heat Transfer, Fluid Mechanics, and Solid Mechanics; Oxford University Press: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Page, A. The biaxial compressive strength of brick masonry. Proc. Inst. Civ. Eng. 1981, 71, 893–906. [Google Scholar] [CrossRef]
- Agency, F.E.M. Evaluation of Earthquake Damaged Concrete and Masonry Wall Buildings; FEMA: Washington, DC, USA, 2013.
- Essawy, A.S.; Drysdale, R.G. Macroscopic failure criterion for masonry assemblages. In Proceedings of the 4th Canadian Masonry Symposium, Fredericton, NB, Canada, 2–4 June 1986; Volume 1, pp. 263–277. [Google Scholar]






| Design Variable | Description | Lower Bound | Upper Bound |
|---|---|---|---|
| EC | Modulus of elasticity of the brick material | 4688.43 MPa | 4826.33 MPa |
| EM | Modulus of elasticity of the mortar material | 2757.90 MPa | 2895.80 MPa |
| ψ | Dilation angle in the p–q plane of the brick material | 0.1 | 40 |
| ε | Flow potential eccentricity | 0 | 1 |
| σb0/σc0 | Ratio of initial equibiaxial compressive yield stress to initial uniaxial compressive yield stress | 1.1 | 1.2 |
| Kc | Ratio of the second stress invariant on the tensile meridian to that on the compressive meridian at initial yield | 0.51 | 1 |
| νM | Poisson ratio of the mortar material | 0.1 | 0.4 |
| σc0,C | Initial yield stress value of brick material in compression for crushing strain equal to 0.0 | 6.89 MPa | 41.37 MPa |
| σc0,M | Initial yield stress value of mortar material in compression, for crushing strain equal to 0.0 | 3.45 MPa | 34.47 MPa |
| εtf | Cracking strain in tension, for failure stress value equal to 1/10 of the failure stress value for cracking strain equal to 0.0 | 10−4 | 10−3 |
| Model | Part | Element Type | Elements | Nodes |
|---|---|---|---|---|
| meshRefB1M1 | Mortar | CPS4R | 10,108 | 19,570 |
| Bricks | CPS4R | 1568 | 3528 | |
| meshRefB1M2 | Mortar | CPS4R | 34,941 | 50,822 |
| Bricks | CPS4R | 1568 | 3528 | |
| meshRefB2M1 | Mortar | CPS4R | 10,108 | 19,570 |
| Bricks | CPS4R | 3528 | 6272 | |
| meshRefB2M2 | Mortar | CPS4R | 34,941 | 50,822 |
| Bricks | CPS4R | 3528 | 6272 | |
| meshRefB3M1 | Mortar | CPS4R | 10,108 | 19,570 |
| Bricks | CPS4R | 6272 | 9800 | |
| meshRefB3M2 | Mortar | CPS4R | 34,941 | 50,822 |
| Bricks | CPS4R | 6272 | 9800 |
| Design Variable | Optimum Value |
|---|---|
| EC | 4744.97 MPa |
| EM | 2819.13 MPa |
| ψ | 8.88 |
| ε | 0.61 |
| σb0/σc0 | 1.112 |
| Kc | 0.84 |
| νM | 0.294 |
| σc0,C | 15.547 MPa |
| σc0,M | 9.067 MPa |
| 1.01 × 10−4 |
| Description | Constant Input | Varying Input | Outputs | Conclusion | |
|---|---|---|---|---|---|
| Shear Stress (τ) MPa | Lateral Dis (U) mm | ||||
| Influence of Vertical Compressive Stress | l/heff = 1.5 f’m = 11 MPa μ = 0.5 τo = 0.69 MPa. f’t = 2.06 MPa | σv = 0.344 MPa σv = 0.69 MPa σv = 1.03 MPa σv = 1.37 MPa σv = 1.72 MPa | (0.72) a (0.78) a (0.83) a (0.88) a (0.91) a | (15.24) b (15.24) b (15.24) b (15.24) b (15.24) b | Note 1 |
| Influence of Aspect Ratio | f’m = 20.69 MPa μ = 0.5 τo = 0.69 MPa. σv = 1.03 MPa f’t = 2.06 MPa | l/heff = 0.55 l/heff = 1.3 l/heff = 1.5 | (0.32) a (0.63) a (0.96) a | (15.24) b (15.24) b (15.24) b | Note 2 |
| Influence of Material Sensitivity: Flexural Tensile Strength | l/heff = 1.5 μ = 0.5 τo = 0.69 MPa σv = 1.03 MPa f’m = 11 MPa | f’t = 0.069 MPa f’t = 0.344 MPa f’t = 0.69 MPa | (0.40) a (0.54) a (0.59) a | (15.24) b (15.24) b (15.24) b | Note 3 |
| Influence of Material Sensitivity: Compressive Strength | l/heff = 1.5 μ = 0.5 τo = 0.69 MPa σv = 1.03 MPa f’t = 2.06 MPa | f’m = 6.9 MPa f’m = 13.78 MPa f’m = 20.68 MPa | (0.72) a (0.83) a (0.72) a | (15.24) b (15.24) b (15.24) b | Note 4 |
| Influence of Material Sensitivity: Coefficient of Friction | l/heff = 1.5 f’m = 11 MPa τo = 0.69 MPa. σv = 1.03 MPa f’t = 2.06 MPa | μ = 0.5 μ = 0.7 μ = 0.9 | (0.80) a (0.83) a (0.85) a | (15.24) b (15.24) b (15.24) b | Note 5 |
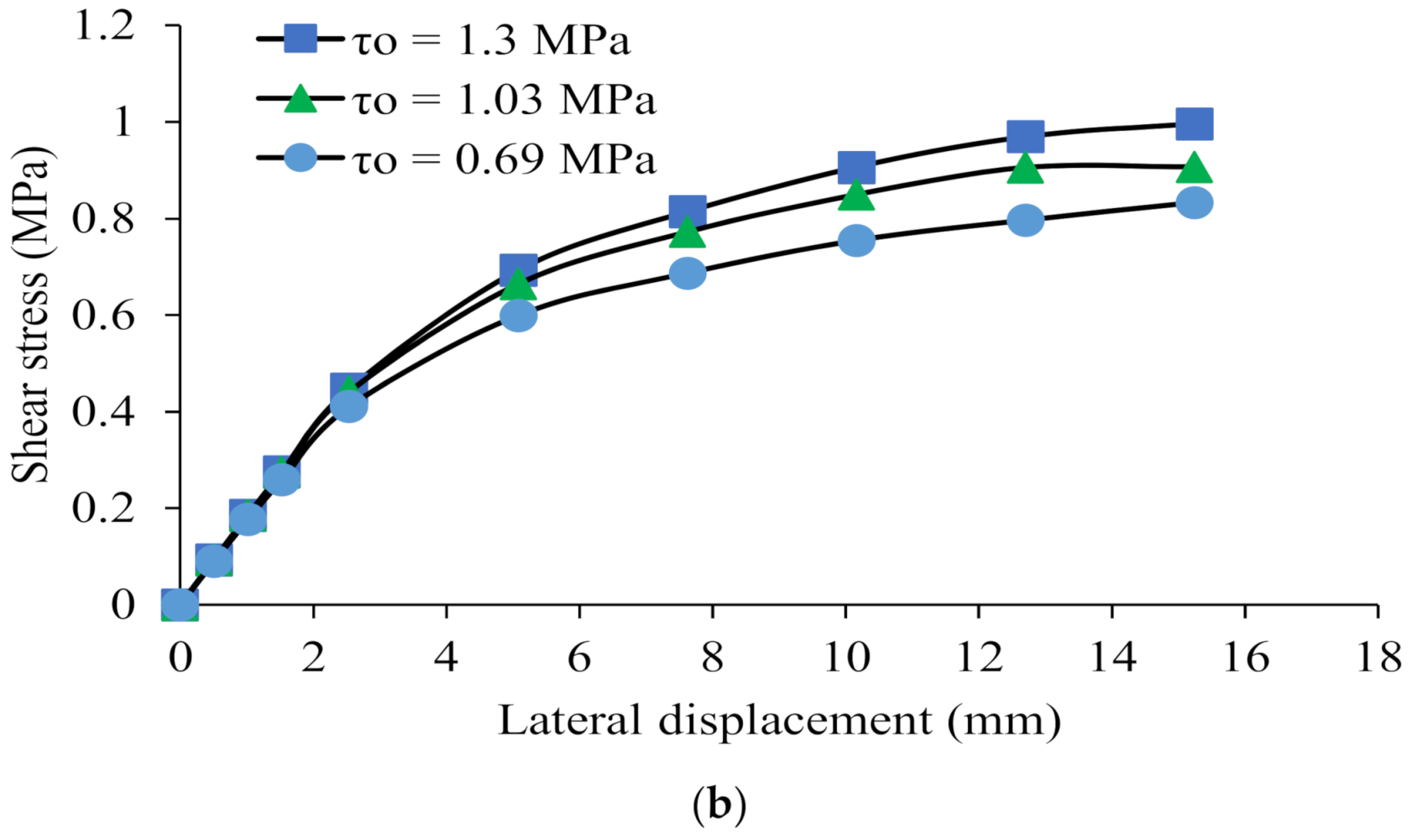
| Influence of Material Sensitivity: Cohesion Stress | l/heff = 1.5 f’m = 11 MPa μ = 0.5 σv = 1.03 MPa f’t = 2.06 MPa | τo = 0.69 MPa. τo = 1.03 MPa. τo = 1.3 MPa | (0.83) a (0.90) a (0.99) a | (15.24) b (15.24) b (15.24) b | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albu-Jasim, Q.; Papazafeiropoulos, G. A Neural Network Inverse Optimization Procedure for Constitutive Parameter Identification and Failure Mode Estimation of Laterally Loaded Unreinforced Masonry Walls. CivilEng 2021, 2, 943-968. https://doi.org/10.3390/civileng2040051
Albu-Jasim Q, Papazafeiropoulos G. A Neural Network Inverse Optimization Procedure for Constitutive Parameter Identification and Failure Mode Estimation of Laterally Loaded Unreinforced Masonry Walls. CivilEng. 2021; 2(4):943-968. https://doi.org/10.3390/civileng2040051
Chicago/Turabian StyleAlbu-Jasim, Qudama, and George Papazafeiropoulos. 2021. "A Neural Network Inverse Optimization Procedure for Constitutive Parameter Identification and Failure Mode Estimation of Laterally Loaded Unreinforced Masonry Walls" CivilEng 2, no. 4: 943-968. https://doi.org/10.3390/civileng2040051
APA StyleAlbu-Jasim, Q., & Papazafeiropoulos, G. (2021). A Neural Network Inverse Optimization Procedure for Constitutive Parameter Identification and Failure Mode Estimation of Laterally Loaded Unreinforced Masonry Walls. CivilEng, 2(4), 943-968. https://doi.org/10.3390/civileng2040051







