Abstract
This paper presents a review of research on underwater explosions (UNDEX) with a focus on the structural response of concrete or reinforced concrete (RC) structures. First, the physical phenomena of UNDEX and its effects are discussed describing both the theory and considerations of the event. Then a brief description of the standard UNDEX experiment is followed by computational methods that employ governing equations that are used for verification of those methods. Lastly, a discussion on structural response for UNDEX is presented with a particular focus on concrete structures.
1. Introduction
This paper presents a review on analyzing underwater explosion (UNDEX) effects on structures. The threat of terrorism attacks and accidents, such as gas explosions or construction overblasting on civil infrastructure, have increased in recent years. Research into the effects of UNDEX largely began in World War II due to the war effort. Much of this research including fundamental equations and observations was compiled into widely accessible work by the efforts of Cole and Weller [1]. The need for understanding UNDEX remained critical due to its effects on infrastructure and human lives. While the effect of air blast on civil infrastructure is studied to a greater length, published research on the effect of UNDEX in civil engineering structures is scant.
This paper presents the fundamentals of UNDEX, the physical and computational methods of analyzing its parameters, and the effects of UNDEX on select structures such as reinforced concrete dams and columns. First, the physical background and mechanics of UNDEX are discussed. Second, the methods of physical and computational modeling of are covered. Third, a series of experiments based on various structures are discussed with a focus on concrete and RC-based structures. Lastly, concluding thoughts as well as potential direction for further research are covered.
2. Physical Background of UNDEX
At the beginning of every UNDEX event is the detonation of the explosive charge. After the initial detonation, the major event of an UNDEX event is the initial shock wave. When the explosive charge is detonated, a pressure wave is released from the charge location and expands outwards in a roughly spherical shape with the gas bubble following behind as shown in Figure 1 [2]. This pressure wave moves at such a speed that it is considered a shock wave and exerts a large amount of pressure on any point or surface it encounters. This shock wave travels at a highly nonlinear rate while still within 2–3 charge radii of the charge, and then moves linearly past that threshold [3]. Shock waves decay over time with their pressure values decreasing exponentially in the initial stages. Thus, the shock wave’s loading effects decrease with increased distance between the point or surface of interest and the charge distance, otherwise known as the stand-off distance.
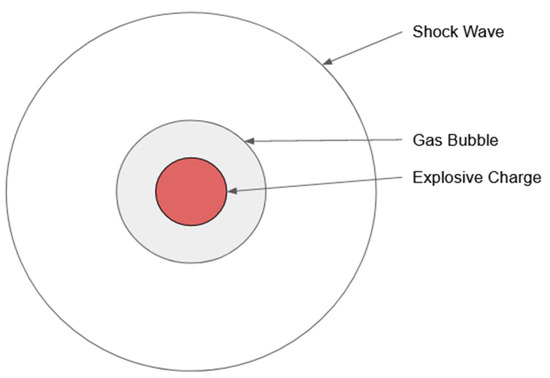
Figure 1.
Diagram of shockwave and gas bubble propagation—reproduced from [2].
In the case of shock waves impacting on a surface or interface, such as a concrete slab or the boundary between air and water, a reflected wave is produced. This reflected wave will ‘bounce’ back away from the impacted surface and propagate outwards, similar to the original shock wave. The properties of this reflected wave vary on the impedance difference between the surface and the medium that the shockwave was traveling through. Costanzo [2], as shown in Figure 2, provided details of a reflected wave originating from an UNDEX event and reflecting off the air–water interface that has a tensile characteristic as opposed to the normal compressive characteristic. This is important because the reflected wave hits the analysis point of interest and lessens any compressive load placed on it from the original shock wave. This phenomenon is critical to the bulk cavitation effect discussed later.
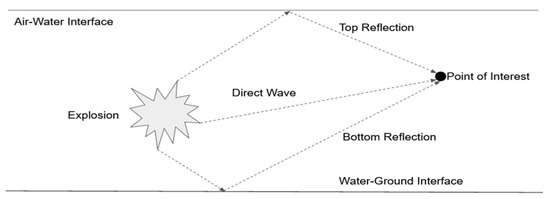
Figure 2.
Diagram of a Reflected Shock wave bouncing off the Air-Water Interface—Reproduced from [2].
Once the initial shock wave has propagated away, the second part of the UNDEX event begins. As the gases left over from the explosion expand, the hydrostatic pressure of the water begins to bear down on the gases and shrink the gas bubble. When a threshold of shrinkage is reached, the gas bubble pushes back against the water and a shock wave is produced. This shock wave is called a bubble pulse. This cycle repeats itself and the gas bubble moves towards the air–water interface. This cycle continues with the gas bubble reaching a smaller peak radius value each time until either the gas bubble breaks or the gas vents towards the surface [4]. Figure 3 shows this cycle of expansion and compression of the gas bubble. Note that the effects of each subsequent pulse are lessened due to the dispersion of energy from the previous pulse.
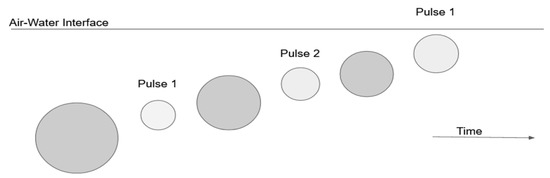
Figure 3.
Multiple bubble pulses rising to the surface in succession—reproduced from [4].
While not considered in all UNDEX shock wave analyses, the impulse delivered from the repeated bubble pulses can be equal to or exceed that of the shock wave [5]. It is noteworthy that the presence of structures can exacerbate the effect of the bubble pulse due to the bubble developing a water jet, which increases its loading properties [5].
The last major phenomenon in UNDEX is cavitation. While the main focus of this review paper is on structural response, understanding the response of the surrounding water is also critical. If water is subjected to enough tensile energy originating from reflected shock waves off of the surface interface, the water cavitates and is unable to transmit any more shock. This cavitated region of water eventually collapses in a motion similar to that of a zipper, creating its own shockwave [2]. Like the bubble pulse, this phenomenon is not typically observed in simulations. However, unlike the bubble pulse, this may be due to the decreased prevalence of cavitation. Not every situation will involve explosives that output such energy that the reflected waves are enough to cavitate the water state. However, for larger structures in which a large quantity of explosive is certainly within the realm of study such as a ship, cavitation can be an important factor. For instance, the research of Ming et al. on ship structures examined the cavitation effects on the ship plating. It was found that the cavitation led to strain relaxation in the areas it affected [6]. Overall, the research on cavitation effects is less reported in literature than that of shock wave effects.
3. Testing and Analysis
3.1. Experimental Testing
The standard setup for testing UNDEX effects is having the tested material submerged in water with pressure gauges placed around it either attached to the surface of the tested material or a specified distance away from the material. The explosive is then placed depending on the circumstance either on the surface or at a certain stand-off distance away. Some experimental setups make use of high-speed cameras as another form of data gathering; however, they provide additional challenges such as water clarity, low light levels, and potential damage to the camera [7]. Once the experiment setup is verified, the experiment begins by detonating the explosive and measuring the quantities of the analyzed material through the sensors mounted. These setups then translate to data used either for analysis based on parameters, such as damage or displacement analyses, or used as validation for computational or numerical models [7]. In terms of the data gathered, pressure-time data, displacement-time data, and strain-time data are common for analyzing the effects of UNDEX.
Logistically, as useful as physical data would be from a full-scale experiment, it is unwieldy to physically test UNDEX effects on full-sized structures such as ships or dams. The financial costs, the difficulty of multiple trials, and potential unforeseen damages create an environment where that sort of experimentation is too unwieldy. Through the testing of physical models, research can be done on smaller scales. However, other issues can arise from effectively shrinking the experimental bounds, specifically scaling for testing involving concrete structures. Due to the nonlinear nature of concrete [8], a certain amount of scaling is required between the concrete and the explosive charge used [9].
Centrifuge testing can also be used in conjunction with the tested model and charge to create behavior similar to a larger, more realistic model [9]. This is done through a series of scaling laws that relate the physical model to the real-life equivalent [10]. Typically, this is done with dam models as it is suitable for scaled down experiments.
When gathering physical data from physical experiments, some form of data-gathering equipment or measurement is imperative. In the case of UNDEX effects, sensors are typically used for measurement [8]. The types of sensors used vary based on the application; however, the usual sensors include pressure sensors and some combination of displacement, stress, and strain sensors. This is the standard suite of data points that are gathered for an analysis of UNDEX on a structure. Most reviewed papers do not mention the specific sensor brands; however, the configuration of these sensors is critical as knowing the relative positions of the charge, structure, and sensor creates a better picture of the scenario. Thus, the sensor configuration is typically included.
The beginning stage of the UNDEX experimental testing starts with the explosive charge. The detonation of the charge is an exothermic chemical reaction that propagates once it has started [2]. This chemical reaction creates extreme heat and pressure that move outwards in a wave originating from the charge location [2]. The intensity of these effects depends on the charge itself, specifically the type, mass, and shape. Table 1 shows a series of explosive types with their chemical formulas, density, and detonation velocity. TNT is mainly employed for experimentation, noted for its use for ‘comparing energy and impulse yields of the other types of explosives’ [2]. RDX is another explosive used for experimentation. Many of the other explosives are varying forms of TNT or RDX with additives added for performance, such as aluminum for longer burn times. The effect of mass is simple for explosive energy; the more mass present at detonation, the more explosive energy is released and, thus, higher levels of pressure and heat are achieved.

Table 1.
Standard explosives with chemical composition, density, and detonation velocity [2].
The shape of the explosive is also an important factor. The typical explosive is spherical in shape; however, by changing the shape, different pressure and energy profiles can be achieved. Huang et al. [11] investigated the effects of changing the explosive shape from spherical to a slender rod with varying degrees of the slenderness ratio. This was achieved by a Multi-Material Arbitrary Lagrangian Eulerian (MM-ALE) method and verified through physical experimentation of varying explosive shapes. They found that the slenderness of the explosive directly affects the resultant pressure field’s shape with the shape becoming more and more nonlinear as the slenderness ratio increases. Additionally, the energy distribution of the slender explosive is similar to that of the spherical explosive; however, the efficacy of the energy is lower. This effect is exacerbated with distance. Overall, the research found that the shape of the explosive affects the pressure but not to such a degree that the load exhibited by the charge changed dramatically [11].
3.2. Analysis via Empirical Equations
The similitude equations, developed by the Naval Ordinance Laboratories (NOL) in the 1950s–1960s, are a series of relationships describing the behavior of shock wave pressure at a given point [4]. These equations are typically used as a form of basic validation for hydrocode for free-field UNDEX. The equations revolve around the use of a decay or time constant defined as the value of time at which a shock wave’s rate of decay drastically decreases from exponential decay [2]. The time constant’s value changes depending on the type of explosive as shown in Table 2 [4]. With these similitude equations, shock wave behavior can be approximated through hydrocode or hand calculations.

Table 2.
Similitude constants and parameters for various explosives [4].
All parameters in Table 2 follow the form shown in Equation (1).
where is the peak pressure, is the reduced time constant, is the reduced impulse, is the reduced energy flux density, is the charge weight in kilograms, and is the slant range in meters. and are similitude constants that are based on the explosive used and the parameter being examined. It is noteworthy to remember that the equations are only valid within the appropriate ranges of validity and that the equations are based on data developed from beyond 130 MPa. Additionally, the similitude equations fit into the portion of the shockwave that is beyond the hump of the wave as opposed to the entire event. Lastly, I and E are integrated to a time equal to , representing 5 times the time constant of the pressure wave.
Typically, shock waves display a reasonably replicable behavior in open-field UNDEX when it comes to the pressure-time history. The pressure acts as an exponential function of time for the UNDEX up to a certain time. This decay is approximately equal to 1/e or about 37% in the time of one decay constant. After one decay constant has passed, the pressure decays at a much slower rate [2].
While the peak pressure graph is easily replicable in free-field scenarios, the presence of structures can affect the pressure values in an UNDEX scenario due to rarefaction and reflection waves [2]. Thus, the use of free-field equations is typically used for validation of hydrocodes [4]. For example, Urgessa and Lohner [12] validated results from a computational fluid dynamics code using data obtained from physical testing results of a free-field UNDEX event.
The case of structural equations depends on the type of structures that are being analyzed. As an example, the equations used for analyzing vertical cylinders are not the same as the equations used to analyze dams. However, they are still based on the same concepts of developing from the empirical equations and from underlying physical principles such as the Navier–Stokes equations for fluid behavior. For example, Wang et al. [13] presented extensive formulas and models for the purposes of analyzing vertical cylinders subjected to UNDEX through the similitude equations and other prior known equations.
3.3. Analysis via Numerical Methods/Hydrocodes
According to Mair [14], hydrocodes are computational continuum mechanics tools that simulate the response of both solid and fluid material under such highly dynamic situations that shock wave propagation is a dominant feature. They are designed to model the environment as well as the matter during which dynamic events occur, such as UNDEX. Hydrocodes are built towards specific problems much like any intensive computer code [14]. However, there is a common architecture, methodology, and workflow between hydrocodes from how the meshes interact with materials to how the data of the problem are processed. This difference in methodology is a main form of categorizing hydrocodes in terms of their mesh generation and their treatment of data points.
Among all hydrocodes is an underlying set of processes that generate the required solutions [15]. The basic flow of work in hydrocodes relies on the Newtonian laws of motion, the equation(s) of state, and the constitutive model. These three pillars direct how matter acts in the hydrocode simulation and yield forces and respective responses. These are seen on the mesh generated by the hydrocode, which discretizes the elements present in the simulation [15]. These meshes can be generated in varying ways based on the application and, thus, elements can interact accordingly with the mesh. With the generation of the mesh as well as the element interaction comes two general forms of hydrocode categorization: Lagrangian and Eulerian.
The categorization of Lagrangian and Eulerian falls in how the mesh interacts with the elements of the hydrocode. For Lagrangian, the mesh follows the elements and remains fixed on them for the duration of the simulation [14]. The implication here is that because the mass element is fixed, the mass flux at the boundaries between elements must be calculated. Deformation of the elements (such as material deformation) causes the mesh to distort and create reductions in time steps or breakdowns in problem advancement. For this reason, the mesh tends to respond better to triangular/tetrahedral elements rather than quadrilateral/hexahedral elements due to the former being more forgiving of distortion [14]. This sort of mesh is well suited for solid structures, as the material does not distort as easily as a fluid such as water or air. Other forms of Lagrangian methods include free Lagrangian method (FLM) and total Lagrangian method (TLM), which affect mesh behavior and individual elements’ time steps, respectively [14].
On the other hand, Eulerian meshes are static in the analyses field as opposed to being fixed on the materials. This negates the problem of mesh distortion and time-step variation between cells as well as allowing for observation of bubble pulses in UNDEX. The weakness of a full-Eulerian mesh is that, because the mesh is static while the simulated materials are not, the cells become mixed between different materials and, thus, the physical characteristics inside those cells change. Additionally, the presence of solids in a Eulerian mesh creates a need for the solid structure to be defined in the mesh and, thus, have precise zoning for the solid–fluid interface [14]. Eulerian meshes are best used for fluids in meshes.
The categorization of Lagrangian and Eulerian, however, is not exclusive. A combination of the techniques used in both types of meshes can be used in both Combined Lagrangian-Eulerian (CLE) and Arbitrary Lagrangian-Eulerian (ALE) methods. CLE splits the meshes based on the materials analyzed with Lagrangian representing solids and Eulerian representing fluids. The interface between the two meshes is handled by a coupling mechanism that either develops its own elements or incorporates Lagrangian elements into the Eulerian meshes. This method has clear uses in mixed-state problems such as analyzing airplane foils’ impact from air flow or UNDEX effects on structures [14]. However, the method is weak to situations that create a rift in the Eulerian elements with the Lagrangian structures. The Lagrangian elements split the Eulerian elements apart at the cell, causing computational issues [14]. Despite this, CLE is still a popular method of simulation for UNDEX events.
The alternative to CLE is ALE, which is based on the concept of incorporating Lagrangian algorithms into a Eulerian mesh. This is done by analyzing the mesh at every time step by determining Lagrangian motion and if the mesh needs to be rezoned or not, thus combining the Eulerian and Lagrangian mesh styles. This algorithm can be performed with varying degrees of intensity by either only focusing on one material or by focusing on multiple materials with regards to mesh deformation [14]. This creates a difference of stability and computational speed. ALE is better suited for structure-fluid coupling due to the interface between the two being Lagrangian in nature rather than Eulerian; however, it can still fail in the same manner due to a ‘pinching’ nature of the Lagrangian elements when coupling the fluid-structure regions through matching element nodes [14].
Separate from the Lagrangian-Eulerian categorization is the Smoothed Particle Hydrodynamics (SPH) method. This method revolves around assigning each particle present in the mesh physical characteristics as opposed to the elements [15]. These particles are then tracked throughout the simulation and analyzed based on the forces exerted upon them. This is a form of Lagrangian analysis due to following the individual particles as opposed to the static Eulerian mesh; however, the elements in this mesh are not considered. This method is fairly simplistic due to only following the particles; however, it does run into complications when tackling complex boundary conditions and large density disparities. Despite these issues, SPH is a satisfactory algorithm for fluid problems with low densities and inflow or outflow conditions as well as problems with self-gravity such as solar systems.
Liu et al. [16] presented a smoothed particle hydrodynamics (SPH) method to simulate UNDEX problems. Their work provides extensive details on the numerical procedures, including the use of artificial viscosity, smoothing length evolution, treatment of solid boundary, material interface consideration, and the Leapfrog time integration scheme. They showed the effectiveness of the SPH method using three case studies: one-dimensional TNT slab detonation, underwater explosion in free space, and underwater explosion in a confined chamber.
Afrasiabi and Mohammadi [17] presented a newly developed stabilized SPH method by implementing a velocity field smoothing technique. They also incorporated an adaptive smoothing length and the penalty force exertion scheme. The stabilized SPH method was applied to analyze spatial and temporal variations of density, pressure, internal energy, and velocity in UNDEX in addition to bubble formation and evolution.
Zhang et al. [18] used SPH to simulate a shaped-charge detonation, formation of a metal jet, and penetration of a steel plate in UNDEX. The SPH method was shown to be effective because the numerical simulation results were all in good agreement with experimental results.
4. Structures Encountered in UNDEX Analysis
Due to the nature of threats that UNDEX can present, the types of structures that can be affected are numerous. In this paper, the following structures are discussed:
- Ships;
- Concrete dams;
- Reinforced concrete (RC) slabs;
- Reinforce concrete/bridge columns;
- Miscellaneous structures.
4.1. Ships
Ships are a popular subject for analysis in UNDEX events. The prevalence of naval military conflict as well as accidents creates a need for inspections on ships’ abilities to withstand UNDEX. As noted before, it is unwieldy to do physical testing on a full-sized ship, so smaller models are typically used as study subjects and references for hydrocode. For example, Ming et al. [6] used air-backed steel plating to examine UNDEX effects on a ship’s hull. The tests generated a series of damage profiles of a ship subjected to UNDEX effects, mainly characteristics of bulging, discing, and petaling. Steel cylinders is another option for analyzing steel behavior or as a rudimentary model of an entire ship’s body, more specifically submarines. As an example, Gannon [19] used this approach for hydrocode verification on submarine analysis. These models are then used for verification of hydrocode models and have been found to be reliable tools for analyzing ship response. The important note in comparing the analysis of ships to civil infrastructure such as concrete structures is that the behavior of steel is linear or plastic unlike concrete [19]. So, while the methodology of the experimentation to data collecting is the same, the specific equations and relationships will differ considerably. Despite that this review paper’s focus is on the response of concrete structures to UNDEX, the prevalence of ship analysis is noteworthy.
4.2. Concrete Dams
Among the concrete structures analyzed for UNDEX in literature, dams are among the most common due to the verification of their safety for terrorist attacks and structural failures. While dams suffer from the same logistical issues as ships, the solution of creating scaled-down models involves the usage of centrifugal modeling, as described in a previous section. Additionally, the nonlinear behavior of concrete compared to steel creates a need for a different computational model through differing hydrocodes and equations of state.
Vanadit-Ellis and Davis [9] verified the centrifugal laws for dams through the use of practical models and hydrocodes. The model dams were made in-house through a basic concrete pour over a wooden mold and steel base plating. These models were then subjected to hardness tests to verify strength, then subjected to UNDEX yielding. The concrete can fail in three ways: material failure due to crushing/spalling, localized failure due to tensile/shear stresses, and structural failure due to tensile bending stresses.
It was found that these failure modes had different intensities depending on the stand-off distance of the explosion as well as the thickness of the dam [9]. For thick panels, detonations nearby the panel surface can cause the concrete to fail due to crushing and back-face spalling due to coupled stresses moving directly through the concrete. For thinner panels and slightly greater stand-offs, the panels fail in a “punching shear” mode, which is localized for relatively small charges. For still greater stand-offs, the pressures applied to the panel are too low to cause either of the first two modes of failure but are distributed over an area wide enough for the total load to break the panel in a beam-type (or cantilever) structural bending failure. It was found that the centrifugal laws accurately depicted the structural response of a concrete dam and that the experimental data provided can be of use for further research purposes as hydrocode validation [9].
Ren et al. [20] studied the numerical verification of hydrocode based on dam analysis. This verification was undertaken by comparing Vanadit-Ellis and Davis’ physical experiment and Ren’s hydrocode. Ren’s code differentiates itself through modeling the dam completely as opposed to analyzing the dam in stages or ‘slices’. This was achieved using a 3D full coupling model developed through ABAQUS, allowing for the full 3D damage profiles of the dam to be obtained, which cannot be done with the slice method. This model was then subjected to simulated UNDEX and analyzed using a rate-dependency damage-plasticity model that then generated the damage and failure data. It was found that this series of methods accurately represented the same data that were physically determined by Vanadit-Ellis and Davis. Ren et al. found that dams affected by UNDEX suffer mainly tensile damage, which is concentrated in the upstream surface of the dam as well as the dam head. This damage decreased with increased stand-off distance, but also increased the number of abnormal data points in the breach area. Ren recommended the countermeasures of increased tensile strength as well as reinforcement of the dam head, upstream surface, and the inside part of the dam [20].
Due to the nonlinear nature of concrete, analyzing it within hydrocode can pose problems due to simulations failing for a variety of reasons such as suboptimal damage models or oversimplification. The development of a concrete damage plasticity (CDP) model could solve those problems through accurately modeling the concrete throughout various states such as compression, tension, and other effects. This model was put forward by Moradloo et al. [21], who designed a set of behaviors, parameters, damage and stiffness recovery algorithms, and governing equations to accurately depict concrete throughout the UNDEX event. This model was verified through testing an UNDEX event on an aluminum cylinder similar to the experiment performed by Kwon and Fox examined by Evans [4]. The model was then used to model an arch concrete dam that was then subjected to a series of UNDEX simulations. It was found that the CDP model was valid with the simulations put forward with the analysis of the damage profiles showing similar behaviors from previous dam research such as increased damage with increased stand-off distance. Additionally, charge depth increased the damage of the dam due to the bubble pulse not venting towards the surface and instead the energy imparting onto the reservoir face [21].
4.3. Reinforced Concrete (RC) Slabs
RC slabs are used as load-bearing members for many marine structures such as docks, piers, and factories. Thus, an examination on their UNDEX resistance should be examined. Hai et al. [22] studied the damage profiles of air-backed RC slabs. To develop proper data for these profiles, physical experimentation was done by subjecting an RC slab that was air-backed on one side and submerged in water on the other to an UNDEX event. This experiment yielded pressure-time and strain-time histories that were replicable in LS-DYNA through a hydrocode simulation. This hydrocode simulation was then used to conduct a more thorough investigation into the UNDEX event and its effects on the slab. It was found that much of the displacement of the slab occurred during the bubble pulse timing and not due to the initial shock wave. Additionally, increased stand-off distance exacerbated the damage on the RC slab with the concrete nearest to the charge location being crushed during the shock wave and having cracks propagate throughout the rest of the UNDEX event [22]. Hai et al. also developed two different computational models for capturing the failure of concrete. One model was based on the concrete damage-plasticity model (CDPM). This model allows for the concrete to be accurately simulated through multi-axial and rate-dependent loadings. This is done through a series of stress-strain equations and classical damage parameter equations. The other was based on the bond-based peridynamic (PD) theory that replaces the partial differential equations that are the typical standard for modeling concrete with integral equations. The PD model uses a series of equations relating the density of body, displacement vector, the peridynamic horizon, body force density, and the pairwise bond force density to form its material defining equations [22]. The PD model came from a need for a model that can accurately model cracks, fractures, and other discontinuities that could not be modeled by classic continuum mechanics. The integral equations remain valid throughout the failure process of the concrete and thus are a good choice for modeling the RC slabs [22]. Both of these models were found to be sufficient for modeling concrete as it undergoes the UNDEX event.
Zhao et al. [23] conducted a series of experiments regarding proper modeling of RC slabs. This comparison was conducted by analyzing the damage profiles of each method of an RC slab subjected to both UNDEX and air explosions (AIREX) [23]. This was done through testing the hydrocode formulations of CEL, SPH, and coupled finite element method-SPH (FEM-SPH). The benefit of FEM-SPH over standard SPH is that the FEM nodes can model the smaller deformations while the SPH particles model the larger deformations as well as the model explosion [23]. Both sets of nodes and particles are linked to each other and exchange information, allowing them to complete the same calculations as standard SPH at a faster time. Due to this trait, it was found that the FEM-SPH method is best at modeling as it is faster than SPH and more accurate than the CEL method, which was found to be unable to properly model the steel reinforcements inside the tested RC slab [23]. The results of the damage profile as well as the analysis of the RC slab’s behavior during the UNDEX event were investigated. It was found that under UNDEX, the main failures were through spalling and punching failures with areas of the slab, notably the top surface and the lower layer steel reinforcement, which suffered heavy damage and complete failure [23].
4.4. Reinforced Concrete/Bridge Columns
RC columns, like RC slabs, are used as load-bearing members of structures and thus can be vulnerable to blast loadings. While the effects of air blasts on RC columns are well-known, UNDEX effects are less documented. Yang et al. [24] analyzed RC columns under both of these effects. For the UNDEX analysis, a fully coupled 3D Lagrangian and Eulerian numerical method was used to simulate its effects on RC columns with varying cross-sections. This numerical model was validated through the use of physical experimentation conducted on an RC column with a square cross-section of 400 mm by 400 mm [24].
The numerical CLE model was found to be accurate through a comparison of the damage profiles and dynamic response of both the numerical and experimental methods. With the numerical model verified, analysis of the different RC columns was conducted with a focus on cross-section shapes. It was found that circular cross-sections worked best for anti-knock purposes due to the diffraction of the shock waves and the compounding of stress waves in the square RC column from the corners of the column. Furthermore, Yang et al. conducted a parametric study on anti-knock measures and their effectiveness. This was done by examining varying concrete properties, reinforcement spacings, and reinforcement thickness. It was found that the use of ultra-performance concrete works best for damage control with decreasing the reinforcement spacing with introducing more reinforcements to the column being the next best measure [24].
Zhuang et al. [25] studied the dynamic response and damage model of circular RC columns through physical experimentation of UNDEX effects on a scaled-down RC circular column and a steel column. The main consideration for the physical experimentation was the load distribution; thus, the data for pressure, acceleration, strain, and displacement were used. The RC column and steel column were subjected to charges with varying masses between 0.05 and 0.8 kg depending on the experimental parameters and purpose set. Due to the expectation that the RC column would deform under UNDEX while the steel column would not, the displacement, acceleration, and strain sensors were placed on the RC column while the pressure sensors were placed on the steel column [25]. These columns were then subjected to UNDEX and the data sets for displacement, acceleration, strain, and pressure were recorded.
The physical data suggest that the shock wave loading refracts due to the round surface of the column with the diffracted pressure being less than that of the shock pressure. This observation is affected by the explosive quantity, proportional stand-off distance, and the detonation depth. Additionally, the bubble pulse is severely hampered due to the proximity of the air–water surface, which causes the energy caused by the bubble pulse to be dispersed upwards into the air as opposed to into the column. This causes low explosive quantities to generate smaller bubble pulses and thus less energy, while higher explosive quantities create a larger bubble pulse that vents to the surface and thus does not create a fully realized bubble pulse. Lastly, Zhuang et al. drew several relationships for predicting shock wave load including the neglecting free surface effects due to explosive quantity and detonation depth, the inverse relation of the diffraction coefficient (equal to the ratio of shock wave peak pressure and diffracted shock wave pressure) with proportional stand-off distance following the least square method, and the calculation of net peak pressure of the shock wave through the reflected and diffracted shock wave peak pressures [25].
With the physical data, a series of parametric studies was performed with an analysis on the effects of explosive quantity, stand-off distance, detonation depth, and proportional stand-off distance on the damage profiles of the columns. The damage and displacement of the RC column was increased with increased explosive quantity. It was found that for explosive quantities, a weight of 0.2 kg of TNT caused the existence of two separate pressure peaks in the pressure-time graph (with the second peak being caused by bubble pulse), while any amount above that resulted in only the shock wave being seen. This correlates with the observations mentioned earlier. For increasing stand-off distance, the shock wave load decreased dramatically with decreased stand-off distance, with the reflected and diffracted shock wave loads acting similarly. With regard to the detonation depth, the larger detonation depths resulted in higher bubble pulse effects with an observed critical value of non-dimensional detonation depth (ratio of detonation depth and cube root of charge mass) of 1.71 below which no bubble pulsation effects were observed. Additionally, once the detonation depth reached a value below 0.34 m, it was considered a non-factor with regards to damage.
The damage profiles observed indicated failure modes of bending, bending shear, and punching. These failure modes take different priorities depending on the situation. Bending failures typically took precedence in situations of small charge masses and large stand-off distances. Shearing failure occurs near the ends of the columns with an increase of charge mass and decrease in stand-off distance. Finally, punching failure occurs after the stand-off distance is within a certain threshold [25].
Further research into damage effects, and specifically safety distances, has been conducted by Loomis [8] for the purposes of bridge safety from UNDEX. This study was conducted through a CLE numerical model developed through DYSMAS that includes sand elements as well as the titular air, water, explosive, and concrete elements. This model is a representation of the foundations of a concrete bridge and thus would accurately depict UNDEX effects. The model also generates a damage parameter for each element that determines the damage state of that element. It was found that the damage parameter will rise as long as the simulations are able to run due to concrete’s tendency to degrade from crumbling past the UNDEX effect [8]. This is critical as this allows for long-term damage effects to be simulated. Through the simulation of this model, two parametric studies were conducted: a depth study and a sensitivity study. For the depth study, the depth and stand-off distances of the explosive charge (50 kg of TNT) were varied from shallow to deep depths and near to far stand-off distances. Damage was measured through measuring stress of each foundation element during and after the UNDEX event. It was determined that the configuration of intermediate depth and nearby stand-off distance creates the most damage. This is due in part to the weakness of the foundation corners, which causes more load to be imparted onto the top and sides of the foundation. The nearby stand-off distance ensures that the UNDEX shock wave is not excessively dissipated by the water before reaching the foundation. Additionally, the deep depth caused relatively little damage due to the shock wave, only hitting the sides of the foundation and the deeper depth, thus causing more energy to be expended overcoming the higher hydrostatic pressure [8].
The sensitivity study was split into three sub-categories: the load sensitivity, the reinforcement orientation sensitivity, and the reinforcement volume fraction sensitivity. These were done in order to develop the parameters for an accurate, high-fidelity model. The load sensitivity was conducted through applying five different loads onto the foundation to analyze the change in the damage parameter. It was found that the damage parameter did increase with increased load but to such an extent that it was considered insensitive to the load changes and, thus, the models were not changed with varying load sizes. The reinforcement orientation study found that the z-direction rebar placed perpendicular to the shockwave was the most critical element in the reinforcement assembly and should be depicted most accurately within the model. Lastly, the reinforcement volume fraction was analyzed. It was found that as the reinforcement volume fraction increased, the damage parameter decreased at varying rates [8].
A practical example of a load-bearing column would be an RC pile, which is typically used to support structures over water such as docks or wharfs. In the case of UNDEX targeting these piles, the structural response would be similar to that of a typical RC column under similar conditions. Yan et al. [26] conducted research on the RC pile with an analysis on the effects of various parameter alterations on the safety distance of the UNDEX. This was done by physical and numerical modeling. The physical model was an RC concrete column submerged partially with water and subjected to near-field UNDEX. The numerical model consisted of a CLE model designed with AUTODYN that incorporates the standard elements of air, water, explosives, and concrete. The model was verified through the comparison of the final displacements and damage of both the physical and numerical models undergoing the same UNDEX event. It was found that the models correlated, and the numerical model was satisfactory.
The numerical model was then used to conduct a series of studies regarding the damage and failure assessments of the RC pile as well as certain effects on the safety distance of the piles. The damage and failure assessments of the RC piles found that with near-field UNDEX, local failure would take precedence and gradually give way to bending then shearing failure as the stand-off distance was increased. Additionally, the damage on the concrete increases with increased depth with more damage being shown at the bottom end of the pile. It was also found that most of the damage was caused through the bubble pulsation event, not the shock wave. Through this analysis, an assessment method for the damage called the damage index was used to perform the damage analysis, which also found that increased stand-off distance decreased damage. With the results of the damage and failure analyses, a series of parametric studies were conducted with a focus on the safety distance. The parameters examined were the charge quantity, blasting depth, steel hooping ratio, concrete strength, and longitudinal reinforcement ratio. It was found that the safety distance shared a direct relationship with the charge quantity while holding an inverse relationship with the steel hooping ratio, concrete strength, and longitudinal reinforcement ratio [26]. The relationship with the safety distance and the blasting depth initially starts as inverse but becomes direct as the depth increases. With these parameters, a safety distance formula was proposed.
4.5. Other Structures
Wang et al. [12] focused on the development of a substructure method for analyzing the transient response of cylinders undergoing UNDEX shock waves. This was done through a numerical model that was verified via a comparison of the numerical response and the results of the Liaw and Chopra [27]. The numerical model was developed through AUTODYN and mathematical formulation. It was found that there are three sub-pressure waves that occur in UNDEX that affect the cylinders: the incident shock wave pressure, the scattered wave pressure, and the radiation pressure from the cylinder displacement during the UNDEX event. It was also found that the transient response can be reduced through the stand-off distance of the charge and the radiation wave, with the effects being more apparent for slender cylinders [12].
Explosive effects on underground structures such as tunnels are also a concern. These explosive effects can be tested physically through the use of a centrifuge similar to the Vanadit-Ellis/Davis experiments. De et al. [10] developed a series of experiments involving physical and numerical simulation of a tunnel covered in soil that was then covered in water [10]. The physical simulation was performed with the use of a geotechnical centrifuge, which allowed the physical experiment to make use of the centrifugal scaling laws similar to those used in the dam experiments by Vanadit-Ellis and Davis and Ren [9]. Data collection on the physical model included a series of strain gauges and pore pressure transducers. The resultant data were then used to develop a model in ANSYS using the CLE method. Multiple parametric studies were conducted to develop relationships between the various materials present in the simulation. It was found that the depth of the water simultaneously increased the total pressure imparted by the explosive charge on the tunnel and created higher strain within the soil [10].
5. Conclusions
This paper presents a state-of-the-art review of the research on UNDEX effects on structures with a particular focus on concrete structures. The fundamentals of the UNDEX event and the analysis models are presented. The UNDEX event is a multi-step process with each step being impactful to the entire scope of the event. Physical experimentation is difficult due to the nature of UNDEX; however, proper facilitation and mathematical scaling laws allow for physical models to be fabricated. Variations in computer algorithms and hydrocodes have allowed these events to be accurately portrayed in a variety of cases and successfully resemble the physical experiments. Steel and concrete structures are the standard subjects of analysis with the behavior of both varying due to their physical properties. Several concrete structures, including dams, columns, and slabs subjected to UNDEX are discussed with brief descriptions provided for the studies presented on ships and tunnels. Further direction for research could include the exploration of UNDEX effects on wooden structures, further testing on anti-blast measures such as high-performance composite fibers, and testing of explosive effects in partial submerged scenarios.
Author Contributions
Conceptualization, J.S. and G.U.; methodology, J.S.; resources, G.U. and R.L.; data curation, J.S. and G.U.; writing—original draft preparation, J.S.; writing—review and editing, G.U. and R.L.; visualization, J.S. and G.U.; supervision, G.U.; project administration, G.U. and R.L.; funding acquisition, G.U. and R.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge a grant received from the Defense Threat Reduction Agency supporting this work.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Cole, R.H.; Weller, R. Underwater Explosions. Phys. Today 1948, 1, 35. [Google Scholar] [CrossRef]
- Costanzo, F.A. Underwater Explosion Phenomena and Shock Physics. In Structural Dynamics; Proulx, T., Ed.; Springer: New York, NY, USA, 2011; Volume 3, pp. 917–938. [Google Scholar]
- Cooper, P.W. Explosives Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Evans, A. Structural Response in Underwater Explosions; George Mason University: Fairfax, VA, USA, 2017. [Google Scholar]
- Hsu, C.-Y.; Liang, C.-C.; Nguyen, A.-T.; Teng, T.-L. A numerical study on the underwater explosion bubble pulsation and the collapse process. Ocean. Eng. 2014, 81, 29–38. [Google Scholar] [CrossRef]
- Ming, F.; Zhang, A.; Xue, Y.; Wang, S. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions. Ocean. Eng. 2016, 117, 359–382. [Google Scholar] [CrossRef]
- Brett, J.M.; Buckland, M.; Turner, T.; Killoh, C.G.; Kiernan, P. An Experimental Facility for Imaging of Medium Scale Underwater Explosions. Defence Science and Technology Organisation Victoria (Australia) Platform Sciences Lab. 1 May 2003. Available online: https://apps.dtic.mil/sti/citations/ADA417894 (accessed on 1 August 2021).
- Loomis, J.B. Impact of Underwater Explosions on Concrete Bridge Foundations. Naval Postgraduate School Monterey ca Monterey United States. 1 June 2016. Available online: https://apps.dtic.mil/sti/citations/AD1026694 (accessed on 1 August 2021).
- Vanadit-Ellis, W.; Davis, L.K. Physical modeling of concrete gravity dam vulnerability to explosions. In Proceedings of the 2010 International WaterSide Security Conference, Carrara, Italy, 3–5 November 2010; pp. 1–11. [Google Scholar]
- De, A.; Niemiec, A.; Zimmie, T.F. Physical and Numerical Modeling to Study Effects of an Underwater Explosion on a Buried Tunnel. J. Geotech. Geoenviron. Eng. 2017, 143, 04017002. [Google Scholar] [CrossRef]
- Huang, C.; Liu, M.; Wang, B.; Zhang, Y. Underwater explosion of slender explosives: Directional effects of shock waves and structure responses. Int. J. Impact Eng. 2019, 130, 266–280. [Google Scholar] [CrossRef]
- Urgessa, G.; Lohner, R. Preliminary Efforts in Validation of Feflo for Underwater Explosion; Auburn University: Aubur, AL, USA, 2020. [Google Scholar]
- Wang, P.; Zhang, Z.; Yan, Q.; Zhang, C. A substructure method for the transient response of vertical cylinders subjected to shock wave of underwater explosion. Ocean. Eng. 2020, 218, 108128. [Google Scholar] [CrossRef]
- Mair, H.U. Review: Hydrocodes for Structural Response to Underwater Explosions. Shock. Vib. 1999, 6, 81–96. [Google Scholar] [CrossRef] [Green Version]
- Collins, G.S. An Introduction to Hydrocode Modeling; Imperial College London: London, UK, 2002; pp. 2–11. [Google Scholar]
- Liu, M.; Liu, G.R.; Lam, K.Y.; Zong, Z. Smoothed particle hydrodynamics for numerical simulation of underwater explosion. Comput. Mech. 2003, 30, 106–118. [Google Scholar] [CrossRef]
- Afrasiabi, M.; Mohammadi, S. Analysis of bubble pulsations of underwater explosions by the smoothed particle hydro-dynamics method. In Proceedings of the ECCOMAS International Conference on Particle Based Methods, Barcelona, Spain, 25–27 November 2009. [Google Scholar]
- Zhang, Z.; Wang, L.; Silberschmidt, V.V. Damage response of steel plate to underwater explosion: Effect of shaped charge liner. Int. J. Impact Eng. 2017, 103, 38–49. [Google Scholar] [CrossRef] [Green Version]
- Gannon, L. Simulation of underwater explosions in close-proximity to a submerged cylinder and a free-surface or rigid boundary. J. Fluids Struct. 2019, 87, 189–205. [Google Scholar] [CrossRef]
- Ren, X.; Shao, Y. Numerical Investigation on Damage of Concrete Gravity Dam during Noncontact Underwater Explosion. J. Perform. Constr. Facil. 2019, 33, 04019066. [Google Scholar] [CrossRef]
- Moradloo, A.J.; Adib, A.; Pirooznia, A. Damage analysis of arch concrete dams subjected to underwater explosion. Appl. Math. Model. 2019, 75, 709–734. [Google Scholar] [CrossRef]
- Hai, L.; Ren, X. Computational investigation on damage of reinforced concrete slab subjected to underwater explosion. Ocean. Eng. 2020, 195, 106671. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, G.; Lu, W.; Yan, P.; Chen, M.; Zhou, C. Damage features of RC slabs subjected to air and underwater contact explosions. Ocean. Eng. 2018, 147, 531–545. [Google Scholar] [CrossRef]
- Yang, G.; Wang, G.; Lu, W.; Zhao, X.; Yan, P.; Chen, M. Cross-section shape effects on anti-knock performance of RC columns subjected to air and underwater explosions. Ocean. Eng. 2019, 181, 252–266. [Google Scholar] [CrossRef]
- Zhuang, T.-S.; Wang, M.-Y.; Wu, J.; Yang, C.-Y.; Zhang, T.; Gao, C. Experimental investigation on dynamic response and damage models of circular RC columns subjected to underwater explosions. Def. Technol. 2020, 16, 856–875. [Google Scholar] [CrossRef]
- Yan, Q.; Liu, C.; Wu, J.; Zhuang, T. Experimental and Numerical Investigation of Reinforced Concrete Pile Subjected to Near-Field Non-Contact Underwater Explosion. Int. J. Struct. Stab. Dyn. 2020, 20, 2040003. [Google Scholar] [CrossRef]
- Liaw, C.-Y.; Chopra, A.K. Dynamics of towers surrounded by water. Earthq. Eng. Struct. Dyn. 1974, 3, 33–49. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).