Abstract
Complex networks make an enticing research topic that has been increasingly attracting researchers from control systems and various other domains over the last two decades. The aim of this paper was to survey the interest in control related to complex networks research over time since 2000 and to identify recent trends that may generate new research directions. The survey was performed for Web of Science, Scopus, and IEEEXplore publications related to complex networks. Based on our findings, we raised several questions and highlighted ongoing interests in the control of complex networks.
1. Introduction
Network science [1] has become an important field of research in the last 20 years [2,3] and is the result of the convergence of many other research fields [4]. Network science is “the study of the theoretical foundations of network structure/dynamic behavior and the application of networks to many subfields” [4] (p. 5). The study of networks has roots in graph theory [5] since real-world networks can be mathematically represented by graphs [6,7].
Network science provides powerful methods that transform our understanding of complex systems [8]: complex networks (CNs) are a subset of complex systems [9], and many complex systems can be described using network structures [10]. Complex networks are systems that provide a universal language to understand patterns of interaction [7], organization, and network topology [11].
Complex systems consist of individual entities (subsystems), self-organize, are large scale, emergent, nonlinear, and heterogeneous, and have no single point of control [9,12,13]. Complex systems can be defined as systems “in which there are non-trivial relationships between cause and effect: each effect may be due to multiple causes; each cause may contribute to multiple effects; causes and effects may be related as feedback loops, both positive and negative; and cause-effect chains are cyclic and highly entangled rather than linear and separable” [14] (p. 14). Usually, complex systems’ definitions emphasize the interconnections between (many) component subsystems, whether they focus on causality, nonlinearities, scale, resilience, or nestedness.
Complex networks are networks with nontrivial topological features [15,16]. Real-world complex networks are ubiquitous in our everyday lives [15] and share several common characteristics [17], such as small-world [18], scale-free [19], hierarchical structure [20], etc. Examples of real-world complex networks include the Internet, electric power grids, metabolic networks, supply chains, the world trade web, and urban road networks, among many others [21].
Emergence is an essential characteristic of complex systems [22] and a basic feature of complex networks [23], reflected in system-wide processes such as evolution, adaptation, or self-organization [12]. Strong emergence is a holistic property of the complex system as a whole, irreducible to its component subsystems, whereas weak emergence is the predictable integration of intrinsic properties of the subsystems and their localized interactions [24]. Emergence can be defined as “the phenomena that emerges (is not reduced) from nonlinear interactions among (large-scale) lower-lever inter-independent components and can be observed only in higher or system level” [12] (p. 3577).
In the world of complexity, systems of systems (SoSs) [25] and complex networks are terminologically different, but in actuality, the difference between them is found in the way each of them reflects the concept of multi-resolution. SoSs focus on nestedness, while CNs on clusters, seemingly “flatter” in structure than SoSs [26]. In actuality, access to a CN cluster works the same as access to a nested component of an SoS: few paths into a smaller world of interconnected processes. The control issues of SoSs apply to CNs, revealing an ever-increasing need for specialized tools and frameworks. As such, control engineering faces challenges related to heterogeneity (pertaining to structure, information, and resource access, communication and interaction methodologies), remote monitoring and control, scalability, geographical distribution (in the case of large-scale systems), flexibility, and configurability [27].
The aim of this paper was to survey the interest in control related to complex networks research over time since 2000 and to identify recent notable contributions that may generate new research directions. To understand the evolution of research in the field of network science, we extracted the number of publications for each year since 2000 and until the present from the following digital libraries: Web of Science [28], Scopus [29], IEEEXplore [30], and ACM-DL [31]. We considered the following keywords as our survey was focused on emergence and complex network control contributions: “Network Science”, “Complex Network”, “Complex Network Control”, “Networked Control”, “Decentralized Network Control”, and “Distributed Network Control”. Table 1 and Figure 1 show comparative results. We noticed that for ACM-DL, the six keywords returned similar numbers and trends, indicating a possible overlap in the returned results, and so were deemed unsuitable for comparative analysis.

Table 1.
Network-Science-related publications on the Web of Science, Scopus, and IEEEXplore from 2000 to 2021.
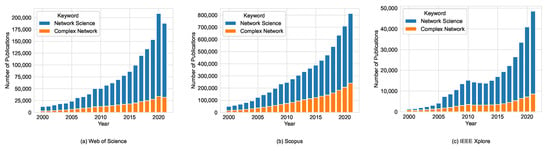
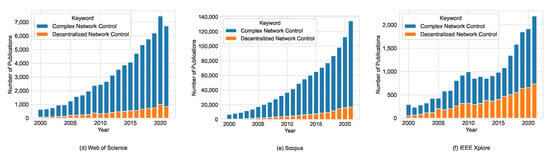
Figure 1.
Total number of “Network Science” related publications over time from 2000 to 2021.
Although complex networks is one of the main topics of network science, we noticed that many authors do not use the word complex when referring to complex networks. As shown in Figure 1a–c, the number of papers using the “Network Science” keyword is higher than the number of papers using the “Complex Network” keyword. For instance, papers related to neural networks [32], wireless networks [33], supply chain networks [34], social networks [35], etc., used complex networks and graph theory concepts.
This survey is structured as follows: Section 2 presents contributions to the field of networked control systems. Section 3 present contributions to the control of complex networks. Section 4 discusses decentralized control in the context of complex networks. Section 5 presents open research questions and Section 6 the conclusions.
2. Control vs. Networks
2.1. Control vs. Networks: Are We Speaking the Same Language?
The control vs. networks problem is a historical coin with two facets: (a) control of the network and (b) control over the network [36]. Despite intersecting characteristics, this disambiguation is necessary due to the intrinsically dichotomous nature as processes and as approaches to solving the control problems.
Control of the network revolves around the challenges posed by the communication network [36]. This field studies problems that deal with the network itself, which can lead the system to instability and low performance: data transmission, management and routing of data packages, connectivity and security, and communication delays.
Control over the network refers to distributed and decentralized control design based on a physical network [36]. This field deals with control problems within a network, seen as an interconnected and interacting set of subsystems, with issues related to network overload, available processing power, delays, and bandwidth.
In the world of control theory and applications, a hefty portion of current research is centered on the control of the network, rather than design methodologies for control systems structured as complex networks. If, for instance, a handful of cascaded loops are difficult to design, how does this translate to networks of hundreds or thousands of loops? Interestingly, the overlap between control of and over the network resides in delays. An indubitable source of closed-loop instability, delays generated by communication can affect the performance of a control system that uses said network. An improperly managed communication medium impedes the achievement of control objectives, and as a result, these two fields have somewhat merged in applications.
A note on terminology: even though publications [37,38,39] often classify networked control systems in these two categories, control of the network would be more accurately referred to as network control, while control over the network would be networked control. The first one uses a noun, the second one an adjective, signifying a property rather than a type of process. In network science terms, the first category deals with the edges (the medium for information transmission), while the second one with the nodes (each local loop as a whole, i.e., the connected set of plant, sensor, controller, and actuator). In what follows, we use the acronym NCS to mean control over the network.
In the mid-to-late 2000s, along with the increase in computing power, control of complex networks emerged (Figure 1). The question now is: Where does it fit? Is it about connectivity, managing states, or something entirely different?
2.2. Control of the (Communication) Network
Communication networks are defined as (large) sets of interconnected nodes capable of receiving and transmitting information [40]. They predate the concept of control over the network [40], have been and still are well studied [41], tackled from the synchronization [42], load balancing (routing, scheduling) [43], and structural (topology) [44,45,46,47,48,49] perspectives, with implementations in wired (e.g., telephone, cable, computer) or wireless (e.g., mobile communication, sensors) forms. From the control angle, communication network challenges concern real-time performance, traffic management, and communication protocols. While the terminology might appear different, the underlying issues to be solved are the same.
Real-time operation of networks as the backbone of communication for control systems introduces performance requirements related to the time in which information is produced (by the control system components) and transmitted (by the network) and translates to time synchronization issues across the network [50], or more precisely, the phase and frequency synchronization of tick generators [40,51]. Recent surveys indicate an increasing interest toward wireless networks [52,53,54,55,56].
Traffic management aims for efficient communication without congestion. Load balancing solutions [40] look at both real-time traffic distribution throughout the network and at the computational resource distribution of the nodes, or resource allocation problems [57]. Oftentimes, the latter leads to sacrificing node performance for the sake of network optimization [58]. Recent surveys look at wireless networks [59] and redefining network architectures to manage big data loads, i.e., software-defined networks [60].
Communication protocols require compatibility across nodes, infrastructure, and transmission mediums and usually prescribe to ensuring real-time performance and traffic management requirements [61,62]. Security is an overarching issue with rapid-paced research as new loopholes are exposed [63,64,65].
2.3. Control over the Network
Over-the-network NCSs are control systems where the loop is closed through a real-time communication network (Figure 2). They exist outside the restrictions of the traditional point-to-point wired control structures [66]. The key advantage of NCSs is that the required information, no matter its type or purpose, is exchanged through a network between the loop components (sensors, controllers, actuators, etc.). Other benefits that put NCSs in the spotlight of the research community relate to the decentralization of control, resource sharing, remote operation, reduced wiring and simple installation, modularity, mobility, flexibility in introducing or removing components to and from the network, and the easy design of large-scale control systems [26,67,68].
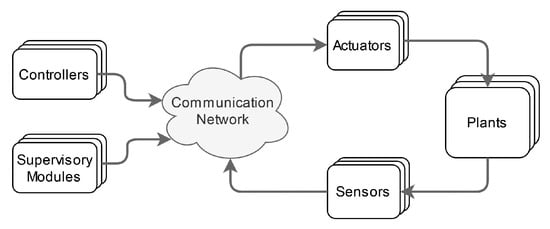
Figure 2.
Networked control systems concept.
NCSs exist over a shared communication network and have remote control capabilities. The NCS design process aims to ensure quality of service (e.g., efficient transmission rates, minimal communication errors) and quality of control (loop performance) [69]. While performance requirements can be described for each control system, their placement in the network comes with a series of challenges [68]. Issues such as packet loss and synchronous communication are solved within the design communication network itself (i.e., the control of the network field). However, two types of network-introduced challenges affect the very performance of the control loops that are ultimately reflected in the controller computation: asynchronous behavior and time delays.
Asynchronous behavior in NCSs has two causes: data quantization generating different sampling times for the nodes and event-triggered methods. The latter appeared in response to the Zeno behavior, in which excessive redundant commands or sensor measurements are transmitted in between loop components, exercising unneeded strain on actuators and increasing network traffic unnecessarily [70]. A widely adopted solution against the Zeno behavior is known as event-triggered control [70,71,72,73], which functions based on the principle that information should be sent over the network only when an event (internal, for instance a change in operating point, or external, for instance a disturbance) has caused a marginally significant change in the variable to be transmitted. Both heterogeneous sampling times and event-triggered communication demand asynchronicity from the communication network, which, at first glance, might seem incongruous with the synchronization requirement. The solution arrived from real-time control [74,75,76,77,78,79], which, through effective combinations of deadlines and interruptions, allows for the asynchronous behavior of control systems to be compatible with the synchronous functioning of the communication network.
Time delays generated by the communication network affect the control loops as any other time delays, pushing them closer to instability regions [80]. They are caused by node processing (stalling task execution), queuing (waiting to access resources), transmission, and propagation (paths through multiple nodes) [81,82]. Moreover, these time delays can be constant, varying, random, and usually difficult, if not impossible, to estimate even though attempts are found throughout the literature [27,83,84,85,86,87]. Controller designs that account for network-induced delays are also widespread, ranging from formal robust and optimal control, to intelligent and heuristic approaches [88,89,90,91,92,93,94,95]. A recent survey [96] summarized time delay approaches to NCSs and how they fit with event-triggered and scheduling methods.
Issues of security and safety are also tackled in NCSs. Approaches based on control systems principles have been popular, ensuring network resilience against attacks [97,98,99,100,101,102,103], and complementing fault tolerance research [104,105,106,107,108,109].
A large amount of research on control systems has made use of the NCS’s features and benefits in the past two decades, with the popularity of the field reflected in a plethora of surveys every few years that either discuss NCSs in overview or focus on particular issues [26,36,37,38,39,67,68,110,111,112]. Although it is not clear yet how the rise in complex networks affects general NCSs, we expect overlapping issues to make way for an increase in the diversity and ingenuity of control approaches and applications.
2.4. Predictive Control: A Deserving Hero
In NCSs, the need to integrate the management of time delays in the controller design [110,113] has been answered, among others [114], by predictive control approaches. In this survey, we focused on predictive control because it has the capacity to maintain control performance even for unknown and varying time delays. The main (and better-known) types of control systems with predictive properties are model predictive control (MPC) and Smith predictors. Where MPC has most often a discrete implementation, Smith predictors are usually continuous controllers, although the opposites exist. They are both based on a priori knowledge of the plant model and time delays, but display robustness to variance in time delay.
MPC controllers are inherently robust, offering optimal or suboptimal solutions with good performance even when disturbances are unknown [115] or uncertainties are significant [116]. Networked MPC considers various configurations: event-triggered [117], buffered [118], and nonlinear [119]. While specific surveys on networked MPC have eluded our searches, MPC techniques are included in NCS surveys [120,121], and the literature makes up for it in application diversity [122,123,124,125,126,127,128,129,130,131].
A properly tuned Smith predictor can maintain loop stability and performance for significant variations of time delay [132] or even for unknown or assumed plant dynamics [133]. Application to NCSs range from UAV network control [134], packet loss management [135], combinations with generalized predictive control [136] or fuzzy controllers [137], and others [138,139,140,141].
In light of these results, we have to wonder: Will predictive control be the instigator of merging requirements for both NCSs and communication networks? Moreover, since time delay management is performed at the node level in the predictive approach, it raises the question whether the future of the combined control of and over the network fields resides in complete decentralization for both.
3. Control of Complex Networks: Is Emergence Lost?
Complex networks consist of vertices (nodes) and edges (links) [17]. Information, energy, or matter is processed by the nodes and transmitted through the links. The manner in which these processes are understood and represented dictates the type of models, control, and purpose of control for complex networks.
Many natural complex systems are important to everyday life and can be modeled as networks [142]. Undesirable behavior in complex networks (e.g., epidemics [143], power outages [144], economic crises [145], abuse of dominant position [146]) have motivated the research in the field of complex network control [42,142].
The purpose of complex network control is to obtain a specified or desired behavior across the entire network. This can be achieved by driving or maintaining the network to/in a desired state. The very nature of complex systems means that there is no central authority; therefore, all control actions must originate from nodes toward other nodes. However, are design approaches respecting this decentralization of decision (bottom-up), or is the hand of the designer dictating overall patterns from a central control position (top-down), which is to ask: is emergence lost, or is it an inherent part of complex network control?
From the systems theory point of view, nodes are systems and links are the medium for transporting signals, which opens the playing field to dynamic modeling of complex networks as interconnected systems. Often, the formal approach to complex dynamics is centered on state-space representations [147], which can become very large in size [148] and have created interest in defining and managing the observability, controllability, and stability of complex networks. Matters of robustness follow. The information-theoretic perspective adds another set of measures in complex networks, related to entropy [149,150], which might open doors to controlling links and not only node states. This reminds us of the duality control of and control over the network, but in the case of complex systems, a clear classification is impossible because the dichotomy between network as a whole and network as a bunch of nodes must not exclude the very essence of complexity, which is that subsystem interactions matter [151,152].
In the case of nonlinear state-space network models, the control problem shifts to approaches common to nonlinear dynamic systems in general, such as attractor basins for state-space trajectories of cyclic behaviors due to oscillation dynamics or due to cycles within the network (paths through nodes that reconnect with themselves). Here, the control problem looks at chaotic behavior and synchronization in complex networks. Ultimately, controlling node behavior means controlling node dynamics, which returns us to the same control purpose of managing node states or, better said, state transitions.
Controlling a network is not a trivial task, as a node can control at most one of its immediate neighbors if there are no cycles in the network [142] (as it happens, for instance, in global value chain networks [153]).
Complex network applications focused on network resilience explore the question: How many nodes or links can be removed from the network before it fails? As such, this is not a control problem, but an optimization of design issue. In the current literature, these applications fall under the scope of fault tolerance [154], often moving away from the characteristics that define complex networks. While structure-based control of complex networks might allude to resilience, its purpose is still that of managing network states (while extracting information from its structure), but not the structure itself [155].
Complex network control was explored by various researchers using traditional control theory concepts such as PID control [156], predictive control [157], optimal control [158], etc., but it appears that all these methods rely on the pinning control concept. This is because complex networks are defined by their topology and their nodes, and it is practically impossible to control a network without altering either the topology or the nodes. The pinning control problem deals with finding how many controllers are required and where to pin them in the network to effectively control the network [159].
Controlling each node in a complex network is expensive and practically impossible; thus, pinning control was introduced [159], and the minimum number of control points is correlated with the degree distribution of the network [142]. Pinning control is an effective strategy that takes into account both the topology and node dynamics [159], e.g., local linear feedback controllers are designed for nodes to control the network [160].
Many real-world scenarios require only a small fraction of nodes to be controlled [161], and in many cases, it is not feasible to control the full network [162]. Target control aims to control only a subset of network nodes instead of the full network [163], and this problem is equivalent to the maximum network flow problem [164].
3.1. Observability, Controllability, and Stability
A dynamical system is controllable if it can be driven from any initial state to a desired state within a finite time [165]. Kalman’s controllability rank condition is the mathematical condition for controllability [165], but is computationally infeasible in the case of complex networks [166].
Structural controllability theory facilitates inferring the controllability of a network [167] as a function of its interconnection graph independent of the edge weights [168], providing a tool for directed networks [169]. The main focus of structural controllability is linear time-invariant systems, but network controllability can be analyzed using the Lyapunov-based technique in the case of nonlinearities and stochastic disturbances [42].
In large networks, it is often impractical to monitor the states of all nodes; therefore, determining if the network is observable is important [170]. A dynamical system is observable if the state of the system can be determined based on the input and measured output variables [171]. The condition for observability is a rank condition of the observability matrix, computationally unfeasible in the case of complex networks [42]. However, the number of sensors required to estimate the internal state of a complex system can be determined using the graphical approach [42].
The science of complex systems relies heavily on linear stability analysis [172]. Linear stability analysis essentially assesses the state of a dynamic system by examining the dominant curvature of the potential energy function near the state as per the Lyapunov exponents [172]. However, the linearization-based approach to stability is too local [42]; therefore, the basin stability approach [172] was proposed. Basin stability is a measure that is easy to apply, non-local, and nonlinear [42,172].
Robustness is the ability of networks to adapt to changes and can be measured using entropy methods [173,174]. Jiang et al. [174] proposed the uncertainty of node importance as a measure of robustness where node importance is determined by the node degree and betweenness centrality [174]. According to Safar et al. [173], the robustness of a complex network is correlated with its capability to handle internal feedback loops within the network.
Entropy in information theory is analogous to entropy in thermodynamics [175] and is related to the system’s ability to possess new states and the system degree of chaos [173]. In complex networks, entropy may be used to analyze global value chain networks as it can provide information about import and export diversification [153], can help identify influential nodes [176], or can predict human mobility as it can determine the degree of predictability of a time series [177].
3.2. Synchronization in Complex Networks
Synchronization is an important topic for complex networks and has been observed in natural networks from various fields such as cell biology [178], neuroscience [179], etc. Certain networks require synchronization, for example power grids require synchronization to achieve a steady state [42], and for this reason, synchronization attracted much interest in complex network research.
Chaos theory has roots in nonlinear dynamic systems [180]. When there is simultaneous and positive and negative feedback, a system is in a chaotic state [181]. The bifurcation phenomenon emerges in dense networks [182], and this was observed in both random and scale-free networks [183]. For example, Liu and Chen [184] showed that a double-scrolling attractor emerged in an undirected network with eight nodes.
In 1990, Pecora and Carroll [185] discovered that two identical chaotic systems can be synchronized by coupling them with a common signal. Since then, chaos control and synchronization have received a great deal of attention [186] as synchronization can be used to explain natural phenomena, secure communications, image processing, etc. [184].
In many complex network models, stochastic uncertainty influences the system dynamics through sensor and actuation unreliability, communication failure, coupling uncertainty, or model inaccuracy [187], and this may lead to synchronization challenges. Lu and Chen [188] noted that synchronization can be chaotic or non-chaotic and proposed network synchronization criteria based on the Jacobian matrix for time-varying and time-invariant networks.
Network synchronization can be analyzed using criteria based on the Lyapunov and master stability functions [189]. Mai et al. showed [190] that chaos can be quenched by deriving stability conditions for the system using Lyapunov stability theory. However, is the emergence lost if the chaos is quenched by means of pinning control and synchronization? Is chaotic behavior the only emergent pattern of complex networks?
3.3. Emergence
According to De Wolf and Holvoet [191], there are four schools of research that regard emergence from different perspectives: (1) complex adaptive systems theory, (2) the synergetics school, (3) nonlinear dynamical systems theory and chaos theory, and (4) far-from-equilibrium thermodynamics. In complex adaptive systems theory, emergence results from interacting agents as macro-level patterns [192], while the synergetics school regards emergence as a macro-level coherent phenomenon influenced by an order parameter [191,193]. The central concept of attractors in chaos theory is an emergent behavior that occurs naturally in many types of systems [194,195]. Under far-from-equilibrium conditions, a thermodynamic system can transition to spontaneous organization, a dissipative structure [196].
Emergence can be engineered [197]; therefore, it is not necessarily lost when the system is controlled, but certain emergent patterns such as chaotic behavior can be quenched [190]. According to Mittal and Rainey [198], emergence is positive if it maintains the component subsystems operational and fulfills the purpose of the SoS or complex system as a whole and negative when it leads to cascaded failures, load hot-swapping, etc.
The question now is: How exactly can we engineer emergence? Does control theory hold the key? Would a properly designed control system be able to maintain the resilience of emergent patterns and even guide the switch to other, desired patterns?
4. Engineering Emergence: Decentralized Control over Complex Networks
4.1. Distributed vs. Decentralized Control
The second disambiguation of this paper pertains to decentralized vs. distributed control systems as major structural players in control architectures. In what follows, we do not use the acronym “DCS” for either to avoid confusion. Figure 3 illustrates the centralized, distributed (hierarchical), and decentralized structures.
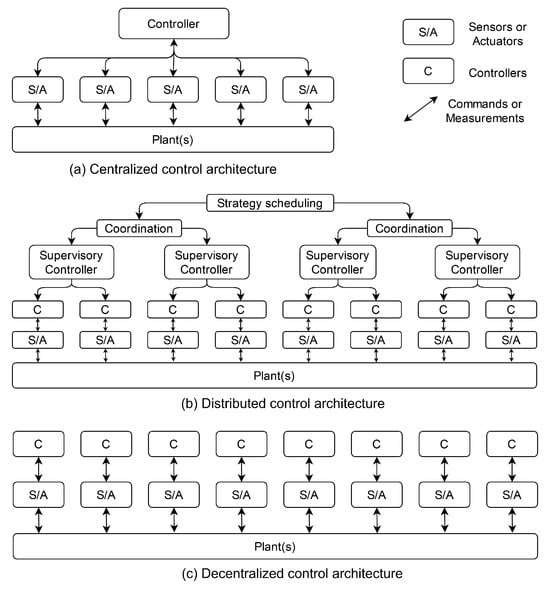
Figure 3.
Control architectures.
Centralized control architectures pertain to structures in which commands are computed by one “central” entity, which is designated as the controller of the system [199]. All sensor information is received by the controller, and all commands are transmitted by the controller. The functioning and task execution of the entire system are dependent on the controller, and so, centralized architectures are not reliable in large networks due to load, traffic, and resource issues.
Distributed control architectures have hierarchical structures [200] supported by a control level in which local commands are computed at the location of the plant. On the next level, supervisory modules assign tasks to the controllers (i.e., change operating points or modes). Further up the hierarchy are two coordination levels that deal with the high-level goals and objectives of the control system. Distributed control systems have been a staple of the manufacturing world [201]. While the plant-level control is not centralized, there is still a guiding action originating from a central entity.
Decentralized control architectures rely exclusively on local node control. Each control subsystem is only sensitive to and reacts to local events (i.e., within a predetermined vicinity of itself) [202,203]. Through the interaction of these components, desired global patterns are obtained. There is no entity inside the system with an overview of the whole system; at most an observer exists, external to the system, to recognize patterns. The decentralized approach is suitable for systems that can be decomposed, are geographically distributed, or exchange large quantities of data [204]. The design and behavior of decentralized systems are bottom-up processes.
Terminology problems arise when “decentralized” and “distributed” are used interchangeably [205], which often happens in the field of multi-agent systems (MASs). Although in MASs, these terms describe the behavior of the group as a result of the local interaction of agents (i.e., emergent behavior), they are not necessarily related to the control system. However, through a strange conjecture, a significant amount of advances in decentralized control have been made under the umbrella of MASs as swarms, robot groups, and other multi-agent applications tackled by control designers. We now have research in industrial automation (manufacturing) and MASs using the same word “distributed” to mean different concepts. Therefore, where do we draw the line, or better yet, should we draw a line? It is our opinion that perhaps the moment for a widely accepted set of unambiguous definitions has passed; what we can do, moving forward, is to keep this unintended diffusion of meaning in mind and apply it appropriately to each paper based on the context of the research.
4.2. Emergence and Consensus through Decentralized Control in Complex Networks
Extrapolating from the MAS concepts, we can define the problem of decentralized control over a complex network as an objective optimization problem [206] to be solved by the nodes of the network. Depending on how the optimization problem is posed, network behavior can be analyzed from the points of view of cooperation and coordination. Cooperation requires nodes to work together toward the achievement of their individual or common goals, while coordination refers to managing interdependencies (e.g., shared resource access). In cooperative control, while the objective of the network is global, the nodes solve the optimization problem locally and display a high level of interaction [207]. In non-cooperative control, nodes work toward their own, independent objectives [208]. The mechanisms for node interactions are either explicit—negotiation, consensus—or non-explicit—structured or emergent. Both cooperative and non-cooperative schemes fit into the decentralized structure if no supervisory type of entities exist in the network, which brings consensus and emergence to our attention in this survey.
Consensus refers to nodes that, while only having access to local knowledge or measurements, reach an agreement regarding a piece of information or state. The latter is of particular interest in control, as consensus mechanisms can guide the state of the network from one operating point to another [209]. Approaches to consensus are plentiful in the control world [210,211,212,213], although not many deal with complex networks specifically. A recent review [214] on consensus shed light on applications such as rendezvous, formation control, or wireless sensor networks.
In complex networks, consensus approaches are applied to clustering, connectivity, or network dynamics: managing stochastic fluctuations [215], robustness based on connectivity [216], positive edge constraints [217], behavioral consensus in evolutionary dynamics [218], observer-type protocols [219], nonlinear dynamics [220], three-body interactions [221], heterogeneous timescales [222], etc. When consensus requires that nodes in a complex network agree on aligning one of their internal states or parameters, temporarily or not, it becomes a case of synchronization (Section 3.2).
Emergence leads to patterns in the complex network, related to node location, degree, states, observable outputs, etc. While not necessarily resulting in synchronization, emergent behavior can produce agreements among the network nodes. From the control perspective, emergence becomes a problem of self-organization. In complex adaptive systems, for instance, nodes adapt (i.e., self-govern) to information exchanges and interactions with neighbors in their vicinity. However, whichever complex network behavior we look at, the matter of self-organization and thus emergence is a local control problem within a decentralized structure.
Research into self-organization is plentiful, especially in MASs [223,224]. In complex networks, self-organization is often regarded as a modeling problem [225,226,227,228]. The fact that deterministic models can be developed for microscopic dynamics [229] keeps these results relevant, even though control design has not yet been applied to all complex network types of self-organization models.
Thus, it is our opinion that emergence can be engineered (i.e., patterns at the network level can governed) through the objectives and design of local node controllers.
The simplest node control is open loop, known as reactive control in mobile robotics and MASs, in which nodes react to inputs without the presence of a feedback loop. One of the most famous applications for reactive laws is Boids [230], but newer applications have moved to local feedback in inventive configurations [231,232,233,234]. These results are fairly recent and not always explicit as concerns the design of local controllers.
Looking at node dynamics, the possibilities of control are indubitably as many as there are controller types out there in the control field, e.g., [235]; in this survey, we looked at predictive control as a connecting point between NCSs and decentralized control of complex networks. In decentralized schemes, local MPC controllers [236] are applied to energy networks [237], traffic [238,239], economic models [240], water management [241,242], supply chains [243], etc. Not all papers dealing with MPC’s decentralized solutions mention complex networks explicitly, but the application processes are usually complex in nature (e.g., traffic networks).
We close with our own example of nested emergence engineered through self-organization: eSCAPE is a scalable control architecture for urban areas that supports bottom-up design in SoSs. In eSCAPE, emergence is reflected by its capacity to generate ad hoc on-demand control loops [244]. The nestedness of eSCAPE comes from the self-organization of agents (representing controllers, actuators, sensors, and nuclei with specialized communication units) in minimal cells (i.e., local control loops) and, if needed, in extended cells (in which the roles for acting and sensing might be taken by other cells). The architecture supports various mechanisms, such as negotiation [245] and decentralized control [204].
5. Open Questions and Perspectives
Network science and complex networks have become an increasingly popular research topic over the last 20 years. Although considerable progress has been made so far, there are still questions that are left unanswered. Throughout the paper, we raised a few questions that we highlight in this section.
The first question we raised (Section 2.1) refers to the place of complex network control under the wider umbrella of network-related control systems. Complex network research has been motivated by a deep need to understand the interconnected world in which biological systems (human or others), urban infrastructures, and developing technology come together to create new complex structures, from energy distribution networks to social media platforms that foster information exchange. Network science has a wide range of applications, and complex topological features arise in all types of networks, allowing the same complex network analysis tools to be used to extract information about networks from various fields.
Control of complex networks is rooted in established control practices, but at the same time reveals itself to be a stand-alone field, due to the infusion of ideas coming from understanding complexity in innovative ways. At the time of writing this paper, it is our belief that only creativity is the limit as concerns the future of complex network control, with the caveat that we expect furthering of efficient resource utilization and sustainability in real-world applications.
In Section 2.4, we launched the hypothesis that predictive control will be the instigator of merging requirements for both NCSs and communication networks. In classical control theory, the predictive control approach enables the control of systems by managing time delays through the controller design. We estimate that predictive approaches will undoubtedly spread toward complex network control in bottom-up design strategies.
Emergent behavior in nature is ubiquitous. In complex systems at large, emergence is an important and defining characteristic. In Section 3.2 and Section 3.3, we raised questions related to the nature and place of emergence in complex network control. Thus, we ask: Can we create artificial emergence? Is it possible to drive emergence through design, or is it a phenomenon spawning out of nowhere, only to slip through our engineering fingers as sand? The answer resides in decentralized control.
In complex systems modeling, the generative experiment [246] brought forth two bottom-up strategies for obtaining and analyzing emergent patterns: the predicting approach in which local node interactions are known, but not the overall emergent pattern, which can be observed under various created conditions, and the evolving approach in which patterns are “grown” out of local interactions with which the designer can experiment to obtain a desired global effect. We already see the former in chaotic systems approaches, and we see the latter compatible with decentralized control. Thus, we believe the answer to engineering emergence to be found in enhancing node agency through control capabilities.
Finally, we ask: Is there a metric for emergence or a metric that helps us classify emergence for all complex networks? If various distinct emergent patterns are observed in complex networks, based on node level interactions and the behavior of the whole network, what quantitative and qualitative conclusions can be drawn? Engineering emergence is a research ground in its infancy when it comes to control, but it shows great potential for new and exciting directions in control systems design.
6. Conclusions
In this paper, we performed a survey on complex networks in an attempt to identify potential research directions and unsolved problems related to control and emergence. We found that a considerable amount of progress was made in the field of complex networks since 2000 and the total number of contributions increased every year. The research field of complex networks is broad and multidisciplinary, so we focused our search on complex network control and the emergent behavior of complex networks. Network control can be regarded from three different perspectives we covered in this survey: control of the network, control over the network, and control of complex networks. We found interesting approaches to these problems, and we raised several questions throughout the paper. Although complex network control has received much attention over the last few years, network science is a field in full development and is currently better suited to represent our current interconnected world.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Molontay, R.; Nagy, M. Two decades of network science: As seen through the co-authorship network of network scientists. In Proceedings of the 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Vancouver, BC, Canada, 27–30 August 2019; pp. 578–583. [Google Scholar]
- Vespignani, A. Twenty years of network science. Nature 2018, 558, 528–529. [Google Scholar] [CrossRef] [PubMed]
- Lewis, T.G. Network Science; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Börner, K.; Sanyal, S.; Vespignani, A. Network science. Annu. Rev. Inf. Sci. Technol. 2007, 41, 537–607. [Google Scholar] [CrossRef]
- Biagini, F.; Kauermann, G.; Meyer-Brandis, T. Network Science; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Serrano, D.H.; Hernández-Serrano, J.; Gómez, D.S. Simplicial degree in complex networks. Applications of topological data analysis to network science. Chaos Solitons Fractals 2020, 137, 109839. [Google Scholar] [CrossRef]
- Rathkopf, C. Network representation and complex systems. Synthese 2018, 195, 55–78. [Google Scholar] [CrossRef]
- Huang, J.; Feng, Y.; Zhang, S. Research of complex system theory application on reliability analysis of network system. In Proceedings of the 2009 8th International Conference on Reliability, Maintainability and Safety, Chengdu, China, 20–24 July 2009; pp. 1141–1145. [Google Scholar]
- Yang, Y.; Yang, H. Complex network-based time series analysis. Phys. A Stat. Mech. Its Appl. 2008, 387, 1381–1386. [Google Scholar] [CrossRef]
- Telesford, Q.K.; Simpson, S.L.; Burdette, J.H.; Hayasaka, S.; Laurienti, P.J. The brain as a complex system: Using network science as a tool for understanding the brain. Brain Connect. 2011, 1, 295–308. [Google Scholar] [CrossRef]
- Zhang, Z.; Jia, L.; Chai, Y.; Guo, M. On conceptual and methodological issues in control of complex systems. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 3576–3581. [Google Scholar]
- Akundi, A.; Smith, E.; Tseng, T.L.; Rubio, I. An attempt to understand information processing capability in complex networks. In Proceedings of the 2018 Annual IEEE International Systems Conference (SysCon), Vancouver, BC, Canada, 23–26 April 2018; pp. 1–6. [Google Scholar]
- Sillitto, H.; Martin, J.; McKinney, D.; Griego, R.; Dori, D.; Krob, D.; Godfrey, P.; Arnold, E.; Jackson, S. Systems engineering and system definitions. In Proceedings of the INCOSE, Biarritz, France, 11–13 September 2019. [Google Scholar]
- Qiao, S.; Han, N.; Gao, Y.; Li, R.H.; Huang, J.; Sun, H.; Wu, X. Dynamic community evolution analysis framework for large-scale complex networks based on strong and weak events. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6229–6243. [Google Scholar] [CrossRef]
- Ling, B.W.K.; Stewart, P.; Teo, K.L.; Chi, K.T. Study of near consensus complex social networks using eigen theory. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 2107–2110. [Google Scholar]
- Du, F.; Xuan, Q.; Wu, T.J. Simplification of complex networks by folding. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010; pp. 4667–4670. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Ravasz, E.; Somera, A.L.; Mongru, D.A.; Oltvai, Z.N.; Barabási, A.L. Hierarchical organization of modularity in metabolic networks. Science 2002, 297, 1551–1555. [Google Scholar] [CrossRef]
- Wu, J.; Barahona, M.; Tan, Y.J.; Deng, H.Z. Spectral measure of structural robustness in complex networks. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2011, 41, 1244–1252. [Google Scholar] [CrossRef]
- Nan-nan, Z.; Xin-yu, O. Summary on emergence of complex systems. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 668–671. [Google Scholar]
- Liu, F.; Xiao, B.; Li, H.; Xue, J. Complex Network Node Centrality Measurement Based on Multiple Attributes. In Proceedings of the 2018 10th International Conference on Modelling, Identification and Control (ICMIC), Guiyang, China, 2–4 July 2018; pp. 1–5. [Google Scholar]
- Karcanias, N.; Hessami, A.G. Complexity and the notion of system of systems: Part (I): General systems and complexity. In Proceedings of the 2010 World Automation Congress, Kobe, Japan, 19–23 September 2010; pp. 1–7. [Google Scholar]
- Boardman, J.; Sauser, B. System of Systems-the meaning of of. In Proceedings of the 2006 IEEE/SMC International Conference on System of Systems Engineering, Los Angeles, CA, USA, 24–26 April 2006; pp. 77–82. [Google Scholar]
- Gupta, R.A.; Chow, M.Y. Networked control system: Overview and research trends. IEEE Trans. Ind. Electron. 2009, 57, 2527–2535. [Google Scholar] [CrossRef]
- Fan, Z.; Yu, X.; Wan, H.; Kang, M.; Liu, Y.; He, Y.; Xiao, G. A Time-Delay-Bounded Data Scheduling Algorithm for Delay Reduction in Distributed Networked Control Systems. Math. Probl. Eng. 2020, 2020, 8290879. [Google Scholar] [CrossRef]
- Web of Science. Available online: http://webofscience.com/ (accessed on 12 January 2022).
- Scopus. Available online: https://www.scopus.com/ (accessed on 12 January 2022).
- IEEEXplore. Available online: https://ieeexplore.ieee.org/ (accessed on 12 January 2022).
- ACM-DL. Available online: https://dl.acm.org/ (accessed on 12 January 2022).
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Backhaus, M.; Schaefer, G. Towards the Complexity of the Widest Path Problem in Hybrid Multi-Channel WMNs. In Proceedings of the 2020 16th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob) (50308), Thessaloniki, Greece, 12–14 October 2020; pp. 378–381. [Google Scholar]
- Zhu, S.; Xu, Y. Complexity measure of supply chain networks. In Proceedings of the IEEE 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 2220–2224. [Google Scholar]
- Zhou, B.; Pei, J. Preserving privacy in social networks against neighborhood attacks. In Proceedings of the 2008 IEEE 24th International Conference on Data Engineering, Cancun, Mexico, 7–12 April 2008; pp. 506–515. [Google Scholar]
- Mittal, S.; Siddiqui, A.S. Networked control system: Survey and directions. J. Eng. Res. Stud. 2010, 1, 35–50. [Google Scholar]
- Zhang, X.M.; Han, Q.L.; Yu, X. Survey on recent advances in networked control systems. IEEE Trans. Ind. Inform. 2015, 12, 1740–1752. [Google Scholar] [CrossRef]
- Cancan, G.; Chen, P.; Jin, Z.; Dacheng, P. A survey on networked control systems subject to limited network resources. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 4958–4965. [Google Scholar]
- Bemporad, A.; Heemels, M.; Johansson, M. Networked Control Systems; Springer: Berlin/Heidelberg, Germany, 2010; Volume 406. [Google Scholar]
- Proskurnikov, A.V.; Fradkov, A.L. Problems and methods of network control. Autom. Remote Control 2016, 77, 1711–1740. [Google Scholar] [CrossRef]
- Fencl, T.; Burget, P.; Bilek, J. Network topology design. Control Eng. Pract. 2011, 19, 1287–1296. [Google Scholar] [CrossRef]
- Tang, Y.; Qian, F.; Gao, H.; Kurths, J. Synchronization in complex networks and its application—A survey of recent advances and challenges. Annu. Rev. Control 2014, 38, 184–198. [Google Scholar] [CrossRef]
- Xiao, Y.; Xue, Y.; Nazarian, S.; Bogdan, P. A load balancing inspired optimization framework for exascale multicore systems: A complex networks approach. In Proceedings of the 2017 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Irvine, CA, USA, 13–16 November 2017; pp. 217–224. [Google Scholar]
- Papagianni, C.; Papadopoulos, K.; Pappas, C.; Tselikas, N.D.; Kaklamani, D.; Venieris, I.S. Communication network design using particle swarm optimization. In Proceedings of the 2008 International Multiconference on Computer Science and Information Technology, Wisla, Poland, 20–22 October 2008; pp. 915–920. [Google Scholar]
- Pimentel, J.; Arif, J. Communication Network Optimization for Subsea Processing Fields Development. In Proceedings of the 2019 Petroleum and Chemical Industry Conference Europe (PCIC EUROPE), Paris, France, 7–9 May 2019; pp. 1–8. [Google Scholar]
- Altiparmak, F.; Dengiz, B. A cross entropy approach to design of reliable networks. Eur. J. Oper. Res. 2009, 199, 542–552. [Google Scholar] [CrossRef]
- You, K.; Xie, L. Network topology and communication data rate for consensusability of discrete-time multi-agent systems. IEEE Trans. Autom. Control 2011, 56, 2262–2275. [Google Scholar] [CrossRef]
- Sharma, P.; Bucci, D.J.; Brahma, S.K.; Varshney, P.K. Communication network topology inference via transfer entropy. IEEE Trans. Netw. Sci. Eng. 2019, 7, 562–575. [Google Scholar] [CrossRef]
- Jia, G.; Zhu, Y.; Li, Y.; Zhu, Z.; Zhou, L. Analysis of the Effect of the Reliability of the NB-Iot Network on the Intelligent System. IEEE Access 2019, 7, 112809–112820. [Google Scholar]
- Kim, K.D.; Kumar, P. The importance, design and implementation of a middleware for networked control systems. In Networked Control Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–29. [Google Scholar]
- Bregni, S. Fast algorithms for TVAR and MTIE computation in characterization of network synchronization performance. Networks 2001, 5, 12. [Google Scholar]
- Al-Mekhlafi, Z.G.; Hanapi, Z.M.; Saleh, A.M.S. Firefly-inspired time synchronization mechanism for self-organizing energy-efficient wireless sensor networks: A survey. IEEE Access 2019, 7, 115229–115248. [Google Scholar] [CrossRef]
- Hasan, K.F.; Wang, C.; Feng, Y.; Tian, Y.C. Time synchronization in vehicular ad-hoc networks: A survey on theory and practice. Veh. Commun. 2018, 14, 39–51. [Google Scholar] [CrossRef]
- Yiğitler, H.; Badihi, B.; Jäntti, R. Overview of time synchronization for iot deployments: Clock discipline algorithms and protocols. Sensors 2020, 20, 5928. [Google Scholar] [CrossRef]
- Puttnies, H.; Danielis, P.; Sharif, A.R.; Timmermann, D. Estimators for Time Synchronization—Survey, Analysis, and Outlook. IoT 2020, 1, 398–435. [Google Scholar] [CrossRef]
- Wang, S.; Shi, M.; Li, D.; Du, T. A survey of time synchronization algorithms for wireless sensor networks. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 6392–6397. [Google Scholar]
- Lee, H.; Lee, K.J.; Kim, H.; Clerckx, B.; Lee, I. Resource allocation techniques for wireless powered communication networks with energy storage constraint. IEEE Trans. Wirel. Commun. 2015, 15, 2619–2628. [Google Scholar] [CrossRef]
- Banner, R.; Orda, A. Bottleneck routing games in communication networks. IEEE J. Sel. Areas Commun. 2007, 25, 1173–1179. [Google Scholar] [CrossRef]
- Soo, W.K.; Ling, T.C.; Maw, A.H.; Win, S.T. Survey on load-balancing methods in 802.11 infrastructure mode wireless networks for improving quality of service. ACM Comput. Surv. (CSUR) 2018, 51, 1–21. [Google Scholar] [CrossRef]
- Neghabi, A.A.; Navimipour, N.J.; Hosseinzadeh, M.; Rezaee, A. Load balancing mechanisms in the software defined networks: A systematic and comprehensive review of the literature. IEEE Access 2018, 6, 14159–14178. [Google Scholar] [CrossRef]
- Reindl, A.; Wetzel, D.; Balbierer, N.; Meier, H.; Niemetz, M.; Park, S. Comparative Analysis of CAN CAN FD and Ethernet for Networked Control Systems. In Proceedings of the Embedded World Conference Digital, Virtual, 1–5 March2021. [Google Scholar]
- Kawamoto, Y.; Nishiyama, H.; Kato, N. Toward terminal-to-terminal communication networks: A hybrid MANET and DTN approach. In Proceedings of the 2013 IEEE 18th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), Berlin, Germany, 25–27 September 2013; pp. 228–232. [Google Scholar]
- Lu, K.; Qian, Y.; Chen, H. A secure and service-oriented network control framework for WiMAX networks. IEEE Commun. Mag. 2007, 45, 124. [Google Scholar] [CrossRef]
- Xia, Y.; Hill, D.J. Attack vulnerability of complex communication networks. IEEE Trans. Circuits Syst. II Express Briefs 2008, 55, 65–69. [Google Scholar] [CrossRef]
- Bhatt, S.; Ragiri, P.R. Security trends in Internet of Things: A survey. SN Appl. Sci. 2021, 3, 121. [Google Scholar]
- Zhang, W.; Branicky, M.S.; Phillips, S.M. Stability of networked control systems. IEEE Control Syst. Mag. 2001, 21, 84–99. [Google Scholar]
- Zhang, X.M.; Han, Q.L.; Ge, X.; Ding, D.; Ding, L.; Yue, D.; Peng, C. Networked control systems: A survey of trends and techniques. IEEE/CAA J. Autom. Sin. 2019, 7, 1–17. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, H.; Kaynak, O. Network-induced constraints in networked control systems—A survey. IEEE Trans. Ind. Inform. 2012, 9, 403–416. [Google Scholar] [CrossRef]
- Wu, F.G.; Sun, F.C.; Xue, D.Q.; Sun, Z.Q. Problems and strategies of networked control systems. In Proceedings of the 2002 IEEE Region 10 Conference on Computers, Communications, Control and Power Engineering (TENCOM’02), Beijing, China, 28–31 October 2002; Volume 3, pp. 1692–1695. [Google Scholar]
- Abdolmaleki, B.; Shafiee, Q.; Seifi, A.R.; Arefi, M.M.; Blaabjerg, F. A zeno-free event-triggered secondary control for ac microgrids. IEEE Trans. Smart Grid 2019, 11, 1905–1916. [Google Scholar] [CrossRef]
- Nowzari, C.; Cortés, J. Zeno-free, distributed event-triggered communication and control for multi-agent average consensus. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 2148–2153. [Google Scholar]
- Sun, Z.; Huang, N.; Anderson, B.D.; Duan, Z. A new distributed zeno-free event-triggered algorithm for multi-agent consensus. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 3444–3449. [Google Scholar]
- Yu, H.; Chen, T. On Zeno behavior in event-triggered finite-time consensus of multi-agent systems. IEEE Trans. Autom. Control 2020, 66, 4700–4714. [Google Scholar] [CrossRef]
- Wittenmark, B.; Nilsson, J.; Torngren, M. Timing problems in real-time control systems. In Proceedings of the 1995 American Control Conference (ACC’95), Seattle, WA, USA, 21–23 June 1995; Volume 3, pp. 2000–2004. [Google Scholar]
- Englehart, K.; Hudgins, B. A robust, real-time control scheme for multifunction myoelectric control. IEEE Trans. Biomed. Eng. 2003, 50, 848–854. [Google Scholar] [CrossRef] [PubMed]
- Campisano, A.; Cabot Ple, J.; Muschalla, D.; Pleau, M.; Vanrolleghem, P.A. Potential and limitations of modern equipment for real time control of urban wastewater systems. Urban Water J. 2013, 10, 300–311. [Google Scholar] [CrossRef]
- Dotoli, M.; Epicoco, N.; Falagario, M.; Turchiano, B.; Cavone, G.; Convertini, A. A decision support system for real-time rescheduling of railways. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 696–701. [Google Scholar]
- Creaco, E.; Campisano, A.; Fontana, N.; Marini, G.; Page, P.; Walski, T. Real time control of water distribution networks: A state-of-the-art review. Water Res. 2019, 161, 517–530. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Imran, M.A.; Pang, Z.; Chen, Z.; Li, L. Toward real-time control in future wireless networks: Communication-control co-design. IEEE Commun. Mag. 2018, 57, 138–144. [Google Scholar] [CrossRef]
- Ge, Y.; Tian, L.; Liu, Z. Survey on the stability of networked control systems. J. Control Theory Appl. 2007, 5, 374–379. [Google Scholar] [CrossRef]
- Zhang, W.A.; Yu, L. Modelling and control of networked control systems with both network-induced delay and packet-dropout. Automatica 2008, 44, 3206–3210. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Hamdan, M.M. Fundamental issues in networked control systems. IEEE/CAA J. Autom. Sin. 2018, 5, 902–922. [Google Scholar] [CrossRef]
- Jungers, M.; Castelan, E.B.; Moraes, V.M.; Moreno, U.F. A dynamic output feedback controller for NCS based on delay estimates. Automatica 2013, 49, 788–792. [Google Scholar] [CrossRef]
- Chunmao, L.; Jian, X. Adaptive delay estimation and control of networked control systems. In Proceedings of the 2006 International Symposium on Communications and Information Technologies, Bangkok, Thailand, 18–20 October 2006; pp. 707–710. [Google Scholar]
- Ghanaim, A.; Borges, G.A.; Frey, G. Estimating delays in networked control systems using colored Petri nets and Markov chain models. In Proceedings of the 2009 IEEE Conference on Emerging Technologies & Factory Automation, Palma de Mallorca, Spain, 22–25 September 2009; pp. 1–6. [Google Scholar]
- Yang, Y.; Wang, Y.J. Modeling and control for NCS with time-varying long delays. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 3, pp. 1407–1411. [Google Scholar]
- Feng, H.; Macedo, H.D.; Larsen, P.G. Estimating the maximum allowable delay bound for networked control systems using co-simulation and design space exploration. In Control Strategy for Time-Delay Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 257–280. [Google Scholar]
- Hespanha, J.P.; Naghshtabrizi, P.; Xu, Y. A survey of recent results in networked control systems. Proc. IEEE 2007, 95, 138–162. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Q.; Qiu, Z. Feedback control of NCS with time-delay and data packet dropout. Syst. Eng. Electron. 2007, 29, 262–268. [Google Scholar]
- Lian, F.L.; Moyne, J.; Tilbury, D. Modelling and optimal controller design of networked control systems with multiple delays. Int. J. Control 2003, 76, 591–606. [Google Scholar] [CrossRef]
- Gabel, O.; Litz, L. QoS-adaptive control in NCS with variable delays and packet losses-a heuristic approach. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC) (IEEE Cat. No. 04CH37601), Nassau, Bahamas, 14–17 December 2004; Volume 2, pp. 1586–1591. [Google Scholar]
- Zhao, H.; Wu, M.; Liu, G.; She, J. H-infinity control for networked control systems (NCS) with time-varying delays. J. Control Theory Appl. 2005, 3, 157–162. [Google Scholar] [CrossRef]
- Li, F.; Gao, L.; Dou, G.; Zheng, B. Dual-side event-triggered output feedback H∞ control for NCS with communication delays. Int. J. Control Autom. Syst. 2018, 16, 108–119. [Google Scholar] [CrossRef]
- Awad, O.A. Fuzzy PID Gain Scheduling Controller for Networked Control System. Iraqi J. Sci. 2021, 210–216. [Google Scholar] [CrossRef]
- Zhao, S. Model Reference Scheduling and Robust Resilient H-infinity Control Co-design with Time-delay. In Proceedings of the 2021 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 8–11 August 2021; pp. 537–541. [Google Scholar]
- Liu, K.; Selivanov, A.; Fridman, E. Survey on time-delay approach to networked control. Annu. Rev. Control 2019, 48, 57–79. [Google Scholar] [CrossRef]
- Amin, S.; Cárdenas, A.A.; Sastry, S.S. Safe and secure networked control systems under denial-of-service attacks. In Proceedings of the International Workshop on Hybrid Systems: Computation and Control, San Francisco, CA, USA, 13–15 April 2009; pp. 31–45. [Google Scholar]
- Sollfrank, M.; Pirehgalin, M.F.; Vogel-Heuser, B. Integration of safety aspects in modeling of Networked Control Systems. In Proceedings of the 2017 IEEE 15th International Conference on Industrial Informatics (INDIN), Emden, Germany, 24–26 July 2017; pp. 405–412. [Google Scholar]
- Pang, Z.H.; Fan, L.Z.; Sun, J.; Liu, K.; Liu, G.P. Detection of stealthy false data injection attacks against networked control systems via active data modification. Inf. Sci. 2021, 546, 192–205. [Google Scholar] [CrossRef]
- Hussain, A.; Amin, S. NCS security experimentation using DETER. In Proceedings of the 1st international conference on High Confidence Networked Systems, Beijing, China, 17–18 April 2012; pp. 73–80. [Google Scholar]
- Mo, Y.; Garone, E.; Casavola, A.; Sinopoli, B. False data injection attacks against state estimation in wireless sensor networks. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 5967–5972. [Google Scholar]
- Peng, C.; Sun, H.; Yang, M.; Wang, Y.L. A survey on security communication and control for smart grids under malicious cyber attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1554–1569. [Google Scholar] [CrossRef]
- Ding, D.; Han, Q.L.; Xiang, Y.; Ge, X.; Zhang, X.M. A survey on security control and attack detection for industrial cyber-physical systems. Neurocomputing 2018, 275, 1674–1683. [Google Scholar] [CrossRef]
- Fang, H.; Ye, H.; Zhong, M. Fault diagnosis of networked control systems. Annu. Rev. Control 2007, 31, 55–68. [Google Scholar] [CrossRef]
- Wang, Y.L.; Lim, C.C.; Shi, P. Adaptively adjusted event-triggering mechanism on fault detection for networked control systems. IEEE Trans. Cybern. 2016, 47, 2299–2311. [Google Scholar] [CrossRef]
- Mao, Z.; Jiang, B.; Shi, P. Protocol and fault detection design for nonlinear networked control systems. IEEE Trans. Circuits Syst. II Express Briefs 2009, 56, 255–259. [Google Scholar]
- Zeng, W.; Chow, M.Y. Resilient distributed control in the presence of misbehaving agents in networked control systems. IEEE Trans. Cybern. 2014, 44, 2038–2049. [Google Scholar] [CrossRef] [PubMed]
- Sauter, D.; Li, S.; Aubrun, C. Robust fault diagnosis of networked control systems. Int. J. Adapt. Control Signal Process. 2009, 23, 722–736. [Google Scholar] [CrossRef]
- Ding, S.X. Advanced Methods for Fault Diagnosis and Fault-Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Baillieul, J.; Antsaklis, P.J. Control and communication challenges in networked real-time systems. Proc. IEEE 2007, 95, 9–28. [Google Scholar] [CrossRef]
- Merrad, W.; Rachedi, A.; Busawon, K.; Binns, R. A survey on smart traffic network control and optimization. In Proceedings of the 2016 International Conference Multidisciplinary Engineering Design Optimization (MEDO), Belgrade, Serbia, 14–16 September 2016; pp. 1–6. [Google Scholar]
- Hu, J.; Zhang, H.; Liu, H.; Yu, X. A survey on sliding mode control for networked control systems. Int. J. Syst. Sci. 2021, 52, 1129–1147. [Google Scholar] [CrossRef]
- Heemels, W.M.H.; Teel, A.R.; Van de Wouw, N.; Nešić, D. Networked control systems with communication constraints: Tradeoffs between transmission intervals, delays and performance. IEEE Trans. Autom. Control 2010, 55, 1781–1796. [Google Scholar] [CrossRef]
- Sun, H.; Sun, J.; Chen, J. Analysis and synthesis of networked control systems with random network-induced delays and sampling intervals. Automatica 2021, 125, 109385. [Google Scholar] [CrossRef]
- Allan, D.A.; Bates, C.N.; Risbeck, M.J.; Rawlings, J.B. On the inherent robustness of optimal and suboptimal nonlinear MPC. Syst. Control Lett. 2017, 106, 68–78. [Google Scholar] [CrossRef]
- Yu, S.; Reble, M.; Chen, H.; Allgöwer, F. Inherent robustness properties of quasi-infinite horizon MPC. IFAC Proc. Vol. 2011, 44, 179–184. [Google Scholar] [CrossRef]
- Berner, P.S.; Mönnigmann, M. A comparison of four variants of event-triggered networked MPC. In Proceedings of the 2016 IEEE Conference on Control Applications (CCA), Buenos Aires, Argentina, 19–22 September 2016; pp. 1519–1524. [Google Scholar]
- Bianchi, D.; Ferrara, A.; Di Benedetto, M.D. Networked model predictive traffic control with time varying optimization horizon: The Grenoble South Ring case study. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 4039–4044. [Google Scholar]
- Grüne, L.; Pannek, J.; Worthmann, K. A networked unconstrained nonlinear MPC scheme. In Proceedings of the 2009 European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 371–376. [Google Scholar]
- Xia, Y.Q.; Gao, Y.L.; Yan, L.P.; Fu, M.Y. Recent progress in networked control systems—A survey. Int. J. Autom. Comput. 2015, 12, 343–367. [Google Scholar] [CrossRef]
- Yang, T.C. Networked control system: A brief survey. IEE Proc.-Control Theory Appl. 2006, 153, 403–412. [Google Scholar] [CrossRef]
- Onat, A.; Naskali, T.; Parlakay, E.; Mutluer, O. Control over imperfect networks: Model-based predictive networked control systems. IEEE Trans. Ind. Electron. 2010, 58, 905–913. [Google Scholar] [CrossRef]
- Shu, S.; Lin, F. Predictive networked control of discrete event systems. IEEE Trans. Autom. Control 2016, 62, 4698–4705. [Google Scholar] [CrossRef]
- Liu, K.; Ma, A.; Xia, Y.; Sun, Z.; Johansson, K.H. Network scheduling and control co-design for multi-loop MPC. IEEE Trans. Autom. Control 2019, 64, 5238–5245. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Qiu, H. Networked coordination-based distributed model predictive control for large-scale system. IEEE Trans. Control Syst. Technol. 2012, 21, 991–998. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, L.; Chen, T. Model predictive control for networked control systems. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2009, 19, 1016–1035. [Google Scholar] [CrossRef]
- Wang, T.; Gao, H.; Qiu, J. A combined adaptive neural network and nonlinear model predictive control for multirate networked industrial process control. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 416–425. [Google Scholar] [CrossRef]
- Vafamand, N.; Khooban, M.H.; Dragičević, T.; Blaabjerg, F. Networked fuzzy predictive control of power buffers for dynamic stabilization of DC microgrids. IEEE Trans. Ind. Electron. 2018, 66, 1356–1362. [Google Scholar] [CrossRef]
- Zhu, B.; Guo, K.; Xie, L. A new distributed model predictive control for unconstrained double-integrator multiagent systems. IEEE Trans. Autom. Control 2018, 63, 4367–4374. [Google Scholar] [CrossRef]
- Li, A.; Sun, J. Self-triggered Model Predictive Control for Nonlinear Continuous-time Networked System via Ensured Performance Control Samples Selection. Int. J. Control 2021, 1–18. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, Y.; Shi, P. Design and stability analysis of networked predictive control systems. IEEE Trans. Control Syst. Technol. 2012, 21, 1495–1501. [Google Scholar] [CrossRef]
- Pătraşcu, M. Smith predictor approximation for industrial control applications with genetic algorithms. In Proceedings of the 2021 International Conference on Applied Artificial Intelligence (ICAPAI), Halden, Norway, 19–21 May 2021; pp. 1–6. [Google Scholar]
- Vişcoţel, L.A.; Pătraşcu, M. Design of Stabilizing Predictor-based Controller for Closed Loop Traffic Control with Real-Coded Genetic Algorithms. In Proceedings of the 2021 European Control Conference (ECC), Delft, The Netherlands, 29 June–2 July 2021; pp. 23–28. [Google Scholar]
- Silveira, A.; Sodre, L.; Silva, A.; Conde, L.; Borges, J.; Souza, Y.; Klautau, A. Smith Predictor-based Adaptive Control of Network-Controlled UAVs. In Proceedings of the XV Simposio Brasileiro de Automacao Inteligente SBAI. Sociedade Brasileira de Automatica (SBA), Virtual Event, 17–20 October 2021. [Google Scholar]
- Bonala, S.; Subudhi, B.; Ghosh, S. On delay robustness improvement using digital Smith predictor for networked control systems. Eur. J. Control 2017, 34, 59–65. [Google Scholar] [CrossRef]
- Feng, D.; Qingquan, Q. Networked control systems based on generalized predictive control and modified Smith predictor. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 7859–7863. [Google Scholar]
- Du, W.; Du, F. Novel smith predictor and fuzzy control for networked control systems. In Proceedings of the 2009 Asia-Pacific Conference on Information Processing, Shenzhen, China, 18–19 July 2009; Volume 1, pp. 75–78. [Google Scholar]
- Du, F.; Qian, Q.; Du, W. Networked control systems based on new smith predictor. J. Southwest Jiaotong Univ. 2010, 45, 65–69. [Google Scholar]
- Zhang, H.; Shi, Y.; Wang, J.; Chen, H. A new delay-compensation scheme for networked control systems in controller area networks. IEEE Trans. Ind. Electron. 2018, 65, 7239–7247. [Google Scholar] [CrossRef]
- Du, F.; Qian, Q. Fuzzy immune self-regulating PID control based on modified Smith Predictor for networked control systems. In Proceedings of the 2008 IEEE International Conference on Networking, Sensing and Control, Sanya, China, 6–8 April 2008; pp. 424–428. [Google Scholar]
- Cuenca, A.; Salt, J.; Casanova, V.; Pizá, R. An approach based on an adaptive multi-rate Smith predictor and gain scheduling for a networked control system: Implementation over Profibus-DP. Int. J. Control Autom. Syst. 2010, 8, 473–481. [Google Scholar] [CrossRef]
- Ruths, J.; Ruths, D. Control profiles of complex networks. Science 2014, 343, 1373–1376. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G. Complex networks: Small-world, scale-free and beyond. IEEE Circuits Syst. Mag. 2003, 3, 6–20. [Google Scholar] [CrossRef]
- Motter, A.E.; Myers, S.A.; Anghel, M.; Nishikawa, T. Spontaneous synchrony in power-grid networks. Nat. Phys. 2013, 9, 191–197. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, H.; Lin, W.; Lai, Y.C.; Wang, X. Growth, collapse and self-organized criticality in complex networks. Sci. Rep. 2016, 6, 1–12. [Google Scholar] [CrossRef]
- Angelidis, G.; Ioannidis, E.; Makris, G.; Antoniou, I.; Varsakelis, N. Competitive Conditions in Global Value Chain Networks: An Assessment Using Entropy and Network Analysis. Entropy 2020, 22, 1068. [Google Scholar] [CrossRef]
- Pasemann, F. Complex dynamics and the structure of small neural networks. Netw. Comput. Neural Syst. 2002, 13, 195–216. [Google Scholar] [CrossRef]
- Dufour, C.; Mahseredjian, J.; Bélanger, J. A combined state-space nodal method for the simulation of power system transients. IEEE Trans. Power Deliv. 2010, 26, 928–935. [Google Scholar] [CrossRef]
- De Domenico, M.; Biamonte, J. Spectral entropies as information-theoretic tools for complex network comparison. Phys. Rev. X 2016, 6, 041062. [Google Scholar] [CrossRef]
- Dehmer, M. Information-theoretic concepts for the analysis of complex networks. Appl. Artif. Intell. 2008, 22, 684–706. [Google Scholar] [CrossRef]
- Csányi, G.; Szendrői, B. Fractal–small-world dichotomy in real-world networks. Phys. Rev. E 2004, 70, 016122. [Google Scholar] [CrossRef]
- Provan, K.G.; Fish, A.; Sydow, J. Interorganizational networks at the network level: A review of the empirical literature on whole networks. J. Manag. 2007, 33, 479–516. [Google Scholar] [CrossRef]
- Papadimitriou, F. Spatial Entropy of Directional Geographical Data and Landscape Networks. In Spatial Entropy and Landscape Analysis; Springer: Berlin/Heidelberg, Germany, 2022; pp. 31–55. [Google Scholar]
- Ledmi, A.; Bendjenna, H.; Hemam, S.M. Fault tolerance in distributed systems: A survey. In Proceedings of the 2018 3rd International Conference on Pattern Analysis and Intelligent Systems (PAIS), Tebessa, Algeria, 24–25 October 2018; pp. 1–5. [Google Scholar]
- Zañudo, J.G.T.; Yang, G.; Albert, R. Structure-based control of complex networks with nonlinear dynamics. Proc. Natl. Acad. Sci. USA 2017, 114, 7234–7239. [Google Scholar] [CrossRef]
- Gu, H.; Liu, P.; Lü, J.; Lin, Z. PID control for synchronization of complex dynamical networks with directed topologies. IEEE Trans. Cybern. 2021, 51, 1334–1346. [Google Scholar] [CrossRef]
- Alejandro, J.; Arce, A.; Bordons, C. An integrated framework for distributed model predictive control of large-scale power networks. IEEE Trans. Ind. Inform. 2013, 10, 197–209. [Google Scholar]
- Klickstein, I.; Shirin, A.; Sorrentino, F. Energy scaling of targeted optimal control of complex networks. Nat. Commun. 2017, 8, 15145. [Google Scholar] [CrossRef]
- Chen, G. Pinning control and synchronization on complex dynamical networks. Int. J. Control Autom. Syst. 2014, 12, 221–230. [Google Scholar] [CrossRef]
- Huang, W.; Sun, H.; He, W. Pinning control of complex networks with general topology. In Proceedings of the IEEE ICCA 2010, Xiamen, China, 9–11 June 2010; pp. 360–364. [Google Scholar]
- Zhang, X.; Wang, H.; Lv, T. Efficient target control of complex networks based on preferential matching. PLoS ONE 2017, 12, e0175375. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Liu, Y.Y.; D’souza, R.M.; Barabási, A.L. Target control of complex networks. Nat. Commun. 2014, 5, 5415. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Tang, P.; Chen, X.; Xiao, G.; Meng, M.; Ma, C.; Shi, L. Target control and expandable target control of complex networks. J. Frankl. Inst. 2020, 357, 3541–3564. [Google Scholar] [CrossRef]
- Li, G.; Chen, X.; Tang, P.; Xiao, G.; Wen, C.; Shi, L. Target control of directed networks based on network flow problems. IEEE Trans. Control Netw. Syst. 2019, 7, 673–685. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Controllability of complex networks. Nature 2011, 473, 167–173. [Google Scholar] [CrossRef]
- Wang, L.; Wang, L.; Kong, Z. Two controllable canonical forms for single input complex network. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 1467–1472. [Google Scholar]
- Mousavi, S.S.; Haeri, M.; Mesbahi, M. On the structural and strong structural controllability of undirected networks. IEEE Trans. Autom. Control 2017, 63, 2234–2241. [Google Scholar] [CrossRef]
- Menara, T.; Bassett, D.S.; Pasqualetti, F. Structural controllability of symmetric networks. IEEE Trans. Autom. Control 2018, 64, 3740–3747. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhao, C.; Di, Z.; Wang, W.X.; Lai, Y.C. Exact controllability of complex networks. Nat. Commun. 2013, 4, 2447. [Google Scholar] [CrossRef]
- Fatemi, M.; Setoodeh, P.; Haykin, S. Observability of stochastic complex networks under the supervision of cognitive dynamic systems. J. Complex Netw. 2017, 5, 433–460. [Google Scholar] [CrossRef]
- Leitold, D.; Vathy-Fogarassy, Á.; Abonyi, J. Controllability and observability in complex networks—The effect of connection types. Sci. Rep. 2017, 7, 151. [Google Scholar] [CrossRef] [PubMed]
- Menck, P.J.; Heitzig, J.; Marwan, N.; Kurths, J. How basin stability complements the linear-stability paradigm. Nat. Phys. 2013, 9, 89–92. [Google Scholar] [CrossRef]
- Safar, M.H.; Sorkhoh, I.Y.; Farahat, H.M.; Mahdi, K.A. On maximizing the entropy of complex networks. Procedia Comput. Sci. 2011, 5, 480–488. [Google Scholar] [CrossRef]
- Jiang, Y.; Hu, A.; Song, Y. The evaluation of complex networks’ robustness based on entropy measure. In Proceedings of the 2014 Communications Security Conference (CSC 2014), Beijing, China, 22–24 May 2014; pp. 1–5. [Google Scholar]
- Weilenmann, M.; Kraemer, L.; Faist, P.; Renner, R. Axiomatic relation between thermodynamic and information-theoretic entropies. Phys. Rev. Lett. 2016, 117, 260601. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Yang, L.; Chen, X.; Chen, D.; Gao, H.; Ma, J. Influential nodes identification in complex networks via information entropy. Entropy 2020, 22, 242. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef]
- Banfalvi, G. Cell Cycle Synchronization; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Fell, J.; Axmacher, N. The role of phase synchronization in memory processes. Nat. Rev. Neurosci. 2011, 12, 105–118. [Google Scholar] [CrossRef]
- Lawande, Q.V.; Maiti, N. Role of Nonlinear Dynamics and Chaos in Applied Sciences; Technical Report; Bhabha Atomic Research Centre: Mumbai, India, 2000; Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:31049284 (accessed on 12 January 2022).
- Dhillon, G.S.; Ward, J. Chaos theory as a framework for studying information systems. In Advanced Topics in Information Resources Management; IGI Global: Hershey, PA, USA, 2003; Volume 2, pp. 320–337. [Google Scholar]
- Zhang, X.; Zhu, Y.; Zhao, Y. Altering control modes of complex networks by reversing edges. Phys. A Stat. Mech. Its Appl. 2021, 561, 125249. [Google Scholar] [CrossRef]
- Jia, T.; Liu, Y.Y.; Csóka, E.; Pósfai, M.; Slotine, J.J.; Barabási, A.L. Emergence of bimodality in controlling complex networks. Nat. Commun. 2013, 4, 2002. [Google Scholar] [CrossRef]
- Liu, X.; Chen, T. Synchronization of nonlinear coupled networks via aperiodically intermittent pinning control. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 113–126. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Chen, G.; Lü, J. On pinning synchronization of complex dynamical networks. Automatica 2009, 45, 429–435. [Google Scholar] [CrossRef]
- Diwadkar, A.; Vaidya, U. Synchronization in large-scale nonlinear network systems with uncertain links. Automatica 2019, 100, 194–199. [Google Scholar] [CrossRef]
- Lu, J.; Chen, G. A time-varying complex dynamical network model and its controlled synchronization criteria. IEEE Trans. Autom. Control 2005, 50, 841–846. [Google Scholar]
- Chen, M. Chaos synchronization in complex networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 1335–1346. [Google Scholar] [CrossRef]
- Mai, X.H.; Zhang, B.; Luo, X.S.; Wei, D.Q. Controlling chaos in complex motor networks by environment. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 603–607. [Google Scholar] [CrossRef]
- De Wolf, T.; Holvoet, T. Emergence versus self-organisation: Different concepts but promising when combined. In Proceedings of the International Workshop on Engineering Self-Organising Applications, New York, NY, USA, 20 July 2004; pp. 1–15. [Google Scholar]
- O’Toole, E.; Nallur, V.; Clarke, S. Towards decentralised detection of emergence in complex adaptive systems. In Proceedings of the 2014 IEEE Eighth International Conference on Self-Adaptive and Self-Organizing Systems, London, UK, 8–12 September 2014; pp. 60–69. [Google Scholar]
- Fonseca, S.T.; Souza, T.R.; Verhagen, E.; Van Emmerik, R.; Bittencourt, N.F.; Mendonça, L.D.; Andrade, A.G.; Resende, R.A.; Ocarino, J.M. Sports injury forecasting and complexity: A synergetic approach. Sports Med. 2020, 50, 1757–1770. [Google Scholar] [CrossRef]
- Miconi, T.; McKinstry, J.L.; Edelman, G.M. Spontaneous emergence of fast attractor dynamics in a model of developing primary visual cortex. Nat. Commun. 2016, 7, 13208. [Google Scholar] [CrossRef]
- Keller, E.F. Organisms, machines, and thunderstorms: A history of self-organization, part two. Complexity, emergence, and stable attractors. Hist. Stud. Nat. Sci. 2009, 39, 1–31. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; De Bari, B.; Dixon, J.A. Dissipative structures, organisms and evolution. Entropy 2020, 22, 1305. [Google Scholar] [CrossRef]
- Giammarco, K. Practical modeling concepts for engineering emergence in systems of systems. In Proceedings of the 2017 12th System of Systems Engineering Conference (SoSE), Waikoloa, HI, USA, 18–21 June 2017; pp. 1–6. [Google Scholar]
- Mittal, S.; Rainey, L. Harnessing emergence: The control and design of emergent behavior in system of systems engineering. In Proceedings of the Conference on Summer Computer Simulation, Chicago, IL, USA, 26–29 July 2015; pp. 1–10. [Google Scholar]
- Espín-Sarzosa, D.; Palma-Behnke, R.; Núñez-Mata, O. Energy management systems for microgrids: Main existing trends in centralized control architectures. Energies 2020, 13, 547. [Google Scholar] [CrossRef]
- Jogwar, S.S.; Daoutidis, P. Community-based synthesis of distributed control architectures for integrated process networks. Chem. Eng. Sci. 2017, 172, 434–443. [Google Scholar] [CrossRef]
- Zou, J.; Chang, Q.; Arinez, J.; Xiao, G. Data-driven modeling and real-time distributed control for energy efficient manufacturing systems. Energy 2017, 127, 247–257. [Google Scholar] [CrossRef]
- Meissner, H.; Ilsen, R.; Aurich, J.C. Analysis of control architectures in the context of Industry 4.0. Procedia Cirp 2017, 62, 165–169. [Google Scholar] [CrossRef]
- Dragicevic, T.; Wu, D.; Shafiee, Q.; Meng, L. Distributed and decentralized control architectures for converter-interfaced microgrids. Chin. J. Electr. Eng. 2017, 3, 41–52. [Google Scholar]
- Patrascu, M.; Ion, A.; Constantinescu, V. Agent based simulation applied to the design of control systems for emergency vehicles access. In Proceedings of the 2015 14th International Conference on ITS Telecommunications (ITST), Copenhagen, Denmark, 2–4 December 2015; pp. 50–54. [Google Scholar]
- Elliott, C.M. Distributed multi-agent systems-a literature survey and inquisitive discussion. In Proceedings of the 2014 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014; pp. 1–7. [Google Scholar]
- Carli, R.; Dotoli, M. Decentralized control for residential energy management of a smart users’ microgrid with renewable energy exchange. IEEE/CAA J. Autom. Sin. 2019, 6, 641–656. [Google Scholar] [CrossRef]
- Srinivasan, D.; Choy, M. Hybrid multi-agent systems. In Innovations in Multi-Agent Systems and Applications-1; Springer: Berlin/Heidelberg, Germany, 2010; pp. 29–42. [Google Scholar]
- Hannebauer, M. Autonomous Dynamic Reconfiguration in Multi-Agent Systems: Improving the Quality and Efficiency of Collaborative Problem Solving; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2427. [Google Scholar]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Sabău, Ş.; Sperilă, A.; Oară, C.; Jadbabaie, A. Network Realization Functions for Optimal Distributed Control. arXiv 2021, arXiv:2112.09093. [Google Scholar]
- Hui, Q.; Haddad, W.M. Distributed nonlinear control algorithms for network consensus. Automatica 2008, 44, 2375–2381. [Google Scholar] [CrossRef]
- Münz, U.; Papachristodoulou, A.; Allgöwer, F. Delay robustness in consensus problems. Automatica 2010, 46, 1252–1265. [Google Scholar] [CrossRef]
- Carli, R.; Cavone, G.; Epicoco, N.; Di Ferdinando, M.; Scarabaggio, P.; Dotoli, M. Consensus-Based Algorithms for Controlling Swarms of Unmanned Aerial Vehicles. In Proceedings of the International Conference on Ad-Hoc Networks and Wireless, Bari, Italy, 19–21 October 2020; pp. 84–99. [Google Scholar]
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artif. Intell. Rev. 2021, 1–39. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Fortunato, S. Consensus clustering in complex networks. Sci. Rep. 2012, 2, 336. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Sundaram, S. Robustness of complex networks with implications for consensus and contagion. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3426–3432. [Google Scholar]
- Su, H.; Wu, H.; Chen, X.; Chen, M.Z. Positive edge consensus of complex networks. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 2242–2250. [Google Scholar] [CrossRef]
- Tan, S.; Lu, J.; Lin, Z. Emerging behavioral consensus of evolutionary dynamics on complex networks. SIAM J. Control Optim. 2016, 54, 3258–3272. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z.; Chen, G.; Huang, L. Consensus of multiagent systems and synchronization of complex networks: A unified viewpoint. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 57, 213–224. [Google Scholar]
- Homs-Dones, M.; Devriendt, K.; Lambiotte, R. Nonlinear consensus on networks: Equilibria, effective resistance, and trees of motifs. SIAM J. Appl. Dyn. Syst. 2021, 20, 1544–1570. [Google Scholar] [CrossRef]
- Shang, Y. A system model of three-body interactions in complex networks: Consensus and conservation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2022, 478. [Google Scholar] [CrossRef]
- Liang, K.; He, W. Secure Consensus Control of Two-timescale Networks Subject to Sequential Scaling Attacks. In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar]
- Ye, D.; Zhang, M.; Vasilakos, A.V. A survey of self-organization mechanisms in multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 441–461. [Google Scholar] [CrossRef]
- Hrabia, C.E.; Lützenberger, M.; Albayrak, S. Towards adaptive multi-robot systems: Self-organization and self-adaptation. Knowl. Eng. Rev. 2018, 33, 1–24. [Google Scholar] [CrossRef]
- Niazi, M.; Hussain, A. Agent-based tools for modeling and simulation of self-organization in peer-to-peer, ad hoc, and other complex networks. IEEE Commun. Mag. 2009, 47, 166–173. [Google Scholar] [CrossRef]
- Song, C.; Havlin, S.; Makse, H.A. Self-similarity of complex networks. Nature 2005, 433, 392–395. [Google Scholar] [CrossRef] [PubMed]
- Caldarelli, G.; Garlaschelli, D. Self-organization and complex networks. In Adaptive Networks; Springer: Berlin/Heidelberg, Germany, 2009; pp. 107–135. [Google Scholar]
- Fei, C.; Zeng-Qiang, C.; Zhu-Zhi, Y. A realistic model for complex networks with local interaction, self-organization and order. Chin. Phys. 2007, 16, 287. [Google Scholar] [CrossRef]
- Aoki, T.; Yawata, K.; Aoyagi, T. Self-organization of complex networks as a dynamical system. Phys. Rev. E 2015, 91, 012908. [Google Scholar] [CrossRef] [PubMed]
- Schlotterbeck, G.; Raievsky, C.; Lefevre, L. Decentralized estimation of forest fire spread using reactive and cognitive mobile sensors. Nat. Comput. 2018, 17, 537–551. [Google Scholar] [CrossRef]
- Asaamoning, G.; Mendes, P.; Rosário, D.; Cerqueira, E. Drone Swarms as Networked Control Systems by Integration of Networking and Computing. Sensors 2021, 21, 2642. [Google Scholar] [CrossRef]
- Gates, A.J.; Rocha, L.M. Control of complex networks requires both structure and dynamics. Sci. Rep. 2016, 6, 24456. [Google Scholar] [CrossRef]
- Mahmoodi, K.; West, B.J.; Grigolini, P. Self-organizing complex networks: Individual versus global rules. Front. Physiol. 2017, 8, 478. [Google Scholar] [CrossRef]
- Silva, C.J.; Cantin, G. Synchronization and self-organization in complex networks for a tuberculosis model. Math. Comput. Sci. 2021, 15, 107–120. [Google Scholar] [CrossRef]
- Bakule, L.; Rehák, B.; Papík, M. Decentralized H-infinity control of complex systems with delayed feedback. Automatica 2016, 67, 127–131. [Google Scholar] [CrossRef]
- Vaccarini, M.; Longhi, S.; Katebi, M.R. Unconstrained networked decentralized model predictive control. J. Process Control 2009, 19, 328–339. [Google Scholar] [CrossRef]
- Sandou, G.; Font, S.; Tebbani, S.; Hiret, A.; Mondon, C.; Tebbani, S.; Hiret, A.; Mondon, C. Predictive control of a complex district heating network. In Proceedings of the IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; Volume 44, p. 7372. [Google Scholar]
- Bianchi, D.; Borri, A.; Di Benedetto, M.D.; Ferrara, A. Decentralized model predictive control of freeway traffic systems over lossy communication networks. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 1074–1079. [Google Scholar]
- Lin, S.; De Schutter, B.; Xi, Y.; Hellendoorn, H. Efficient network-wide model-based predictive control for urban traffic networks. Transp. Res. Part C Emerg. Technol. 2012, 24, 122–140. [Google Scholar] [CrossRef]
- Li, A.; Sun, J. Stability of nonlinear system under distributed Lyapunov-based economic model predictive control with time-delay. ISA Trans. 2020, 99, 148–153. [Google Scholar] [CrossRef] [PubMed]
- Ocampo-Martinez, C.; Puig, V.; Cembrano, G.; Quevedo, J. Application of predictive control strategies to the management of complex networks in the urban water cycle [applications of control]. IEEE Control Syst. Mag. 2013, 33, 15–41. [Google Scholar]
- Barcelli, D.; Ocampo-Martinez, C.; Puig, V.; Bemporad, A. Decentralized model predictive control of drinking water networks using an automatic subsystem decomposition approach. IFAC Proc. Vol. 2010, 43, 572–577. [Google Scholar] [CrossRef]
- Fu, D.; Ionescu, C.M.; Aghezzaf, E.H.; De Keyser, R. Decentralized and centralized model predictive control to reduce the bullwhip effect in supply chain management. Comput. Ind. Eng. 2014, 73, 21–31. [Google Scholar] [CrossRef]
- Ion, A.; Patrascu, M. A Scalable Algorithm for Self-Organization in Event-Triggered Networked Control Systems. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 2725–2730. [Google Scholar]
- Ion, A.; Berceanu, C.; Patrascu, M. Applying agent based simulation to the design of traffic control systems with respect to real-world urban complexity. In Multi-Agent Systems and Agreement Technologies; Springer: Berlin/Heidelberg, Germany, 2015; pp. 395–409. [Google Scholar]
- Bertolotti, T. Generative and Demonstrative Experiments. In Model-Based Reasoning in Science and Technology; Springer: Berlin/Heidelberg, Germany, 2014; pp. 479–498. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).