A Comparative Analysis of DNN and Conventional Signal Detection Techniques in SISO and MIMO Communication Systems
Abstract
1. Introduction
2. Theoretical Foundation
2.1. Signal Detection Techniques
- Conventional methods: These include statistical approximation and optimization techniques such as MLD, MMSE, and ZF. These methods, while effective, face limitations in complex MIMO systems due to increased computational demands and the need for precise channel information.
- Machine learning-based approaches: These approaches focus on learning complex patterns and making data-driven decisions. Deep learning techniques, such as DNN, have shown promising results in various applications, including signal detection in wireless communication systems.
2.1.1. Maximum Likelihood Detection (MLD)
2.1.2. MMSE Detection
2.1.3. ZF Detection
2.2. Machine Learning (ML) for Signal Detection
3. Literature Review
4. Methodology
4.1. Evaluation of Conventional Methods
4.2. Designing the DNN-Based Detection Model
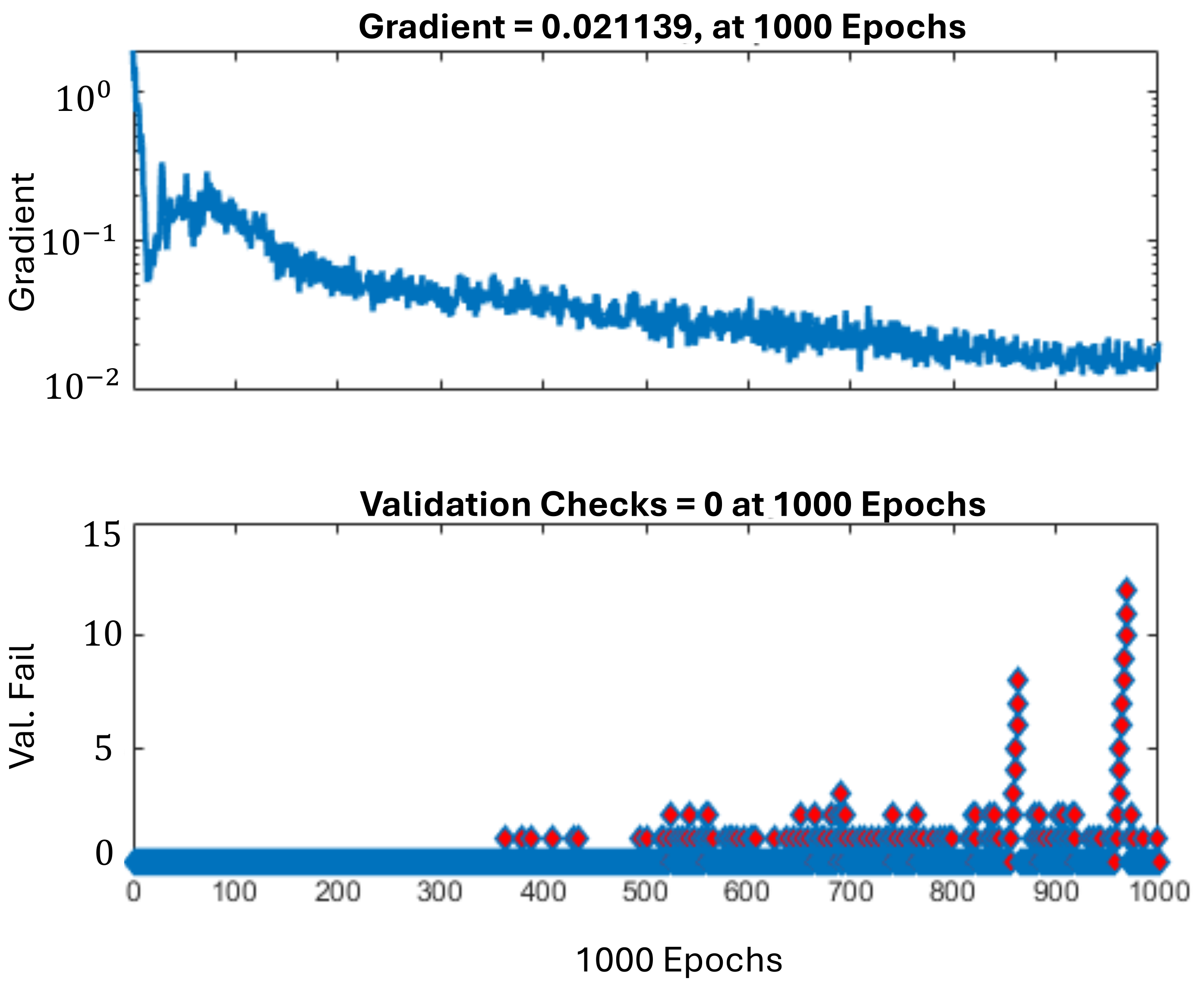
4.3. DNN Architecture and Training
5. Results and Analysis
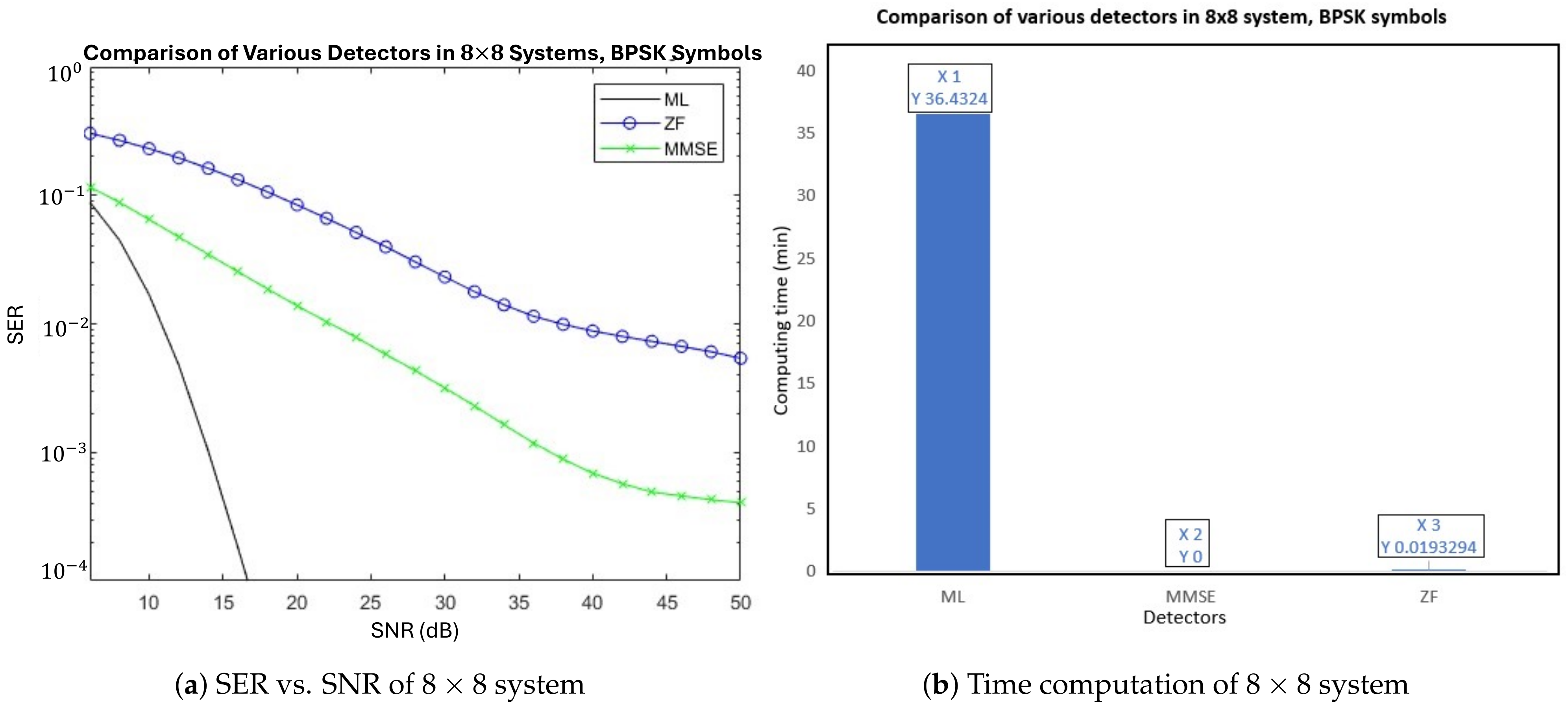
5.1. Performance of Conventional Methods
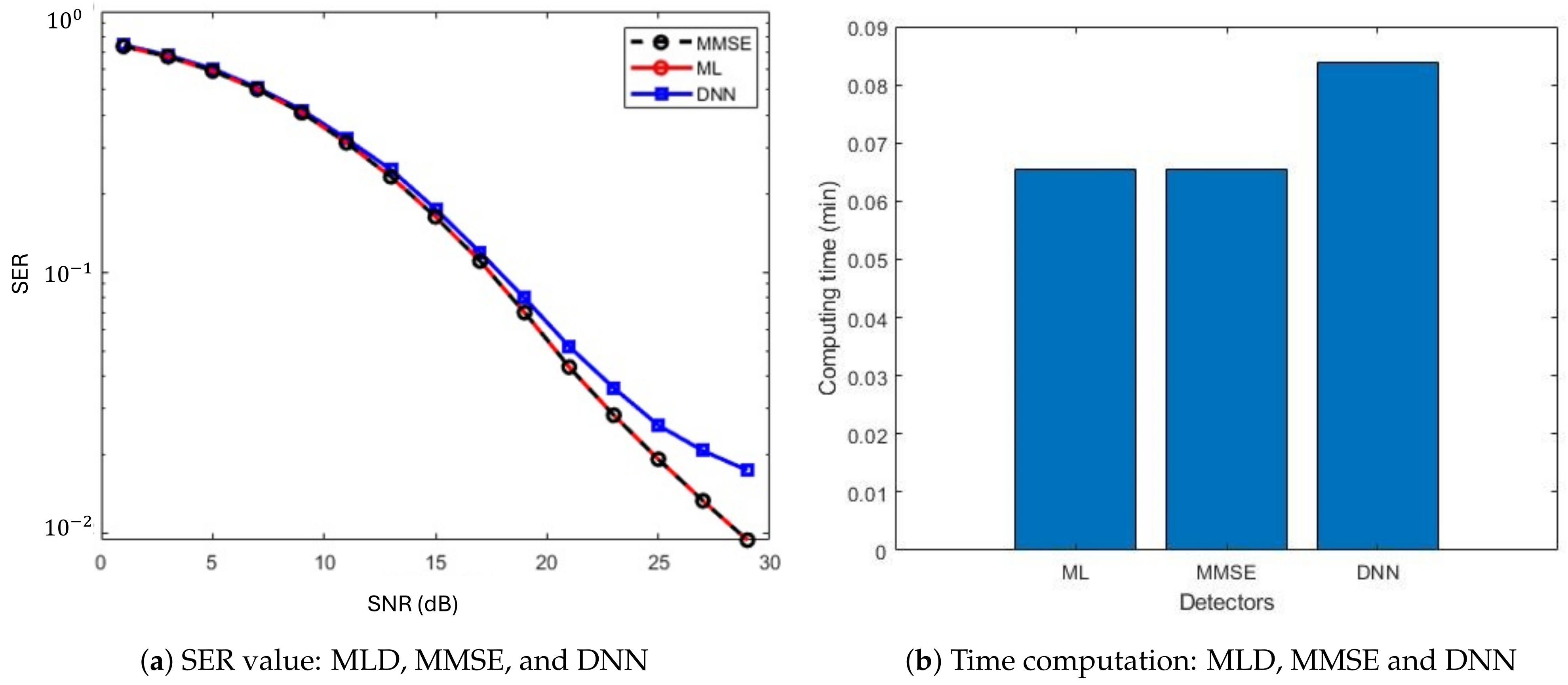
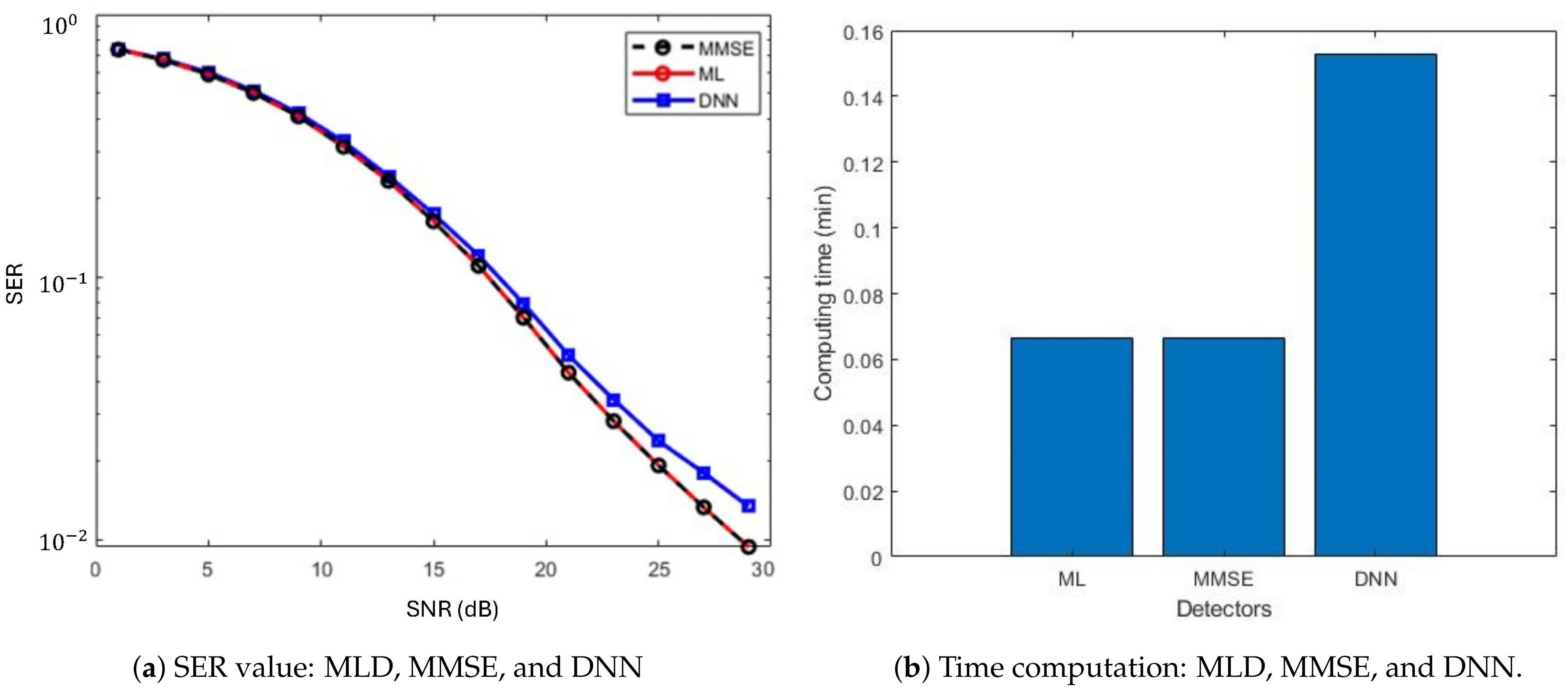
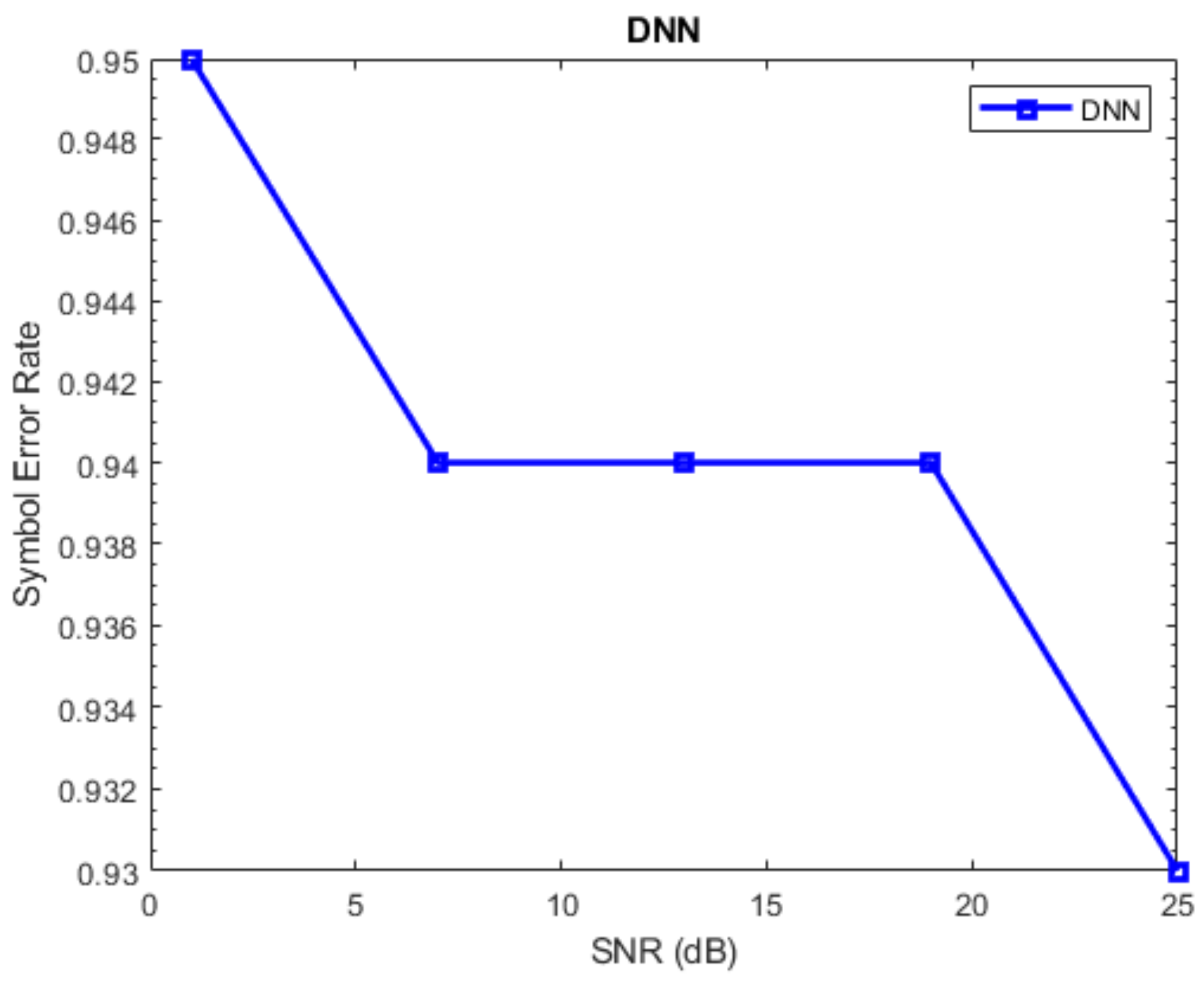
5.2. Performance of DNN-Based Detector
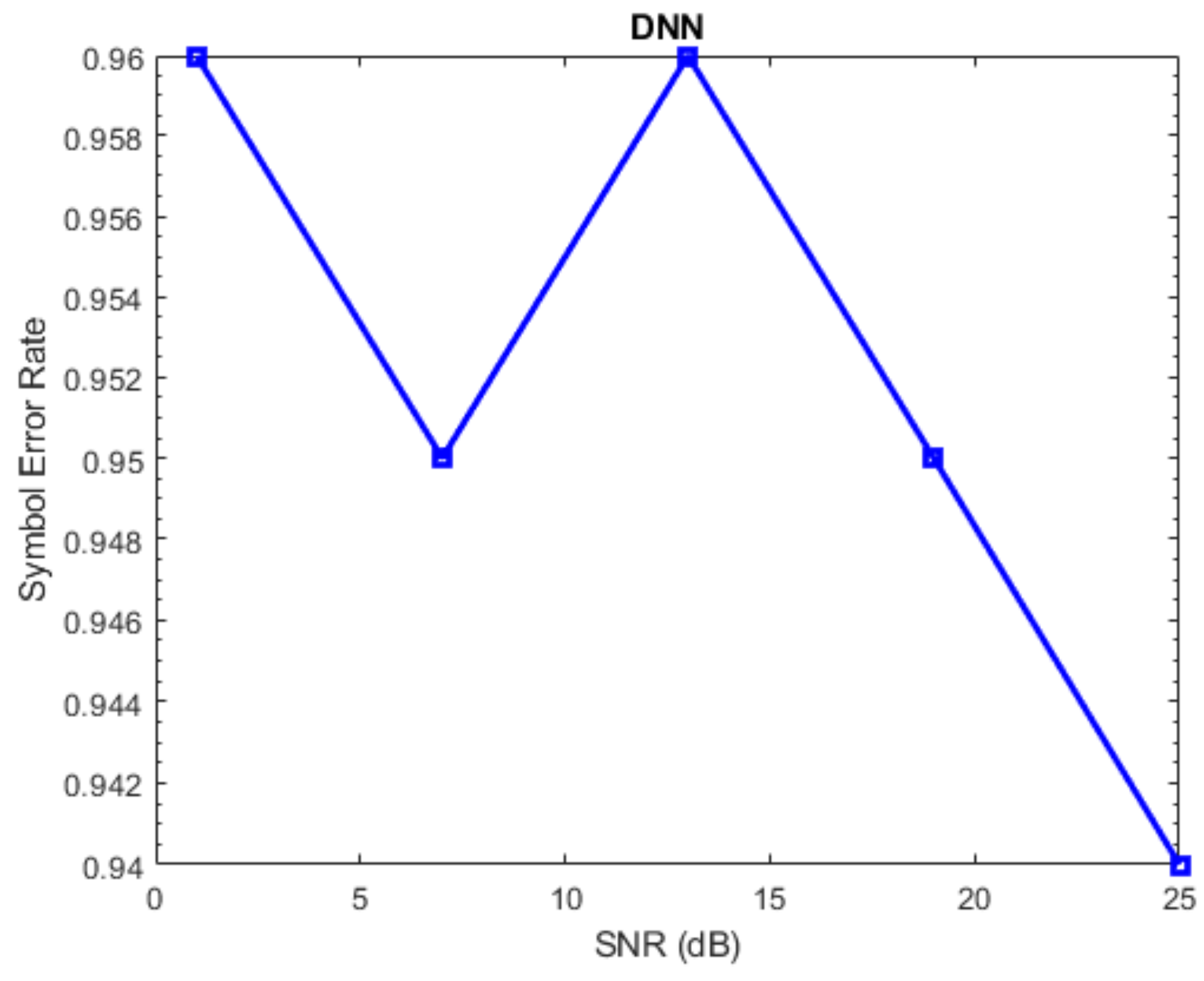
5.3. MIMO-Based DNN Signal Detection Model
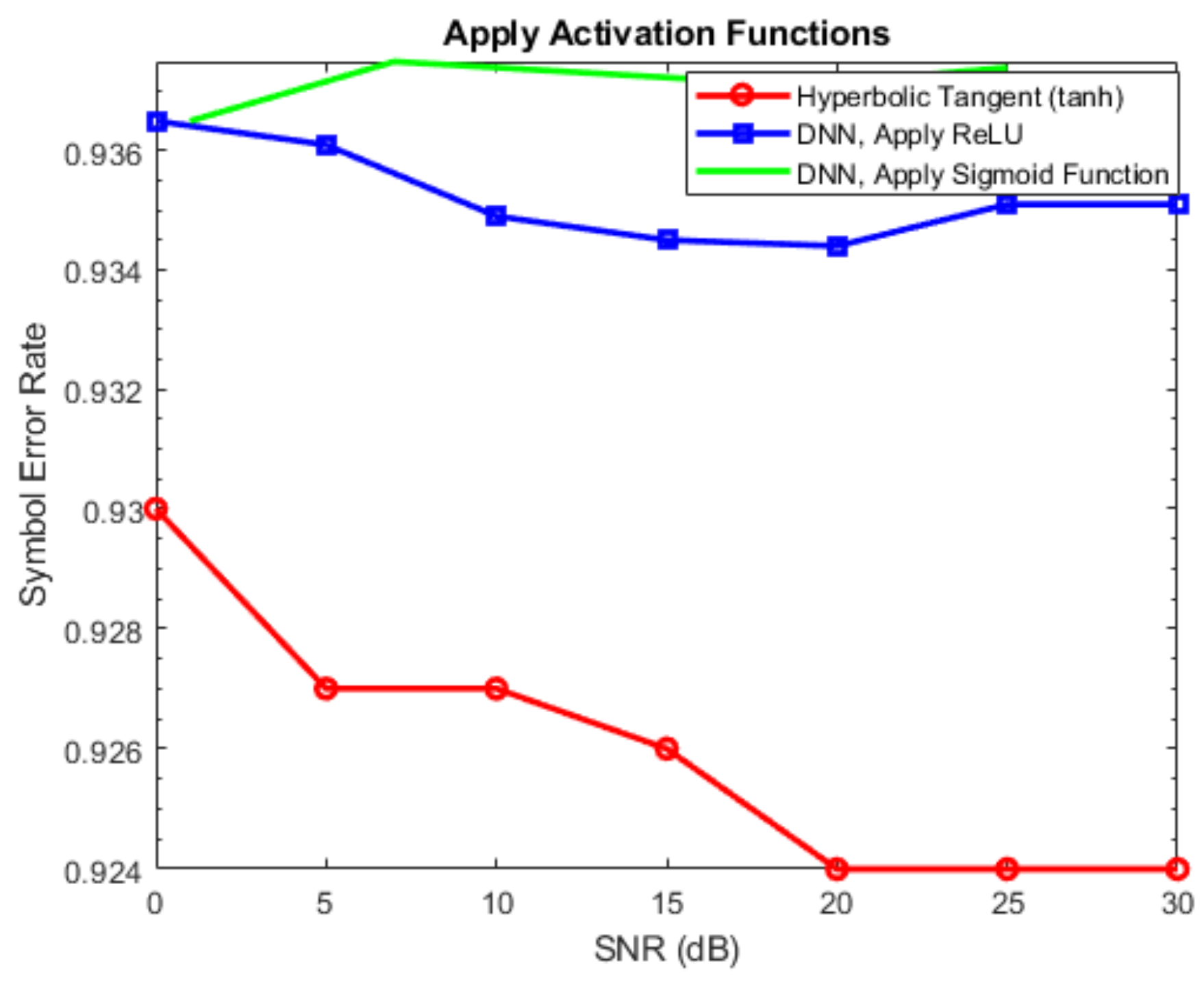
5.4. Impact of Activation Functions
5.5. Impact of Training Algorithms
5.6. Comparison with Conventional MIMO Methods
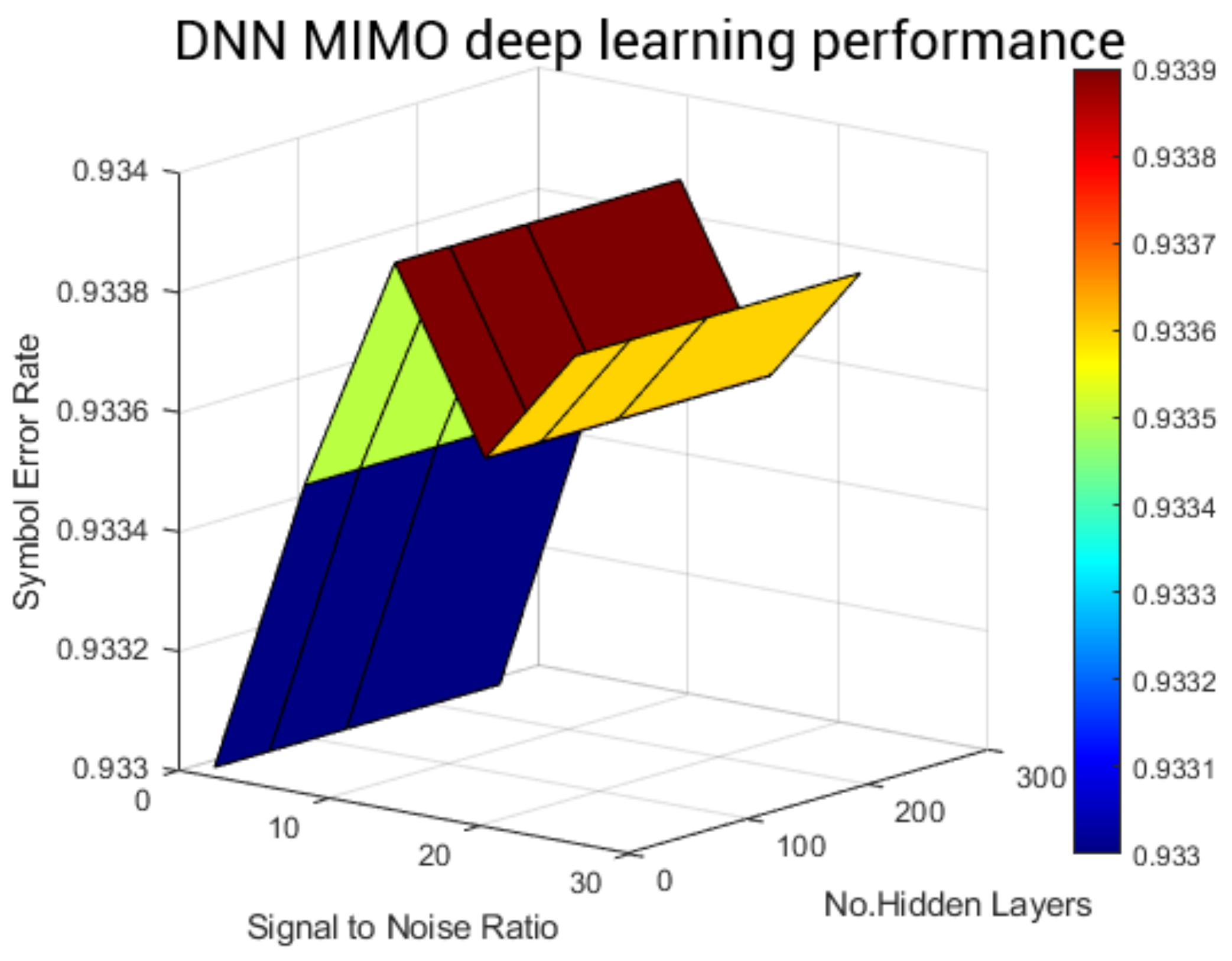
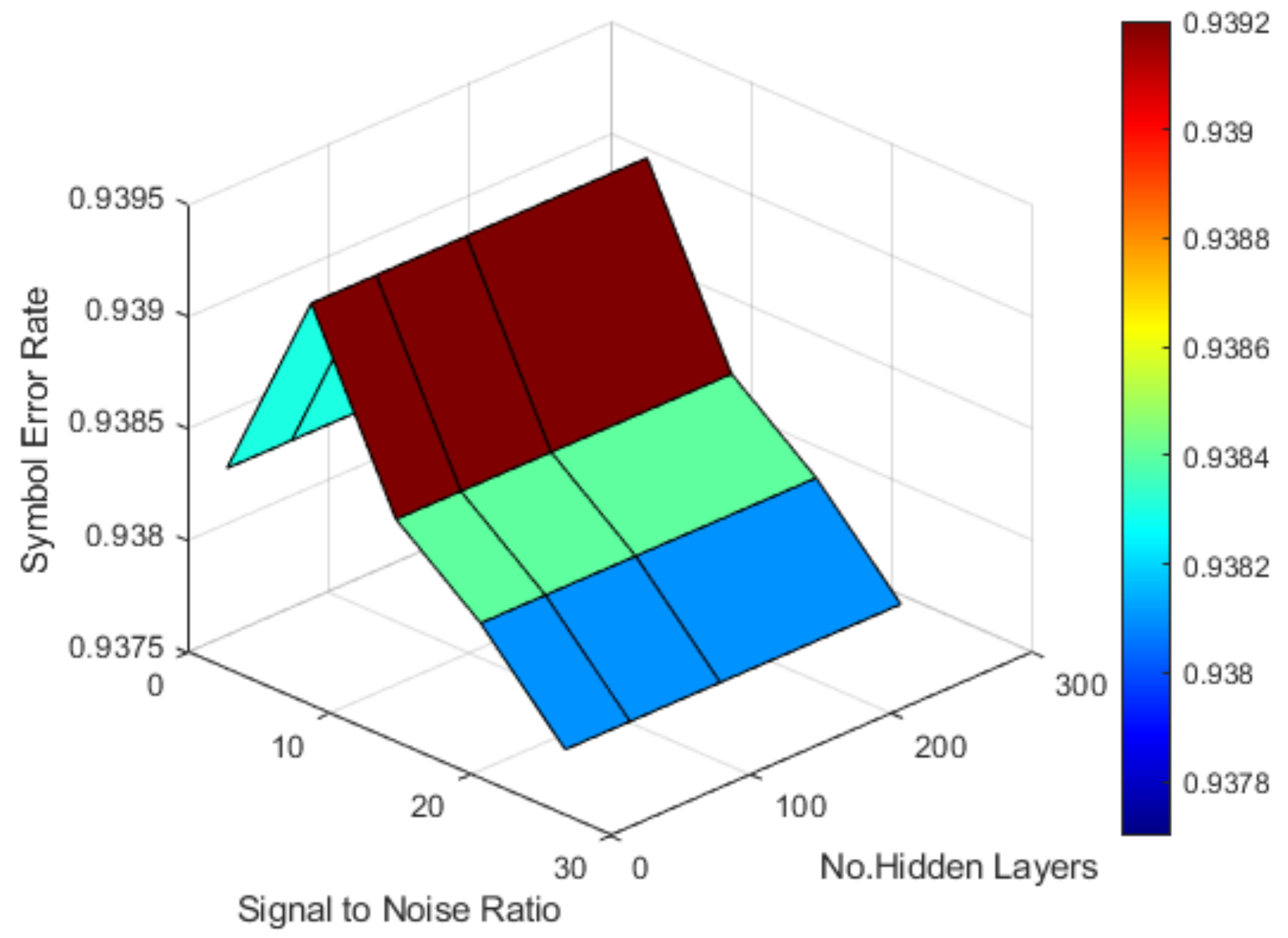
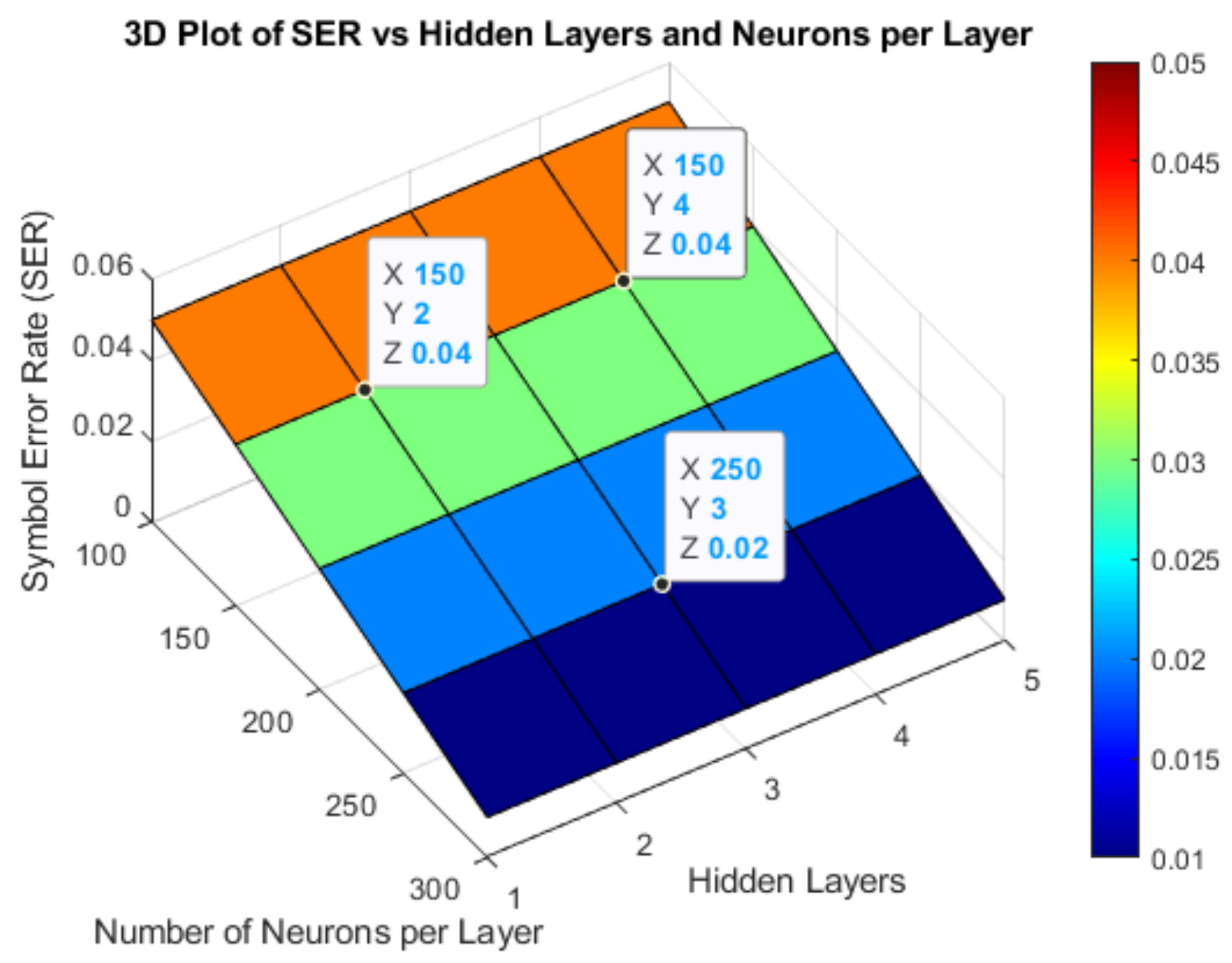
5.7. 3D Visualization of DNN Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Y.; Sun, S.; Duan, X.; Chen, Z. A study on Deep Neural Networks framework. In Proceedings of the 2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 3–5 October 2016; pp. 1519–1522. [Google Scholar] [CrossRef]
- Dixit, G.K.; Ch, V.; Barbosa, V.J.; Jeelani, S.H.; Johari, L.; Shukla, S.K. Comparative Analysis of Neural Networks and Deep Learning using Wireless Communication. In Proceedings of the 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, India, 28–29 April 2022; pp. 1585–1588. [Google Scholar] [CrossRef]
- Angra, S.; Ahuja, S. Machine learning and its applications: A review. In Proceedings of the 2017 International Conference on Big Data Analytics and Computational Intelligence (ICBDAC), Chirala, Andhra Pradesh, India, 23–25 March 2017; pp. 57–60. [Google Scholar] [CrossRef]
- Jha, K.K.; Jha, R.; Jha, A.K.; Hassan, M.A.M.; Yadav, S.K.; Mahesh, T. A Brief Comparison on Machine Learning Algorithms Based on Various Applications: A Comprehensive Survey. In Proceedings of the 2021 IEEE International Conference on Computation System and Information Technology for Sustainable Solutions (CSITSS), Bangalore, India, 16–18 December 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Fujii, S.; Hayashi, H. Comparison of Performance by Activation Functions on Deep Image Prior. In Proceedings of the 2019 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Okinawa, Japan, 11–13 February 2019; pp. 255–258. [Google Scholar] [CrossRef]
- Khurshid, K.; Khan, A.A.; Siddiqui, M.H.; Hadi, M.U.; Rashid, I.; Imran, M. Optimality of Linear MIMO Detection for 5G Systems via 1-Opt Local Search. J. Electr. Eng. Technol. 2021, 16, 1099–1108. [Google Scholar] [CrossRef]
- Gebre, A.; Shaikh, J.; Kebede, T.; Gelete, F.Z. Comparative Performance Analysis of Channel Estimation Techniques for Massive MIMO System. In Proceedings of the 2021 IEEE Indian Conference on Antennas and Propagation (InCAP), Jaipur, Rajasthan, India, 13–16 December 2021; pp. 236–239. [Google Scholar] [CrossRef]
- Lyu, T.K. Capacity of multi-user MIMO systems with MMSE and ZF precoding. In Proceedings of the 2016 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), San Francisco, CA, USA, 10–14 April 2016; pp. 1083–1084. [Google Scholar] [CrossRef]
- Wei, S. Simulation and Analysis of the Impact of MIMO System on Communication Quality. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 341–344. [Google Scholar] [CrossRef]
- Albreem, M.A.; Juntti, M.; Shahabuddin, S. Massive MIMO Detection Techniques: A Survey. IEEE Commun. Surv. Tutorials 2019, 21, 3109–3132. [Google Scholar] [CrossRef]
- Daha, M.Y.; Rafferty, J.; Ashraf, M.I.; Usman Hadi, M. DM-DETECT—A Deep MIMO Detector for Beyond 5G Networks. In Proceedings of the 2023 Second International Conference on Augmented Intelligence and Sustainable Systems (ICAISS), Trichy, India, 23–25 August 2023; pp. 1381–1385. [Google Scholar] [CrossRef]
- Daha, M.Y.; Rafferty, J.; Ashraf, M.I.; Hadi, M.U. AIDETECT—AI-based Integratable Detection for Beyond 5G Networks. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Tenerife, Canary Islands, Spain, 19–21 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, L.; Chen, H.; Liu, Q. Comparative Analysis of ML and MMSE Methods in Massive MIMO Systems for Future Wireless Networks. In Proceedings of the IEEE International Conference on Communications (ICC), Seoul, Republic of Korea, 16–20 May 2022. [Google Scholar]
- Sarangi, A.K.; Datta, A. Capacity Comparison of SISO, SIMO, MISO and MIMO Systems. In Proceedings of the 2018 Second International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 15–16 February 2018; pp. 798–801. [Google Scholar] [CrossRef]
- Gonzalez, R.; Patel, K. Machine Learning Applications in Advanced MIMO Technologies for 6G and Beyond. In Advances in Wireless Communications: Technologies for Future Networks; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Doe, J.; Smith, A. Introduction to Machine Learning in Data Detection for Wireless Communication Systems. Wirel. Commun. Mob. Comput. 2021, 10, 100–120. [Google Scholar]
- Wang, H.; Wang, Y.; Lou, Y.; Song, Z. The Role of Activation Function in CNN. In Proceedings of the 2020 2nd International Conference on Information Technology and Computer Application (ITCA), Guangzhou, China, 18–20 December 2020; pp. 429–432. [Google Scholar] [CrossRef]
- Ding, B.; Qian, H.; Zhou, J. Activation functions and their characteristics in deep neural networks. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 1836–1841. [Google Scholar] [CrossRef]
- Shojaeifard, A.; Wong, K.K.; Tong, K.F.; Chu, Z.; Mourad, A.; Haghighat, A.; Hemadeh, I.; Nguyen, N.T.; Tapio, V.; Juntti, M. MIMO Evolution Beyond 5G through Reconfigurable Intelligent Surfaces and Fluid Antenna Systems. Proc. IEEE 2022, 110, 1244–1265. [Google Scholar] [CrossRef]
- Parhi, R.; Nowak, R.D. The Role of Neural Network Activation Functions. IEEE Signal Process. Lett. 2020, 27, 1779–1783. [Google Scholar] [CrossRef]
- Varshney, R.; Jain, P.; Vijay, S. Massive MIMO Systems In Wireless Communication. In Proceedings of the 2018 2nd International Conference on Micro-Electronics and Telecommunication Engineering (ICMETE), Ghaziabad, India, 20–21 September 2018; pp. 39–44. [Google Scholar] [CrossRef]
- Wang, S.; Li, F.; Li, T.; Ji, W.; Liang, Y. A Deep Learning Detector for 3D Massive MIMO Systems with Impulsive Noise. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–6. [Google Scholar] [CrossRef]






| Aspect | Description |
|---|---|
| Architecture | 7 hidden layers, each with 100 neurons |
| Activation function (hidden layers) | ReLU |
| Training Process | |
| Dataset preparation | Large dataset of received signals and corresponding transmitted symbols |
| Train/test split | 70% training data, 30% testing data |
| Optimization algorithm | Stochastic gradient descent (SGD) |
| Learning rate | 0.01 |
| Loss function | Mean squared error (MSE) |
| Training epochs | 1000 with early stopping |
| Evaluation Metrics | SER, SNR, computational Time |
| Aspect | Description |
|---|---|
| Input layer | Corresponds to input signal dimension |
| Hidden layer | Extract higher-level features, more nodes initially for complex patterns |
| Output layer | Determined according to classification/regression task (e.g., transmitted symbols) |
| Number of nodes | Tuned empirically using cross-validation (grid search, validation set) |
| Regularization | Techniques like dropout and early stopping to avoid overfitting |
| SER | CT | ||||||
|---|---|---|---|---|---|---|---|
| N | M | MLD | MMSE | ZF | MLD | MMSE | ZF |
| 2 | 2 | 0.000325 | 0.00567 | 0.00823 | 0.11714 | 0.00132964 | 0.0016907 |
| 4 | 4 | 0.005705 | 0.015575 | 0.518657 | 0.00273238 | 0.0033708 | |
| 6 | 6 | 0.00602 | 0.0257517 | 5.41947 | 0.00967891 | 0.0118022 | |
| 8 | 8 | 0.00395 | 0.0307313 | 36.4324 | - | 0.0193294 | |
| 10 | 10 | 0.002195 | 0.030952 | 390.642 | - | - | |
| 12 | 12 | 0.00260917 | 0.0370992 | 288.854 | - | - | |
| SER | CT | ||||||
|---|---|---|---|---|---|---|---|
| N | M | MLD | MMSE | ZF | MLD | MMSE | ZF |
| 2 | 2 | 0.007245 | 0.00978 | 0.105489 | 0.00127795 | 0.00160855 | |
| 2 | 4 | 0.000021 | 0.000022 | 0.0107284 | 0.00136752 | 0.00173983 | |
| 2 | 6 | 0.114222 | 0.00154409 | 0.00198467 | |||
| 2 | 8 | 0.116254 | 0.00189622 | 0.0021896 | |||
| 2 | 10 | 0.132713 | 0.00255674 | 0.00321228 | |||
| 2 | 12 | 0.12416 | 0.0025504 | 0.00324025 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shoukat, H.; Khurshid, A.A.; Daha, M.Y.; Shahid, K.; Hadi, M.U. A Comparative Analysis of DNN and Conventional Signal Detection Techniques in SISO and MIMO Communication Systems. Telecom 2024, 5, 487-507. https://doi.org/10.3390/telecom5020025
Shoukat H, Khurshid AA, Daha MY, Shahid K, Hadi MU. A Comparative Analysis of DNN and Conventional Signal Detection Techniques in SISO and MIMO Communication Systems. Telecom. 2024; 5(2):487-507. https://doi.org/10.3390/telecom5020025
Chicago/Turabian StyleShoukat, Hamna, Abdul Ahad Khurshid, Muhammad Yunis Daha, Kamal Shahid, and Muhammad Usman Hadi. 2024. "A Comparative Analysis of DNN and Conventional Signal Detection Techniques in SISO and MIMO Communication Systems" Telecom 5, no. 2: 487-507. https://doi.org/10.3390/telecom5020025
APA StyleShoukat, H., Khurshid, A. A., Daha, M. Y., Shahid, K., & Hadi, M. U. (2024). A Comparative Analysis of DNN and Conventional Signal Detection Techniques in SISO and MIMO Communication Systems. Telecom, 5(2), 487-507. https://doi.org/10.3390/telecom5020025






