Polar-Coded Differential/Quadrature Chaos Shift Keying Communication Systems for Underwater Acoustic Channels
Abstract
1. Introduction
2. Polar Code
3. UWA Channel and Noise Models
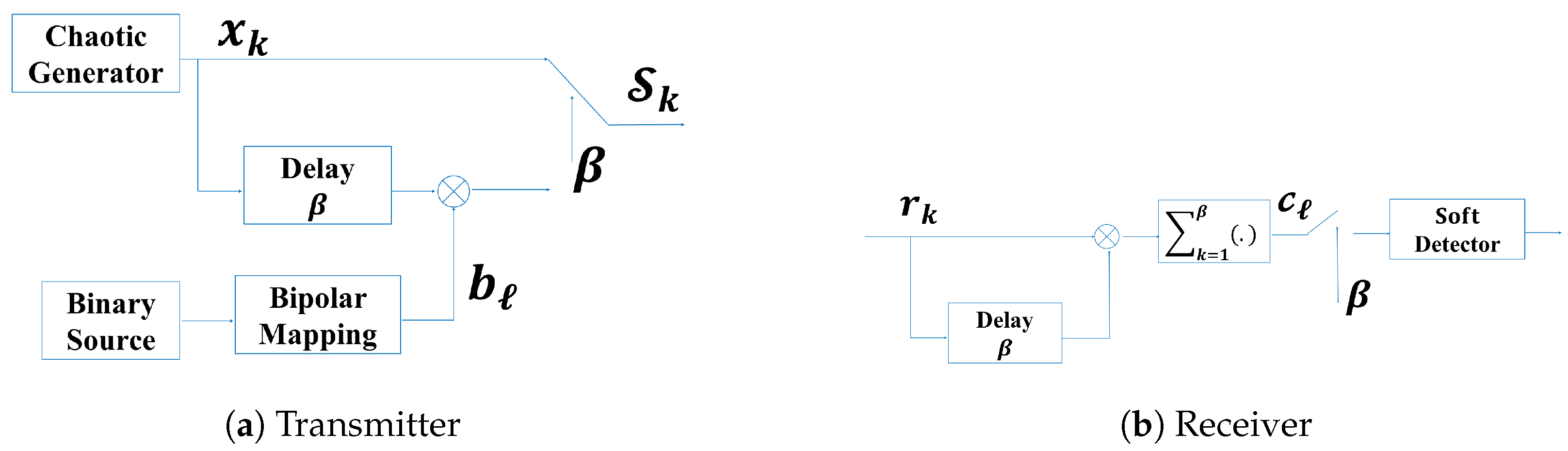
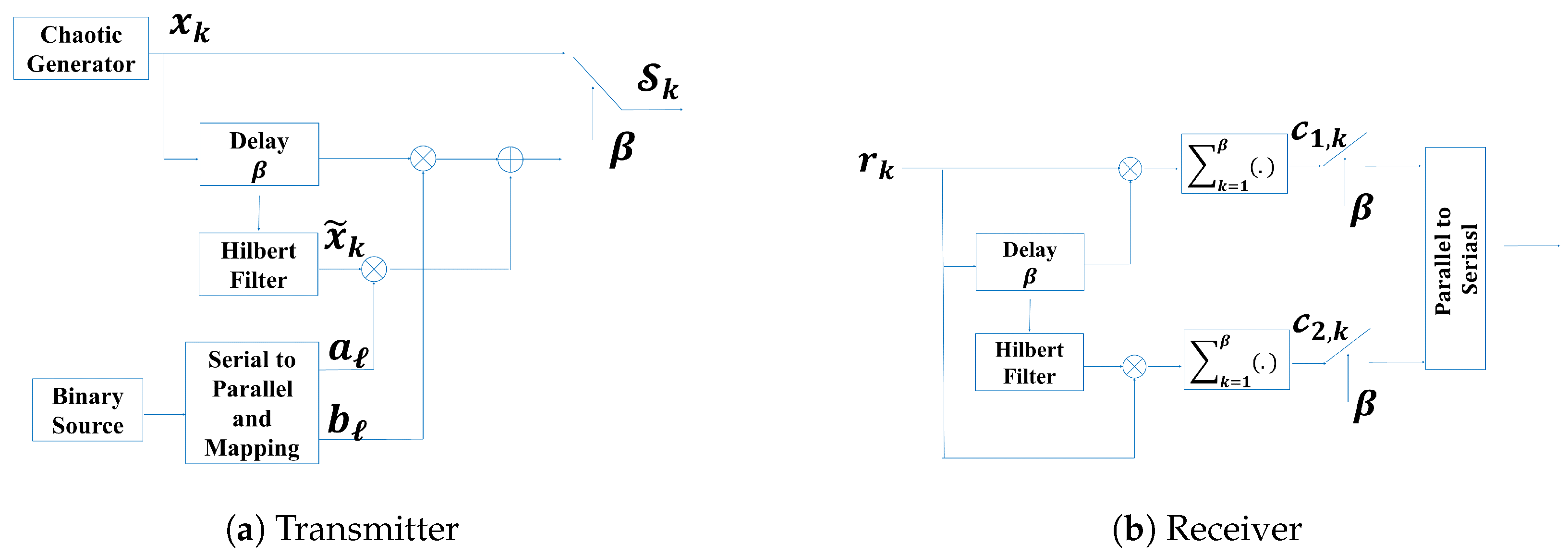
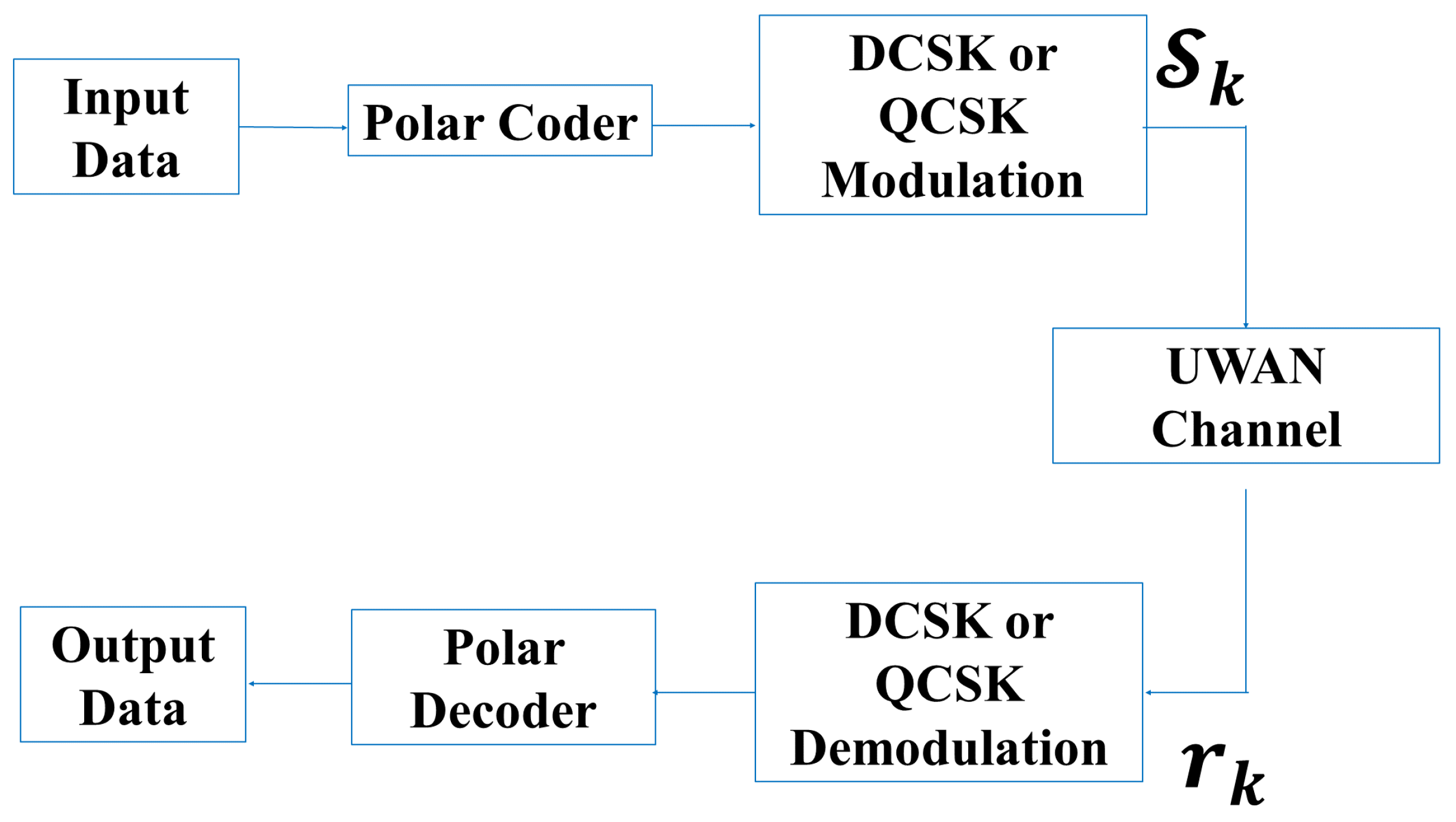
4. DCSK and QCSK Communication Systems for UWA
5. BER Analysis of DCSK and QCSK Systems under the UWA Channel
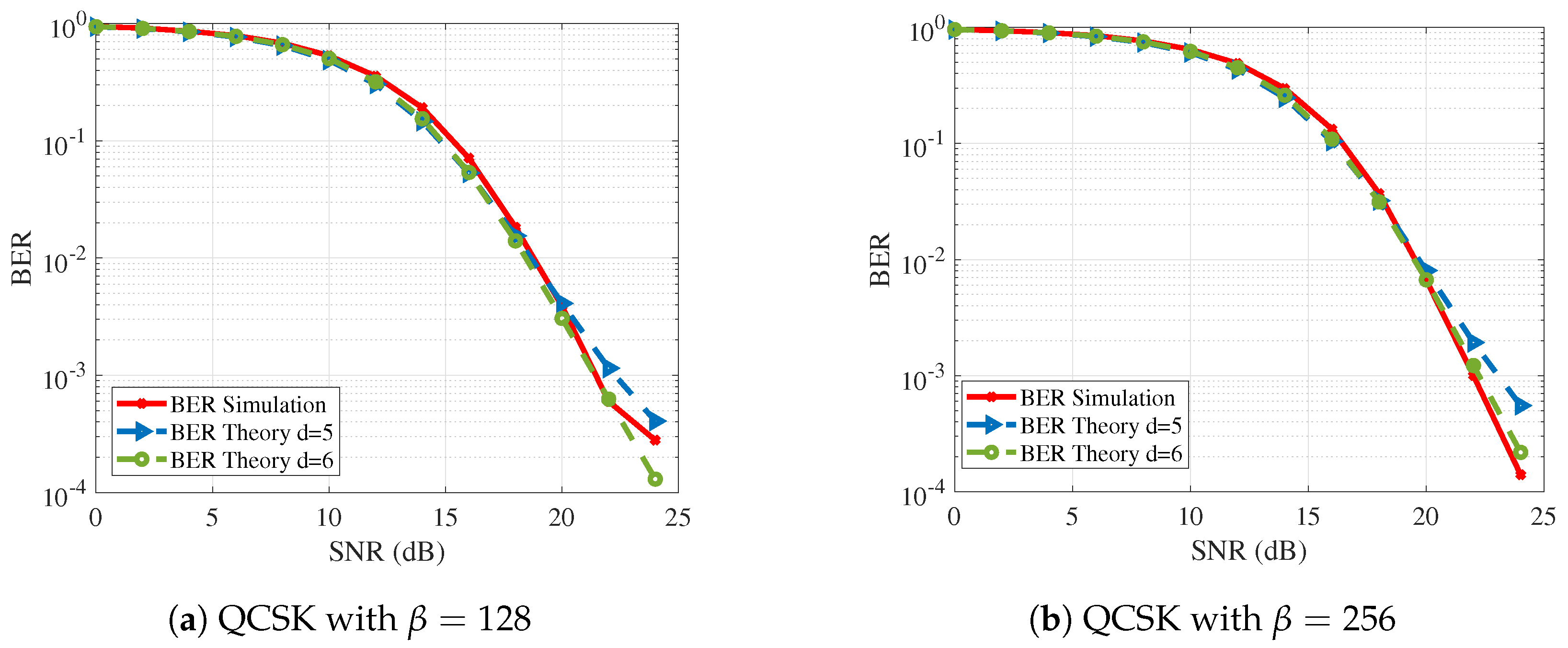
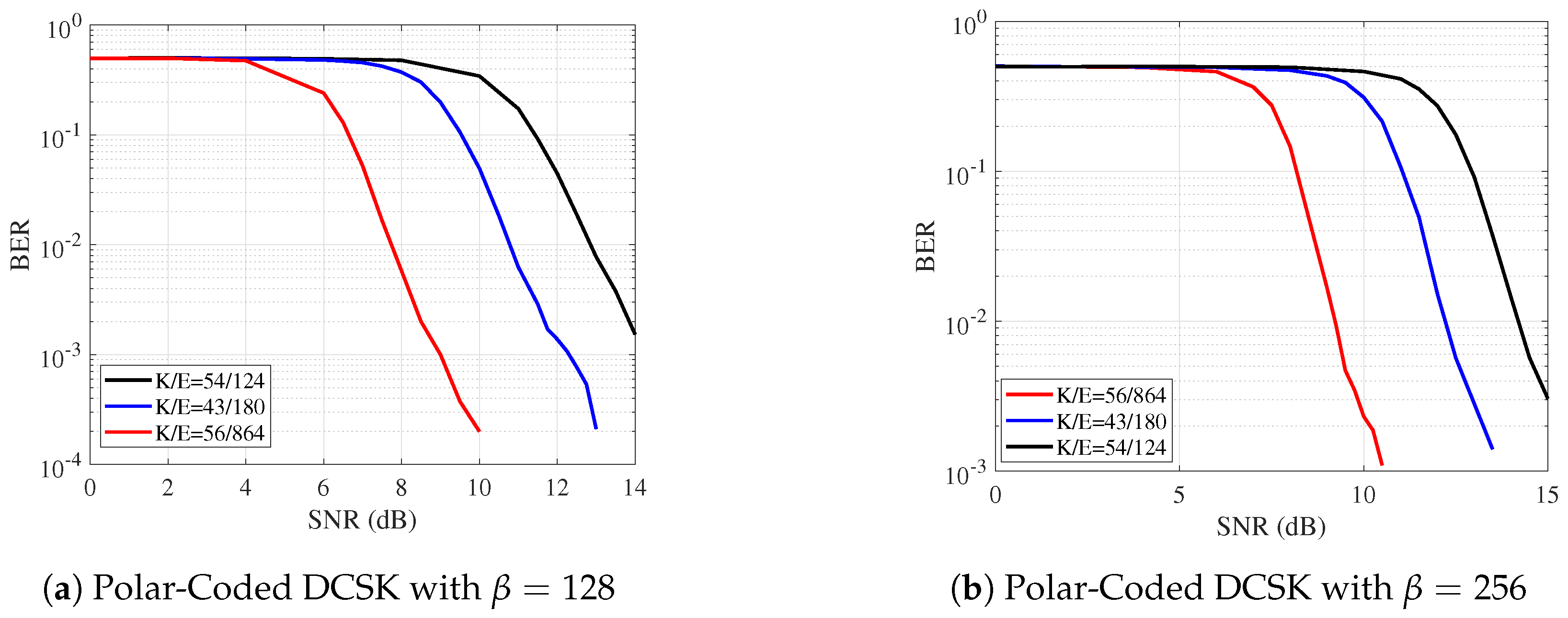
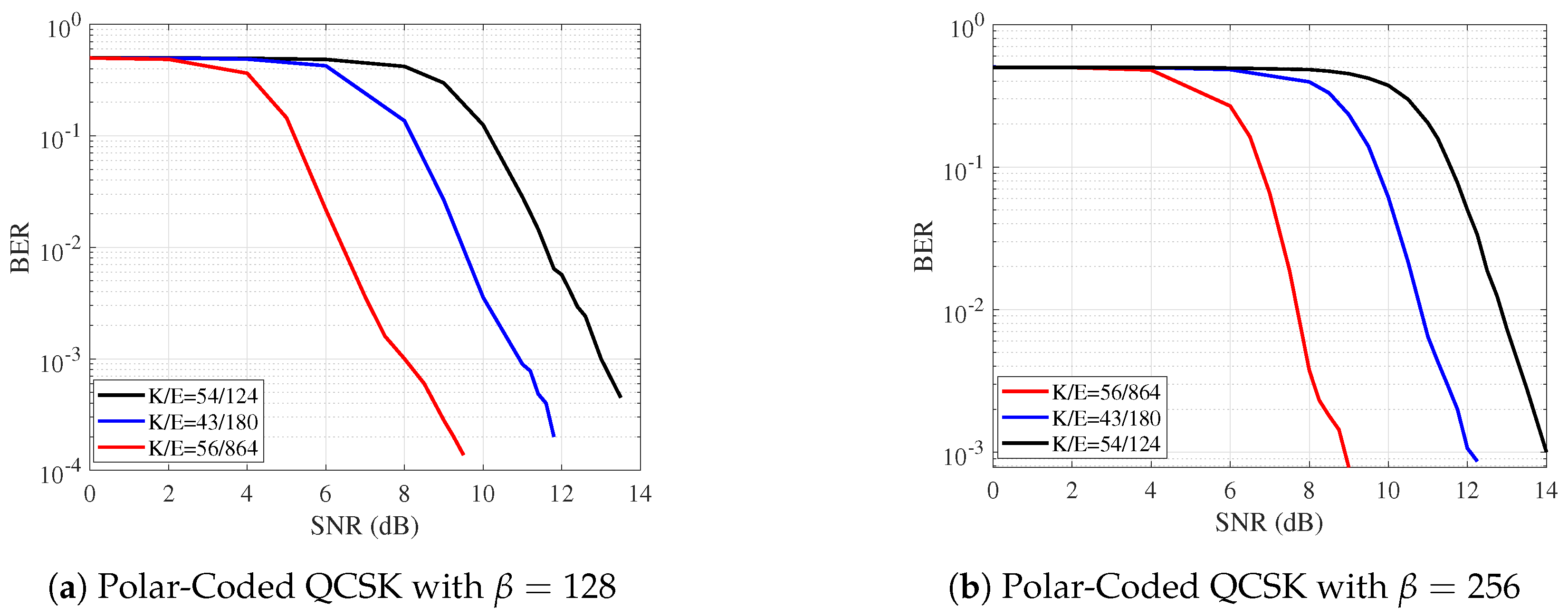
6. Simulation and Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UWA | Underwater acoustic |
| SNR | Signal-to-noise ratio |
| BER | Bit error rate |
| DCSK | Differential chaos shift keying |
| QCSK | Quadrature chaos shift keying |
| Probability density function |
References
- Sha’ameri, A.Z.; Al-Aboosi, Y.Y.; Khamis, N.H. Underwater acoustic noise characteristics of shallow water in Tropical Seas. In Proceedings of the International Conference on Computer and Communication Engineering, Kuala Lumpur, Malaysia, 23–25 September 2014. [Google Scholar] [CrossRef]
- Chen, P.; Rong, Y.; Nordholm, S.; He, Z.; Duncan, A.J. Joint channel estimation and impulsive noise mitigation in underwater acoustic OFDM communication systems. IEEE Trans. Wirel. Commun. 2017, 16, 6165–6178. [Google Scholar] [CrossRef]
- Chitre, M.; Ong, S.H.; Potter, J. Performance of coded OFDM in very shallow water channels and snapping shrimp noise. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Shah, N.S.M.; Ghawbar, F.; Jawhar, Y.A.; Almohammedi, A.A. Filtered-OFDM with channel coding based on T-distribution noise for underwater acoustic communication. J. Ambient. Intell. Humaniz. Comput. 2020, 13, 3379–3392. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Zhu, M. Nonbinary LDPC code for noncoherent underwater acoustic communication under non-Gaussian noise. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Xiamen, China, 22–25 October 2017. [Google Scholar] [CrossRef]
- Yousif Al-Aboosi, Y.; Zuri Sha’ameri, A. Improved underwater signal detection using efficient time–frequency de-noising technique and pre-whitening filter. Appl. Acoust. 2017, 123, 93–106. [Google Scholar] [CrossRef]
- Panaro, J.; Lopes, F.; Barreira, L.; Souza, F. Underwater acoustic noise model for shallow water communications. In Proceedings of the Brazilian telecommunication symposium, Brasilia, Brazil, 13–16 September 2012. [Google Scholar] [CrossRef][Green Version]
- Mohd Shah, N.S.; Al-Aboosi, Y.Y.; Ahmed, M.S. Error performance analysis in underwater acoustic noise with non-Gaussian distribution. Telecommun. Comput. Electron. Control 2018, 16, 681. [Google Scholar] [CrossRef]
- Qarabaqi, P.; Stojanovic, M. Statistical characterization and computationally efficient modeling of a class of underwater acoustic communication channels. IEEE J. Ocean. Eng. 2013, 38, 701–717. [Google Scholar] [CrossRef]
- Ren, H.-P.; Kong, Q.-J.; Bai, C. A chaotic spread spectrum system for underwater acoustic communication. In Proceedings of the 2015 IEEE International Wireless Symposium, Shenzhen, China, 30 March–1 April 2015. [Google Scholar] [CrossRef]
- Chen, M.; Xu, W.; Wang, D.; Wang, L. Statistical Multi-carrier chaotic communication scheme for underwater acoustic communications. IET Commun. 2019, 13, 2097–2105. [Google Scholar] [CrossRef]
- Morozs, N.; Gorma, W.; Henson, B.T.; Shen, L.; Mitchell, P.D.; Zakharov, Y.V. Channel modeling for underwater acoustic network simulation. IEEE Access 2020, 8, 136151–136175. [Google Scholar] [CrossRef]
- Zanaj, E.; Gambi, E.; Zanaj, B.; Disha, D.; Kola, N. Underwater wireless sensor networks: Estimation of acoustic channel in shallow water. Appl. Sci. 2020, 18, 6393. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, W.; Sun, X.; Wan, L.; Tao, Y.; Xu, X. Environment-aware communication channel quality prediction for underwater acoustic transmissions: A machine learning method. Appl. Acoust. 2021, 181, 108–128. [Google Scholar] [CrossRef]
- Wang, S.; He, Z.; Niu, K.; Chen, P.; Rong, Y. New results on joint channel and impulsive noise estimation and tracking in underwater acoustic OFDM systems. IEEE Trans. Wirel. Commun. 2020, 19, 2601–2612. [Google Scholar] [CrossRef]
- Wei, Y.; Quan, L.; Xu, W.; Wang, D.; Wang, L. An in-phase/quadrature index modulation-aided spread spectrum communication system for underwater acoustic communication. Electronics 2023, 12, 2919. [Google Scholar] [CrossRef]
- Arikan, E. Channel Polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Coladarci, T.; Cobb, C.D.; Minium, E.W.; Clarke, R.C. Fundamentals of Statistical Reasoning in Education; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Al-Askery, A.J.; Tsimenidis, C.C.; Boussakta, S.; Chambers, J.A. Performance analysis of coded massive MIMO-OFDM systems using effective matrix inversion. IEEE Trans. Commun. 2017, 65, 5244–5256. [Google Scholar] [CrossRef]
- Al-Askery, A.; Al-Naji, A.; Alsabah, M. Improving the performance of turbo-coded systems under Suzuki fading channels. J. Low Power Electron. Appl. 2019, 9, 13. [Google Scholar] [CrossRef]
- Xia, Y.; Tse, C.K.; Lau, F.C.M. Performance of differential chaos-shift-keying digital communication systems over a multipath fading channel with delay spread. IEEE Trans. Circuits Syst. II Express Briefs 2004, 51, 680–684. [Google Scholar] [CrossRef]
- Galias, Z.; Maggio, G.M. Quadrature chaos-shift keying: Theory and performance analysis. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2001, 48, 1510–1519. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Askery, A.J.; Hasan, F.S.; Yassin, Y.A. Polar-Coded Differential/Quadrature Chaos Shift Keying Communication Systems for Underwater Acoustic Channels. Telecom 2024, 5, 476-486. https://doi.org/10.3390/telecom5020024
Al-Askery AJ, Hasan FS, Yassin YA. Polar-Coded Differential/Quadrature Chaos Shift Keying Communication Systems for Underwater Acoustic Channels. Telecom. 2024; 5(2):476-486. https://doi.org/10.3390/telecom5020024
Chicago/Turabian StyleAl-Askery, Ali Jaber, Fadhil Sahib Hasan, and Yaser Atta Yassin. 2024. "Polar-Coded Differential/Quadrature Chaos Shift Keying Communication Systems for Underwater Acoustic Channels" Telecom 5, no. 2: 476-486. https://doi.org/10.3390/telecom5020024
APA StyleAl-Askery, A. J., Hasan, F. S., & Yassin, Y. A. (2024). Polar-Coded Differential/Quadrature Chaos Shift Keying Communication Systems for Underwater Acoustic Channels. Telecom, 5(2), 476-486. https://doi.org/10.3390/telecom5020024




