Non-Premixed Filtered Tabulated Chemistry: Filtered Flame Modeling of Diffusion Flames
Abstract
:1. Introduction
2. Materials and Methods
2.1. Flamelet Equations
2.2. Filtered Reactive Flow Governing Equations
2.3. Non-Premixed Filtered Tabulated Chemistry Closure
2.4. Coflow Flame Configuration
2.5. Numerical Setup
2.6. Filtered Chemical Database
3. Results
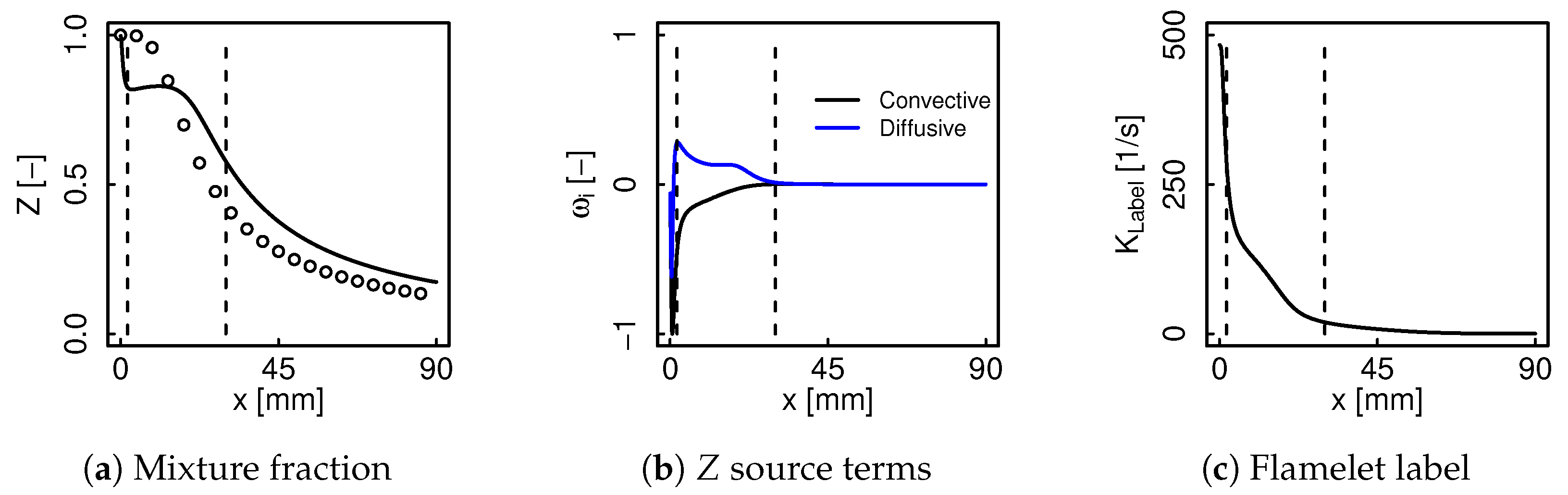
3.1. Filtered Tabulated Chemistry Problem
Filtered Manifold Transformation
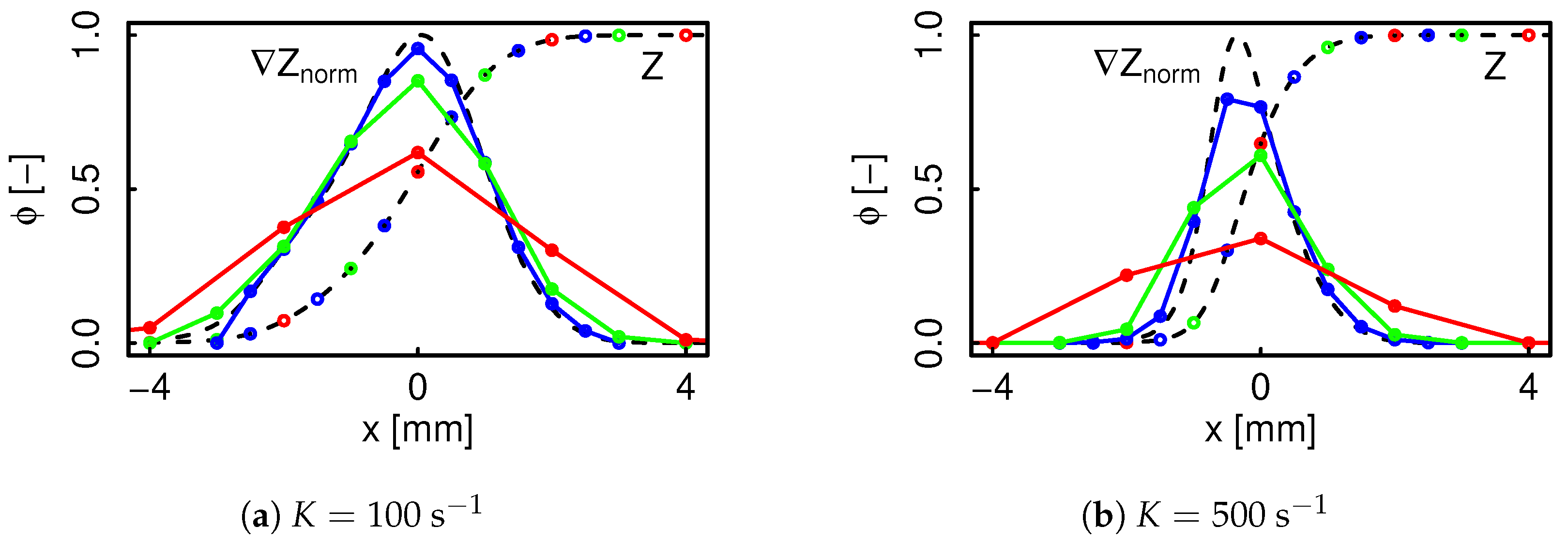
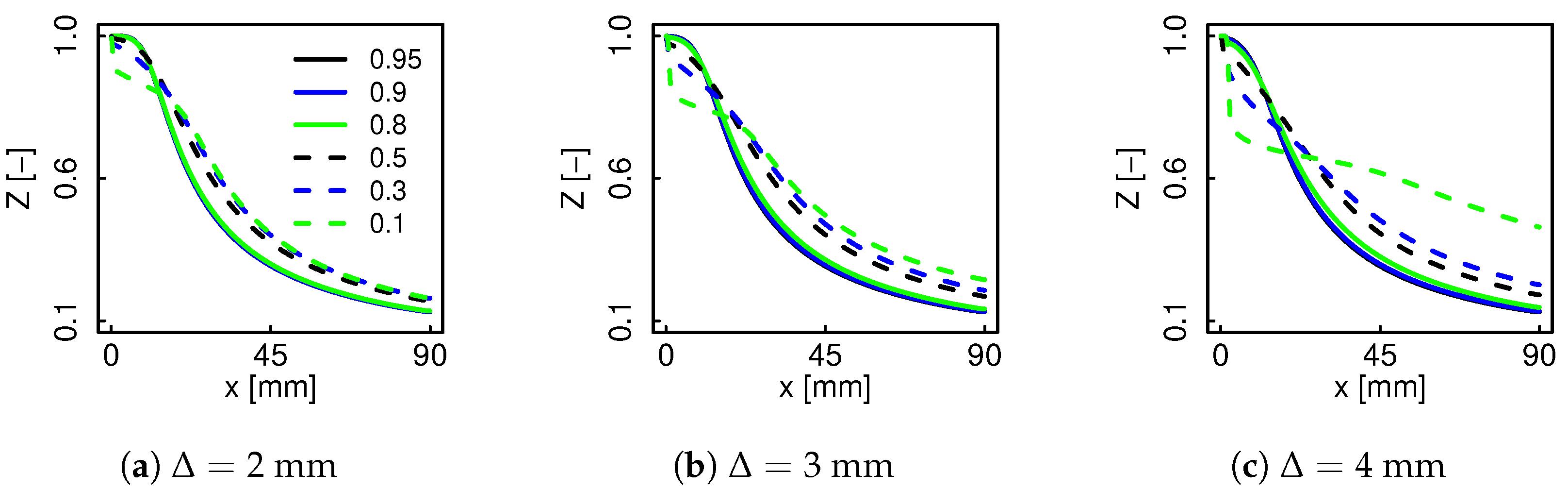
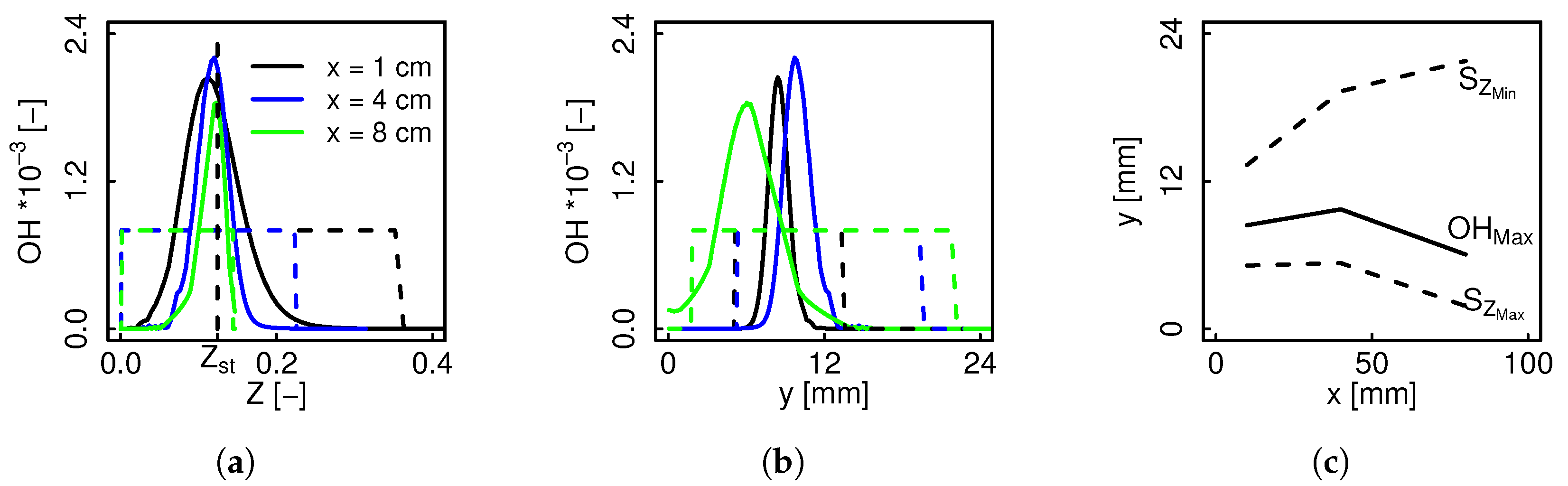
3.2. Flame Sensor
3.2.1. Justification
3.2.2. Proposed Definition
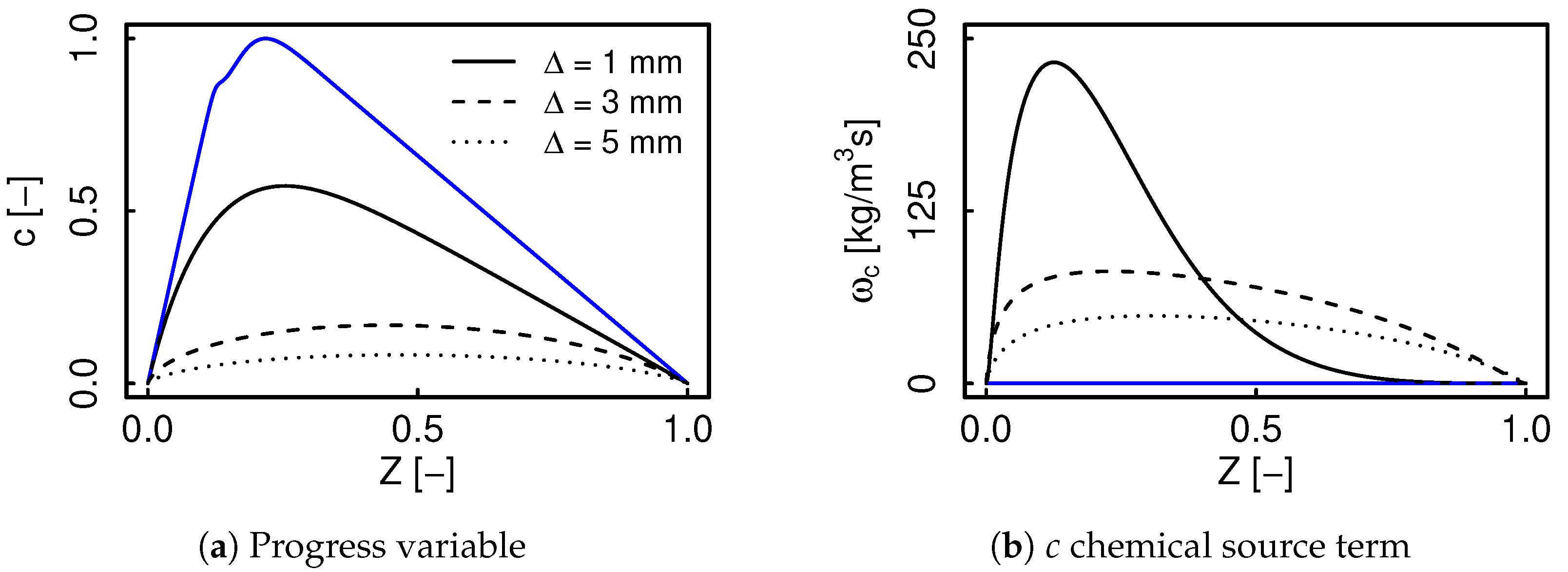
3.3. Filtered Tabulated Chemistry Results
4. Discussion
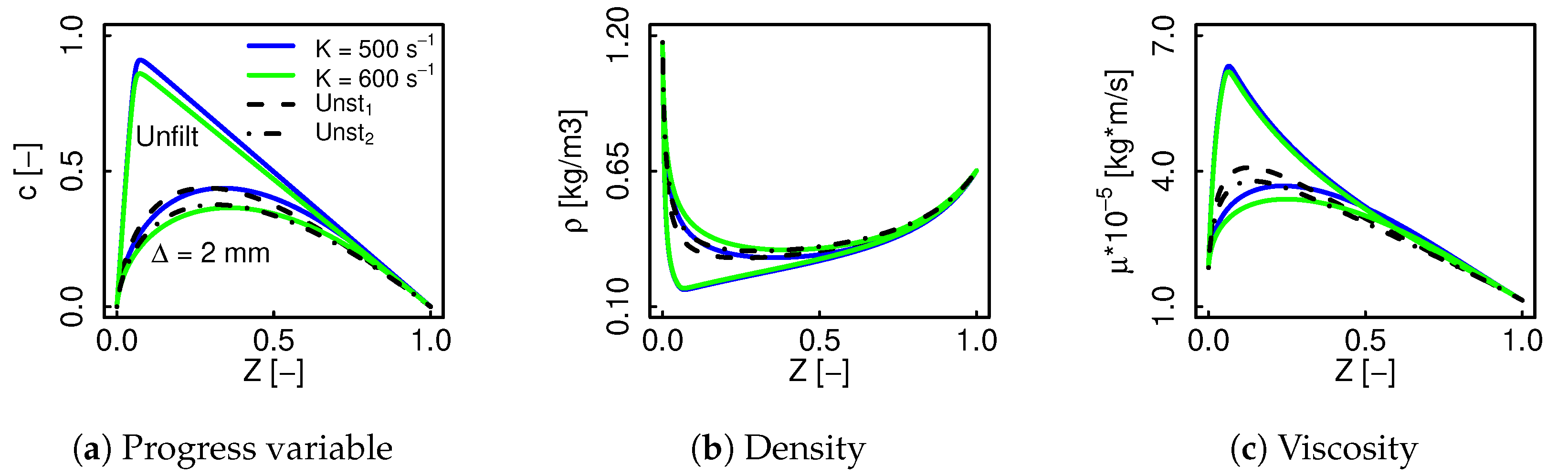
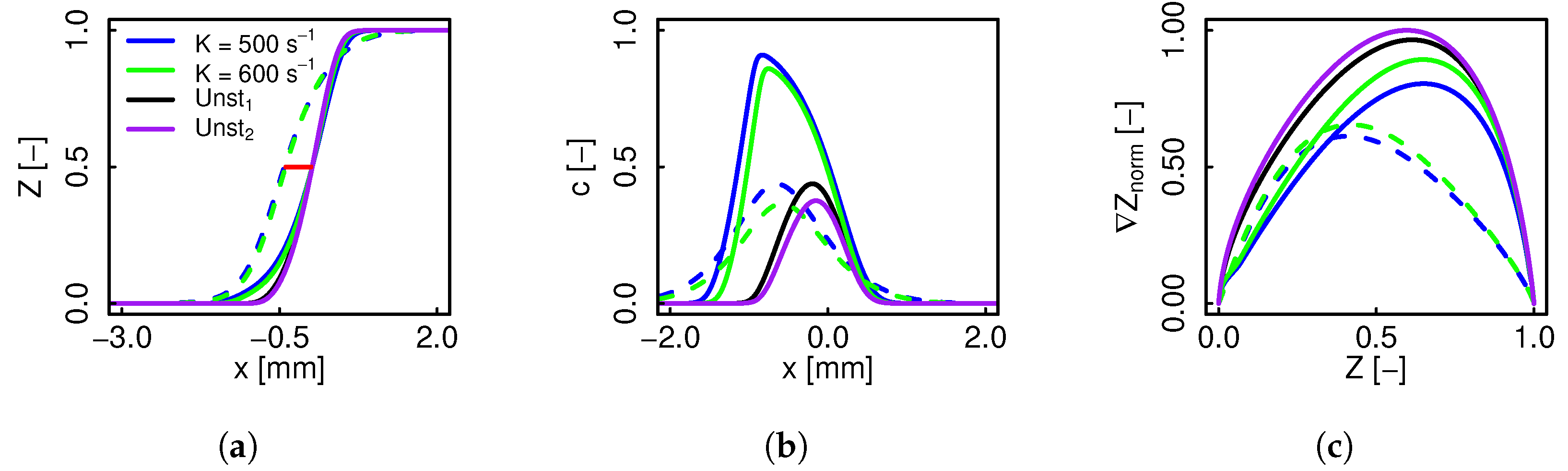
4.1. Flame Structure
4.2. Model Correction Terms Sensitivity
4.3. Sensor Performance
5. Conclusions
- Far from the centerline the flame front does not only satisfy the counterflow hypothesis, but the flamelet identifier remains unaltered after the filtering operation, what can be understood as the filtering of the same trajectory, namely of the same flamelet.
- The effect of a modified filtered profile at the reaction zone is then transported through convection and diffusion towards higher Z zones, and is the cause for the centerline profile modifications, where the model is not active.
- The profile extension due to the filtering process is mainly driven by the model correction terms, while the decrease in the peak values of non monotonically evolving variables depends on the filtered parameters that enter the transport equation.
- The sensor adequately identifies the multidimensional effect at the centerline, and its active range both in Z as in physical space changes throughout the domain, in accordance with the strain rate decrease and higher flame thickness.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Greek letters | |
| Unresolved diffusive contribution | |
| Progress variable species i weight factor | |
| Flame thickness | |
| Thermal conductivity | |
| Specific value of a parameterizing variable | |
| Mass density | |
| Laminar viscous tensor | |
| Chemical production rate | |
| Filter size | |
| Numerical grid spacing | |
| Unresolved convective contribution | |
| Latin letters | |
| c | Progress variable |
| Specific heat at constant pressure | |
| h | Enthalpy |
| p | Pressure |
| s | Spatial coordinate perpendicular to the flame front |
| u | Velocity |
| D | Molecular diffusivity |
| K | Strain rate |
| Flamelet label | |
| Lewis number | |
| S | Flame sensor |
| Mass fraction of species i | |
| Z | Mixture fraction |
References
- Curran, H.J. Developing detailed chemical kinetic mechanisms for fuel combustion. Proc. Combust. Inst. 2019, 37, 57–81. [Google Scholar] [CrossRef]
- Van Oijen, J.; Donini, A.; Bastiaans, R.; ten Thije Boonkkamp, J.; De Goey, L. State-of-the-art in premixed combustion modeling using flamelet generated manifolds. Prog. Energy Combust. Sci. 2016, 57, 30–74. [Google Scholar] [CrossRef]
- van Oijen, J.A. Flamelet-Generated Manifolds: Development and Application To Premixed Laminar Flames; Technische Universiteit Eindhoven Eindhoven: Eindhoven, The Netherlands, 2002. [Google Scholar]
- Gicquel, O.; Darabiha, N.; Thévenin, D. Liminar premixed hydrogen/air counterflow flame simulations using flame prolongation of ILDM with differential diffusion. Proc. Combust. Inst. 2000, 28, 1901–1908. [Google Scholar] [CrossRef]
- Pierce, C.D.; Moin, P. Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech. 2004, 504, 73–97. [Google Scholar] [CrossRef]
- Ihme, M.; Cha, C.M.; Pitsch, H. Prediction of local extinction and re-ignition effects in non-premixed turbulent combustion using a flamelet/progress variable approach. Proc. Combust. Inst. 2005, 30, 793–800. [Google Scholar] [CrossRef]
- Sacomano Filho, F.L.; Hosseinzadeh, A.; Sadiki, A.; Janicka, J. On the interaction between turbulence and ethanol spray combustion using a dynamic wrinkling model coupled with tabulated chemistry. Combust. Flame 2020, 215, 203–220. [Google Scholar] [CrossRef]
- Colin, O.; Ducros, F.; Veynante, D.; Poinsot, T. A thickened flame model for large eddy simulations of turbulent premixed combustion. Phys. Fluids 2000, 12, 1843–1863. [Google Scholar] [CrossRef]
- Mahmoud, R.; Jangi, M.; Ries, F.; Fiorina, B.; Janicka, J.; Sadiki, A. Combustion Characteristics of a Non-Premixed Oxy-Flame Applying a Hybrid Filtered Eulerian Stochastic Field/Flamelet Progress Variable Approach. Appl. Sci. 2019, 9, 1320. [Google Scholar] [CrossRef]
- Sarkar, S. Large Eddy Simulation of Flows of Engineering Interest: A Review. In 50 Years of CFD in Engineering Sciences; Springer: Berlin/Heidelberg, Germany, 2020; pp. 363–400. [Google Scholar]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion; R.T. Edwards Inc.: Montgomery, PA, USA, 2005. [Google Scholar]
- Gicquel, L.Y.; Staffelbach, G.; Poinsot, T. Large eddy simulations of gaseous flames in gas turbine combustion chambers. Prog. Energy Combust. Sci. 2012, 38, 782–817. [Google Scholar] [CrossRef]
- Luo, G.; Dai, H.; Dai, L.; Qian, Y.; Sha, C.; Zhang, Y.; Wu, B. Review on Large Eddy Simulation of Turbulent Premixed Combustion in Tubes. J. Therm. Sci. 2020, 29, 853–867. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Garnier, E.; Adams, N.; Sagaut, P. Large Eddy Simulation for Compressible Flows; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Celik, I.; Klein, M.; Janicka, J. Assessment measures for engineering LES applications. J. Fluids Eng. 2009, 131, 031102. [Google Scholar] [CrossRef]
- Grigoriadis, D.G.; Geurts, B.J.; Kuerten, H.; Fröhlich, J.; Armenio, V. Direct and Large-Eddy Simulation X; Springer International Publishing: New York, NY, USA, 2018. [Google Scholar]
- Salvetti, M.V.; Geurts, B.; Meyers, J.; Sagaut, P. Quality and Reliability of Large-Eddy Simulations II; Springer Science & Business Media: New York, NY, USA, 2010; Volume 16. [Google Scholar]
- Veynante, D.; Vervisch, L. Turbulent combustion modeling. Prog. Energy Combust. Sci. 2002, 28, 193–266. [Google Scholar] [CrossRef]
- Fiorina, B.; Vicquelin, R.; Auzillon, P.; Darabiha, N.; Gicquel, O.; Veynante, D. A filtered tabulated chemistry model for LES of premixed combustion. Combust. Flame 2010, 157, 465–475. [Google Scholar] [CrossRef]
- Auzillon, P.; Gicquel, O.; Darabiha, N.; Veynante, D.; Fiorina, B. A filtered tabulated chemistry model for LES of stratified flames. Combust. Flame 2012, 159, 2704–2717. [Google Scholar] [CrossRef]
- Mercier, R.; Auzillon, P.; Moureau, V.; Darabiha, N.; Gicquel, O.; Veynante, D.; Fiorina, B. Les modeling of the impact of heat losses and differential diffusion on turbulent stratified flame propagation: Application to the tu darmstadt stratified flame. Flow Turbul. Combust. 2014, 93, 349–381. [Google Scholar] [CrossRef]
- Wang, L. Analysis of the filtered non-premixed turbulent flame. Combust. Flame 2017, 175, 259–269. [Google Scholar] [CrossRef]
- Chan, W. A Higher-Order Flamelet Model for Turbulent Combustion Simulations. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2016. [Google Scholar]
- Coussement, A.; Schmitt, T.; Fiorina, B. Filtered Tabulated Chemistry for non-premixed flames. Proc. Combust. Inst. 2015, 35, 1183–1190. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Donini, A.; Bastiaans, R.; van Oijen, J.; de Goey, L. A 5-D implementation of FGM for the large eddy simulation of a stratified swirled flame with heat loss in a gas turbine combustor. Flow, Turbul. Combust. 2017, 98, 887–922. [Google Scholar] [CrossRef] [PubMed]
- De Goey, L.; ten Thije Boonkkamp, J. A flamelet description of premixed laminar flames and the relation with flame stretch. Combust. Flame 1999, 119, 253–271. [Google Scholar] [CrossRef]
- De Goey, L.; ten Thije Boonkkamp, J. A mass-based definition of flame stretch for flames with finite thickness. Combust. Sci. Technol. 1997, 122, 399–405. [Google Scholar] [CrossRef]
- Ramaekers, W.; Van Oijen, J.; De Goey, L. A priori testing of flamelet generated manifolds for turbulent partially premixed methane/air flames. Flow Turbul. Combust. 2010, 84, 439–458. [Google Scholar] [CrossRef]
- Verhoeven, L.; Ramaekers, W.; Van Oijen, J.; De Goey, L. Modeling non-premixed laminar co-flow flames using flamelet-generated manifolds. Combust. Flame 2012, 159, 230–241. [Google Scholar] [CrossRef]
- Ries, F.; Obando, P.; Shevchuck, I.; Janicka, J.; Sadiki, A. Numerical analysis of turbulent flow dynamics and heat transport in a round jet at supercritical conditions. Int. J. Heat Fluid Flow 2017, 66, 172–184. [Google Scholar]
- Caretto, L.; Gosman, A.; Patankar, S.; Spalding, D. Two calculation procedures for steady, three-dimensional flows with recirculation. In Proceedings of the Third International Conference on Numerical Methods in Fluid Mechanics, Paris, France, 3–7 July 1972; pp. 60–68. [Google Scholar]
- Greenshields, C.J. OpenFOAM Programmer’s Guide, 2.4.0 ed.; OpenFOAM Foundation: London, UK, 2015. [Google Scholar]
- Somers, B. The Simulation of Flat Flames with Detailed and Reduced Chemical Models. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 1994. [Google Scholar]
- Smith, G.P. GRI-3.0. 2000. Available online: http://www.me.berkeley.edu/gri_mech/ (accessed on 14 December 2016).
- Malik, M.R.; Vega, P.O.; Coussement, A.; Parente, A. Combustion modeling using Principal Component Analysis: A posteriori validation on Sandia flames D, E and F. Proc. Combust. Inst. 2020, in press. [Google Scholar] [CrossRef]
- Ren, S.; Wang, X. NOx emission and its reduction mechanism investigation in one diffusion-like vortex-tube combustor. J. Clean. Prod. 2020, 274, 123138. [Google Scholar] [CrossRef]
- Gopal, A.; Volpiani, P.S.; Yellapantula, S.; Larsson, J. Computational investigation of real fluid effects in cryogenic laminar premixed CH4–O2 flames. J. Supercrit. Fluids 2020, 168, 105045. [Google Scholar] [CrossRef]
- Fiolitakis, A.; Arndt, C. Transported PDF simulation of auto-ignition of a turbulent methane jet in a hot, vitiated coflow. Combust. Theory Model. 2020, 24, 326–361. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, G.; Deng, H.; Wen, X.; Wang, F.; Zhang, A.; Sheng, W. Experimental and numerical study of the effects of oxygen-enriched air on the laminar burning characteristics of biomass-derived syngas. Fuel 2021, 285, 119183. [Google Scholar] [CrossRef]
- Parente, A.; Sutherland, J.C.; Tognotti, L.; Smith, P.J. Identification of low-dimensional manifolds in turbulent flames. Proc. Combust. Inst. 2009, 32, 1579–1586. [Google Scholar] [CrossRef]
- Pitsch, H.; Chen, M.; Peters, N. Unsteady flamelet modeling of turbulent hydrogen-air diffusion flames. Symp. Combust. 1998, 27, 1057–1064. [Google Scholar] [CrossRef]
- Pitsch, H. Unsteady flamelet modeling of differential diffusion in turbulent jet diffusion flames. Combust. Flame 2000, 123, 358–374. [Google Scholar] [CrossRef]
- Durand, L.; Polifke, W. Implementation of the thickened flame model for large eddy simulation of turbulent premixed combustion in a commercial solver. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, American Society of Mechanical Engineers, Montreal, QC, USA, 14–17 May 2007; pp. 869–878. [Google Scholar]
- Schmitt, T.; Sadiki, A.; Fiorina, B.; Veynante, D. Impact of dynamic wrinkling model on the prediction accuracy using the F-TACLES combustion model in swirling premixed turbulent flames. Proc. Combust. Inst. 2013, 34, 1261–1268. [Google Scholar] [CrossRef]
- Proch, F.; Kempf, A.M. Numerical analysis of the Cambridge stratified flame series using artificial thickened flame LES with tabulated premixed flame chemistry. Combust. Flame 2014, 161, 2627–2646. [Google Scholar] [CrossRef]
- Scholtissek, A.; Chan, W.L.; Xu, H.; Hunger, F.; Kolla, H.; Chen, J.H.; Ihme, M.; Hasse, C. A multi-scale asymptotic scaling and regime analysis of flamelet equations including tangential diffusion effects for laminar and turbulent flames. Combust. Flame 2015, 162, 1507–1529. [Google Scholar] [CrossRef]
- Claramunt, K.; Consul, R.; Carbonell, D.; Pérez-Segarra, C. Analysis of the laminar flamelet concept for nonpremixed laminar flames. Combust. Flame 2006, 145, 845–862. [Google Scholar] [CrossRef]
- Cuoci, A.; Frassoldati, A.; Faravelli, T.; Ranzi, E. A computational tool for the detailed kinetic modeling of laminar flames: Application to C2H4/CH4 coflow flames. Combust. Flame 2013, 160, 870–886. [Google Scholar] [CrossRef]
- Cuoci, A.; Frassoldati, A.; Faravelli, T.; Ranzi, E. Numerical modeling of laminar flames with detailed kinetics based on the operator-splitting method. Energy Fuels 2013, 27, 7730–7753. [Google Scholar] [CrossRef]
- Cuoci, A.; Frassoldati, A.; Faravelli, T.; Ranzi, E. OpenSMOKE++: An object-oriented framework for the numerical modeling of reactive systems with detailed kinetic mechanisms. Comput. Phys. Commun. 2015, 192, 237–264. [Google Scholar] [CrossRef]
- Auzillon, P.; Fiorina, B.; Vicquelin, R.; Darabiha, N.; Gicquel, O.; Veynante, D. Modeling chemical flame structure and combustion dynamics in LES. Proc. Combust. Inst. 2011, 33, 1331–1338. [Google Scholar] [CrossRef]
- Delhaye, S.; Somers, L.; Van Oijen, J.; De Goey, L. Incorporating unsteady flow-effects in flamelet-generated manifolds. Combust. Flame 2008, 155, 133–144. [Google Scholar] [CrossRef]
- Vreman, A.; Albrecht, B.; Van Oijen, J.; De Goey, L.; Bastiaans, R. Premixed and nonpremixed generated manifolds in large-eddy simulation of Sandia flame D and F. Combust. Flame 2008, 153, 394–416. [Google Scholar] [CrossRef]
- Sacomano Filho, F.L.; Kuenne, G.; Chrigui, M.; Sadiki, A.; Janicka, J. A consistent Artificially Thickened Flame approach for spray combustion using LES and the FGM chemistry reduction method: Validation in Lean Partially Pre-Vaporized flames. Combust. Flame 2017, 184, 68–89. [Google Scholar] [CrossRef]
- Ihme, M.; See, Y.C. LES flamelet modeling of a three-stream MILD combustor: Analysis of flame sensitivity to scalar inflow conditions. Proc. Combust. Inst. 2011, 33, 1309–1317. [Google Scholar] [CrossRef]
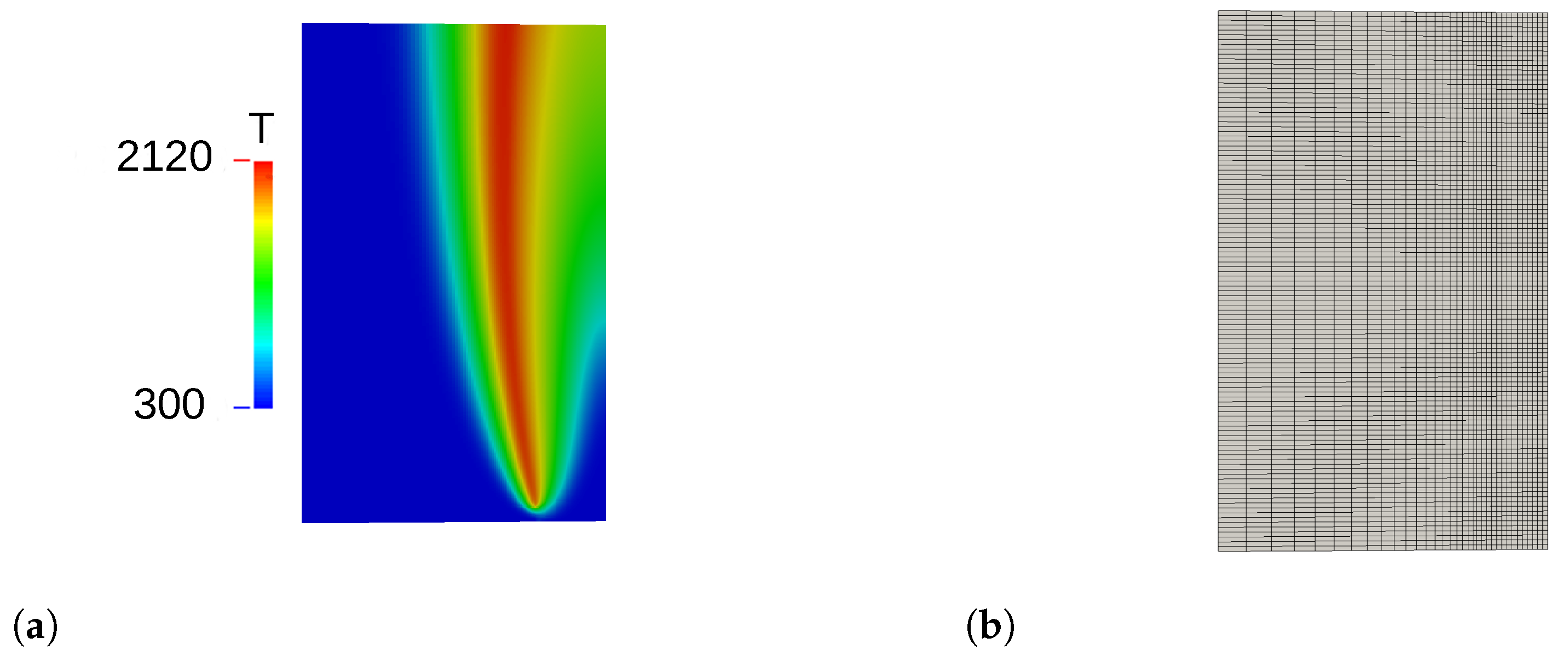





| Mesh | NoCells | [mm] | [mm] | [mm] |
|---|---|---|---|---|
| NU1 | 127,658 | 0.1 | 0.23 | 0.13 |
| NU2 | 33,300 | 0.2 | 0.45 | 0.24 |
| NU3 | 9225 | 0.4 | 0.82 | 0.45 |
| Z | c | u [m/s] | p [Pa] | |
|---|---|---|---|---|
| Jet | 1 | 0 | parabolic profile, 0.23 | z.G. |
| Coflow | 0 | 0 | 0.23 | z.G. |
| Side wall | 0 | 0 | no-slip | z.G. |
| Outflow | z.G. | z.G. | z.G. | 101,325 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obando Vega, P.J.; Coussement, A.; Sadiki, A.; Parente, A. Non-Premixed Filtered Tabulated Chemistry: Filtered Flame Modeling of Diffusion Flames. Fuels 2021, 2, 87-107. https://doi.org/10.3390/fuels2020006
Obando Vega PJ, Coussement A, Sadiki A, Parente A. Non-Premixed Filtered Tabulated Chemistry: Filtered Flame Modeling of Diffusion Flames. Fuels. 2021; 2(2):87-107. https://doi.org/10.3390/fuels2020006
Chicago/Turabian StyleObando Vega, Pedro Javier, Axel Coussement, Amsini Sadiki, and Alessandro Parente. 2021. "Non-Premixed Filtered Tabulated Chemistry: Filtered Flame Modeling of Diffusion Flames" Fuels 2, no. 2: 87-107. https://doi.org/10.3390/fuels2020006
APA StyleObando Vega, P. J., Coussement, A., Sadiki, A., & Parente, A. (2021). Non-Premixed Filtered Tabulated Chemistry: Filtered Flame Modeling of Diffusion Flames. Fuels, 2(2), 87-107. https://doi.org/10.3390/fuels2020006







