Abstract
The effect of poroelastic properties of the shale matrix on gas storage and transport mechanisms has gained significant attention, especially during history-matching and hydrocarbon production forecasting in unconventional reservoirs. The common oil and gas industry practice in unconventional reservoir simulation is the extension of conventional reservoir simulation that ignores the dynamic behavior of matrix porosity and permeability as a function of reservoir effective net stress. This approach ignores the significant impact of the poroelastic characteristics of the shale matrix on hydrocarbon production. The poroelastic characteristics of the shale matrix highly relate to the shale matrix geomechanical properties, such as the Young’s Modulus, Poisson’s ratio, bulk modulus, sorption behavior, total organic content (TOC), mineralogy and presence of natural fractures in the multi-scale shale structure. In this study, in order to quantify the effect of the poroelasticity of the shale matrix on gas production, a multi-continuum approach was employed in which the shale matrix was divided into organic materials, inorganic materials and natural fractures. The governing equations for gas transport and storage in shale were developed from the basic fundamentals of mass and momentum conservation equations. In this case, gas transport in organics was assumed to be diffusive, while gas transport in inorganics was governed by convection. Finally, a fracture system was added to the multi-scale shale gas matrix, and the poroelastic effect of the shale matrix on transport and storage was investigated. A modified Palmer and Mansoori model (1998) was used to include the pore compression, matrix swelling/shrinkage and desorption-induced deformation of shale organic matter on the overall pore compressibility of the shale matrix. For the inorganic part of the matrix, relations between rock mechanical properties and the pore compressibility were obtained. A dual Langmuir–Henry isotherm was also used to describe the sorption behavior of shale organic materials. The coupled governing equations of gas storage and transport in the shale matrix were then solved using the implicit finite difference approach using MATLAB. For this purpose, rock and fluid properties were obtained using actual well logging and core analysis of the Marcellus gas well. The results showed the importance of the poroelastic effect on the pressure response and rate of gas recovery from the shale matrix. The effect was found to be mainly due to desorption-induced matrix deformation at an early stage. Coupling the shale matrix gas production including the poroelastic effect in history-matching the gas production from unconventional reservoirs will significantly improve engineering completion design optimization of the unconventional reservoirs by providing more accurate and robust production forecasts for each hydraulic fracture stage.
1. Introduction
Over the last two decades, shale gas has become one of the most important sources of natural gas supply. Figure 1, shows the history and projections of energy production in the U.S. in which dry natural gas is projected to contribute to our economy more than nuclear, hydro and other renewable energies combined [1]. As a result, more attention has been paid to this source of energy and ways to optimize the gas production in a much cheaper, safer and cleaner manner. Among the main areas of the investigation to achieve this goal is the completion design and drawdown optimization of the long horizontal wells drilled in shale gas reservoirs [2,3,4]. Recent studies have shown the significant economic impact of completion design efficiency on both short-and long-term hydrocarbon production from these unconventional reservoirs [5]. Typically, 6 to 12 months of production data are required to evaluate the efficiency of the completion design tested in unconventional shale reservoirs. There are various tools that can be used to evaluate the productivity of a well in unconventional shale reservoirs. Calculating the estimated ultimate recovery (EUR) using various types of decline curve analysis (DCA) or using rate transient analysis (RTA) is a widely used method to determine the flow capacity and strength of a well in conjunction with another to correspond to completion design [6,7]. Recently, our team used different types of curves, diagnostic plots and unconventional models in IHS harmony commercial software to quantify the well performance of six lateral wells drilled and completed in Marcellus shale in which three of them were completed using geomechanical/engineering design and three wells were completed using geometrical design. Among the infill wells, the wells with engineering completion design showed the highest flow capacity per foot of lateral well. This observation clearly confirmed the importance of considering the geomechanical properties and fracture distributions of the rock in completion design optimization [4].
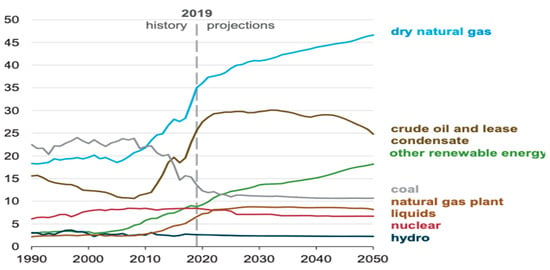
Figure 1.
Energy production in quadrillion British thermal units (AEO2020).
As previously discussed, comprehensive engineering completion design depends on drilling mechanics, fracture interpretations, geomechanical properties and completion monitoring. However, this approach still ignores the poroelastic effect of the shale matrix on hydrocarbon production, which is stress-dependent rock properties, such as pore compressibility and permeability, matrix shrinkage and the adsorption effect [8,9]. In this study, we developed a multi-continuum model to account for such properties and investigated their impact on gas transport and storage in the shale matrix to be employed in engineering completion design optimization.
Previous studies, such as those by [10,11,12,13,14], have reported the relation between stress and the formation permeability in organic rich reservoirs. The majority of these approaches are introduced based on the experiments on coalbed methane cores and field data. Shale core samples have also shown similar sensitivity to the change in the mechanical properties of the formation and the effective stress. The sensitivity of the shale matrix properties to the change in stress comes as a result of the intricate nature of the shale matrix which consists of organic and inorganic components [15,16]. Each of these components have different pore structures and thus different storage and transport characteristics as a function of changes in the net effective stress of the reservoir. In this study, in order to quantify the effect of the poroelasticity of the shale, a multi-continuum approach was chosen to represent the shale matrix. The governing equations for the model were developed from the basic fundamentals of mass and momentum conservation equations of flow and transport in naturally fractured porous media. A multi-continuum approach was used to develop the governing equations where the shale matrix is assumed to consist of organic and inorganic materials. In this case, gas transport in organics is assumed to be diffusive, while gas transport in inorganics is governed by convection. Finally, a fracture system was added to the multi-scale shale gas matrix, and the poroelastic effect of the shale matrix on transport and storage was investigated. A modified model [10] was used to include the effects of pore compression, matrix shrinkage and desorption-induced deformation of shale organic matter on the overall pore compressibility of the shale matrix. Relations between rock mechanical properties and the pore compressibility of the inorganic part of the matrix were obtained following [17,18,19].
The purpose of this study was to develop governing equations describing gas transport and storage in shale gas reservoirs, including the multi-scale nature of the shale matrix, gas sorption behavior and poroelastic effects due to changes in effective net stress. Governing equations were derived based on mass and momentum balance under isothermal conditions using analytical techniques and solved using the implicit finite difference approach. The sensitivity analysis of the different poroelastic parameters of the shale matrix under specified initial and boundary conditions was performed.
2. Theoretical Models
The transport process in the shale matrix consists of a combination of different transport mechanisms, including viscous flow, pore and solid diffusion and adsorption/desorption. The storage mechanisms include free gas storage in the matrix and fracture and also adsorbed gas storage on the organic surface area. Adsorption in inorganic matrix and fracture and gas dissolution is ignored due to a negligible amount in comparison to the aforementioned storage mechanisms. During the development of this poroelastic model, the compressible nature of the gas is considered, and the real gas law is used to represent the thermodynamic behavior of the gas. Porosity is treated as a function of reservoir pressure, adsorption parameters and stress. The governing equations describing mass balance in the matrix organic material, matrix inorganic material and fracture are coupled following the Warren and Root coupling approach [20]. Here, the shale matrix is assumed to be a quad-porosity dual-permeability system, i.e., adsorption sites, organic and inorganic porosity in the matrix and fracture porosity and also inorganic and fracture permeability. The conceptual multi-continuum model is assumed to have hydraulic communication in series where gas will be released from adsorption sites following the dual Langmuir–Henry isotherm model and will be transported by pore and solid diffusion in organic materials of the shale (the permeability in organic materials is so low, in the order of nano-Darcy, that convective gas transport can be ignored). Gas then will be released to the inorganic shale matrix following the Warren and Root coupling approach and transported by convection (Darcy type flow). Gas will then be released from the shale inorganic matrix to the fractures and transported in the fractures by convention and dispersion transport mechanism. Note here that the rate of change in kerogen porosity with pressure is defined using [10] modified model used for coalbed methane reservoirs, while inorganic porosity variation as a function of pressure obtained using [18,19] definitions for bulk and pore volume compressibility. In this study, we used a multi-continuum approach in which there explicit representation of the natural fractures is not required. However, the application of multi-continua requires that each porous medium be distributed continuously in space and hold porous medium conditions specified by [21]. In addition to that, we assumed the fracture porosity to be constant; the natural fracture gas adsorption and dissolution were ignored; and natural fractures were in series hydraulic communication with the matrix and hydraulic fracture.
Equations (1) and (2) describe the one-dimensional material balance in terms of gas concentration in organic materials of the shale matrix. In Equation (1), the left-hand side describes the free gas ( storage in the organic pore structure and adsorbed gas ( storage on the organic matrix, while the right-hand side describes the free and adsorbed gas transport following pore and solid diffusions ( Equation (2) describes the dual Langmuir–Henry isotherm model described by Green and Selby (1994) [22].
Equations (3) and (4) describe the gas mass balance in inorganic materials. The gas transport in inorganic material is governed by convection, assuming real gas behavior and mass exchange between matrix organic and inorganic materials to be in series and following [20].
Equations (5) and (6) describe the gas mass balance in fractures. The gas transport in fractures governed by convection and dispersion and mass exchange between the matrix inorganic materials and fractures are assumed to be in series and following Warren and Roots flow coupling.
Equation (7) is a modified Palmer and Mansoori (1998) poroelastic model following [13] to include the macropore volume strain increments under the influence of sorption and constant overburden stress.
- : macropore compression;
- : shrinkage/swelling due to gas dissolution;
- : desorption-induced matrix deformation effect.
Equation (8) defines the inorganic porosity as a function of geomechanical properties of the rock (i.e., Young’s modulus and Poisson’s ratio) and Biot’s coefficient.
Here, x-t are the space and time coordinate. C and Cμ are the free and adsorbed gas concentrations, k is matrix permeability, μ is gas viscosity, Z is a gas compressibility, R is a universal gas constant and T is temperature. is the total porosity changing with time due to the poroelastic effects of the shale matrix. represents the solid volume over bulk volume of the shale matrix. is the adsorbed gas surface diffusion coefficient, and is the pore diffusion of free gas in the matrix. is Poisson’s ratio, E is Young’s modulus, is Biot’s coefficient, M is the bulk modulus in 1/Pascal and is the swelling strain of the matrix. is the fracture dispersion coefficient, and is the fracture shape factor. The subscripts k, I, f and 0 stand for matrix organic, inorganic, fracture and initial conditions, respectively. Temperature is assumed to be constant; therefore, fluid thermal expansivity is ignored. Furthermore, for low porosity systems and by assuming there is no change in overburden stress, porosity then can be related to the permeability using Mckee’s cubic relationship:
Thus, from the equation above, the permeability is expressed as a function of Poisson’s ratio, Young’s modulus, initial porosity, adsorption and pressure change. However, we should mention that the theory works relatively well when the change in porosity is less than a factor of 2; therefore, permeability change should be less than factor of 10. The Palmer and Mansoori model heavily relies on the effective stress calculation that controls the porosity change as a function of pressure. This is essential since the pressure dependent permeability is controlled predominantly by effective net stress; hence, effective stress is a function of vertical or overburden stress, Biot’s coefficient and pore pressure.
In Equation (11), is the average density of the formation that can be obtained using density log for each zone, and TVD is the true vertical depth of the formation. The pore pressure gradient of the 0.65 psi/ft was used for our Marcellus shale case study.
3. Numerical Simulation
An analytical model was developed using a set of equations defined in Equation (1) through (11) and solved numerically using the implicit finite difference approach in MATLAB. Figure 2, shows the schematic of the problem that was solved. It is a one-dimensional model with a quad porosity matrix, including organic micropores, inorganic macropores, natural fractures and adsorption. Numerical simulation was performed on half of the stage length assuming symmetric production with no flow boundary in the middle of stage (i.e., left boundary condition) and Neuman boundary condition at the right boundary (i.e., hydraulic fracture). At the initial condition, single-component, single-phase methane was assumed to be in equilibrium between the matrix and fracture. Parameters used to develop the base case model to investigate the poroelastic effect on the storage and transport in the organic rich shale gas matrix were obtained using well log and core sample measurements of the Marcellus shale well. The properties of the sample used for adsorption measurements are as follows:
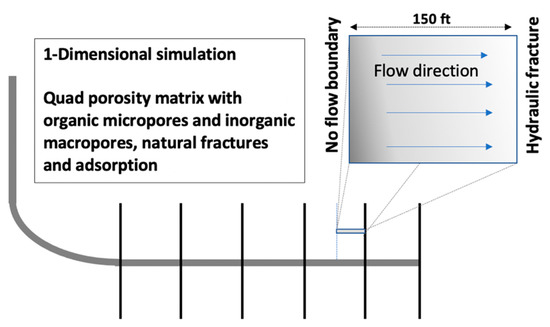
Figure 2.
Schematic of the numerical model that was solved.
- Depth: 7971 ft;
- TOC: 12.4;
- Temp: 148 F;
- As received moisture: 0.75%.
In addition to the adsorption measurements shown in Figure 3, and Table 1, the rock geomechanical properties were also measured, and static and dynamic elastic properties were obtained using triaxial core test measurements as presented in Table 2. Parameters used to develop the base case model to investigate the poroelastic effect on the storage and transport in the organic rich shale gas matrix are shown in Table 3. Well logging information (i.e., Gamma ray, resistivity, density, neutron, sonic, and geomechanical log) and core property measurements (adsorption, permeability/porosity and triaxial geomechanical test) using a core plug under the reservoir effective stress condition was used to obtain the shale matrix properties. Transport coefficients and mass exchange shape factors for organic material were obtained by history-matching the pressure pulse decay using a simulation-based non-linear optimization technique, i.e., randomized maximum likelihood method (RML).
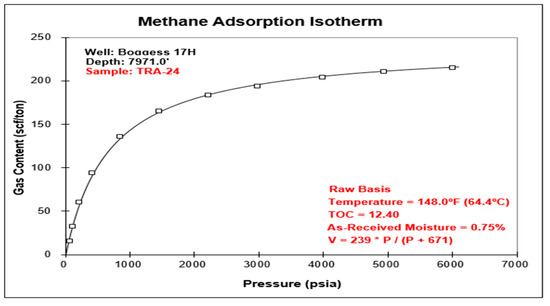
Figure 3.
Methane adsorption measurements.

Table 1.
Summary of Langmuir adsorption parameters courtesy of Schlumberger Reservoir Laboratory 20 July 2020.

Table 2.
Geomechanical properties courtesy of Schlumberger Reservoir Laboratory 2 September 2020.

Table 3.
Model base case parameters.
4. Results and Discussion
Gas transport and sorption in organic rich shale was investigated using a multi-scale, multi-continuum approach under the poroelastic effect of the shale matrix. Pore and rock compressibility effects were investigated using pressure decay and ultimate gas recovery predictions. The poroelastic effect can be seen in both organic and inorganic materials. In organic materials, it includes three components of matrix pore compression, matrix swelling and shrinkage and the desorption-induced matrix deformation effect. All these effects were coupled through Equation (7), in which the change in organic porosity is a function of three terms, namely, a1 (macropore compression), a2 (shrinkage and swelling) and a3 (desorption-induced matrix deformation). Organic porosity defined using Equation (7) was then coupled with the reset of the governing equations through Equations (1) and (4). The main parameters affecting the poroelastic effect in organic materials were the Young’s modulus, Poisson’s ratio and desorption constant.
In inorganic materials, the poroelastic effect was introduced in both the change in porosity and permeability through Equations (8) and (9), which were coupled with transport in the matrix using the mass exchange term as presented in Equations (3) and (6). The Biot’s coefficient affected the poroelastic effect in inorganic material through both porosity and permeability. In low-pressure gradient reservoirs, such as Marcellus Shale, we found this effect to be minimal numerically (here) and in the real field, as presented in our earlier study [7].
Figure 4, shows that the poroelastic effect introduced in the governing equations of gas transport and storage in shale reservoirs had a significant positive impact on pressure response as well as the rate of gas recovery at an early stage when the pressure gradient was relatively large. Figure 4 includes all the poroelastic effects (both organic and inorganic materials). Next, we tried to decouple the terms by eliminating the poroelastic effect in inorganic materials first and then in organic materials by eliminating a1, a2 and a3 terms, as defined in Equation (7). Due to the low TOC content, the matrix swelling and shrinkage effect were negligible in the case of shale gas reservoirs. The pore compressibility effect also showed a minimal impact on the ultimate recovery and pressure response; however, gas desorption-induced matrix deformation showed the greatest impact on both pressure and ultimate recovery, as shown in Figure 5. The effect was pronounced at an early stage, when the pressure gradient was larger. A greater pore pressure drop accelerated the desorption process, which led to an increase in desorption-induced matrix deformation. This effect was also reported by [23], using a finite element method and the dual permeability model. In Figure 5, without a poroelastic effect, the curve is associated with the case where constant porosity and permeability in both organic and inorganic matrices were assumed. The poroelastic effect curve includes both porosity and permeability pressure dependent on both organic and inorganic materials. The desorption-induced matrix deformation only curve corresponds to the case where inorganic porosity and permeability were assumed constant and there was no macropore compression or shrinkage and swelling effect .
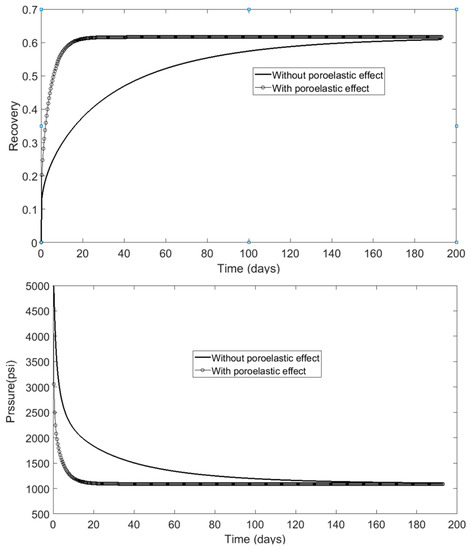
Figure 4.
Pressure decay (bottom) and ultimate recovery (top) comparisons of models with and without poroelastic effect.
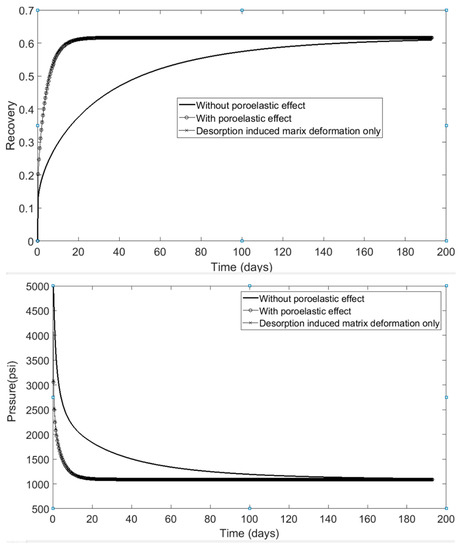
Figure 5.
Pressure decay (bottom) and ultimate recovery (top) comparisons of models with desorption-induced matrix deformation only.
Figure 6, compares the effect of a1 (organic macropore compression), a2 (shrinkage and swelling) and a3 (desorption-induced matrix deformation) on pressure response and ultimate recovery. As discussed earlier, the organic macropore compression and shrinkage and swelling showed a minimal impact, while the desorption-induced matrix deformation showed a major impact on both pressure and ultimate recovery.

Figure 6.
Comparisons of the effects of (organic macropore compression), (shrinkage and swelling) and (desorption-induced matrix deformation) on pressure decay (bottom) and ultimate recovery (top).
Figure 7, shows the impact of Poisson’s ratio on the poroelastic effects of the shale matrix, affecting pressure response and gas recovery rate. Increasing the Poisson’s ratio led to a higher ductility of the rock and a tendency towards viscous deformation. This effect showed a negative impact on pressure response and rate of recovery, which led to a decrease in the recovery rate at an early stage. In this figure, only the desorption deformation effect is considered. Finally, Figure 8, depicts the impact of Biot’s coefficient on pressure decay and ultimate gas recovery, where the inorganic poroelastic effect was considered through changes in both the porosity and permeability of inorganic materials with fixed Young’s modulus, as defined in the base case. Increasing the Biot’s coefficient increased the matrix bulk compressibility and showed low sensitivity in both pressure and ultimate recovery curves.

Figure 7.
Impact of changes in Poisson’s ratio on pressure decay (bottom) and ultimate recovery (top).
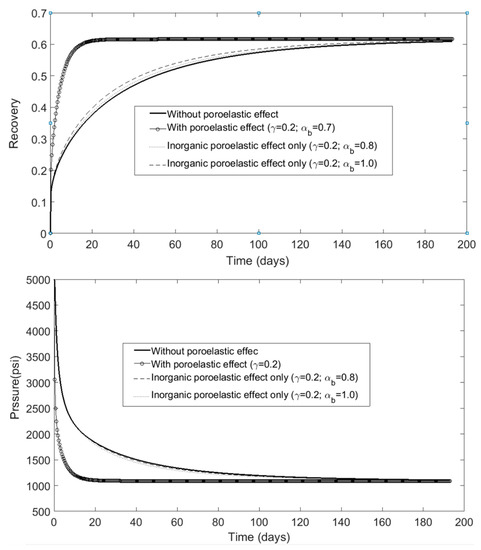
Figure 8.
Impact of changes in Biot’s coefficient on pressure decay (bottom) and ultimate recovery (top).
5. Conclusions
The poroelastic effect on the rate of recovery of gas production from naturally fractured shale gas reservoirs was simulated using quad-porosity dual-permeability systems. The poroelastic effect of the organic and inorganic material of the shale matrix was coupled with gas transport and storage mechanisms. The dual Langmuir–Henry isotherm was also used to describe the sorption dynamic equilibrium. Furthermore, the matrix deformation captured through porosity variation was coupled with permeability using Mckee’s cubic relationship. The numerical simulation of the coupled governing equations using the implicit finite difference approach showed the importance of the poroelastic effect on the pressure response and rate of gas recovery of the shale matrix. The effect was found to be mainly due to desorption-induced matrix deformation at an early stage. The Biot’s coefficient affected the poroelastic effect on inorganic material through both porosity and permeability. In low-pressure gradient reservoirs, such as Marcellus, we found this effect to be minimal numerically (here) and in the real field, as presented in our earlier study [3]. Coupling the gas transport in the shale matrix with hydraulic fractures (including poroelastic and geomechanical properties of the rock) when history-matching the gas production from unconventional reservoirs will significantly help in engineering completion design optimization. Shale reservoirs are extremely heterogeneous, and rock properties could be significantly different even in a single well; however, the findings of this study were valid in reservoirs with pressure gradients in the order of 0.68 psi/ft, such as Marcellus shale reservoirs. We suspect the results would be different in overpressured reservoirs with pressure gradients in the order of 0.85–0.95 psi/ft, such as those in the Utica shale. We have shown in different studies [3] that the poroelastic effect is more pronounced in higher pressure gradient reservoirs. For a more complete understanding of the impact of the poroelastic effect on completion design optimization of the unconventional reservoirs, a future study will be performed where the multi-continuum model developed here will be integrated with gas transport in hydraulic fractures.
Author Contributions
Conceptualization, E.F.; methodology, E.F.; software, B.J.; validation, F.B.; formal analysis, E.F.; investigation, B.J.; resources, E.F.; data curation, F.B.; writing—original draft preparation, E.F. and B.J.; writing—review and editing, E.F., F.B.; visualization, F.B.; supervision, E.F.; project administration, E.F.; funding acquisition, E.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded through the U.S.DOE National Energy Technology Lab part of their Marcellus Shale Energy and Environmental Laboratory (MSEEL) (DOE Award No.: DE-FE0024297). We appreciate Northeast Natural Energy LLC. For providing data and technical support.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Annual Energy Outlook 2021. Available online: www.eia.gov/aeo (accessed on 13 April 2021).
- Jenkins, A.; Fathi, E.; Belyadi, F. Stress field behavior induced by hydraulic fracture in shale reservoirs: A practical view on cluster spacing. J. Nat. Gas. Sci. Eng. 2017, 48, 186–196. [Google Scholar] [CrossRef]
- Belyadi, H.; Fathi, E.; Belyadi, F. Drawdown Key to Well Performance. J. Am. Oil Gas Report. 2017, 60, 69–73. [Google Scholar]
- Li, L.; Kavousi, P.; Li, B.; Carney, B.J.; Carr, T. Data Integration for Engineered Completion Design in the Marcellus Shale. AAPG ACE 2020. Available online: ACE.AAPG.org (accessed on 1 October 2020).
- Parsegov, S.G.; Niu, G.; Schechter, D.S. Benefits of Engineering Fracture Design. Lessons Learned from Underperformers in the Midland Basin. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 23–25 January 2018. [Google Scholar]
- Belyadi, H.; Fathi, E.; Belyadi, F. Hydraulic Fracturing in Unconventional Reservoirs: Theories, Operations, and Economic Analysis, 2st ed.; Gulf Professional Publishing: Oxford, UK, 2019. [Google Scholar]
- Belyadi, H.; Fathi, E.; Belyadi, F. Hydraulic Fracturing in Unconventional Reservoirs: Theories, Operations, and Economic Analysis, 1st ed.; Gulf Professional Publishing: Oxford, UK, 2016. [Google Scholar]
- Jabbar, B. Poroelastic Effect on Gas Transport and Storage in Organic Rich Shale Reservoir. Master’s Thesis, PNGE West Virginia University, Morgantown, WV, USA, 2014. [Google Scholar]
- Yi, X.; Ong, S.H.; Russell, J.E. Characterizing Pore Compressibility, Reservoir Compaction and Stress Path under Uniaxial Strain Condition for Nonlinear Elastic Rock; American Rock Mechanics Association: Alexandria, VA, USA, 2005. [Google Scholar]
- Palmer, I.; Mansoori, J. How Permeability Depends on Stress and Pore Pressure in Coalbeds: A New Model. Soc. Pet. Eng. 1998, 1, 539–544. [Google Scholar] [CrossRef]
- Seidle, J.P.; Jeansonne, M.W.; Erickson, D.J. Application of Matchstick Geometry to Stress Dependent Permeability in Coals. Soc. Pet. Eng. 1992. [Google Scholar]
- Shi, J.-Q.; Durucan, S. A Model for Changes in Coalbed Permeability During Primary and Enhanced Methane Recovery. Soc. Pet. Eng. 2005, 8, 291–299. [Google Scholar] [CrossRef]
- Yi, J.; Akkutlu, Y.; Ozgen, K.; Claekson, C.R. Gas sorption and transport in coal: A poroelastic medium approach. Int. J. Coal Geol. 2008, 77, 137–144. [Google Scholar] [CrossRef]
- Gao, Q.; Cheng, Y.; Fathi, E.; Ameri, S. Analysis of stress-field variations expected on subsurface faults and discontinuities in the vicinity of hydraulic fracturing. SPE Reserv. Eval. Eng. 2016, 19, 54–69. [Google Scholar] [CrossRef]
- Takbiri-Borujeni, A.; Fathi, E.; Kazemi, M.; Belyadi, F. An integrated multiscale model for gas storage and transport in shale reservoirs. Fuel 2019, 237, 1228–1243. [Google Scholar] [CrossRef]
- Gupta, N.; Fathi, E.; Belyadi, F. Effects of nano-pore wall confinements on rarefied gas dynamics in organic rich shale reservoirs. Fuel 2018, 220, 120–129. [Google Scholar] [CrossRef]
- Raaen, A.M. Pore volume compressibility under uniaxial strain conditions from Biot-Gassmann theory. In Proceedings of the 15th European Forms Evaluation Symposium, Stavanger, Norway, 5–7 May 1993; pp. 1–9. [Google Scholar]
- Fjær, E.; Holt, R.; Horsrud, P.; Raaen, A.; Risnes, R. Petroleum Related Rock Mechanics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Zimmerman, R. Coupling in poroelasticity and thermoelasticity. Int. J. Rock Mech. Min. Sci. 2000, 37, 79–87. [Google Scholar] [CrossRef]
- Warren, J.; Root, P. The Behavior of Naturally Fractured Reservoirs. SPE J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. Introduction to Modeling of Transport Phenomena in Porous Media; Kluwer Academic Publ.: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Green, T.K.; Selby, T.D. Pyridine sorption isotherms of Argonne premium coals—Dual-mode sorption and coal microporosity. Energy Fuels 1994, 8, 213–218. [Google Scholar] [CrossRef]
- Huang, J.; Ghassemi, A. A poroelastic model for evolution of fractured reservoirs during gas production. J. Pet. Sci. Eng. 2015, 135, 626–644. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).