Structural and Electronic Properties of Small Perovskite Nanoparticles of the Form ABX3 (A = MA, DEA, FA, GA, B = Pb, Sn, X = Cl, Br, I)
Abstract
:1. Introduction
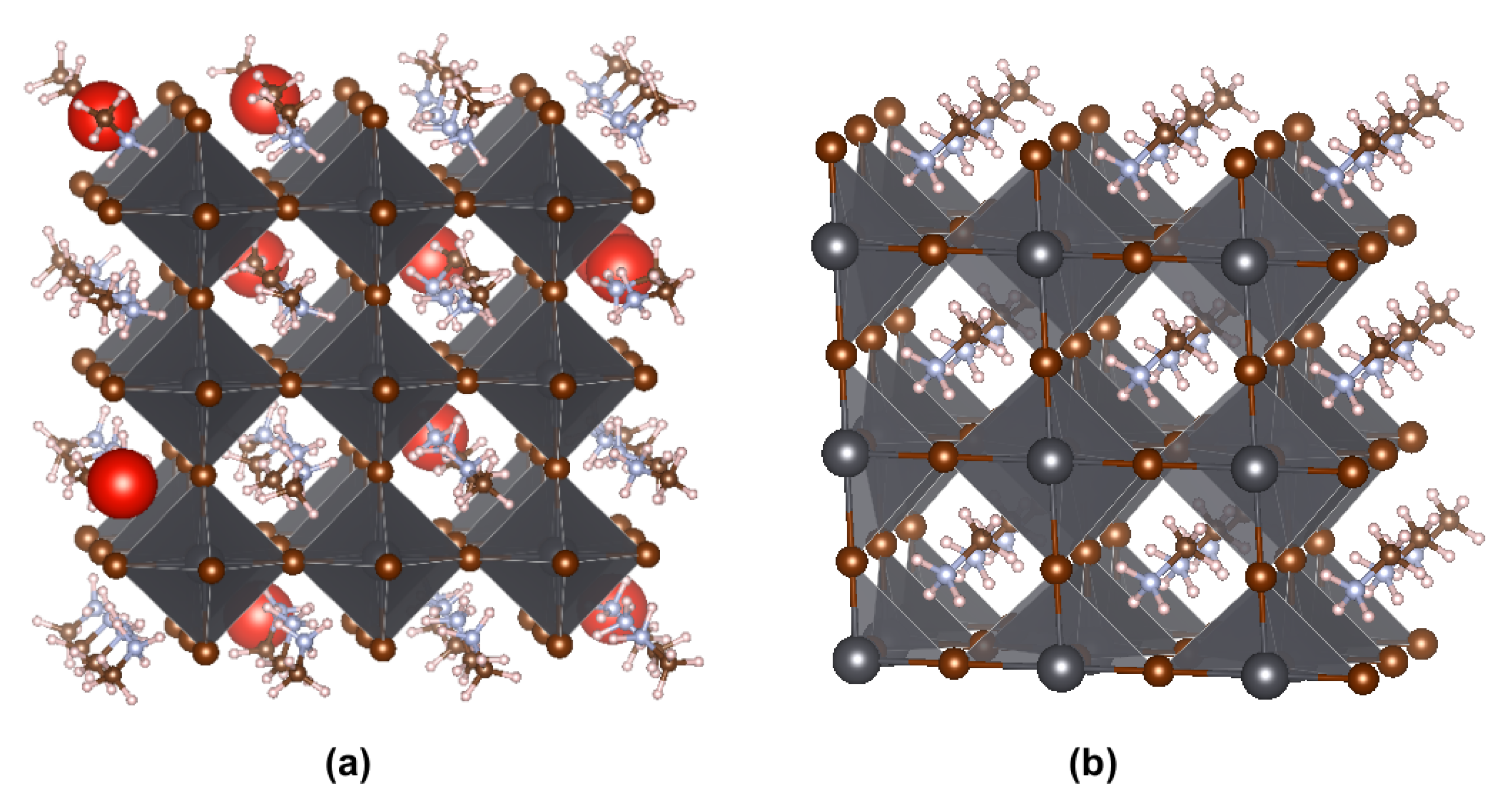
2. Outline of Calculations
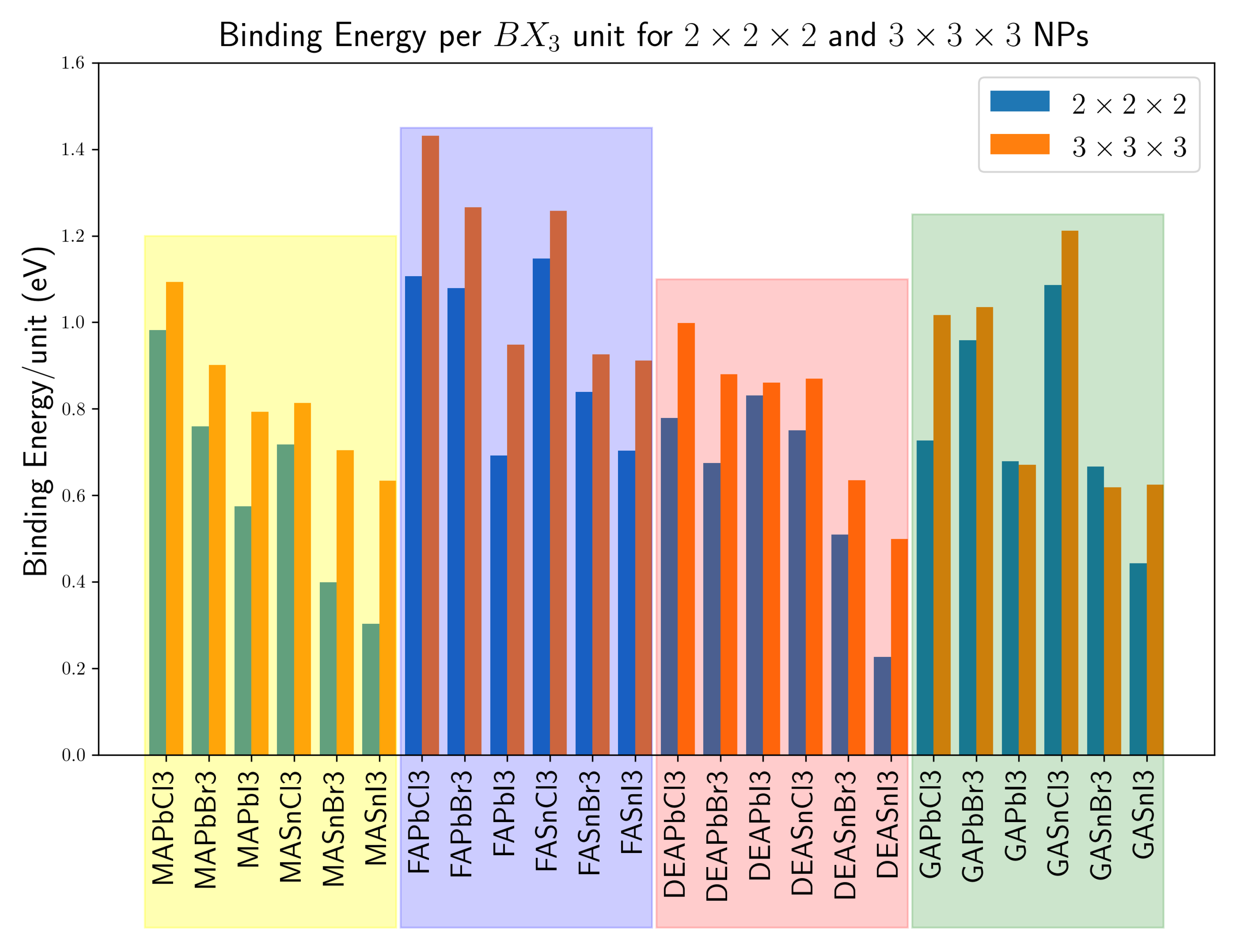
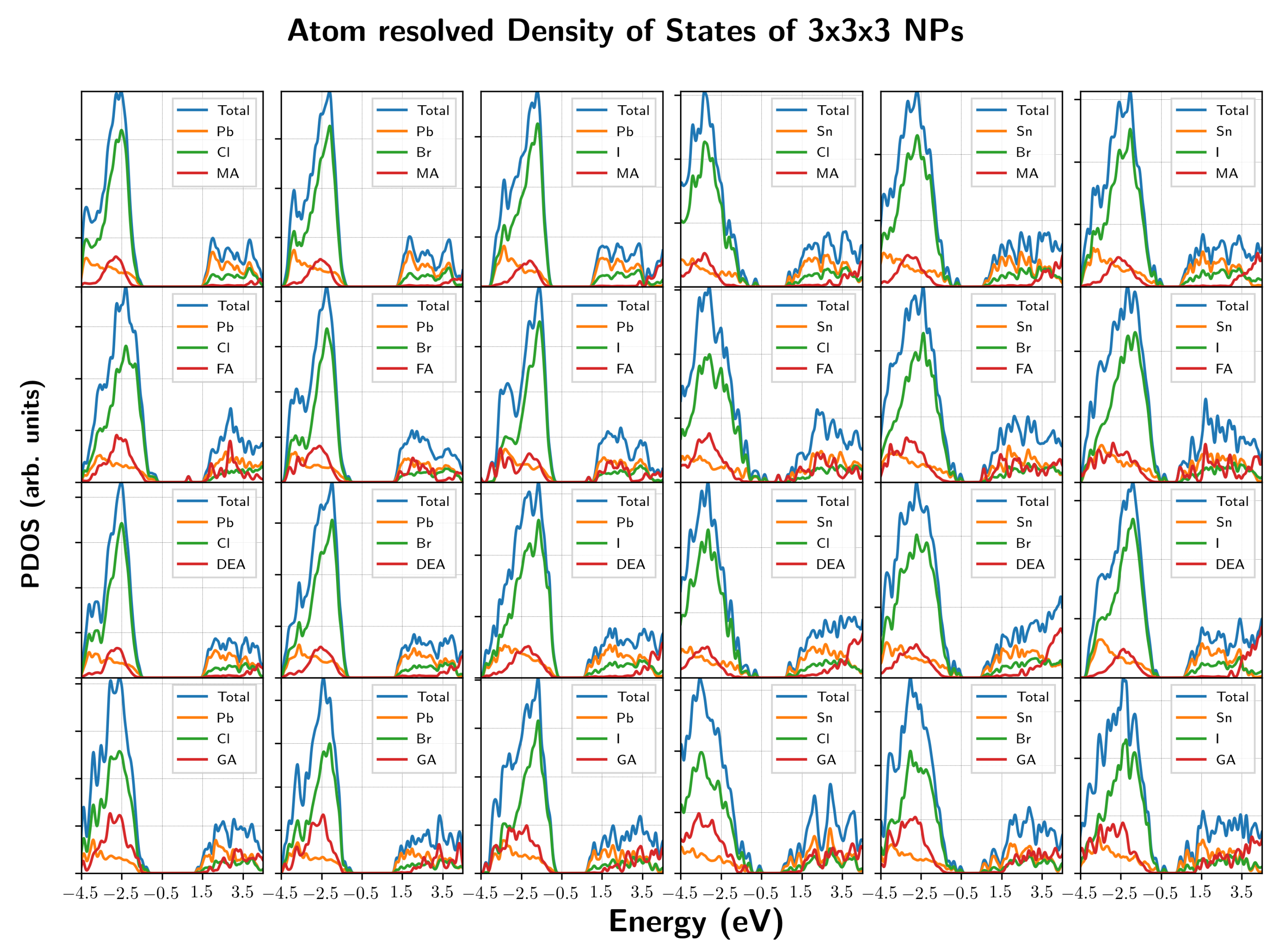
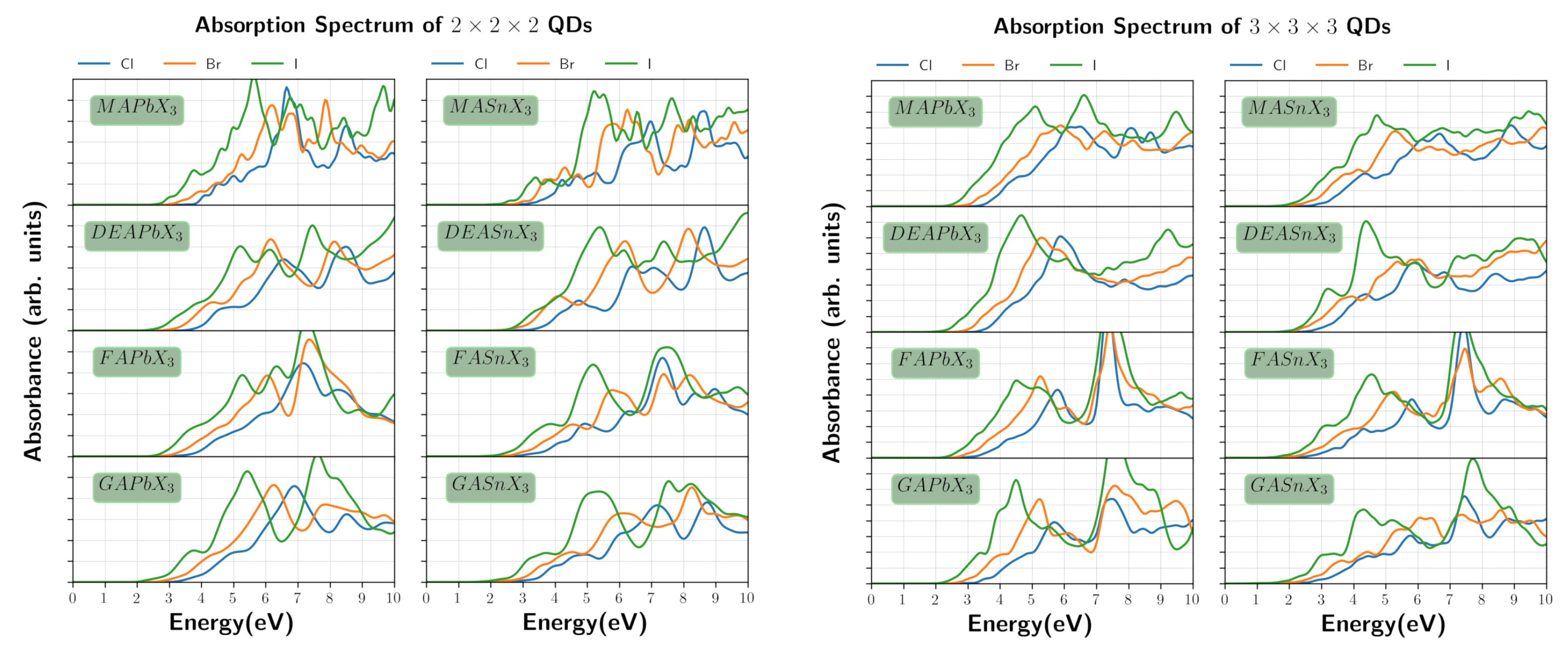
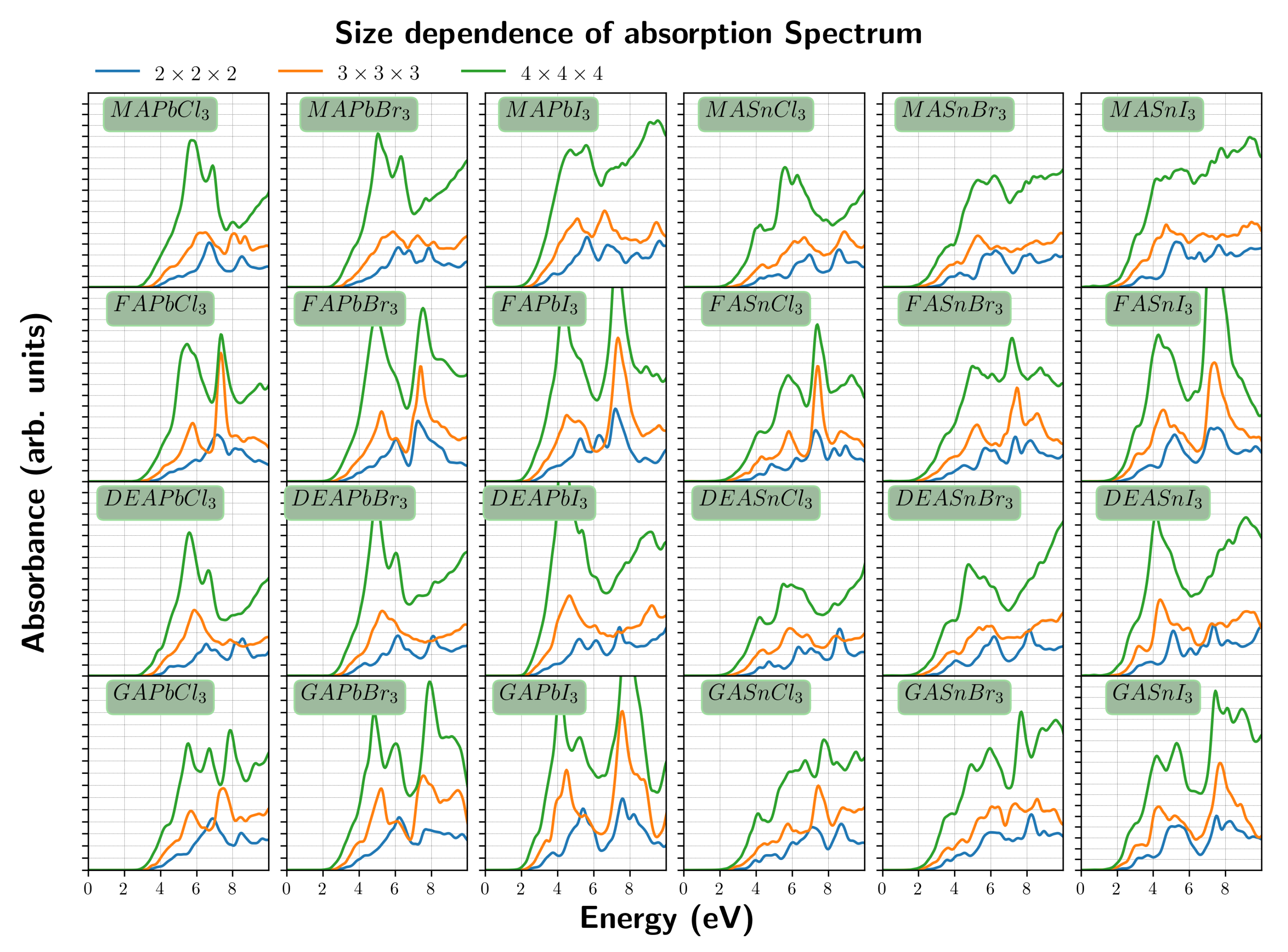
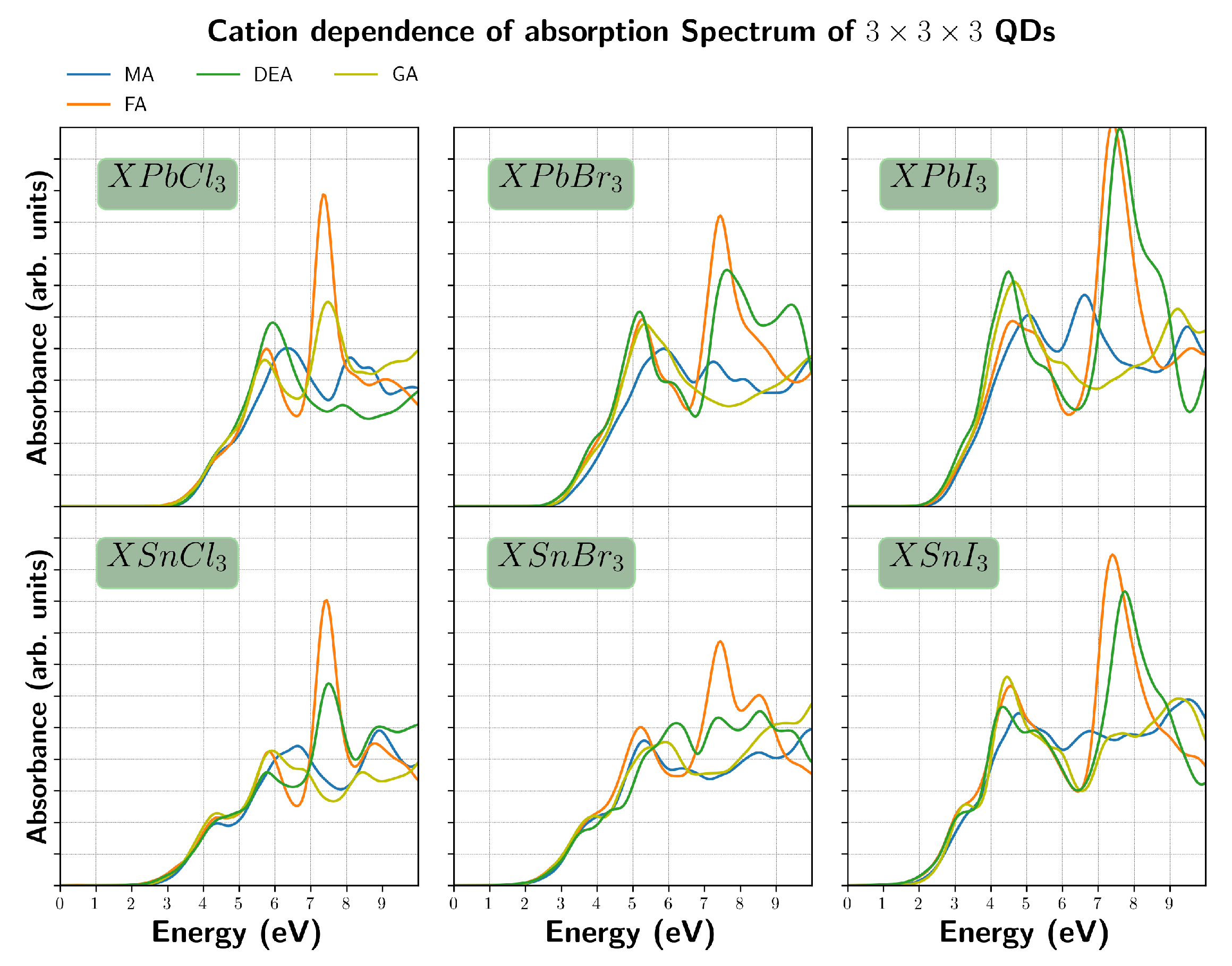
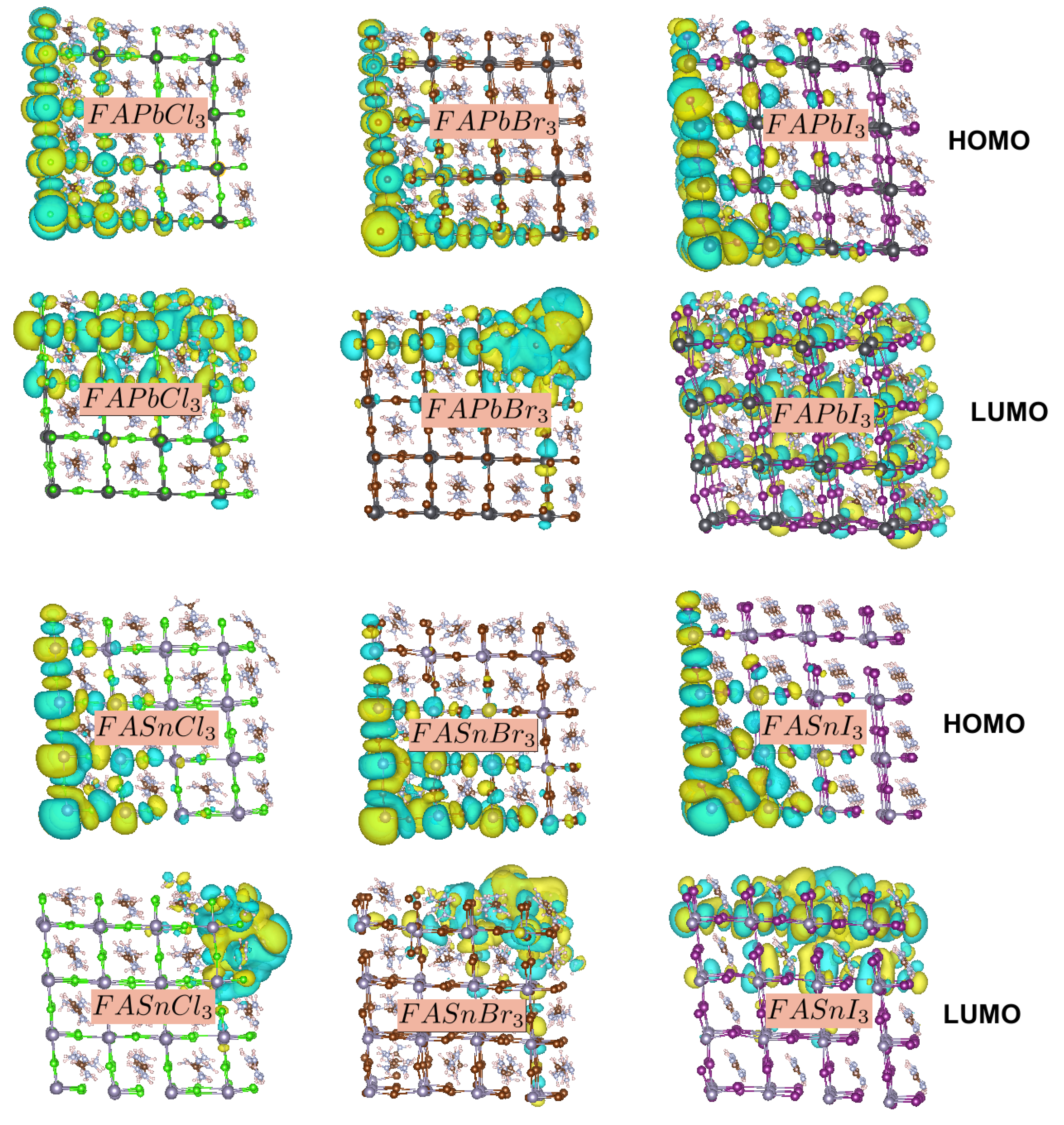
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pena, M.A.; Fierro, J.L.G. Chemical structure and performance of perovskite oxides. Chem. Rev. 2001, 101, 1981. [Google Scholar] [CrossRef]
- Chen, Q.; De Marco, N.; Yang, Y.M.; Song, T.B.; Chen, C.C.; Zhao, H.; Hong, Z.; Zhou, H.; Yang, Y. Under the spotlight: The organic–inorganic hybrid halide perovskite for optoelectronic applications. Nano Today 2015, 10, 355–396. [Google Scholar] [CrossRef] [Green Version]
- Hoefler, S.F.; Trimmel, G.; Rath, T. Progress on lead-free metal halide perovskites for photovoltaic applications: A review. Monatsh. Chem. 2017, 148, 795. [Google Scholar] [CrossRef] [Green Version]
- Román-Vázquez, M.; Vidyasagar, C.; Muũnoz Flores, B.M.; Jiménez-Pérez, V.M. Recent advances on synthesis and applications of lead- and tin-free perovskites. J. Alloys Compd. 2020, 835, 155112. [Google Scholar] [CrossRef]
- Yang, L.; Barrows, A.T.; Lidzey, D.G.; Wang, T. Recent progress and challenges of organometal halide perovskite solar cells. Rep. Prog. Phys. 2016, 79, 026501. [Google Scholar] [CrossRef]
- Yang, G.L.; Zhong, H.Z. Organometal halide perovskite quantum dots: Synthesis, optical properties, and display applications. Chin. Chem. Lett. 2016, 27, 1124. [Google Scholar] [CrossRef]
- Johnston, M.B.; Herz, L.M. Hybrid perovskites for photovoltaics: Change-Carrier recombination, diffusion, and radiative efficiencies. Acc. Chem. Res. 2016, 49, 146. [Google Scholar] [CrossRef] [Green Version]
- Brittman, S.; Adhyaksa, G.W.P.; Garnett, E.C. The expanding world of hybrid perovskites: Materials properties and emerging applications. MRS Commun. 2015, 5, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frost, J.M.; Butler, K.T.; Brivio, F.; Hendon, C.H.; van Schilfgaarde, M.; Walsh, A. Atomistic origins of high-performance in hybrid halide perovskite solar cells. Nano Lett. 2014, 14, 2584. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Filippetti, A.; Mattoni, A. Hybrid perovskites for photovoltaics: Insights from first principles. Phys. Rev. B 2014, 89, 125203. [Google Scholar] [CrossRef]
- Albero, J.; Asiri, A.M.; Garcia, H. Influence of the composition of hybrid perovskites on their performance in solar cells. J. Mater. Chem. 2016, 4, 4353. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Zhu, K. Organic-inorganic hybrid lead halide perovskites for optoelectronic and electronic applications. Chem. Soc. Rev. 2016, 45, 655. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, M.; Game, O.S.; Wu, W.; Kwun, J.; Strauss, M.A.; Yan, Y.; Huang, J.; Zhu, K.; Padture, N.P. Manipulating crystallization of organolead mixed-halide thin films in antisolvent baths for wide-bandgap perovskite solar cells. ACS Appl. Mater. Interfaces 2016, 8, 22322237. [Google Scholar] [CrossRef]
- Quarti, C.; Mosconi, E.; Ball, J.M.; DInnocenzo, V.; Tao, C.; Pathak, S.; Snaith, H.J.; Petrozza, A.; De Angelis, F. Structural and optical properties of methylammonium lead iodide across the tetragonal to cubic phase transition: Implications for perovskite solar cells. Energy Environ. Sci. 2016, 9, 155. [Google Scholar] [CrossRef]
- Koliogiorgos, A.; Baskoutas, S.; Galanakis, I. Electronic and gap properties of lead-free perfect and mixed hybrid halide perovskites: An ab-initio study. Comput. Mater. Sci. 2017, 138, 92. [Google Scholar] [CrossRef] [Green Version]
- Kovalenko, M.V.; Protesescu, L.; Bodnarchuk, M.I. Properties and potential optoelectronic applications of lead halide perovskite nanocrystals. Science 2017, 358, 745750. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hwang, J.; Rao, R.R.; Giordano, L.; Katayama, Y.; Yu, Y.; Shao-Horn, Y. Perovskites in catalysis and electrocatalysis. Science 2017, 358, 751756. [Google Scholar] [CrossRef] [Green Version]
- Green, M.A. Silicon solar cells: Evolution, high-efficiency design and efficiency enhancements. Semicond. Sci. Technol. 1993, 8, 1. [Google Scholar] [CrossRef]
- Grätzel, M. The light and shade of perovskite solar cells. Nat. Mater. 2014, 13, 838. [Google Scholar] [CrossRef] [PubMed]
- Correa-Baena, J.P.; Saliba, M.; Buonassisi, T.; Grätzel, M.; Abate, A.; Tress, W.; Hagfeldt, A. Promises and challenges of perovskite solar cells. Science 2017, 358, 739744. [Google Scholar] [CrossRef] [Green Version]
- Ono, L.K.; Qi, Y.; Liu, S. Progress toward Stable Lead Halide Perovskite Solar Cells. Joule 2018, 2, 1961. [Google Scholar] [CrossRef] [Green Version]
- Sahare, S.; Ghoderao, P.; Khan, S.B.; Chan, Y.; Lee, S.L. Recent progress in hybrid perovskite solar cells through scanning tunneling microscopy and spectroscopy. Nanoscale 2020, 12, 15970. [Google Scholar] [CrossRef]
- Xie, H.; Yin, X.; Guo, Y.; Liu, J.; Que, W.; Wang, G. Recent Progress of Flexible Perovskite Solar Cells. Phys. St. Solidi RRL 2019, 13, 1800566. [Google Scholar] [CrossRef]
- Jošt, M.; Kegelmann, L.; Korte, L.; Albrecht, S. Monolithic Perovskite Tandem Solar Cells: A Review of the Present Status and Advanced Characterization Methods Toward 30% Efficiency. Adv. Energy Mater. 2020, 10, 1904102. [Google Scholar] [CrossRef]
- Daboczi, M.; Kim, J.; Lee, J.; Kang, H.; Hamilton, I.; Lin, C.T.; Dimitrov, S.D.; McLachlan, M.A.; Lee, K.; Durrant, J.R.; et al. Towards Efficient Integrated Perovskite/Organic Bulk Heterojunction Solar Cells: Interfacial Energetic Requirement to Reduce Charge Carrier Recombination Losses. Adv. Funct. Mater. 2020, 30, 2001482. [Google Scholar] [CrossRef]
- Asghar, M.; Zhang, J.; Wang, H.; Lunda, P.D. Device stability of perovskite solar cells-A review. Renew. Sust. Energ. Rev. 2017, 77, 131. [Google Scholar] [CrossRef] [Green Version]
- Saliba, M.; Correa-Baena, J.P.; Grätzel, M.; Hagfeldt, A.; Abate, A. Perovskite Solar Cells: From the Atomic Level to Film Quality and Device Performance. Angew. Chem. Int. Ed. 2018, 57, 2554. [Google Scholar] [CrossRef] [PubMed]
- Shekhirev, M.; Goza, J.; Teeter, J.D.; Lipatov, A.; Sinitskii, A. Synthesis of Cesium Lead Halide Perovskite Quantum Dots. J. Chem. Educ. 2017, 94, 1150. [Google Scholar] [CrossRef]
- Hou, J.; Cao, S.; Wu, Y.; Gao, Z.; Liang, F.; Sun, Y.; Lin, Z.; Sun, L. Inorganic Colloidal Perovskite Quantum Dots for Robust Solar CO2 Reduction. Chem.-Eur. J. 2017, 23, 9481. [Google Scholar] [CrossRef]
- Bohn, B.J.; Tong, Y.; Gramlich, M.; Lai, M.L.; Döblinger, M.; Wang, K.; Hoye, R.L.Z.; Muüller-Buschbaum, P.; Stranks, S.D.; Urban, A.S.; et al. Boosting Tunable Blue Luminescence of Halide Perovskite Nanoplatelets through Postsynthetic Surface Trap Repair. Nano Lett. 2018, 18, 5231. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Zou, Y.; Li, P.; Liu, Q.; Wu, L.; Hu, H.; Xu, Y.; Sun, B.; Zhang, Q.; Lee, S.T. Large-scale synthesis of ultrathin cesium lead bromide perovskite nanoplates with precisely tunable dimensions and their application in blue light-emitting diodes. Nano Energy 2018, 47, 235. [Google Scholar] [CrossRef]
- Tong, Y.; Fu, M.; Bladt, E.; Huang, H.; Richter, A.F.; Wang, K.; Muller-Buschbaum, P.; Bals, S.; Tamarat, P.; Lounis, B.; et al. Chemical Cutting of Perovskite Nanowires into Single-Photon Emissive Low-Aspect-Ratio CsPbX3 (X = Cl, Br, I) Nanorods. Angew. Chem. Int. Ed. 2018, 57, 16094. [Google Scholar] [CrossRef] [PubMed]
- Bai, Z.; Zhong, H. Halide perovskite quantum dots: Potential candidates for display technology. Sci. Bull. 2015, 60, 1622. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Zhong, H.; Chen, C.; Wu, X.g.; Hu, X.; Huang, H.; Han, J.; Zou, B.; Dong, Y. Brightly Luminescent and Color-Tunable Colloidal CH3NH3PbX3 (X = Br, I, Cl) Quantum Dots: Potential Alternatives for Display Technology. ACS Nano 2015, 9, 4533. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, K.; Takahashi, T.; Ban, T.; Kondo, T.; Uchida, K.; Miura, N. Comparative study on the excitons in lead-halide-based perovskite-type crystals CH3NH3PbBr3 CH3NH3PbI3. Solid State Commun. 2003, 127, 619. [Google Scholar] [CrossRef]
- Mali, S.S.; Shim, C.S.; Hong, C.K. Highly stable and efficient solid-state solar cells based on methylammonium lead bromide (CH3NH3PbBr3) perovskite quantum dots. Npg Asia Mater. 2015, 7, 208. [Google Scholar] [CrossRef] [Green Version]
- Castañeda, J.A.; Nagamine, G.; Yassitepe, E.; Bonato, L.G.; Voznyy, O.; Hoogland, S.; Nogueira, A.F.; Sargent, E.H.; Cruz, C.H.B.; Padilha, L.A. Efficient Biexciton Interaction in Perovskite Quantum Dots Under Weak and Strong Confinement. ACS Nano 2016, 10, 8603. [Google Scholar] [CrossRef]
- Peng, L.; Geng, J.; Ai, L.; Zhang, Y.; Xie, R.; Yang, W. Room temperature synthesis of ultra-small, near-unity single-sized lead halide perovskite quantum dots with wide color emission tunability, high color purity and high brightness. Nanotechnology 2016, 27, 335604. [Google Scholar] [CrossRef]
- Chen, X.; Peng, L.; Huang, K.; Shi, Z.; Xie, R.; Yang, W. Non-injection gram-scale synthesis of cesium lead halide perovskite quantum dots with controllable size and composition. Nano Res. 2016, 9, 1994. [Google Scholar] [CrossRef]
- Buin, A.; Comin, R.; Ip, A.H.; Sargent, E.H. Perovskite Quantum Dots Modeled Using ab Initio and Replica Exchange Molecular Dynamics. J. Phys. Chem. C 2015, 119, 13965. [Google Scholar] [CrossRef]
- He, J.; Vasenko, A.S.; Long, R.; Prezhdo, O.V. Halide Composition Controls Electron–Hole Recombination in Cesium–Lead Halide Perovskite Quantum Dots: A Time Domain Ab Initio Study. J. Phys. Chem. Lett. 2018, 9, 1872. [Google Scholar] [CrossRef]
- Koliogiorgos, A.; Garoufalis, C.S.; Galanakis, I.; Baskoutas, S. Electronic and optical properties of ultrasmall ABX3 (A = Cs, CH3NH3, B = Ge, Pb, Sn, Ca, Sr, X = Cl, Br, I) perovskite quantum dots. ACS Omega 2018, 3, 18917. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef] [PubMed]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef] [Green Version]
- Pracht, P.; Bohle, F.; Grimme, S. Automated exploration of the low-energy chemical space with fast quantum chemical methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations. J. Chem. Theory Comput. 2019, 15, 2847–2862. [Google Scholar] [CrossRef]
- Mortensen, J.J.; Hansen, L.B.; Jacobsen, K.W. Real-space grid implementation of the projector augmented wave method. Phys. Rev. B 2005, 71, 035109. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Larsen, A.H.; Mortensen, J.J.; Blomqvist, J.; Castelli, I.E.; Christensen, R.; Dułak, M.; Friis, J.; Groves, M.N.; Hammer, B.; Hargus, C.; et al. The atomic simulation environment—A Python library for working with atoms. J. Phys. Condens. Matter 2017, 29, 273002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walter, M.; Häkkinen, H.; Lehtovaara, L.; Puska, M.; Enkovaara, J.; Rostgaard, C.; Mortensen, J.J. Time-dependent density-functional theory in the projector augmented-wave method. J. Chem. Phys. 2008, 128, 244101. [Google Scholar] [CrossRef] [Green Version]
- Kuisma, M.; Sakko, A.; Rossi, T.P.; Larsen, A.H.; Enkovaara, J.; Lehtovaara, L.; Rantala, T.T. Localized surface plasmon resonance in silver nanoparticles: Atomistic first-principles time-dependent density-functional theory calculations. Phys. Rev. B 2015, 91, 115431. [Google Scholar] [CrossRef] [Green Version]
| A = MA | ||||||
|---|---|---|---|---|---|---|
| Pb | Sn | |||||
| Cl | Br | I | Cl | Br | I | |
| 3.55 | 2.97 | 2.50 | 2.78 | 2.10 | 1.84 | |
| 3.34 | 2.84 | 2.28 | 1.80 | 1.62 | 1.25 | |
| 2.87 | 2.38 | 1.48 | 1.48 | 1.16 | 0.45 | |
| A = FA | ||||||
| Pb | Sn | |||||
| Cl | Br | I | Cl | Br | I | |
| 2.36 | 1.81 | 1.94 | 0.97 | 1.36 | 0.86 | |
| 1.82 | 2.49 | 1.87 | 1.01 | 1.22 | 0.83 | |
| 2.55 | 1.88 | 1.53 | 0.65 | 0.73 | 0.90 | |
| A = DEA | ||||||
| Pb | Sn | |||||
| Cl | Br | I | Cl | Br | I | |
| 3.50 | 2.95 | 2.46 | 2.82 | 2.01 | 2.16 | |
| 3.29 | 2.65 | 1.65 | 1.80 | 1.40 | 1.65 | |
| 2.90 | 2.50 | 1.50 | 1.69 | 0.85 | 0.55 | |
| A = GA | ||||||
| Pb | Sn | |||||
| Cl | Br | I | Cl | Br | I | |
| 3.21 | 2.90 | 2.29 | 2.33 | 2.16 | 1.67 | |
| 2.71 | 2.35 | 1.79 | 1.40 | 1.22 | 0.84 | |
| 2.62 | 2.00 | 1.42 | 0.73 | 0.78 | 0.76 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garoufalis, C.S.; Galanakis, I.; Zeng, Z.; Hayrapetyan, D.B.; Baskoutas, S. Structural and Electronic Properties of Small Perovskite Nanoparticles of the Form ABX3 (A = MA, DEA, FA, GA, B = Pb, Sn, X = Cl, Br, I). Electron. Mater. 2021, 2, 382-393. https://doi.org/10.3390/electronicmat2030026
Garoufalis CS, Galanakis I, Zeng Z, Hayrapetyan DB, Baskoutas S. Structural and Electronic Properties of Small Perovskite Nanoparticles of the Form ABX3 (A = MA, DEA, FA, GA, B = Pb, Sn, X = Cl, Br, I). Electronic Materials. 2021; 2(3):382-393. https://doi.org/10.3390/electronicmat2030026
Chicago/Turabian StyleGaroufalis, Christos S., Iosif Galanakis, Zaiping Zeng, David B. Hayrapetyan, and Sotirios Baskoutas. 2021. "Structural and Electronic Properties of Small Perovskite Nanoparticles of the Form ABX3 (A = MA, DEA, FA, GA, B = Pb, Sn, X = Cl, Br, I)" Electronic Materials 2, no. 3: 382-393. https://doi.org/10.3390/electronicmat2030026
APA StyleGaroufalis, C. S., Galanakis, I., Zeng, Z., Hayrapetyan, D. B., & Baskoutas, S. (2021). Structural and Electronic Properties of Small Perovskite Nanoparticles of the Form ABX3 (A = MA, DEA, FA, GA, B = Pb, Sn, X = Cl, Br, I). Electronic Materials, 2(3), 382-393. https://doi.org/10.3390/electronicmat2030026








