Sterically Stabilized Multilayer Graphene Nanoshells for Inkjet Printed Resistors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Nanoparticle Structure
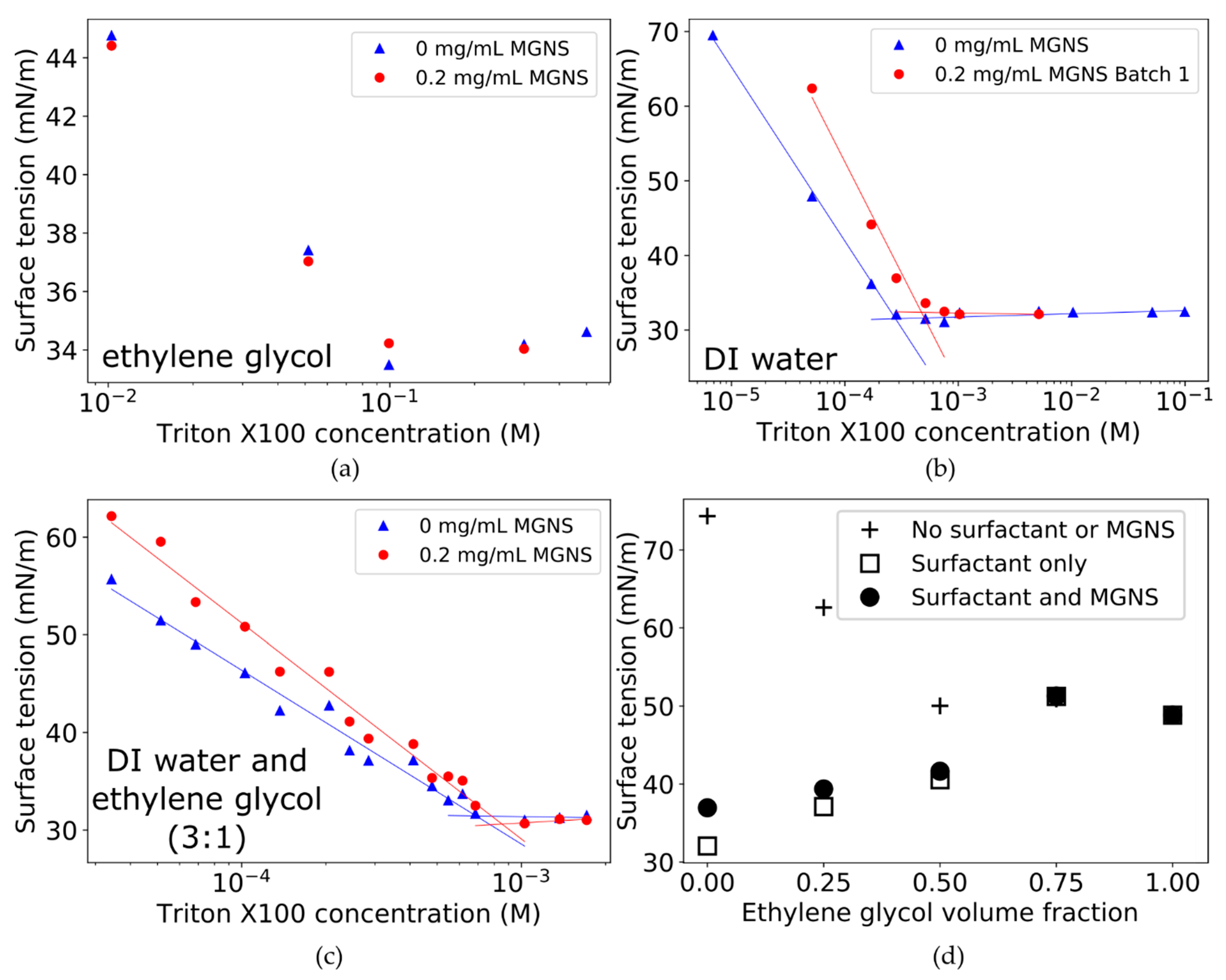
2.2. Surface Tension-Based Adsorption Analysis
2.3. Ink Synthesis
2.4. Inkjet Printing
2.5. Electrical Characterization
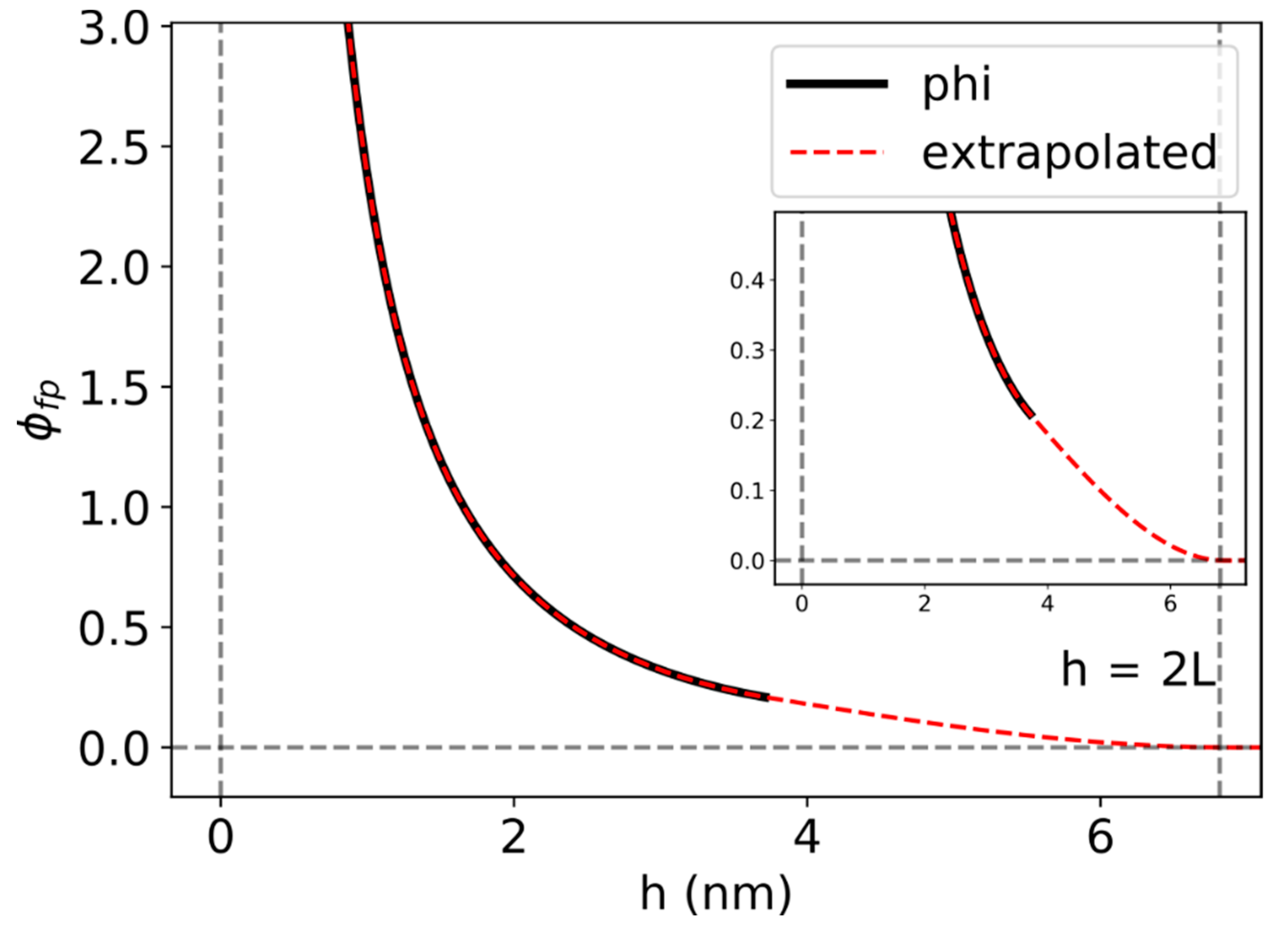
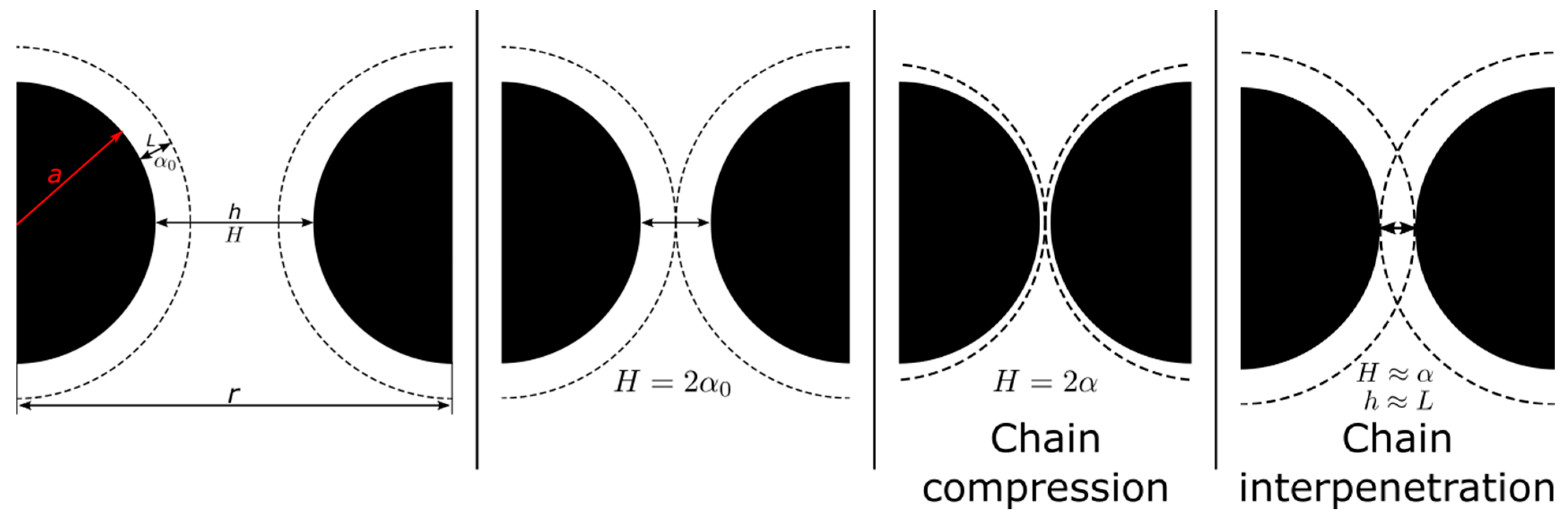
2.6. Geometric Model
- : carbon-carbon bond length in phenyl group;
- : carbon-hydrogen bond length in phenyl group;
- : carbon-oxygen bond length;
- : carbon-carbon bond length (not in phenyl group);
- Lftprnt: molecule footprint length;
- Wftprnt: molecule footprint width;
- Aftprnt: molecule footprint area.
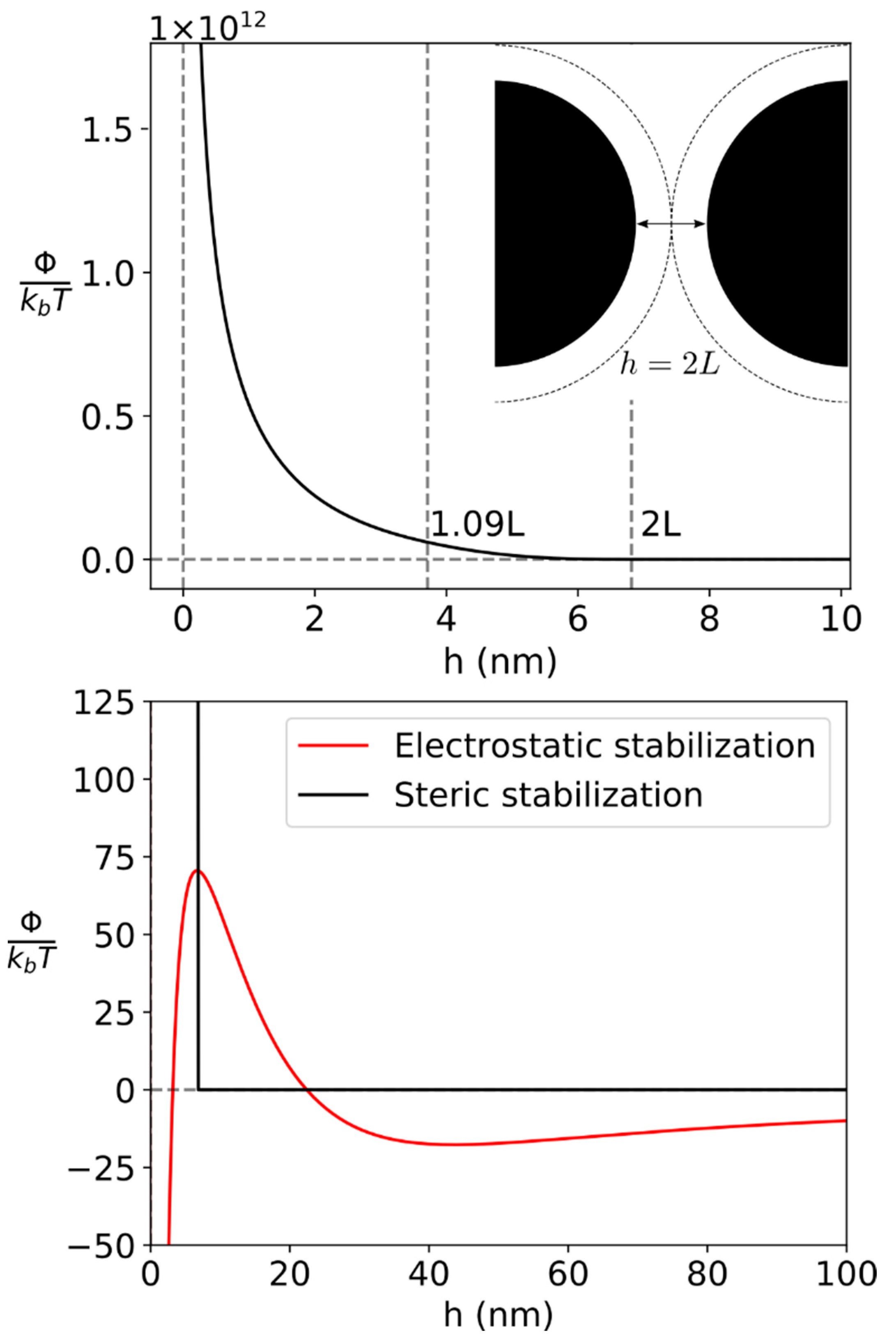
2.7. Inter-Particle Potential Model
- : interparticle potential;
- : particle radii;
- : particle – particle center separation;
- : particle – particle surface separation;
- number of polymer segments = 9.5 for Triton X100 [];
- : stabilizing segment chain length = 0.6 for poly(oxyethylene) [];
- : polymer segment density;
- polymer segment – segment excluded volume ;
- : physical volume of segment ;
- : surface density of polymer chains = ;
- : full retarded Hamaker constant;
- : adsorbed layer thickness;
- : dimension layer thickness of an isolated adsorbed layer;
- : dimensionless layer thickness;
- : dimensionless particle – particle surface separation;
- : dimensionless surface density of adsorbed polymer;
- : ratio of excluded volume per chain to volume occupied by chain at ideal conditions.
3. Results
3.1. Surface Tension Coverage Analysis
3.2. Geometric Absorption Model
3.3. Energetic Potential Model
3.4. Ink Properties
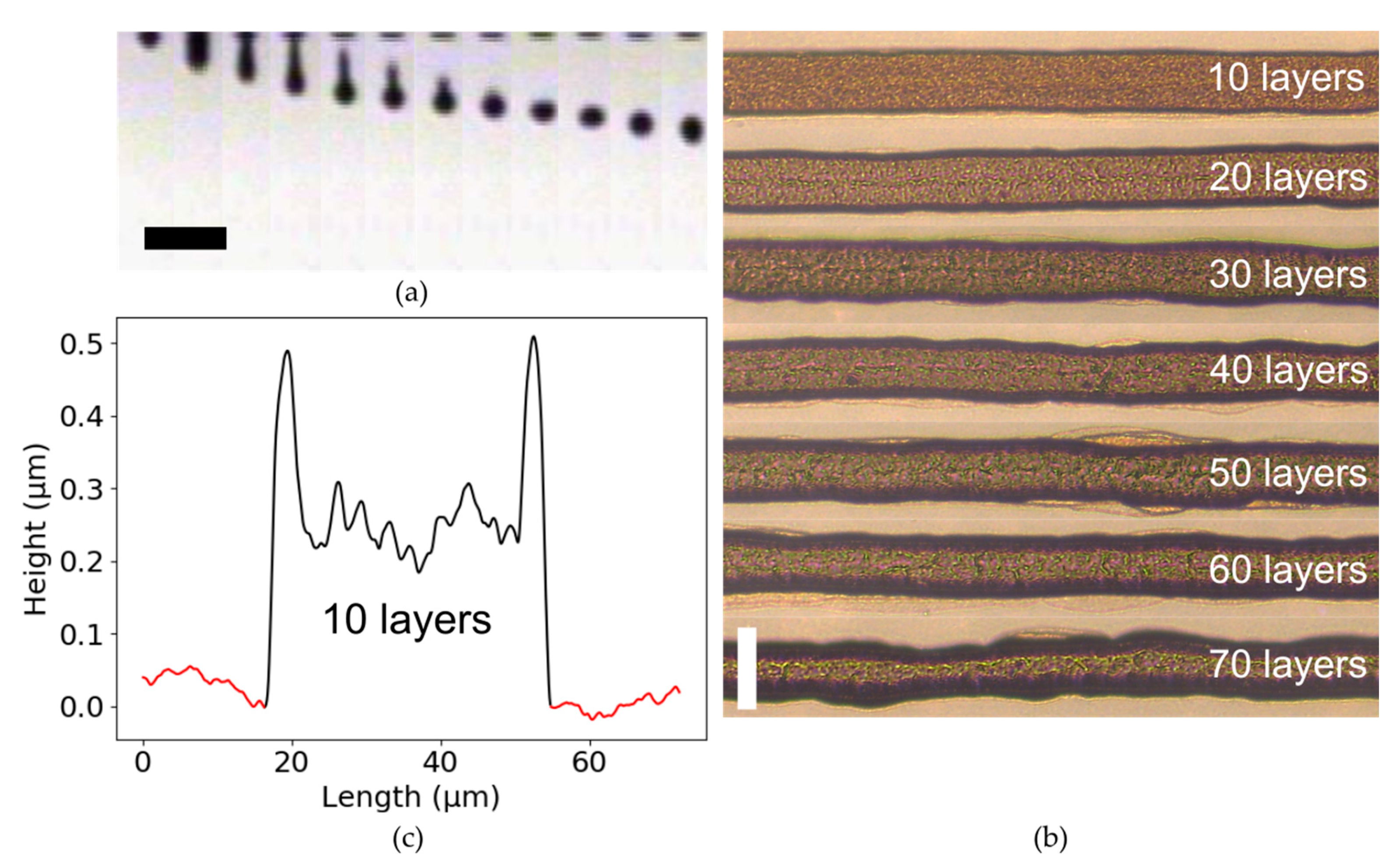
3.5. Printing Results
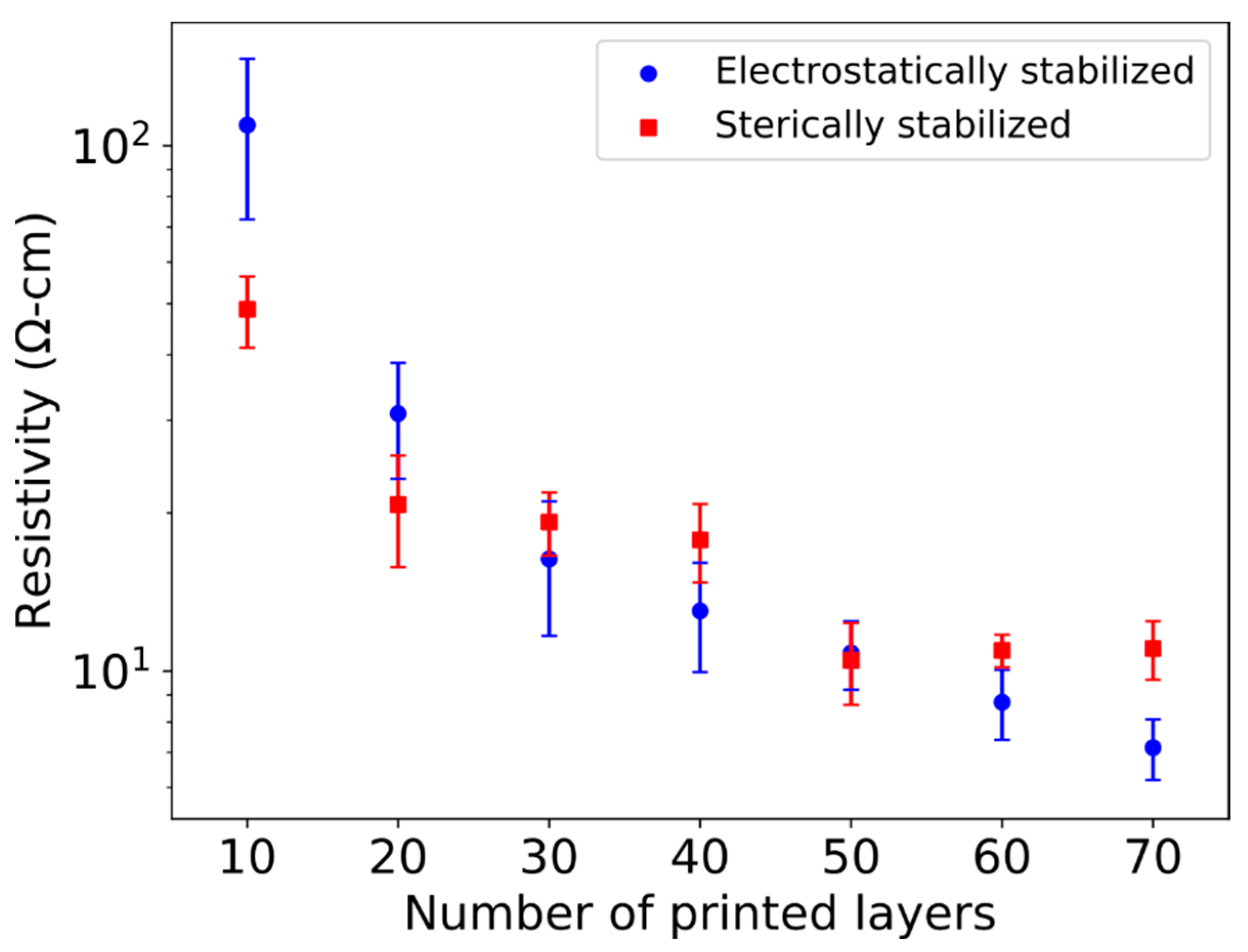
3.6. Electrical Characteristics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Sairajan, K.K.; Aglietti, G.S.; Mani, K.M. A Review of Multifunctional Structure Technology for Aerospace Applications. Acta Astronaut. 2016, 120, 30–42. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Zhang, T. Flexible Sensing Electronics for Wearable/Attachable Health Monitoring. Small 2017, 13, 1602790. [Google Scholar] [CrossRef]
- Liu, Y.; Pharr, M.; Salvatore, G.A. Lab-on-Skin: A Review of Flexible and Stretchable Electronics for Wearable Health Monitoring. ACS Nano 2017, 11, 9614–9635. [Google Scholar] [CrossRef]
- Luo, N.; Dai, W.; Li, C.; Zhou, Z.; Lu, L.; Poon, C.C.Y.; Chen, S.-C.; Zhang, Y.; Zhao, N. Flexible Piezoresistive Sensor Patch Enabling Ultralow Power Cuffless Blood Pressure Measurement. Adv. Funct. Mater. 2016, 26, 1178–1187. [Google Scholar] [CrossRef]
- Amjadi, M.; Kyung, K.-U.; Park, I.; Sitti, M. Stretchable, Skin-Mountable, and Wearable Strain Sensors and Their Potential Applications: A Review. Adv. Funct. Mater. 2016, 26, 1678–1698. [Google Scholar] [CrossRef]
- Khan, Y.; Garg, M.; Gui, Q.; Schadt, M.; Gaikwad, A.; Han, D.; Yamamoto, N.A.D.; Hart, P.; Welte, R.; Wilson, W.; et al. Flexible Hybrid Electronics: Direct Interfacing of Soft and Hard Electronics for Wearable Health Monitoring. Adv. Funct. Mater. 2016, 26, 8764–8775. [Google Scholar] [CrossRef]
- Santhiago, M.; Corrêa, C.C.; Bernardes, J.S.; Pereira, M.P.; Oliveira, L.J.M.; Strauss, M.; Bufon, C.C.B. Flexible and Foldable Fully-Printed Carbon Black Conductive Nanostructures on Paper for High-Performance Electronic, Electrochemical, and Wearable Devices. ACS Appl. Mater. Interfaces 2017, 9, 24365–24372. [Google Scholar] [CrossRef]
- Zhang, Y.; Anderson, N.; Bland, S.; Nutt, S.; Jursich, G.; Joshi, S. All-Printed Strain Sensors: Building Blocks of the Aircraft Structural Health Monitoring System. Sens. Actuators A Phys. 2017, 253, 165–172. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Rieutort-Louis, W.; Sanz-Robinson, J.; Huang, L.; Glisic, B.; Sturm, J.C.; Wagner, S.; Verma, N. Large-Scale Sensing System Combining Large-Area Electronics and CMOS ICs for Structural-Health Monitoring. IEEE J. Solid State Circuits 2014, 49, 513–523. [Google Scholar] [CrossRef]
- Brandon, E.; West, W.; Zhou, L.; Jackson, T.; Theriot, G.; Devine, R.A.B.; Binkley, D.; Verma, N.; Crawford, R. Flexible Electronics for Space Applications. MRS Proc. 2004, 814, I9.7. [Google Scholar] [CrossRef] [Green Version]
- Mattoni, B.; Pagliaro, F.; Gugliermetti, L.; Bisegna, F.; Cellucci, L. A Territorial Based Strategy for the Distribution of Sensor Networks in Smart Cities. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 653–658. [Google Scholar]
- Zhan, Y.; Mei, Y.; Zheng, L. Materials Capability and Device Performance in Flexible Electronics for the Internet of Things. J. Mater. Chem. C 2014, 2, 1220–1232. [Google Scholar] [CrossRef]
- MacDonald, W.A.; Looney, M.K.; MacKerron, D.; Eveson, R.; Adam, R.; Hashimoto, K.; Rakos, K. Latest Advances in Substrates for Flexible Electronics. J. Soc. Inf. Disp. 2007, 15, 1075–1083. [Google Scholar] [CrossRef]
- Ahn, B.Y.; Duoss, E.B.; Motala, M.J.; Guo, X.; Park, S.-I.; Xiong, Y.; Yoon, J.; Nuzzo, R.G.; Rogers, J.A.; Lewis, J.A. Omnidirectional Printing of Flexible, Stretchable, and Spanning Silver Microelectrodes. Science 2009, 323, 1590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perelaer, J.; de Gans, B.-J.; Schubert, U.S. Ink-Jet Printing and Microwave Sintering of Conductive Silver Tracks. Adv. Mater. 2006, 18, 2101–2104. [Google Scholar] [CrossRef]
- Sivaramakrishnan, S.; Chia, P.-J.; Yeo, Y.-C.; Chua, L.-L.; Ho, P.K.-H. Controlled Insulator-to-Metal Transformation in Printable Polymer Composites with Nanometal Clusters. Nat. Mater. 2007, 6, 149–155. [Google Scholar] [CrossRef]
- Kim, H.-S.; Dhage, S.R.; Shim, D.-E.; Hahn, H.T. Intense Pulsed Light Sintering of Copper Nanoink for Printed Electronics. Appl. Phys. A 2009, 97, 791. [Google Scholar] [CrossRef] [Green Version]
- Ko, S.H.; Pan, H.; Grigoropoulos, C.P.; Luscombe, C.K.; Fréchet, J.M.J.; Poulikakos, D. Air Stable High Resolution Organic Transistors by Selective Laser Sintering of Ink-Jet Printed Metal Nanoparticles. Appl. Phys. Lett. 2007, 90, 141103. [Google Scholar] [CrossRef] [Green Version]
- Perelaer, J.; Klokkenburg, M.; Hendriks, C.E.; Schubert, U.S. Microwave Flash Sintering of Inkjet-Printed Silver Tracks on Polymer Substrates. Adv. Mater. 2009, 21, 4830–4834. [Google Scholar] [CrossRef]
- Grouchko, M.; Kamyshny, A.; Mihailescu, C.F.; Anghel, D.F.; Magdassi, S. Conductive Inks with a “Built-In” Mechanism That Enables Sintering at Room Temperature. ACS Nano 2011, 5, 3354–3359. [Google Scholar] [CrossRef]
- Magdassi, S.; Grouchko, M.; Berezin, O.; Kamyshny, A. Triggering the Sintering of Silver Nanoparticles at Room Temperature. ACS Nano 2010, 4, 1943–1948. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.-S.; Khang, D.-Y. Room-Temperature Chemical Welding and Sintering of Metallic Nanostructures by Capillary Condensation. Nano Lett. 2016, 16, 3550–3556. [Google Scholar] [CrossRef]
- Orrill, M. Ink Synthesis and Inkjet Printing of Multilayer Graphene Nanoshells. Ph.D Thesis, The George Washington University, Washington, DC, USA, 2020. [Google Scholar]
- Orrill, M.; Abele, D.; Wagner, M.; LeBlanc, S. Ink Synthesis and Inkjet Printing of Electrostatically Stabilized Multilayer Graphene Nanoshells. J. Colloid Interface Sci. 2020, 566, 454–462. [Google Scholar] [CrossRef] [PubMed]
- Herbert, R.; Kim, J.-H.; Kim, Y.S.; Lee, H.M.; Yeo, W.-H. Soft Material-Enabled, Flexible Hybrid Electronics for Medicine, Healthcare, and Human-Machine Interfaces. Materials 2018, 11, 187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, T.; Hou, Z.; Johnson, R.W.; Castillo, L.D.; Moussessian, A.; Greenwell, R.; Blalock, B.J. Flexible Electronics: Thin Silicon Die on Flexible Substrates. IEEE Trans. Electron. Packag. Manuf. 2009, 32, 291–300. [Google Scholar] [CrossRef]
- Leber, D.E.; Meek, B.N.; Leija, S.D.; Wilson, D.G.; Chaney, R.L.; Hackler, D.R. Electromechanical Reliability Testing of Flexible Hybrid Electronics Incorporating FleX Silicon-On-Polymer Ics. In Proceedings of the 2016 IEEE Workshop on Microelectronics and Electron Devices (WMED), Boise, ID, USA, 15 April 2016; pp. 1–4. [Google Scholar]
- Kim, M.; Alrowais, H.; Pavlidis, S.; Brand, O. Size-Scalable and High-Density Liquid-Metal-Based Soft Electronic Passive Components and Circuits Using Soft Lithography. Adv. Funct. Mater. 2017, 27, 1604466. [Google Scholar] [CrossRef]
- Ostfeld, A.E.; Deckman, I.; Gaikwad, A.M.; Lochner, C.M.; Arias, A.C. Screen Printed Passive Components for Flexible Power Electronics. Sci. Rep. 2015, 5, 15959. [Google Scholar] [CrossRef]
- Chang, J.; Zhang, X.; Ge, T.; Zhou, J. Fully Printed Electronics on Flexible Substrates: High Gain Amplifiers and DAC. Org. Electron. 2014, 15, 701–710. [Google Scholar] [CrossRef] [Green Version]
- Jung, S.; Sou, A.; Gili, E.; Sirringhaus, H. Inkjet-Printed Resistors with a Wide Resistance Range for Printed Read-Only Memory Applications. Org. Electron. 2013, 14, 699–702. [Google Scholar] [CrossRef]
- Cao, M.; Jochem, K.; Hyun, W.J.; Francis, L.F.; Frisbie, C.D. Self-Aligned Inkjet Printing of Resistors and Low-Pass Resistor–Capacitor Filters on Roll-to-Roll Imprinted Plastics with Resistances Ranging from 10 to 10 6 Ω. Flex. Print. Electron. 2018, 3, 045003. [Google Scholar] [CrossRef]
- Wagner, M.; Banek, N.; Hays, K. Hollow Carbon Nanosphere Based Secondary Cell Electrodes. U.S. Patent US8262942B2, 11 September 2012. [Google Scholar]
- Matarredona, O.; Rhoads, H.; Li, Z.; Harwell, J.H.; Balzano, L.; Resasco, D.E. Dispersion of Single-Walled Carbon Nanotubes in Aqueous Solutions of the Anionic Surfactant NaDDBS. J. Phys. Chem. B 2003, 107, 13357–13367. [Google Scholar] [CrossRef]
- Russel, W.B.; Saville, D.A.; Schowalter, W.R. Electrostatic Stabilization. In Colloidal Dispersions; Cambridge Monographs on Mechanics; Cambridge University Press: Cambridge, UK, 1989; pp. 168, 310–314. [Google Scholar]
- Brandrup, J.; Immergut, E.H.; Grulke, E.A. Polymer Handbook, 4th ed.; Brandrup, J., Immergut, E.H., Grulke, E.A., Eds.; John Wiley & Sons Inc.: New York, NY, USA, 1999; ISBN 978-0-471-47936-9. [Google Scholar]
- Hough, D.B.; White, L.R. The Calculation of Hamaker Constants from Liftshitz Theory with Applications to Wetting Phenomena. Adv. Colloid Interface Sci. 1980, 14, 3–41. [Google Scholar] [CrossRef]
- Cordero, B.; Gómez, V.; Platero-Prats, A.E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent Radii Revisited. Dalton Trans. 2008, 21, 2832–2838. [Google Scholar] [CrossRef] [PubMed]
- Jang, D.; Kim, D.; Moon, J. Influence of Fluid Physical Properties on Ink-Jet Printability. Langmuir 2009, 25, 2629–2635. [Google Scholar] [CrossRef] [PubMed]
- Derby, B. Inkjet Printing of Functional and Structural Materials: Fluid Property Requirements, Feature Stability, and Resolution. Annu. Rev. Mater. Res. 2010, 40, 395–414. [Google Scholar] [CrossRef]
- Reis, N.; Derby, B. Ink Jet Deposition of Ceramic Suspensions: Modeling and Experiments of Droplet Formation. MRS Proc. 2000, 625, 117. [Google Scholar] [CrossRef]
- Xin, F.; Xu, G.Z. The Effect of Triton® X-100 on CNT/PP Composite’s Electrical Conductivity. Adv. Mater. Res. 2011, 284–286, 1836–1841. [Google Scholar] [CrossRef]
- Sidim, T. Some Physicochemical Properties Of Octylphenol Ethoxylate Nonionics (Triton X-100, Triton X-114 And Triton X-405) And The Temperature Effect On This Properties. Trak. Univ. J. Nat. Sci. 2016, 13, 101–116. [Google Scholar]





| Parameter | Value | Unit |
|---|---|---|
| Triton X100 parameters | ||
| lC-C | 152 | pm |
| lC-O | 142 | pm |
| lC-C Phenyl | 139 | pm |
| lC-H Phenyl | 107 | pm |
| Lftprnt | 572 | pm |
| Wftprnt | 426 | pm |
| Aftprnt | 0.24 | nm2 |
| molar density | 1.71 × 10−3 | mol/mL |
| MGNS particle parameters | ||
| RMGNS inner | 15 | nm |
| RMGNS outer | 25 | nm |
| MGNS surface area per particle | 1.1 × 10−14 | m2 |
| MGNS volume per particle | 5.1 × 10−23 | m3 |
| MGNS mass per particle | 1.28 × 10−16 | g/particle |
| MGNS 1 BET surface area | 323 | m2/g |
| ρgraphite | 2230 | kg/m3 |
| ρwater | 997.05 | kg/m3 |
| Result | Model | Surface Tension | Unit | Ratio |
|---|---|---|---|---|
| Optimal dosage | ||||
| DI water | 1.8 × 10−6 | 2.7 × 10−6 | mol/m2 | 1.5 |
| 5.7 × 10−7 | 8.7 × 10−7 | mol/mg | ||
| DI water/EG mixture | 1.8 × 10−6 | 2.4 × 10−6 | mol/m2 | 1.3 |
| 5.7 × 10−7 | 7.7 × 10−7 | mol/mg | ||
| Footprint for monolayer | ||||
| DI water | 0.24 | 0.16 | nm2 | 1.5 |
| DI water/EG mixture | 0.24 | 0.18 | nm2 | 1.3 |
| Solvent System | Solid loading (mg/mL) | Viscosity (Pa.s) | Density (kg/m3) | Surface Tension (N/m) | Z = 1/Oh |
|---|---|---|---|---|---|
| water | 5.47 | 8.53 × 10−4 | 1005 | 3.50 × 10−2 | 32.2 |
| water/ethylene glycol | 4.83 | 1.68 × 10−3 | 1044 | 3.27 × 10−2 | 16.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orrill, M.; Abele, D.; Wagner, M.J.; LeBlanc, S. Sterically Stabilized Multilayer Graphene Nanoshells for Inkjet Printed Resistors. Electron. Mater. 2021, 2, 394-412. https://doi.org/10.3390/electronicmat2030027
Orrill M, Abele D, Wagner MJ, LeBlanc S. Sterically Stabilized Multilayer Graphene Nanoshells for Inkjet Printed Resistors. Electronic Materials. 2021; 2(3):394-412. https://doi.org/10.3390/electronicmat2030027
Chicago/Turabian StyleOrrill, Michael, Dustin Abele, Michael J. Wagner, and Saniya LeBlanc. 2021. "Sterically Stabilized Multilayer Graphene Nanoshells for Inkjet Printed Resistors" Electronic Materials 2, no. 3: 394-412. https://doi.org/10.3390/electronicmat2030027
APA StyleOrrill, M., Abele, D., Wagner, M. J., & LeBlanc, S. (2021). Sterically Stabilized Multilayer Graphene Nanoshells for Inkjet Printed Resistors. Electronic Materials, 2(3), 394-412. https://doi.org/10.3390/electronicmat2030027





