Winding Numbers in Discrete Dynamics: From Circle Maps and Fractals to Chaotic Poincaré Sections

Abstract

Winding numbers are key indices in the depiction, modelling, and testing of dynamical processes. They capture phase progression on closed curves and are robust for quasiperiodic dynamics, but their status for chaotic Poincaré sections is unclear. This study tests whether any non-trivial winding-type index can be extracted from chaotic Poincaré maps using three approaches: (i) phase-angle analysis, (ii) Kabsch optimal-rotation estimation, and (iii) local turning-angle averaging. To benchmark feasibility and error, we compare four systems: the standard circle map, the same circle map embedded on two planar fractal curves (Koch snowflake and Hilbert curve), a quasiperiodic Duffing–van der Pol (DVP) Poincaré map, and a chaotic DVP Poincaré map. For the quasiperiodic map, all methods yield consistent, accurate winding numbers. For the transitional systems (circle map and its fractal embeddings), indices remain non-trivial but more deviated. In stark contrast, chaotic Poincaré maps produce only trivial indices across all methods. These results indicate a crucial fact about the modelling of chaotic Poincaré maps. That is, although being fractal, they are not merely chaotic maps on fractal curves; rather, they reflect a tighter coupling of geometry and dynamics. Practically, the recoverability of a non-trivial winding index offers a simple diagnostic to distinguish quasiperiodicity from chaos in Poincaré data or corresponding models. The constructed chaotic-map-on-fractal systems also act as test-bed models that bridge ideal one-dimensional mappings and realistic two-dimensional Poincaré sections.

1. Introduction

The Poincaré map of a three-dimensional chaotic system can be represented as a mapping on a two-dimensional plane. Such maps are classical tools for characterizing dynamical behaviours. Chaotic Poincaré maps are known to exhibit fractal geometries. However, the extent to which the dynamics on these fractal geometries contain regularities that can be mathematically described remains unclear [1,2,3,4]. In other words, it is not yet well-established whether some quantitative indices can be extracted that describe the dynamics, such as the winding behaviour, on such a fractal Poincaré attractor [5,6,7]. Investigating whether such a winding-type index can be meaningfully extracted from chaotic Poincaré maps would clarify the extent to which these maps exhibit hidden order.

The winding number is a powerful index used to characterize significant properties of dynamical systems and is widely applied in one-dimensional quasiperiodic and chaotic systems [8]. For the motion of a point along a closed curve, the winding number quantifies how the phase angle evolves with time/iteration along the curve. A typical application of the winding number appears in the analysis of phase locking and the devil’s staircase [9,10], both of which are essential for modelling the dynamical processes and their testing. Despite its success in one-dimensional contexts, it has rarely been applied to chaotic Poincaré maps, and its behaviour in such maps remains largely unexplored.

Nevertheless, chaotic motion can exhibit winding-like behaviour. It is widely accepted that chaotic systems are mixing. Specifically, when examining the motion of a set of Poincaré points under the system’s governing equation, it is observed that the point set stretches, folds, and winds around until it returns to a shape resembling the initial configuration [11,12,13]. Nevertheless, it remains an open question how such a combination of stretching, folding, and winding can be modelled. Therefore, it appears promising to extract indices that describe the winding behaviour of a point set under the Poincaré map. However, these intuitive observations require rigorous definitions and metrics. Thus, it is critical to develop a method that can compute a winding number from a Poincaré map.

This attempt faces several challenges. The most significant aspect is that the applicability of the winding number method depends heavily on certain topological properties of the examined geometry [8]. Specifically, the winding number is well defined only on a Jordan curve. However, there is no evidence that the chaotic Poincaré sections form Jordan curves. Even more basic properties, such as whether being perfect or dense, have not been established for chaotic Poincaré sections, although certain fractal sets are known to be Jordan curves [14,15] and perfect sets [16].

Another challenge lies in the fact that defining and computing the winding number requires a reference point placed within the interior of the curve of interest. Yet, there is no guarantee that a chaotic Poincaré map even has an interior. This problem has rarely been addressed, although many types of fractals have been shown or constructed to possess interiors [17].

An alternative to defining the winding number is to use the rotation number. Both of them are well-developed tools that are applied in the analysis of one-dimensional systems. The concepts are used interchangeably in many contexts, particularly in the study of orientation-preserving homeomorphism [18,19,20]. However, subtle differences exist. McSharry and Ruffino defined the two indices differently and discussed their distinctions [21]. Despite these nuances, in many cases, the two indices either represent the same quantity or yield the same value. Therefore, the rotation number is also used in this study as an alternative. A notable advantage of the rotation number is that it does not require a central reference point, which helps maintain generality.

Because a Poincaré map has a different dimensionality from a one-dimensional mapping, some special models are constructed to bridge the two. A chaotic one-dimensional mapping is redefined to iterate on artificially constructed fractal structures. These models resemble Poincaré maps in terms of spatial distribution and fractal properties. However, unlike chaotic Poincaré maps, they can be confidently regarded as having well-defined and known winding numbers.

With the aid of these artificially constructed chaotic mapping systems, this research investigates potential methods for computing the winding number of chaotic mappings and identifies any inherent differences between the two types of systems studied. Furthermore, when these methods are applied, any observed differences between quasiperiodic and chaotic Poincaré maps, whether in terms of numerical values or computational feasibility, can serve as criteria to distinguish quasiperiodicity from chaos. Additionally, certain topological features of chaotic Poincaré maps are illustrated.

2. Motivation

2.1. Regularity and Modelling of the Poincaré Map

In a differential dynamical system, the motion of Poincaré points in iterations can be either regular or irregular. The distinction between these two behaviours may indicate whether the system is chaotic. Figure 1 illustrates these differences in Duffing–van der Pol (DVP) systems. In the quasiperiodic case, the Poincaré points form a closed curve [22]. When a small number of these points are plotted sequentially, they wind around the curve with a consistent angle at each iteration. This regular angle increment can be described using a winding number, which reflects the ratio between two frequencies in the motion. This quantity has clear physical significance and is relatively easy to extract. With the help of such an index, the behaviour and dynamical process of a system on the Poincaré section can be readily modelled as a winding process on a curve.

In contrast, the Poincaré points of a chaotic system appear to move randomly at each iteration. It is difficult to identify any regularity in their distribution, density, motion pattern, or the geometry they form. Therefore, the accuracy and effectiveness of chaotic process modelling can be limited when the underlying governing equation is unknown. However, since chaos is not merely randomness but is thought to possess intricate structure, it is both challenging and potentially rewarding to investigate whether any index analogous to the winding number can be extracted from a chaotic Poincaré map. Such findings may help characterize the nature of chaos and quasiperiodicity or provide a way to quantify the complexity of chaotic motion. Moreover, such an index may be used to test the effectiveness of a model of a chaotic Poincaré map.

2.2. Review of the Winding Number

It is then necessary to review and extend the classic definition of winding number, especially from a dynamical perspective. Arnold first systematically studied the standard circle map:

$${\theta }_{i+1}={\theta }_i+\mathrm{\Omega }-{\displaystyle \frac{K}{2\pi }}\sin \left(2\pi {\theta }_i\right)$$

(1)

For $K$ values in [0, 1], the map only has periodic or quasiperiodic behaviours, and its winding number is defined as:

$$w=\underset{i\to \infty }{\lim }{\displaystyle \frac{{\theta }_i-{\theta }_0}{i}}$$

(2)

When the system is periodic, the winding number is rational, while for quasiperiodic, its winding number is irrational. With the winding number, the standard circle map can be modelled with its topological conjugate, namely, the rotation map. With the increase of $K$, chaotic behaviour emerges, but it does not stop the calculation of a well-defined winding value. This fact suggests the possibility of extracting the winding number from chaotic maps, even those as complicated as the Poincaré maps of differential systems.

Another similar but distinct definition of winding number is the number of times a closed curve winds around a center point, as shown in Figure 2. The curve winds about the red center point for two revolutions, and one revolution about the green one. Now consider a mapping on the curve that takes four iterations to return to its initial point; it is justifiable to define such a mapping to hold a winding number of 0.5 around the red center point. This is the desirable winding number that is to be extracted in this study.

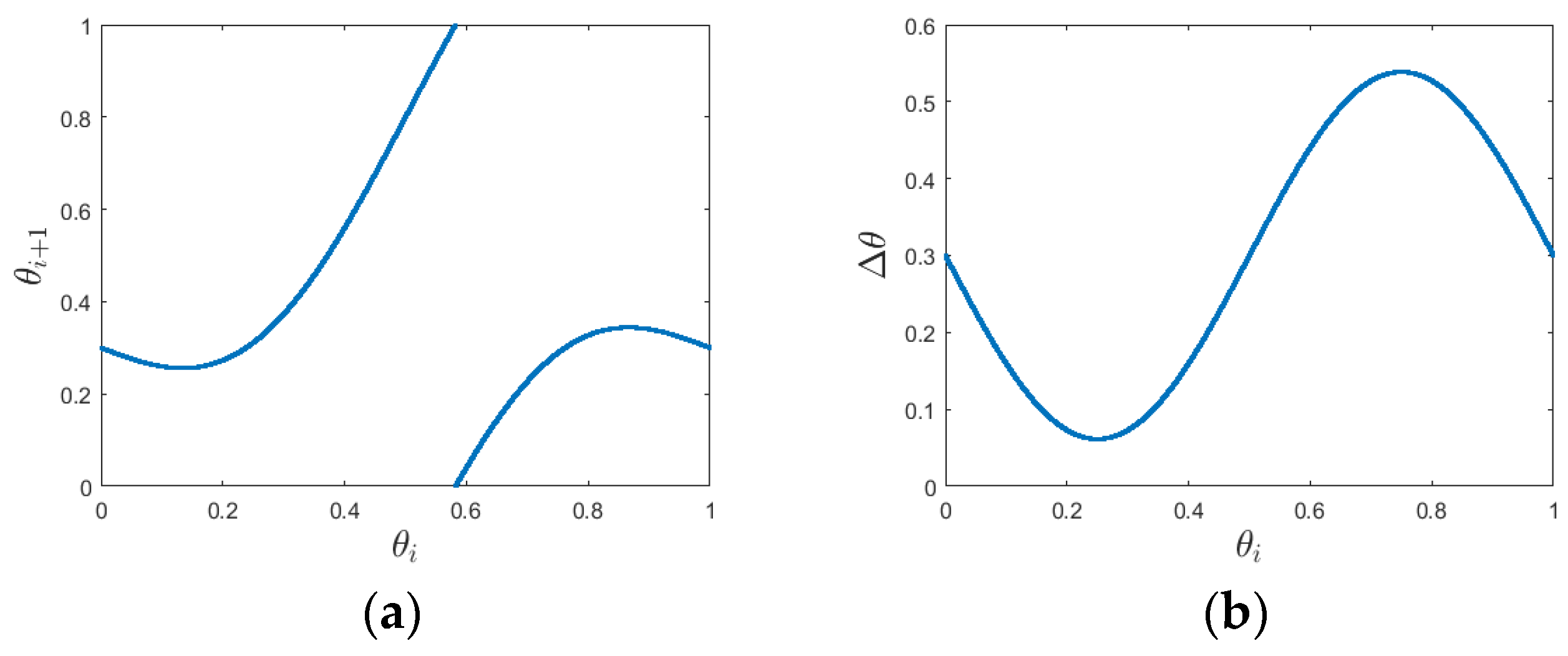
3. Model Systems Analyzed

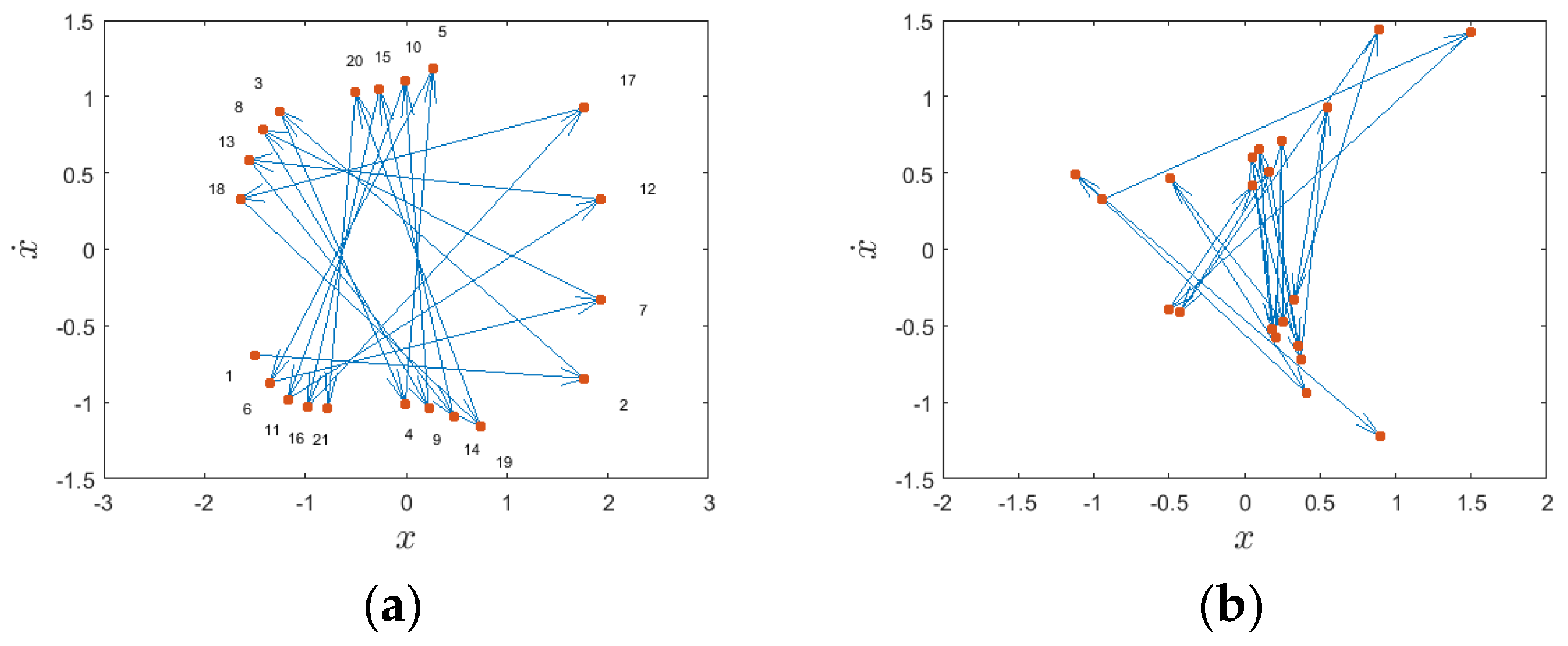
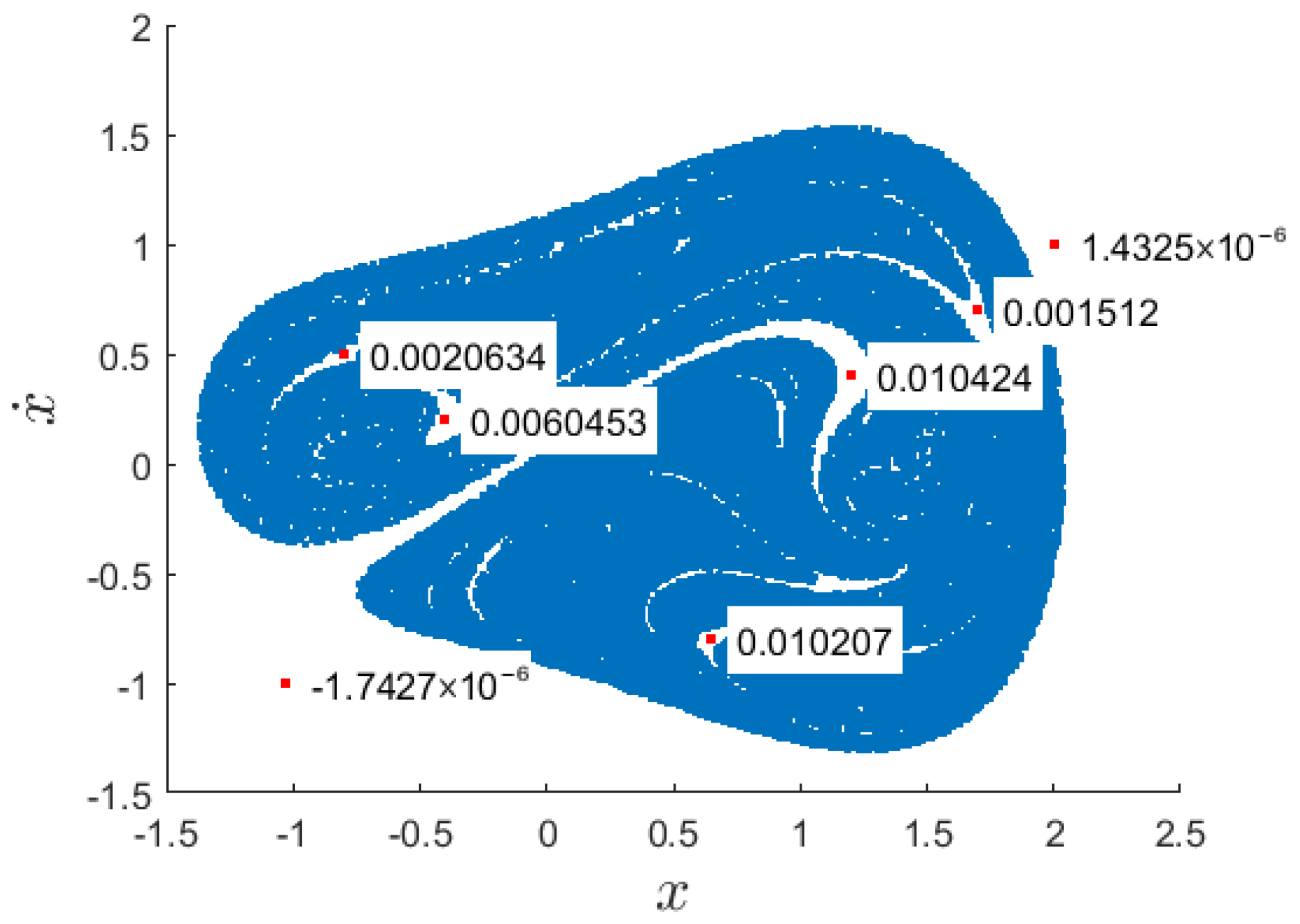
3.1. Poincaré Maps

DVP systems are used to generate examples of chaotic and quasiperiodic Poincaré maps, as has been shown in Figure 1. Depending on the parameter values, this system can exhibit periodic, quasiperiodic, or chaotic attractors [23,24], therefore widely used in modelling and as a benchmark.

$$\ddot{x}-\mu \left(1-x^2\right)\dot{x}+\alpha x+\beta x^3=f\cos \omega t$$

(3)

To maintain consistency with existing studies, the same parameter set $\alpha =-0.5$, $\beta =0.5$, $\mu =0.1$ is used. The system has a double-well potential and exhibits a large orbit motion. Illustrations of the system’s behaviours can be found in the literature [22,23].

3.2. Chaotic Map on Fractals

As mentioned in the introduction, due to the complexity of this task, it is necessary to design model systems that are neither too simple, such as low-dimensional systems with well-defined topology like the standard circle map or logistic map [25], nor too complex and topologically ambiguous like the chaotic Poincaré map. The ideal models should be embedded in two-dimensional space, possess well-defined and easily computable winding numbers, and exhibit useful topological features.

Here, the desired models are constructed in two steps. First, a bijection is established from the interval [0, 1) to a fractal curve. Then, the standard circle map is used to define the iteration of points along this fractal curve. Two types of regular fractals are used: the Koch snowflake and the Hilbert curve. For each real number in [0, 1), there exists one and only one corresponding point on the fractal. In this way, the point sequences iterate with a well-defined winding number along curves with desirable topological properties embedded in the two-dimensional plane. These models should share the same winding number as the underlying standard circle map, and this value serves to validate the results obtained by the proposed methods. It is worth noting that since the Hilbert curve is not closed, two mirrored copies are used to form a closed curve. By constructing these models, chaotic maps are created that lie “in between” the very simple and regular standard circle map and the complex, difficult-to-analyze chaotic Poincaré map. Figure 3 shows the point distributions of the designed models. For the snowflake, the distribution appears relatively regular. However, for the Hilbert curve, the points are dense in the second quadrant ($x<0$, $y>0$) and sparse in the others. This asymmetry arises from the uneven distribution caused by the standard circle map, as illustrated in Figure 4.

The two constructed models exhibit discrepancies, in addition to the visual one. The Koch snowflake is a Jordan curve with a well-defined interior. In contrast, the Hilbert curve has an empty interior and thus is not a rigorous Jordan curve. Additionally, the Koch snowflake has a fractal dimension of $\ln (4)/\ln (3)$, while the Hilbert curve has a dimension of 2, which is even larger than that of any two-dimensional Poincaré point set. A third difference is that the mapping from [0, 1) to the snowflake preserves continuity, whereas the mapping to the Hilbert curve does not. In this respect, the Hilbert curve system is more similar to chaotic Poincaré maps.

Due to these differences, the Koch snowflake is expected to be easier to analyze, and the winding number computed from it is expected to be more accurate, closer to that of the underlying standard circle map. Figure 5 illustrates how points wind as iterated by these models. The motion on the Koch snowflake remains relatively regular and somewhat predictable, whereas the motion on the Hilbert curve appears random and unpredictable.

3.3. Hypotheses

Based on the discussion above, it can be proposed as a hypothesis that a chaotic circle map on a fractal curve will retain a detectable winding-type index, although the geometric complexity affects the accuracy of extraction. In contrast, a chaotic Poincaré map will not yield a consistent non-trivial winding-type index, regardless of the method used.

4. Methodology and Results

This section presents and evaluates three distinct approaches for computing the winding number in discrete dynamical systems. In the context of one-dimensional mappings, particularly the standard circle map, the terms “winding number” and “rotation number” are frequently used interchangeably. While previous studies have proposed distinctions between the two, these definitions remain context-dependent and often reflect individual methodological preferences. In the present work, the two terms are treated as equivalent in value, insofar as they pertain to the conventional application of winding metrics to two-dimensional mappings. Accordingly, the methods explored here either directly implement the classical definition of the winding number or examine the rotational transformation between point configurations before and after mapping. As demonstrated in the subsequent analysis, this treatment proves practically justified across a range of systems.

4.1. Phase Angle Analysis

Among the methods examined, reducing each point to its associated phase angle represents the most intuitive approach to estimating the winding number in two-dimensional mappings. For a given point $\left(x_i,y_i\right)$ in the sequence, its position relative to a fixed reference point $\left(x_c,y_c\right)$ can be expressed as $\left(x_i-x_c,y_i-y_c\right)$, and the phase angle can be computed as:

$${\theta }_i={\displaystyle \frac{\mathrm{atan}2\left(y_i-y_c,x_i-x_c\right)}{2\pi }}$$

(4)

Such phase angles are illustrated in Figure 6a. For quasiperiodic systems, despite the choice of the center, the relationship between ${\theta }_i$ and $i$ shows a certain level of regularity, as shown in Figure 6b. Now, recall the definition of the winding number in Equation (2), and rewrite it as:

$$w=\underset{i\to \infty }{\lim }{\displaystyle \frac{{\theta }_i-{\theta }_0}{i}}=\underset{i\to \infty }{\lim }{\displaystyle \frac{{\theta }_{i+1}-{\theta }_1}{i}}=\underset{i\to \infty }{\lim }{\displaystyle \frac{1}{i}}{\displaystyle \sum _i{\theta }_{i+1}-{\theta }_i=}\underset{i\to \infty }{\lim }{\displaystyle \frac{1}{i}}{\displaystyle \sum _i\mathrm{\Delta }{\theta }_i}=\underset{i\to \infty }{\lim }〈\mathrm{\Delta }{\theta }_i〉$$

(5)

In this way, the calculation of the winding number becomes the calculation of the average phase angle increment $\mathrm{\Delta }{\theta }_i={\theta }_{i+1}-{\theta }_i$. Therefore, by plotting $\mathrm{\Delta }{\theta }_i$ vs. $i$, the value of $〈\mathrm{\Delta }{\theta }_i〉$ can be estimated, as shown in Figure 6c. Despite the vague regularity in Figure 6b,c, the relationship between $\mathrm{\Delta }{\theta }_i$ and ${\theta }_i$ can be clear and simple, as shown in Figure 6d,e. For this quasiperiodic DVP system ($f=0.1$, $\omega =0.5$), the relationship exhibits strong regularity, yielding a winding number of 0.4057. This is consistent with the regularity mentioned in the motivation section.

For the standard circle map, this ${\theta }_{i+1}$ vs. ${\theta }_i$ relation is highly structured, as illustrated in Figure 7. Although not directly continuous, continuity can be restored in the plot by adjusting the second segment of the curve by adding 1 or by plotting $\mathrm{\Delta }{\theta }_i$ vs. ${\theta }_i$. Calculated as $w=〈\mathrm{\Delta }\theta 〉$, the computed winding number is 0.2289 in the example shown.

While the method is straightforward in systems with well-behaved geometries, it suffers from a key limitation: the accuracy of the result depends on the ability to consistently “unwrap” phase angle discontinuities. Determining whether a given angle ${\theta }_i$ should be treated as ${\theta }_i+k$, where $k$ is an integer indicating the number of revolutions per iteration, introduces a degree of ambiguity that may reduce the method’s robustness in more complex systems.

For the standard circle map transformed onto the Koch snowflake, a similar procedure is employed, using the geometric center of the snowflake as the reference point. The resulting relations are presented in Figure 8. Although these curves deviate in form from that of the one-dimensional standard circle map, they still exhibit a clear and regular structure. Notably, the same winding number of 0.2289 is recovered, confirming the method’s consistency under geometric transformation onto the snowflake.

In contrast, the obtained relations become less deterministic for the standard circle map transformed onto the Hilbert curve. As shown in Figure 9, the mapping produces bands rather than well-defined curves, indicating that the corresponding ${\theta }_{i+1}$ values span a range with non-negligible variance for a given angle value ${\theta }_i$. This lack of functional determinism introduces uncertainty and necessitates manual adjustment, making the process less automatable. Additionally, the presence of negative phase increments further complicates the analysis. Nonetheless, by leveraging underlying geometric regularity, a winding number of 0.2289 is still obtainable, albeit with more effort and reduced clarity.

However, for the chaotic DVP system ($f=0.2$, $\omega =0.5$), illustrated in Figure 10, no reference point produces a manageable or interpretable relation between ${\theta }_i$ and ${\theta }_{i+1}$. Regardless of the chosen center, the resulting plot does not form a band but rather a complex, area-filling structure, with potential fractal nature. In such cases, the computed winding number becomes trivial (0.0104 or 0.0015, respectively), indicating the method’s failure to extract meaningful winding information.

Figure 11 presents winding number estimates obtained by applying the same analysis using different reference points to demonstrate this limitation further. None of the results are significant or non-trivial, reinforcing the conclusion that the method is inadequate for chaotic Poincaré maps.

Note that the ${\theta }_{i+1}$ vs. ${\theta }_i$ relationship obtained in the process also has modelling significance. If both the ${\theta }_{i+1}$ vs. ${\theta }_i$ relationship and the relationship of corresponding distance to the center point can be described, then the dynamical process is accordingly modelled.

4.2. Kabsch Algorithm

As demonstrated in the previous subsection, the phase angle increment often exhibits bounded variation. This observation motivates the use of the Kabsch algorithm, which extracts the dominant rotational component of a geometric transformation.

The Kabsch algorithm identifies the optimal rotation matrix that minimizes the root mean square deviation between two sets of points under a rigid rotation. Formally, consider two corresponding point sets $P$ and $Q$, representing positions before and after iteration, respectively. The algorithm computes the rotation matrix $R$:

$$H=P^{T}Q$$

(6)

$$R={(H^{T}H)}^{1/2}{H}^{-1}$$

(7)

The optimal rotation angle can then be extracted from the matrix by:

$${\theta }_{opt}={\cos }^{-1}\left(R_{11}\right)$$

(8)

where $R_{11}$ indicates the first element of the matrix $R$. The normalized angle ${\theta }_{opt}/2\pi$ serves as an estimate of the winding number induced by a single iteration of the map. It is important to note that the two sets $P$ and $Q$ produce exactly the same plot, namely, the Poincaré attractor, as:

$${\left\{\begin{array}{c}P=\left[\begin{array}{ccccc}{x}_1& x_2& x_3& \dots & x_{n-1}\\ y_1& y_2& y_3& \dots & y_{n-1}\end{array}\right]\hfill \\ Q={\left[\begin{array}{ccccc}{x}_2& x_3& x_4& \dots & x_n\\ y_2& y_3& y_4& \dots & y_n\end{array}\right]}^T\hfill \end{array}\right.}^T$$

(9)

When applying this method to the Koch snowflake and the Hilbert curve, Figure 12 shows that although the point set after the rotation defined by the extracted angle does not overlap with the initial set, the optimal angle still provides an estimate of the winding number, albeit with limited accuracy. This suggests that the results are non-trivial and may reflect the rotational characteristics of the mapping. Also, $Q$ is not necessarily chosen as the image of $P$ after a single iteration. When the mapping is applied twice, the rotation angle should be divided by two to estimate the winding number. The values computed from different iteration counts are listed in

Table 1. Winding numbers computed using the Kabsch algorithm for different systems.

Iteration Count	Circle Map	Koch Snowflake	Hilbert Curve	Quasiperiodic Poincaré Map	Chaotic Poincaré Map
1	0.2089	0.2159	0.1803	0.4056	0.0024
2	0.2253	0.2131	0.2062	0.0963	0.0258
3	0.0822	0.0847	0.0773	0.0734	0.0028
4	0.0125	0.0107	0.0061	0.0942	0.0100

.

Interestingly, for some systems, applying the mapping twice yields the most accurate estimate of the winding number. However, it is unsurprising that with too many iterations, the estimated winding number gradually converges to 0, as the rotation from $P$ to $Q$ may exceed a revolution, making it difficult to interpret.

However, when the same method is applied to the chaotic Poincaré map, the outcome is remarkably different. The estimated winding number remains trivial regardless of the iteration count, yielding a result that reflects statistical insignificance, as shown in Figure 13.

4.3. Turning Angle Analysis

The third method involves computing the turning angles formed by each three consecutive points in the point sequence. Namely, for points $(x_i,y_i)$, $(x_{i+1},y_{i+1})$, $(x_{i+2},y_{i+2})$, the normalized turning angle is:

$${\theta }_i=\mathrm{atan}2\left(y_{i+2}-y_{i+1},x_{i+2}-x_{i+1}\right)-\mathrm{atan}2\left(y_{i+1}-y_i,x_{i+1}-x_i\right)$$

(10)

$${\theta }_{norm,i}={\displaystyle \frac{{\theta }_i}{2\pi }}-⌊{\displaystyle \frac{{\theta }_i}{2\pi }}⌋$$

(11)

The winding number is then estimated as $\underset{i\to \infty }{\lim }〈{\theta }_{norm,i}〉$. This method relies on the classical geometric result that the sum of external angles of any polygon is always 2π, regardless of its shape.

Figure 14 shows the effect of using the method on the quasiperiodic DVP system. Due to the regularity of the Poincaré map, the normalized turning angle fluctuates in a very narrow range (0.38, 0.43), making the results clear and robust, yielding an accurate winding number of 0.4057.

For the Koch snowflake and the Hilbert curve, it still produces non-trivial results of 0.2289 and 0.1828, respectively. In the case of the snowflake, the winding number obtained via exterior angles closely matches the analytical value. However, for the Hilbert curve, the result significantly deviates by 25% from the analytical value. This discrepancy indicates that the method is unreliable for complex geometries. The special distributions of the normalized angles are shown in Figure 15 and appear to be continuous functions of the coordinates.

When applied to chaotic Poincaré maps, the result remains relatively close to zero (0.0805), suggesting that it is still trivial and incapable of capturing the winding nature of such a geometry.

Moreover, Figure 16 shows that both the regions with positive and negative exterior angles exhibit fractal structures. These regions intertwine, making it difficult to predict the precise exterior angles within any specific small area of the graph, regardless of the resolution.

The turning angles analysis also has modelling significance, as the Poincaré map can be modelled as a point turning and then moving for a certain distance in its direction. Recall that the L-system, the classic fractal-generating algorithm, also adopts turning and moving along a direction as its commonly used elements. This implies the possibility of generating chaotic Poincaré map-like systems through L-system-like processes.

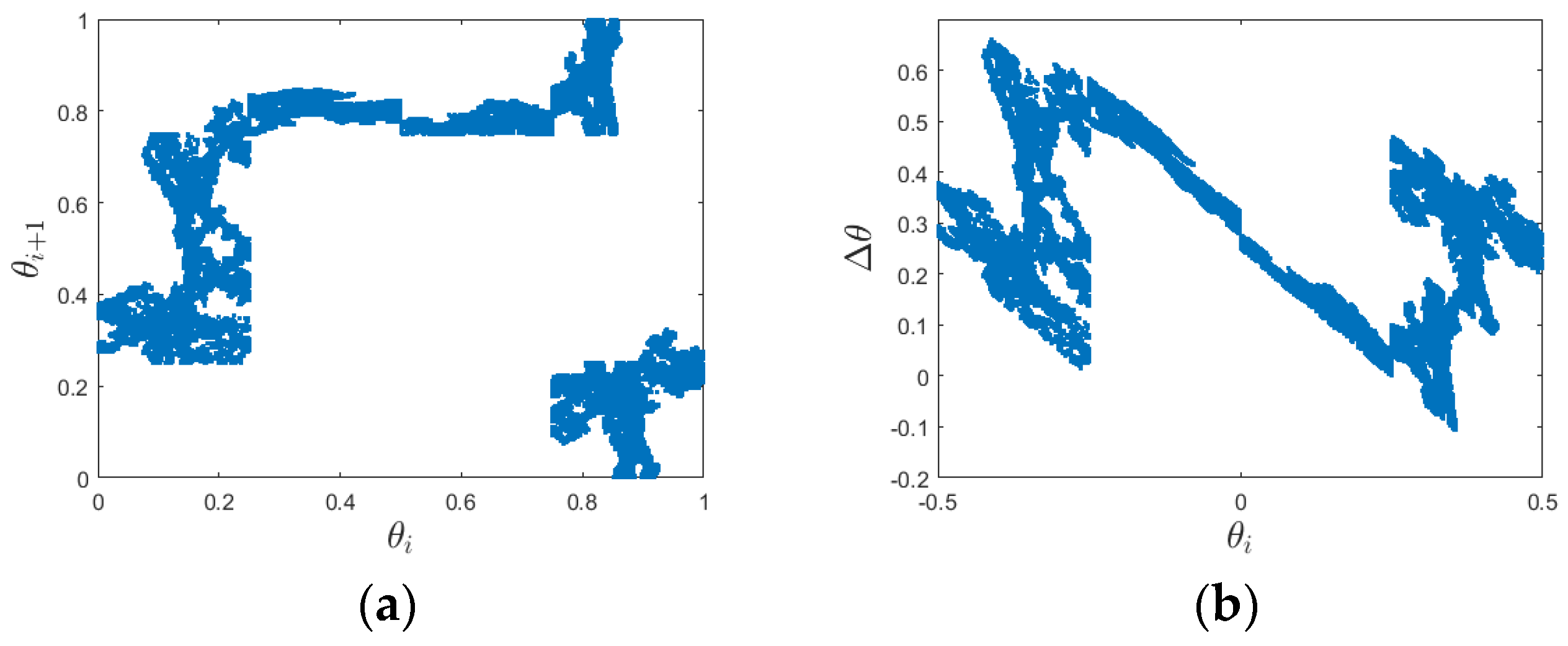
5. Discussion

All the results from the previous section are summarized in

Table 2. Winding numbers computed by different methods across various systems.

Methods	Circle Map	Koch Snowflake	Hilbert Curve	Quasiperiodic Poincaré Map	Chaotic Poincaré Map
Phase angle	0.2289	0.2289	0.2289	0.4057	0.0104
Kabsch	0.2089	0.2159	0.1803	0.4056	0.0024
Turning angle	0.2292	0.2289	0.1828	0.4057	0.0805

. The differences between systems and methods are readily apparent, and several possible explanations exist for these discrepancies.

The inaccuracy of the Kabsch method is easily explained: it analyzes the point set as a whole, whereas the other methods evaluate each point individually. Additionally, because the method aligns one point set to another via rotation, the norm of each column vector in the matrices can influence the result.

It is also understandable why the quasiperiodic Poincaré map yields the most consistent results across all methods. As the only non-chaotic system, it exhibits the most regular geometry and dynamics. Since it is topologically conjugate to a rotation, methods that capture winding behaviour in point sets are particularly well-suited for its analysis.

Among the chaotic-circle-map-based systems, the 1D circle map and the Koch snowflake yield relatively accurate results, whereas the Hilbert curve results show greater error. The differences between these systems, as previously discussed, stem from their distinct fractal dimensions and topological properties.

For the chaotic Poincaré map, no method proves effective in quantifying its winding behaviour. All the results are trivial and lack physical significance. This suggests that such systems either lack a non-trivial winding number or possess one that is too difficult to extract using the proposed methods. In either case, this result may still serve as a useful indicator for characterizing chaos. For a non-periodic Poincaré map, the presence of a reliable, non-trivial winding number indicates quasiperiodicity; its absence suggests chaos.

Another observation from the results is that the chaotic Poincaré map, albeit being both fractal and chaotic, is more complex than a chaotic map defined on a fractal. In other words, the chaotic dynamics and the fractal geometry are tightly coupled and cannot be easily separated. This insight eliminates some futile attempts at chaos modelling.

The results also highlight the role of folding in chaotic mapping systems. The relative ease and accuracy of computing the winding number on the Koch snowflake are largely due to its minimal folding compared to the Hilbert curve. Folding, widely regarded as a key contributor to the mixing behaviour of chaotic systems, is difficult to quantify and may be inseparable from winding and stretching effects.

The results also inspire approaches for quantifying the complexity of mapping systems, for example, by measuring the area of the ${\theta }_{i+1}$ vs. ${\theta }_i$ plots. Notably, even though the Hilbert curve has a higher fractal dimension, its ${\theta }_{i+1}$ vs. ${\theta }_i$ plot covers a smaller area than that of the chaotic Poincaré map. Additional indices may be extracted from Figure 15 and Figure 16 to describe the complexity of these plots. Generally, greater plot complexity implies greater complexity in the mapping system.

Although the standard circle map is a typical 1D chaotic map with a known winding number, other 1D chaotic maps may have winding numbers that are difficult to define. An example is:

$$x_{i+1}=10x_i\left(\mathrm{mod}1\right)$$

(12)

This map is extremely simple, yet its winding number is already difficult to define.

6. Conclusions

This research is inspired by the regular winding behaviour observed in quasiperiodic Poincaré maps and shows that no non-trivial winding-type index exists for chaotic Poincaré maps under the tested metrics. Three methods are proposed to quantify such regularity and to distinguish between chaotic and quasiperiodic Poincaré maps. The 1D standard circle map and its embeddings on two fractals serve as transitional systems between different types of Poincaré maps. For the quasiperiodic system, the results are highly consistent and accurate. For the constructed systems, the obtained winding numbers are less consistent and less precise. For the chaotic Poincaré map, all results are trivial. The key conclusions are summarized below:

• The quasiperiodic Poincaré map can be modelled as a winding mapping, and all proposed methods yield highly accurate winding numbers for it.
• For the transitional test-bed models (1D circle map, circle map on the Koch snowflake, circle map on the Hilbert curve), the methods produce non-trivial winding numbers that reflect the underlying winding dynamics.
• Among the chaotic transition systems, the 1D circle map allows for easy and accurate evaluation of the winding number, while the Hilbert curve is the most challenging, exhibiting the largest error.
• Among the three proposed methods, phase angle analysis provides the most accurate estimates of the winding number for the transitional systems, while the Kabsch method yields the least accurate results.
• None of the methods can extract a non-trivial winding number from chaotic Poincaré maps. This outcome highlights some differences between the Poincaré maps of distinct dynamical behaviours. Moreover, certain methods reveal intriguing features of the chaotic Poincaré map. In phase angle analysis, the relationship between ${\theta }_i$ and ${\theta }_{i+1}$ appears complex and potentially fractal. In turning angle analysis, the turning angles themselves form a fractal pattern, with rapid local fluctuations.
• The methods can be used to test the models of chaotic Poincaré maps. Even if a model reproduces the apparent unpredictability and fractal geometry of a chaotic Poincaré map, a non-trivial winding number would indicate that it still fails to capture the true winding properties of the Poincaré map.