ANN-Based Prediction of Tartrazine Adsorption on Chitosan–Polyvinyl Alcohol Hydrogel Beads: A Comparison with Kinetic Models

Abstract

The release of industrial wastewater containing synthetic dyes poses a major environmental issue because of their toxicity and persistence. Among treatment options, natural materials, specifically chitosan–polyvinyl alcohol (chitosan–PVA) hydrogel, have shown high effectiveness in dye removal due to their abundant functional groups and proven adsorption capacity. However, optimizing these systems experimentally is often time-consuming and requires many resources. This study introduces an artificial neural network (ANN) model to predict the adsorption capacity ($q_e$) and the time needed to reach equilibrium during the removal of tartrazine dye using chitosan–PVA hydrogel beads of different mean sizes, categorized as small, medium and large (2.1, 2.5, and 3.2 mm, respectively) at temperatures of 10, 30, and 50 °C The ANN model was compared with traditional kinetic models: pseudo-first-order, pseudo-second-order, and Elovich. Results showed that the ANN outperformed conventional models in predicting $q_e$ and equilibrium time, especially for small beads at 10 °C, where it predicted $q_e$ = 945 mg/g in 40 h with an $R^2$ of $0.9428$. Across all conditions, the ANN achieved strong correlation coefficients ($R^2>0.94$) and significantly shortened prediction times. Although the pseudo-second-order model achieved high $R^2$ values (up to $0.9929$), it took over 72 h to reach equilibrium prediction. These results demonstrate that ANN-based modeling can reduce experimental effort by up to 50% in prediction time while maintaining high predictive accuracy ($R^2>0.94$), offering a sustainable and efficient approach for designing wastewater treatment processes.

1. Introduction

The discharge of industrial wastewater into aquatic environments is a significant global environmental issue because of the presence of persistent and toxic pollutants, including synthetic dyes [1,2]. These compounds can negatively impact aquatic ecosystems and human health, even at low levels. Different treatment methods have been developed to reduce this impact, such as adsorption, photodegradation, ozonation, membrane filtration, and reverse osmosis [3,4]. Among these, adsorption is notable for its high efficiency, simplicity, and affordability in removing contaminants like dyes, heavy metals, and organic pollutants [5].

Natural adsorbents such as agricultural residues, clays, and biopolymers like chitosan are increasingly favored for their sustainability, biodegradability, and low toxicity [1,5]. Chitosan, derived from chitin, has demonstrated excellent performance in dye removal because of its abundant amino and hydroxyl functional groups, which enable electrostatic interactions with anionic dyes like tartrazine [6]. For example, it has been reported to achieve up to 584 mg/g for the removal of tartrazine using a chitosan/polyaniline composite [7]. However, optimizing adsorption processes through experiments often takes a lot of time and resources, which limits quick process development [8]. In this sense, computational modeling has become a useful tool for predicting system behavior and decreasing experimental workload.

Artificial neural networks (ANNs) have attracted attention for their ability to model complex, nonlinear relationships without requiring explicit physical equations. Unlike traditional kinetic models (e.g., pseudo-first-order, pseudo-second-order or Langmuir and Freundlich isotherms), which depend on simplified assumptions, ANNs can incorporate multiple variables, including pH, temperature, contact time, initial concentration, and adsorbent dose, to deliver accurate predictions [3].

Several studies have successfully utilized ANNs in adsorption processes. Pauletto et al. [9] developed an ANN for multicomponent adsorption, enhancing prediction accuracy in complex systems. Avci et al. [10] employed multilayer perceptron (MLP) and convolutional neural networks (CNNs) to model dye adsorption on carbonaceous materials, achieving ($R^2>0.95$) and low mean square errors. Alardhi et al. [11] showed high agreement between ANN predictions and experimental data for dye adsorption on natural materials. Al-Hameed et al. [12] combined response surface methodology (RSM) with ANN to optimize dye removal (Yellow 105) using an adsorbent based on Zeolitic Imidazolate Framework-67 modified with ${\mathrm{Fe}}_3{\mathrm{O}}_4$ nanoparticles, reaching ($R^2>0.96$). Similarly, Karam et al. [5] demonstrated the effectiveness of ANN in comparing adsorbents for textile dye removal, with efficiencies approaching 100%, and determination coefficients higher than $0.90$. Additionally, da Silva et al. [13] emphasized the potential of ANNs to reduce experimental trials and support sustainable process design.

In this context, this study presents an ANN model to predict the adsorption of tartrazine (FD&C Yellow No. 5) using chitosan–polyvinyl alcohol (chitosan–PVA) hydrogel beads. The model aims to estimate both the equilibrium adsorption capacity ($q_e$) and the time needed to reach equilibrium under different conditions (bead size and temperature). This approach reduces dependence on extensive experimentation and promotes more sustainable, efficient wastewater treatment design.

2. Treatment Methods for Dye Removal

Synthetic dyes are widely used in various industries, including textiles, food, paper, and cosmetics. Tartrazine (Yellow No. 5), a water-soluble azo dye, is commonly used in food products due to its bright yellow color, stability, and low cost [14]. However, its release into wastewater poses environmental risks due to its toxicity, persistence, and resistance to biodegradation [15].

Various methods for dye removal include (a) physical approaches (adsorption, filtration), (b) chemical processes (advanced oxidation, coagulation), and (c) biological methods (microbial degradation) [16]. Among these, adsorption is regarded as one of the most effective and affordable techniques, particularly when utilizing natural, renewable adsorbents like chitosan–PVA hydrogel.

Adsorption is a process where solute molecules, such as dyes, adhere to the surface of a solid adsorbent. This technique is highly effective for removing dissolved contaminants from water because of the adsorbents’ high capacity and versatility [17]. The process’s effectiveness depends on factors like the type of adsorbent, contaminant concentration, pH, temperature, and contact time [18,19].

Chitosan is a biodegradable, non-toxic biopolymer derived from chitin, found in crustacean shells. Its amino groups enable strong electrostatic interactions with anionic dyes, making it highly effective for tartrazine removal [6,7].

Adsorption Kinetic Models

Understanding and optimizing the adsorption process involves analyzing kinetics, which explains how quickly adsorption happens. Kinetic models describe how the contaminant concentration changes over time and help predict system behavior [6].

There are three key adsorption kinetic models commonly used to describe the adsorption process: (1) the Lagergren model, in Equation (1), also known as the pseudo-first-order model, assumes the rate of occupation of adsorption sites is proportional to the number of unoccupied sites [20]; (2) the Ho and McKay model described by Equation (2), or pseudo-second-order model, considers that the adsorption rate depends on the square of the number of unoccupied sites, often providing a better fit for chemisorption processes [21]; and (3) the Elovich model, in Equation (3), is often used for systems with heterogeneous surfaces and describes adsorption kinetics over a wide range of times, considering the complexity of the adsorption process [22]. These models are fitted to experimental data to estimate kinetic parameters and assess mechanism suitability.

$$q_t=q_e\left(1-e^{-k_{1}t}\right)$$

(1)

$$q_t={\displaystyle \frac{k_2{q}_e^{2}t}{1+k_2{q}_{e}t}}$$

(2)

$$q_t={\displaystyle \frac{1}{\beta }}ln\left(\alpha \beta \right)+{\displaystyle \frac{1}{\beta }}ln\left(t\right)$$

(3)

where

• $q_t$: adsorption capacity at time t (mg/g). It represents the amount of adsorbate adsorbed over time.
• $q_e$: equilibrium adsorption capacity (mg/g).
• $k_1$: pseudo-first-order rate constant (1/time).
• $k_2$: pseudo-second-order rate constant (g/mg·time).
• $\alpha$: initial adsorption rate (mg/g·time).
• $\beta$: desorption constant related to surface coverage (1/time).
• t: contact time.

3. Artificial Neural Networks

ANNs are computational models inspired by biological neural systems. They learn complex input–output relationships from data [23], making them ideal for modeling nonlinear processes like adsorption.

MLP is one of the most widely used architectures of artificial neural networks (see Figure 1). It is composed of an input layer that receives the variables, one or more hidden layers that transform the inputs through activation functions (e.g., sigmoid, ReLU), and an output layer that generates the predictions. The training process is carried out using backpropagation, where the weights are iteratively updated to minimize the prediction error [24,25].

An MLP employs the backpropagation algorithm to iteratively update its weights through forward and backward passes, enabling the capture of complex, nonlinear relationships between variables [25]. This capability makes MLPs particularly effective for modeling systems influenced by multiple interacting factors [24].

In adsorption studies, ANNs have proven effective in predicting behavior under diverse conditions without relying on simplified physical assumptions [26]. Their universal approximation capability makes them particularly suitable when traditional models fail to capture system complexity.

4. Methodology

This section is structured into four main stages to provide a comprehensive understanding of the proposed approach: (1) data collection, (2) application of traditional kinetic models, (3) development of an MLP model, and finally, (4) training and validation of the MLP.

4.1. Dataset

In the first stage, a dataset of 297 experimental points was compiled. Each experiment involved mixing a fixed volume of tartrazine solution with chitosan–PVA hydrogel beads classified into three groups based on their size, as exhibited in

Table 1. Size characterization of chitosan–PVA hydrogel beads used in the adsorption experiments.

Bead Identification	Diameter Range (mm)	Mean Diameter (mm)
Small	2.00–2.20	2.1
Medium	2.35–2.57	2.5
Large	3.10–3.45	3.2

. Testing temperatures of 10, 30, and 50 °C were used. The experiments were conducted under continuous agitation using a Heidolph Unimax 1010 refrigerated orbital shaker, which ensured temperature control and uniform mixing at 150 rpm. Samples were collected at intervals of 0.5, 1, 4, 8, 16, 24, 32, 40, 48, 63, and 72 h. Adsorption capacity ($q_t$) was measured in mg dye per gram of adsorbent. Prior to the experiments, the chitosan–PVA hydrogel beads were stored under refrigeration (at approximately 4 °C) to preserve their structural integrity.

While this study focuses on the predictive modeling of adsorption kinetics, it is essential to note that a detailed characterization of the surface morphology, specific surface area, and internal structure of the chitosan–polyvinyl alcohol hydrogel beads was not performed.

The primary objective of this work is to develop and evaluate an artificial neural network model for predicting equilibrium adsorption capacity and time to equilibrium based on experimental kinetic data. Our analysis centers on the influence of macroscopic parameters, specifically bead size and temperature, on adsorption performance, rather than on the physicochemical properties of the adsorbent material itself.

4.2. Kinetic Models Fitting

The second stage focuses on the utilization of the three above-mentioned traditional kinetic models, pseudo-first-order (Equation (1)), pseudo-second-order (Equation (2)), and Elovich (Equation (3)), which were fitted to the experimental data using nonlinear regression [27]. The equilibrium adsorption capacity, $q_e$ was determined to assess their predictive performance.These models serve as a baseline for comparison with the artificial neural network model.

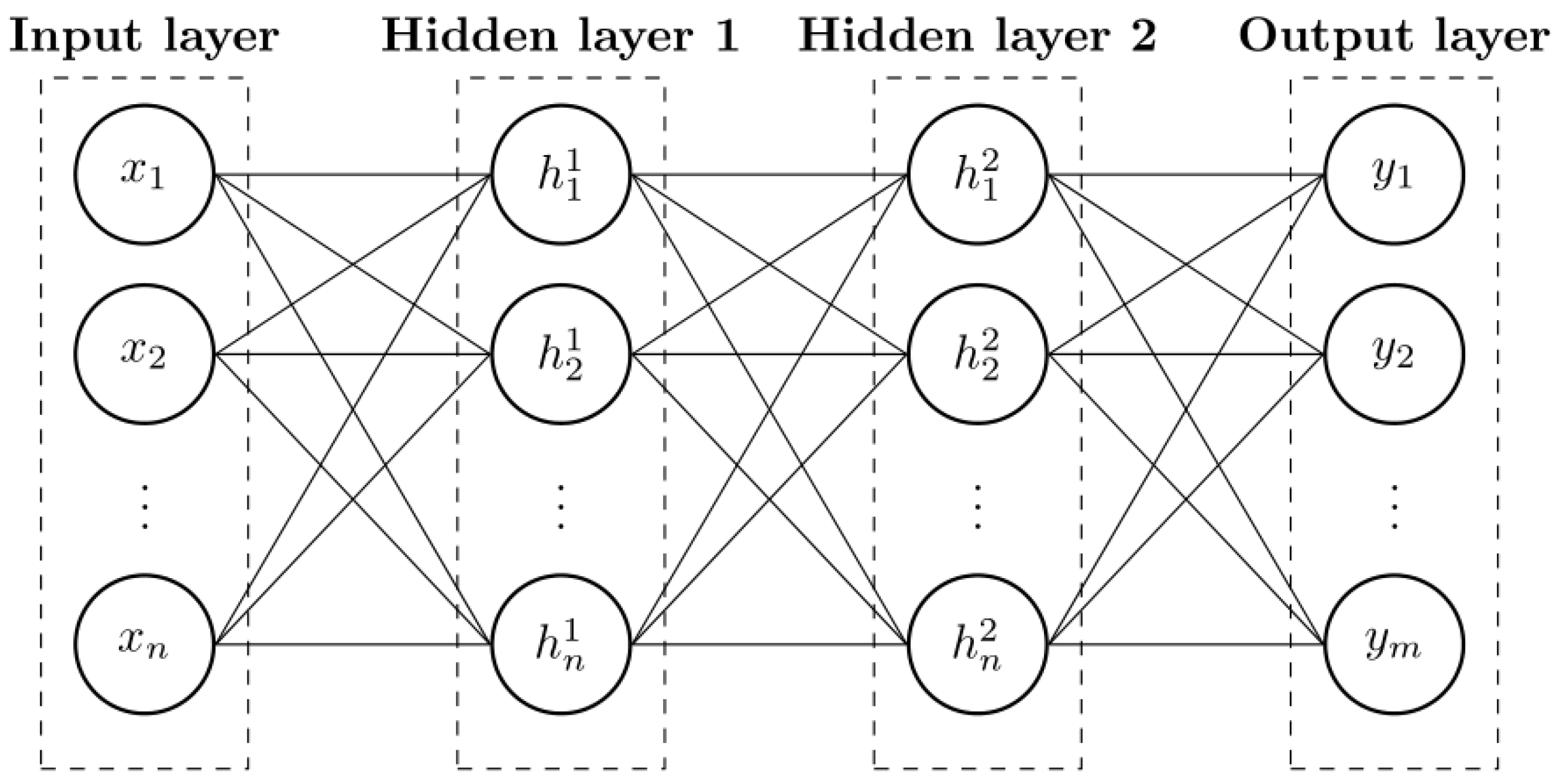
4.3. ANN Design

The third stage addresses the ANN modeling, with the MLP architecture. Considering the experimental data characteristics of the specifically acquired dataset, two variables were selected as inputs: time (t, measured in h), representing the different sampling points, and the adsorbate removal ($q_t$) at time t. On the other hand, the equilibrium adsorption capacity ($q_e$) was assigned as the output variable.

An MLP with two hidden layers was developed to represent the adsorption process and predict $q_e$ (see Figure 1). The model’s output, denoted as $z_j$, is computed as Equation (4):

$$q_e=z_j=g\left(s_j\right)$$

(4)

where $g\left(s_j\right)$ is the logistic sigmoid activation function, applied to the output layer, which gives

$$z_j={\left(1+e^{-s_j}\right)}^{-1}$$

(5)

Considering that,

$$s_j=\sum _m{y}_m{U}_{mj},p_l=\sum _n{x}_n{V}_{nl},r_m=\sum _l{a}_l{W}_{ml}$$

(6)

In Equation (6), $U_{mj}$ represents the weights of the output layer, $x_n$ is the n-th input to the neural network, $V_{nl}$ belongs to the initial weights, and $W_{ml}$ are the weights of first hidden layer. Aditionally, if logistic sigmoid activation functions $a_l=f\left(p_l\right)$, $y_m=h\left(r_m\right)$ are applied to both hidden layers, it yields

$$a_l={\left(1+e^{-p_l}\right)}^{-1},y_m={\left(1+e^{-r_m}\right)}^{-1}$$

(7)

Optimization of the model parameters was performed using partial derivatives, according to the structural equations of the ANN (see Equations (6) and (7)). When obtaining the partial derivatives for each variable, the final expression, which is the product of all partial derivatives (chain rule for backpropagation), $q_e$, is shown in Equation (8):

$$qe={\displaystyle \frac{\partial z_j}{\partial V_{nl}}}=\left({\displaystyle \frac{\partial z_j}{\partial s_j}}\right)\left({\displaystyle \frac{\partial s_j}{\partial y_m}}\right)\left({\displaystyle \frac{\partial y_m}{\partial r_m}}\right)\left({\displaystyle \frac{\partial r_m}{\partial a_l}}\right)\left({\displaystyle \frac{\partial a_l}{\partial p_l}}\right)\left({\displaystyle \frac{\partial p_l}{\partial V_{nl}}}\right)$$

(8)

The chain rule in backpropagation is a fundamental mathematical principle that allows neural networks like MLPs to compute gradients of the loss function with respect to every model parameter. The essence of the chain rule is to decompose the derivative of a composite function into a product of derivatives at each layer, enabling the model to adjust weights to minimize prediction error [28].

In this sense, after substituting, developing, and simplifying the derivatives of each term from Equation (8), the partial derivative of the output $z_j$ with respect to the input weight $V_{nl}$ is computed using the chain rule, as expressed in Equation (9):

$$q_e=z_j(-1+z_j)·U_{mj}·y_m(-1+y_m)·W_{ml}·a_l(-1+a_l)·V_{nl}$$

(9)

This approach allowed effective fitting of the model to the experimental adsorption data and precise identification of the adsorption equilibrium point $q_e=z_j$.

4.4. ANN Evaluation

In the final stage, the ANN was implemented in the C programming language and trained using the experimental dataset, which was partitioned into training (70%), validation (15%), and testing (15%) subsets. Prior to training, input variables were normalized to the range [0,1]. The purpose of normalizing variables in training an MLP is to make sure all input features have equal influence on the training process, resulting in faster and more stable convergence during gradient descent [29]. Normalization prevents input variables with larger ranges from having a disproportionate effect on the model, and it helps avoid numerical problems like vanishing or exploding gradients, thereby improving the training process and the model’s ability to generalize.

The network architecture consisted of an input layer with two neurons, corresponding to time (t) and adsorption capacity at time t ($q_t$), followed by two hidden layers, each containing 30 neurons with sigmoid activation functions, and an output layer with one neuron that provided the predicted equilibrium adsorption capacity ($q_e=z_j$).

Training was carried out using the backpropagation algorithm, which applies the chain rule of calculus (using Equation (8)) to compute the gradient of the output with respect to each network parameter. This gradient information guides the iterative adjustment of connection weights to minimize the prediction error. The latter is basis of the learning process of a neural network as an iterative process in which the calculations are carried out forward and backward through each layer in the network until the error is minimized [30]. In our case, the process was executed over 5000 iterations with a fixed learning rate of 0.009.

The hyperparameters, including the number of neurons per hidden layer and the learning rate, were selected through a trial-and-error approach, as no universal configuration exists for ANNs applied to adsorption systems. Thus, with this configuration, the model was designed to capture adsorption behavior as a function of bead size and system temperature, and its performance was evaluated using the coefficient of determination ($R^2$), which served as the primary metric for assessing the model’s accuracy, as it quantifies the degree of agreement between predicted and experimental values.

5. Results

The following section shows the results of predicting adsorption capacity ($q_t$) over time using different kinetic models. Chitosan–PVA hydrogel spheres of three sizes (small, medium, and large) were tested at three temperature conditions (10, 30, and 50 °C). For each case, experimental data were compared with predictions from three traditional kinetic models (Lagergren, Ho–McKay, and Elovich) as well as the MLP model. The goodness of fit of each model are examined in comparison to the experimental data.

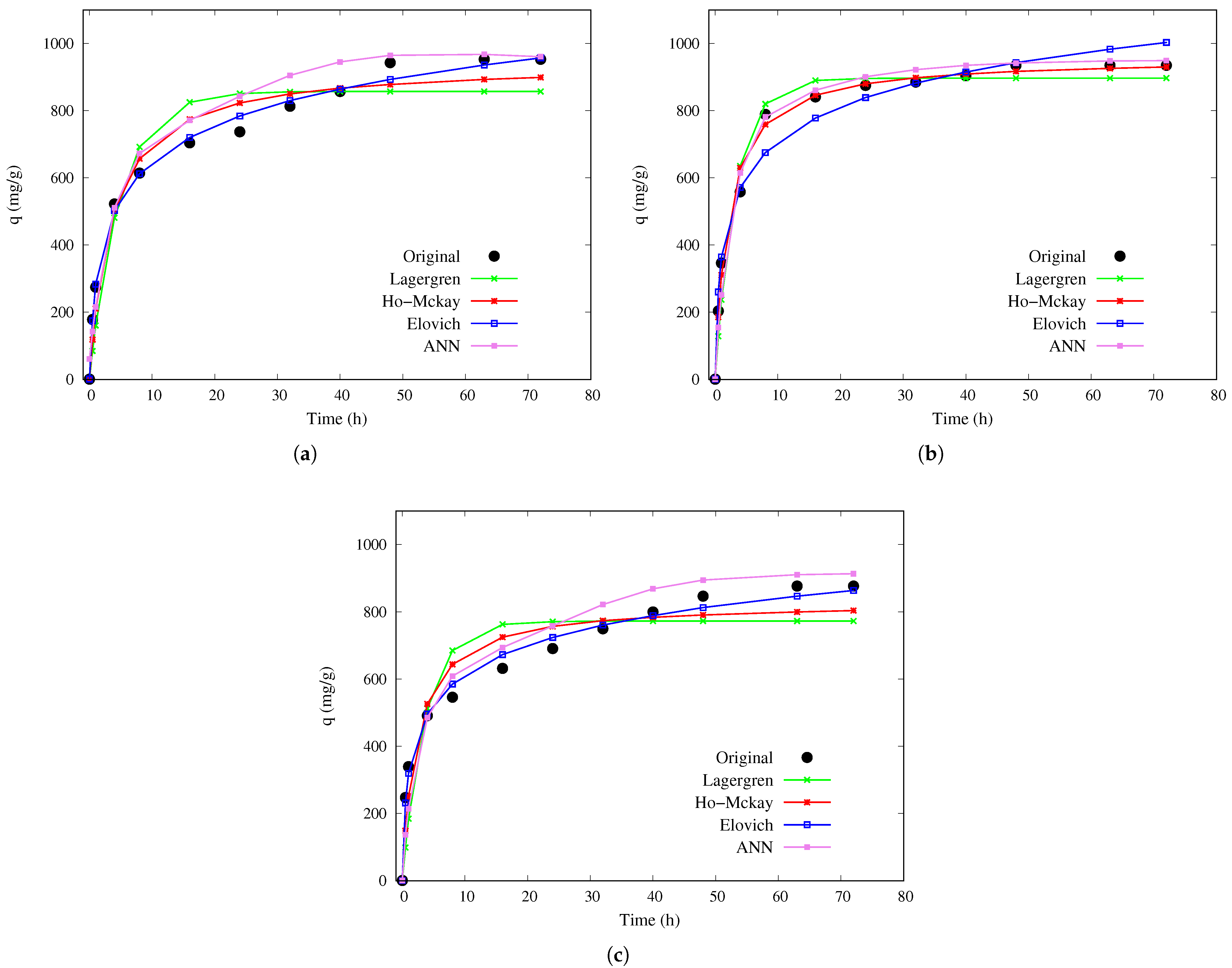
For the small sphere, Figure 2 presents the adsorption capacity over time at the three selected temperature conditions. Experimental data, indicated by black dots, are compared with model predictions (both ANN and kinetic). The ANN demonstrates excellent agreement with experimental data across all temperatures. At 10 °C, traditional kinetic models exhibit greater variability during the initial adsorption stages; however, at 30 and 50 °C, the ANN more accurately reproduces the adsorption profile, particularly in the intermediate and final phases, consistently outperforming the traditional models.

In addition to the graphical results,

Table 2. Predicted equilibrium adsorption capacity ($q_e$), time to reach equilibrium, and coefficient of determination ($R^2$) for kinetic models and ANN in tartrazine removal using small chitosan–PVA hydrogel beads.

Model	Temperature (°C)	${\mathit{q}}_{\mathit{e}}$ (mg/g)	Time (h)	${\mathit{R}}^2$
ANN	10	945	40	0.9428
	30	934	40	0.9721
	50	869	40	0.8830
Lagergren	10	857	57	0.9258
	30	897	44	0.9729
	50	773	48	0.8614
Ho-Mckay	10	943	72	0.9701
	30	957	+72	0.9929
	50	830	+72	0.9335
Elovich	10	-	-	0.9946
	30	-	-	0.9752
	50	-	-	0.9913

summarize the numerical values obtained for each prediction method. It provides a detailed comparison between traditional models and the MLP in predicting the adsorption capacity ($q_e$), the time required to reach equilibrium, and the coefficient of determination ($R^2$).

For the small chitosan–PVA hydrogel beads in Table 2, the MLP model exhibited a strong correlation with the experimental data, with $R^2$ values ranging from 0.883 to 0.972. It accurately predicted an adsorption capacity ($q_e$) of up to 945 mg/g within just 40 h at 10 °C. In comparison, traditional kinetic models took longer, exceeding 72 h, to estimate equilibrium. Although the pseudo-second-order (Ho-McKay) model achieved a high coefficient of determination (up to 0.9929), it predicted significantly longer equilibrium times, resulting in slower convergence. The Elovich model also showed high $R^2$ values, indicating good data fitting; however, it does not provide explicit estimates of $q_e$ or the time to reach equilibrium, which limits its practical usefulness for process prediction and optimization.

The predicted equilibrium adsorption capacity of 945 mg/g at 10 °C for small chitosan–PVA hydrogel beads is remarkable, and its explanation involves favorable physicochemical interactions, a higher surface-to-volume ratio, and specific experimental conditions. The smaller bead size (mean diameter of 2.1 mm) provides a significantly higher external surface area per unit mass compared to medium and large beads [31]. This increases the number of available active sites for tartrazine molecules to interact with functional groups on chitosan, at lower temperatures where molecular diffusion is slower but electrostatic attraction remains strong. Also, the use of a chitosan–polyvinyl alcohol hydrogel enhances mechanical stability and prevents excessive swelling or dissolution, allowing the beads to maintain their structural integrity over long exposure times up to 72 h [32]. This enables gradual but continuous uptake, which the ANN model accurately captures and extrapolates to a high $q_e$.

Figure 3 shows the adsorption capacity results for the medium size beads. The ANN again provides a more accurate depiction of the experimental trends. As temperature increases, adsorption capacity stabilizes more quickly, and the ANN maintains superior predictive performance even near equilibrium. Although the Ho–McKay model offers a reasonable approximation, the ANN delivers a more precise overall fit, especially during the early stages of adsorption.

For medium-sized beads (

Table 3. Performance comparison of kinetic models and ANN in estimating $q_e$ and equilibrium time for tartrazine adsorption on medium-sized chitosan–PVA hydrogel beads, with corresponding $R^2$ values.

Model	Temperature (°C)	${\mathit{q}}_{\mathit{e}}$ (mg/g)	Time (h)	${\mathit{R}}^2$
ANN	10	777	63	0.9658
	30	823	48	0.9114
	50	762	32	0.9754
Lagergren	10	729	+72	0.9405
	30	747	49	0.9465
	50	721	35	0.9716
Ho-Mckay	10	819	+72	0.9732
	30	815	+72	0.9829
	50	773	+72	0.9958
Elovich	10	-	-	0.9865
	30	-	-	0.9946
	50	-	-	0.9817

), the ANN model again demonstrated strong predictive performance, achieving $R^2$ values between 0.911 and 0.975, and accurately estimated a maximum adsorption capacity of 823 mg/g within 48 h at 30 °C. In contrast, traditional kinetic models required longer times, exceeding 72 h, to predict equilibrium. Although the pseudo-second-order (Ho–McKay) model exhibited high correlation (0.9958), it consistently overestimated the time to reach equilibrium, reducing its practical utility. The Elovich model also yielded high $R^2$ values, indicating good data fitting; however, as with the other bead sizes, it does not provide explicit estimates of $q_e$ or equilibrium time.

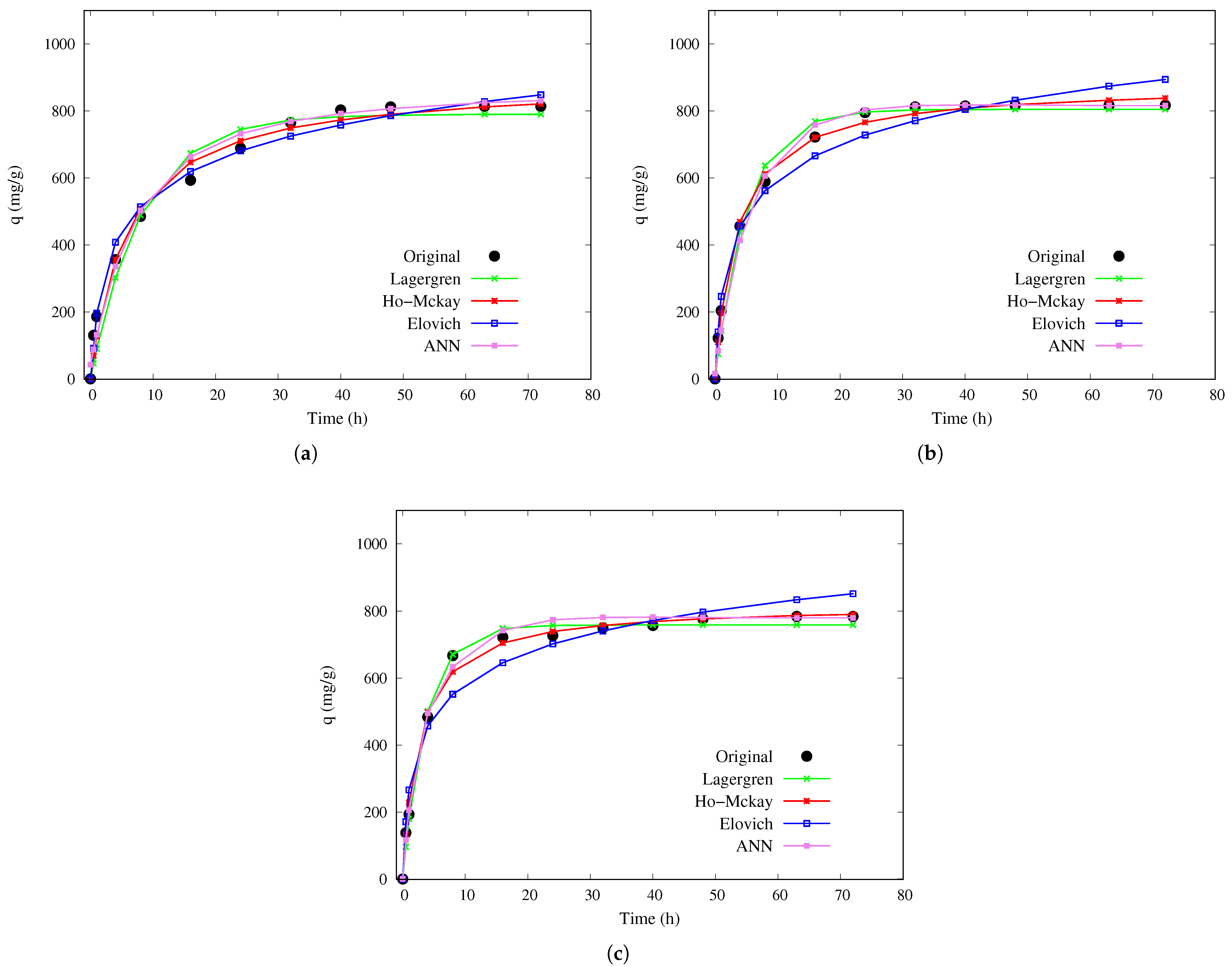
Finally, for the large sphere, Figure 4 displays the adsorption curves predicted by the models. In this case, the ANN and the Ho–McKay model show closer agreement with the experimental data (black dots), while the Elovich model deviates more significantly from the observed values. These results emphasize the superior predictive ability of the ANN and the Ho–McKay model for adsorption capacity in large chitosan–PVA hydrogel spheres under the tested temperature conditions.

Table 4. Model-predicted adsorption capacity ($q_e$) and equilibrium time for tartrazine removal using large chitosan–PVA hydrogel beads, highlighting the efficiency of the ANN approach.

Model	Temperature (°C)	${\mathit{q}}_{\mathit{e}}$ (mg/g)	Time (h)	${\mathit{R}}^2$
ANN	10	807	48	0.9810
	30	818	48	0.9876
	50	781	40	0.9893
Lagergren	10	790	+72	0.9682
	30	805	62	0.9890
	50	759	45	0.9938
Ho-Mckay	10	890	+72	0.9869
	30	879	+72	0.9973
	50	819	+72	0.9951
Elovich	10	-	-	0.9883
	30	-	-	0.9792
	50	-	-	0.9621

shows the results for large chitosan–PVA hydrogel beads. The ANN model demonstrated high robustness, achieving $R^2$ values between 0.981 and 0.9893, and accurately predicted an adsorption capacity ($q_e$) of 807 mg/g within 48 h at 10 °C. In contrast, traditional kinetic models, particularly the pseudo-second-order (Ho–McKay) model, exhibited slightly higher coefficients of determination (up to 0.9973) but required more than 72 h to reach equilibrium, significantly overestimating the time needed to achieve steady state. The Elovich model also produced competitive $R^2$ values; however, it does not provide explicit estimates of $q_e$ or equilibrium time, limiting its predictive utility. These results further confirm that the ANN offers a more efficient and versatile approach for modeling adsorption dynamics.

6. Discussion

While traditional kinetic models, such as the pseudo-first-order, pseudo-second-order, and Elovich models, are widely employed in adsorption studies due to their versatility and relative ease of application, they are inherently limited by a series of simplifying assumptions that restrict their predictive power and mechanistic interpretability.

A primary limitation lies in their assumption of surface homogeneity and uniform activation energy across adsorption sites. These conditions are rarely met in real-world systems involving heterogeneous materials like chitosan–polyvinyl alcohol hydrogel beads. These models often fail to account for complex phenomena such as simultaneous physisorption and chemisorption, pore diffusion effects, or multi-step adsorption mechanisms [33]. Furthermore, their parameters are typically treated as time-independent and disconnected from initial experimental conditions [34].

The pseudo-first-order model assumes that the rate of adsorption is proportional to the number of unoccupied sites, making it most applicable to systems dominated by physical adsorption. However, it frequently fails to accurately describe adsorption at higher concentrations or over extended time periods, especially when equilibrium is reached slowly. Its linearized form is also sensitive to systems with low adsorption, which can lead to significant errors in parameter estimation [35].

Similarly, the pseudo-second-order model, despite its widespread use and high correlation coefficients (as seen in this work), assumes that the adsorption rate is proportional to the number of unoccupied sites, making it suitable primarily for physisorption-dominated processes [35]. This assumption may lead to misleading mechanistic interpretations when applied to systems where mass transfer, diffusion, or electrostatic interactions are the rate-limiting steps [36]. Moreover, as demonstrated in this study, the model consistently overestimates the time required to reach equilibrium, reducing its practical utility for process optimization.

The Elovich model, commonly used for heterogeneous surfaces, predicts an exponential decrease in the adsorption rate with increasing surface coverage [35]. While it provides good data fitting (with $R^2$ values of up to 0.9946 in our results), it does not yield direct estimates of equilibrium adsorption capacity ($q_e$) or the time to reach equilibrium. Its empirical nature results in parameters lacking clear physical meaning, and its formulation implies continuous adsorption without a defined saturation point, which is highly dependent on experimental conditions, and potentially limits its generalization capabilities [34].

In contrast, the ANN model presented in this work does not rely on predefined mechanistic assumptions. Instead, it learns complex, nonlinear relationships directly from the data, enabling accurate predictions of both $q_e$ and equilibrium time under diverse conditions [37]. This flexibility makes the ANN a more robust and practical tool for modeling and optimizing adsorption processes, especially when dealing with variable operational parameters such as bead size and temperature, as we used in this research.

The results show that the ANN achieves high predictive accuracy ($R^2>0.94$) and significantly shortens the estimated time to reach equilibrium, ranging from 32 to 63 h, compared to over 72 h for traditional kinetic models. This improved efficiency, along with the ANN’s ability to incorporate multiple process variables, demonstrates its potential as a reliable and practical tool for optimizing adsorption processes, reducing experimental time. These benefits are also evident in the graphical analyses, where the ANN consistently provided a closer fit to the experimental data across all tested bead sizes and temperatures.

The superior performance of the ANN model demonstrated in this study is strongly supported by recent advances in computational modeling of adsorption processes. Various studies have highlighted the effectiveness of ANNs in predicting dye removal efficiency and optimizing operational parameters across diverse adsorbent systems.

For instance, Karam et al. [5] applied ANN to compare nano zerovalent iron, activated carbon, and green-synthesized nanoparticles for textile wastewater decolorization, reporting removal efficiencies of up to 100% under optimized conditions and confirming the ANN’s ability to accurately simulate complex adsorption behavior. Similarly, Alardhi et al. [11] used an ANN to model methyl orange adsorption on date seed-derived activated carbon, achieving high predictive accuracy ($R^2\approx 0.99$) with low error margins, while Al-Hameed et al. [12] demonstrated that an ANN outperformed response surface methodology in modeling reactive yellow 105 removal using zeolitic materials, with minimal MSE.

These findings align with broader trends showing that ANNs are particularly effective in capturing nonlinear relationships in multi-variable adsorption systems. Recent studies applying ANN to chitosan-based composites, though targeting different dyes or incorporating layered double hydroxides or metal–organic frameworks, have reported similarly high predictive accuracy [38]. In fact, computational approaches using ANN and machine learning on chitosan matrices consistently yield values close to unity when modeling dye adsorption as a function of pH, concentration, time, and dosage [39]. Furthermore, research on chitosan–polyvinyl alcohol (PVA) hydrogels specifically has shown that hybrid models, including ANN and Random Forest algorithms, can reliably predict removal efficiency and optimize process conditions [40].

Therefore, the integration of ANN into adsorption modeling represents a methodological advancement and is a necessary evolution toward more efficient, data-driven environmental engineering. While some of the cited works utilize modified adsorbents and other experimental conditions, the core principles of ANN application (namely, nonlinear pattern recognition, multi-parameter integration, and predictive optimization) are transferable to chitosan–PVA hydrogel systems. This growing body of evidence confirms that ANNs offer a robust, reliable, and versatile alternative to conventional kinetic models [41].

7. Conclusions

This study demonstrates the capability of ANNs in modeling the adsorption kinetics of tartrazine onto chitosan–PVA alcohol hydrogel beads across varying sizes (small, medium, large) and temperatures (10, 30, 50 °C). The ANN model achieved high predictive accuracy for both equilibrium adsorption capacity ($q_e$) and time-to-equilibrium, with all $R^2$ values exceeding 0.94. For small beads at 10 °C, it predicted $q_e$ = 945 mg/g within 40 h ($R^2$ = 0.9428), showcasing its reliability and precision.

Compared to traditional kinetic models, the ANN significantly reduced prediction time, by estimating equilibrium in 32 to 63 h, versus over 72 h required by the pseudo-second-order model, even though the latter showed slightly higher $R^2$ values, up to 0.9973, this reduction highlights the ANN’s potential to accelerate process evaluation and minimize reliance on prolonged experimental trials. In contrast, while the Elovich model exhibited strong data fitting ($R^2$ = 0.9946), it does not yield direct estimates of equilibrium time, limiting its utility for practical design. These findings establish the ANN as an efficient and practical tool compared to traditional models for optimizing dye removal.

Despite these advantages, a key limitation remains: the current dependence on trial-and-error for hyperparameter selection (number of neurons, learning rate), which hinders standardization and reproducibility. Thus, future work should explore optimization techniques, such as genetic algorithms or Bayesian optimization, to automate network configuration. Furthermore, validating the model with other dyes, adsorbents, and real wastewater matrices will be essential to assess its generalizability under complex conditions.