Abstract
The theoretical model for a packed porous catalytic particle of the slab, cylindrical, and spherical geometries shape in fixed-bed electrochemical reactors is discussed. These particles have internal mass concentration and temperature gradients in endothermic or exothermic reactions. The model is based on a nonlinear reaction–diffusion equation containing a nonlinear term with an exponential relationship between intrinsic reaction rate and temperature. The porous catalyst particle’s concentration is obtained by solving the nonlinear equation using Akbari-Ganji’s method. A simple and closed-form analytical expression of the effectiveness factor for slab, cylindrical, and spherical geometries was also reported for all values of Thiele modulus, activation energy, and heat reaction. The accordance with results of a reliable numerical method shows the good accuracy that their approximate solution yields.
1. Introduction
Scientists have been inspired to create more effective electrochemical reactors by the significant contribution of electrochemical engineering in pollution control (in water, air, and soil) and electrochemical synthesis [1]. Furthermore, due to the fixed bed electrochemical reactor’s excellent space–time yield, numerous studies have focused on its performance features, such as mass transfer and current distribution, in recent years [2]. Mass transfer behaviour in chemical reactor with a mathematical approach is given in the books by Bird et al. [3] and Treybal [4].
The uniform current distribution in this electrochemical reactor is an advantage widely desired for electro-organic synthesis, since it results in a high degree of selectivity [1]. In addition, the inner surface of the inner tubular electrode of the reactor can be employed as a heat exchanger to remove extra heat produced during electrolysis from the cell. However, the annular flow electrochemical reactor’s primary drawback is its small area-to-volume ratio, reducing diffusion-controlled reactions.
By increasing the rate of mass transfer using various methods, such as surface roughness [2], turbulence-promoting screens [5], gas generation at the working electrode [6,7], gas sparging [8], swirl flow [9,10], and pulsating flow [11], various authors have attempted to address this defect. In addition, some research has been done on the impact of inert beds on the mass transfer behaviour of the electrochemical reactors in single-phase flow [12,13,14] and two-phase flow. The effectiveness factor for a reaction with arbitrary kinetics occurring inside a porous catalyst pellet is predicted by Paterson et al. [15] using the orthogonal collocation method. Tavera [16] calculated the effectiveness factor, expressed in terms of special functions and exponential integrals for a porous slab of catalyst pellet under non-isothermal conditions.
When analyzing chemical reaction kinetics based on externally observable parameters, the behavior of a porous particle in an electrochemical reactor can differ significantly from appropriate chemical kinetics. The particle’s mass and heat transfer influence the overall reaction rate in heterogeneous gas–solid systems. In both isothermal [17] and non-isothermal systems [18], the influence of diffusion resistance and heat of reaction in solid-catalyzed processes have been characterized using the effectiveness factor. Depending on the reaction conditions, the gas–solid interaction has both interfacial and homogeneous reactions [19,20,21,22]. When combined with transient conditions, heat and mass transfer play an essential role in gas–solid reaction systems [23,24,25].
Weisz et al. [18] studied the behavior of porous catalyst particles in the presence of internal mass concentration and temperature gradients. Finally, Lucia and co-workers [26] present the numerical solution of the non-linear equations for simultaneous mass and heat diffusion effects. Sevukaperumal and Rajendran [27] developed a mathematical model of porous catalyst particles in endothermic and exothermic processes.
However, no exact analytical expression for the concentration of a reactant at the catalyst’s surface of general geometries has been reported. Therefore, this communication aims to derive a simple approximate analytical expression for concentration and effectiveness factors, for all possible reaction/diffusion parameter values for the slab, cylinder, and spherical geometries. The approximate analytical results (concentration, and effectiveness factor) obtained using the Akbari-Ganji’s method (AGM) will help control the operational variables (heat of the reaction, activation energy, and Thiele modulus) in designing the components and the scale-up of electrochemical reactors.
2. Mathematical Formulation of the Problem
The nonlinear mass balance equation involving heterogeneous reaction kinetics on electrochemical fixed-bed reactors of general geometries (slab, cylindrical, and spherical) can be written as follows (Appendix A):
The dimensionless boundary conditions are
where is the dimensionless concentration of reactant, is the dimensionless pellet radius and is the dimensionless activation energy, is the dimensionless heat of reaction, and is the Thiele modulus. The values of the geometrical shape parameter fall n within the range 0 to 2 for all simply connected regions of the pellet. The limits of these regions are: the infinite slab (n = 0), cylinder (n = 1), and the sphere (n = 2).
The effectiveness factor is
3. Approximate Analytical Expression of the Concentration and Effectiveness Factor Using Akbari-Ganji’s Method
Solving nonlinear differential equations analytically is more complicated than solving linear differential equations. Recently, many asymptotic methods for solving nonlinear differential equations have been developed, such as the homotopy perturbation method [28,29,30], Adomian decomposition method [31,32,33], Variational iteration method [34,35,36], Taylor series method [37,38], Akbari-Ganji method [39,40,41,42,43,44], and Rajendran–Joy method [45]. The AGM may be considered a powerful algebraic (semi-analytic) approach for solving such problems. The approximate analytical expression of a reactant concentration for all dimensionless parameters is obtained using this method (Appendix B) as follows:
where m is obtained by solving the equation
Equation (5) is the new analytical expression of a reactant concentration for all values of dimensionless parameters , and . The Ying Buzu algorithm [46,47] can be used to find the unknown parameter m. The numerical value of for the given values of , and can be obtained by solving Equation (6) by any mathematical software. Additionally, when m is small, Equation (6) becomes (Appendix C):
and for large values of m, we have
Substituting the value of in Equation (5) gives the closed-form of approximate analytical expression of a reactant concentration, for all dimensionless parameters.
The regular false method and the secant algorithm were also used to determine this parameter. The Ying Buzu algorithm method offers an extremely fast convergent result. The effectiveness factor response can be obtained as follows:
4. Numerical Simulation
The nonlinear diffusion Equation (1) for the boundary conditions (Equations (2) and (3)) is also solved numerically. We have used the function pdex1 in MATLAB software to numerically solve the initial-boundary value problems for the nonlinear differential equations (Appendix D).
The simulation results are compared with our approximate analytical results in Table 1, Table 2, Table 3 and Table 4 for spherical catalyst pellets. The maximum average error percentage between numerical and our approximate analytical results is 3.6% for all values of the activation energy, heat of reaction, and Thiele modulus.

Table 1.
Comparison of dimensionless concentration of species for spherical catalyst pellets with simulation results for various values of parameter when .

Table 2.
Comparison of dimensionless concentration of species for spherical catalyst pellets with simulation results for various values of parameter when

Table 3.
Comparison of dimensionless concentration of species for spherical catalyst pellets with simulation results for various values of parameter when

Table 4.
Comparison of dimensionless concentration of species for spherical catalyst pellets with simulation results for various values of parameter when .
5. Discussion
Equation (5) is the new closed and simple new approximate analytical expressions’ concentration of reactant. The concentration depends on the parameters (dimensionless activation energy), (dimensionless heat of reaction), and (Thiele modulus).
5.1. Influence of the Parameters (Thiele Modulus, Heat of the Reaction, and Activation Energy) on the Concentration Profile
The Thiele modulus is the ratio of reaction to diffusion rates. Figure 1a–c represent the concentration of species for various value parameters. Figure 1a illustrates the concentration profile for various values of the Thiele modulus. When is low, the diffusional resistance is inadequate to limit the reaction rate. Therefore, uniform concentration CA/CAS can be maintained. However, when is large, a significant diffusional resistance prevents a constant concentration profile of A within the catalyst particle and thus lowers the observed rate. From the figure, it is observed that the concentration increases when the Thiele modulus decreases. Additionally, the concentration is uniform when . From Figure 1b,c, it is inferred that concentration decreases when the heat of the reaction ( and activation energy () decreases.
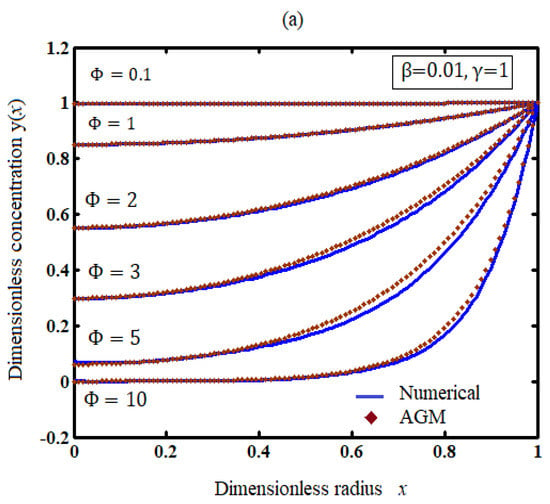
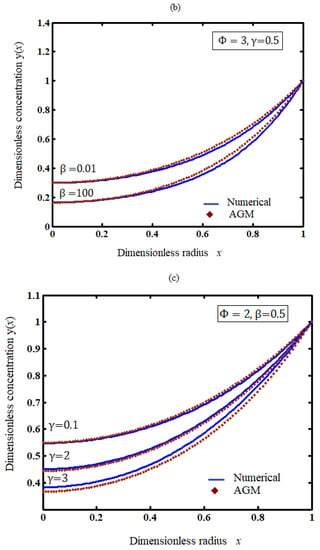
Figure 1.
Effect of the parameters on concentration of the reactant for spherical catalyst pellet using Equation (5). (a) Various values of (b) various values of and (c) various values of .
5.2. Influence of the Parameters (Thiele Modulus, Heat of the Reaction, and Activation Energy) on the Effectiveness Factor
The overall reaction rate in a catalytic pellet is often expressed by the effectiveness factor η, which measures the total reaction rate as a scalar multiple of a homogeneous reaction rate at the surface concentration.
Equation (9) represents the new approximate analytical expression of the effectiveness factor for all values of parameters. It is observed that the value of the effectiveness factor increases as the Thiele modulus increases initially, reaches the maximum value, and then decreases. The peak value of the effectiveness factor increases when the heat of the reactant or activation energy increases. The heat of the reaction value is negative for an exothermic reaction. In this case, the effectiveness factor is less than one (see Figure 2a).
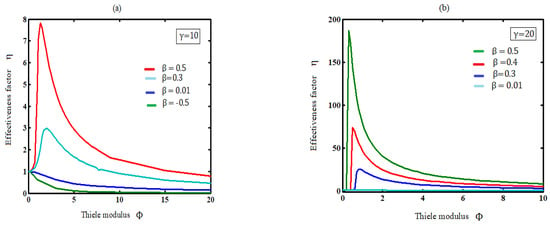
Figure 2.
Plot of the effectiveness factor (spherical catalyst pellets) versus the Thiele modulus for various values of parameter (a) when (b) when using Equation (9).
Figure 3 shows the effectiveness factor versus Thiele modulus for flat, cylindrical, and spherical catalyst pellets. It is observed that the peak value of the effectiveness factor for spherical geometrics is higher than for cylindrical and slab geometries. Furthermore, it is concluded that for all geometries, the effectiveness increases when the Thiele modulus increases to attain the maximum value before it decreases.
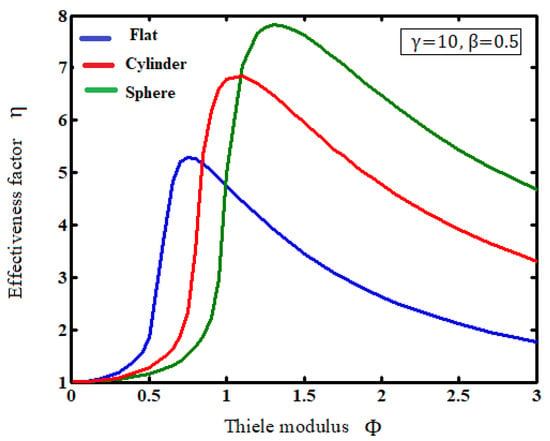
Figure 3.
The effectiveness factor versus of the Thiele modulus for the flat, cylindrical, and spherical catalyst pellet.
5.3. A limiting Case: The Dimensionless Heat of Reaction Is Zero
When , Equation (1) becomes
In this case, we can obtain the well-known exact analytical expression of concentration and effectiveness factors when n = 0, 1, 2. In Table 5, the exact results for the limiting cases, i.e., n = 0, 1, 2 (Equations. (11) to (16)), and approximate general analytical results (Equations. (17) to (19)) for all cases (this work) are summarized.

Table 5.
The concentration and effectiveness factors when
This limiting case result for the concentration of species for cylindrical catalyst pellets is compared with our approximate analytical results in Table 6, where satisfactory agreement is noted.

Table 6.
Comparison of dimensionless concentration of species for cylindrial catalyst pellets with simulation results for various values of parameter when
Here we have presented an analysis to compute the effectiveness factor in a reaction/diffusion system of general geometry. The value for the effectiveness factor is also valid for a modified electrode, since the reaction flux is defined by the concentration gradient at x = 1. Therefore, the analysis for a polymer-modified electrode and a packed bed reactor are equivalent. Consequently, the theory applies to both electrochemical and catalytic problems, hence the concept applies equally to electrochemical and catalytic problems. The concept of effectiveness factor is beneficial for polymer-modified electrodes since it presents the degree of utilization of the layer in catalysis. The electrochemical polymer-modified electrode problem is equivalent to packed bed catalysis.
6. Conclusions
The mass transfer behavior in fixed electrochemical reactors was discussed. The nonlinear differential equation for coupled heat and mass transfer in a slab, cylindrical, and spherical non-isothermal kinetics was solved analytically using the efficient Akbari-Ganji method. The approximate analytical expressions for the reactant concentration and effectiveness factor were obtained for all values of parameters. The numerical simulation results provided by Matlab, and theoretical predictions, were found to be in satisfactory agreement. The derived approximate analytical results were employed to analyze the effect of the behavior of porous catalyst particles subject to both internal mass concentration gradients and temperature gradients in endothermic or exothermic reactions. The theoretical model in this study and the derived approximate analytical solution can be extended to study the electrosynthesis of chemicals and drugs, redox flow batteries, fuel cells, water disinfection, and electrodialysis.
Author Contributions
Conceptualization, M.E.G.L. and L.R.; methodology, M.E.G.L.; software, P.J.; validation, M.A. and P.J.; formal analysis, M.A.; investigation, M.E.G.L.; resources, P.J.; data curation, P.J.; writing—original draft preparation, M.A.; writing—review and editing, P.J.; visualization, L.R.; supervision, M.E.G.L. and L.R.; project administration, M.E.G.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors have not received any funds.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
List of Symbols
| Concentration of reactant inside the catalyst pellet | |
| Concentration of reactant at the surface of catalyst pellet | |
| Effective diffusivity inside the catalyst pellet | |
| Activation energy | |
| Reference reaction constant | |
| Effective thermal conductivity inside the catalyst pellet | |
| Arrhenius reaction rate | |
| Radius of a sphere | |
| Gas constant | |
| Temperature inside the catalyst pellet | |
| Reference temperature | |
| Temperature at the surface of catalyst pellet | |
| Dimensionless radius of the spherical catalyst pellet | |
| Dimensionless concentration | |
| Heat of reaction | |
| Thiele modulus | |
| Dimensionless heat of reaction | |
| Dimensionless activation energy | |
| Effectiveness factor | |
| Flux |
Appendix A. Physicochemical Formulation of the Problem
Many industrial reactors use heterogeneous reaction kinetics of packed catalytic pellets in fixed-bed reactors (Equation (A1)). A single porous catalyst pellet can be viewed as a porous media through which reactants diffuse as interaction occurs.
The species mass balance equation is
where is the Laplacian operator and the rate constant k is a negative exponential function of temperature
The boundary conditions are given by
where is the concentration of reactant inside the catalyst pellet, is concentration of reactant at the surface of catalyst pellet, is a length parameter (radius in case of a sphere), is the reference reaction constant, is the activation energy, is a gas constant, is a reference temperature, is a temperature at the surface of catalyst pellet, and is the effective diffusivity inside the catalyst pellet. The schematic concentration profile showing boundary condition for slab, cylindrical, and spherical catalytic is represented in Figure A1.
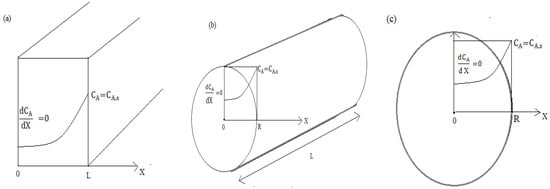
Figure A1.
(a) Slab, (b) cylindrical, and (c) spherical catalytic pellet, and schematic concentration profile showing boundary condition.
The analogous equation for heat diffusion is
where is the thermal conductivity and is a function of T.
and
Here, and are the boundary values. The boundary conditions are
Using the relation Equation (A8), we can write the reaction rate Equation (A6) in terms of one variable instead of both c and Using the following dimensionless variable
The nonlinear equation and boundary conditions can be written as in Equations (1)–(3) in the main manuscript.
Appendix B. Approximate Analytical Expression of a Substrate Concentration in Species
There are numerous analytical and numerical techniques for solving linear differential equations, however, nonlinear differential equation techniques are far more difficult to use [48,49]. Here, we can use a novel algebraic method AGM for solving nonlinear differential equations proposed by Akbari et al. [50]. In the AGM, it is initially assumed that a solution function with unknown constant coefficients will satisfy both the initial conditions and the differential equation. Then, using algebraic equations obtained for the initial condition and their derivatives, the unknown coefficients are calculated. Assume that the solution to Equation (1) is the following Akbari Ganji’s method.
where , and are constant. The values of are found easily from boundary conditions (2) and (3), that is
As a result, Equation (A12) becomes
We use the general form of Equation (1) to find the constant m in Equation (B3). We write Equation (1) in the form
By substituting Equation (A14) into Equation (B4) and letting , we obtain
Appendix C. Approximate Analytical Solution of Nonlinear Equation (6)
The approximate solution of the nonlinear equation in non-isothermal kinetics
for the boundary conditions and is given by
where is obtained by solving the equation
Case 1: is sufficiently small.
In this case, we have
Hence, Equation (A19) becomes
where
If we assume that . Then . Hence,
which reduces to
Case (2). Assume m is large, that is > > 1. Then
That is . Hence, For large . In other words,
and consequently Equation (A19) becomes
Solving (A25) for m gives
and in simplified from,
Appendix D. MATLAB Code for Numerical Solution of the Non-Linear Equation (1)
function pdex1
m = 1;
x = linspace(0,1);
t = linspace(0,1000);
sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);
u1 = sol(:,:,1);
figure
plot(x,u1(end,:))
title(‘u1(x,t)’)
xlabel(‘Distance x’)
ylabel(‘u1(x,2)’)
% --------------------------------------------------------------
function [c,f,s] = pdex1pde(x,t,u,DuDx)
c = 1;
f = DuDx;
p = 10;b = 0.01;r = 3;
s =-(p^2)*u*exp(r*b*(1-u)/(1 + b*(1-u)));
function u0 = pdex1ic(x)
u0 = 1;
function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)
pl = 0;
ql = 1;
pr = ur-1;
qr = 0;
References
- Walsh, F. A First Course in Electrochemical; The Electrochemical Consultancy: Hants, UK, 1993. [Google Scholar]
- Sedahmed, G.H.; Shemilt, L.W. Forced convection mass transfer at rough surfacesin annuli. Lett. Heat Mass Transf. 1976, 3, 499–511. [Google Scholar] [CrossRef]
- Bird, R.; Stewart, W.; Lightfoot, E. Transport Phenomena, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2002. [Google Scholar]
- Treybal, R.E. Mass Transfer Operations; McGraw Hill: New York, NY, USA, 1980; p. 466. [Google Scholar]
- Zaki, M.; Nirdosh, I.; Sedahmed, G.H. Effect of surface roughness induced bywoven metallic screens wrapped on the inner surface of an annulus on the rate of turbulent flow mass transfer. Ind. Eng. Chem. Res. 1996, 35, 4354–4359. [Google Scholar] [CrossRef]
- El-Sherbiny, M.F.; Zatout, A.A.; Hussien, M.; Sedahmed, G.H. Mass transfer at the gas evolving inner electrode of a concentric cylinder reactor. J. Appl. Electrochem. 1991, 21, 537–542. [Google Scholar] [CrossRef]
- Fahidy, T.Z. Electrolysis in an annular flow cell with gas generation. J. Appl. Electrochem. 1979, 9, 101–108. [Google Scholar] [CrossRef]
- Sedahmed, G.H.; Hosny, A.Y.; Fadally, O.A.; El-Mekkawy, I.M. Mass transfer at rough gas-sparged electrodes. J. Appl. Electrochem. 1994, 24, 139–144. [Google Scholar] [CrossRef]
- de Sa, M.S.; Shemilt, L.W.; Soegiarto, I.V. Mass transfer in the entrance region for axial and swirling annular flow. Can. J. Chem. Eng. 1991, 69, 294–299. [Google Scholar] [CrossRef]
- Legentilhomme, P.; Legrand, J. Overall mass transfer in swirling decaying flow in an annular electrochemical cells. J. Appl. Electrochem. 1990, 20, 216–222. [Google Scholar] [CrossRef]
- Zaki, M.M.; Nirdosh, I.; Sedahmed, G.H. Mass transfer behavior of annular ducts under developing flow with superimposed pulsating flow. Chem. Eng. Technol. 2011, 34, 475–481. [Google Scholar] [CrossRef]
- Storck, A.; Coeuret, F. Mass transfer between a flowing liquid and a wall or animmersed surface in fixed and fluidized beds. Chem. Eng. J. 1980, 20, 149–154. [Google Scholar] [CrossRef]
- Hutin, D.; Storck, A.; Coeuret, F. Local study of wall to liquid mass transfer influidized and packed beds. II. Mass transfer in packed beds. J. Appl. Electrochem. 1979, 9, 361–367. [Google Scholar] [CrossRef]
- Ramana Rao, M.V.; Rao, C.V. Mass transfer in square channels. Part II–ionic mass transfer in packed beds. Ind. J. Technol. 1970, 8, 44–47. [Google Scholar]
- Paterson, W.R.; Cresswell, D.L. A simple method for the calculation of effectiveness factors. Chem. Eng. Sci. 1971, 26, 605–616. [Google Scholar] [CrossRef]
- Tavera, E.M. Analytical expression for the non-isothermal effectiveness factor: The nth-order reaction in a slab geometry. Chem. Eng. Sci. 2005, 60, 907–916. [Google Scholar] [CrossRef]
- Thiele, E.W. Relation between catalytic activity and size of particle. Ind. Eng. Chem. 1936, 31, 916–920. [Google Scholar] [CrossRef]
- Weisz, P.; Hicks, J. The behaviour of porous catalyst particles in view of internal mass and heat diffusion effects. Chem. Eng. 1962, 17, 265–275. [Google Scholar] [CrossRef]
- Ishida, M.; Wen, C.; Shirai, T. Comparison of zone-reaction model and unreacted-core shrinking model in solid-gas reactions—II non-isothermal analysis. Chem. Eng. Sci. 1971, 26, 1043–1048. [Google Scholar] [CrossRef]
- Kimura, S.; Tone, S.; Otake, T. Reaction order in the grain model with grain size distribution. J. Chem. Eng. Jpn. 1981, 14, 491–493. [Google Scholar] [CrossRef][Green Version]
- Wang, S.C.; Wen, C.Y. Experimental evaluation of nonisotheral solid-gas reaction model. AIChE J. 1972, 18, 1231–1238. [Google Scholar] [CrossRef]
- Weisz, P.B.; Goodwin, R.D. Combustion of carbonaceous deposits within porous catalyst particles I. Diffusion-controlled kinetics. J. Catal. 1963, 2, 397–404. [Google Scholar] [CrossRef]
- Cannon, K.J.; Denbigh, K.G. Studies on gas-solid reactions—I: The oxidation rate of zinc sulphide. Chem. Eng. Sci. 1957, 6, 145–154. [Google Scholar] [CrossRef]
- Costa, E.C.; Smith, J.M. Kinetics of noncatalytic, nonisothermal, gas-solid reactions: Hydrofluorination of uranium dioxide. AIChE J. 1971, 17, 947–957. [Google Scholar] [CrossRef]
- Shettigar, U.R.; Hughues, R. Prediction of transient temperature distribution in gas—Solid reactions. Chem. Eng. J. 1972, 3, 93–99. [Google Scholar] [CrossRef]
- Lucia, A.; Gattupalli, R.R. A barrier-terrain methodology for global optimization. Ind. Eng. Chem. Res. 2008, 47, 2666–2680. [Google Scholar] [CrossRef]
- Renugadevi, M.; Sevukaperumal, S.; Rajendran, L. The Approximate analytical solution of non-linear equation for simultaneous internal mass and heat diffusion effects. Nat. Sci. 2016, 8, 284–294. [Google Scholar] [CrossRef]
- Nadeem, M.; He, J.H. The homotopy perturbation method for fractional differential equations: Part 2, two-scale transform. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 559–567. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. Homotopy perturbation method with three expansions for Helmholtz-Fangzhu oscillator. Int. J. Mod. Phys. B 2021, 35, 2150244. [Google Scholar] [CrossRef]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Rajendran, L.; Lyons, M.E.G. Amperometric biosensors and coupled enzyme nonlinear reactions processes: A complete theoretical and numerical approach. Electrochim. Acta 2022, 415, 140236. [Google Scholar] [CrossRef]
- Hasan, Y.Q.; Zhu, L.M. A note on the use of modified Adomian decomposition method for solving singular boundary value problems of higher-order ordinary differential equations. Commun. Nonlinear Sci. Numer. Simulat. 2009, 14, 3261–3265. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Kannan, M.; Rajendran, L. Approximate analytical solutions of biofilm reactor problem in applied biotechnology. Theor. Found. Chem. Eng. 2021, 55, 851–861. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Abukhaled, M.; Kannan, M. Semi-analytical expressions for the concentrations and effectiveness factor for the three general catalyst shapes. React. Kinet. Mech. Catal. 2022, 135, 1739–1754. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Variational iteration method: New development and applications. Comput. Math. Appl. 2007, 54, 881–894. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A comparison between the variational iteration method and Adomian decomposition method. J. Comput. Appl. Math. 2007, 207, 129–136. [Google Scholar] [CrossRef]
- Abukhaled, M. Variational iteration method for nonlinear singular two-point boundary value problems arising in human physiology. J. Math. 2013, 1–4. [Google Scholar] [CrossRef]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Rajendran, L.; Abukhaled, M. Solving nonlinear reaction–diffusion problem in electrostatic interaction with reaction-generated pH change on the kinetics of immobilized enzyme systems using Taylor series method. J. Math. Chem. 2021, 59, 1332–1347. [Google Scholar] [CrossRef]
- He, J.H. Taylor series solution for a third order boundary value problem arising in Architectural Engineering. Ain Shams Eng. J. 2022, 11, 1411–1414. [Google Scholar] [CrossRef]
- Manimegalai, B.; Lyons, M.E.G.; Rajendran, L. A kinetic model for amperometric immobilized enzymes at planar, cylindrical and spherical electrodes: The Akbari-Ganji method. J. Electroanal. Chem. 2021, 880, 114921. [Google Scholar] [CrossRef]
- Salomi, R.J.; Sylvia, S.V.; Rajendran, L.; Abukhaled, M. Electric potential and surface oxygen ion density for planar, spherical and cylindrical metal oxide grains. Sens. Actuators B Chem. 2020, 321, 128576. [Google Scholar] [CrossRef]
- Saranya, K.; Mohan, V.; Rajendran, L. Steady-state concentrations of carbon dioxide absorbed into phenyl glycidyl ether solutions by residual method. J. Math. Chem. 2020, 58, 1230–1246. [Google Scholar] [CrossRef]
- Akbari, M.R.; Akbari, S.; Kalantari, E.; Ganji, D.D. Akbari-Ganji’s method “AGM” to chemical reactor design for non-isothermal and non-adiabatic of mixed flow reactors. J. Chem. Eng. Mater. Sci. 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Mary, M.L.C.; Devi, M.C.; Meena, A.; Rajendran, L.; Abukhaled, M. Mathematical modeling of immobilized enzyme in porous planar, cylindrical, and spherical particle: A reliable semi-analytical approach. React. Kinet. Mech. Catal. 2021, 134, 641–651. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Lyons, M. Reaction-diffusion in a packed-bed reactors: Enzymatic isomerization with Michaelis-Menten Kinetics. J. Electroanal. Chem. 2022, 910, 116184. [Google Scholar] [CrossRef]
- Salomi, R.J.; Rajendran, L. Cyclic voltammetric response of homogeneous catalysis of electrochemical reactions: Part 1. A theoretical and numerical approach for EE’C scheme. J. Electroanal. Chem. 2022, 918, 116429. [Google Scholar] [CrossRef]
- Lakshmi Narayanan, K.; Shanthi, R.; Usha Rani, R.; Lyons, M.E.G.; Rajendran, L. Mathematical modelling of forced convection in a porous medium for a general geometry: Solution of thermal energy equation via Taylor’s series with Ying Buzu algorithms. Int. J. Electrochem. Sci. 2022, 17, 220623. [Google Scholar] [CrossRef]
- Manimegalai, B.; Swaminathan, R.; Lyons, M.E.G.; Rajendran, L. Application of Taylor’s series with Ying Buzu Shu algorithm for the nonlinear problem in amperometric biosensors. Int. J. Electrochem. Sci. 2022, 17, 22074. [Google Scholar] [CrossRef]
- Fucik, S.; Kufner, A. Nonlinear Differential Equations; Elsevier: Prague, Czech Republic, 2014; pp. 1–136. [Google Scholar]
- Hermann, M.; Seravi, M. Nonlinear Ordinary Differential Equations; Springer: New Delhi, India, 2016. [Google Scholar]
- Akbari, M.R.; Ganji, D.D.; Nimafar, M.; Ahmadi, A.R. Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Front. Mech. Eng. 2014, 9, 390–401. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).