Review of Shearography for Dual-Directional Measurement
Abstract
:1. Introduction
2. Theory
2.1. The Principle of Digital Shearography
2.2. Temporal Phase Shift
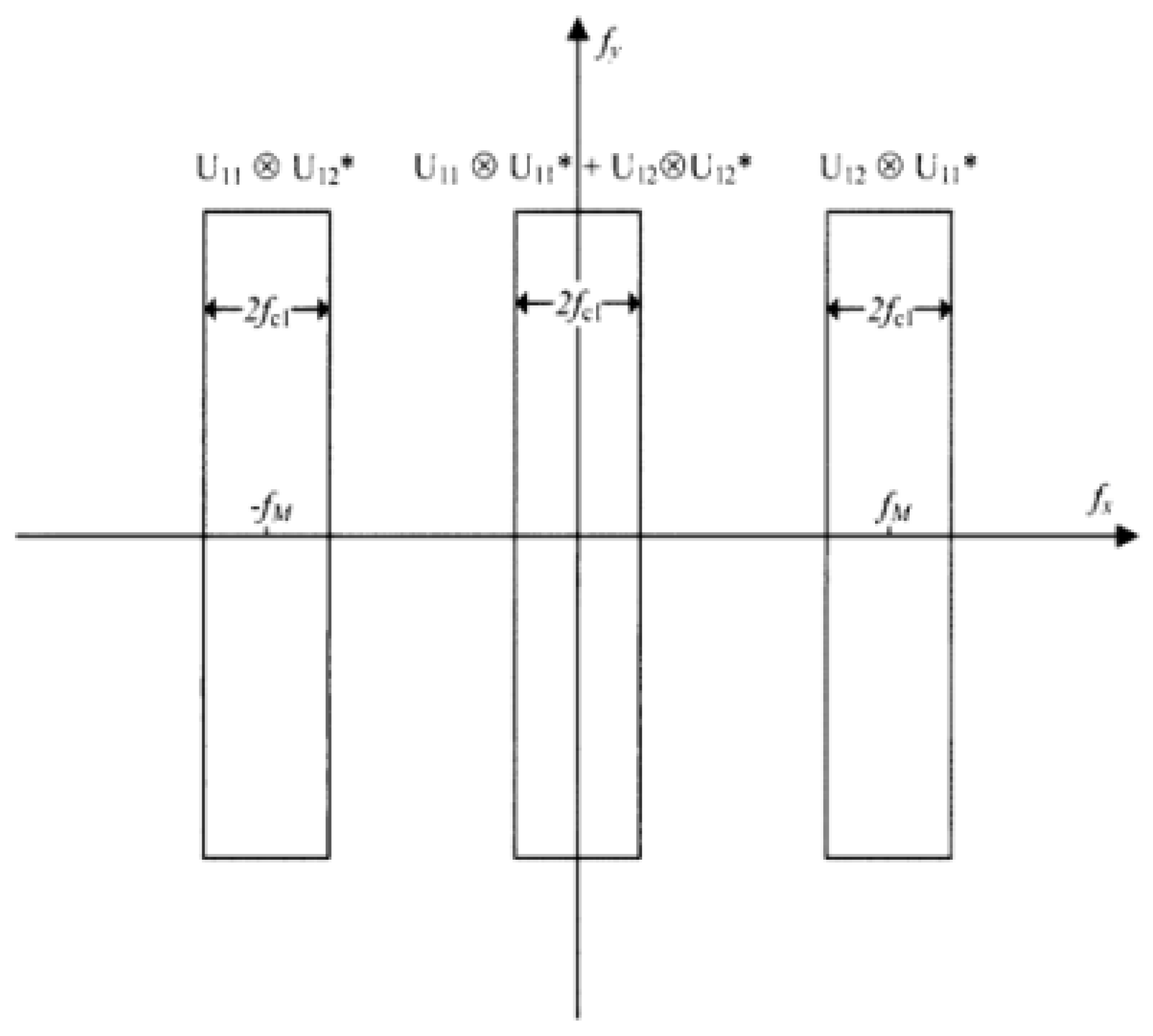
2.3. Spatial Phase Shift
2.4. The Significance of Dual-Directional Shearography Measurement
3. Development in Dual-Directional Shearography Technique
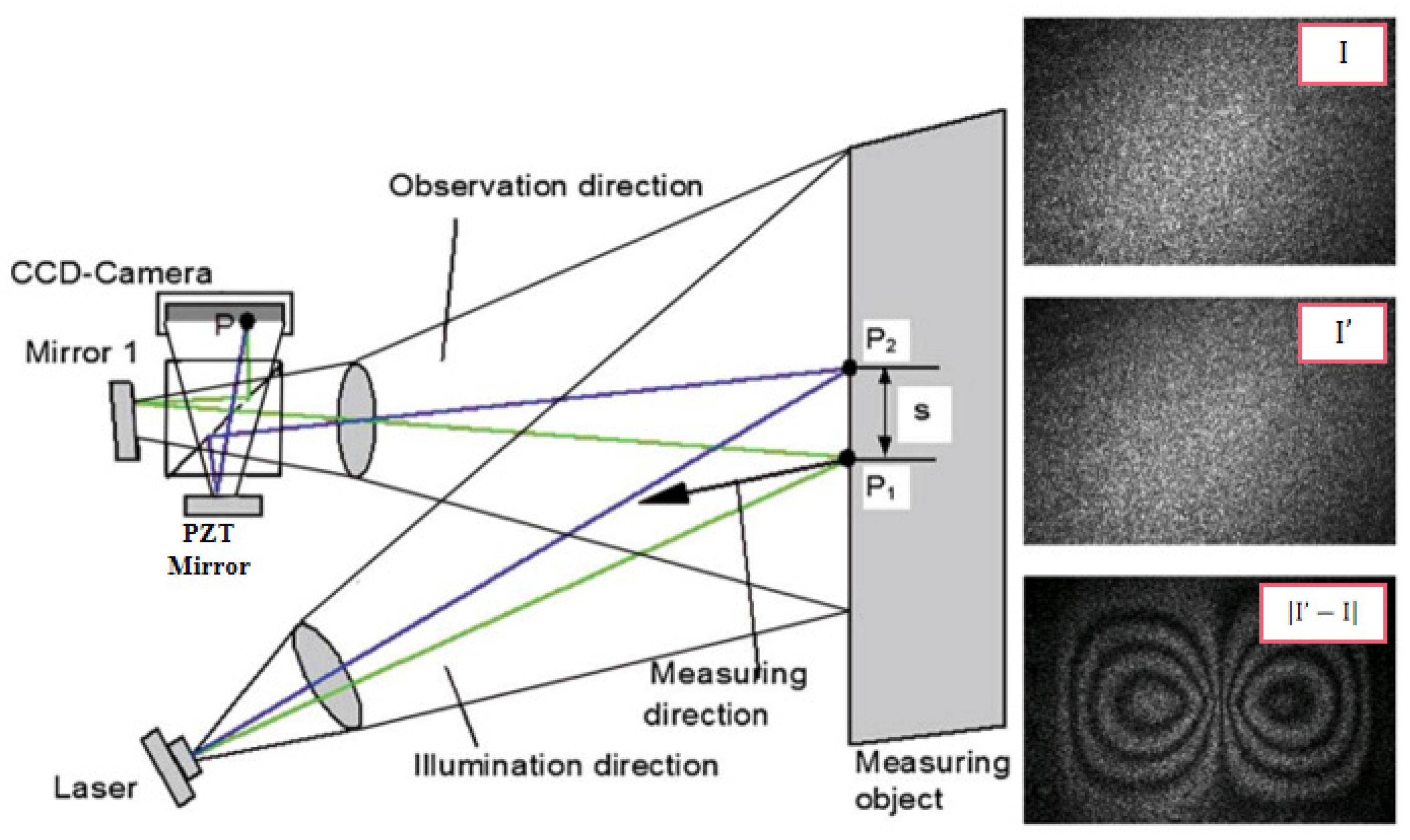
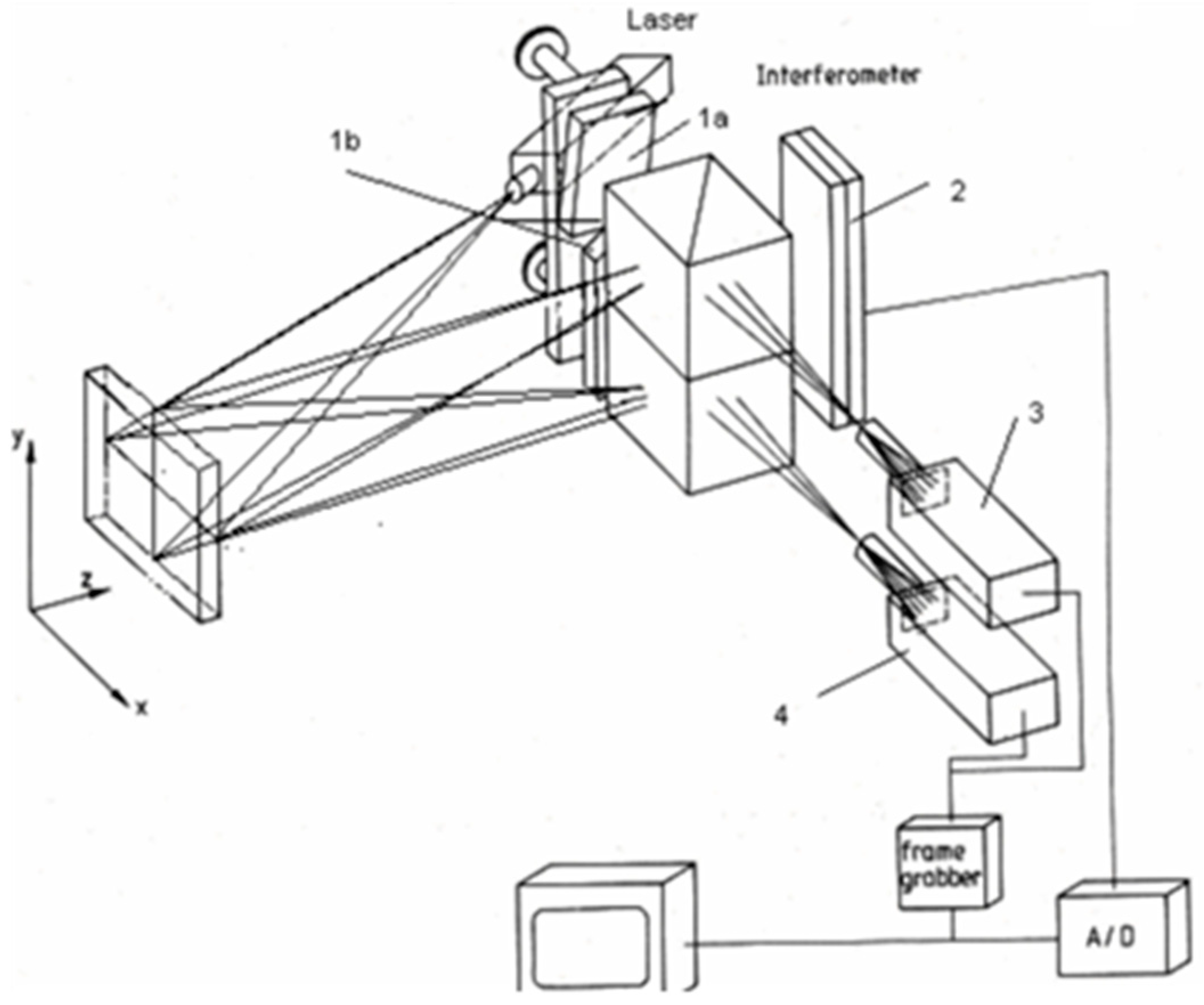
3.1. Dual-Directional Measurement Application in Temporal Phase-Shift (TPS) Technique
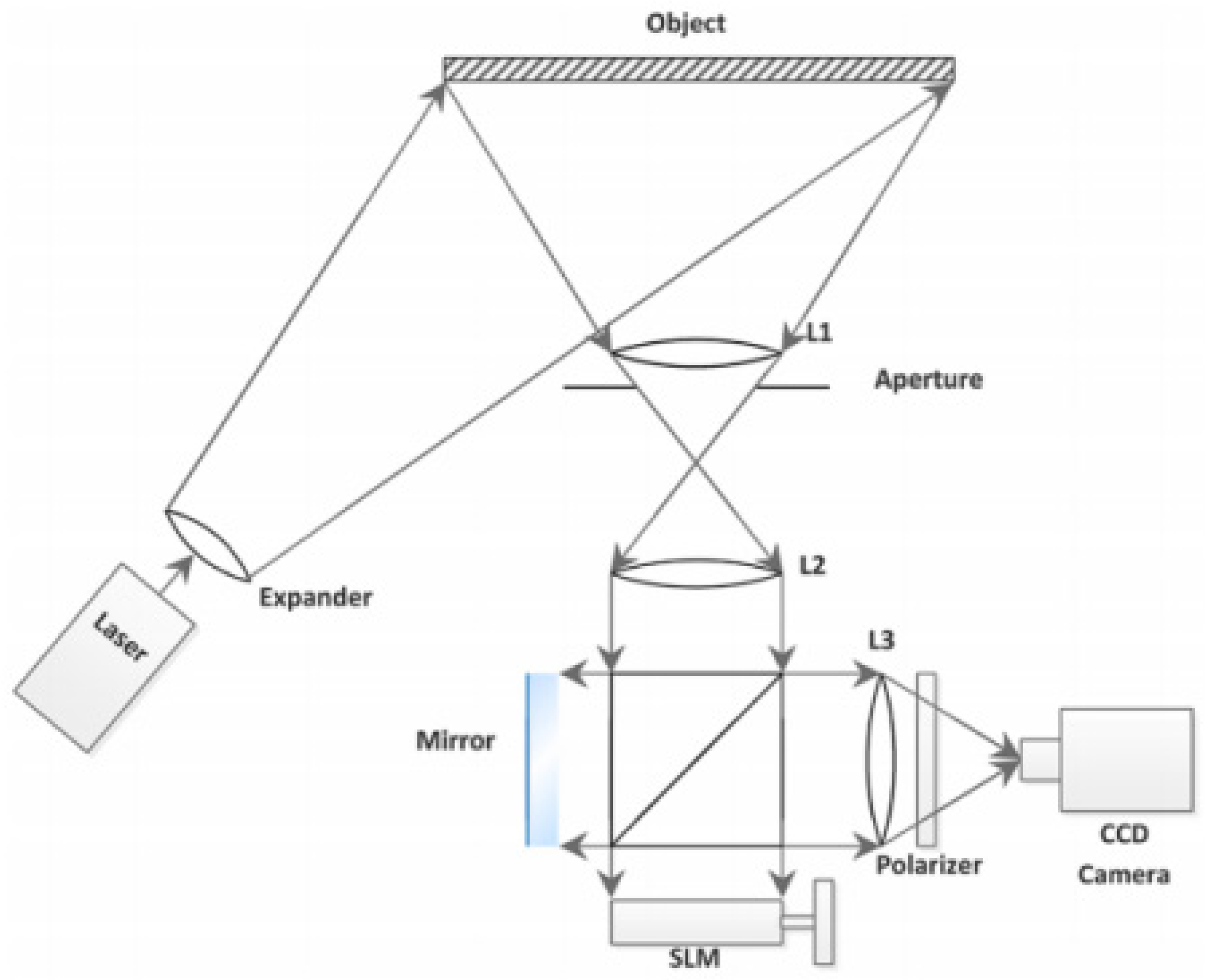
3.1.1. Dual-Directional Temporal Phase-Shift Technique
3.1.2. Recent Developments in Dual-Directional TPS Technique
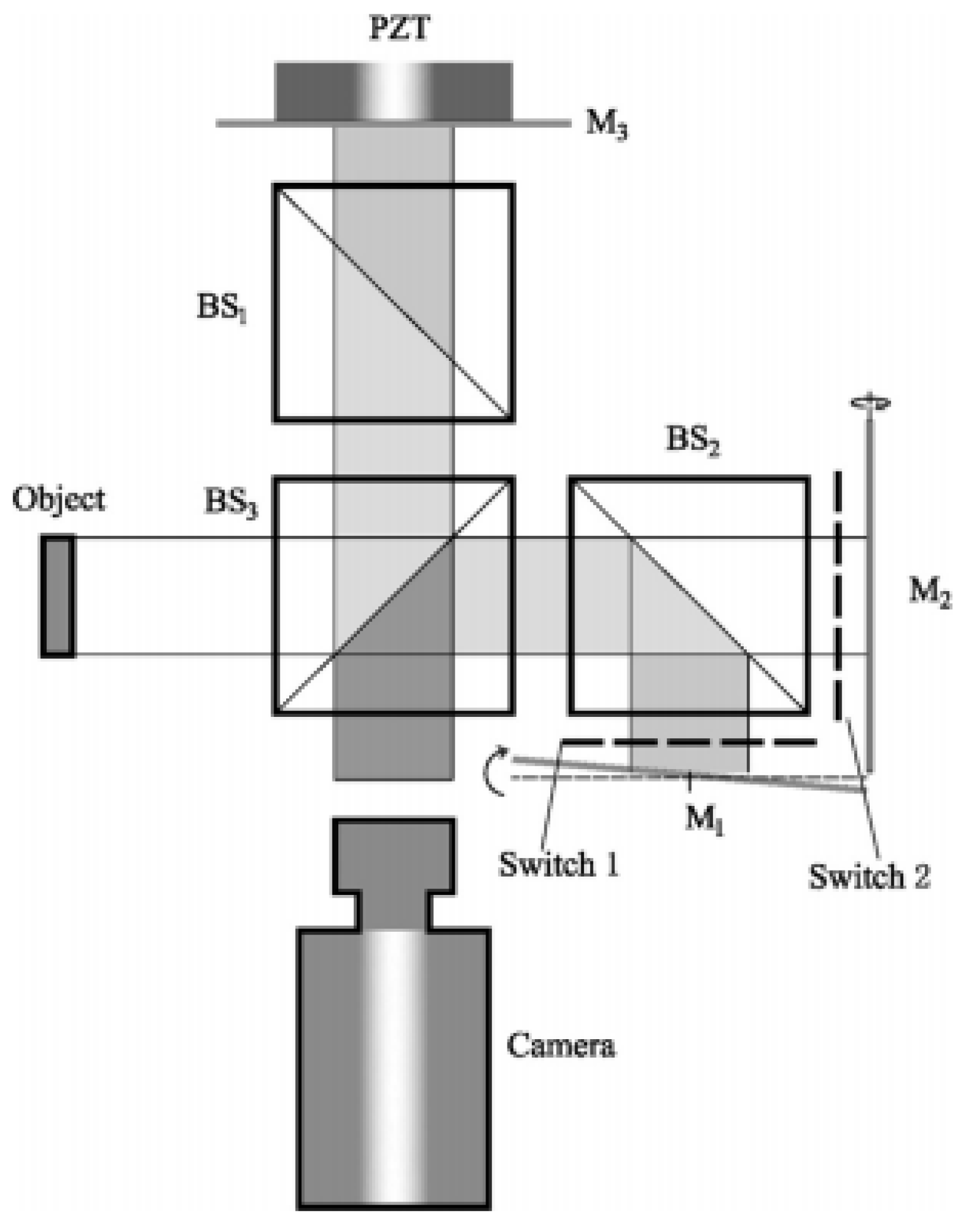
3.2. Dual-Directional Measurement Application in Spatial Phase-Shift (SPS) Technique
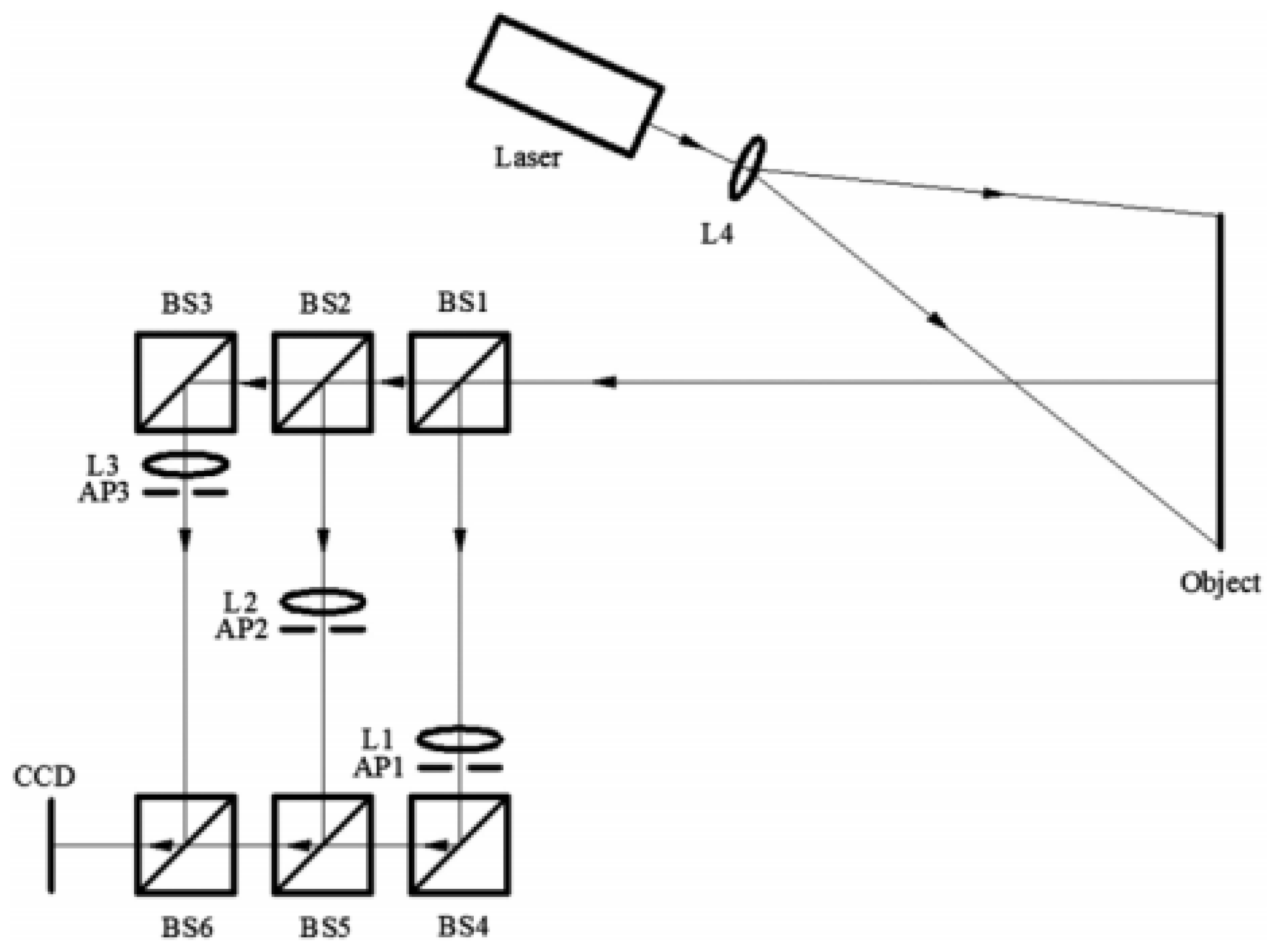
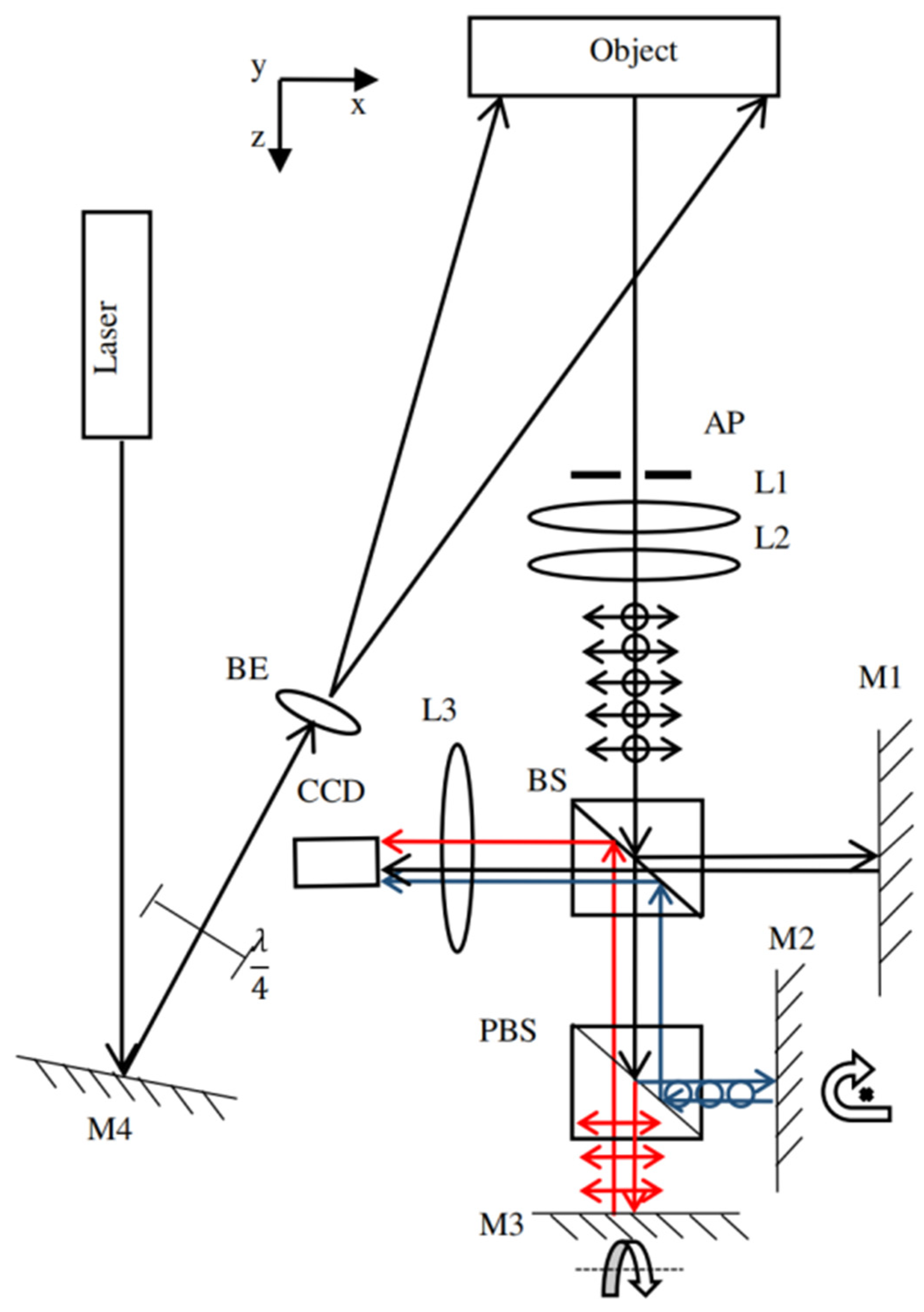
3.2.1. Dual-Directional Spatial Phase-Shift Technique
3.2.2. Recent Developments in Dual-Directional SPS Technique
4. Potentials and Limitations
4.1. Potentials
- In the basic shearography system, a single shearing-direction shearography system may fail to detect the defect if the wrong shearing direction is selected. The dual-directional measurement shearography technique solves the problem by quantifying the first derivative of two different directions of deformation simultaneously.
- Two different directional measurements need to be carried out, twice successively with orthogonal shearing directions. However, in practice, the measurement conditions and the loading events are not reproducible. In the dual-directional measurement shearography technique, different directional measurements are executed simultaneously. Therefore, it enhances the precision compared to the basic shearography system.
- The process of simultaneous measurement will reduce cost and calibration effort and lower susceptibility.
- The technique has broad development prospects, as it can also be developed for three-dimensional, radial, and lateral measurements.
4.2. Limitations
- The dual-directional measurement technique applied in the TPS system can only measure static conditions. However, the phase-map quality for the dual-directional SPS technique is still not as good as that for dual-directional TPS.
- As the dual-directional measurement will require multiple optical components, the cost of the system cannot be ignored.
- For the dual-directional SPS system, the shearing amount needs to be large enough to separate the spectrums on the Fourier domain to obtain a better quality phase map. However, a larger shearing amount will reduce the size of the area of interest that can be captured and measured with accuracy.
- The Michelson interferometer application cannot adjust carrier frequency and shearing amount separately, limiting the system sensitivity.
- The technique improves the sensitivity of shearography. As an interference-based technique with many optical components, the higher sensitivity allows the system to more easily be impacted by environmental disturbances that rise in setup, thus resulting in greater error accumulation.
- A large amount of energy from the laser is lost due to the number of beam splitters and polarization beam splitters used in dual-directional shearography systems, so high-intensity lasers and system stability are required.
- For the multi-wavelength dual-directional measurement shearography technique, different wavelength beams create different carrier frequencies, allowing the condition of overlapping spectra to be avoided. However, it may not be possible to eliminate the influence of interference completely.
- Even though the SLM technique solves most problems, the high cost of devices makes it not suitable for the industry.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, B.; Zhong, S.; Lee, T.L.; Fancey, K.S.; Mi, J. Non-destructive testing and evaluation of composite materials/structures: A state-of-the-art review. Adv. Mech. Eng. 2020, 12. [Google Scholar] [CrossRef] [Green Version]
- Schnars, U.; Jüptner, W.P. Digital recording and numerical reconstruction of holograms. Meas. Sci. Technol. 2002, 13, R85. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, P.; Liu, S.; Samala, P.R.; Su, M.; Yokota, H. Measurement of strain distributions in mouse femora with 3D-digital speckle pattern interferometry. Opt. Lasers. Eng. 2007, 45, 843–851. [Google Scholar] [CrossRef] [Green Version]
- Xu, N.; Xie, X.; Harmon, G.; Gu, R.; Yang, L. Quality inspection of spot welds using digital shearography. SAE Int. J. Mater. 2012, 5, 96–101. [Google Scholar] [CrossRef]
- Chen, X.; Yang, L.; Xu, N.; Xie, X.; Sia, B.; Xu, R. Cluster approach based multi-camera digital image correlation: Methodology and its application in large area high temperature measurement. Opt. Laser. Technol. 2014, 57, 318–326. [Google Scholar] [CrossRef]
- Petry, M.E.C.; Schuth, M. Spatial phase shift shearography for enhanced NDT. NDT E. Int. 2018.SHM-NDT 2018. Available online: https://www.ndt.net/article/shmndt2018/papers/SHM-NDT-2018_paper_39.pdf (accessed on 4 January 2022).
- Hooshmand-Ziafi, H.; Hassani, K.; Dashtdar, M. Dual-sensitive spatial phase-shifting shearography based on a common-path configuration. Opt. Eng. 2019, 58, 114104. [Google Scholar] [CrossRef]
- Steinchen, W.; Yang, L.X.; Kupfer, G.A.; Mäckel, P.; Vössing, F. Strain analysis by means of digital shearography: Potential, limitations and demonstration. J. Strain. Anal. Eng. Des. 1998, 33, 171–182. [Google Scholar] [CrossRef]
- Shang, H.M.; Hung, Y.Y.; Luo, W.D.; Chen, F. Surface profiling using shearography. Opt. Eng. 2000, 39, 23–31. [Google Scholar] [CrossRef]
- Zhao, Q.; Dan, X.; Sun, F.; Wang, Y.; Wu, S.; Yang, L. Digital shearography for NDT: Phase measurement technique and recent developments. Am. J. Appl. Sci. 2018, 8, 2662. [Google Scholar] [CrossRef] [Green Version]
- Steinchen, W.; Yang, L.X. Digital Shearography; SPIE Press: Bellingham, DC, USA, 2003. [Google Scholar]
- Bhaduri, B.; Mohan, N.K.; Kothiyal, M.P. Simultaneous measurement of out-of-plane displacement and slope using a multiaperture DSPI system and fast Fourier transform. J. Appl. Opt. 2007, 46, 5680–5686. [Google Scholar] [CrossRef] [PubMed]
- Burke, J.; Helmers, H. Spatial versus temporal phase shifting in electronic speckle-pattern interferometry: Noise comparison in phase maps. J. Appl. Opt. 2000, 39, 4598–4606. [Google Scholar] [CrossRef] [PubMed]
- Pedrini, G.; Osten, W.; Gusev, M.E. High-speed digital holographic interferometry for vibration measurement. J. Appl. Opt. 2006, 45, 3456–3462. [Google Scholar] [CrossRef] [PubMed]
- Xie, X. Development of Michelson Interferometer Based Spatial Phase-Shift Digital Shearography. Ph.D. Dissertation, Oakland University, Oakland, MI, USA, 2016. [Google Scholar]
- Wang, Y.; Gao, X.; Xie, X.; Wu, S.; Liu, Y.; Yang, L. Simultaneous dual directional strain measurement using spatial phase-shift digital shearography. Opt. Lasers Eng. 2016, 87, 197–203. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, F.; Yang, L.; Yang, L. Spatial-light-modulator-based dual shearing direction shearography. J. Appl. Opt. 2020, 59, 11080–11086. [Google Scholar] [CrossRef]
- Yang, L.X.; Steinchen, W.; Schuth, M.; Kupfer, G. Precision measurement and nondestructive testing by means of digital phase shifting speckle pattern and speckle pattern shearing interferometry. Measurement 1995, 16, 149–160. [Google Scholar] [CrossRef]
- Siebert, T.; Schmitz, B. New shearing setup for simultaneous measurement of two shear directions. Int. J. Opt. Photon. 1999, 3637, 225–230. [Google Scholar]
- Bai, P.; Zhu, F.; He, X. Out-of-plane displacement field measurement by shearography. Opt. Laser Technol. 2015, 73, 29–38. [Google Scholar] [CrossRef]
- Groves, R.M.; James, S.W.; Tatam, R.P. Polarization-multiplexed and phase-stepped fiber optic shearography using laser wavelength modulation. Meas. Sci. Technol. 2000, 11, 1389. [Google Scholar] [CrossRef]
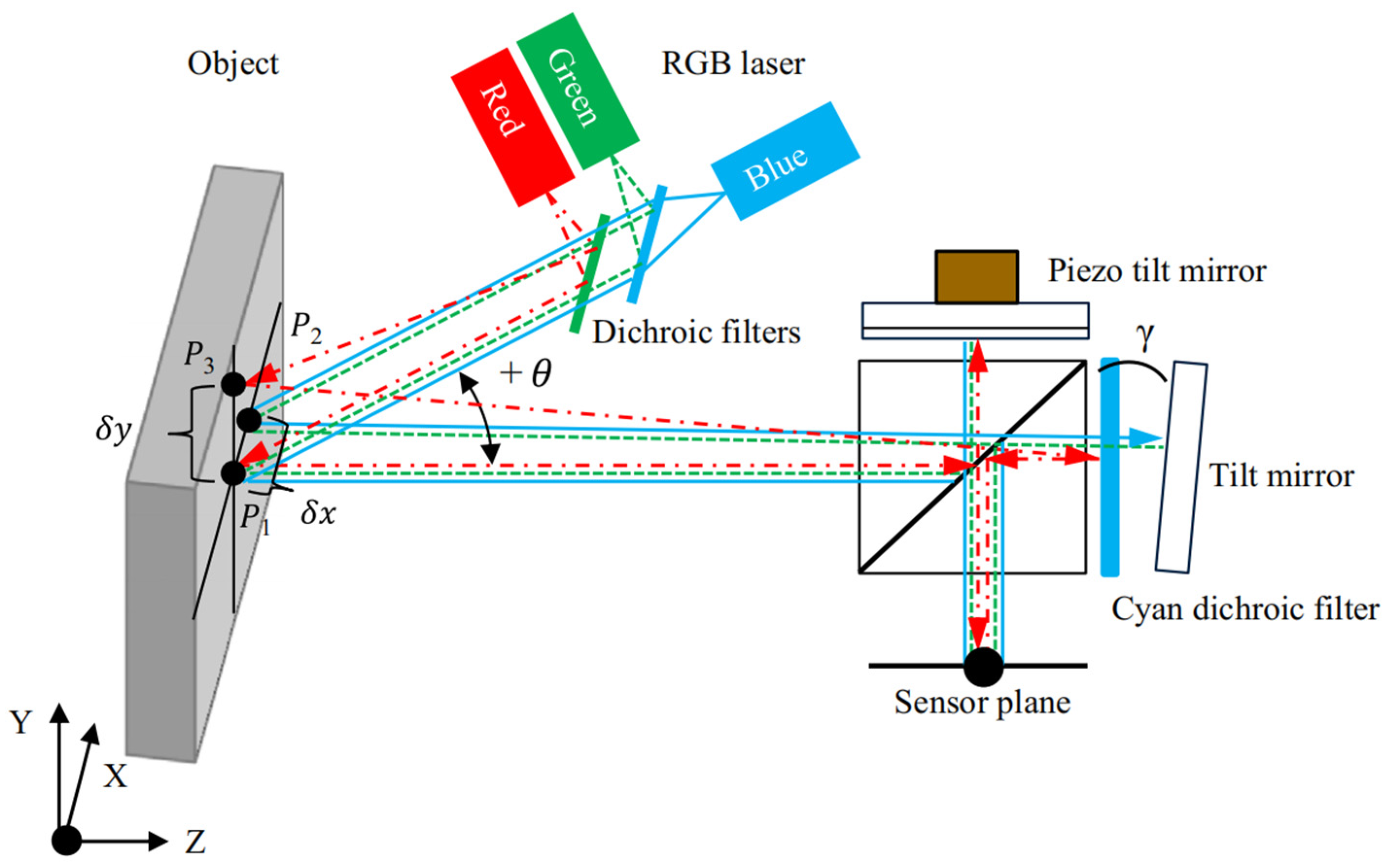
- Richoz, G.L.; Schajer, G.S. Simultaneous two-axis shearographic interferometer using multiple wavelengths and a color camera. Opt. Lasers Eng. 2016, 77, 143–153. [Google Scholar] [CrossRef]
- Jiang, H.; Ma, Y.; Dai, M.; Dai, X.; Yang, F.; He, X. Panoramic dual-directional shearography assisted by a bi-mirror. J. Appl. Opt. 2020, 59, 5812–5820. [Google Scholar] [CrossRef] [PubMed]
- Burnett, M.; Bryanston-Cross, P.J. Measurements of transonic shock structures using shearography. In Laser interferometry VIII: Applications. Int. J. Opt. Photon. 1996, 2861, 124–135. [Google Scholar]
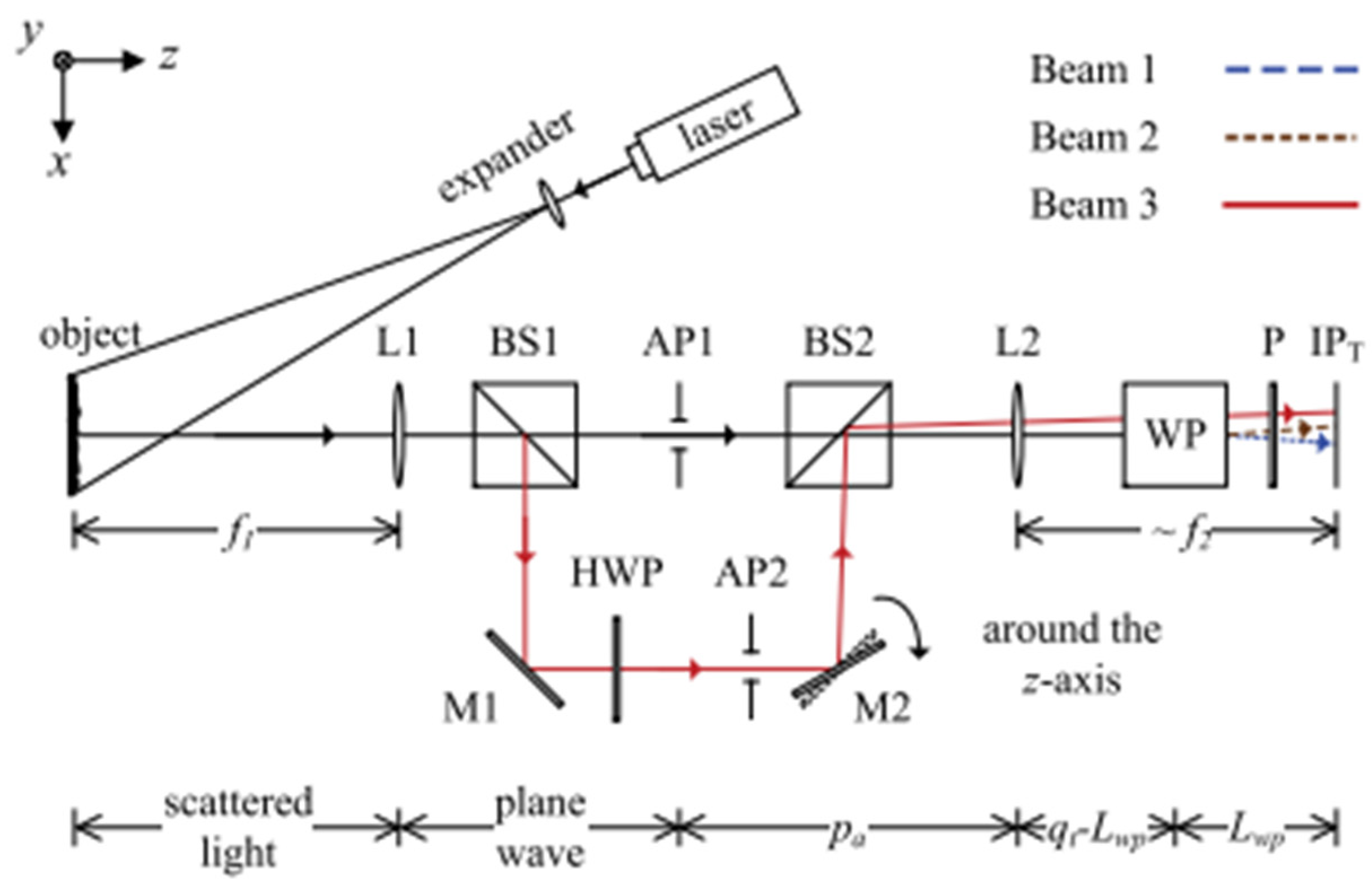
- Wang, S.; Dong, J.; Pöller, F.; Dong, X.; Lu, M.; Bilgeri, L.M.; Koch, A.W. Dual-directional shearography based on a modified common-path configuration using spatial phase shift. J. Appl. Opt. 2019, 58, 593–603. [Google Scholar] [CrossRef] [PubMed]
- Duffy, D.E. Moiré gauging of in-plane displacement using double aperture imaging. J. Appl. Opt. 1972, 11, 1778–1781. [Google Scholar] [CrossRef] [PubMed]
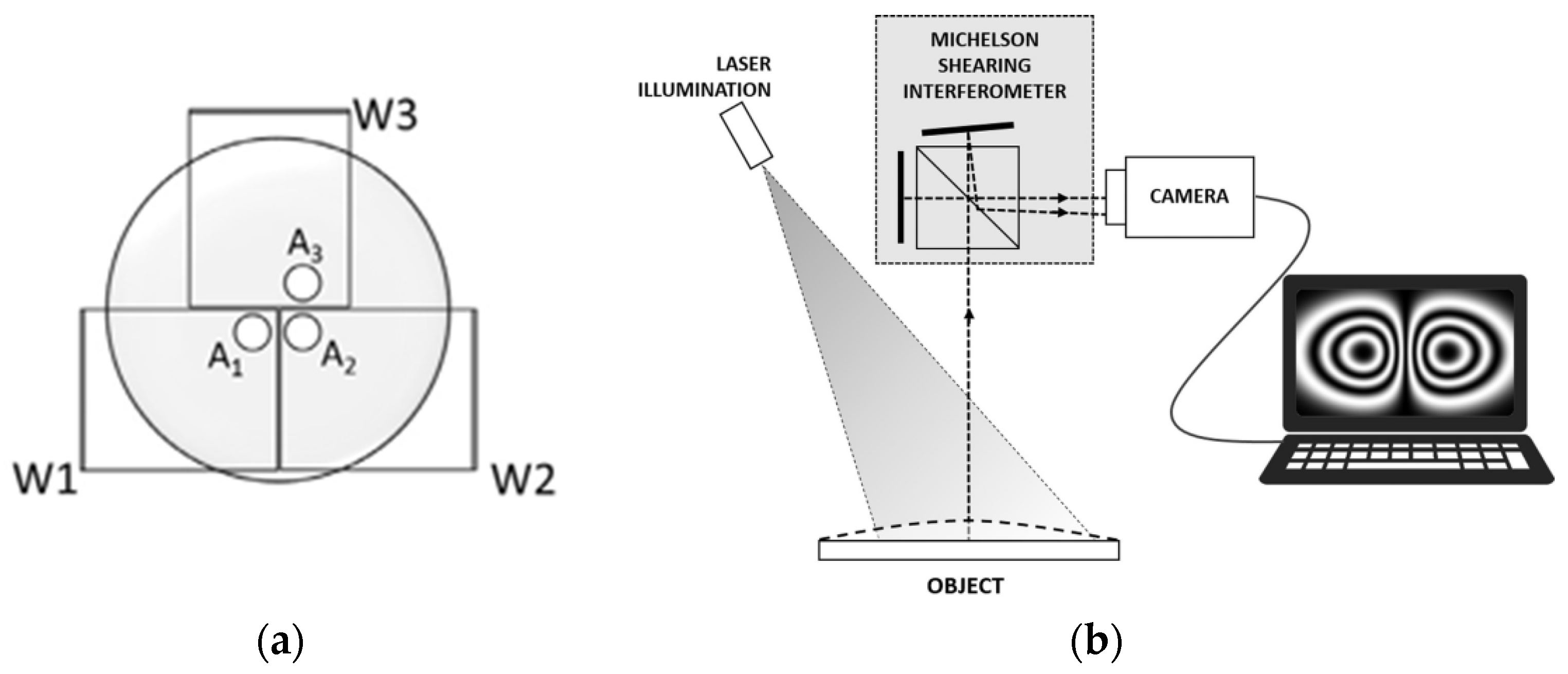
- Barrera, E.S.; Fantin, A.V.; Willemann, D.P.; Benedet, M.E.; Goncalves, A.A., Jr. Multiple-aperture one-shot shearography for simultaneous measurements in three shearing directions. Opt. Lasers Eng. 2018, 111, 86–92. [Google Scholar] [CrossRef]
- Zhong, S.; Sun, F.; Wu, S.; Bao, F.; Wang, Y. Multi-directional shearography based on multiplexed Mach–Zehnder interference system. J. Mod. Opt. 2020, 67, 346–354. [Google Scholar] [CrossRef]
- Yan, P.; Sun, F.; Dan, X.; Zhao, Q.; Wang, Y.; Lu, Y. Spatial phase-shift digital shearography for simultaneous measurements in three shearing directions based on adjustable aperture multiplexing. Opt. Eng. 2019, 58, 054105. [Google Scholar] [CrossRef]
- Xie, X.; Lee, C.P.; Li, J.; Zhang, B.; Yang, L. Polarized digital shearography for simultaneous dual shearing directions measurements. Rev. Sci. Instrum. 2016, 87, 083110. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, W.; Li, J.; Siebert, T.; Yang, L. Modified Michelson interferometer based dual shearing single camera digital sherography. Exp. Tech. 2020, 44, 187–195. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, B.; Zhang, B.; Zheng, X.; Fang, S.; Fang, Y.; Sia, B.; Yang, L. Review of Shearography for Dual-Directional Measurement. Optics 2022, 3, 117-137. https://doi.org/10.3390/opt3020014
Guo B, Zhang B, Zheng X, Fang S, Fang Y, Sia B, Yang L. Review of Shearography for Dual-Directional Measurement. Optics. 2022; 3(2):117-137. https://doi.org/10.3390/opt3020014
Chicago/Turabian StyleGuo, Bicheng, Boyang Zhang, Xiaowan Zheng, Siyuan Fang, Yue Fang, Bernard Sia, and Lianxiang Yang. 2022. "Review of Shearography for Dual-Directional Measurement" Optics 3, no. 2: 117-137. https://doi.org/10.3390/opt3020014
APA StyleGuo, B., Zhang, B., Zheng, X., Fang, S., Fang, Y., Sia, B., & Yang, L. (2022). Review of Shearography for Dual-Directional Measurement. Optics, 3(2), 117-137. https://doi.org/10.3390/opt3020014





