Resolution Limit of Correlation Plenoptic Imaging between Arbitrary Planes
Abstract
:1. Introduction
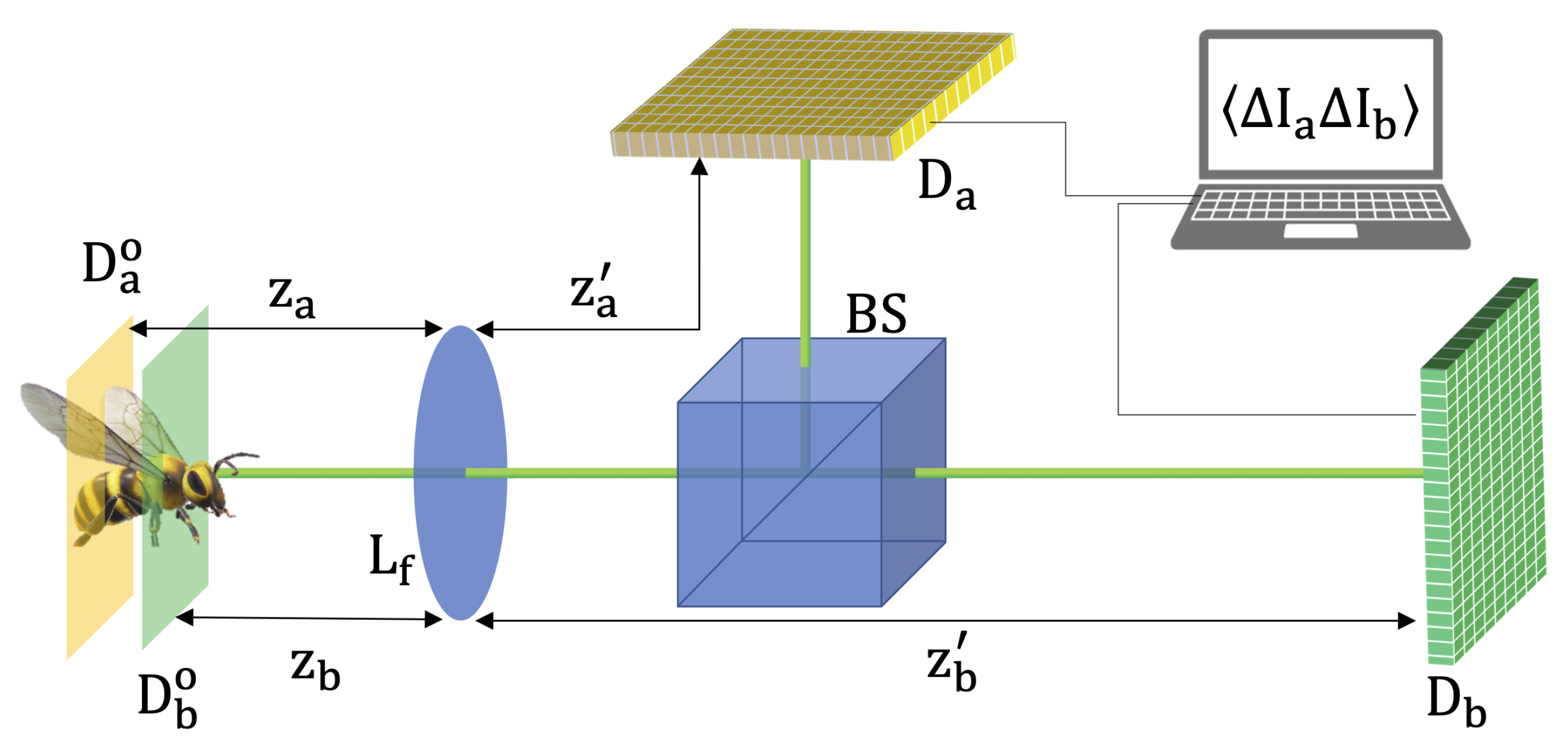
2. Methods
3. Results
- While the spread of the direct intensity image is independent of a, the spread of the refocused CPI-AP image is monotonically decreasing with the object width. The dependence of the correlation image on the object is related to the role of as an “effective aperture” in correlation imaging;
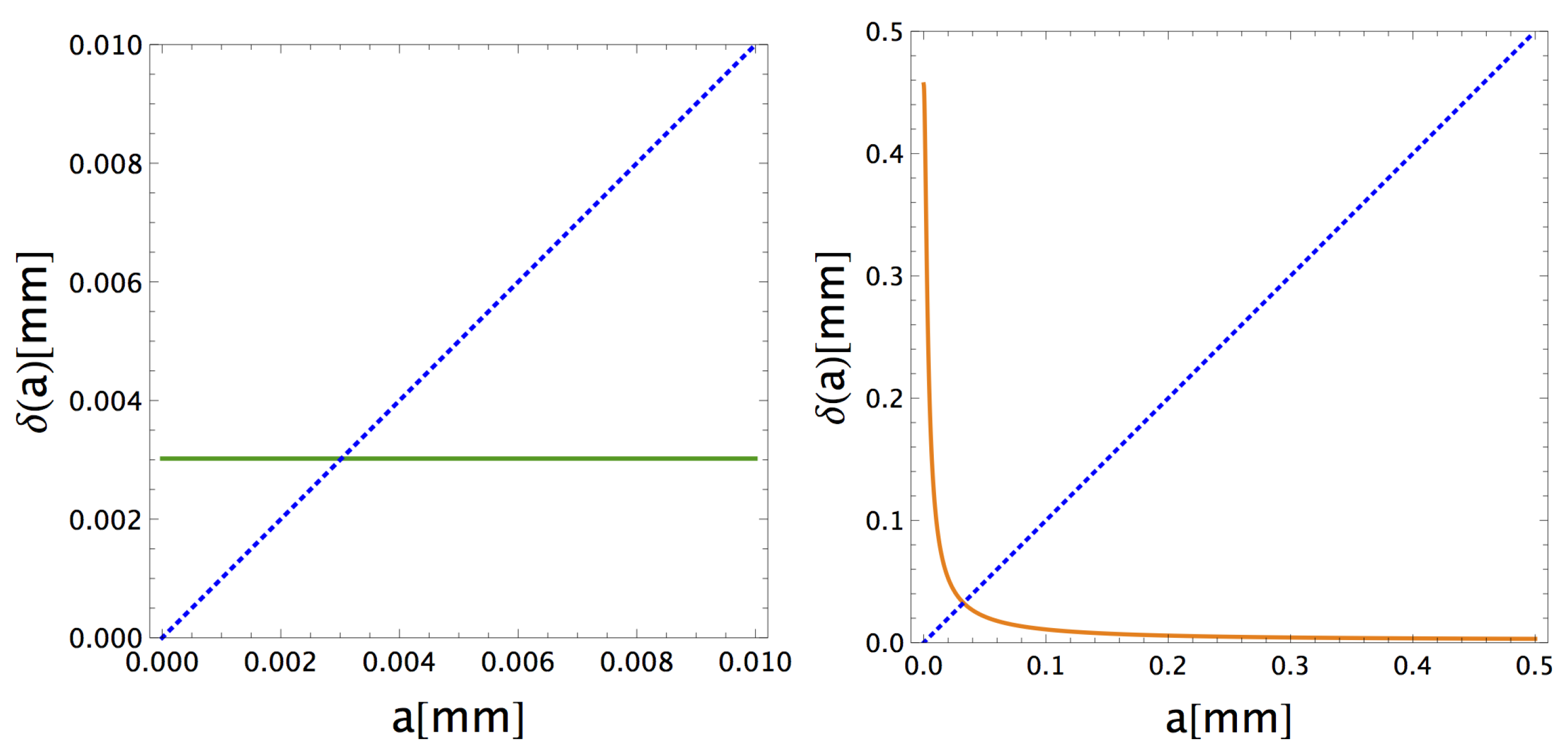
- Consistent with the previous point, in Equation (22) is monotonically decreasing with the object size a. This entails that the total image width can have a counterintuitive non-monotonous behaviour with a, with a minimum for , unless the object is very close to one of the reference planes, namelyNoticeably, the value is always finite, unlike in previously analysed cases [20];
- As expected, in the out-of-focus case, the direct intensity image cannot provide a faithful representation of the object, even for ,since a residual purely geometrical spread, proportional to the lens aperture, is still present. Moreover, as the distance from the focused plane increases, the dependence of on a becomes progressively weaker, making objects of different widths indistinguishable. This is not the case for CPI-AP, since:refocusing provides a perfectly resolved image of , independent of the distance from the focused planes;
- The resolution and depth-of-field limits of traditional plenoptic imaging devices [14] are determined by the properties of the collected sub-images, obtained by reducing the main lens numerical aperture of a factor , with the number of directional resolution cells per line. Therefore, the image width is obtained by the replacementin Equation (25). Besides negatively affecting the resolution of the focused image, such a change entails a limitation to the image width at , which is qualitatively similar to the case reported in Equation (27) for standard imaging, although quantitatively attenuated.
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PI | Plenoptic imaging |
| CPI | Correlation plenoptic imaging |
| CPI-AP | Correlation plenoptic imaging between arbitrary planes |
| MTF | Modulation transfer function |
References
- Adelson, E.H.; Wang, J.Y. Single lens stereo with a plenoptic camera. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 99. [Google Scholar] [CrossRef] [Green Version]
- Levoy, M.; Ng, R.; Adams, A.; Footer, M.; Horowitz, M. Light field microscopy. ACM Trans. Graph. (TOG) 2006, 25, 924. [Google Scholar] [CrossRef]
- Broxton, M.; Grosenick, L.; Yang, S.; Cohen, N.; Andalman, A.; Deisseroth, K.; Levoy, M. Wave optics theory and 3-D deconvolution for the light field microscope. Opt. Express 2013, 21, 25418. [Google Scholar] [CrossRef]
- Glastre, W.; Hugon, O.; Jacquin, O.; de Chatellus, H.G.; Lacot, E. Demonstration of a plenoptic microscope based on laser optical feedback imaging. Opt. Express 2013, 21, 7294. [Google Scholar] [CrossRef] [Green Version]
- Prevedel, R.; Yoon, Y.G.; Hoffmann, M.; Pak, N.; Wetzstein, G.; Kato, S.; Schrödel, T.; Raskar, R.; Zimmer, M.; Boyden, E.S.; et al. Simultaneous whole-animal 3D imaging of neuronal activity using light-field microscopy. Nat. Methods 2014, 11, 727. [Google Scholar] [CrossRef] [PubMed]
- Muenzel, S.; Fleischer, J.W. Enhancing layered 3D displays with a lens. Appl. Opt. 2013, 52, D97. [Google Scholar] [CrossRef]
- Levoy, M.; Hanrahan, P. Light field rendering. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques; ACM: New York, NY, USA, 1996; pp. 31–42. [Google Scholar]
- Wu, C.W. The Plenoptic Sensor. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2016. [Google Scholar]
- Lv, Y.; Wang, R.; Ma, H.; Zhang, X.; Ning, Y.; Xu, X. SU-G-IeP4-09: Method of Human Eye Aberration Measurement Using Plenoptic Camera Over Large Field of View. Med. Phys. 2016, 43, 3679. [Google Scholar] [CrossRef]
- Wu, C.; Ko, J.; Davis, C.C. Using a plenoptic sensor to reconstruct vortex phase structures. Opt. Lett. 2016, 41, 3169. [Google Scholar] [CrossRef]
- Wu, C.; Ko, J.; Davis, C.C. Imaging through strong turbulence with a light field approach. Opt. Express 2016, 24, 11975. [Google Scholar] [CrossRef]
- Fahringer, T.W.; Lynch, K.P.; Thurow, B.S. Volumetric particle image velocimetry with a single plenoptic camera. Meas. Sci. Technol. 2015, 26, 115201. [Google Scholar] [CrossRef]
- Hall, E.M.; Thurow, B.S.; Guildenbecher, D.R. Comparison of three-dimensional particle tracking and sizing using plenoptic imaging and digital in-line holography. Appl. Opt. 2016, 55, 6410. [Google Scholar] [CrossRef] [PubMed]
- Ng, R.; Levoy, M.; Brédif, M.; Duval, G.; Horowitz, M.; Hanrahan, P. Light field photography with a hand-held plenoptic camera. Comput. Sci. Tech. Rep. CSTR 2005, 2, 1. [Google Scholar]
- Shademan, A.; Decker, R.S.; Opfermann, J.; Leonard, S.; Kim, P.C.; Krieger, A. Plenoptic cameras in surgical robotics: Calibration, registration, and evaluation. In Proceedings of the Robotics and Automation (ICRA), 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 708–714. [Google Scholar]
- Le, H.N.; Decker, R.; Opferman, J.; Kim, P.; Krieger, A.; Kang, J.U. 3-D endoscopic imaging using plenoptic camera. In CLEO: Applications and Technology; Optical Society of America: Washington, DC, USA, 2016; paper AW4O.2. [Google Scholar]
- Carlsohn, M.F.; Kemmling, A.; Petersen, A.; Wietzke, L. 3D real-time visualization of blood flow in cerebral aneurysms by light field particle image velocimetry. Proc. SPIE 2016, 9897, 989703. [Google Scholar]
- Xiao, X.; Javidi, B.; Martinez-Corral, M.; Stern, A. Advances in three-dimensional integral imaging: Sensing, display, and applications [Invited]. Appl. Opt. 2013, 52, 546. [Google Scholar] [CrossRef] [PubMed]
- D’Angelo, M.; Pepe, F.V.; Garuccio, A.; Scarcelli, G. Correlation plenoptic imaging. Phys. Rev. Lett. 2016, 116, 223602. [Google Scholar] [CrossRef] [Green Version]
- Pepe, F.V.; Di Lena, F.; Mazzilli, A.; Edrei, E.; Garuccio, A.; Scarcelli, G.; D’Angelo, M. Diffraction-limited plenoptic imaging with correlated light. Phys. Rev. Lett. 2010, 119, 243602. [Google Scholar] [CrossRef] [Green Version]
- Pittman, T.; Shih, Y.; Strekalov, D.; Sergienko, A. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429. [Google Scholar] [CrossRef]
- Gatti, A.; Brambilla, E.; Bache, M.; Lugiato, L.A. Ghost imaging with thermal light: Comparing entanglement and classicalcorrelation. Phys. Rev. Lett. 2004, 93, 093602. [Google Scholar] [CrossRef] [Green Version]
- D’Angelo, M.; Shih, Y. Quantum imaging. Laser Phys. Lett. 2005, 2, 567–596. [Google Scholar] [CrossRef]
- Valencia, A.; Scarcelli, G.; D’Angelo, M.; Shih, Y. Two-photon imaging with thermal light. Phys. Rev. Lett. 2005, 94, 063601. [Google Scholar] [CrossRef] [Green Version]
- Scarcelli, G.; Berardi, V.; Shih, Y. Can two-photon correlation of chaotic light be considered as correlation of intensity fluctuations? Phys. Rev. Lett. 2006, 96, 063602. [Google Scholar] [CrossRef] [PubMed]
- Pepe, F.V.; Vaccarelli, O.; Garuccio, A.; Scarcelli, G.; D’Angelo, M. Exploring plenoptic properties of correlation imaging with chaotic light. J. Opt. 2017, 19, 114001. [Google Scholar] [CrossRef] [Green Version]
- Pepe, F.V.; Scarcelli, G.; Garuccio, A.; D’Angelo, M. Plenoptic imaging with second-order correlations of light. Quantum Meas. Quantum Metrol. 2016, 3, 20. [Google Scholar] [CrossRef]
- Pepe, F.V.; Di Lena, F.; Garuccio, A.; Scarcelli, G.; D’Angelo, M. Correlation Plenoptic Imaging With Entangled Photons. Technologies 2016, 4, 17. [Google Scholar] [CrossRef] [Green Version]
- Abbattista, C.; Amoruso, L.; Burri, S.; Charbon, E.; Di Lena, F.; Garuccio, A.; Giannella, D.; Hradil, Z.; Iacobellis, M.; Massaro, G.; et al. Towards Quantum 3D Imaging Devices. Appl. Sci. 2021, 11, 6414. [Google Scholar] [CrossRef]
- Di Lena, F.; Massaro, G.; Lupo, A.; Garuccio, A.; Pepe, F.V.; D’Angelo, M. Correlation plenoptic imaging between arbitrary planes. Opt. Express 2020, 28, 35857–35868. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to fourier optics. McGraw Hill 1996, 10, 160. [Google Scholar] [CrossRef] [Green Version]
- Scala, G.; D’Angelo, M.; Garuccio, A.; Pascazio, S.; Pepe, F.V. Signal-to-noise properties of correlation plenoptic imaging with chaotic light. Phys. Rev. A 2019, 99, 053808. [Google Scholar] [CrossRef] [Green Version]
- Howland, B. New test patterns for camera lens evaluation. Appl. Opt. 1983, 22, 1792–1793. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scattarella, F.; D’Angelo, M.; Pepe, F.V. Resolution Limit of Correlation Plenoptic Imaging between Arbitrary Planes. Optics 2022, 3, 138-149. https://doi.org/10.3390/opt3020015
Scattarella F, D’Angelo M, Pepe FV. Resolution Limit of Correlation Plenoptic Imaging between Arbitrary Planes. Optics. 2022; 3(2):138-149. https://doi.org/10.3390/opt3020015
Chicago/Turabian StyleScattarella, Francesco, Milena D’Angelo, and Francesco V. Pepe. 2022. "Resolution Limit of Correlation Plenoptic Imaging between Arbitrary Planes" Optics 3, no. 2: 138-149. https://doi.org/10.3390/opt3020015
APA StyleScattarella, F., D’Angelo, M., & Pepe, F. V. (2022). Resolution Limit of Correlation Plenoptic Imaging between Arbitrary Planes. Optics, 3(2), 138-149. https://doi.org/10.3390/opt3020015







